フラクタル指数とハースト指数の財務時系列を予測する能力の評価
Roman Korotchenko | 17 7月, 2019
イントロダクション
現代の金融相場は、複雑でありつつ、バランスの取れたシステムです。 一方で、相場は多くの参加者の影響を受けているため、かなり混沌としています。 同時に、相場は、相場参加者の行動によって決定される明確な安定したプロセスによって特徴付けられます。 エコノフィジックスのタスクの1つは、交換で観察される価格ダイナミクスを形成する社会的相互作用プロセスの記述によるものです。 したがって、このようなデータを他の自然プロセスと区別する財務時系列の特性を定義し、提示することが望ましいと考えられます。 現代の理論では、価格シリーズは異なるスケールのフラクタル(数分から数十年)として定義されています。
それらは多くのモデルと自然なプロセスよりもはるかに複雑な動作を示します。[3] そのような行動の詳細を見つけるためのツールの一つは、シリーズの数値分析であり、その目的は、シリーズのダイナミクスを研究することです。 フラクタルディメンションの信頼性の高い評価の典型的なアルゴリズムは、大きなデータセット(約10,000〜100,000サンプル)を必要とします。 実際のトレードタスクでは、シリーズのローカルフラクタル特性を決定する方法が必要です。 この記事では、[1, 2] で説明する数値方法を使用して、一連の価格配列のフラクタルディメンションを決定する方法について説明し、デモンストレーションします。
フラクタルディメンションの概念と時系列の統計的特性
フラクタル ディメンションは、データ セットがスペースを占有する方法を推定します。 フラクタルディメンションを推定するメソッドは多数あります。 共通の特徴は、ボリュームまたはエリアが、このセットが配置されているスペースで計算されることです。 終値 {Close(t)} で構成される金融商品の時系列の例を使用してみましょう。 {Close(t)} 系列レベルが独立している場合、シンボル チャートには明確なトレンドはありませんが、動作は "ホワイトノイズ"に似ています。 フラクタルディメンション Dの値は、平面のトポロジディメンションの値に近いです。言い換えればD->2になります。 {Close(t)} 系列レベルが独立していない場合、D 値は 2 より大幅に小さいため、時系列に "memory"が含まれます。つまり、非定義期間と交互に、ある時点で上下のトレンドが観察されます(図1)。
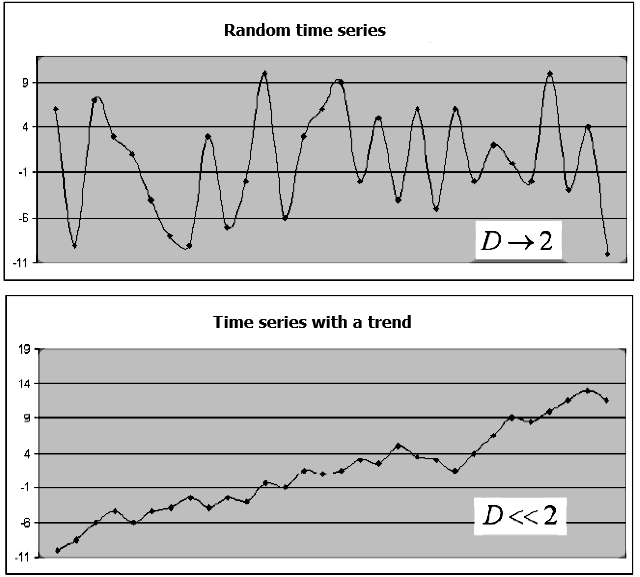
図1. トレンドを持つランダム系列、および対応するフラクタルディメンションの例
フラクタルディメンション評価方法とその特徴
時系列のフラクタルディメンションを計算するメソッドはいくつかあります。 ハースト指数を利用した評価方法を考えてみましょう。
ハースト指数Hは、次の式に基づいて決定されます。
![]() (1a)
(1a)
ここで、かぎかっこは時間の平均化を示します。 ハースト指数とフラクタルディメンションの関係は、正規化された範囲のメソッドまたは以下の方程式に基づくR/S分析によって得られます。
DH = 2-HH = log(R/ S) / log(N / 2) (1b)
ここで R — max{Close(t)} - min {Close(t)}, i = 1..N は Close(t) 系列偏差の範囲であり、S は Close(t) 値の標準偏差です。 このメソッドは、ドミトリー・ピスカレフによる ハースト指数の計算に関する記事で詳しく説明しました。
時系列のハースト指数が 0.5 ~ 1 の範囲にある場合、このような系列は永続的またはトレンドに強いと見なされ、{Close(t)} 系列がランダムではなく、トレンドが含まれており、系列の動作を良好に予測できます。 H 値が 1 に近いほど、{Close(t)} 系列値間の相関が大きくなります。
このメソッドの欠点は、ハースト指数の信頼性の高い推定値を得るために大量のデータ(数千のデータ系列値)が必要であり、そうでなければ得られた推定値が間違っている可能性があることです。 さらに、系列値には正規分布法が必要です。 DHとHの両方の信頼性の高い計算は、大量のデータとの大きな代表的なサンプルを必要とするので、系列挙動は関連する長いトレード期間中に繰り返し変化する可能性があります。 解析されたプロセスの局所ダイナミクスを観測した系列のフラクタルディメンションとリンクするには、 D 次元を局所的に決定する必要があります。
最小カバー領域に基づくフラクタルディメンション推定
計量法系列を予測する場合の効率的な方法は、最小カバレッジディメンション [1, 2] の計算に基づくメソッド
![]() です。
1919年、Hausdorff(ハウドルフ)はフラクタルを決定するための次の式を提案しました。
です。
1919年、Hausdorff(ハウドルフ)はフラクタルを決定するための次の式を提案しました。
![]() .
.
このセットをカバーする、最小のボール半径
![]() の場所です。
の場所です。
![]() 元のセットがユークリッド空間にある場合、ボールを使用してセットをカバーする代わりに、ジオメトリ係数を使用して設定近似に他のシンプルなシェイプ(セルなど)を使用できます。
元のセットがユークリッド空間にある場合、ボールを使用してセットをカバーする代わりに、ジオメトリ係数を使用して設定近似に他のシンプルなシェイプ(セルなど)を使用できます。
![]()
たとえば、f(t)関数は [a, b] で設定されます。 wm = [a=t0<t1<t2...tm=b] 分割の範囲は、
![]() 例えばセルサイズを使用してセットをカバーする場合と定義されますが、
例えばセルサイズを使用してセットをカバーする場合と定義されますが、
![]() 因子が減少した場合、
因子が減少した場合、
![]() パワー法に従ってセルNの数が増加します。
パワー法に従ってセルNの数が増加します。
![]()
ここで D はフラクタルディメンションです。
セル法を用いてDディメンションを決定する場合、時系列チャートが配置されている表面はサイズのセルに分割
![]() され、その後、少なくとも1つにセルN()
され、その後、少なくとも1つにセルN()
![]() の数をカウントする計算が行われます。
次に、
の数をカウントする計算が行われます。
次に、
![]() N(
N(
![]() )
関数チャートが二重対数状態でプロットされます。 また、得られたポイントのセットは、最小2乗(LS)法を使用して近似されます。 Dは、ラインスロープに基づいて決定されます。
)
関数チャートが二重対数状態でプロットされます。 また、得られたポイントのセットは、最小2乗(LS)法を使用して近似されます。 Dは、ラインスロープに基づいて決定されます。
このスケールの関数チャートの最小カバレッジ領域は、[a, b]間隔で、ベースを持つ4角形の面積の合計
![]() と、変動値と等しくなります。
と、変動値と等しくなります。
![]() e
f(t)は各[ti-1, ti]間隔で機能します。 最小カバレッジエリア
e
f(t)は各[ti-1, ti]間隔で機能します。 最小カバレッジエリア
![]() は、次の式を使用して計算できます。
は、次の式を使用して計算できます。
![]() (2)
(2)
![]() [a, b]間隔における関数f(t) の振幅変動の合計の場所。 この推定値は、
[a, b]間隔における関数f(t) の振幅変動の合計の場所。 この推定値は、
![]() 選択した大きさによって異なります。
小さければ小さいほど、
選択した大きさによって異なります。
小さければ小さいほど、
![]() 計算がより正確になります。
計算がより正確になります。
![]() この場合、値は、
この場合、値は、
![]() 変更時にパワーレイに応じて変化します。
変更時にパワーレイに応じて変化します。
![]()
![]() (3)
(3)
ただし、
![]() .
この値
.
この値
![]() は
"最小カバーのディメンション" と呼ばれ、インデックス
は
"最小カバーのディメンション" と呼ばれ、インデックス
![]() はフラクタル
インデックスと呼ばれます。
はフラクタル
インデックスと呼ばれます。
32個の観測値からなる時系列の異なる
![]() 値からの最小カバー領域の依存性を図2に示します。
値からの最小カバー領域の依存性を図2に示します。
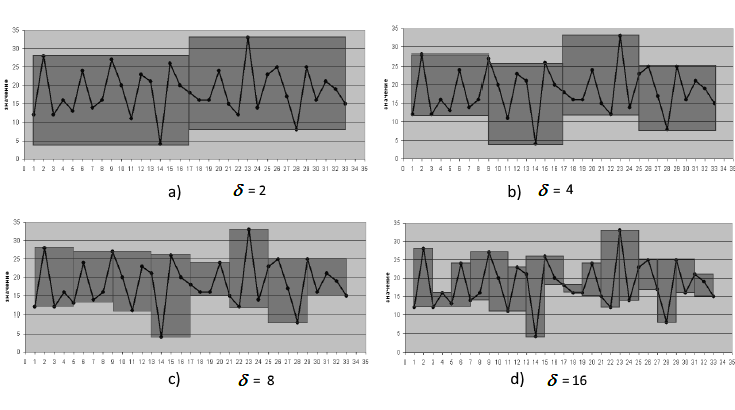
図2. さまざまな値を持つカバー領域の計算
![]()
参照[2]は、関数の変動に基づいて、セルカバーと長方形でカバーを使用して計算されるフラクタルディメンションが一致することを述べています。 関数のバリエーションを使用するアルゴリズムの重要なプロパティは、はるかに高速な収束で、小さな値セットを使用して、時系列フラクタルディメンション値をローカルで決定することができます。
(3) に対数を適用すると、次の情報が得されます。
![]() (4)
(4)
決定
![]() するために、依存(3)チャートは、最小2乗(LS)法を使用して二重対数座標でプロットされ、直線角の接線が決定されます。
式(4)に基
するために、依存(3)チャートは、最小2乗(LS)法を使用して二重対数座標でプロットされ、直線角の接線が決定されます。
式(4)に基
![]() づいて、時系列の局所特性であるフラクタル指数を計算します。
参考[1]に示すように、
づいて、時系列の局所特性であるフラクタル指数を計算します。
参考[1]に示すように、
![]() 決定精度は、
決定精度は、
![]() ハースト指数に基づいて計算されたセルディメンションなどの他のフラクタル特性を決定する精度がはるかに高いです。
さらに、このメソッドには系列の分布に制限
ハースト指数に基づいて計算されたセルディメンションなどの他のフラクタル特性を決定する精度がはるかに高いです。
さらに、このメソッドには系列の分布に制限
![]() はありません。
参照[1]はまた、時系列が32以上の観測値を含む場合に信頼性の高い推定値を得ることができることを示
はありません。
参照[1]はまた、時系列が32以上の観測値を含む場合に信頼性の高い推定値を得ることができることを示
![]() します。
通常、財務セットのヒストリーは長くなります。 このアプローチでは、フラクタルインデックスを時間の関数として使用
します。
通常、財務セットのヒストリーは長くなります。 このアプローチでは、フラクタルインデックスを時間の関数として使用
![]() し、各値が時系列の前の
32 の値に基づいて決定されます。
し、各値が時系列の前の
32 の値に基づいて決定されます。
![]()
図3は、
![]() 近似直線の角度に基づくフラクタル指数の計算例を示します。
図によると、依存性に近似する回帰
式R2
の決定係数は0.96に等しく、フラクタル指数0.4544が正確に計算されたことを示します。
近似直線の角度に基づくフラクタル指数の計算例を示します。
図によると、依存性に近似する回帰
式R2
の決定係数は0.96に等しく、フラクタル指数0.4544が正確に計算されたことを示します。
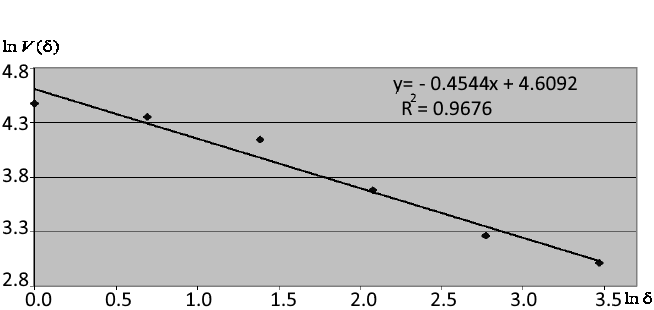
図3.
![]() 二重対数座標における依存性の近似とフラクタル指数の決定
二重対数座標における依存性の近似とフラクタル指数の決定
フラクタルディメンションは、セルディメンション法またはハーストインデックスのいずれかを使用して評価できます。 例として、今世紀の初めに起こった危機の直前のLukoilの株価(MICEX)を考えてみましょう。 この時、緩やかな増加(永続的系列)の安定したトレンドとして解釈することができます。 図4は、1999年のフラクタルディメンション評価の結果を示します。
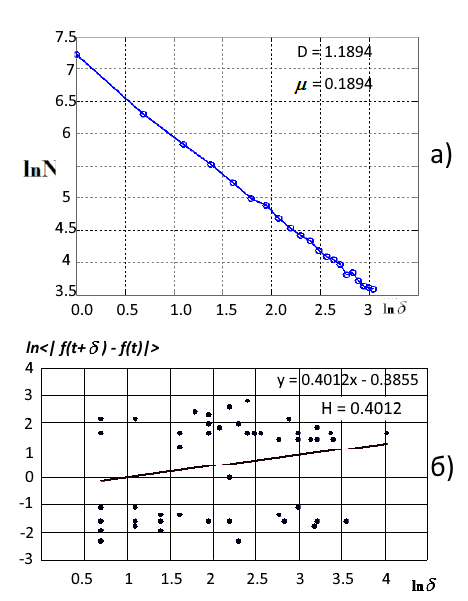
図4. a) セルカバーを用いたフラクタルメジャーのLS近似(D=1.1894)、b)ハーストパラメータの数値推定値のログログプロット(D=1.6)
この一連のD = 1.18のフラクタルディメンションは、その持続的なトレンディな性質を指します。 1に近い値は、2000-2001年に起こったトレンドの終わりに近いことを示します。 ハースト指数値はH=0.40. 信頼区間が 0.95 の場合、決定 R 2= 0.56 の比較的低い係数に注意してください。 数式 (1) によると、ハースト指数によって計算されたフラクタルディメンションはD = 1.6 に等しく、系列のランダムな動作と確率の増加レベルを示します。 しかし、1999年の期間のLukoil株には関係ありません。
フラクタル指数とハースト指数のローカルインジケータのまた別の興味深い例は、参照[2]にあります。 このパラメータ評価は、時系列の運用定性および定量的挙動の相場分析に関連するトレードタスクに適します。 8145ポイントを含むAlcoa
Inc.のソース価格シリーズは、それぞれ32日の8113の重複間隔に分割され、1日ずつ互いに相対的にシフトしました。 計算精度パラメータとして使用されました:
Hの信頼区間95%の幅
![]() と、理論線K
=1-R2
に当たる実点の精度評価、R2
は、決定係数(正確にラインに入り、次にR
2=1 とK=0)です。
と、理論線K
=1-R2
に当たる実点の精度評価、R2
は、決定係数(正確にラインに入り、次にR
2=1 とK=0)です。
次の値は、8113 間隔のそれぞれで計算されました。
- H— ハースト指数;
-
 —
fractal index;
—
fractal index; -
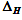 — H
の信頼区間の幅 95%
— H
の信頼区間の幅 95% -
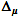 — 信頼区間の幅
95%
— 信頼区間の幅
95%
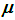 ;
; -
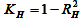 - Hの実験と得られた直線の対応の精度;
- Hの実験と得られた直線の対応の精度; -
 -
実験の対応の精度と得られた
-
実験の対応の精度と得られた
 直線.
直線.
関数
![]() のチャートの典型的な断片、
のチャートの典型的な断片、
![]() そして、
そして、
![]() インターバルに構築され、時間tと一致する正しい値を
インターバルに構築され、時間tと一致する正しい値を
![]() 図5aおよび5bに示します。
数字から見ると、ほとんどの場合、インデックス
図5aおよび5bに示します。
数字から見ると、ほとんどの場合、インデックス
![]() はHよりもはるかに正確に決定されます。
はHよりもはるかに正確に決定されます。
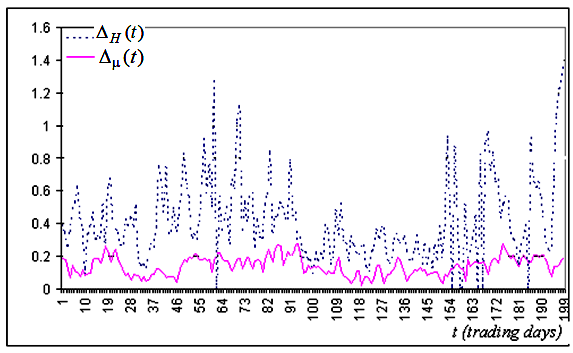
図5a。Alcoa(アルコア)社の終値に基づいて作成された信頼区間の幅の時系列の典型的なフラグメント.
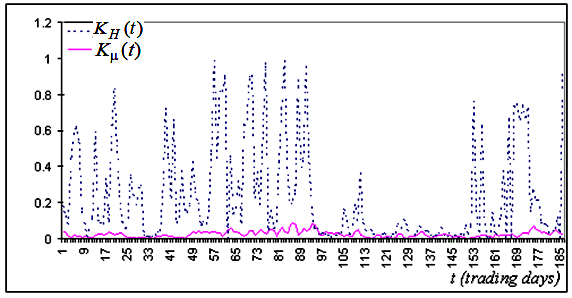
図5b。実験点の一致の精度と理論線の精度を示す値に対する対応する系列フラグメントは、同じ系列用に構築されています。
画像に基づいて、圧倒的多数の場合にフラクタル指数
![]() は
Hよりもはるかに正確に決定されると、結論付けることが可能です。
は
Hよりもはるかに正確に決定されると、結論付けることが可能です。
![]() 他のフラクタルインジケータ(特にハースト指数を含む)に関連するインデックスの主な利点は、対応する
他のフラクタルインジケータ(特にハースト指数を含む)に関連するインデックスの主な利点は、対応する
![]() 値がすぐに漸近的モードに入ることです。
これより、
値がすぐに漸近的モードに入ることです。
これより、
![]() その正確な決定のスケールのオーダーがプロセス状態を決定する主なスケールと一致するので、初期プロセスのダイナミクスを決定することにより、ローカル特性としての使用が可能です。
このような状態には、相対的な穏やかな期間(レンジ)と長期的な上向きまたは下降の動き期間(トレンド)が含まれます。 値を系列挙動とリンクするための効率的なソリューション
その正確な決定のスケールのオーダーがプロセス状態を決定する主なスケールと一致するので、初期プロセスのダイナミクスを決定することにより、ローカル特性としての使用が可能です。
このような状態には、相対的な穏やかな期間(レンジ)と長期的な上向きまたは下降の動き期間(トレンド)が含まれます。 値を系列挙動とリンクするための効率的なソリューション
![]() は、t
は、t
![]()
![]() の前の最小間隔で決定される値
の前の最小間隔で決定される値
![]() として関数を追加することです。
として関数を追加することです。
時系列の性質とフラクタルインデックスの相関
フラクタルインデックスに基づくインジケータを使用する人は、その特定の関数のいくつかを知っておく必要があります [2].
このシリーズの動作は、
![]() 値を定義します。
値を定義します。
-
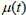 =
0.5 はランダム価格ウォークを意味します。(Wienerプロセス). 投資家は独立してふるまい、価格の行動に明白な傾向はありません。
この場合、価格は外部の影響に弱く依存しているため、"フィードバック"が存在せず、アービトラージの機会がないため、価格は"normal"安定性があると言えます。
=
0.5 はランダム価格ウォークを意味します。(Wienerプロセス). 投資家は独立してふるまい、価格の行動に明白な傾向はありません。
この場合、価格は外部の影響に弱く依存しているため、"フィードバック"が存在せず、アービトラージの機会がないため、価格は"normal"安定性があると言えます。 -
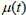 <0.5
は、価格が外部の影響に対して高い安定性があることを示唆しており、関連する会社の安定性に対する投資家の信頼と相場に新しい情報がないことを示している可能性があります。 この場合、株価は狭い価格帯で変動します。
価格が上昇しても十分な売り手が残っていて、価格が下がっても十分な買い手がいて、それらの行動は価格を最初の範囲に戻します。 "相関" はマイナスであり、安定した価格行動を維持しながら株価の変化を軽減します。
<0.5
は、価格が外部の影響に対して高い安定性があることを示唆しており、関連する会社の安定性に対する投資家の信頼と相場に新しい情報がないことを示している可能性があります。 この場合、株価は狭い価格帯で変動します。
価格が上昇しても十分な売り手が残っていて、価格が下がっても十分な買い手がいて、それらの行動は価格を最初の範囲に戻します。 "相関" はマイナスであり、安定した価格行動を維持しながら株価の変化を軽減します。 -
 >
0.5 は、価格の安定性の低下に対応します。 新しい情報の出現と、この情報に対する反応を示している可能性があります。
すべての相場参加者が受けとった情報をほぼ均等に見積もると仮定することと、受けとった情報に対応する価格の動きにトレンドが現れます。 状況によっては、株価の急激な変動につながります。
>
0.5 は、価格の安定性の低下に対応します。 新しい情報の出現と、この情報に対する反応を示している可能性があります。
すべての相場参加者が受けとった情報をほぼ均等に見積もると仮定することと、受けとった情報に対応する価格の動きにトレンドが現れます。 状況によっては、株価の急激な変動につながります。
フラクタルインデックスとハースト指数は
![]() =1-Hとして関連しており、カオス時系列からの亜種の継承を可能にします。
=1-Hとして関連しており、カオス時系列からの亜種の継承を可能にします。
-
 =
0.5 の場合、時系列はウィーナー プロセス ("brown" ノイズ) です。 このプロセスの主なプロパティは、メモリの不在です。つまり、系列の進化は、以前の値に接続されていません。
=
0.5 の場合、時系列はウィーナー プロセス ("brown" ノイズ) です。 このプロセスの主なプロパティは、メモリの不在です。つまり、系列の進化は、以前の値に接続されていません。 - 0.5 <=
 1,
0 <= H <0.5の場合、プロセスは "ピンク" ノイズと見なされます。 "ネガティブ" メモリが特徴で、過去に正の増分があった場合は、負の増分が続く可能性があります。その逆もしかりです。
1,
0 <= H <0.5の場合、プロセスは "ピンク" ノイズと見なされます。 "ネガティブ" メモリが特徴で、過去に正の増分があった場合は、負の増分が続く可能性があります。その逆もしかりです。 - 0 <=
 <
0.5 , 0.5 < H <=1の場合、時系列は正のメモリを持つ "ブラック" ノイズです。
<
0.5 , 0.5 < H <=1の場合、時系列は正のメモリを持つ "ブラック" ノイズです。
フラクタル指数とハースト指数を評価するためのインジケータ
日、週、月単位で成功したトレードは、金融時系列の混沌とした状態の理解に関連付けられています。 短いデータ断片におけるフラクタル指数の安定的な評価に基づいて、トレーダーが金融時系列を識別し、予測するのに役立つ株式(多数の人々の意志によって決定されるの進化)のインジケータを開発することができます。
このインジケータは、フラクタル指数、信頼区間、決定係数の値、ハースト指数を評価します。 以下のチャートは、前述の、
![]()
![]()
![]() 関数チャートを示します。
関数チャートを示します。
このインジケータでは、計算が実行され、パラメータ評価ウィンドウが提供される時系列セグメントの長さを設定することができます。 インジケータの起動時に、このシリーズは終値に沿って計算され、ウィンドウは1カウントずつシフトされます。 評価ウィンドウの長さ(間隔)は2の二乗に等しいため、セットの線形近似を行うことで値のセットを取得し、フラクタルインデックスを評価することができます。
double CFractalIndexLine::CalculateFractalIndex(const double &series[],const int N0,const int N1, const double hourSampling,int CountFragmentScale=0) { //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // series[] - time series // N0, N1 - the left and right boundary points of the series[] array fragment, based on which the fractal index will be estimated // hourSampling - discretization between points in HOURS // CountFragmentScale - the number of requested scales to form a set of points, for which the fractal index is calculated // // RESULT // the fractal index (Mu), the Hurst index (Hurst), the Confidence interval 95% (ConfInterval[2], // coefficient of determination (R2det) - the closer to 1, the more accurately the calculation points fall on the approximating line // determining stability for coefficient KR2 = 1-R2det. The closer to zero, the more accurate the calculated value of Mu //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. Load the internal fragment with values from the time series LoadFragment(series,N0,N1,hourSampling); // 2. Determine the number of cycles to determine the points of the approximating line int nn2 = (int)floor(Nfrgm/2); // Partition limits - no less than two points int npow2 = (int)ipow2(nn2); // The number of the powers of two in the Possible partitioning limit; if(CountFragmentScale==0) CountFragmentScale=npow2; // default int Count=fmin(CountFragmentScale,npow2); // limiting the number of variants of series fragment division int NumPartDivide; for(int i=0; i<=Count; i++) { NumPartDivide = (int)pow (2,i); // Number of pieces in the series fragment division CalcAmplVariation(NumPartDivide, i); // Calculating a point for the approximating line model i=i; } // 4. Evaluation of the Fractal Index and on the limits of the Index confidence intervals Mu=fCalculateConfidenceIntervalMU(LogDeltaScales,LogAmplVariations,Count,ConfInterval,R2det); Hurst=1-Mu; // Hurst exponent KR2=1-R2det; return Mu; } //----------------------------------------------------------------------------------------------------------------------------------
double CFractalIndexLine::CalcAmplVariation(const int NumPartDivide,int idxAmplVar=-1) { // If idxAmplVar=-1, then index in the array is determined automatically (based on the contribution of the power of two in NumPartDivide) // ALREADY PREVIOUSLY DONE: copying the fragment, setting the time of discretization of the series IN DAYS // - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. DETERMINE THE BORDERS OF INTERVALS CORRESPONDING TO THE SPECIFIC NUMBERS int nCheckPoint=0,nIntervalPoints=0; // the number of points to check in one division interval double dayDeltaScales=BoundaryArray(NumPartDivide,fragment,0,Nfrgm-1,hSampling,Boundaries,nIntervalPoints); // 2. GO THROUGH INTERVALS TO DETERMINE LIMIT VALUES OF FUNCTIONS AND OF AMPLITUDE VARIATION int countInterval=Boundaries.CountNonEmty(); int maxFuncIdx=0,minFuncIdx=0; double A,V=0.; nCheckPoint=(int)(Boundaries.y[0]-Boundaries.x[0])+1; for(int i=0; i<countInterval; i++) { maxFuncIdx = ArrayMaximum(fragment,(int)Boundaries.x[i],nCheckPoint); // INDEX WITH MAX. VALUE minFuncIdx = ArrayMinimum(fragment,(int)Boundaries.x[i],nCheckPoint); A = fragment[maxFuncIdx] - fragment[minFuncIdx]; V = V+A; i=i; } // 3. ACCUMULATION OF RESULTS IN STORAGE if(idxAmplVar==-1) idxAmplVar=ipow2(NumPartDivide); // index in the storage array LogDeltaScales [idxAmplVar] = log(dayDeltaScales); // log-scale of the current division LogAmplVariations[idxAmplVar] = log(V); // log-Amplitude Variation in the current division scale return V; } //--------------------------------------------------------------------------------------------------------------------------------------
CFragmentIndexLine.mqh ファイル フラグメントは、図2 に示すように、カバー領域の計算にループを実行します。 プログラム内のアクションのシーケンスは、詳細なコメントを通じて説明されます。
実データに対するインジケータ演算のデモンストレーション
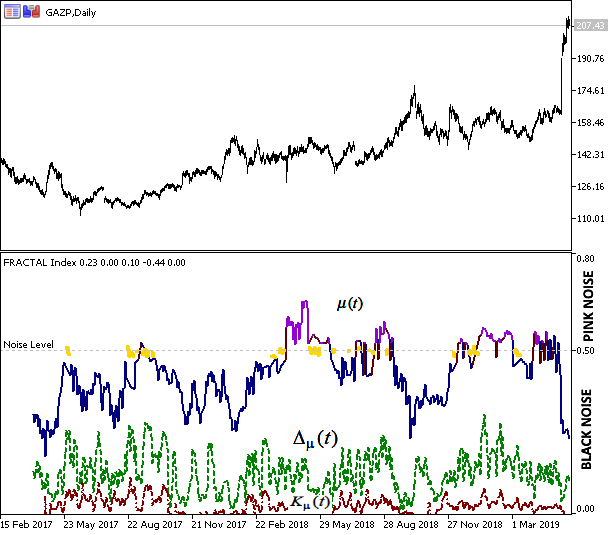
図6 ガスプロムの終値とフラクタル指数評価結果
この図は、インデックス値の相関関係と価格の振る舞いを示します。 インデックスチャートの青色は、システムのトレンド状態に対応し、トレンドの安定性と未来の行動を予測する力を示します。 紫色は"ピンクノイズ" タイプの持続性が高いことを示し、"ネガティブ" メモリとレンジに対応します。 黄色は"ブラウニアンモーション"に対応し、動きはランダムであり、予測できません。
結論
局所的なフラクタル分析は、次の目的においてトレードで興味深いです。
- カオスの決定、すなわち時系列の統計的特性が変化する瞬間の決定です;
- 時系列の予測。
適切な精度でインデックス
![]() を決定するスケールは、ハースト指数 H を計算する場合に同様のスケールよりも 2 桁小さいことを考慮する必要があります。この差により、
を決定するスケールは、ハースト指数 H を計算する場合に同様のスケールよりも 2 桁小さいことを考慮する必要があります。この差により、
![]() インデックスをローカルフラクタルインデックスとして使用できます。
これが、インデックスが
インデックスをローカルフラクタルインデックスとして使用できます。
これが、インデックスが
![]() 時系列の安定性を表していると考えることができる理由です。
時系列の安定性を表していると考えることができる理由です。
![]() <0.5の場合はトレンドとして解釈でき、
<0.5の場合はトレンドとして解釈でき、
![]() >0.5の場合はレンジとして扱うことができます。
~ 0.5 はブラウン運動と見なされます。
>0.5の場合はレンジとして扱うことができます。
~ 0.5 はブラウン運動と見なされます。
![]() したがって、関数
したがって、関数
![]() を使用して初期価格シリーズを分類し、予測をすることができます。
を使用して初期価格シリーズを分類し、予測をすることができます。
参考文献一覧
- Dubovikov M.M., Starchenko N.V. 金融時系列の経済物理学とフラクタル分析
- Dubovikov M.M., Starchenko N.V. 経済物理学と財務時系列の分析と収集. "ECONOPHYSICS. 経済理論を求めた現代物理学"
- Peters, J.によるカオスと資本相場におけるオーダー サイクル、価格、相場のボラティリティの新しい見方
- Krivonosova
E.K., Pervadchuk V.P., Krivonosova E.A.経済インジケータの時系列のフラクタル特性の比較
- Starchenko N.V. 物理アプリケーションにおける局所フラクタル解析。