¿Qué son las tendencias y cómo es la estructura de los mercados: de tendencia o plana?

Maxim Romanov | 4 diciembre, 2020

Introducción

Antes de comenzar, vamos a echar un vistazo a la definición de "tendencia" que nos da internet. Esta es la definición ofrecida por la wikipedia: 

Según una de las definiciones del diccionario Merriam-Webster, una tendencia sería el movimiento general a lo largo del tiempo de un cambio estadísticamente detectable, así como la curva estadística que refleja dicho cambio. En matemáticas, las tendencias pueden ser descritas con varias ecuaciones: lineales, logarítmicas, polinomiales, etcétera. El tipo de tendencia real se establece usando como base la selección de su modelo funcional con la ayuda de métodos estadísticos o suavizando la serie temporal inicial. 

También tenemos esta otra definición:

En economía, sería la dirección de movimiento predominante de los indicadores económicos. Generalmente, se considera dentro del marco del análisis técnico que implica la dirección del movimiento del precio o los valores de los índices. Según Charles Dow, una tendencia alcista se caracteriza porque cada pico subsiguiente en un gráfico se encuentra por encima de los anteriores, mientras que una tendencia bajista conlleva que cada valle subsiguiente debe encontrarse por debajo de los anteriores (ver Teoría de Dow)). Existen varios tipos de tendencia: alcista, bajista y lateral (plana). Con frecuencia, en el gráfico se dibuja una línea de tendencia que conecta en la tendencia alcista dos o más valles de precio (la línea se ubica debajo del gráfico, como si lo apoyara y lo empujara visualmente hacia arriba); en el caso de la tendencia bajista, la línea de tendencia conecta dos o más picos de precios (la línea se halla sobre el gráfico, como si ofreciera resistencia y lo empujara visualmente hacia abajo). Las líneas de tendencia sirven como soporte (para una tendencia alcista) y resistencia (para una tendencia bajista).

En realidad, a nosotros no nos importa tanto cómo suena esto, sino cómo ganar dinero usando esta definición y lo que significa en general. Leyendo las definiciones anteriores, no queda muy claro qué debemos hacer para ganar dinero y cómo describirlo todo matemáticamente. Las definiciones que todos conocemos parecen crearse de forma intencionalmente vaga, de manera que tengan más de una interpretación y la gente pueda "pensar" en algo por sí misma. La ciencia, en cambio, prefiere la precisión. Las definiciones deben ser claras, comprensibles e inequívocas, de manera que cualquier persona que utilice el método pueda reproducir los resultados de otra persona que haya usado el mismo método antes.

Fundamentos de una estrategia comercial rentable

Antes de pasar a los conceptos de tendencia y mercado plano, primero debemos entender los conceptos básicos, es decir, qué tenemos que hacer para ganar dinero. Nos guste o no, cualquier estrategia comercial se basa en el hecho de que necesitamos obtener una ganancia esperada superior a 0. Para los entendidos en matemáticas, todo esto está claro, y no requiere mayor explicación, pero para el resto, debemos explicar qué es la esperanza matemática, ya que será clave en el futuro. En palabras simples, la esperanza matemática es el beneficio promedio. Lo lógico es que el beneficio promedio sea superior a 0, de lo contrario, si es 0, no ganaremos nada, y si es inferior a 0, perderemos dinero.

La esperanza matemática se compone de la probabilidad de una transacción rentable, el beneficio promedio y las pérdidas promedio de las transacciones. La fórmula es simple: multiplicamos la probabilidad del beneficio por el beneficio promedio y restamos del resultado la probabilidad de pérdidas multiplicada por las pérdidas promedio. 

m=(P(tp)*tp)-(P(sl)*sl), 

donde

• m — esperanza matemática del beneficio,
• P(tp) — probabilidad de una transacción rentable, 
• P(sl) — probabilidad de una transacción no rentable,
• tp — tamaño medio de las transacciones rentables,
• sl — tamaño medio de las transacciones no rentables.

Esto significa que si la probabilidad de una transacción rentable es del 50% y el tamaño medio de una transacción rentable es igual al tamaño de una transacción con pérdidas, entonces el valor esperado será 0, lo cual significa que no ganaremos nada. Por ejemplo, el tamaño medio de una transacción con beneficios y de una transacción con pérdidas = 10$, luego m=(50*10)-(50*10)=0. Debemos aclarar que la esperanza matemática para una variable aleatoria distribuida normalmente es de 0 (este es un hecho matemático). En el artículo anterior: Discretización de series temporales con generación aleatoria de "ruidos", vimos que la distribución de los incrementos en los mercados reales es muy parecida a la normal, y sospechosamente similar a un paseo aleatorio. 

Para obtener beneficios, tenemos que aumentar la probabilidad de lograr una transacción rentable, o bien aumentar el tamaño promedio de una transacción rentable y reducir el tamaño promedio de una transacción con pérdidas. Supongamos que incrementamos la probabilidad de una transacción rentable hasta un 60%, mientras que la transacción rentable promedio es igual a una transacción con pérdidas promedio = 10$. Entonces, después de completar 100 transacciones, ganaremos m=(60*10)-(40*10)=200$. Si la probabilidad de una transacción rentable sigue siendo la misma, obtendremos una ganancia constante. De forma similar, podemos aumentar el tamaño promedio de una transacción rentable, reducir el tamaño promedio de una transacción perdedora y dejar la probabilidad en un 50%, por lo que también quedaremos en positivo.

Aquí es donde con frecuencia sucede un sesgo cognitivo en muchos tráders, especialmente en los principiantes, que piensan: "bien, voy a hacer que el tamaño promedio de una transacción rentable sea 2 veces el tamaño promedio de una transacción perdedora, y luego abriré posiciones... digamos, en el cruce de los promedios" (el algoritmo de entrada no importa, puede sustituirlo por uno propio). El tráder pretende conseguir de forma inconsciente el resultado: m=(50*20)-(50*10)=500$ de beneficios, pero, en la práctica, obtiene una esperanza matemática m=(33.3*20)-(66.6*10)=0, o dicho de otra manera, acaba sufriendo las pérdidas derivadas del spread y las comisiones. En este artículo, no vamos a considerar el spread y las comisiones, ya que aquí no son importantes. Otros tráders podrían caer en la trampa opuesta, decidiendo obtener un beneficio dos veces inferior a las pérdidas, puesto que, según sus observaciones, las transacciones rentables deberían activarse con más frecuencia en este caso. Como resultado de ello, también obtendrán pérdidas, por las comisiones y el spread, ya que la recompensa real esperada de dicho sistema es m=(66,6*10)-(33,3*20)=0. Así, podemos aumentar considerablemente un stop loss y reducir los beneficios, lo cual aumentará la probabilidad de obtener beneficios al 90-99% y más, pero todo ese beneficio finalmente se compensará con pérdidas. Aquí también podemos incluir todos los sistemas de martingale que no cambian la esperanza matemática; si dicha esperanza era igual a 0, permanecerá igual, pero podemos sufrir pérdidas con bastante retardo temporal.

El motivo de esto es que no se han encontrado patrones rentables, y sin patrones correctos, los tráders realizan transacciones basadas ​​en paseos aleatorios. La esperanza matemática de un paseo aleatorio es 0. Si la esperanza matemática es igual a 0, la probabilidad de realizar una transacción rentable seguirá siendo del 50%. Lo único que cambiará son las proporciones (de ahora en adelante, nos referiremos a esto como "equilibrio del 50%"). En nuestro caso, la probabilidad de realizar una transacción rentable aumenta, y el tamaño de la transacción rentable disminuye proporcionalmente; o al contrario, la probabilidad de una transacción rentable disminuye, pero su tamaño aumenta también proporcionalmente. Ahora, necesitamos romper de alguna forma este "equilibrio del 50%" y alcanzar una rentabilidad esperada superior a cero. Debemos destacar que el desarrollo de un sistema no rentable es igualmente difícil. Los tráders pierden dinero por la existencia de las comisiones correspondientes y porque los depósitos son finitos.

Pasando de los gráficos de velas a los gráficos de bloques

Como estamos comerciando con los cambios del precio, y estos se dan en puntos (entendemos por punto el cambio de precio mínimo posible), y el beneficio depende de cuántos puntos haya superado el precio, entonces, para que todo resulte más comprensible, deberemos apartarnos de la forma estándar de representación del precio como velas/barras, porque estas deforman mucho la imagen y dificultan la comprensión del proceso. Vamos a adoptar un método de visualización que considera solo el movimiento del precio en puntos. En el artículo, usaremos un indicador propio que construye bloques después de que el precio haya superado una cierta cantidad de puntos. El indicador se adjunta al artículo. No obstante, podemos usar cualquier otro método. En la figura 1, se muestra la construcción de los bloques. Los bloques pueden tener cualquier tamaño, desde un punto hasta el infinito, usando incrementos de un punto. Si el tamaño del bloque es de 10 puntos, entonces el bloque se cerrará después de que el precio haya superado verticalmente los 10 puntos, y entonces comenzará a formarse un nuevo bloque, que podrá cerrarse en incrementos de 10 puntos hacia arriba o hacia abajo. El bloque representa los precios open, high, low, close, y estos indican las mismas funciones que sus velas análogas. Vamos a considerar que un bloque es un salto. Esto será importante más adelante.

Figura 1.

Para pasar al concepto de tendencia, necesitamos partir de algún tipo de muestra en la que apoyarnos. En el paseo aleatorio, cada paso posterior no depende del anterior: el proceso carece de memoria, y la probabilidad de que el siguiente salto cambie de dirección es del 50%. Pero, ¿el paseo aleatorio se basa en una tendencia o es plano? Vamos a echar un vistazo al gráfico del paseo aleatorio en la figura 2.

Figura 2.

Algunos tráders encontrarán en la figura 2 tanto áreas de tendencia, como planas, pero, en realidad, este es un gráfico de paseo aleatorio muestreado por velas H1. La probabilidad de que cada salto subsiguiente suba o baje aquí es del 50%, y no depende de la dirección del salto anterior. Al desarrollar el concepto de tendencia, usaremos el paseo aleatorio como base ya que, como hemos dicho anteriormente, la esperanza matemática en este caso es 0. Esto se debe a que la probabilidad de que cada paso subsiguiente cambie o mantenga su dirección aquí es del 50%. Al abrir una posición, independientemente del número de saltos que la mantengamos, la pérdida promedio siempre permanecerá igual al beneficio promedio. La probabilidad de adivinar la dirección también será del 50%. Por consiguiente, asumiremos que el gráfico del paseo aleatorio no se basa ni en la tendencia ni en el mercado plano: es aleatorio.

Así, como ahora disponemos de una referencia con la que comparar la serie de precios que estamos investigando, vamos a decidir si esta serie de precios se basa en una tendencia o es plana.

Desarrollando el modelo de referencia

En la figura 2, mostramos el gráfico de un paseo aleatorio muestreado por velas H1. Esta representación no resulta demasiado intuitiva, y distorsiona la percepción del proceso. Vamos a ver su código fuente, mostrado en la figura 3. Adjuntamos a continuación la serie en formato CSV. El lector podrá descargarla en el terminal.

Figura 3.

La figura 3 muestra el gráfico de un paseo aleatorio con un salto de 1 punto, y el mismo gráfico como bloques con un tamaño de 1 punto. Los bloques son necesarios para hacer los saltos más visibles; en esencia, son el mismo gráfico, la única diferencia es visual. Como creemos que el paseo aleatorio será un estándar para definir aún más la tendencia de una serie de precios, con objeto de comparar la serie de precios reales con la estándar, vamos a construir un gráfico con la distribución de la densidad de probabilidad de los incrementos para un paseo aleatorio. Podemos resolver este problema de forma analítica utilizando una función gaussiana, pero no está tan claro, y ni siquiera todos los tráders familiarizados con las matemáticas comprenderán completamente lo que significa esta o aquella forma de la distribución obtenida. Por eso, para construir la distribución de referencia de la densidad de la probabilidad, crearemos con la ayuda de las reglas combinatorias el fragmento que mostramos en la figura 4. El recuadro completo se adjuntará al artículo en un archivo aparte en formato excel.

Figura 4.

El recuadro nos permite valorar cuánto puede recorrer verticalmente el paseo aleatorio en 40 saltos. Con la ayuda del coeficiente qs (en la fórmula del recuadro), estableceremos el número de muestras para las que se construye el recuadro. En el ejemplo, el recuadro ha sido creado para 100.000 muestras. La columna "vertical steps" indica el número de saltos que la función realiza verticalmente, mientras que la columna "probability of event %", indica la frecuencia de estos saltos verticales. Por ejemplo, el proceso realiza 40 saltos en total, y es capaz de subir o bajar 40 saltos; tenemos 100.000 muestras (medidas), de promedio, el proceso se desplaza 40 saltos verticales 0.00000009 veces de 100,000. En este caso, además, 38 saltos verticales se hacen 0.0000036 veces de 100,000, mientras que 36 saltos se realizan 0.00007 veces de 100,000. Por consiguiente, estableciendo la matriz de valores en la columna "probability of event %", podemos construir el gráfico de distribución de densidad de la probabilidad del incremento que se muestra en la figura 5.

Figura 5.

El recuadro nos permite ver la distribución de referencia de la densidad de la probabilidad del incremento en 40 saltos para un proceso con una probabilidad de cambio de dirección y continuación de cada salto subsiguiente igual al 50%. Para asegurarnos de que todo esté correcto, podemos medir la distribución de la densidad de la probabilidad para el paseo aleatorio y compararla con la referencia. Realizaremos las medidas para el paseo aleatorio cuyos fragmentos se muestran en las figuras 2 y 3. Mediremos cuántos saltos verticales ha realizado la función dentro de 40 saltos y 100.000 muestras (medidas). Los resultados se muestran en la figura 6. El eje Х indica las amplitudes de -40...0... 40 saltos verticales, mientras que el eje Y muestra el número de eventos para cada número de saltos verticales.

Figura 6.

La distribución de referencia para 100.000 muestras de 40 saltos cada una (calculada según el recuadro) se muestra en rojo, mientras que el histograma blanco muestra las 100.000 muestras realmente medidas del paseo aleatorio generado. Como podemos ver, la distribución de referencia y el histograma son casi idénticos. Las desviaciones son mínimas; cuantas más muestras utilicemos, con mayor precisión se corresponderán los valores medidos realmente con los de referencia. Ahora, podemos determinar cuánto se diferencia la distribución de una serie respecto a la de referencia. Considerando la distribución de la probabilidad del incremento, actualmente podemos concluir que la serie analizada coincide al máximo posible con el paseo aleatorio. Más adelante, explicaremos por qué es necesario esto. 

Distribución de los incrementos en el mercado real

Para realizar las mediciones, utilizaremos un gráfico GBPUSD real y lo transformaremos en un gráfico de bloques con un tamaño de bloque de 0.00022. Al igual que en el ejemplo anterior, calcularemos cuánto se ha desplazado verticalmente el precio en 40 saltos utilizando 100.000 muestras, y compararemos el resultado con la referencia en la figura 7.

Figura 7.

Como antes, la distribución de referencia se muestra en rojo, mientras que la distribución medida se muestra en blanco. Ahora, vamos a necesitar simplificar de la forma que hicimos antes, es decir, usaremos la combinatoria en lugar de la función de Gauss, porque no todos los tráders entendidos en matemáticas pueden sacar la conclusión correcta; es más, ni siquiera quienes conocen bien las matemáticas podrían sacar ninguna conclusión en absoluto. Podemos ver que la distribución de los incrementos de GBPUSD es simétrica alrededor del cero. La simetría alrededor del cero indica que no existe una propensión acusada hacia las tendencias alcistas o bajistas. Es decir, la probabilidad de que después de cada bloque hacia arriba se encuentre un bloque hacia abajo es igual a la probabilidad de que después de cada bloque hacia abajo se encuentre un bloque hacia arriba. En otras palabras, no existe una tendencia pronunciada de movimiento de precios hacia arriba o hacia abajo. 

Resulta mucho más interesante que el gráfico de distribución de GBPUSD sea más bajo y más ancho que la referencia. Esto indica que el precio llega a cero en 40 saltos con mucha menor frecuencia de lo que debería para un paseo aleatorio, y al contrario: con frecuencia, hay más bloques a lo largo de la vertical de lo que debería para un paseo aleatorio. Y esto conlleva que la probabilidad de cambiar de dirección en cada salto subsiguiente no es del 50%, sino ligeramente menor. Mirando el gráfico, podemos deducir que si ha habido un bloque en crecimiento, entonces, con una probabilidad de más del 50%, aparecerá un bloque en crecimiento después de aquel, y con una probabilidad de más del 50%, aparecerá un bloque en caída.

¿Qué podemos extraer de esta información? Recordemos la fórmula de la esperanza matemática con la que podíamos valorar el beneficio. En ella, todo el problema referente a la obtentención de beneficios radicaba en el hecho de que si la probabilidad de una entrada "correcta" era superior al 50%, entonces permaneceríamos en el beneficio, siempre que la pérdida promedio fuera igual al beneficio promedio. Para ganar dinero, era necesario romper el "equilibrio del 50%". Ahora, no hemos estimado el valor exacto de la probabilidad de un viraje (podemos calcularlo simplemente a partir del gráfico), pero si suponemos que en este gráfico la probabilidad de continuación es del 55%, y la probabilidad de viraje es del 45%, y el beneficio promedio será igual a las pérdidas promedio e igual a 10 saltos (con un tamaño de salto de 0,00022*10=0.0022), entonces la esperanza matemática m=(55*0.0022)-(45*0.0022)=0.121-0.099=0.022. A su vez, esto significará que, después de completar 100 transacciones, permaneceremos en positivo: 0.022. Si comerciamos con 0.1 lotes de GBPUSD, entonces tendremos unos beneficios de 220$.

Sabiendo que la probabilidad de que la tendencia continúe es superior al 50%, podemos usar una estrategia comercial para continuar la tendencia, es decir, si el bloque en crecimiento está cerrado, al abrir una posición de compra para continuar la tendencia, ganaremos dinero. En otras palabras, si sabemos que la probabilidad de que la tendencia continúe es superior al 50%, utilizaremos la estrategia de tendencia y permaneceremos en positivo. Por el contrario, si sabemos que la probabilidad de un viraje (es decir, de que surja un bloque descendente después de un bloque ascendente) es superior al 50%, abriremos una posición Sell cada vez que se cierre el bloque ascendente y, usando una estrategia plana (de contratendencia), nos mantendremos en positivo.

Definición: qué entendemos por tendencia/mercado plano

La definición de la tendencia y el mercado plano procede directamente de la estrategia que podemos usar para ganar dinero en un mercado concreto. Si la probabilidad de que la tendencia prosiga en un paseo aleatorio es del 50% y el paseo aleatorio no es de tendencia ni plano, entonces:

Un movimiento de tendencia comprenderá la situación en la que la probabilidad de una continuación de la tendencia será superior a la probabilidad de un viraje de la misma. Si el precio ha superado 10 puntos, entonces en una situación de tendencia con una probabilidad superior al 50%, el precio se desplazará otros 10 puntos en la dirección del movimiento anterior.

Un movimiento plano comprenderá la situación en la que la probabilidad de un cambio en la dirección del movimiento será superior a la probabilidad de la continuación de la tendencia. Si el precio se ha desplazado 10 puntos en una situación plana, entonces, con una probabilidad de más del 50%, virará y se desplazará 10 puntos en la dirección opuesta.

Si representamos el precio en forma de bloques (como hemos descrito anteriormente) de 10 puntos, entonces, en una situación de tendencia, será rentable abrir una posición de compra después del cierre de cada bloque ascendente subsiguiente y abrir una posición de venta después de cada bloque descendente subsiguiente. En una situación plana, por el contrario, después de cerrar un bloque ascendente, será rentable abrir una posición de venta, y después de un bloque descendente, será rentable abrir una posición de compra.

En otras palabras, si el mercado está en tendencia, solo tendremos que comerciar para la continuación de la tendencia, y será rentable. Si el mercado es plano, entonces deberemos comerciar para el viraje de la tendencia, y será rentable. Si el mercado no se encuentra en tendencia o plano, no abra posiciones.

No estamos afirmando que no se pueda ganar dinero con un paseo aleatorio, pero este tema merece un profundo estudio aparte.

Comprobando la afirmación

Al parecer, las afirmaciones lógicas no siempre resultan ser verdaderas. Por consiguiente, pondremos a prueba nuestros hallazgos usando un modelo simple. Para ello, vamos a crear 2 procesos; el primero tendrá una probabilidad de viraje superior al 80%, y se muestra en la figura 8. El segundo proceso tendrá un 20% de probabilidad de viraje, y se muestra en la figura 9.

Figura 8.

Figura 9.

En la figura 8, vemos que la distribución de la densidad de la probabilidad medida es mucho más estrecha que la referencia, y el proceso retorna a cero con mucha mayor frecuencia. En la figura 9, vemos que la distribución de la densidad de la probabilidad medida es mucho más amplia que la referencia, y el proceso retorna a cero con mucha menor frecuencia. Por consiguiente, podemos deducir que las transacciones efectuadas anteriormente son correctas, al igual que la lógica. Si la probabilidad de un viraje es inferior al 50%, la distribución resultará más amplia que la de referencia, y esta lógica podrá utilizarse para analizar el grado de tendencia de un determinado instrumento. Aquí, vamos a presentar un concepto de "tendencia" que muestra cuantitativamente la inclinación del proceso a continuar la tendencia.

Valorando el grando de tendencia de un instrumento

Disponiendo de un valor de referencia, podemos evaluar en valores absolutos el grado de tendencia de los diferentes marcos temporales de un instrumento y de los distintos instrumentos. Pero, antes de ello, necesitamos desarrollar un método para comparar valores absolutos. Sugerimos 2 métodos:

1. Según la desviación de la densidad. Seleccionamos un intervalo de amplitudes y calculamos cuántos eventos han entrado en dicho intervalo para la referencia. A continuación, hacemos lo mismo con los valores medidos. Luego, dividimos el valor de referencia por el medido para obtener unidades absolutas. Si el valor es superior a 1, la serie será de tendencia; si es inferior a 1, la serie será plana. Por ejemplo, el intervalo de amplitud completo es -40...0...40. No tiene sentido calcular cuántos valores han entrado en -40...40, porque el 100% de los valores se dan allí, así que tomaremos otro valor. Según la teoría de la probabilidad, "aproximadamente el 68% de los valores de la distribución normal se hallan a una distancia no superior a una desviación estándar σ del promedio; aproximadamente el 95 % de los valores se hallan dentro de dos desviaciones estándar, mientras que el 99,7 % puede ubicarse en no más de tres desviaciones estándar". Es decir, se considera normal comparar cuántos eventos entran en un intervalo particular y comparar esto con la distribución normal. No obstante, no hemos medido la desviación estándar en nuestro trabajo, ya que no resulta necesario. Por consiguiente, usaremos números absolutos. Preferimos el método siguiente: 
• Establecemos en la referencia el porcentaje de muestra que nos interese. Por ejemplo, el 80% de las muestras: esto significa que deberemos definir el intervalo en el que se encuentra este 80% de muestras. Nuestro ejemplo tiene 100,000 muestras, lo cual implica que el 80% son 80,000 muestras. Vamos a calcular el intervalo de amplitud en el que se encuentran estas 80 000 muestras. El 84,6% de las muestras se hallan en el intervalo de -8...8, mientras que el 73,18% de las muestras se encuentran en el rango de -6...6. El 84,6% se encuentra más cerca del 80%, así que tenemos que registrar cuántas muestras se hallan en el intervalo de -8...8, a saber, 84,614 muestras. 
• A continuación, medimos cuántas muestras entran en el intervalo de -8...8 en la distribución construida para una serie con el 80% de probabilidad de viraje. En nuestro caso, el intervalo tiene 100.000 muestras. Ahora, dividimos 84.614/100.000=0,8416. Por consiguiente, el grado de tendencia es 0,8416 para el gráfico de la figura 8. 
• Vamos a comprobar el grado de tendencia del gráfico en la figura 9. El intervalo de -8...8 presenta 52034 muestras, y obtenemos un grado de tendencia para la serie con una probabilidad de viraje del 20%, es decir, 84,614/52,325=1.617.
2. Según la amplitud media. También podemos usar otro método. Gracias al teorema del límite central, podemos deducir que la amplitud vertical promedio del paseo aleatorio es proporcional a la potencia de 0.5 del número de saltos. Antes, creamos un recuadro para construir la distribución de referencia que mostramos parcialmente en la figura 4. Aparte de otras cosas, contenía la celda "average block vertically", donde se calculaba el número promedio de saltos verticales superados ​​por el paseo aleatorio de referencia. Esta cifra se hallaba como la suma de la columna "amplitude frequency" para el intervalo de 0...40 saltos verticales dividida por el número de muestras (aquí es 100.000). En el recuadro, el valor es igual a 5.0148. Esto significa que, de media, el paseo aleatorio supera -5.0148...5.0148 saltos verticales para 40 saltos, lo cual es proporcional a la potencia 0,437 del número de saltos. La desviación de la potencia 0.5 procede del hecho de que solo damos 40 saltos, y el teorema del marinero borracho afirma que el paseo aleatorio debe ser aproximadamente proporcional a la potencia 0.5 del número de saltos. Usando el recuadro, hemos obtenido el valor exacto para el número especificado de saltos.
• Si medimos el número promedio de saltos verticales superados ​​por el proceso con una probabilidad de viraje del 50% que mostramos en las figuras 2 y 3, obtendremos 5.0363. Vamos a definir el grado de tendencia de una serie con un 50% de probabilidad de viraje. Para ello, dividiremos el valor de referencia por el medido 5,0148/5,0363=0,9957. Como podemos ver, el grado de tendencia es casi igual a 1, lo que indica que la serie está lo más cerca posible del paseo aleatorio, y nuestra lógica es correcta.
• Ahora, calculamos el grado de tendencia de un proceso con una probabilidad de reversión del 80%. Para hacerlo, medimos su amplitud promedio, que resulta igual a 1,6495. A continuación, dividimos el valor medido por el de referencia 1,6495/5,0148=0,3289. El valor es mucho menor que 1, lo cual indica que la serie analizada es de baja tendencia.
• Ahora, calculamos el grado de tendencia de un proceso con una probabilidad de reversión del 20%. Para hacerlo, medimos su amplitud promedio, que resulta igual a 9,95. A continuación, dividimos el valor medido por el de referencia 9,95/5,0148=1,98. El valor es casi 2 veces superior a 1, lo cual indica que la serie analizada tiene un alto grado de tendencia.
  

Con una herramienta de este tipo, podemos comparar directamente los grados de tendencia en diferentes escalas (marcos temporales) de un mismo instrumento y valorar visualmente sus parámetros estadísticos. Como ejemplo, vamos a utilizar los 2 mismos procesos con un 20% y un 80% de probabilidad de viraje, valorando visualmente sus parámetros estadísticos en diferentes escalas. Antes, usamos un tamaño de bloque igual a 1 punto. Ahora, crearemos bloques de mayor tamaño multiplicando cada tamaño del bloque subsiguiente por una proporción de 1,1. Por consiguiente, obtendremos varias escalas con tamaños de bloque de 1; 1,1; 1,21; 1.33..... 6.12. La figura 10, mostramos cómo cambia la tendencia al incrementar la escala del proceso con una probabilidad de viraje del 80%. En la figura 11, se muestra lo mismo para un proceso con una probabilidad de viraje del 20%.

Figura 10.

Figura 11.

En las figuras 10 y 11, la escala menor (1 punto) se encuentra a la izquierda, mientras que la mayor se halla a la derecha en el eje X. El eje Y muestra el grado de tendencia de un instrumento calculado utilizando el grado de "amplitud promedio". Podemos ver que en la figura 10, donde el proceso de probabilidad de viraje del 80% es inicialmente plano, la primera columna del histograma posee un bajo nivel de tendencia, pero, a medida que aumenta la escala, la tendencia tiende a 1 (el valor del paseo aleatorio de referencia). Esto indica que, a pesar de que la probabilidad de inversión en la escala más pequeña es alta, eso mismo no resulta cierto para escalas mayores, donde el proceso pierde "memoria" y se convierte en un paseo aleatorio. En la figura 11 vemos una imagen similar. Si bien inicialmente el proceso tiene un alto grado de tendencia, 2.053, luego disminuye y tiende al valor de referencia del paseo aleatorio en escalas mayores. 

Las figuras 10 y 11 muestran que el proceso tiene "memoria" solo en la escala más pequeña, pareciéndose cada vez más a un paseo aleatorio a medida que aumenta la escala. Esta conclusión respalda totalmente cómo han sido creadas las series. Al generar estos dos procesos, solo se ha considerado la dirección del salto anterior. Los saltos restantes no se han tomado en cuenta, por lo que el efecto de la "memoria" se disipa rápidamente conforme aumenta la escala.

Construyendo la dependencia entre el grado de tendencia y el número de pasos

Los mercados reales son diferentes de las series generadas sintéticamente, y para detectar los patrones se requieren más herramientas analíticas. Por consiguiente, resultaría útil no solo analizar el grado de tendencia en un número fijo de saltos, sino también valorar cómo cambia la tendencia del mercado al aumentar en el número de saltos pasados. Como los recuadros de referencia se pueden construir para un número distinto de saltos, podemos ver simultáneamente no solo cómo se comporta la herramienta al incrementar el tamaño del salto, sino también cómo se comporta cuando aumenta el número de estos. En la figura 12, podemos ver la dinámica del grado de tendencia de GBPUSD para 10,000 muestras con un tamaño de bloque de 0.00314, para un número de saltos de 10 a 100. La columna del histograma más a la izquierda se ha construido para 10 saltos, mientras que la columna más a la derecha se ha construido para 100 saltos. En cada columna del histograma, el número de saltos aumenta en 2. 

Figura 12.

De acuerdo con la figura 12, en la escala actual, la tendencia de GBPUSD supera 1 y vacila en el intervalo de 1.133-1.166, dependiendo del número de saltos para los que se realiza el análisis. La figura 13 refleja cómo varía el grado de tendencia al aumentar la escala. El gráfico se ha construido para 10,000 muestras de 40 saltos cada una, para tamaños de salto de 0,00021 a 0,00495. La columna de histograma más a la izquierda se ha construido para un tamaño de bloque de 0,00021, mientras que cada columna subsiguiente del histograma supera a la anterior 1,1 veces.

Figura 13.

En la figura 13, vemos cómo disminuye el grado de tendencia al aumentar la escala. Si bien es igual a 1.425 para la escala menor, ya tiende a 1 y es igual a 1.062 en la mayor. Conforme la escala aumenta, el comportamiento de GBPUSD se parece más al comportamiento de una serie sintética con una probabilidad del 20%.

Este enfoque nos permite valorar de forma dinámica la velocidad de cambio del grado de tendencia de un instrumento comercial. La siguiente animación muestra la dinámica de la distribución de la densidad de la probabilidad de un incremento para acciones de AMD en relación con la distribución de referencia. Como base, se usan las velas de marco temporal M1. La animación se ha construido para 40 saltos, 1000 muestras. El tamaño del bloque varía de forma dinámica, dependiendo de la volatilidad promedio actual.

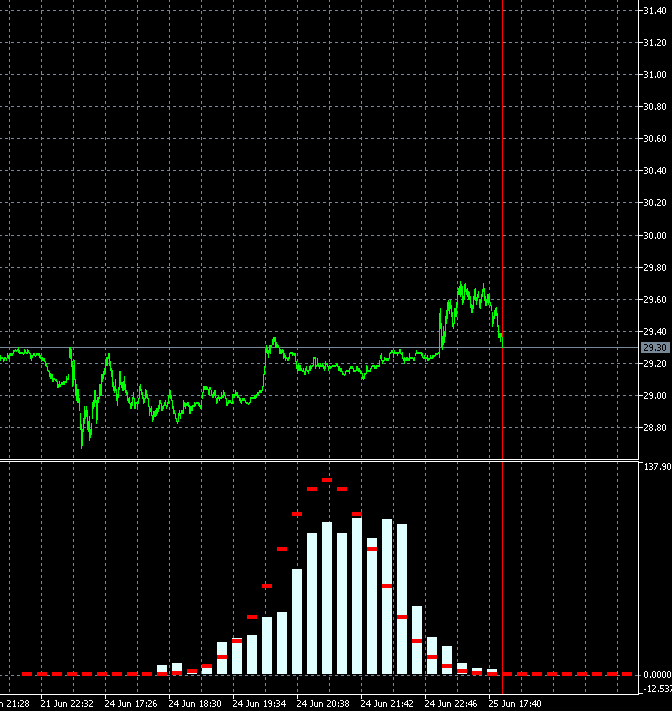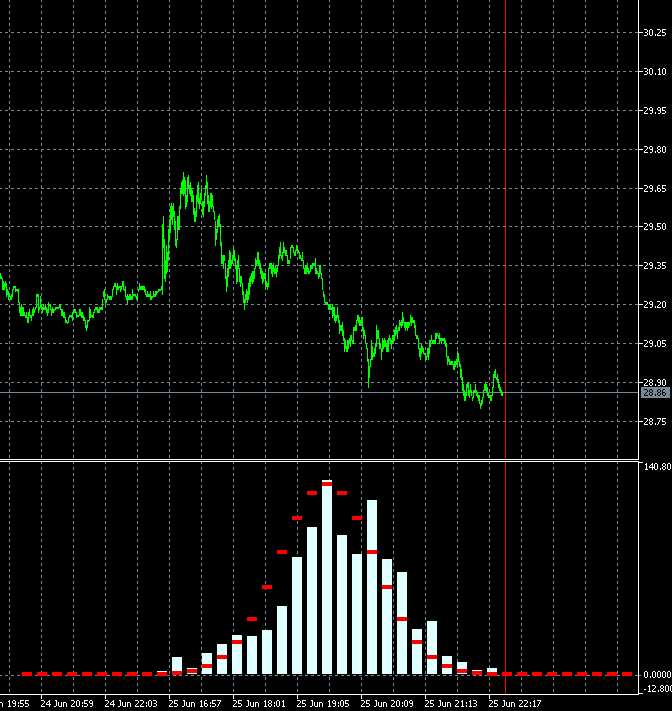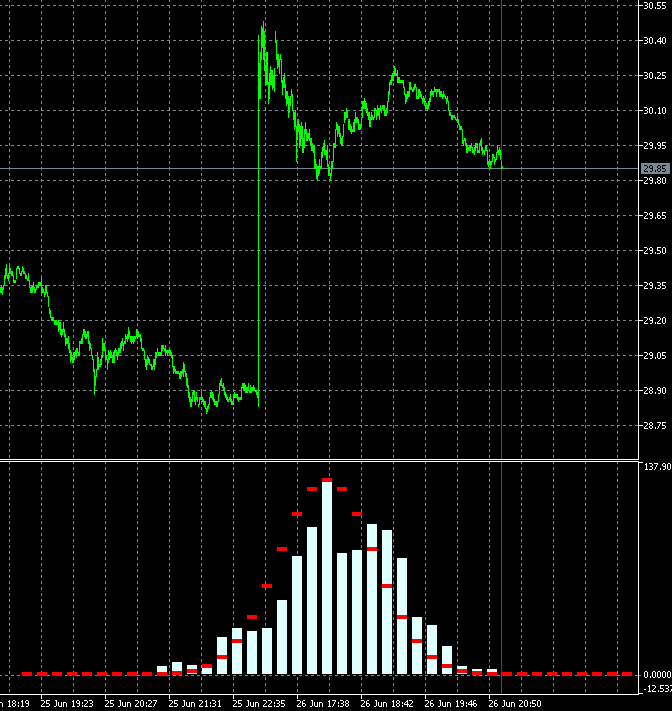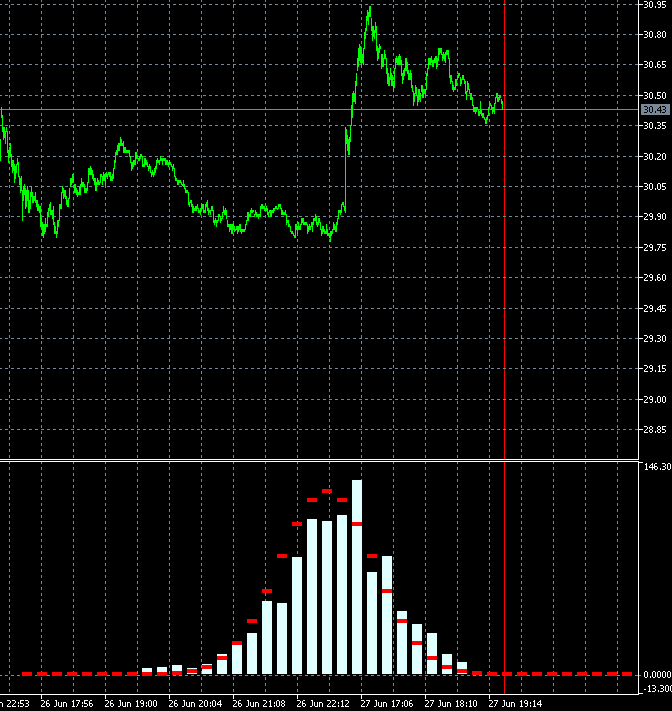
A diferencia del GBPUSD, la distribución de la densidad de la probabilidad del incremento de las acciones de AMD no resulta simétrica respecto a cero. Podemos ver un claro componente de tendencia alcista. Esto implica que la probabilidad de que la tendencia continúe es ligeramente superior cuando un salto ascendente es seguido por otro ascendente, en comparación con el caso cuando un salto descendente sigue a otro. Esto indica que es más razonable abrir transacciones de compra en dicho instrumento. En este caso, podemos mantener la rentabilidad incluso entrando en el mercado en puntos aleatorios. 

¿La estructura del mercado es de tendencia o plana?

Considerando todo lo mencionado, podemos preguntarnos si los mercados son predominantemente de tendencia, planos o aleatorios. Dando respuesta a esta pregunta, podremos definir qué estrategia aplicar y qué tipo de análisis seguir desarrollando. Hemos analizado más de 30 parejas de divisas, más de 50 acciones de los mercados ruso y estadounidense, y también de los mercados de criptomonedas y materias primas. Los mercados de productos básicos incluían metales, energía y alimentos. Una vez finalizada la investigación, podemos concluir que:

• La mayoría de las parejas de divisas desarrolladas tienen una tendencia débil que disminuye conforme aumenta la escala y el volumen de las transacciones. Por ejemplo, EURUSD demuestra menos nivel de tendencia que GBPUSD. La densidad de la distribución de la probabilidad en fórex se encuentra próxima a la distribución normal.
• El mercado de valores muestra un mayor nivel de tendencia que las divisas, pero la tendencia se sigue reduciendo conforme aumenta la escala. Los activos que se desarrollan de forma más activa muestran mayor nivel de tendencia que los activos de empresas desarrolladas. Cuanto menos tienda una empresa al desarrollo y menos potencial posea, menor tendencia mostrarán sus acciones. Los activos en absoluto "interesantes" pueden mostrar un movimiento plano. Cuanto mayor sea la liquidez del instrumento, menor será el grado de tendencia. El análisis de la distribución de las tendencias utilizando la escala como medida nos permite comprender la estructura de los flujos de capital. Por ejemplo, podemos ver que, a escalas pequeñas, una acción demuestra tedencia, mientras que a escalas mayores se muestra plana. Esto indica que la empresa no se está desarrollando, mientras que el dinero se invierte solo con perspectivas a corto plazo. Dicho de otra manera, las formas de distribución muestran si un instrumento se usa para invertir o para especular. Así, el gráfico permite valorar la calificación crediticia de una empresa, aunque sea de forma indirecta.
• El mercado de materias primas tiene instrumentos tanto de tendencia como planos, dependiendo de la actual demanda de materias primas y el nivel de producción. Si la demanda aumenta mientras que la producción no cambia, el instrumento adquiere mayor nivel de tendencia. De forma semejante, si la demanda baja, el grado de tendencia también aumentará siempre que el nivel de producción permanezca sin cambios. Si la oferta y la demanda de productos básicos se encuentra próxima al equilibrio, su movimiento se volverá más plano.
• Las criptomonedas muestran una mayor tendencia en la etapa cuando aumentan tanto interés por las mismas como su circulación. El mercado se vuelve más plano cuando disminuye el interés público. Como resultado, el precio de toda su historia tiende al paseo aleatorio. Pero, en cuanto comienza una nueva ola, el instrumento vuelve a mostrar un buen nivel de tendencia. 

Aquí, podemos sacar conclusiones más amplias, pero este tema ya da para otro artículo.

Más abajo, vemos algunos gráficos que describen las características de los instrumentos comerciales.

• Como ya hemos mencionado antes, en algunas escalas, BTCUSD se vuelve plano cuando disminuye el entusiasmo por las criptomonedas. Curiosamente, la distribución de la densidad de la probabilidad para las criptomonedas es simétrica respecto al cero, a pesar de que visualmente parece que las criptomonedas presentan una tendencia alcista. 
• Las acciones de AMD y AAPL muestran una tendencia constante con algunas caídas poco significativas. La distribución de la densidad de la probabilidad se desplaza hacia la derecha respecto al cero en la dirección de los movimientos ascendentes. Además, resulta visualmente obvio que estas acciones tienen una tendencia ascendente constante. 
• Asimismo, el petróleo tiene una tendencia general, incluso si aumentamos la escala.
• En EURUSD, la tendencia prácticamente se disipa a gran escala. El instrumento se vuelve plano en algunas escalas, pero, en general, tiende a la distribución de la densidad de la probabilidad del paseo aleatorio más que otros.
  
• Los líderes del mercado ruso se asemejan entre sí, mostrando tendencias estables a pequeña escala y prácticamente ninguna tendencia a gran escala.

En el próximo artículo, trataremos de explicar por qué un instrumento muestra mayor nivel de tendencia en una escala menor, y un carácter más plano en una escala mayor. Asimismo, desarrollaremos un algoritmo basado en la investigación actual, y también comprobaremos si es rentable.

Conclusión

Los conceptos de tendencia y mercado plano se pueden definir de forma clara y completa. También podemos comparar el nivel de tendencia de diferentes instrumentos, así como el de un solo instrumento en diferentes escalas. Este tipo de análisis nos permite valorar las características y peculiaridades de los instrumentos y construir algoritmos comerciales tendiendo en cuenta el comportamiento individual de cada instrumento.

Partiendo de las características estadísticas de un instrumento y su cambio a lo largo del tiempo, tendremos la posibilidad de descartar diferentes parámetros de optimización al desarrollar un algoritmo comercial. En lugar de ello, podremos realizar mediciones y modificar a voluntad los parámetros del algoritmo comercial en función de las características estadísticas del instrumento negociado.

A continuación, mostramos varios archivos que contienen gráficos con una probabilidad de viraje del 20%, el 50% y el 80%. Además, incluimos un archivo de Excel para construir la distribución de referencia, y también el indicador que ha construido los bloques utilizados para el análisis.

Autor del algoritmo del indicador: Maxim Romanov. Autor del código del indicador: Konstantin Gruzdev.