Combinatoria y teoría de la probabilidad en el trading (Parte IV): Lógica de Bernoulli
Evgeniy Ilin | 8 diciembre, 2021
Contenido
- Introducción
- ¿Por qué una presentación correcta de los datos es tan importante para el análisis?
- Estados dobles
- Estados múltiples
- Implementación programática de los estados múltiples
- Conclusión
- Enlaces
Introducción
En los artículos anteriores de esta serie, describimos los fractales como una herramienta útil para describir el mercado y, concretamente, los precios. Este modelo describe perfectamente el mercado, lo cual hemos confirmado con cálculos y simulaciones. Todo esto se inició no solo para describir las formas más simples de fijación de precios, sino también para poder describir con mayor detalle cualquier serie de vectores que tenga un conjunto de parámetros similar a la fijación de precios. Y es que, si pensamos en lo que representa una transacción en general, entenderemos que supone un trozo de mercado con una duración temporal y una cierta probabilidad de suceder en el proceso comercial. Tanto el precio como las transacciones se pueden usar para crear curvas arbitrarias, que, en el caso del precio, se denominan historia de precios y, en el caso de las transacciones, se conocen como historia de transacciones.
En el caso del precio, todo está mucho más claro, porque todos los miembros de dicha serie siempre se ubican claramente y uno tras otro. Claro que dichas series se pueden componer partiendo de los precios que se superpondrán unos a otros, pero dicho análisis resultará totalmente inútil para nosotros, ya que no nos reportará ningún beneficio práctico. En el caso de los backtests o la historia comercial, las cosas cambian un poco. Estudiando estos procesos, hemos llegado a la conclusión inequívoca de que, a la hora de lograr un comercio rentable y estable, se ha conseguido trazar un camino mucho más fácil y correcto al respecto usando precisamente el análisis de la historia comercial o los backtests. Dedicaremos el artículo final a la descripción de uno de estos enfoques, pero, por ahora, es demasiado pronto para hablar de ello.
¿Por qué una presentación correcta de los datos es tan importante para el análisis?
Si profundizamos en un análisis superficial de las posibilidades de describir la historia comercial y los backtests en el lenguaje de las matemáticas, en primer lugar, deberemos entender por qué necesitamos tal análisis y qué nos ofrecerá al final. ¿Hay algún valor añadido en semejante análisis? En realidad, aunque resulte imposible dar una respuesta clara de entrada, sí que existe dicha respuesta, y esta nos conducirá paulatinamente al hallazgo de soluciones simples y funcionales. No obstante, primero tendremos que meternos en las zarzas. Considerando la experiencia de los artículos anteriores, nos interesan de inmediato las siguientes preguntas:
- ¿Podemos reducir cualquier estrategia a una descripción fractal del comercio?
- Y si dicha reducción es posible, ¿para qué sirve?
- Si la reducción no siempre es posible, ¿cuáles son las condiciones para que esta resulte?
- Si se cumplen las condiciones de reducción, se dará el desarrollo de un algoritmo de reducción
- Estudio de otras opciones para describir la estrategia y realizar la generalización
Responderemos de inmediato a todas estas preguntas. Resulta posible reducir algunas estrategias a una descripción fractal: ya hemos desarrollado este algoritmo, que describiremos más adelante. Nos será útil en general, no solo para estos fines (porque es universal). No obstante, esto no es lo principal. Ahora, vamos a pensar un poco para intentar responder a la pregunta: ¿qué es la historia comercial en el lenguaje de los números aleatorios y la teoría de probabilidad? La respuesta es simple: se trata de un conjunto de entidades o vectores aislados, cuya aparición en un determinado periodo temporal tiene una cierta probabilidad y coeficiente de uso del tiempo. La característica principal de cada una de estas entidades es la probabilidad de su aparición. La tasa de utilización del tiempo supone simplemente una medida auxiliar que ayuda a determinar cuánto tiempo disponible se utiliza para comerciar. Para comprender mejor de qué estamos hablando, podemos dibujar una ilustración:
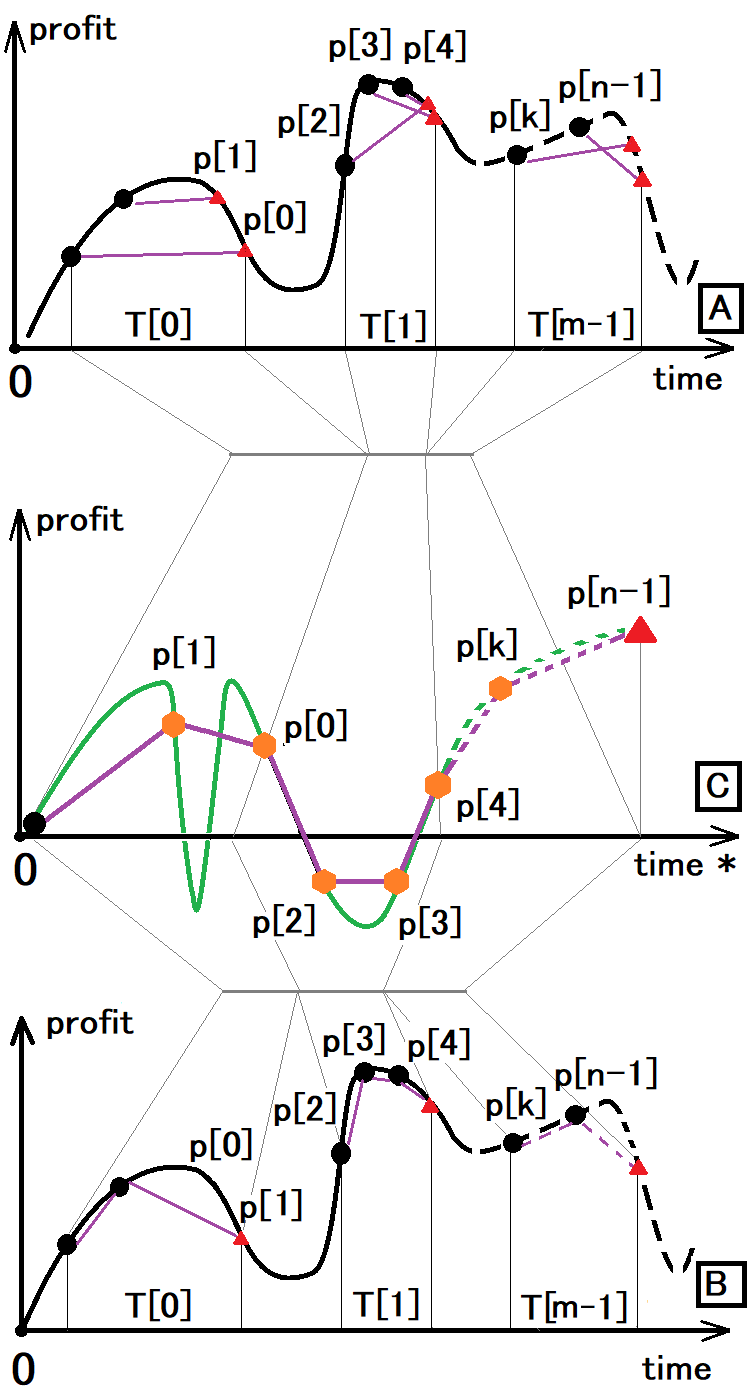
La figura tiene las siguientes designaciones:
- Punto negro: inicio del comercio
- Triángulo rojo: final de la próxima transacción
- Hexágono naranja: simultáneamente el final de la transacción anterior y el inicio de la siguiente
- T[i] - hora de la sigiente ventana comercial
- P[i] - beneficio o pérdidas de la próxima transacción
- n - número de transacciones
- m - número de ventanas comerciales
La figura representa específicamente 3 gráficos para mostrar que las opciones "A" y "B" se pueden reducir a la opción "C". Vamos a averiguar cuáles son estas opciones:
- La opción "A" es cómo vemos el comercio aleatorio usando todas las técnicas posibles, la administración de dinero y otros trucos.
- La opción “B” es la misma, pero considerando que solo se puede abrir 1 orden a la vez en la cuenta correspondiente.
- La opción "C" es cómo vemos el comercio, ya sea en el servicio de señales o en el backtest.
Debemos señalar que la opción "C" es lo más informativa posible y, en la mayoría de los casos, confiamos en esta misma representación para comerciar; además, resulta interesante que absolutamente cualquier estrategia se puede reducir a este tipo, y todo porque la característica principal de cualquier backtest o señal comercial es la línea de equidad. Esta línea muestra el beneficio o las pérdidas reales en el momento actual.
Si analizamos la línea de equidad de una estrategia aleatoria, resultará que los puntos de apertura y cierre de las transacciones siguientes pueden colocarse de forma absolutamente arbitraria si la línea de equidad permanece sin cambios. Esto nos indica que podemos representar una estrategia comercial en particular de muchas formas distintas, y todos estos métodos serán equivalentes entre sí, ya que sus líneas de equidad serán equivalentes. En este caso, no tiene sentido buscar todas las opciones equivalentes y, lo más importante, ¿para qué buscarlas?
Si tomamos una estrategia de tipo "B", su transformación en el tipo "C" será una operación extremadamente simple, en el sentido de que solo necesitaremos unir en uno solo los intervalos temporales en el orden en que estén ubicados: el simulador y el servicio de señales, respectivamente, se encargan precisamente de ello. Otra cosa distinta es si estamos tratando de convertir el tipo "A" en el tipo "C": aquí todo resulta completamente diferente. Para realizar dichas conversiones, primero deberemos reducir el tipo "A" al tipo "B", y después de ello, realizar la conversión al tipo "C". Ahora sabemos cómo funciona el simulador de estrategias y el servicio de señales.
En sí misma, esta transformación no tiene ningún valor práctico para el comercio, pero puede desarrollar la comprensión de cosas más profundas; por ejemplo, nos puede ayudar a concluir que existen los siguientes tipos de estrategias:
- Descritas por dos estados
- Descritas por varios estados
- Descritas por un número infinito de estados
En este artículo, mostraremos ejemplos de los dos primeros tipos de estrategias. El tercer tipo de estrategia es más complejo, así que la analizaremos aparte en otro artículo. Realizaremos estas consideraciones a su debido tiempo, pero por ahora, para entender el tercer tipo de estrategia, deberemos aclararnos con los dos primeros. Estos dos tipos ayudarán a nuestra mente a madurar para llegar al tercer y último tipo de estrategia general.
Estados dobles
Los fractales descritos en artículos anteriores no son más que un modelo de dos estados. En este caso, los estados son el movimiento descendente y el movimiento ascendente. Si aplicamos el modelo a la línea de balance comercial, y no a la formación de precios, este modelo funcionará exactamente igual. El modelo se basa en el esquema de Bernoulli. El esquema de Bernoulli describe el fractal más simple con dos estados:
- P[k] = C(n,k)*Pow(p,k)*Pow(q,n-k) — fórmula de Bernoulli ( P[k] – probabilidad de que se dé una combinación específica )
- p - probabilidad de ocurrencia del estado “1” como resultado de una única experiencia
- q - probabilidad de ocurrencia del estado “2” como resultado de una única experiencia
Estas fórmulas son capaces de calcular la probabilidad de que después de “n” saltos, obtengamos una curva de balance o cualquier otra curva en la que haya “k” primeros estados y “nk” segundos estados; no tiene que tratarse necesariamente de los beneficios de las transacciones. Estos estados pueden simbolizar cualquier vector de parámetros en el que veamos unicidad. Lo más interesante es que la suma de todas esas probabilidades de una combinación particular deberá formar un grupo completo, lo cual implica que la suma de todas esas probabilidades deberá ser igual a uno. Dicho hecho simboliza que una de estas combinaciones tendrá que aparecer después de “n”saltos:
- Summ(0...k…n)[ P[k] ] = 1
En este caso, nos interesa utilizar estas cosas para describir los precios o los backtests y las señales. Imaginemos que nuestra estrategia consta de transacciones que se cierran en stops equidistantes, pero, al mismo tiempo, sabemos que resulta imposible calcular el movimiento de precios esperado en el futuro, entonces la distribución de estas probabilidades tendrá el aspecto que sigue:
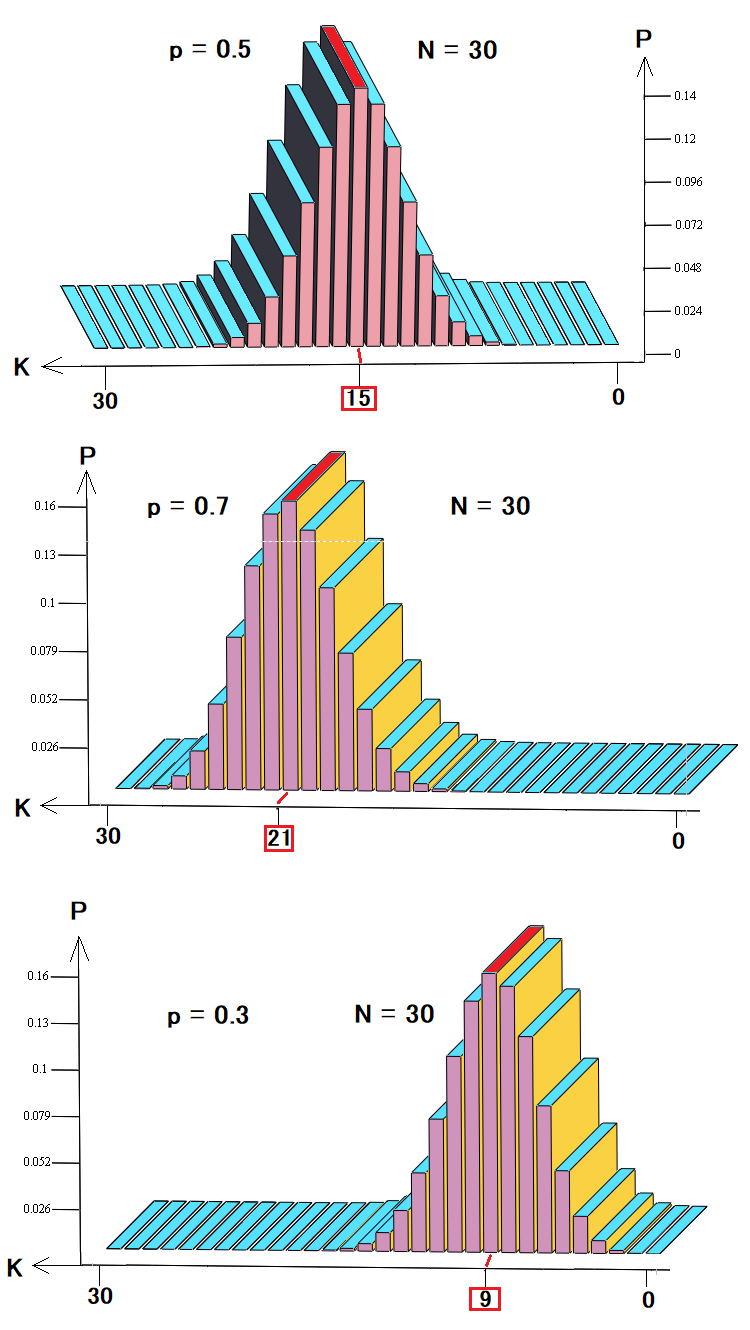
En estas tres figuras se muestran:
- La distribución de probabilidad para paseos o comercio aleatorios
- La distribución de probabilidad para un comercio rentable o una tendencia alcista
- La distribución de probabilidad para una transacción perdedora o una tendencia bajista
Como podemos ver en estos diagramas, dependiendo de la probabilidad de que se dé un salto hacia arriba, las probabilidades de ciertas combinaciones cambian, y el caso más probable se desplaza hacia la izquierda o hacia la derecha, al igual que el resto de probabilidades. Este modelo de presentación de backtest o formación de precios es el más sencillo y preferible para el análisis. Si bien un modelo de este tipo puede bastar para describir los precios, a la hora de describir el comercio, obviamente, resulta insuficiente. En la práctica, nos encontramos con que la curva de balance puede contener una amplísima variedad de transacciones, tanto en términos de duración como de beneficio. Dependiendo de qué indicadores comerciales sean más importantes para nosotros, podemos seleccionar no dos, sino tantos estados como necesitemos.
Estados múltiples
Analicemos ahora un ejemplo ilustrativo. Imaginemos que, como antes, solo nos importa el tamaño del beneficio o las pérdidas de la próxima transacción, pero sabemos que estos pueden adoptar estrictamente tres valores fijos, y conocemos las probabilidades de ocurrencia de cada uno de esos valores. Si todo es así, podemos decir que tenemos un sistema con tres estados. Ahora, intentemos preguntarnos: ¿resulta posible describir todos los desarrollos posibles de los eventos como un sistema con dos estados? En realidad, sí que es posible. Vamos a modificar ligeramente el esquema de Bernoulli para que pueda funcionar con un sistema con tantos estados como necesitemos.
Si seguimos la lógica de Bernoulli, deberemos definir los contadores de estado:
- i[0] – número de ocurrencias de los primeros estados en la cadena de pruebas independientes
- i[1] – número de ocurrencias de los segundos estados en la cadena de estados independientes
- i[N] – número de ocurrencias de estados N
- N – número de estados del sistema
- s – número de estado
Si determinamos a su vez el número de ocurrencias de un cierto estado, entonces el número disponible para el siguiente estado será:
- s[i] = N - Summ(0… k … i - 1) [ s[k] ]
Podemos decirlo de forma más simple. Si hemos seleccionado el número de resultados del estado anterior, entonces para el siguiente estado quedará un número de resultados que será menor en una cantidad exactamente igual a los estados seleccionados para el estado anterior. Al igual que sucede en el esquema de Bernoulli, hay cadenas de probabilidad que son inconsistentes y tienen la misma probabilidad. El número de cadenas con un mismo número de todos los estados se calcula de la forma que sigue:
- A[h](N,i[0] ,i[1] ,… i[n]) = C(N , i[0]) * C(N-i[0] , i[1]) *…. C(N-Summ(0…k…n-1)[ i[k] ] , i[n])
- С - combinaciones
- h – siguiente conjunto único de saltos
Así, queda claro que las probabilidades de tales conjuntos se pueden calcular de la misma forma que en el esquema de Bernoulli. Multiplicamos la probabilidad de uno de esos conjuntos por su número:
- P[k] = A[h](N,i[0] ,i[1] ,… i[n]) * Pow(p[0], i[0]) * Pow(p[1], i[1]) … * Pow(1- Summ(0…j…N-1)[ p[j] ] , i[1])
- p[j] - probabilidad de ocurrencia de un estado determinado
Para que todo quede más claro, hemos creado varios gráficos en 3D, como en el ejemplo anterior para los dos estados. De la misma forma, tenemos 30 saltos, pero tomamos ya tres estados en lugar de dos:
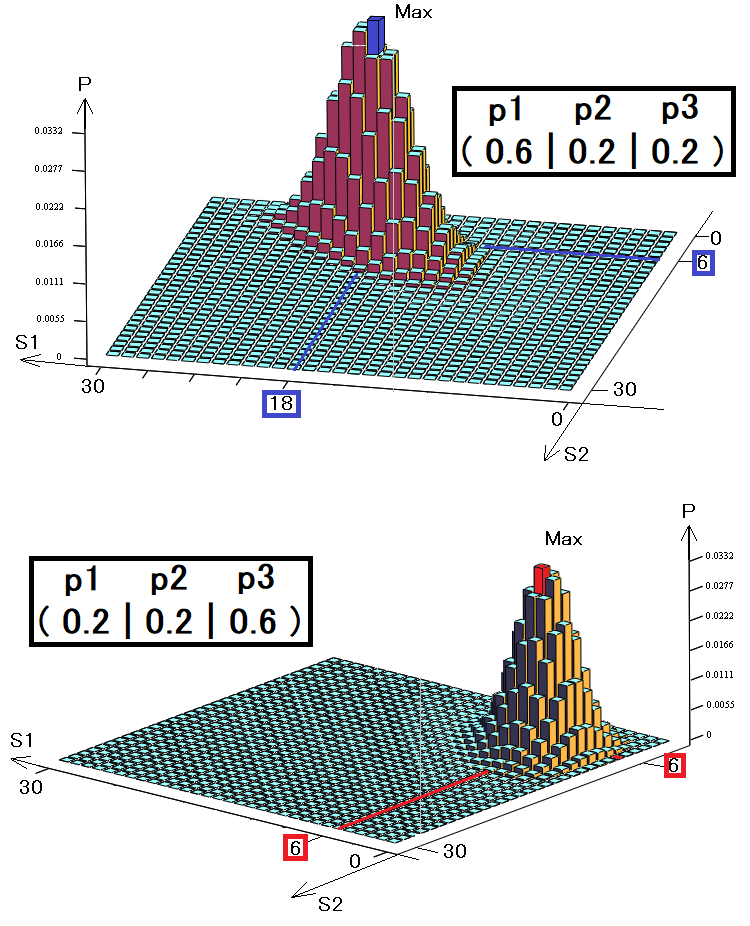
Obviamente, el volumen de este gráfico será exactamente igual a uno, ya que cada barra simboliza un evento inconsistente, y todos estos eventos inconsistentes precisamente forman un grupo completo. Los gráficos muestran dos estrategias distintas con diferentes vectores de probabilidad. Estas probabilidades simbolizan la posibilidad de obtener uno de los tres estados.
- S1 - número de primeros estados descartados
- S2 – número de segundos estados descartados
- S3 = 30 - S1 - S2 - número de terceros estados descartados
Si de repente hay un cuarto estado en nuestro sistema, resultará posible representarlo solo en cuatro dimensiones; si hay cinco estados, el gráfico será de cinco dimensiones, y así sucesivamente. El ojo humano solo puede captar 3 dimensiones, por lo que los sistemas más complejos no se pueden representar gráficamente. No obstante, debemos comprender que las funciones multidimensionales son igual de funcionales que las otras.
Implementación programática de los estados múltiples
Está claro que podemos representar los estados dobles como una matriz de datos unidimensional, pero ¿y si hay más estados? Solo podríamos pensar en una matriz multidimensional. Pero, hasta donde sabemos, todos los lenguajes de programación usan como máximo matrices dobles. Podríamos tener la oportunidad en algún lugar de crear matrices 3D y matrices multidimensionales, pero esto no supondría ni mucho menos la opción más cómoda. Para estos fines, resulta mejor usar colecciones o tuplas:
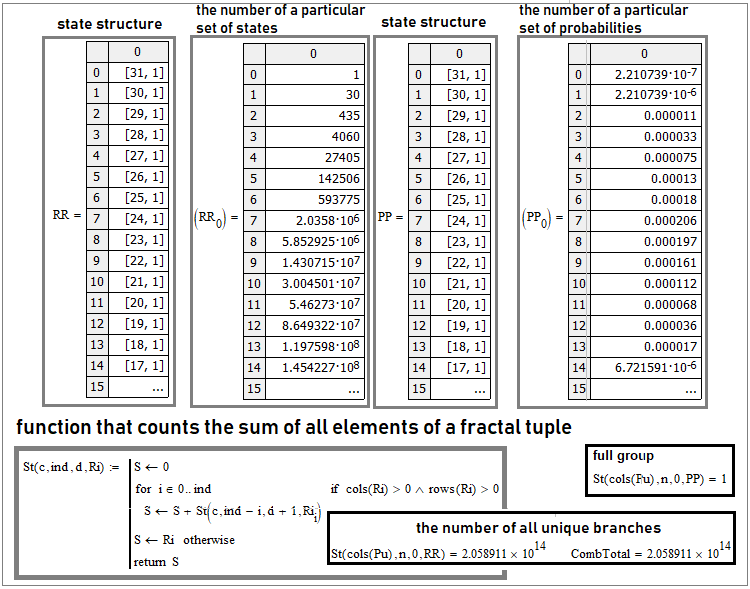
Aquí tenemos precisamente la situación con “30” saltos. Las columnas primera y tercera reflejan la estructura interna de la tupla. Podemos ver que se trata solo de una matriz dentro de otra. Donde está escrito, por ejemplo, “[31,1]”, significa que este elemento de la matriz también es una matriz con “31” filas y una columna. Precisamente la propia fórmula de Bernoulli y todo el esquema de Bernoulli son un caso especial de este esquema más general. Si necesitamos dos estados, las tuplas se convertirán en matrices unidimensionales y obtendremos combinaciones simples que jugarán el papel principal en la fórmula de Bernoulli.
Si miramos lo que hay dentro de estas matrices, obtendremos las columnas “2” y “4”. La segunda columna es el número de ramas equivalentes de conjuntos de estados únicos específicos, y la cuarta es la probabilidad total de que se den tales ramas, porque sus probabilidades son iguales.
Un criterio muy claro a la hora de comprobar la exactitud del cálculo de dichas tuplas es verificar el grupo completo de eventos y el número total de todas las ramas únicas. Para ello, podemos construir una función general que sume todos los elementos de estas tuplas complejas, independientemente de la complejidad de su estructura interna. En la captura de pantalla de arriba se ve un ejemplo. Esta función debe ser necesariamente recurrente y llamarse a sí misma por dentro, entonces resultará universal para cualquier número de estados y saltos. En cuanto al número de ramas únicas, el valor real se calcula de la forma siguiente:
- Pow(N,n)
En otras palabras, el número de estados del sistema debe elevarse a la potencia del número de saltos, y así obtendremos todas las combinaciones posibles de cadenas únicas que constan de nuestros estados. En la imagen, este número actúa como variable “CombTotal”; precisamente con ella compararemos lo que hemos obtenido al realizar la suma.
Para contar las propias tuplas, deberemos utilizar funciones similares con la misma estructura recurrente:

Podemos ver que todo sucede de forma similar. Solo hay un par de diferencias. En cada nivel, deberemos multiplicar por el número de combinaciones para los saltos libres restantes. Una vez calculadas las probabilidades, multiplicaremos por la probabilidad del estado que ahora estamos ganando, obviamente, sin olvidar multiplicar por la probabilidad ya recolectada de la cadena. Simplemente recopilamos uno por uno todos los estados hasta que no haya celdas libres: las celdas representan el número de nuestros saltos.
También podemos crear un ejemplo de extracción de estados partiendo de los datos que conocemos. Por ejemplo, sabemos que tenemos estadísticas comerciales, y en estas estadísticas, cada orden contiene información sobre su duración, su volumen de transacciones y otros indicadores, tales como la magnitud de las pérdidas o el beneficio. Como la muestra es finita, el número de estados también será finito. Podemos, por ejemplo, determinar cuántas opciones de beneficio hay en esta muestra, y cada valor único de beneficio se considerará un estado único. Calculamos el número de ocurrencias de todos esos beneficios en toda la muestra y lo dividimos por el número total de transacciones para obtener la probabilidad de que se dé un estado específico. Y hacemos esto para todos los estados. Si luego sumamos todas estas probabilidades, obtendremos la unidad. Si es así, todo se habrá hecho correctamente. Lo mismo se puede hacer, por ejemplo, con la hora, para hacer una clasificación según el tiempo de vida de una orden. En otras palabras, un estado puede ser cualquier característica única de un evento. En este caso, una transacción se considerará un evento y sus parámetros serán solo las características de un evento en particular. Los ejemplos de los estados en nuestro caso podrían ser así:
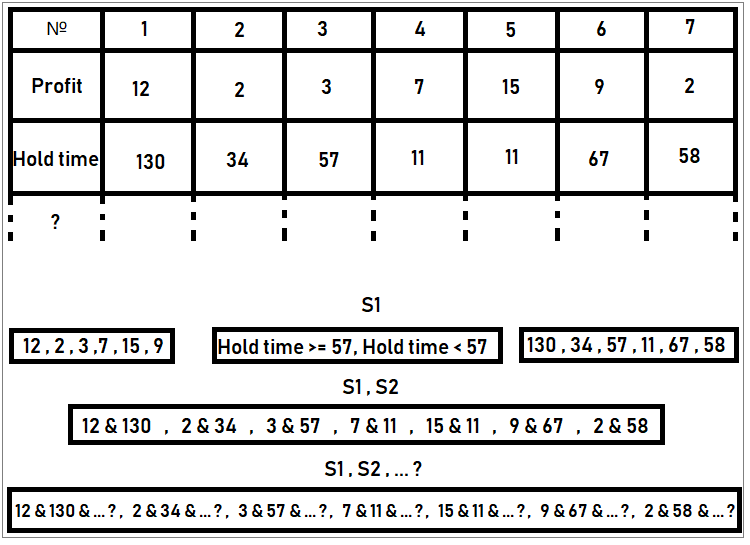
La figura muestra un ejemplo de composición de conjuntos de estados. Según las reglas, los estados deben formar un grupo completo de eventos: en otras palabras, allí no debemos encontrar estados conjuntos. Podemos calcular la probabilidad de estos eventos simplemente dividiendo el número de órdenes en el recuadro con estados específicos por el número total de órdenes; en nuestro caso, este número es “7”. Este es un ejemplo con uso de órdenes, pero se puede emplear cualquier cosa.
Conclusión
En este artículo, hemos intentado mostrar cómo se pueden evaluar muestras de datos; asimismo, hemos mostrado cómo crear nuevas muestras a partir de aquellas, clasificando los datos y combinándolos en conjuntos de estados cuyas probabilidades se pueden calcular. Qué hacer con estos datos depende de usted. A nuestro juicio, el mejor uso es la extracción de muestras y su valoración; esto también se conoce como clusterización de la muestra. La ventaja es que la clusterización de una muestra puede ejercer como un filtro excelente para mejorar el rendimiento comercial de los sistemas existentes, así como para lograr que una estrategia ya existente y en apariencia no rentable comercie de forma rentable; todo lo que necesitamos hacer es clusterizar y encontrar la muestras rentables que todos deseamos. Y lo más importante, estos mecanismos pueden ser una de las etapas del procesamiento de datos en sistemas comerciales escalables. Aplicaremos estos mecanismos en la práctica cuando procedamos a componer un sistema comercial autoadaptable: por ahora, todo esto es solo un ladrillo más.
Enlaces
- Combinatoria y teoría de la probabilidad en el trading (Parte I): Fundamentos
- Combinatoria y teoría de la probabilidad en el trading (Parte II): Fractal universal
- Combinatoria y teoría de la probabilidad en el trading (Parte III): Primer modelo matemático