Risikobewertung durch die Abfolge von Positionen von Finanzanlagen. Fortsetzung
Aleksey Nikolayev | 5 Februar, 2018
Inhaltsverzeichnis
- Vorwort
- Annahmen über Preise und Handelssystems
- Ertragsverteilung. Allgemeine Bemerkungen
- Was kommt als Nächstes?
- Statistiken und Kurslücken
- Statistisches, maschinelles Lernen
- Statistik und Optimierung des Handelssystems
- Anlagen
Vorwort
Fahren wir fort, die Theorie der Risikoeinschätzung zu untersuchen, die im vorhergehenden Artikel begonnen wurde. Sie wird an zwei Beispielen zu einem logischen Abschluss gebracht. Auch andere Anwendungsmöglichkeiten der Wahrscheinlichkeitstheorie und der mathematischen Statistik werden kurz skizziert.
Annahmen über Preise und Handelssystems
Können die Methoden, die im vorhergehenden Artikel betrachtet wurden, für die Analyse der Handelsergebnisse irgendeines Systems verwendet werden? Dazu müssen wir sicher sein, dass die Reihenfolge ihrer Positionen (Deals) eine Folge unabhängiger und identisch verteilter Variablen ist. Leider zeigt jedoch die Praxis, dass dies nicht immer der Fall ist.
Beide Bedingungen können verletzt werden: die Unabhängigkeit und die identische Verteilung. Im Buch "The Mathematics of Money Management" skizziert Ralph Vince Wege zur Lösung dieser Probleme. Er schlägt vor, die Systeme in mehrere Teile (Subsysteme) aufzuteilen, die die geforderten Bedingungen erfüllen. Vince gibt zwei Beispiele. Die erste behandelt ein System mit Abhängigkeiten zwischen den nachfolgenden Positionen. In diesem Fall ist die Sequenz in zwei Teile aufgeteilt. Positionen mit geraden und ungeraden Zahlen werden so behandelt, als wären sie von verschiedenen Systemen. Das zweite Beispiel betrachtet ein "pyramidisierendes" System - das Positionsvolumen wird schrittweise erhöht. Jeder Schritt einer solchen Erhöhung wird als eigenes System betrachtet. Daraus ergibt sich eine Sammlung von mehreren Systemen: Das erste System besteht aus den ersten Schritten, das zweite System enthält die zweiten Schritte und so weiter.
Sobald solche Systemteile untersucht sind, ist es notwendig, einen Weg zu finden, sie wieder zusammenzusetzen, um ein "Mikroportfolio" zu erstellen, das die Abhängigkeiten zwischen ihnen berücksichtigt. Dies erfordert etwas Ähnliches wie die Modern Portfolio Theory von Markowitz.
Das sieht schon recht kompliziert aus, aber es bleibt noch viel mehr zu tun. Betrachten wir ein System, das jede Position zu einem der vorgegebenen Preisniveaus verlässt: pstoploss oder ptakeprofit. Das Verhältnis k=|ptakeprofit-penter|/|pstoploss-penter| variiert von Position zu Position, abhängig vom jeweiligen Indikator. Die Ertragsverteilung jeder Position wird sehr einfach sein - eine diskrete Verteilung mit zwei Werten -1 und k, akzeptiert mit bestimmten Wahrscheinlichkeiten. Aber da der Wert von k für jede Position spezifisch ist, haben verschiedene Positionen auch unterschiedliche Verteilungen. Wenn man also versucht, das System in "Teile" zu zerlegen, wird ihre Anzahl gleich der Anzahl der Positionen sein, was offensichtlich bedeutungslos ist. In der Praxis ist es sehr wahrscheinlich, dass der verwendete Wert von k für alle Positionen gleich ist (einige Durchschnittswerte, charakteristische Werte). Dies ermöglicht die Durchführung der Analyse mit einer vereinfachten Version des Systems, das im realen Handel verwendet wird.
Fassen wir alle möglichen Optionen für die Anwendung der Risikotheorie für reale Handelssysteme zusammen:
- Aufteilen des Handelssystems in mehrere Teile.
- Untersuchen eines vereinfachten Modells des Systems.
- Analysieren der Reihenfolge der Positionen, ohne sie auf Unabhängigkeit und Eindeutigkeit der Verteilung zu überprüfen. Gleichzeitig ist es möglich, den ermittelten Risikowert mit anderen Analysemethoden geringfügig anzupassen.
Diese Art, System zu untersuchen, ist offensichtlich nicht universell und nicht immer anwendbar. Versuchen wir, die Methode systematischer zu gestalten. Dies erfordert mehrere Annahmen über die Preise und Systeme.
- Ein Abfolge von Preisen ist dem Random Walk sehr ähnlich. Wir werden nicht versuchen, die Definition dieser Ähnlichkeit mathematisch zu formulieren, sondern nur davon ausgehen, dass, wenn bestimmte Berechnungen auf einem Zufallsweg und auf realen Preisen durchgeführt werden, die Ergebnisse der ersteren als die Nullannäherung der Ergebnisse der letzteren betrachtet werden können. So werden zum Beispiel die Annahmen über die Verteilung von Zufallsvariablen aus einer Preisreihe getroffen.
- Das System kann mit den die Kurse, die durch einen Random Walk generiert werden, gefüttert werden. In diesem Fall müssen die Zufallspreise "im Durchschnitt" nahe an den realen Preisen liegen. Dies führt zu einer ähnlichen Volatilität in den größeren Zeiträumen, eine ähnliche Verteilung der Preisspitzen der Ticks etc.
- Die Strukturen der Abhängigkeit zwischen den Positionen des Systems (reale Preise und der Random Walk) sind in beiden Fällen eng, während die Ertragsverteilungen sehr unterschiedlich sein können. Wenn z.B. alle Erträge um den gleichen Faktor steigen, ändern sich die Verteilungen (nach rechts verschoben). Die Korrelationskoeffizienten zwischen den Renditen bleiben jedoch unverändert.
- Das System ist so aufgebaut, dass dessen Verteilung der Positionen mit der eines Random Walk identisch ist und nur dann signifikant voneinander abhängig sein können, wenn sie sich zeitlich stark überlappen (die zweite wird geöffnet, bevor die erste geschlossen wird).
Erläutern wir diese Annahmen. Ein Random Walk ist eine umfangreiche Klasse von Zufallsprozessen. Diese können diskret oder kontinuierlich sein. Beide Herangehensweisen werden in analytischen Berechnungen verwendet, während die Modellierung am Computer nur die erste verwendet. Sie sind überdies miteinander verknüpft - ein Random Walk mit kontinuierlicher Zeit kann durch den mit diskreter Zeit einfach mit einer Grenzwertbildung beliebig genau angenähert werden, in dem man die Schrittweite der Zeit gegen Null laufen lässt. Außerdem kann der Random Walk entweder symmetrisch (kein Trend, flach) oder positiv/negativ (aufwärts/abwärts) sein. Am häufigsten wird der symmetrische Random Walk betrachtet. In diesem Fall führt die Annahme über die Preise zu folgendem:
- Die Handelsergebnisse können durch keine Indikatoren vorhergesagt werden. Dies vereinfacht die Modellierung erheblich. Es stellt sich heraus, dass es notwendig ist, nur den Teil des Systems zu studieren, der für das Schließen der Positionen verantwortlich ist. Wo und wie die Position eröffnet wurde, ist völlig unerheblich.
- Der durchschnittliche Gewinn ist Null. Dies schließt nicht aus, dass eine einzelne Position nicht doch irgendeinen Gewinn abwirft. Aber je mehr Positionen eröffnet werden, desto mehr entspricht die Summe ihrer Ergebnisse einer bestimmten Wahrscheinlichkeitsverteilung. Die spezifische Form dieser Verteilung hängt von dem Algorithmus ab, mit dem die Positionen geschlossen werde, aber der Erwartungswert ist immer Null.
Diese Konsequenzen müssen bei den Tests (und insbesondere bei der Optimierung) realer Systeme mit realen Preisen berücksichtigt werden. Es besteht Bedarf an Kriterien, die zeigen, dass die Ergebnisse nicht für einen symmetrischen Random Walk mit ausreichender Zuverlässigkeit erzielt werden. Dies gilt sowohl für die Ertragsverteilung der Positionen als auch für den Nutzwert der technischen Indikatoren. Darüber hinaus kann die Suche nach Abweichungen von einem symmetrischen Random Walk auch bei der Suche nach Ideen für Handelssysteme hilfreich sein. Als ein Beispiel betrachten wir später die Möglichkeit, die Behauptung zu nutzen, dass sich "Lücken immer schließen".
Die oben genannten Annahmen schränken die Handelssysteme ein. Im Allgemeinen erfordern sie Einfachheit, Einheitlichkeit und Transparenz bei den Regeln für den Markteintritt und -austritt. Diese Regeln sollten die Beziehung zwischen den Positionen nicht zusätzlich stärken (z.B. siehe die Kapitalentwicklung), nicht willkürlich die Methoden zum Schließen von Positionen ändern (z.B. zufällige Änderung des Verhältnisses Take-Profit/Stop-Loss), es sollte nicht zu viele Positionen in kurzer Zeit geben etc. Die ungefähre Erfüllung dieser Bedingungen kann entweder theoretisch überprüft oder mit Hilfe der Monte-Carlo-Methode am Computer modelliert werden.
Ertragsverteilung. Allgemeine Bemerkungen
Wir beginnen mit einer Bemerkung über die allgemeine Form der Verteilungen. Wann immer das Konzept der Wahrscheinlichkeitsverteilungsfunktion eingeführt wird, werden in der Regel Diskrete und Kontinuierliche impliziert. Es stellt sich heraus, dass man sie auch kombinieren kann. Das heißt, Verteilungsfunktionen der Form P(x)=γcPc(x)+γdPd(x) sind möglich, wobei γc≥0, γd≥0, γc+γd=1 ist, und Pc(x) und Pd(x) kontinuierliche (mit einer Dichte) und diskrete (schrittweise) Verteilungsfunktionen sind.
Betrachten wir eine einfache Methode Positionen zu schließen als Beispiel - Unveränderliche Stop-Loss und Take-Profit mit einem Verhältnis von k, ergänzt durch eine Begrenzung der Haltezeit von Positionen texit. Vereinfacht ausgedrückt, haben Positionen, die durch Take-Profit/Stop-Loss geschlossen werden, eine diskrete Verteilung, und solche mit einem zeitbedingten Ende eine kontinuierliche Verteilung. Die Gesamtverteilung ergibt sich aus ihrer Kombination. Das erschwert natürlich die weitere Diskussion. Machen wir eine vereinfachte Annahme: Angenommen, dass texit so groß gewählt wurde, dass γc vernachlässigt werden kann. Nehmen wir an P(x)=Pd(x).
Das Schließen einer Position, ausgelöst durch einen unveränderlichen Trailing-Stop, ist eine Beispiel für den Fall γd=0. Es ist auch möglich, dass gleichzeitig gilt γd≠0 und γс≠0. Dies kann z.B. eine Kombination aus beiden betrachteten Beispielen sein. Mit dieser Methode ist der Stop-Loss während der Anfangsphase eine Position unbeweglich, aber sobald eine bestimmte Bedingung erfüllt ist, beginnt er sich ähnlich wie der Trailing-Stop zu bewegen.
Konkretisieren wir die Risikotheorie für beide oben genannten Beispiele (die kombinierte Variante wird nicht berücksichtigt). Nachfolgend werden Skripte zur Berechnung des optimalen Risikowertes ropt für jeden konkreten Fall der Ertragsverteilung bereitgestellt. Aber manchmal sind auch andere Aufgaben von Interesse. Zum Beispiel wird das Risiko festgelegt, und es ist notwendig, δ — das entsprechende Maß an Zuverlässigkeit (oder optional den maximal verfügbaren Wert des durchschnittlichen Gewinns G0) zu berechnen. In diesem Fall ist es notwendig, entweder das Skript zu modifizieren oder es mit verschiedenen Eingabedaten zu starten, um den gewünschten Risikowert zu erreichen.
Unveränderliche Stop-Loss' und Take-Profits
Wie bereits erwähnt, wird eine diskrete Verteilung angenommen. Die Handelsgewinne können zwei Werte annehmen: -1 und k, mit den Wahrscheinlichkeiten P-1 bzw. Pk. Nach der Formel für deren Gesamtwahrscheinlichkeit, P-1+Pk=1. Die Verteilungsfunktion at eine schrittweise Form mit zwei Sprüngen an den Punkten -1 und k, mit den Werten P-1 und Pk. Der Erwartungswert der Verteilung ist M=-1*P-1+k*Pk. Es wird definiert θ=Pk, woraus sich ergibt P-1=1-θ, M=(1+k)θ-1. Es handelt sich also um eine parametrische Familie von Verteilungen, definiert durch die Parameter k>0 und 0≤θ≤1. Im Falle eines symmetrischen Random Walk, M=0, so dass θ=θ0=1/(1+k).
Es sei ai — der jeweilige Gewinn der n Positionen, jede gleich -1 oder k.
- Berechnen der Schätzung des Erwartungswertes M≈Mapr=(a1+a2+...+an)/n=(1+k)nk/n-1, wobei nk die Anzahl der profitablen Positionen. Wenn Mapr≤0, soll das Handelssystem als unprofitabel verworfen werden. Es gibt keine Tricks mit einem Risikomanagement, mit denen aus einem unprofitablen System in ein profitables wird. Wenn Mapr>0, fahren wir mit dem nächsten Schritt fort.
- Es muss gezeigt werden, dass die Positionen nicht das Handelsergebnis eines symmetrischen Random Walks ist. Dafür muss der Schätzwert Mapr deutlich größer als Null sein (mit der Sicherheit δ). Es sei M=0 die Nullhypothese. Der statistische Test ist die Variable S=n(Mapr+1)/(1+k)=nk, die einer standardmäßigen Binomialverteilung B(n,θ0) entspricht, wenn die Nullhypothese erfüllt ist. Die Verteilungsfunktionen sei P(x). Um die Nullhypothese zu akzeptieren, gilt es sicherzustellen, dass P(S)>P(nθ0)+δ/2. Ist das der Fall, fahren wir mit dem nächsten Schritt fort. Falls nicht, wird das Handelssystem verworfen.
- Überprüfen Sie, ob die erforderliche Bedingung für den ausgewählten Wert des Mindest-Durchschnittsertrags G0 erfüllt ist. Dafür sollte G0 nicht größer sein als die δ-Quantile der Verteilung qδ der Zufallsvariablen Λ, die im ersten Teil (arithmetisches Mittel der Erträge) eingeführt wurde. Die Variable Λ stimmt mit Mapr überein, ausgedrückt durch S. Jetzt kann S als eine Binomialverteilung mit den Parametern n und θapr=nk/n angesehen werden. Ist die Bedingung erfüllt, fahren wir mit dem nächsten Schritt fort. Falls nicht, bestimmen wir das Minimum der Positionen n=nmin, das für die geforderte Bedingung erfüllt sein muss (schrittweises Erhöhen von n für ein unveränderliches θapr bis zum Wert, zu dem die geforderte Ungleichheit erfüllt ist).
- Mit Monte-Carlo-Methode, erhalten wir eine empirische Verteilung ρopt. Dafür simulieren wir eine große Anzahl von Gruppen mit n Erträgen der Positionen. Jeder Ertrag ist gleich k mit der Wahrscheinlichkeit Pk, und ist gleich -1 mit der Wahrscheinlichkeit 1-Pk. Für jede Gruppe bestimmen wir ropt,i mit der Methode, die im ersten Teil besprochen wurde. Insgesamt bestimmen wird die empirische Verteilung der Zufallsvariablen ρopt. Um das Risiko ropt zu bestimmen, verwenden wir als Stichprobe das Quantil δ dieser Verteilung.
#include <Math\Stat\Binomial.mqh> #property script_show_inputs input uint na=50; // number of deals in the series input double kt=3; // ratio of take profit to stop loss input double pk=0.5; // probability of profit #define NX 300 // the maximum number of deals in a series (to search for nmin) #define NB 10000 // the number of generated samples for the Monte Carlo method #define NR 1000 // the number of interval partitions for the risk double G0=0.15; // the lowest average yield double D0=0.9; // the lowest minimal gain double dlt=0.05; // significance level void OnStart() { if (D0<=0||D0>=1) {Print("D0 must be positive and less than one"); return;} double m=(1+kt)*pk-1; // expected value if(m<=0) {Print("expected value must be positive"); return;} double s=na*pk; // statistics (average number of profitable deals) double s0=na/(1+kt); // average number of profitable deals at zero expected value int ner; double p=MathCumulativeDistributionBinomial(s,na,1/(1+kt),ner); if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;} double p0=MathCumulativeDistributionBinomial(s0,na,1/(1+kt),ner); if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;} if(p<=p0+dlt/2) {Print("expected value is close to zero"); return;} double q=MathQuantileBinomial(dlt,na,pk,ner),q0=na*(G0+1)/(kt+1); if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;} if(q0>q) { Print("G0 is greater than dlt quantile of the arithmetic mean of the yield"); uint nmin=na+1; for(;nmin<=NX;++nmin) { q=MathQuantileBinomial(dlt,nmin,pk,ner); q0=nmin*(G0+1)/(kt+1); if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;} if(q0<=q) break; } if(nmin<=NX) Print("nmin = ",nmin); else Print("nmin is greater than ",NX); return; } // the Monte Carlo method MathSrand(GetTickCount()); double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR; uint ir; ArrayResize(a,na); ArrayResize(c,na); for(uint ib=0; ib<NB;++ib) { for(uint i=0; i<na;++i) if(MathRandomNonZero()<=pk) a[i]=kt; else a[i]=-1; A=MathMean(a); A0=a[ArrayMinimum(a)]; if(A<G0) {ropt[ib]=0; continue;} if(A0>0) {ropt[ib]=1-stp; continue;} cn1=1; for(ir=1;ir<NR;++ir) { r=ir*stp; cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i]; if(cn2<cn1) {ropt[ib]=r-stp; break;} cn1=cn2; g=(MathPow(cn2,1.0/na)-1)/r; if(g<G0) {ropt[ib]=r-stp; break;} c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]); d=dcalc(c); if(d<D0) {ropt[ib]=r-stp; break;} } } ArraySort(ropt); uint nr=(uint)(dlt*NB); Print("ropt = ",ropt[nr]); } // Die Funktion dcalc() akzeptiert das Array mit c1, c2, ... cN Werten und // gibt den kleinsten Gewinn d zurück. Assume that c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(uint i=1; i<na;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; } //+------------------------------------------------------------------+
Mit den Standard-Argumenten berechnet das Skript folgenden Wert für das Risiko:
- ropt = 0.011
Dies entspricht den 1,1% des Kapitals, die jede Position bei der Eröffnung riskiert.
Unveränderlicher Trailing-Stop
Nehmen wir eine Kaufposition an (die erforderlichen Änderungen für eine Verkaufsposition sind intuitiv). Bezeichnen wir die Differenz zwischen dem Einstiegspreis und dem anfänglichen Stop-Loss durch Δp=penter-pstop. Die Position wird geschlossen, wenn der Preis den Wert pmax-Δp erreicht, wobei pmax der höchste Preis ist, während die Position offen ist. Wird die Preisreihe durch einen Random Walk mit kontinuierlicher Zeit- und Linearverschiebung modelliert, kann die Ertragsverteilung in expliziter Form gefunden werden. Es ist eine Exponentialverteilung, die um eins nach links verschoben ist. Die Verteilungsfunktion wird genau beschrieben durch die Gleichung P(x)=1-exp(-θ(x+1)) if x≥-1, und P(x)=0 if x<-1. Bei einer positiven Verschiebung (Aufwärtstrend) erfüllen die Parameter θ die Ungleichung 0<θ<1, bei einer negativen (Abwärtstrend): θ>1 und bei Null (flach): θ=1. Der Erwartungswert ergibt sich aus der Gleichung M=1/θ-1.
Da wir davon ausgegangen sind, dass die realen Preise in der Nähe eines Random Walk liegen, wird die Ertragsverteilung der Positionen in einer Serie auch als solche betrachtet, mit einem bestimmten Wert des Parameters θ. Dies ergibt eine Ein-Parameter-Familie kontinuierlicher Verteilungen. Ein bestimmter Wert des Parameters θ während eines Trends hängt vom Verhältnis zwischen der Stärke des Trends und dem Trailing-Stop ab. Berechnen wir es mit Methoden der parametrischen Statistik für die exponentielle Verteilung für die verfügbare Historie der Positionen (in diesem Fall mit Hilfe der Maximum-Likelihood-Methode). Für die weiteren Berechnungen ist es auch wichtig, dass die Summe (und das arithmetische Mittel) einer endlichen Anzahl solcher Variablen mit demselben Parameter einer wohl bekannten Gammaverteilung gleicht.
Es sei ai — die Erträge von n Positionen, wobei jede Position ai>-1 erfüllt (unter Vernachlässigung des Schlupfes). Wie im vorherigen Kapitel, schlagen wir einen Plan für weitere Maßnahmen vor.
- Wir berechnen die Schätzung des Erwartungswertes M≈Mapr=(a1+a2+...+an)/n. Wenn Mapr≤0, soll das Handelssystem als unprofitabel verworfen werden. Wenn Mapr>0, fahren wir mit dem nächsten Schritt fort.
- Versuchen wir die Hypothese M=0 zu widerlegen. Zu verifizieren ist S=Mapr+1, eine Gammaverteilung Γ(n,1/n) (Wenn die Nullhypothese M=0 erfüllt ist). Wenn wir die Verteilung P(x) bezeichnen, dann muss die alternative Hypothese, die Ungleichung P(S)≥P(1)+δ/2, erfüllt sein. Wenn die Nullhypothese erfolgreich widerlegt wurde, gehen wir zum nächsten Schritt, und wenn nicht — wird das System verworfen.
- Überprüfen wir die wesentliche Bedingung für G0. Zuerst ist es notwendig, die Schätzung des Parameters θ=θapr zu erhalten. Mit Hilfe der Maximum-Likelihood-Methode erhalten wir θapr=1/(1+Mapr). Der Wert Λ ist entsprechend der um eins nach links verschobenen Gammaverteilung Γ(n,θapr/n) verteilt. Die erforderliche Bedingung ist erfüllt, wenn das Quantil δ dieser Gammaverteilung kleiner ist als G0+1. Ist das erfüllt, fahren wir fort. Ist das nicht erfüllt, müssen wir die kleinste Anzahl von Positionen ermitteln, die diese Bedingung erfüllen. Dazu erhöhen wir schrittweise den Wert von n und nehmen als nmin den von ihnen an, bei dem die geforderte Ungleichung erfüllt ist.
-
Sie wird auf die gleiche Weise wie im vorherigen Kapitel des Artikels ausgeführt. Änderungen betreffen nur die Verteilung, die für die zufällige Generierung von Erträgen verwendet wird. Jetzt wenden wir die Exponentialverteilung mit dem Parameterθ=θapr um Eins nach links verschoben. Die Statistik-Bibliothek von MQL5 verwendet eine etwas andere Form der Parametrisierung der Exponentialverteilung - Parameter μ (Erwartungswert), ausgedrückt durch θ oder M als μ=1/θ or μ=M+1.
#include <Math\Stat\Gamma.mqh> #include <Math\Stat\Exponential.mqh> #property script_show_inputs input uint na=50; // number of deals in the series input double tht=0.65; // parameter of the exponential distribution 0<tht<1 #define NX 300 // the maximum number of deals in a series (to search for nmin) #define NB 10000 // the number of generated samples for the Monte Carlo method #define NR 1000 // the number of interval partitions for the risk double G0=0.15; // the lowest average yield double D0=0.9; // the lowest minimal gain double dlt=0.05; // significance level void OnStart() { if(D0<=0 || D0>=1) {Print("D0 must be positive and less than one"); return;} double m=1/tht-1; // expected value if(m<=0) {Print("expected value must be positive"); return;} int ner; double p=MathCumulativeDistributionGamma(m+1,na,1.0/na,ner); if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;} double p0=MathCumulativeDistributionGamma(1,na,1.0/na,ner); if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;} if(p<=p0+dlt/2) {Print("expected value is close to zero"); return;} double q=MathQuantileGamma(dlt,na,1/tht/na,ner),q0=G0+1; if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;} if(q0>q) { Print("G0 is greater than dlt quantile of the arithmetic mean of the yield"); uint nmin=na+1; for(;nmin<=NX;++nmin) { q=MathQuantileGamma(dlt,nmin,1/tht/nmin,ner); q0=G0+1; if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;} if(q0<=q) break; } if(nmin<=NX) Print("nmin = ",nmin); else Print("nmin is greater than ",NX); return; } // the Monte Carlo method MathSrand(GetTickCount()); double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR; uint ir; ArrayResize(a,na); ArrayResize(c,na); for(uint ib=0; ib<NB;++ib) { for(uint i=0; i<na;++i) { a[i]=MathRandomExponential(m+1,ner); if(!MathIsValidNumber(a[i])) {Print("Error MathRandomExponential()",ner); return;} a[i]-=1.0; } A=MathMean(a); A0=a[ArrayMinimum(a)]; if(A<G0) {ropt[ib]=0; continue;} if(A0>0) {ropt[ib]=1-stp; continue;} cn1=1; for(ir=1;ir<NR;++ir) { r=ir*stp; cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i]; if(cn2<cn1) {ropt[ib]=r-stp; break;} cn1=cn2; g=(MathPow(cn2,1.0/na)-1)/r; if(g<G0) {ropt[ib]=r-stp; break;} c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]); d=dcalc(c); if(d<D0) {ropt[ib]=r-stp; break;} } } ArraySort(ropt); uint nr=(uint)(dlt*NB); Print("ropt = ",ropt[nr]); } // Die Funktion dcalc() akzeptiert das Array mit c1, c2, ... cN Werten und // gibt den kleinsten Gewinn d zurück. Assume that c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(uint i=1; i<na;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; } //+------------------------------------------------------------------+
Mit den Standard-Argumenten wird folgender Wert für das Risiko berechnet:
- ropt = 0.015
Dies entspricht den 1,1% des Kapitals, die jede Position bei der Eröffnung riskiert.
Die Sequenz von dreißig Positionen, die im vorherigen Teil als Beispiel betrachtet wurde, wurde speziell für ein System mit Trailing-Stops, durch die die Positionen geschlossen werden, erhalten. Daher kann unsere Methode auf sie angewandt werden. Ähnlich wie die zuvor betrachtete Methode zeigt sie, dass die Sequenz unter bestimmten Bedingungen (n, δ, G0, D0) nicht handelbar ist. Das Ergebnis ändert sich nicht, auch wenn der Schlupf (Spread) nicht berücksichtigt wird, in dem eine kleine positive Zahl zu allen ai, addiert wird, so dass für alle i=1,...,n die Bedingung ai>-1 erfüllt wäre.
Hinweis: Wenn das Skript die Fehlernummer 4 für die Standardargumente auswirft, sind die notwendigen Aktualisierungen für das Terminal erforderlich. In diesem Fall muss ein Teil des Skripts (Zeilen 21 bis 42) auskommentiert werden. Dieser Teil enthält Berechnungen, die sich auf Gammaverteilung beziehen. Für sie können wir das folgende Skript in R verwenden.
na=50; tht=0.65; dlt=0.05; G0=0.15; nx=300 m=1/tht-1; l1=l2=l3=FALSE l1 = m > 0 if (l1) l2 = pgamma(m+1,na,scale = 1/na) > pgamma(1,na,scale = 1/na)+dlt/2 if (l2) l3 = G0+1 <= qgamma(dlt,na,scale = 1/tht/na) if(!l1) cat("m must be greater 0\n") if(l1 & l3) cat("G0 and na are ok\n") else cat("na too small or G0 too big\n") if(l1 & l2 & !l3) {for (nmin in (na+1):(nx+1)) {if(G0+1 <= qgamma(dlt,nmin,scale = 1/tht/nmin)) break()} if (nmin<=nx) {cat("nmin =",nmin)} else {cat("nmin >",nx)} }
Was kommt als Nächstes?
Es ist klar, dass die oben genannten Methoden nicht als vollständig und endgültig angesehen werden können. Der Einfachheit halber wurden die Positionen als unabhängig betrachtet und als identisch verteilt. Aber dies erfordert eine gründlichere Betrachtung und kann sich als falsch erweisen. Es kann nützlich sein, wenn die Verteilung der Erträge zu einer bestimmten parametrischen Familie gehört oder einer ähnlich sind. Diese Mitgliedschaft kann aber auch zusätzliche Untersuchungen erfordern.
Wir haben uns für Punktschätzungen der Verteilungsparameter entschieden und nicht nach Konfidenzintervallen für diese gesucht. Aber sobald sie konstruiert sind, stellt sich die Frage nach der Stabilität der Rentabilität des Systems, da diese Parameter schwanken.
Eine Vielzahl von möglichen Methoden bedeutet natürlich nicht, dass sie ständig und auf einmal angewendet werden müssen. Aber es ist besser, sie zu kennen und bei Bedarf nutzen zu können, als sich von Zufälligkeiten täuschen zu lassen.
Einige andere mögliche Richtungen für die Anwendung der Wahrscheinlichkeitstheorie werden im weiteren Verlauf des Artikels kurz skizziert.
Statistiken und Kurslücken
Eine Kurslücke ist ein großer Sprung zwischen dem Schlusskurs einer Bar und dem Eröffnungspreis der nächsten. Diese Bars müssen aber auch über einen deutlichen Abstand voneinander haben. Es wird vermutet, dass "Lücken immer gefüllt werden". Das Füllen einer Lücke bedeutet, dass der Preis, nachdem die Lücke aufgetreten ist, schließlich zu dem Schlusskurs der Bar vor der Lücke zurückkehrt. Manchmal versuchen Händler, ein Handelssystem aufzubauen, das auf dieser Regelmäßigkeit basiert. Ist es möglich?
Die Theorie eines symmetrischen Random Walk auf einer Linie besagt, dass jeder Preis in einem ausreichend große Zeitraum erreicht wird, mit einer Wahrscheinlichkeit, die fast gleich Eins ist. Das heißt, "Lücken werden auch unter diesen Bedingungen fast sicher gefüllt". Aber wie wir wissen, ist mit einem symmetrischen Random Walk kein profitables System möglich. Bedeutet dies, dass ein lückenbasiertes System keine Existenzberechtigung hat?
Nicht unbedingt. Nicht nur der Lückenschluss selbst ist wichtig, sondern auch die Art und Weise, wie die Lücke geschlossen wird. Dies bezieht sich nicht auf das Schließen jeder einzelnen Lücke, sondern auf ihr bestimmtes Aggregat. Es ist dann möglich, empirische Wahrscheinlichkeitsverteilungen von Zufallsvariablen, die mit ihnen assoziiert sind, zu berücksichtigen. Es kann einen Unterschied zwischen realen Preisen und einem symmetrischen Random-Walk-Modell geben. Die Unterschiede können sehr erheblich sein. Es kann sein, dass die Bewegung in Richtung der Lücke klein ist, und dass die Zeit vor der Schließung geringer ist als bei einem Random Walk und vieles mehr. Wichtig ist nur, dass das Vorhandensein und die Signifikanz dieser Abweichungen mit den Methoden der Wahrscheinlichkeitstheorie und der mathematischen Statistik bestimmt werden können. Nachdem diese Abweichungen sichergestellt wurden, ist es möglich, Handelssysteme auf deren Basis aufzubauen. Sie können auch versuchen, eine Theorie zu testen, die Lücken klassifiziert.
Wir betrachten die einfachste Version der Suche nach Abweichungen von einem Random Walk. Dies wird ein Maß dafür sein, wie viel sich der Preis in Richtung der Lücke bewegt, bis sie geschlossen wird. Sie können eine empirische Verteilung dieses Wertes aus der Geschichte der Preise erhalten und diese mit der Theorie vergleichen. Einige Gütekriterien können verwendet werden, um zwei Verteilungen miteinander zu vergleichen.
Wir betrachten ein Modell eines symmetrischen Random Walk mit diskreter Zeit. Nehmen wir an, große Lücken darin sind selten (wie bei den realen Preisen), und in den Intervallen zwischen ihnen ist es nahe einem kontinuierlichen Zeit (dem Wiener Prozess). Wir verwenden folgende Notation: g — die Größe der Lücke, m — die größte Bewegung in Richtung der Lücke, bevor sie geschlossen wird. Die Zufallsvariable x=m/g wird eine Verteilungsfunktion haben, die nahe der Funktion P(x) ist — so wie P(x)=1-1/x if x≥1, und P(x)=0 if x<1. Das Bild illustriert die eingeführten Werte:
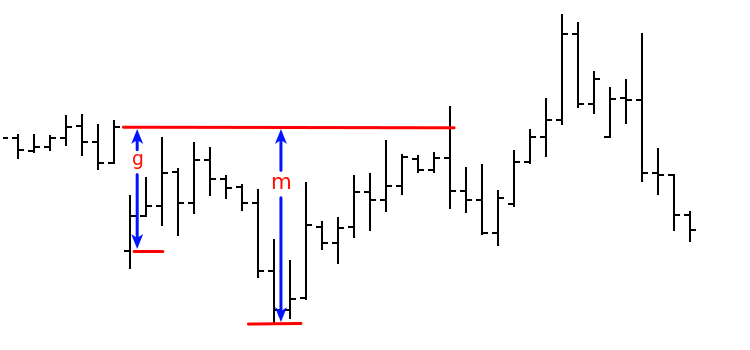
Das aufgeworfene Thema erfordert eine tiefergehende und umfangreichere Untersuchung. Deshalb beschränken wir uns auf die folgenden Ausführungen:
- Das Problem der Lücken-Forschung liegt in ihrer Seltenheit. Dies gilt insbesondere, wenn man versucht, die mit ihnen verbundenen Verteilungen in Abhängigkeit von ihren Parametern zu studieren (ähnlich wie im nächsten Kapitel beschrieben).
- Um die Theorie einer Klassifizierung von Lücken zu überprüfen (z.B. hier), muss ein komplexeres Modell erstellt werden, das nicht nur die Preise von der Lücke bis zu ihrer Füllung berücksichtigt, sondern auch die vorhergehenden und nachfolgenden. Dies führt zu einer Erhöhung der Anzahl der betrachteten Zufallsvariablen. Dies wiederum kann zu Problemen führen, da die oben genannten Daten fehlen.
Statistisches, maschinelles Lernen
Betrachten wir das Schema von folgenden Handelssystem. Für jede Position ist eine Reihe von Parametern h bekannt, deren Werte eindeutig das Volumen und den bestehenden Algorithmus (nicht den Preis!) enthalten. Der Wert von h muss zuverlässig bekannt sein, im Moment der Eröffnung der Position. Es kann sich um Indikatorwerte handeln etc. In den Begriffen des maschinellen Lernens ist h eine Menge von Eigenschaften.
Um sicher zu gehen, machen wir folgende Verfeinerung. Wenn wir über das Handelssystem sprechen, meinen wir normalerweise nicht ein bestimmtes System, sondern ihre parametrische Familie. Die Aufgabe des Testens und Optimierens besteht darin, ein spezifisches System aus dieser Familie auszuwählen, indem ein spezifischer Parameterwert definiert und festgelegt wird. Um die Darstellung nicht zu verkomplizieren (um h nicht mit den Parametern zu verwechseln, die die Wahl des Systems aus der Familie spezifizieren), sprechen wir in diesem Kapitel von einem bestimmten System und nicht von dessen Familie. Die Optimierungsprobleme werden im nächsten Kapitel kurz diskutiert.
Nachdem wir einen bestimmten Wert von h festgelegt haben, erhalten wir einen unveränderlichen Algorithmus für das Eröffnen/Schließen von Positionen. Dadurch ergibt sich eine unveränderliche Verteilung der Wahrscheinlichkeiten. Bitte beachten Sie, dass es für ein und dasselbe h zu unterschiedlichen Erträgen kommen kann. Die Verteilung der Erträge ist unveränderlich, nicht ihr spezifischer Wert.
Dies bringt uns zum Problem der Wiederherstellung der Abhängigkeit des Verteilungesetzes der Erträge mit den Eigenschaften h. Die Ausgangsdaten sind die Historie der Positionen als Paare von Parameterwerten und die entsprechenden Renditen (hi,ai). Solche Probleme werden mit den Methoden des statistischen maschinellen Lernens gelöst. Es stellt sich heraus, dass es keinen grundsätzlichen Unterschied zwischen diesen Methoden und denen des maschinellen Lernens gibt, wenn es darum geht, Probleme bei der Wiederherstellung einer deterministischen (nicht-zufälligen) Abhängigkeit zu lösen.
Formulieren wir das Problem etwas klarer, vorausgesetzt, dass die Verteilung der Erträge zu einer bestimmten Familie gehört. Gegeben sei eine Menge (hi,ai) von Paaren. Die Verteilung der Erträge ai gehört zur Familie mit den Parametern einer Verteilung, die vom Parameter θ abhängen. Es muss die Abhängigkeit θ(h) wiederhergestellt werden. Diese Abhängigkeit wird bei willkürlichen Funktionen nicht angestrebt - die Ausgangsdaten reichen dafür nicht aus. Gewöhnlich wird es unter einer bestimmten parametrischen Familie von Funktionen gesucht: θ(h)=θ(h,β), wobei der Parameter β von der Menge der Paare (hi,ai) bestimmt wird, unter Berücksichtigung der Anforderung einer gewissen Optimalität. Ein breites Spektrum an Funktionsfamilien zum Auffinden von Abhängigkeiten, Optimalitätsbedingungen für die Parameter und Methoden zur Suche nach diesem optimalen Wert definiert die enorme Vielfalt der maschinellen Lernmethoden.
Aus dieser Vielfalt von Methoden ist es notwendig, diejenigen auszuwählen, die aus der Sicht eines Händlers sinnvoll sind (z.B. eine Methode, die hilft, den Gewinn zu erhöhen oder die Inanspruchnahme zu verringern). Dies ist besonders wichtig bei der Auswahl der Optimalitätsbedingung für die Auswahl des Parameters β. Wenn diese Bedingung geändert wird, kann die daraus resultierende Abhängigkeit θ(h,β) stark variieren.
Angenommen, für die gegebene parametrische Familie von Ertragsverteilungen ai wurde das Risikoabschätzungsproblem ähnlich wie in den beiden oben betrachteten Fällen gelöst. Da die Abhängigkeit θ=θ(h) entstanden ist, und es bekannt ist, wie der Risikowert ropt für jedes gegebene θ auszuwählen ist, kennen wir die Abhängigkeit ropt=ropt(h). Damit wäre unser System vollständig.
Statistik und Optimierung des Handelssystems
Betrachten wir die folgende, einfache Variante der Optimierung. Machen wir N Durchläufe mit einem System mit jeweils n Positionen. Wir wählen eine kleine Zahl εN der besten Ergebnisse aus ihnen heraus (mit den höchsten Durchschnittserträgen), wobei 0<ε<<1. Wir bezeichnen den kleinsten Durchschnitt unter diesen ausgewählten Durchläufen als mopt und betrachten das als Anzeichen dafür, wie gut das optimale System sein wird.
Betrachten wir nun ein System, das als Beispiel dafür dient, dass die Optimierungsergebnisse mit Vorsicht zu behandeln sind. Das Beispiel, wenn auch künstlich, reicht aus, um das Wesen des Problems zu erkennen. Betrachten wir nun ein System mit dem Erwartungswert Null für die Erträge und einer zufälligen Abhängigkeit der Parameter.
Dieses System eröffnet zu bestimmten Zeitpunkten die Positionen aber in zufälligen Richtung. Die Richtungen wird mit einem Zufallszahlengenerator mit gleicher Wahrscheinlichkeit gewählt. Der Anfangswert für die Initialisierung dieses Generators vor jedem Testlauf ist eine Funktion der Parameter. So wird immer die gleiche Abfolge von Positionen für jeden Parametersatz erzielt, während die Änderung dieser Parameter die Abfolge in einer völlig zufälligen, unvorhersehbaren Weise ändert. Das Schließen der Positionen wird durch unveränderliche Stop-Loss'/Take-Profits mit einem konstanten Verhältnis k durchgeführt. Wir nehmen auch an, dass es im Testbereich keinen Trend gibt.
Offensichtlich würde das Fehlen eines Trends dazu führen, dass der Erwartungswert der Erträge dieses Systems nahe Null liegt (ein kleines Negativ unter Berücksichtigung des Schlupfes). Die Anzahl der Positionen einer Serie sei n. Das arithmetische Mittel m der Erträge der Serien mit n Positionen ist eine Zufallsvariable. Ausgedrückt als Zufallsvariable nk — die Anzahl der profitablen Positionen der Serie: m=(1+k)nk/n-1. Die Variable nk folgt der Binomialverteilung mit den Parametern 1/(1+k) und n.
Für ausreichend große N wird der Wert mopt nahe dem Quantil (1-ε) der Verteilung von m sein. Wir werden zeigen, dass trotz der scheinbaren Sinnlosigkeit dieses "Handelssystems" (aufgrund der Ertragserwartung von Null) der Wert von mopt ziemlich groß sein wird. Zur Überprüfung setzen wir: k=3, n=50, ε=0.1 und erhalten mopt=2.52.
Offensichtlich ist für reale, sinnvolle Systeme in realen Tests alles anders angeordnet und viel schwieriger. Dennoch kann und sollte man in diesem Fall versuchen zu verstehen, ob der Vorteil eines optimierten Systems nicht zufällig ist.
Anlagen
| Nr. | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | bn.mq5 | Skript | Berechnung des Risikos, wenn Positionen mit unveränderlichen Stop-Loss' und Take-Profits geschlossen werden |
| 2 | exp.mq5 | Skript | Berechnung des Risikos, wenn Positionen mit unveränderlichen Trailing-Stops geschlossen werden |