Statistische Schätzungen
Victor | 7 April, 2016
Einleitung
Heutzutage trifft man häufig auf Beiträge und Veröffentlichungen über Themen, die im Zusammenhang mit Ökonometrie, der Prognose von Preisreihen, der Auswahl und Schätzung der Eignung eines Modells usw. stehen Doch in den meisten Fällen basiert die Argumentation auf der Annahme, dass der Leser mit den Methoden mathematischer Statistiken vertraut ist und die statischen Parameter einer zu analysierenden Sequenz einfach schätzen kann.
Die Schätzung der statistischen Parameter einer Sequenz ist sehr wichtig, weil die meisten mathematischen Modelle und Methoden auf unterschiedlichen Annahmen basieren, beispielsweise dem Normalverteilungsgesetz oder dem Streuungswert oder anderen Parametern. Beim Analysieren und Prognostizieren von Zeitreihen brauchen wir deshalb ein einfaches und bequemes Werkzeug, das es uns ermöglicht, die wichtigsten statistischen Parameter schnell und deutlich zu schätzen. In diesem Beitrag versuchen wir, ein solches Werkzeug zu erstellen.
Dieser Beitrag beschreibt kurz die einfachsten statistischen Parameter einer zufälligen Sequenz und mehrere Methoden für die visuelle Analyse. Er liefert die Umsetzung dieser Methoden in MQL5 und die Methoden der Visualisierung des Ergebnisses der Berechnung mithilfe der Anwendung Gnuplot. Dieser Beitrag sollte keineswegs als Handbuch oder Referenz betrachtet werden. Deshalb enthält er möglicherweise bestimmte Freiheiten in Bezug auf Terminologie und Definitionen.
Analyse von Parametern anhand einer Stichprobe
Nehmen wir an, dass es einen zeitlich endlosen stationären Prozess gibt, der als Sequenz diskreter Auszüge dargestellt werden kann. Bezeichnen wir diese Sequenz von Auszügen als Grundgesamtheit. Ein Teil der Auszüge aus der Grundgesamtheit wird als Stichprobe der Grundgesamtheit oder Stichprobe aus N Auszügen bezeichnet. Nehmen wir zusätzlich an, dass uns keine wahren Parameter bekannt sind, deshalb schätzen wir sie auf Basis einer endlichen Stichprobenentnahme.
Vermeiden von Ausreißern
Bevor wir mit der statistischen Schätzung von Parametern beginnen, sollten wir festhalten, dass die Schätzungsgenauigkeit möglicherweise unausreichend ist, wenn die Stichprobe grobe Fehler (Ausreißer) enthält. Wenn die Stichprobe einen geringen Umfang hat, wirken sich Ausreißer wesentlich auf die Genauigkeit von Schätzungen aus. Ausreißer sind Werte, die sich ungewöhnlich stark vom Zentrum der Verteilung unterscheiden. Solche Abweichungen können durch unterschiedliche unwahrscheinliche Ereignisse und Fehler, die beim Sammeln der statistischen Daten und der Formierung der Sequenz aufgetreten sind, verursacht werden.
Es ist schwer zu entscheiden, ob Ausreißer herausgefiltert werden sollen oder nicht, da es in den meisten Fällen unmöglich ist, eindeutig festzustellen, ob ein Wert ein Ausreißer ist oder zum analysierten Prozess gehört. Wenn also Ausreißer festgestellt werden und beschlossen wird, sie herauszufiltern, stellt sich eine Frage: Was sollen wir mit diesen Fehlerwerten tun? Die logischste Entscheidung wäre, sie aus der Stichprobe auszuschließen, wodurch die Genauigkeit der Schätzung von statistischen Merkmalen erhöht wird. Doch Sie sollten beim Ausschließen von Ausreißern aus Stichproben vorsichtig sein, wenn Sie mit Zeitreihen arbeiten.
Um eine Möglichkeit zu erhalten, Ausreißer aus einer Stichprobe auszuschließen oder sie zumindest zu finden, implementieren wir den im Buch "Statistics for Traders" von S.V. Bulashev.
Laut diesem Algorithmus müssen wir fünf Schätzungswerte des Zentrums der Verteilung berechnen:
- Median;
- Zentrum des 50-prozentigen Interquartilsbereichs (midquartile range, MQR);
- Arithmetisches Mittel der gesamten Stichprobe;
- Arithmetisches Mittel im 50-prozentigen Interquartilsbereich (interquartile mean, IQM);
- Mittelpunkt des Bereichs (midrange) – wird als Durchschnittswert des Maximal- und Minimalwerts in der Stichprobe bestimmt.
Anschließend werden die Ergebnisse der Schätzung des Mittelpunkts der Verteilung in aufsteigender Reihenfolge angeordnet. Der Durchschnittswert oder der dritte Wert wird daraufhin als Mittelpunkt der Verteilung Xcen gewählt. Somit wird die gewählte Schätzung nur minimal durch Ausreißer beeinflusst.
Berechnen wir nun mithilfe der erhaltenen Schätzung des Mittelpunkts der Verteilung Xcen die Standardabweichung s, den Überschuss K und die Zensierungsrate gemäß der empirischen Formel:
![]()
Dabei ist N die Anzahl der Exemplare in der Stichprobe (Stichprobenvolumen).
Damit werden Werte, die außerhalb des Bereichs:
![]()
liegen, als Ausreißer gewertet und müssen aus der Stichprobe ausgeschlossen werden.
Diese Methode wird im Buch "Statistics for Traders" ausführlich beschrieben, widmen wir uns also direkt der Umsetzung des Algorithmus. Der Algorithmus, der das Auffinden und Ausschließen von Ausreißern ermöglicht, ist in der Funktion erremove() enthalten.
Unten sehen Sie das für den Test dieser Funktion geschriebene Script.
//---------------------------------------------------------------------------- // erremove.mq5 // Copyright 2011, MetaQuotes Software Corp. // https://www.mql5.com //---------------------------------------------------------------------------- #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #import "shell32.dll" bool ShellExecuteW(int hwnd,string lpOperation,string lpFile, string lpParameters,string lpDirectory,int nShowCmd); #import //---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[100]; double y[]; srand(1); for(i=0;i<ArraySize(dat);i++)dat[i]=rand()/16000.0; dat[25]=3; // Make Error !!! erremove(dat,y,1); } //---------------------------------------------------------------------------- int erremove(const double &x[],double &y[],int visual=1) { int i,m,n; double a[],b[5]; double dcen,kurt,sum2,sum4,gs,v,max,min; if(!ArrayIsDynamic(y)) // Error { Print("Function erremove() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function erremove() error!"); return(-1); } ArrayResize(a,n); ArrayCopy(a,x); ArraySort(a); b[0]=(a[0]+a[n-1])/2.0; // Midrange m=(n-1)/2; b[1]=a[m]; // Median if((n&0x01)==0)b[1]=(b[1]+a[m+1])/2.0; m=n/4; b[2]=(a[m]+a[n-m-1])/2.0; // Midquartile range b[3]=0; for(i=m;i<n-m;i++)b[3]+=a[i]; // Interquartile mean(IQM) b[3]=b[3]/(n-2*m); b[4]=0; for(i=0;i<n;i++)b[4]+=a[i]; // Mean b[4]=b[4]/n; ArraySort(b); dcen=b[2]; // Distribution center sum2=0; sum4=0; for(i=0;i<n;i++) { a[i]=a[i]-dcen; v=a[i]*a[i]; sum2+=v; sum4+=v*v; } if(sum2<1.e-150)kurt=1.0; kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*(n-1.0)/(n-2.0)/(n-3.0); // Kurtosis if(kurt<1.0)kurt=1.0; gs=(1.55+0.8*MathLog10((double)n/10.0)*MathSqrt(kurt-1))*MathSqrt(sum2/(n-1)); max=dcen+gs; min=dcen-gs; m=0; for(i=0;i<n;i++)if(x[i]<=max&&x[i]>=min)a[m++]=x[i]; ArrayResize(y,m); ArrayCopy(y,a,0,0,m); if(visual==1)vis(x,dcen,min,max,n-m); return(n-m); } //---------------------------------------------------------------------------- void vis(const double &x[],double dcen,double min,double max,int numerr) { int i; double d,yma,ymi; string str; yma=x[0];ymi=x[0]; for(i=0;i<ArraySize(x);i++) { if(yma<x[i])yma=x[i]; if(ymi>x[i])ymi=x[i]; } if(yma<max)yma=max; if(ymi>min)ymi=min; d=(yma-ymi)/20.0; yma+=d;ymi-=d; str="unset key\n"; str+="set title 'Sequence and error levels (number of errors = "+ (string)numerr+")' font ',10'\n"; str+="set yrange ["+(string)ymi+":"+(string)yma+"]\n"; str+="set xrange [0:"+(string)ArraySize(x)+"]\n"; str+="plot "+(string)dcen+" lt rgb 'green',"; str+=(string)min+ " lt rgb 'red',"; str+=(string)max+ " lt rgb 'red',"; str+="'-' with line lt rgb 'dark-blue'\n"; for(i=0;i<ArraySize(x);i++)str+=(string)x[i]+"\n"; str+="e\n"; if(!saveScript(str)){Print("Create script file error");return;} if(!grPlot())Print("ShellExecuteW() error"); } //---------------------------------------------------------------------------- bool grPlot() { string pnam,param; pnam="GNUPlot\\binary\\wgnuplot.exe"; param="-p MQL5\\Files\\gplot.txt"; return(ShellExecuteW(NULL,"open",pnam,param,NULL,1)); } //---------------------------------------------------------------------------- bool saveScript(string scr1="",string scr2="") { int fhandle; fhandle=FileOpen("gplot.txt",FILE_WRITE|FILE_TXT|FILE_ANSI); if(fhandle==INVALID_HANDLE)return(false); FileWriteString(fhandle,"set terminal windows enhanced size 560,420 font 8\n"); FileWriteString(fhandle,scr1); if(scr2!="")FileWriteString(fhandle,scr2); FileClose(fhandle); return(true); } //----------------------------------------------------------------------------
Sehen wir uns die Funktion erremove() im Detail an. Als ersten Parameter der Funktion übergeben wir die Adresse des Arrays x[], in dem die Werte der analysierten Stichprobe gespeichert werden. Das Stichprobenvolumen muss aus mindestens vier Elementen bestehen. Es wird angenommen, dass die Größe des Arrays x[] gleich der Größe der Stichprobe ist, deshalb wird der Wert N des Stichprobenvolumens nicht übergeben. Die Daten im Array x[] werden als Resultat der Ausführung dieser Funktion nicht verändert.
Der nächste Parameter ist die Adresse des Arrays y[]. Bei erfolgreicher Ausführung der Funktion wird dieses Array die Eingabesequenz mit ausgeschlossenen Ausreißern enthalten. Die Größe des Arrays y[] ist um die Menge der aus der Stichprobe ausgeschlossenen Werte geringer als die Größe von x[]. Das Array y[] muss als dynamisches Array deklariert werden. Andernfalls ist es nicht möglich, seine Größe im Körper der Funktion zu ändern.
Der letzte (optionale) Parameter ist das Flag, das für die Visualisierung der Berechnungsergebnisse zuständig ist. Wenn sein Wert gleich eins ist (Standardwert), wird das Diagramm, das die folgenden Informationen anzeigt, vor dem Ende der Ausführung der Funktion in einem separaten Fenster gezeichnet: die Eingabesequenz, die Mittellinie der Verteilung und die Grenzen des Bereichs; Werte, die außerhalb dieser Grenzen liegen, werden als Ausreißer betrachtet.
Die Methode zur Zeichnung von Diagrammen wird später beschrieben. Bei erfolgreicher Ausführung gibt die Funktion die Menge der aus der Stichprobe ausgeschlossenen Werte aus. Liegt ein Fehler vor, gibt sie -1 aus. Werden keine Fehlerwerte (Ausreißer) entdeckt, gibt die Funktion 0 aus und die Sequenz im Array y[] entspricht x[].
Am Anfang der Funktion werden die Informationen aus dem Array x[] nach a[] kopiert und in aufsteigender Reihenfolge angeordnet. Anschließend werden fünf Schätzungen des Mittelpunkts der Verteilung gemacht.
Der Mittelpunkt des Bereichs (midrange) wird als Summe der Grenzwerte des sortierten Arrays a[] geteilt durch zwei bestimmt.
Der Median wird auf folgende Weise für ungerade Volumina der Stichprobe N berechnet:
![]()
und für gerade Volumina der Stichprobe:
![]()
Unter Berücksichtigung, dass die Indizes des sortierten Arrays a[] bei Null beginnen, erhalten wir:
m=(n-1)/2; median=a[m]; if((n&0x01)==0)b[1]=(median+a[m+1])/2.0;
Das Zentrum des 50-prozentigen Interquartilsbereichs (midquartile range, MQR):
![]()
wobei M=N/4 (ganzzahlige Division).
Für das sortierte Array a[] erhalten wir:
m=n/4; MQR=(a[m]+a[n-m-1])/2.0; // Midquartile range
Arithmetisches Mittel im 50-prozentigen Interquartilsbereich (interquartile mean, IQM). 25 % der Auszüge werden von beiden Seiten der Stichprobe abgeschnitten, die verbleibenden 50 % werden für die Berechnung des arithmetischen Mittels verwendet:
![]()
wobei M=N/4 (ganzzahlige Division).
m=n/4; IQM=0; for(i=m;i<n-m;i++)IQM+=a[i]; IQM=IQM/(n-2*m); // Interquartile mean(IQM)
Das arithmetische Mittel (mean) wird für die gesamte Stichprobe bestimmt.
Jeder der bestimmten Werte wird in das Array b[] geschrieben. Anschließend wird das Array in aufsteigender Reihenfolge sortiert. Ein Elementwert des Arrays b[2] wird als Mittelpunkt der Verteilung gewählt. Anhand dieses Wertes berechnen wir weiterhin die unverzerrten Schätzungen des arithmetischen Mittels und des Überschusskoeffizienten. Der Algorithmus der Berechnung wird später beschrieben.
Die erhaltenen Schätzungen werden für die Berechnung des Zensierungskoeffizienten und der Grenzen des Bereichs für das Auffinden von Ausreißern verwendet (die Ausdrücke sind oben abgebildet). Am Ende wird die Sequenz mit ausgeschlossenen Ausreißern im Array y[] geformt und die Funktion vis() für die Zeichnung des Diagramms aufgerufen. Sehen wir uns kurz die in diesem Artikel verwendete Visualisierungsmethode an.
Visualisierung
Zum Anzeigen der Berechnungsergebnisse nutze ich die Freeware-Anwendung gnuplot, die für die Erstellung verschiedener 2- und 3-dimensionaler Diagramme vorgesehen ist. Gnuplot bietet die Möglichkeit, Diagramme auf dem Bildschirm (in einem separaten Fenster) anzuzeigen oder sie in verschiedenen Grafikformaten in eine Datei zu schreiben. Die Befehle für die Zeichnung von Diagrammen können über eine vorab vorbereitete Textdatei ausgeführt werden. Die offizielle Webseite des gnuplot-Projekts ist gnuplot.sourceforge.net. Die Anwendung ist Multiplattform-fähig und wird sowohl in Form von Quelltextdateien als auch von für eine bestimmte Plattform kompilierten Binärdateien bereitgestellt.
Die für diesen Beitrag geschriebenen Beispiele wurden unter Windows XP SP3 und mit gnuplot Version 4.2.2 getestet. Die Zip-Datei gp442win32.zip kann unter http://sourceforge.net/projects/gnuplot/files/gnuplot/4.4.2/ heruntergeladen werden. Ich habe die Beispiele nicht mit anderen Versionen und Builds von gnuplot getestet.
Sobald Sie das Archiv gp442win32.zip heruntergeladen haben, entpacken Sie es. Es wird der Ordner \gnuplot erstellt, der die Anwendung, die Hilfsdatei, die Dokumentation und Beispiele enthält. Um mit Anwendungen zu interagieren, legen Sie den gesamten Ordner \gnuplot im Stammverzeichnis Ihres MetaTrader 5 Client Terminals ab.
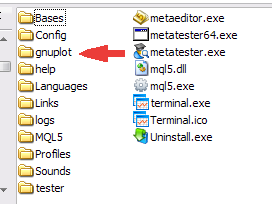
Abbildung 1. Platzierung des Ordners \gnuplot
Sobald der Ordner verschoben wurde, können Sie die Bedienbarkeit der gnuplot-Anwendung anpassen. Führen Sie dazu die Datei \gnuplot\binary\wgnuplot.exe aus und geben Sie in der Befehlseingabe "gnuplot>" den Befehl "plot sin(x)" ein. Als Ergebnis sollte ein Fenster mit eingezeichneter Funktion sin(x) erscheinen. Sie können ebenfalls die in der bereitgestellten Anwendung enthaltenen Beispiele ausprobieren. Wählen Sie dazu den Menüeintrag Datei\Demos und wählen Sie die Datei \gnuplot\demo\all.dem aus.
Wenn Sie nun das Script erremove.mq5 ausführen, wird das in Abbildung 2 dargestellte Diagramm in einem separaten Fenster gezeichnet:
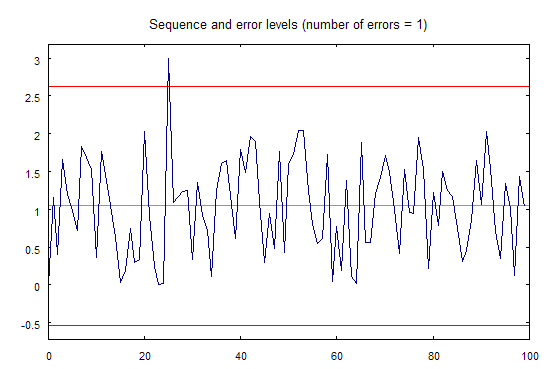
Abbildung 2. Mithilfe des Scripts erremove.mq5 gezeichnetes Diagramm.
Im weiteren Verlauf dieses Beitrags gehen wir nur kurz auf einige Besonderheiten der Benutzung von gnuplot ein, da die Informationen über das Programm und seine Bedienelemente in der Dokumentation, die mit dem Programm bereitgestellt wird, und auf diversen Webseiten wie http://gnuplot.ikir.ru/ einfach zu finden sind.
Die für diesen Beitrag geschriebenen Beispielprogramme nutzen eine äußerst einfache Methode zur Interaktion mit gnuplot zum Zeichnen der Diagramme. Zunächst wird die Textdatei gplot.txt erstellt. Sie beinhaltet die gnuplot-Befehle und die anzuzeigenden Informationen. Anschließend wird die Anwendung wgnuplot.exe mit dem Namen dieser Datei als Argument in der Befehlszeile gestartet. Die Anwendung wgnuplot.exe wird mithilfe der aus der Systembibliothek shell32.dll importierten Funktion ShellExecuteW() aufgerufen. Aus diesem Grund muss der Import von externen DLLs im Client Terminal erlaubt sein.
Die vorliegende Version von gnuplot ermöglicht das Zeichnen von Diagrammen in einem separaten Fenster für zwei Arten von Terminals: wxt und windows. Das wxt-Terminal nutzt Antialiasing-Algorithmen für das Zeichnen von Diagrammen, wodurch im Vergleich zum windows-Terminal ein höher auflösendes Bild ermöglicht wird. Allerdings wurde für das Schreiben der Beispiele für diesen Beitrag das windows-Terminal verwendet. Der Grund dafür ist, dass der Systemprozess, der nach dem Aufruf von "wgnuplot.exe -p MQL5\\Files\\gplot.txt" und dem Öffnen eines Diagrammfensters erstellt wird, bei der Arbeit mit dem windows-Terminal automatisch geschlossen wird, wenn das Fenster geschlossen wird.
Wenn Sie das wxt-Terminal wählen, wird der Systemprozess wgnuplot.exe beim Schließen des Diagrammfensters nicht automatisch geschlossen. Somit können sich mehrere Prozesse ohne jegliche Anzeichen von Aktivität im System ansammeln, wenn Sie das wxt-Terminal verwenden und wgnuplot.exe mehrmals aufrufen. Mit dem Aufruf "wgnuplot.exe -p MQL5\\Files\\gplot.txt" und dem windows-Terminal können Sie die Öffnung unerwünschter Fenster und das Auftreten nicht geschlossener Systemprozesse vermeiden.
Das Fenster, in dem das Diagramm angezeigt wird, ist interaktiv und verarbeitet Mausklicks und Tastatureingaben. Um die Information über Standard-Hotkeys zu erhalten, führen Sie wgnuplot.exe aus, wählen Sie mithilfe des Befehls "set terminal windows" einen Terminal-Typ und zeichnen Sie ein beliebiges Diagramm, beispielsweise mit dem Befehl "plot sin(x)". Wenn das Diagrammfenster aktiv (im Fokus) ist, sehen Sie im Textfenster von wgnuplot.exe einen Tipp, wenn Sie die Taste "h" drücken.
Schätzung von Parametern
Nachdem Sie die Methode zum Zeichnen von Diagrammen nun kennen gelernt haben, kehren wir zur Schätzung der Parameter der Grundgesamtheit auf Basis von endlichen Stichproben zurück. Unter der Annahme, dass keine statistischen Parameter der Grundgesamtheit bekannt sind, nutzen wir nur unverzerrte Schätzungen dieser Parameter.
Die Schätzung des mathematischen Erwartungswerts oder der Mittelpunkt der Stichprobe können als Hauptparameter betrachtet werden, der die Verteilung einer Sequenz bestimmt. Der Mittelpunkt der Stichprobe wird mithilfe der folgenden Formel berechnet:
![]()
Dabei ist N die Anzahl der Exemplare in der Stichprobe.
Der Mittelwert ist eine Schätzung des Mittelpunkts der Verteilung und wird für die Berechnung anderer mit zentralen Punkten in Verbindung stehender Parameter verwendet, was diesen Parameter besonders wichtig macht. Zusätzlich zum Mittelwert nutzen wir die Schätzung der Streuung (dispersion, variance), die Standardabweichung, den Koeffizienten der Schiefe (skewness) und den Koeffizienten des Überschusses (kurtosis) als statistische Parameter.
![]()
Dabei sind m zentrale Punkte.
Zentrale Punkte sind numerische Eigenschaften der Verteilung einer Grundgesamtheit.
Der zweite, dritte und vierte selektive zentrale Punkt werden durch die folgenden Ausdrücke ermittelt:
![]()
Doch diese Werte sind unverzerrt. An dieser Stelle sollten wir k-Statistic und h-Statistic erwähnen. Unter bestimmten Bedingungen ermöglichen sie den Erhalt unverzerrter Schätzungen von zentralen Punkten, also können sie für die Berechnung unverzerrter Schätzungen der Streuung, der Standardabweichung, der Schiefe und der Kurtosis verwendet werden.
Beachten Sie, dass die Berechnungen des vierten Punktes in den k- und h-Schätzungen unterschiedlich durchgeführt werden. Dies führt dazu, dass bei der Verwendung von k oder h unterschiedliche Ausdrücke für die Schätzung der Kurtosis erhalten werden. Beispielsweise wird der Überschuss in Microsoft Excel mithilfe einer Formel berechnet, die der Verwendung von k-Schätzungen entspricht, im Buch "Statistics for Traders" wird die unverzerrte Schätzung der Kurtosis mithilfe von h-Schätzungen durchgeführt.
Entscheiden wir uns für h-Schätzungen und berechnen die erforderlichen Parameter, indem wir 'm' aus dem vorherigen Ausdruck damit ersetzen.
Streuung und Standardabweichung:
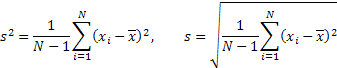
Schiefe:
![]()
Kurtosis:
![]()
Der Koeffizient des Überschusses (Kurtosis), der gemäß dem aufgeführten Ausdruck für die Sequenz mit normalem Verteilungsgesetz berechnet wird, entspricht 3.
Beachten Sie, dass der Wert, den wir durch Abziehen von 3 vom berechneten Wert erhalten, häufig als Kurtosis-Wert verwendet wird. Somit wird der erhaltene Wert relativ zum normalen Verteilungsgesetz normalisiert. Im ersten Fall wird der Koeffizient als "kurtosis" bezeichnet, im zweiten als "excess kurtosis".
Die Berechnung der Parameter gemäß dem aufgeführten Ausdruck findet in der Funktion dStat() statt:
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dStat(const double &x[],statParam &sP) { int i,m,n; double a,b,sum2,sum3,sum4,y[]; ZeroMemory(sP); // Reset sP n=ArraySize(x); if(n<4) // Error { Print("Function dStat() error!"); return(-1); } sP.kurt=1.0; ArrayResize(y,n); ArrayCopy(y,x); ArraySort(y); m=(n-1)/2; sP.median=y[m]; // Median if((n&0x01)==0)sP.median=(sP.median+y[m+1])/2.0; sP.mean=0; for(i=0;i<n;i++)sP.mean+=x[i]; sP.mean/=n; // Mean sum2=0;sum3=0;sum4=0; for(i=0;i<n;i++) { a=x[i]-sP.mean; b=a*a;sum2+=b; b=b*a;sum3+=b; b=b*a;sum4+=b; } if(sum2<1.e-150)return(1); sP.var=sum2/(n-1); // Variance sP.stdev=MathSqrt(sP.var); // Standard deviation sP.skew=n*sum3/(n-2)/sum2/sP.stdev; // Skewness sP.kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)* (n-1.0)/(n-2.0)/(n-3.0); // Kurtosis return(1);Beim Aufruf von dStat() wird die Adresse des Arrays x[] an die Funktion übergeben. Dieses Array beinhaltet die ursprünglichen Daten und den Verweis zur Struktur statParam, die die berechneten Werte der Parameter beinhalten wird. Tritt bei weniger als vier Elementen im Array ein Fehler auf, gibt die Funktion -1 aus.
Histogramm
Zusätzlich zu den in der Funktion dStat() berechneten Parametern ist das Gesetz der Verteilung der Grundgesamtheit von großem Interesse für uns. Um das Verteilungsgesetz der endlichen Stichprobe visuell zu schätzen, können wir ein Histogramm zeichnen. Beim Zeichnen des Histogramms wird der Wertebereich der Stichprobe in mehrere ähnliche Abschnitte unterteilt. Anschließend wird die Anzahl der Elemente in jedem Abschnitt berechnet (Gruppenhäufigkeiten).
Im weiteren Verlauf wird ein Balkendiagramm auf Basis der Gruppenhäufigkeiten gezeichnet. Dieses Diagramm wird als Histogramm bezeichnet. Nach der Normalisierung an die Breite des Bereichs stellt das Histogramm eine empirische Dichte der Verteilung eines zufälligen Werts dar. Nutzen wir den in "Statistics for Traders" beschriebenen empirischen Ausdruck, um die optimale Anzahl von Abschnitten zum Zeichnen des Histogramms zu bestimmen:
![]()
Dabei ist L die erforderliche Anzahl von Abschnitten, N das Volumen der Stichprobe und e die Kurtosis.
Unten sehen Sie die Funktion dHist(), die die Anzahl von Abschnitten bestimmt, die Anzahl der Elemente in jedem von ihnen berechnet und erhaltene Gruppenhäufigkeiten normalisiert.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dHist(const double &x[],double &histo[],const statParam &sp) { int i,k,n,nbar; double a[],max,s,xmin; if(!ArrayIsDynamic(histo)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } nbar=(sp.kurt+1.5)*MathPow(n,0.4)/6.0; if((nbar&0x01)==0)nbar--; if(nbar<5)nbar=5; // Number of bars ArrayResize(a,n); ArrayCopy(a,x); max=0.0; for(i=0;i<n;i++) { a[i]=(a[i]-sp.mean)/sp.stdev; // Normalization if(MathAbs(a[i])>max)max=MathAbs(a[i]); } xmin=-max; s=2.0*max*n/nbar; ArrayResize(histo,nbar+2); ArrayInitialize(histo,0.0); histo[0]=0.0;histo[nbar+1]=0.0; for(i=0;i<n;i++) { k=(a[i]-xmin)/max/2.0*nbar; if(k>(nbar-1))k=nbar-1; histo[k+1]++; } for(i=0;i<nbar;i++)histo[i+1]/=s; return(1); }
Die Adresse des Arrays x[] wird an die Funktion übergeben. Sie beinhaltet die ursprüngliche Sequenz. Die Inhalte des Arrays werden als Resultat der Ausführung dieser Funktion nicht verändert. Der nächste Parameter ist der Verweis zum dynamischen Array histo[], in dem die berechneten Werte gespeichert werden. Die Anzahl der Elemente dieses Arrays entspricht der Anzahl der für die Berechnung verwendeten Abschnitte plus zwei weitere Elemente.
Ein Element, das den Nullwert enthält, wird am Anfang und am Ende des Arrays histo[] eingefügt. Der letzte Parameter ist die Adresse der Struktur statParam, die die vorher berechneten Werte der darin gespeicherten Parameter beinhalten sollte. Falls das Array histo[], das an die Funktion übergeben wird, kein dynamisches Array ist oder das Eingabe-Array x[] weniger als vier Elemente beinhaltet, hält die Funktion ihre Ausführung an und gibt -1 aus.
Sobald Sie ein Histogramm der erhaltenen Werte gezeichnet haben, können Sie visuell schätzen, ob die Stichprobe dem normalen Verteilungsgesetz entspricht. Für eine anschaulichere grafische Darstellung der Entsprechung mit dem normalen Verteilungsgesetz können wir zusätzlich zum Histogramm ein Diagramm mit einer Skala der normalen Wahrscheinlichkeit (Normal Probability Plot) zeichnen.
Normal Probability Plot
Die Grundidee hinter der Zeichnung eines solchen Diagramms ist, dass die X-Achse auf eine Art verzerrt wird, die zur Darstellung der Werte einer Sequenz mit normaler Verteilung auf der gleichen Linie führt. Auf diese Weise kann die Normalitätshypothese grafisch überprüft werden. Detailliertere Informationen über diese Art von Diagrammen finden Sie hier: "Normal probability plot" (dt. "Wahrscheinlichkeitsnetz") oder "e-Handbook of Statistical Methods" (nur englisch).
Für die Berechnung von Werten, die für die Zeichnung des Diagramms der normalen Wahrscheinlichkeit benötigt werden, wird die unten aufgeführte Funktion dRankit() genutzt.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dRankit(const double &x[],double &resp[],double &xscale[],const statParam &sp) { int i,n; double np; if(!ArrayIsDynamic(resp)||!ArrayIsDynamic(xscale)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } ArrayResize(resp,n); ArrayCopy(resp,x); ArraySort(resp); for(i=0;i<n;i++)resp[i]=(resp[i]-sp.mean)/sp.stdev; ArrayResize(xscale,n); xscale[n-1]=MathPow(0.5,1.0/n); xscale[0]=1-xscale[n-1]; np=n+0.365; for(i=1;i<(n-1);i++)xscale[i]=(i+1-0.3175)/np; for(i=0;i<n;i++)xscale[i]=ltqnorm(xscale[i]); return(1); } //---------------------------------------------------------------------------- double A1 = -3.969683028665376e+01, A2 = 2.209460984245205e+02, A3 = -2.759285104469687e+02, A4 = 1.383577518672690e+02, A5 = -3.066479806614716e+01, A6 = 2.506628277459239e+00; double B1 = -5.447609879822406e+01, B2 = 1.615858368580409e+02, B3 = -1.556989798598866e+02, B4 = 6.680131188771972e+01, B5 = -1.328068155288572e+01; double C1 = -7.784894002430293e-03, C2 = -3.223964580411365e-01, C3 = -2.400758277161838e+00, C4 = -2.549732539343734e+00, C5 = 4.374664141464968e+00, C6 = 2.938163982698783e+00; double D1 = 7.784695709041462e-03, D2 = 3.224671290700398e-01, D3 = 2.445134137142996e+00, D4 = 3.754408661907416e+00; //---------------------------------------------------------------------------- double ltqnorm(double p) { int s=1; double r,x,q=0; if(p<=0||p>=1){Print("Function ltqnorm() error!");return(0);} if((p>=0.02425)&&(p<=0.97575)) // Rational approximation for central region { q=p-0.5; r=q*q; x=(((((A1*r+A2)*r+A3)*r+A4)*r+A5)*r+A6)*q/(((((B1*r+B2)*r+B3)*r+B4)*r+B5)*r+1); return(x); } if(p<0.02425) // Rational approximation for lower region { q=sqrt(-2*log(p)); s=1; } else //if(p>0.97575) // Rational approximation for upper region { q = sqrt(-2*log(1-p)); s=-1; } x=s*(((((C1*q+C2)*q+C3)*q+C4)*q+C5)*q+C6)/((((D1*q+D2)*q+D3)*q+D4)*q+1); return(x); }
Die Adresse des Arrays x[] wird in die Funktion eingegeben. Das Array beinhaltet die ursprüngliche Sequenz. Die nächsten Parameter sind Verweise auf die Ausgabe-Arrays resp[] und xscale[]. Nach der Ausführung der Funktion werden die Werte, die für die Zeichnung des Diagramms auf der X- bzw. Y-Achse verwendet werden, in die Arrays geschrieben. Anschließend wird die Adresse der Struktur statParam an die Funktion übergeben. Sie sollte die vorher berechneten Werte der statistischen Parameter der Eingabesequenz beinhalten. Bei einem Fehler gibt die Funktion -1 aus.
Beim Formen der Werte für die X-Achse wird die Funktion Itqnorm() aufgerufen. Sie berechnet die umgekehrte Integralfunktion der Normalverteilung. Der für die Berechnung genutzte Algorithmus wurde "An algorithm for computing the inverse normal cumulative distribution function" entnommen. [Anm. d. Übers.: Diese Seite war zum Zeitpunkt der Übersetzung nicht erreichbar.]
Vier Diagramme
Ich habe vorher die Funktion dStat() erwähnt, in der die Werte der statistischen Parameter berechnet werden. Wiederholen wir kurz deren Bedeutung.
Streuung (variance) – der Mittelwert der zweiten Potenz der Abweichung eines zufälligen Werts von seiner mathematischen Erwartung (Durchschnittswert). Der Parameter, der zeigt, wie groß die Abweichung eines zufälligen Werts vom Mittelpunkt seiner Verteilung ist. Je höher der Wert dieses Parameters ist, desto größer ist die Abweichung.
Standardabweichung (standard deviation) – da die Streuung als zweite Potenz eines zufälligen Werts gemessen wird, wird die Standardabweichung häufig als deutlichere Eigenschaft der Streuung genutzt. Sie entspricht der Quadratwurzel der Streuung.
Schiefe – wenn wir eine Kurve der Verteilung eines zufälligen Werts zeichnen, zeigt die Schiefe, wie asymmetrisch die Kurve der Wahrscheinlichkeitsdichte in Relation zum Mittelpunkt der Verteilung ist. Wenn der Wert der Schiefe größer als Null ist, hat die Kurve der Wahrscheinlichkeitsdichte eine steile Neigung auf der linken Seite und eine flache auf der rechten Seite. Wenn der Wert der Schiefe negativ ist, ist die linke Neigung flach und die rechte steil. Wenn die Kurve der Wahrscheinlichkeitsdichte symmetrisch zum Mittelpunkt der Verteilung ist, ist die Schiefe gleich Null.
Koeffizient des Überschusses (kurtosis) – beschreibt die Schärfe der Spitze der Kurve der Wahrscheinlichkeitsdichte und die Steilheit der Neigungen der Verteilungslinien. Je schärfer die Kurvenspitze nahe des Mittelpunkts der Verteilung ist, desto höher ist der Wert der Kurtosis.
Obwohl die aufgezählten statistischen Parameter eine Sequenz detailliert beschreiben, können Sie eine Sequenz oftmals einfacher charakterisieren – auf Basis des Ergebnisses von Schätzungen in grafischer Form. Beispielsweise kann ein herkömmliches Diagramm einer Sequenz einen Eindruck aus der Analyse der statistischen Parameter hervorragend ergänzen.
An einer früheren Stelle dieses Beitrags habe ich die Funktionen dHist() und dRankit() erwähnt, die die Vorbereitung von Daten für das Zeichnen eines Histogramms oder Diagramms mit der Skala der normalen Wahrscheinlichkeit ermöglichen. Die Darstellung des Histogramms und des Diagramms der normalen Verteilung zusammen mit dem herkömmlichen Diagramm in demselben Arbeitsblatt ermöglicht es Ihnen, die Hauptmerkmale der analysierten Sequenz visuell zu bestimmen.
Die drei aufgezählten Diagramme sollten um ein weiteres ergänzt werden: das Diagramm mit den aktuellen Werten der Sequenz auf der Y-Achse und ihren vorhergehenden Werten auf der X-Achse. Ein solches Diagramm wird als "Korrelogramm" (Lag Plot) bezeichnet. Bei einer starken Korrelation zwischen benachbarten Werten strecken sich die Werte einer Stichprobe über eine gerade Linie aus. Falls es keine Korrelation zwischen benachbarten Werten gibt, beispielsweise bei der Analyse einer zufälligen Sequenz, sind die Werte über das gesamte Diagramm verteilt.
Für eine schnelle Schätzung einer Ausgangsstichprobe schlage ich vor, vier Diagramme in einem Arbeitsblatt zu zeichnen und die berechneten Werte des statistischen Parameters darauf abzubilden. Das ist keine völlig neue Idee. Hier können Sie mehr über die Verwendung der Analyse der vier aufgezählten Diagramme nachlesen: "4-Plot".
Am Ende des Beitrags finden Sie den Abschnitt "Dateien", der das Script s4plot.mq5 enthält, das diese vier Diagramme auf einem Arbeitsblatt zeichnet. Das Array dat[] wird innerhalb der Funktion OnStart() des Scripts erstellt. Es beinhaltet die ursprüngliche Sequenz. Anschließend werden die Funktionen dStat(), dHist() und dRankit() nacheinander aufgerufen, um die Daten zu berechnen, die für die Zeichnung der Diagramme benötigt werden. Als Nächstes wird die Funktion vis4plot() aufgerufen. Sie erstellt eine Textdatei mit den gnuplot-Befehlen auf Basis der berechneten Daten und ruft anschließend die Anwendung für die Zeichnung der Diagramme in einem separaten Fenster auf.
Es wäre nicht zielführend, den gesamten Code des Scripts in diesem Beitrag abzubilden, da die Funktionen dStat(), dHist() und dRankit() bereits beschrieben wurden und die Funktion vis4plot(), die eine Sequenz von gnuplot-Befehlen erstellt, keine wesentlichen Besonderheiten aufweist und die Beschreibung der gnuplot-Befehle den Umfang dieses Beitrags sprengt. Zusätzlich können Sie anstatt der gnuplot-Anwendung eine weitere Methode zum Zeichnen der Diagramme nutzen.
Bilden wir also nur einen Teil von s4plot.mq5 ab: die Funktion OnStart().
//---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[128],histo[],rankit[],xrankit[]; statParam sp; MathSrand(1); for(i=0;i<ArraySize(dat);i++) dat[i]=MathRand(); if(dStat(dat,sp)==-1)return; if(dHist(dat,histo,sp)==-1)return; if(dRankit(dat,rankit,xrankit,sp)==-1)return; vis4plot(dat,histo,rankit,xrankit,sp,6); }
In diesem Beispiel wird eine zufällige Sequenz verwendet, um das Array dat[] mithilfe der Funktion MathRand() mit Ausgangsdaten zu befüllen. Die Ausführung des Scripts sollte zum folgenden Ergebnis führen:
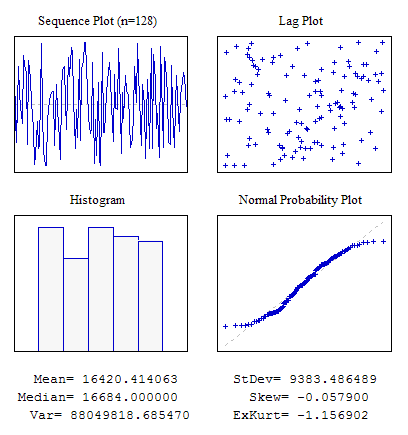
Abbildung 3. Vier Diagramme. Script s4plot.mq5
Beachten Sie den letzten Parameter der Funktion vis4plot(). Er ist für das Format der ausgegebenen numerischen Werte verantwortlich. In diesem Beispiel werden die Werte mit sechs Nachkommastellen ausgegeben. Dieser Parameter entspricht demjenigen, der das Format in der Funktion DoubleToString() bestimmt.
Wenn die Werte der Eingabesequenz zu klein oder zu groß sind, können Sie das wissenschaftliche Format für eine eindeutigere Anzeige nutzen. Legen Sie diesen Parameter hierzu beispielsweise mit -5 fest. Der Wert -5 wird als Standardwert für die Funktion vis4plot() festgelegt.
Um die Eindeutigkeit der Vier-Diagramme-Methode für die Darstellung der Besonderheiten einer Sequenz vorzuführen, benötigen wir einen Generator für solche Sequenzen.
Generator einer pseudo-zufälligen Sequenz
Die Klasse RNDXor128 ist für die Generierung von pseudo-zufälligen Sequenzen vorgesehen.
Nachfolgend sehen Sie den Quellcode der Include-Datei, die diese Klasse beschreibt.
//----------------------------------------------------------------------------------- // RNDXor128.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Generation of pseudo-random sequences. The Xorshift RNG algorithm // (George Marsaglia) with the 2**128 period of initial sequence is used. // uint rand_xor128() // { // static uint x=123456789,y=362436069,z=521288629,w=88675123; // uint t=(x^(x<<11));x=y;y=z;z=w; // return(w=(w^(w>>19))^(t^(t>>8))); // } // Methods: // Rand() - even distribution withing the range [0,UINT_MAX=4294967295]. // Rand_01() - even distribution within the range [0,1]. // Rand_Norm() - normal distribution with zero mean and dispersion one. // Rand_Exp() - exponential distribution with the parameter 1.0. // Rand_Laplace() - Laplace distribution with the parameter 1.0 // Reset() - resetting of all basic values to initial state. // SRand() - setting new basic values of the generator. //----------------------------------------------------------------------------------- #define xor32 xx=xx^(xx<<13);xx=xx^(xx>>17);xx=xx^(xx<<5) #define xor128 t=(x^(x<<11));x=y;y=z;z=w;w=(w^(w>>19))^(t^(t>>8)) #define inidat x=123456789;y=362436069;z=521288629;w=88675123;xx=2463534242 class RNDXor128:public CObject { protected: uint x,y,z,w,xx,t; uint UINT_half; public: RNDXor128() {UINT_half=UINT_MAX>>1;inidat;}; double Rand() {xor128;return((double)w);}; int Rand(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w;} return(0);}; double Rand_01() {xor128;return((double)w/UINT_MAX);}; int Rand_01(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w/UINT_MAX;} return(0);}; double Rand_Norm() {double v1,v2,s,sln;static double ra;static uint b=0; if(b==w){b=0;return(ra);} do{ xor128;v1=(double)w/UINT_half-1.0; xor128;v2=(double)w/UINT_half-1.0; s=v1*v1+v2*v2; } while(s>=1.0||s==0.0); sln=MathLog(s);sln=MathSqrt((-sln-sln)/s); ra=v2*sln;b=w; return(v1*sln);}; int Rand_Norm(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Norm(); return(0);}; double Rand_Exp() {xor128;if(w==0)return(DBL_MAX); return(-MathLog((double)w/UINT_MAX));}; int Rand_Exp(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Exp(); return(0);}; double Rand_Laplace() {double a;xor128; a=(double)w/UINT_half; if(w>UINT_half) {a=2.0-a; if(a==0.0)return(-DBL_MAX); return(MathLog(a));} else {if(a==0.0)return(DBL_MAX); return(-MathLog(a));}}; int Rand_Laplace(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Laplace(); return(0);}; void Reset() {inidat;}; void SRand(uint seed) {int i;if(seed!=0)xx=seed; for(i=0;i<16;i++){xor32;} xor32;x=xx;xor32;y=xx; xor32;z=xx;xor32;w=xx; for(i=0;i<16;i++){xor128;}}; int SRand(uint xs,uint ys,uint zs,uint ws) {int i;if(xs==0&&ys==0&&zs==0&&ws==0)return(-1); x=xs;y=ys;z=zs;w=ws; for(i=0;i<16;i++){xor128;} return(0);}; }; //-----------------------------------------------------------------------------------
Der für die Generierung einer zufälligen Sequenz verwendete Algorithmus wird im Artikel "Xorshift RNGs" von George Marsaglia detailliert beschrieben (siehe xorshift.zip am Ende dieses Beitrags). Methoden der Klasse RNDXor128 werden in der Datei RNDXor128.mqh beschrieben. Mithilfe dieser Klasse können Sie Sequenzen mit gleichmäßiger, normaler oder exponentieller Verteilung oder mit Laplace-Verteilung (doppelt exponentiell) erhalten.
Beachten Sie, dass bei der Erstellung einer Instanz der Klasse RNDXor128 die Basiswerte der Sequenz in ihren ursprünglichen Zustand zurückgesetzt werden. Somit wird im Gegensatz zum Aufruf der Funktion MathRand() bei jedem Neustart eines Scripts oder Indikators, der RNDXor128 nutzt, immer die gleiche Sequenz generiert, genauso wie beim Aufrufen von MathSrand() und dann MathRand().
Beispielsequenzen
Nachfolgend finden Sie als Beispiel die Ergebnisse aus der Analyse von Sequenzen, die sich in ihren Eigenschaften sehr stark voneinander unterscheiden.
Beispiel 1. Eine zufällige Sequenz mit gleichmäßigem Verteilungsgesetz.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_01(); ... }
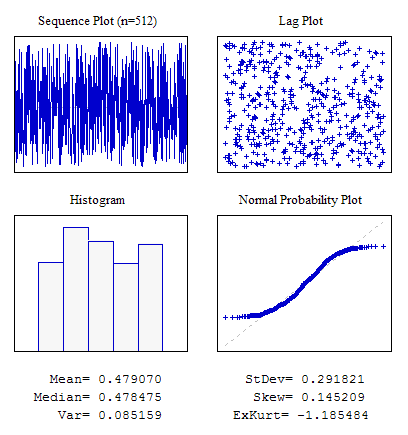
Abbildung 4. Gleichmäßige Verteilung
Beispiel 2. Eine zufällige Sequenz mit normalem Verteilungsgesetz.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Norm(); ... }
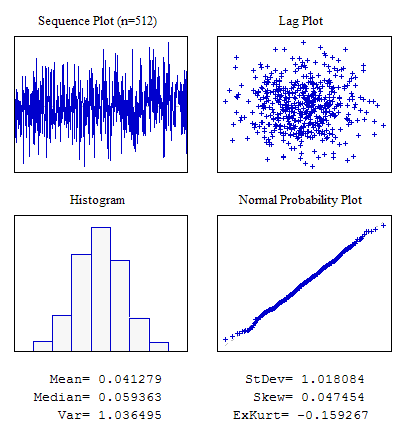
Abbildung 5. Normale Verteilung
Beispiel 3. Eine zufällige Sequenz mit exponentiellem Verteilungsgesetz.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Exp(); ... }
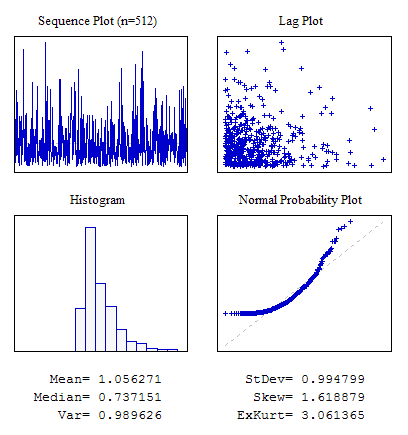
Abbildung 6. Exponentielle Verteilung
Beispiel 4. Eine zufällige Sequenz mit Laplace-Verteilung.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Laplace(); ... }
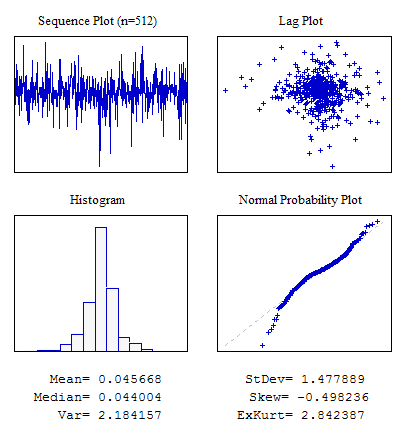
Abbildung 7. Laplace-Verteilung
Beispiel 5. Sinusförmige Sequenz
//---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=MathSin(2*M_PI/4.37*i); ... }
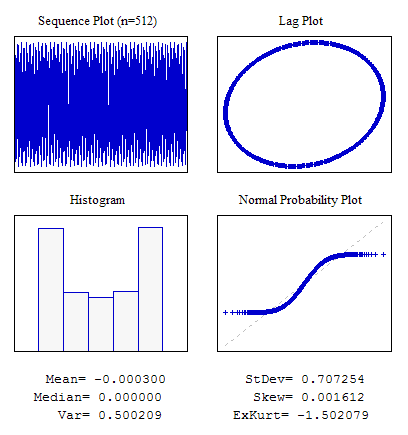
Abbildung 8. Sinusförmige Sequenz
Beispiel 6. Eine Sequenz mit sichtbarer Korrelation zwischen benachbarten Werten.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512],a; for(i=0;i<ArraySize(dat);i++) {a+=Rnd.Rand_Laplace();dat[i]=a;} ... }
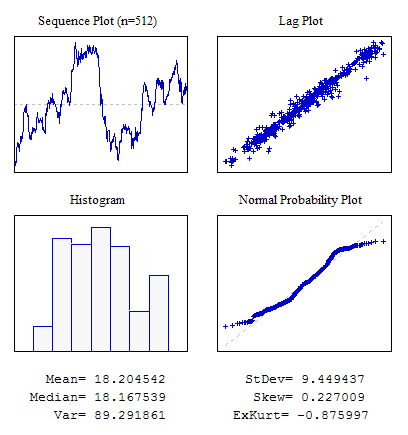
Abbildung 9. Korrelation zwischen benachbarten Werten
Fazit
Die Entwicklung von Programmalgorithmen, die irgendeine Art von Berechnung umsetzen, ist immer harte Arbeit. Der Grund ist die Notwendigkeit, zahlreiche Anforderungen zu berücksichtigen, um die Wahrscheinlichkeit von Fehlern zu verringern, die entstehen können, wenn Variablen gerundet, abgeschnitten oder überfüllt werden.
Beim Schreiben der Beispiele für diesen Beitrag habe ich keinerlei Analyse der Programmalgorithmen durchgeführt. Beim Schreiben der Funktionen wurden die mathematischen Algorithmen "direkt" umgesetzt. Wenn Sie sie also in "ernsthaften" Anwendungen nutzen möchten, sollten Sie ihre Stabilität und Genauigkeit analysieren.
In diesem Beitrag werden keine Funktionen der gnuplot-Anwendung beschrieben. Diese Fragen sprengen einfach den Rahmen dieses Beitrags. Dennoch möchte ich erwähnen, dass gnuplot für die gemeinsame Nutzung mit MetaTrader 5 angepasst werden kann. Zu diesem Zweck müssen Sie einige Korrekturen am Quellcode vornehmen und erneut kompilieren. Zudem ist die Übergabe von Befehlen an gnuplot mithilfe einer Datei wahrscheinlich nicht der optimale Weg, da die Interaktion mit gnuplot über eine Programmierschnittstelle eingerichtet werden kann.
Dateien
- erremove.mq5 – Beispiel eines Scripts, das Fehler aus einer Stichprobe ausschließt.
- function_dstat.mq5 – Funktion zum Berechnen statistischer Parameter.
- function_dhist.mq5 – Funktion zum Berechnen von Werten des Histogramms.
- function_drankit.mq5 – Funktion zum Berechnen von Werten beim Zeichnen eines Diagramms mit Skala der Normalverteilung.
- s4plot.mq5 – Beispiel eines Scripts, das vier Diagramme in einem Arbeitsblatt zeichnet.
- RNDXor128.mqh – Klasse des Generators einer zufälligen Sequenz.
- xorshift.zip - George Marsaglia. "Xorshift RNGs".