
Wahrscheinlichkeitstheorie und mathematische Statistik mit Beispielen (Teil I): Grundlagen und elementare Theorie
Inhalt
- Einführung
- Theoretische Grundlagen
- Elementartheorie
- 3.1. Kombinatorische Wahrscheinlichkeit
- 3.2. Bernoulli-Schema
- Grundlagen der mathematischen Statistik
- Beispiele für die Anwendung der mathematischen Statistik im Rahmen der Elementartheorie
- 5.1. Schätzung von Parametern
- 5.2. Prüfen statistischer Hypothesen
- Schlussfolgerung
- Angehängte Dateien
1. Einführung
Beim Handel geht es immer darum, im Angesicht von Unsicherheit Entscheidungen zu treffen. Das bedeutet, dass die Ergebnisse der Entscheidungen zu dem Zeitpunkt, zu dem diese Entscheidungen getroffen werden, nicht ganz eindeutig sind. Daraus ergibt sich die Bedeutung theoretischer Ansätze für die Konstruktion mathematischer Modelle, die es uns ermöglichen, solche Fälle sinnvoll zu beschreiben. Ich möchte zwei solcher Ansätze hervorheben: Die Wahrscheinlichkeitstheorie und die Spieltheorie. Manchmal werden sie in Themen, die sich auf probabilistische Methoden beziehen, als Theorie der "Spiele gegen die Natur" miteinander kombiniert. Dies zeigt deutlich die Existenz von zwei verschiedenen Arten von Unsicherheit. Die erste (probabilistische) wird gewöhnlich mit Naturphänomenen in Verbindung gebracht. Die zweite (rein spielbezogene) wird mit den Aktivitäten anderer Subjekte (Einzelpersonen oder Gemeinschaften) in Verbindung gebracht. Die Spielunsicherheit ist theoretisch viel schwieriger zu handhaben. Manchmal werden diese Unsicherheiten sogar als "schlecht" und "gut" bezeichnet. Der Fortschritt im Verständnis der anfänglich spielbezogenen Unsicherheit ist oft damit verbunden, sie auf eine probabilistische Form zu reduzieren.
Im Falle der Finanzmärkte ist die Unsicherheit des Spielcharakters offensichtlich wichtiger, da hier die Aktivität der Menschen der Schlüsselfaktor ist. Der Übergang zu probabilistischen Modellen beruht hier in der Regel auf den Überlegungen einer großen Zahl von Spielern, von denen jeder für sich genommen wenig Einfluss auf Preisänderungen hat. Zum Teil ähnelt dies dem in der statistischen Physik verwendeten Ansatz, der zur Entstehung eines wissenschaftlichen Ansatzes mit der Bezeichnung Ökonophysik geführt hat.
Tatsächlich ist das Thema eines solchen Übergangs sehr interessant, nicht trivial und verdient eine detailliertere Betrachtung. Es bleibt zu hoffen, dass die entsprechenden Artikel eines Tages auf unserem Forum erscheinen werden. In diesem Artikel werden wir uns mit den Grundlagen der Wahrscheinlichkeitstheorie und der mathematischen Statistik befassen.
2. Theoretische Grundlagen
Die Wahrscheinlichkeitstheorie basiert auf einem formalen System, das als Kolmogorov-Axiome bekannt ist. Ich werde nicht näher darauf eingehen, zu erklären, was ein "formales System" ist und wie man den mathematischen, axiomatischen Ansatz richtig versteht, da dies allzu komplexe Fragen sind, die zum Bereich der mathematischen Logik gehören. Stattdessen werde ich mich auf das Grundobjekt der Wahrscheinlichkeitstheorie konzentrieren — der Wahrscheinlichkeitsraum. Er besteht aus einem Stichprobenraum, Ereignismenge und der Wahrscheinlichkeit dieser Ereignisse. Lassen Sie uns dies im Detail betrachten:
1) Ein Stichprobenraum ist ein Satz aller möglichen Ergebnisse eines Zufallsexperiments. Er wird normalerweise mit dem griechischen Großbuchstaben "Omega" bezeichnet — Ω und auf Bildern als Zahl dargestellt. Elementare Ereignisse (Beispielpunkte) werden normalerweise durch den griechischen Kleinbuchstaben "Omega" - о - bezeichnet und als Punkt auf Bildern dargestellt. Das einfachste Standardbeispiel, das das Ergebnis eines einzigen Münzwurfs beschreibt: Ω={ω1, ω2}, wobei ω1=H und ω2=T bedeuten, dass die Münze Kopf oder Zahl landet, während geschweifte Klammern eine Menge bezeichnen, die durch die Aufzählung ihrer Elemente gegeben ist.
Die Abbildung unten zeigt ein abstraktes Ω als Rechteck und mehrere Punkte — dazu gehörende elementare Punkte: ω1, ω2 und ω3.
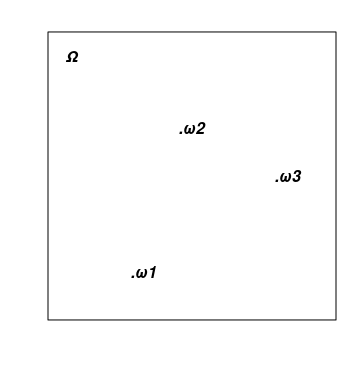
2) Eine Reihe von Zufallsereignissen. Jedes dieser Ereignisse ist eine Menge von Elementarereignissen (eine Teilmenge aller Ω Elementarereignisse). Die Menge der Ereignisse umfasst eine leere Menge ∅={} (ein Ereignis, das nie eintritt) und die gesamte Menge Ω (ein Ereignis, das immer eintritt). Die Kombination (und Schnittmenge) von zwei Ereignissen aus der Menge sollte ebenfalls zur Menge gehören. In der Mathematik wird eine solche Sammlung von Mengen gewöhnlich als Mengenalgebra bezeichnet. Das obige Münzbeispiel hat vier Ereignisse: {}=∅, {H}, {T} und {H,T}=Ω. (Frage zum Selbsttest: Kann ein Elementarereignis als Beispiel für ein Zufallsereignis angesehen werden?)
Zufallsereignisse werden normalerweise als lateinische Großbuchstaben bezeichnet: A, B, C, ... und in Bildern als Formen dargestellt, die sich innerhalb von Ω befinden. Die Kombination und Überschneidung von Ereignissen werden auf unterschiedliche Weise bezeichnet. Manchmal wird ein Eintrag ähnlich der Addition und Multiplikation gewöhnlicher numerischer Variablen verwendet: АВ und А+В, während manchmal die Zeichen ∩ und ∪ verwendet werden: А∩В und А∪В.
Das Bild unten zeigt Ω als Rechteck und zwei sich schneidende А und В Ereignisse.
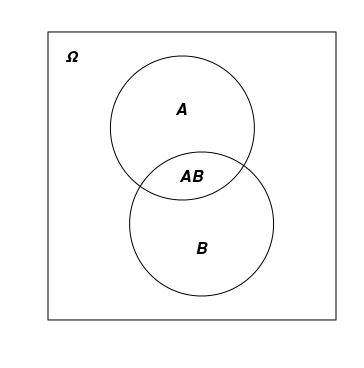
3) Die Wahrscheinlichkeit ist eine numerische Funktion P=P(A), die jedem Zufallsereignis A eine reelle Zahl von 0 bis 1 zuordnet. P(Ω)=1 und P(∅)=0. Außerdem ist die Additivitätsregel erfüllt: Wenn das Ereignis A eine Kombination von sich nicht überlappenden Ereignissen B und C ist, dann gilt P(A)=P(B)+P(C). Zusätzlich zum Begriff "Wahrscheinlichkeit" wendet die Funktion P() die "Wahrscheinlichkeitsverteilung von Ω" an. (oder einfach "Verteilung von Ω"). Verwechseln Sie dieses Konzept nicht mit dem ähnlichen Konzept der "Verteilungsfunktion einer Zufallsvariablen". Sie sind zwar miteinander verwandt, aber dennoch unterschiedlich. Erstere ist eine Funktion, die eine Zahl mit einer Menge vergleicht, während letztere eine gewöhnliche numerische Funktion ist, die eine Zahl mit einer Zahl vergleicht.
Es ist nicht klar, wie die Wahrscheinlichkeitsverteilung in einem Bild dargestellt werden kann, aber intuitiv lässt sie sich mit der Verteilung der Einheitsmasse über das Volumen Ω vergleichen. In diesem Vergleich ist ein Ereignis Teil des Volumens, während die Wahrscheinlichkeit ein Anteil der Masse innerhalb dieses Teils des Volumens ist.
Alle anderen Konzepte der Wahrscheinlichkeitstheorie werden daraus abgeleitet. Lassen Sie uns hier ein sehr wichtiges Konzept der probabilistischen Abhängigkeit (Unabhängigkeit) hervorheben. Dazu werde ich das Konzept der ereignisbedingten Wahrscheinlichkeit А in Abhängigkeit von der Ereignisausführung B, P(B)>0 einführen. Es wird als P(A|B) und per Definition als P(A|B)=P(AB)/P(B) bezeichnet (wie Sie sich vielleicht erinnern, AB bedeutet Schnittpunkt der Ereignisse A und B). Per Definition wird das Ereignis A als unabhängig vom Ereignis B betrachtet, wenn seine bedingte Wahrscheinlichkeit während des Ereignisses B gleich der Wahrscheinlichkeit ist: P(A|B)=P(A). Wenn wir den Ausdruck der bedingten Wahrscheinlichkeit verwenden, kann die Definition der Unabhängigkeit wie folgt umgeschrieben werden: P(A)P(B)=P(AB). Wenn diese Gleichheit nicht erfüllt ist, dann soll das Ereignis A vom Ereignis B abhängen.
Intuitiv bedeutet Unabhängigkeit, dass das Wissen um das Eintreten des Ereignisses B die mit dem Ereignis A verbundene Unsicherheit nicht ändert. Umgekehrt bedeutet Abhängigkeit, dass die Ausführung des B Ereignisses Informationen über das A Ereignis mit sich bringt. Der genaue Ausdruck dieses intuitiven Verständnisses findet sich in Claude Shannons Informationstheorie.
Die elementare Wahrscheinlichkeitstheorie wird gewöhnlich gesondert hervorgehoben. Der Unterschied zwischen der elementaren Theorie und der nicht-elementaren Theorie besteht darin, dass sie Mengen von Elementarereignissen betrachtet, die aus einer endlichen Anzahl von Elementen bestehen. Folglich erweist sich auch die Menge der Zufallsereignisse als endlich (Selbsttestfrage: Warum ist das wahr?). Diese Theorie entwickelte sich lange vor den Kolmogorov-Axiomen und brauchte sie nicht wirklich. Der Rest des Artikels wird sich auf diesen Teil der Theorie konzentrieren. Die nicht-elementare Theorie wird im nächsten Artikel besprochen.
3. Elementartheorie
Da die Anzahl der elementaren Ergebnisse endlich ist, können wir einfach die Wahrscheinlichkeit für Ereignisse festlegen, die genau ein Elementarereignis enthalten (Einheitsmenge). Wir müssen nur sicherstellen, dass die Summe aller solcher Wahrscheinlichkeiten gleich eins ist. Die Wahrscheinlichkeit eines jeden Ereignisses wird gleich der Summe solcher Wahrscheinlichkeiten sein. Diese Anfangswahrscheinlichkeiten sind nicht unbedingt gleich, aber wir werden mit solchen Modellen beginnen, die gewöhnlich unter dem Namen "kombinatorische Wahrscheinlichkeit" zusammengefasst werden.
3.1. Kombinatorische Wahrscheinlichkeit
Es gelte, dass Ω aus genau N elementaren Ergebnissen besteht, dann ist die Wahrscheinlichkeit, dass die Ereignisse diese in der Menge von m enthalten, gleich m/N. Wahrscheinlichkeitsberechnungen bestehen hier aus der Zählung der Anzahl von Optionen. In der Regel werden dazu kombinatorische Methoden verwendet, daher der Name. Hier sind einige Beispiele:
Beispiel 1. Angenommen, wir haben n verschiedene Elemente. Wie viele verschiedene Möglichkeiten gibt es, sie anzuordnen (aneinander zu reihen)? Antwort: n!=1*2*3*....*(n-1)*n. Jeder Weg wird Permutation genannt, und jede Permutation ist ein elementares Ereignis. Daher ist N=n! und die Wahrscheinlichkeit eines Ereignisses, das aus m Permutationen besteht, m/n! (m/N=m/n!).
Lassen Sie uns ein einfaches Problem lösen: Definieren Sie die Wahrscheinlichkeit, dass ein gegebenes Objekt nach einer zufälligen Permutation an der ersten Stelle steht. Wenn der erste Platz durch ein ausgewähltes Objekt besetzt ist, können die verbleibenden n-1 Objekte auf den verbleibenden n-1 Plätzen in (n-1)! platziert werden. Somit ist m=(n-1)!, was bedeutet, dass die gewünschte Wahrscheinlichkeit gleich m/N=m/n!=(n-1)!/n!=1/n ist.
Beispiel 2. Wir haben n verschiedene Elemente. Wie viele verschiedene Gruppen von k (k<=n) Elementen können wir von ihnen trennen? Hier gibt es zwei mögliche Optionen, je nachdem, ob wir zwei Sets, die sich nur in der Reihenfolge der Positionen unterscheiden, als unterschiedlich betrachten. Wenn ja, dann lautet die Antwort n!/(n-k)! Sätze. Wenn nicht, dann sind es k!-mal weniger: n!/((n-k)!*k!). Eine Menge, die die Reihenfolge berücksichtigt, nennt man Zuweisung, eine Menge ohne Berücksichtigung der Reihenfolge nennt man eine Kombination. Bei der Erstellung der Zuordnungsnummer, die auch als Binomialkoeffizientengleichung bekannt ist, werden spezielle Symbole verwendet — in der folgenden Abbildung sind zwei Optionen dargestellt.
![]()
Wenn also die Reihenfolge der Elemente innerhalb der Menge nicht wichtig ist, können wir Kombinationen als eine Menge von Elementarereignissen zur Lösung des Problems verwenden. Wenn die Reihenfolge wichtig ist, dann sollten Zuordnungen verwendet werden.
Beispiel 3. Betrachten wir ein wichtiges Beispiel, das zu der so genannten hypergeometrischen Verteilung führt. Nehmen wir an, dass jeder der Punkte n entweder als "gut" oder als "schlecht" markiert ist. Es seien b, b⋜n, Elemente "schlecht", dann sind die übrigen n-b "gut". Wählen Sie eine Menge von k Elementen aus, ohne ihre Reihenfolge zu berücksichtigen (Kombination). Wie hoch ist die Wahrscheinlichkeit, dass unsere Menge genau x "schlechte" Elemente enthält? Das Problem wird gelöst, indem die Anzahl der übereinstimmenden Kombinationen gezählt wird. Die Antwort ist ziemlich umständlich, und es ist besser, sie durch die Notationen für die Anzahl der Kombinationen aufzuschreiben, wie in der folgenden Abbildung gezeigt, wo die gewünschte Wahrscheinlichkeit über p angegeben und über x ausgedrückt wird, n, b und k.
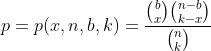
Dieses Beispiel eignet sich gut, um die Logik hinter der Einführung des Konzepts der "Zufallsvariablen" zu verstehen (es wird im nächsten Artikel ausführlicher behandelt). Es kann sich durchaus herausstellen, dass zur Lösung eines spezifischen Problems im Zusammenhang mit der Berechnung der Wahrscheinlichkeiten von Ereignissen die Kenntnis von x, n, b und k völlig ausreichend ist, während die vollständigen Daten über die gesamte ursprüngliche Menge von Ereignissen redundant sind. Dann ist es sinnvoll, das ursprüngliche Modell zu vereinfachen, indem unnötige Informationen weggelassen werden. Lassen Sie uns wie folgt vorgehen:
- n, b und k werden als feste Parameter angenommen.
- Statt des Stichprobenraums Ω konstruieren einen darauf basierenden neuen Ωх={0, 1, ..., k}. Der neue Raum soll aus möglichen х Werten bestehen.
- Jedes Ereignis {х} (bestehend aus einem Elementarereignis) soll mit einer durch die oben gezeigte hypergeometrische Verteilungsgleichung spezifizierten Wahrscheinlichkeit übereinstimmen.
Das resultierende Objekt wird als "diskrete Zufallsvariable" bezeichnet, die eine hypergeometrische Verteilung für ihre möglichen Werte von Ωх aufweist.
3.2. Bernoulli-Schema
Dies ist ein weiteres bekanntes Modell aus dem Bereich der elementaren Wahrscheinlichkeitstheorie. Seine Beispiele beinhalten normalerweise die Modellierung der Ergebnisse von aufeinanderfolgenden Münzwürfen, ich werde das Schema jedoch in einer formelleren Weise konstruieren.
Angenommen, wir haben eine positive ganze Zahl n und ein Paar nicht-negativer reeller Zahlen p und q, so dass p+q=1. Der Stichprobenraum Ω besteht aus Wörtern mit der genauen Länge von n, in denen nur die Buchstaben H und T erlaubt sind (H - Head (Kopf), T - Tail (Zahl). Die Wahrscheinlichkeit für ein aus einem Elementarereignis bestehendes Ereignis wird durch die Gleichung pu({w})=p^nh*q^nt bestimmt, wobei w ein Wort ist, während nh and nt, nh+nt=n entsprechend für die Anzahl der Buchstaben H und T stehen.
Es ist leicht zu erkennen, dass im Gegensatz zur kombinatorischen Wahrscheinlichkeit die Anfangswahrscheinlichkeiten im Allgemeinen nicht gleich sind (sie sind nur dann ähnlich, wenn p=q=0,5).
Betrachten wir n=2 als Beispiel. In diesem Fall gilt Ω={HHH, HT, TH, TT}. Die Anzahl der Elementarereignisse ist hier gleich 4, während die Anzahl der Zufallsereignisse 16 ist. (Selbsttest-Frage: Leiten Sie die allgemeine Form der Gleichungen, die die Abhängigkeit der Elementarereigniszahl und der Anzahl aller Zufallsereignisse beschreiben, aus n für das Bernoulli-Schema ab).
Betrachten wir das Ereignis "H"=kommt zuerst {HHH, HT}. Seine Wahrscheinlichkeit ist pq+p^2=p. Dasselbe gilt für jede Position, die uns erlaubt, über den Parameter p als die "Wahrscheinlichkeit, bei jedem Wurf Zahl zu bekommen" zu sprechen. Jetzt prüfen wir, ob das Ereignis А="H kommt als Zweites"={HH, TH} unabhängig ist vom Ereignis В="H kommt zuerst"={HH, HT}. Verwenden wir die Unabhängigkeitsdefinition − den Schnittpunkt von АВ={HH}, P(A)=p, P(B)=p und P(AB)=p^2. Da P(A)P(B)=p*p=p^2=P(AB), sind die Ereignisse unabhängig.
Die Aussagen über die Wahrscheinlichkeit des Ergebnisses eines jeden Wurfes und ihre Unabhängigkeit erweisen sich für alle n>2 als zutreffend.
Wir hätten die Wahrscheinlichkeit auf andere Weise spezifizieren können, was möglicherweise entweder zur Abwesenheit der gleichen Wahrscheinlichkeit oder zur Abhängigkeit der Wurf-Ergebnisse führen könnte. Der Punkt ist hier, dass das Bernoulli-Schema nicht das einzige gültige Modell ist, das den Ablauf der Ereignisse beschreibt, und wir sollten uns nicht darauf beschränken.
Berechnen wir nun die Wahrscheinlichkeit eines Ereignisses, das aus den Wörtern besteht, wobei H genau k mal vorkommt, oder (weniger formal) die Wahrscheinlichkeit einer Zahl ist gleich k bei n Würfen. Die Antwort auf diese Frage kann über die in der folgenden Abbildung dargestellte sogenannte Binomialverteilungsgleichung gefunden werden. pb steht für die gesuchte Wahrscheinlichkeit in Abhängigkeit von k, n, p and q.
![]()
Betrachten wir ein weiteres Beispiel, das die Beziehung zwischen der Binomialverteilung und der oben betrachteten hypergeometrischen Verteilung zeigt. Sie ist sowohl an sich als auch im Zusammenhang mit ihren Anwendungen in der mathematischen Statistik wichtig (Exakter Test nach Fisher). Die Frage ist aus mathematischer Sicht recht komplex und aussagekräftig. Lassen Sie uns alle Argumentationspunkte Punkt für Punkt hervorheben.
- Basierend auf dem Stichprobenraum des Bernoulli-Schemas Ω, konstruieren wir den neuen − Ω1, der nur die Wörter enthält, in denen H genau b mal vorkommt.
- Da jedes Ereignis A innerhalb von Ω1 auch ein Ereignis innerhalb von Ω ist, ist die Wahrscheinlichkeit P(A) dafür definiert. Ausgehend von dieser Tatsache führen wir die Wahrscheinlichkeit P1 von Ω1 gemäß der Gleichung P1(A)=P(A)/Р(Ω1) ein. Die bedingte Wahrscheinlichkeitsgleichung P1(A)=P(A|О1) wird hier tatsächlich verwendet.
- Betrachten wir nun die Wahrscheinlichkeit P1() des Ereignisses "das Suffix eines Wortes der Länge k genau x Anzahl von H Buchstaben enthält" aus Ω1. Es stellt sich heraus, dass diese Wahrscheinlichkeit durch die oben angegebene hypergeometrische Verteilungsgleichung genau festgelegt ist. Insbesondere hat die Gleichung keinen Einfluss auf den Parameter p.
4. Grundlagen der mathematischen Statistik
Der Unterschied zwischen der mathematischen Statistik und der Wahrscheinlichkeitstheorie wird gewöhnlich als ein Unterschied in der Art der Probleme beschrieben, die sie lösen. In der Wahrscheinlichkeitstheorie wird in der Regel davon ausgegangen, dass das probabilistische Modell vollständig bekannt ist und einige Schlussfolgerungen daraus gezogen werden sollten. In der mathematischen Statistik ist das Wissen über das Modell unvollständig, aber es gibt zusätzliche Informationen in Form von experimentellen Daten, die zur Verfeinerung des Modells beitragen. Daher sind alle im vorigen Kapitel behandelten Fragen Probleme der Wahrscheinlichkeitstheorie.
Die Definition der mathematischen Statistik, die ich soeben gegeben habe, kann als konventionell betrachtet werden. Es gibt auch einen anderen, moderneren Ansatz zur Definition der mathematischen Statistik. Sie kann als Teil der Entscheidungstheorie definiert werden. In diesem Fall liegt der Schwerpunkt auf der Konstruktion von Entscheidungsregeln, die im Sinne einer Minimierung der durchschnittlichen Kosten eines Fehlers optimal sind. Es besteht hier eine sehr starke Konvergenz mit Methoden des maschinellen Lernens. Ein wesentlicher Unterschied zu ihnen besteht darin, dass in der mathematischen Statistik die Art des angewandten mathematischen Modells recht eindeutig bestimmt wird (z.B. innerhalb der Genauigkeit eines unbekannten Parameters). Beim maschinellen Lernen erstreckt sich die Unsicherheit in der Regel auch auf den Modelltyp.
Betrachten wir nun Beispielprobleme der mathematischen Statistik in ihrem herkömmlichen Sinn.
5. Beispiele für die Anwendung der mathematischen Statistik im Rahmen der Elementartheorie
Es gibt zwei Arten von Problemen − die Schätzung eines Parameters und die Überprüfung von Hypothesen.
Beginnen wir mit der Schätzung von Parametern. Sie setzt das Vorhandensein beliebiger numerischer (nicht zufälliger, deterministischer) Variablen im probabilistischen Modell voraus. Ihr genauer numerischer Wert ist unbekannt, aber wir können ihren Näherungswert anhand von Daten berechnen, die als Ergebnis eines Zufallsexperiments erhalten wurden.
5.1. Schätzung von Parametern
Der allgemeinste Ansatz besteht hier in der Anwendung der Maximum-Likelihood-Methode. Wenn irgendein Elementarereignis ω als Ergebnis eines Zufallsexperiments realisiert wurde, ist die Wahrscheinlichkeitsfunktion die Wahrscheinlichkeit des {ω} Ereignisses (das nur aus diesem Elementarereignis besteht). Sie wird insofern als Funktion bezeichnet, als sie vom Wert des Modellparameters abhängt. Die Maximum-Likelihood-Methode (ML) ist der Parameterwert, bei dem diese Funktion ihr Maximum erreicht.
Neben der ML kann es mehrere verschiedene Parameterschätzungen geben, aber, wie in der mathematischen Statistik bewiesen, ist die ML in Bezug auf die Genauigkeit die beste. Ich überlasse die Erklärung dessen, was hier mit dem Wort "Präzision" gemeint ist, dem nächsten Artikel, der sich mit Zufallsvariablen befasst. In jedem Fall sollten wir uns vor Augen halten, dass die statistische Schätzung fast immer vom wahren Wert des Parameters abweicht. Daher ist es sehr wichtig, zwischen ihnen zu unterscheiden. Zum Beispiel die Wahrscheinlichkeit eines Ereignisses im Bernoulli-Schema und ihre Schätzung in der Form einer Häufigkeit.
Lassen Sie uns mit der Berechnung der ML anhand von Beispielen fortfahren.
Beispiel 1. Schätzung des Parameters b in der hypergeometrischen Verteilung. Es gibt eine Anzahl von n=1000 Werkstücken. Nach der Überprüfung von k=20 davon wurde ein fehlerhaftes Werkstück erkannt: x=1. Schätzen Sie die Anzahl der fehlerhaften Werkstücke in der gesamten Charge.
Unten sehen Sie das in Python geschriebene Skript hyperg_be.py, das dieses Problem löst, indem es alle möglichen Optionen für b aufzählt. Die Antwort ist Schätzung be, bei der der Wahrscheinlichkeitswert, bestimmt durch die hypergeometrische Verteilungsgleichung, maximal ist.
from scipy.stats import hypergeom n = 1000 k = 20 x = 1 lhx = 0.0 be = 0 for b in range(x, n - k + x): lh = hypergeom.pmf(x, n, b, k) if lh > lhx: be = b lhx = lh print("be =",be)
Antwort: be = 50, was durchaus zu erwarten ist (jedes 20-zigste Werkstück).
Beispiel 2. Schätzung des Parameters n in der hypergeometrischen Verteilung. Es soll die Menge der Fische im Wasserbehälter geschätzt werden. Zu diesem Zweck wurden b=50 Fische mit einem Netz gefangen, markiert und wieder freigelassen. Danach wurden k=55 Fische gefangen, von denen sich x=3 als markiert herausstellte.
Unten ist hyperg_ne.py ein in Python geschriebenes Skript, das dieses Problem löst, indem es mögliche Optionen für n aufzählt. Die Antwort ist die Schätzung ne mit dem höchsten Wahrscheinlichkeitswert. Etwas anders ausgedrückt reichen die möglichen Werte für n theoretisch von 50+(55-3)=102 bis unendlich. Dies könnte zu einer endlosen Aufzählungsschleife führen. Es stellt sich jedoch heraus, dass die Wahrscheinlichkeitsfunktion bis zu einem Wert von n wächst. Dann beginnt sie abzunehmen und tendiert gegen Null. Dementsprechend ist die Antwort der erste Wert ne, bei dem der Wert der Wahrscheinlichkeitsfunktion größer ist als ihr Wert bei ne+1.
from scipy.stats import hypergeom b = 50 k = 55 x = 3 lh0 = 0.0 ne = b + k - x - 1 while True: lh = hypergeom.pmf(x, ne+1, b, k) if lh < lh0: break else: lh0 = lh ne += 1 print("ne =",ne)
Antwort: ne = 916, was auch eigentlich erwartet wurde (ne/b ist ungefähr gleich k/x, woraus sich ergibt, dass ne ist ungefähr gleich b*k/x).
Alle nachstehenden Beispiele beziehen sich auf das Bernoulli-Schema oder seine Modifikationen. Die herkömmliche Handelsinterpretation dieses Modells besteht darin, es mit einer diskretisierten Version eines Vermögenswertpreises abzugleichen. Zum Beispiel kann ein Renko- oder Point-and-Figure-Chart verwendet werden, um eine solche Darstellung zu erhalten.
Halten wir uns an diese konventionelle Methode. Anstelle der Buchstaben H und T werden wir uns Zahlen-Sequenzen von 1 und -1 ansehen, die offensichtlich diskreten Preisschritten (nach oben bzw. nach unten) entsprechen. Im Allgemeinen kann die Preisstufe als das Erreichen einer neuen Stufe in einem Preisraster definiert werden. Diese Stufenraster werden in der Regel so definiert, dass entweder die Differenz oder das Verhältnis zwischen jeder Stufe und ihrem unteren Nachbarn gleich bleibt. Ich werde die zweite Methode verwenden. Der Nachteil dieser Methode ist die Unmöglichkeit ihrer Anwendung für Anlagen mit negativen Preisen, während es ein Vorteil ist, keine Schrittgröße für jede einzelne Anlage angeben zu müssen. Außerdem besteht eine gewisse Willkür bei der Wahl einer Nullschwelle. Deren Rolle wird der allererste Preis sein, die diskretisiert werden.
Unten sehen Sie ein einfaches Skript, das den Preis mit einem bestimmten Prozentschritt in einem bestimmten Intervall diskretisiert. Die Datei Discr.mqh enthält nur die Funktion setmv(), in der die Preisdiskretisierung tatsächlich stattfindet. Der Einfachheit halber werden nur die Eröffnungspreise der Minutenbalken als Startpreise genommen.
// Constructing the array of discrete mv[] movements // at a specified time interval and with a specified percentage step void setmv(int& mv[], datetime t1, datetime t2, double dpr) { int ND = 1000; ArrayResize(mv, 0, ND); // Get price history double price[]; int nprice = CopyOpen(Symbol(), PERIOD_M1, t1, t2, price); if(nprice < 2) { Print("not enough price history"); return; } // Construct mv[] int lvl = 0, dlvl, nmv = 0, dmv; double lp0 = log(price[0]), lstep = log(1 + 0.01 * dpr); for(int i = 1; i < nprice; ++i) { dlvl = (int)((log(price[i]) - lp0) / lstep - lvl); if(dlvl == 0) continue; lvl += dlvl; dmv = 1; if(dlvl < 0) { dmv = -1; dlvl = -dlvl; } ArrayResize(mv, nmv + dlvl, ND); for(int j = 0; j < dlvl; ++j) mv[nmv + j] = dmv; nmv += dlvl; } }
Das Skript discret_prices.mq5 zeigt das Ergebnis als Sequenz von 1 und -1 an, sowie ein Diagramm eines diskreten Analogons des Ausgangspreises.
#include <Discr.mqh> #include <Graphics\Graphic.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input datetime tstart = D'2020.05.20 00:00'; // start of the considered time interval input datetime tstop = D'2020.06.20 00:00'; // end of the considered time interval input double dprcnt = 0.5; // price discretization step in % //+------------------------------------------------------------------+ void OnStart() { int mv[], nmv; setmv(mv, tstart, tstop, dprcnt); nmv = ArraySize(mv); if(nmv < 1) { Print("not enough moves"); return; } // Display mv[] as a sequence of 1 and -1 string res = (string)mv[0]; for(int i = 1; i < nmv; ++i) res += ", " + (string)mv[i]; Print(res); // Display the mv[] cumulative sum chart ChartSetInteger(0, CHART_SHOW, false); CGraphic graphic; graphic.Create(0, "G", 0, 0, 0, 750, 350); double x[], y[]; ArrayResize(x, nmv + 1); ArrayResize(y, nmv + 1); x[0] = y[0] = 0.0; for(int i = 1; i <= nmv; ++i) { x[i] = i; y[i] = y[i-1] + mv[i-1]; } ArrayPrint(x); ArrayPrint(y); graphic.CurveAdd(x, y, CURVE_LINES, "discret_prices"); graphic.CurvePlotAll(); graphic.Update(); Sleep(30000); ChartSetInteger(0, CHART_SHOW, true); graphic.Destroy(); }
In allen Beispielen unten werde ich die Ergebnisse der Preisdiskretisierung für EURUSD mit der Erhöhung um 0,5% vom 20. Mai bis 20. Juni 2020 verwenden. Das Ergebnis ist die folgende Sequenz von diskreten Schritten: 1, -1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1. Die Charts des Originalkurses und seines diskreten Analogons werden zur besseren Übersichtlichkeit unten angezeigt.
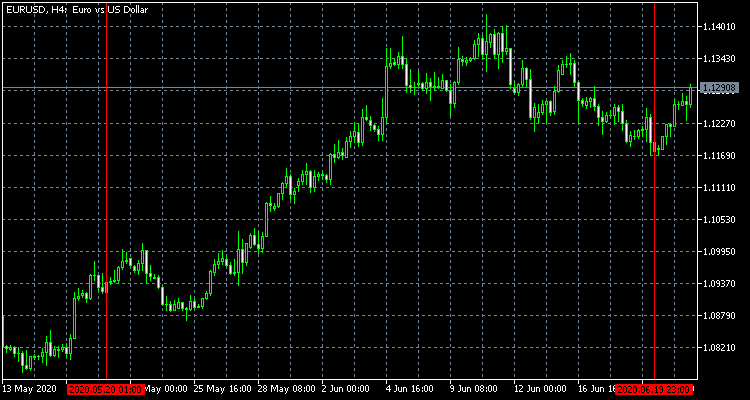
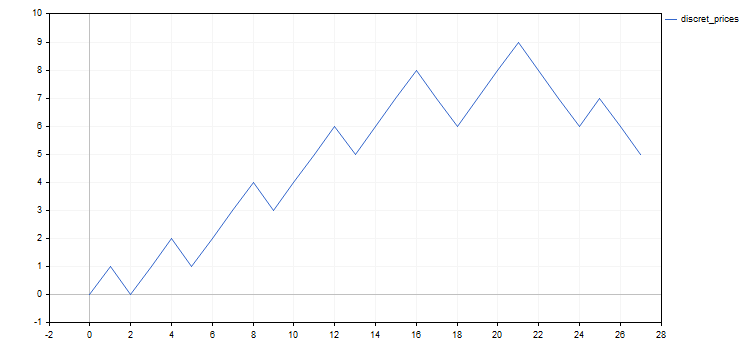
Neben der Untersuchung des Verhaltens des diskretisierten Preises gibt es möglicherweise noch andere Möglichkeiten, das Bernoulli-Schema oder seine Modifikationen anzuwenden. Lassen Sie uns auf zwei davon hinweisen, die sich auf den Handel beziehen.
- Ergebnisse des Handels, bei dem die Aufträge mit festen Stop-Loss, Take-Profit und Volumen getätigt werden. Alle Gewinne in einer Reihe von Handelsgeschäften sind einander ungefähr gleich, und dasselbe gilt für Verluste. Daher ist die Wahrscheinlichkeit eines Gewinns ein ausreichender Parameter, um das Handelsergebnis zu beschreiben. Wir können zum Beispiel die Frage aufwerfen, ob die Wahrscheinlichkeit, einen Gewinn zu erzielen, in der bestehenden Abfolge von Geschäften hoch genug ist.
- Auswahl von Vermögenswerten für Investitionen. Nehmen wir an, dass wir zu Beginn der Periode eine große Auswahl an Investitionsmethoden haben. Jede von ihnen kann mit einer gewissen Wahrscheinlichkeit am Ende zu einem vollständigen Verlust der investierten Mittel führen. Wenn es eine Möglichkeit gibt, Vermögenswerte auszuwählen, dann kann die Frage nach dem Unterschied in der Wahrscheinlichkeit eines Konkurses zwischen den ausgewählten Vermögenswerten im Vergleich zu den abgelehnten Vermögenswerten gestellt werden.
Lassen Sie uns zu den Beispielen zurückkehren.
Beispiel 3. Schätzung des Parameters p im Bernoulli-Schema. Dies ist der seltene Fall, in dem ein Problem auf dem Papier gelöst werden kann. Die Wahrscheinlichkeitsfunktion sieht wie folgt aus: p^nup*(1-p)^ndn. Wir leiten nach p ab und setzen das mit Null gleich, um den erwarteten Wert für die Schätzung von р als Frequenz zu erhalten: pe=nup/(nup+ndn)=nup/nmv. Wie üblich wird nicht nach dem Maximum der Wahrscheinlichkeitsfunktion gesucht, sondern nach ihrem Logarithmus, was wesentlich einfacher ist. Die Antwort ist dieselbe, da der Logarithmus eine streng ansteigende Funktion ist und das Maximum mit dem gleichen Parameterwert erreicht wird. Unten ist das Skript p_model.mq5, das diese Schätzung berechnet.
#include <Discr.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input datetime tstart = D'2020.05.20 00:00'; // start of the considered time interval input datetime tstop = D'2020.06.20 00:00'; // end of the considered time interval input double dprcnt = 0.5; // price discretization step in % //+------------------------------------------------------------------+ void OnStart() { int mv[]; setmv(mv, tstart, tstop, dprcnt); if(ArraySize(mv) < 1) { Print("not enough moves"); return; } double pe = calcpe(mv); Print("pe=", pe); } //+------------------------------------------------------------------+ // Calculate the probability estimation double calcpe(int& mv[]) { int nmv = ArraySize(mv); if(nmv < 1) return 0.0; int nup = 0; for(int i = 0; i < nmv; ++i) if(mv[i] > 0) ++nup; return ((double)nup) / nmv; }
Antwort: pe = 0.59 (gerundet)
Beispiel 4. Schätzung des Parameters im modifizierten Bernoulli-Schema. Wie ich oben geschrieben habe, kann das Bernoulli-Schema sehr wohl geändert werden, wenn es für unsere Modellierungszwecke erforderlich ist. Lassen Sie uns eine mögliche Modifizierungsoption in Betracht ziehen.
Vielleicht ist die einfachste Option, die Sequenz der Bewegungen in zwei kleinere zu unterteilen, die nacheinander ablaufen und mit ihren Parametern dem Bernoulli-Schema entsprechen: n1, p1, n2=n-n1 und p2, wobei n die Länge der kumulativen Sequenz ist.
Es müssen also drei Parameter geschätzt werden − n1, p1 und p2. Die Maximierung der log-Wahrscheinlichkeitsfunktion relativ zu p1 und p2 erlaubt es uns, sie analytisch über n1 auszudrücken. Die Schätzung von n1 sollte durch eine einfache Suche gefunden werden, indem die Ausdrücke p1 und p2 durch die log-Wahrscheinlichkeitsfunktion ersetzt werden.
Unten finden Sie das Skript für p1p2_model.mq5 für die Berechnung von Parameterschätzungen.
#include <Discr.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input datetime tstart = D'2020.05.20 00:00'; // start of the considered time interval input datetime tstop = D'2020.06.20 00:00'; // end of the considered time interval input double dprcnt = 0.5; // price discretization step in % //+------------------------------------------------------------------+ void OnStart() { int mv[]; setmv(mv, tstart, tstop, dprcnt); if(ArraySize(mv) < 2) { Print("not enough moves"); return; } double p1e, p2e; int n1e; calc_n1e_p1e_p2e(mv, n1e, p1e, p2e); Print("n1e=", n1e, " p1e=", p1e, " p2e=", p2e); } //+------------------------------------------------------------------+ // Calculate the probability estimation void calc_n1e_p1e_p2e(int& mv[], int& n1e, double& p1e, double& p2e) { n1e = 0; p1e = p2e = 0.0; int nmv = ArraySize(mv); if(nmv < 2) return; n1e = 1; double llhx = llhx_n1(mv, 1, p1e, p2e), llh, p1, p2; for(int n1 = 2; n1 < nmv; ++n1) { llh = llhx_n1(mv, n1, p1, p2); if(llh > llhx) { llhx = llh; n1e = n1; p1e = p1; p2e = p2; } } } //+------------------------------------------------------------------+ // log-likelihood function maximum depending on n1 double llhx_n1(int& mv[], int n1, double& p1, double& p2) { p1 = p2 = 0.0; int nmv = ArraySize(mv); if(nmv < 2 || n1 < 1 || n1 >= nmv) return 0.0; int nu1 = 0, nu2 = 0; for(int i = 0; i < n1; ++i) if(mv[i] > 0) ++nu1; for(int i = n1; i < nmv; ++i) if(mv[i] > 0) ++nu2; double l = 0.0; if(nu1 > 0) { p1 = ((double)nu1) / n1; l += nu1 * log(p1); } if(nu1 < n1) l += (n1 - nu1) * log(((double)(n1 - nu1)) / n1); if(nu2 > 0) { p2 = ((double)nu2) / (nmv - n1); l += nu2 * log(p2); } if(nu2 < nmv - n1) l += (nmv - n1 - nu2) * log(((double)(nmv - n1 - nu2)) / (nmv - n1)); return l; }
Antwort: n1e = 21; p1e = 0.71; p2e = 0.17 (Zahlen gerundet). Es scheint ziemlich offensichtlich zu sein - unser Modell "erkannte" die Preisrichtungsänderung (oder Korrektur) am Ende seines Segments. Dies deutet darauf hin, dass der Übergang zu einem komplexeren Modell in diesem Fall nicht vergeblich war.
Beispiel 5. Im vorherigen Beispiel hing die Wahrscheinlichkeit der Aufwärtsbewegung von ihrer Zahl (in der Zeit) ab. Betrachten wir eine weitere Modifikation des Bernoulli-Schemas, bei der diese Wahrscheinlichkeit von der vorherigen Bewegung selbst abhängt. Konstruieren wir ein Modell als Beispiel einer einfachsten Markov-Kette mit zwei Zuständen.
Nehmen wir an, dass die Bewegungen von 0 bis n nummeriert sind. Für eine Nullbewegung wird die Wahrscheinlichkeit einer Aufwärtsbewegung einfach gleich 0,5 gesetzt, da es dafür keine vorherige Bewegung gibt. Für andere Positionen ist die Wahrscheinlichkeit einer Aufwärtsbewegung gleich p1, wenn ihr eine Aufwärtsbewegung vorausgegangen ist, und p2, wenn ihr eine Abwärtsbewegung vorausgegangen ist. Die Wahrscheinlichkeiten von Abwärtsbewegungen sind in diesen beiden Fällen entsprechend gleich >q1=1-p1 und q2=1-p2. Zum Beispiel ist die Wahrscheinlichkeit eines Ereignisses mit einem Elementarereignis "down-up-up-down" 0.5*p2*p1*q1.
Wir haben ein Modell mit zwei Parametern erhalten, die mit Hilfe der ML geschätzt werden können. Hier können alle Berechnungen wieder auf dem Papier durchgeführt werden, insbesondere wenn wir die Log-Likelihood-Funktion maximieren. Wie im Fall des Bernoulli-Schemas läuft die Antwort auf Frequenzen hinaus. Die Anzahl, wie oft die Abwärtsbewegung nach der Aufwärtsbewegung auftritt, wird als nud (u - nach oben, d - nach unten) festgelegt. Auf ähnliche Weise führen wir nuu, ndd and ndu ein. Die Schätzungen für p1 and p2 werden über p1e und p2e angegeben. Dann werden diese Schätzungen mit Hilfe der Gleichungen p1e=nuu/(nuu+nud) und p2e=ndu/(ndu+ndd) gefunden.
Unten gibt es das Skript markov_model.mq5, das diese Schätzungen berechnet.
#include <Discr.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input datetime tstart = D'2020.05.20 00:00'; // start of the considered time interval input datetime tstop = D'2020.06.20 00:00'; // end of the considered time interval input double dprcnt = 0.5; // price discretization step in % //+------------------------------------------------------------------+ void OnStart() { int mv[]; setmv(mv, tstart, tstop, dprcnt); if(ArraySize(mv) < 2) { Print("not enough moves"); return; } double p1e, p2e; calcpes(mv, p1e, p2e); Print("p1e=", p1e, " p2e=", p2e); } //+------------------------------------------------------------------+ // Calculate probability estimations void calcpes(int& mv[], double& p1e, double& p2e) { p1e = p2e = 0; int nmv = ArraySize(mv); if(nmv < 2) return; int nuu = 0, nud = 0, ndu = 0, ndd = 0, nu, nd; for(int i = 0; i < nmv - 1; ++i) if(mv[i] > 0) { if(mv[i + 1] > 0) ++nuu; else ++nud; } else { if(mv[i + 1] > 0) ++ndu; else ++ndd; } nu = nuu + nud; nd = ndu + ndd; if(nu > 0) p1e = ((double)nuu) / nu; if(nd > 0) p2e = ((double)ndu) / nd; }
Antwort: p1e = 0.56; p2e = 0.60 (Zahlen gerundet). Dass beide Wahrscheinlichkeiten nahezu gleich groß sind, deutet darauf hin, dass es keine Abhängigkeit zwischen benachbarten Bewegungen gibt. Wenn beide Wahrscheinlichkeiten größer als 0,5 sind, deutet dies auf einen Aufwärtstrend hin. Beide Wahrscheinlichkeitsschätzungen, die nahe an der Wahrscheinlichkeitsschätzung für ein einfacheres Modell (das einfache Bernoulli-Schema aus dem dritten Beispiel) liegen, deuten darauf hin, dass sich der Übergang zu diesem komplizierten Modell in diesem speziellen Fall als unnötig erwiesen hat.
5.2. Prüfen statistischer Hypothesen
Auf demselben Stichprobenraum können verschiedene Wahrscheinlichkeitsverteilungen eingestellt werden. Eine Hypothese ist eine Aussage, die die Art der Verteilung angibt. Es sollte mehrere Hypothesen (mindestens zwei) geben, da die Lösung in der Bevorzugung einer Hypothese gegenüber den anderen liegt. Eine Hypothese wird als einfach bezeichnet, wenn sie die Art der Verteilung eindeutig bestimmt.
Geben wir Beispiele für das Bernoulli-Schema: die Hypothese der Gleichheit des Parameters p zu einer bestimmten Zahl — eine einfache Hypothese (nur ein möglicher Parameterwert, der die Verteilung eindeutig bestimmt), während die Hypothese, dass der Parameter die angegebene Zahl überschreitet, eine komplexe Hypothese (unendlich viele mögliche Parameterwerte) ist.
Als Nächstes werden wir uns mit der Auswahl einer der beiden Hypothesen befassen. Eine von ihnen wird Null genannt, und die andere ist die Alternative. Die Hypothese wird anhand eines statistischen Kriteriums ausgewählt. Im Grunde handelt es sich dabei nur um eine Funktion mit Werten von 0 und 1 innerhalb des Stichprobenraums, wobei 0 bedeutet, die Nullhypothese zu akzeptieren, während 1 bedeutet, die Alternativhypothese zu akzeptieren.
Wir können also entweder die Nullhypothese akzeptieren oder die Nullhypothese ablehnen. Dementsprechend wird die Alternativhypothese entweder abgelehnt oder akzeptiert. Jede dieser Entscheidungen kann entweder richtig oder falsch sein. Folglich gibt es vier mögliche Ergebnisse der Annahme der Hypothese, von denen zwei richtig und zwei falsch sind.
- Fehler vom Typ 1 — fälschliche Ablehnung der Nullhypothese.
- Typ-2-Fehler − fälschliche Annahme der Nullhypothese.
Die Wahrscheinlichkeiten der Fehler vom Typ 1 und 2 werden über a1 und a2 angegeben. Natürlich wäre es gut, diese Wahrscheinlichkeiten so weit wie möglich zu verringern. Aber leider ist das unmöglich. Durch die Verringerung der Wahrscheinlichkeit von Fehlern eines bestimmten Typs werden wir zudem erwartungsgemäß mit der Erhöhung der Wahrscheinlichkeit von Fehlern eines anderen Typs konfrontiert. Aus diesem Grund wird normalerweise ein gewisser Kompromiss zwischen diesen Fehlern eingegangen.
1-a1 wird die Testsignifikanz genannt, während 1-a2 seine Potenz genannt wird. Die Testleistung kann schwierig zu berechnen sein, insbesondere bei einer komplexen Hypothese. Daher wird in der Regel nur die Testsignifikanz verwendet.
Ein Kriterium basiert im Allgemeinen auf einer numerischen Funktion (die ebenfalls auf der Grundlage eines Stichprobenraums definiert wird), die als Teststatistik bezeichnet wird. Ihre mehrfachen Werte werden in zwei Bereiche unterteilt. Einer der Bereiche entspricht der Annahme der Nullhypothese, während der andere der Ablehnung der Nullhypothese entspricht. Der Bereich, in dem die Nullhypothese abgelehnt wird, wird als kritisch bezeichnet.
Im Folgenden wird eine wichtige Anmerkung über die Hypothese "Minus zuerst" gemacht. Dieser Begriff bedeutet, dass wir uns im Voraus vergewissern sollten, dass eine unserer beiden Hypothesen erfüllt ist. Grob gesagt, wenn wir Chihuahuas von Hunden anderer Rassen nach Gewicht trennen, dann müssen wir sicher sein, dass wir immer einen Hund auf der Waage haben (keinen Elefanten, keine Maus oder Katze). Andernfalls ist unser Test bedeutungslos. Dieses Prinzip wird am häufigsten verletzt, wenn die in der Ökonometrie verwendeten statistischen Kriterien ungenau angewendet werden.
Nachstehend finden Sie Beispiele für das Testen von Hypothesen für das Bernoulli-Schema.
Beispiel 1. Testen der Nullhypothese p=p0 im Bernoulli-Schema. Diese Hypothese ist einfach. Die Alternativhypothese kann eine der beiden folgenden Optionen sein (sie ist in beiden Fällen komplex). kup (Anzahl der Aufwärtsbewegungen in der Sequenz) wird in beiden Fällen als statistisches Kriterium verwendet, obwohl der kritische Bereich unterschiedlich definiert ist.
- p>p0, der kritische Bereich befindet sich rechts kup⋝kr
- p<p0, der kritische Bereich befindet sich links kup⋜kl
Spezifische Werte für kr und kl werden unter der Bedingung gefunden, dass die Wahrscheinlichkeit, dass die Statistik in den kritischen Bereich fällt, die gewählte Wahrscheinlichkeit eines Fehlers vom Typ 1 nicht überschreitet. Wie ich bereits erwähnt habe, werden all diese Wahrscheinlichkeiten unter der Bedingung berechnet, dass die Nullhypothese erfüllt ist (durch die Bernoulli-Verteilung mit dem Parameter p=p0).
Überprüfen wir diese Hypothese für p0=0,5 auf die gleiche diskretisierte Preisfolge. Der Wert für p0 ist insofern großartig, als er dem "random walk" Hypothese ("fair coin") entspricht.
Unten finden Sie das Skript p0_Hypothese.mq5, das diese Hypothese testet.
#include <Math\Stat\Binomial.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input int nm = 27; // total number of movements in the series input int kup = 16; // number of upward movements input double p0 = 0.5; // checked probability value input double alpha1 = 0.05; // type 1 error probability //+------------------------------------------------------------------+ void OnStart() { int kl, kr, er; kr=(int)MathQuantileBinomial(1.0-alpha1,nm,p0,er); kl=(int)MathQuantileBinomial(alpha1,nm,p0,er); Print("kl=", kl, " kup=", kup, " kr=", kr); Print("kup<=kl = ", kup<=kl); Print("kup>=kr = ", kup>=kr); }
Antwort:
- kl=9; kup=16; kr=18
- kup<=kl = false
- kup>=kr = false
Das Ergebnis zeigt, dass die Nullhypothese auf diesem Signifikanzniveau nicht zugunsten einer der Alternativen abgelehnt werden kann.
Beispiel 2. Nehmen wir an, wir hätten zwei Sequenzen mit den Längen n1 und n2, entnommen aus zwei Bernoulli-Schemata mit den Parametern p1 und p2. Die Nullhypothese liegt hier in der Aussage, dass die Gleichheit p1=p2 erfüllt ist, während die möglichen Alternativen verschiedene Arten ihrer Ungleichheit sind, von denen es hier ebenfalls zwei gibt. k2 wird in all diesen Fällen als statistisches Kriterium verwendet − Anzahl der Aufwärtsbewegungen in die zweite von zwei Sequenzen, wobei der kritische Bereich unterschiedlich definiert ist.
- p2>p1, der kritische Bereich liegt rechts k2⋝kr
- p2<p1, der kritische Bereich liegt links k2⋜kl
Der signifikante Unterschied zum vorherigen Beispiel besteht darin, dass es sich hier nicht um Aussagen handelt, die sich auf genaue p1 und p2 Werte beziehen, sondern nur um deren Verhältnis. Die kritischen Regionen werden auf die gleiche Weise wie im vorherigen Beispiel definiert, aber die Verteilung der Statistiken unter der Nullhypothese ist hypergeometrisch und nicht binomisch. In der mathematischen Statistik ist dieses Kriterium als Exakter_Test_nach_Fisher bekannt.
Unten sehen Sie das Skript p1p2_hypothesis.py in Python, das dieses Problem für die diskretisierte Preisspaltung in zwei Teile löst. Ich verwende die Aufteilung, die im vierten Beispiel aus dem vorigen Absatz erhalten wurde.
from scipy.stats import hypergeom n1 = 21; n2 = 6 k1 = 15; k2 = 1 alpha1 = 0.05 kl = int(hypergeom.ppf(alpha1, n1 + n2, k1 + k2, n2)) kr = int(hypergeom.ppf(1.0 - alpha1, n1 + n2, k1 + k2, n2)) print("kl =", kl, " k2 =", k2, " kr =", kr) print("k2<=kl =", k2<=kl) print("k2>=kr =", k2>=kr)
Antwort:
- kl = 2; k2 = 2; kr = 6
- k2<=kl = True
- k2>=kr = False
6. Schlussfolgerung
Der Artikel hat so wichtige Themen der mathematischen Statistik wie deskriptive Statistik, Schätzung von Intervallparametern, asymptotische Schätzungen und den bayesschen Ansatz in der Statistik nicht behandelt. Der Grund dafür ist, dass ich das Konzept einer Zufallsvariablen für ihre sinnvolle Verwendung erklären muss. Ich habe mich entschieden, dies im nächsten Artikel zu tun, um den aktuellen Artikel kompakt genug zu machen.
7. Angehängte Dateien
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | hyperg_be.py | Python script | Berechnung der Schätzung des hypergeometrischen Verteilungsparameters b. Example 5.1.1 |
| 2 | hyperg_ne.py | Python script | Berechnung der Schätzung des hypergeometrischen Verteilungsparameters n. Example 5.1.2 |
| 3 | Discr.mqh | MQL5 header file | Die Datei mit der Funktion setmv(), die in allen MQL5-Beispielen unten für die Preisdiskretisierung verwendet wird. |
| 4 | discret_prices.mq5 | MQL5 script | Das Skript, das die Preisdiskretisierung durchführt und das Ergebnis als eine Folge von 1 und -1 und auf einem Chart anzeigt |
| 5 | p_model.mq5 | MQL5 script | Berechnung der Parameterschätzung p im Bernoulli-Schema. Example 5.1.3 |
| 6 | p1p2_model.mq5 | MQL5 script | Berechnung der Parameterschätzungen von n1, p1 und p2 im Modell, das zwei Bernoulli-Schemata enthält. Example 5.1.4 |
| 7 | markov_model.mq5 | MQL5 script | Berechnung der Parameterschätzungen von p1 und p2 einer Markov-Kette. Example 5.1.5 |
| 8 | p0_hypothesis.mq5 | MQL5 script | Überprüfung der Hypothese, dass der Parameter des Bernoulli-Schemas gleich einer bestimmten Zahl ist. Example 5.2.1 |
| 9 | p1p2_hypothesis.py | Python script | Exakter Test nach Fisher Example 5.2.2 |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8038
 Über Methoden zum Erkennen überkaufter/überverkaufter Zonen. Teil I
Über Methoden zum Erkennen überkaufter/überverkaufter Zonen. Teil I
 Schnelle Werkzeuge für den manuellen Handel: Arbeiten mit offenen Positionen und Pending-Orders
Schnelle Werkzeuge für den manuellen Handel: Arbeiten mit offenen Positionen und Pending-Orders
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.