单一资产交易顺序中的风险评估. 续篇
Aleksey Nikolayev | 30 一月, 2018
目录
前言
让我们继续研究在前一篇文章中开始的风险评估理论,它将在两个例子中得出合乎逻辑的结论。另外,还将简要介绍概率论和数理统计的其它可能的应用。
对价格和交易系统的假定
上一篇文章中所用的方法可以用来分析任何系统的交易结果吗?为此,我们必须确定它的序列是一个独立的同分布变量序列。然而不幸的是,实践表明情况并非总是如此。
这两个条件都可能受到违反:既独立又同分布。在“资金管理的数学(The Mathematics of Money Management)”一书中, Ralph Vince 概述了解决这些问题的方法。他建议将系统分成满足所需条件的几个部分(子系统)。Vince 给出了两个例子,第一个讨论了一个在后续交易中有依赖性的系统。在这个例子中,顺序被分为两个部分,偶数和奇数的交易被视为是从不同的系统接收的。第二个例子探讨了一个金字塔系统 — 分步增加仓位的交易量,每步这样的增加都当成是一个独立的系统,这就形成了一个多系统的集合: 第一个包含第一步,第二个包含第二步,以此类推。
一旦研究了这样的系统"片段", 就需要找到一种方法来综合它们,创建一个“微型投资组合”来考量它们之间的依赖关系。这就需要类似于马科维茨的现代投资组合理论(Markowitz's Modern Portfolio Theory)的方法。
这已经看起来非常复杂了,但是还有更多要做的。让我们考虑一个系统,它的每个仓位都位于预先确定的价格水平: pstoploss 或者 ptakeprofit. 其比率k=|ptakeprofit-penter|/|pstoploss-penter| 根据指定指标在各个交易中有所不同。每个交易中的收益分布将非常简单 — 使用两个数值根据某种概率确定的分离的分布 -1 和 k。但是因为k的值对于每个交易都是特定的,不同的交易也就将有不同的分布。这样,当试图把系统分成“片段”的时候,他们的编号将等于交易的数量,这完全没有意义。在实际中,所使用的k的值在所有交易中可能是一样的(一些平均,典型值),这可以使得在真实交易中在简化版本的系统中进行分析。
综合所有可能的选项来对真实交易系统作风险分析:
- 把交易系统分成几个部分.
- 研究系统的简化版本.
- 分析交易序列,而不检验分布的独立和一致性。同时,可以使用其他分析方法来少许调整取得的风险值。
这种研究系统的方法明显不是通用的,并且不是一直适用。让我们让方法更加系统化一些,这要求对价格和系统作一些假定。
- 价格序列类似于随机波动,我们将不会尝试用数学公式来定义这个过程,而只是假定可以在真实价格上做某种计算而使它随机游走,前者的结果可以认为与后者一样。例如,这就是如何从价格序列中获得随机变量的分布的假设。
- 系统可以接收随机波动生成的报价,在这种情况下,随机价格“在平均程度”上必须接近真实价格。这就以为着要在较高时段有类似的动荡,在分时上有类似的价格波动分布,等等。
- 在系统(真实价格和随机波动)中交易之间依赖的结构在两种情况下也类似,而收益分布则可能相差很大。例如,如果所有的收益都增加同样的数量,分布就会有变化(向右平移),但是收益之间的相关系数还是会保持不变。
- 系统是这样处理的,它的交易全都是随机分布的,只有在时间上紧密连接(第二个交易在第一个交易关闭后再开启)的时候才会有大的内部依赖。
让我们详细描述一下这些假定,随机游走是一类扩展的随机过程,它可以是分离的或者连续的,两种类型都在分析计算中使用,而在计算机建模中只是用前者。这些类型是相关的 — 在连续时间内的随机游走可以从把分离的时间距离限制到趋向于0来达到。另外,随机游走可以使对称的(无趋势,平盘) 或者有正向/反向偏移 (上涨/下跌趋势)。最常考虑的是对称的随机游走,在这种情况下,假定的价格是这样变化的:
- 交易的结果不能使用任何指标来预测,这使建模大为简化。这样就只要研究用于退出交易的系统部分了,交易是在哪里和怎样开启就完全没有关系了。
- 平均情况下,利润为0。这并不妨碍任何的单个交易来取得任何数量的利润。但是开启了更多的交易后,它们结果的聚集会对应着某种概率分布。这种分布的具体形式取决于市场退出算法,但其期望值总是零。
这些推论时必须考虑在真实系统中使用真实价格测试(特别是优化时)。有必要的标准表明,得到的结果不是对称的具有足够可靠性的随机游走。这对两种交易收益分布和技术指标应用角度都是适用的。另外,从对称随机游走中搜索偏差在寻找交易系统想法的过程中也可能是有用的。作为例子,我们晚些时候将会探讨使用常言“跳空永远会被回填”的可能性。
叙述完交易系统的假设之后我们看一下它的限制,通常,它们需要在市场的入场和出场规则中具有简单性、统一性和透明性。这些规则不应当再额外加强交易之间的关系 (例如,参考余额曲线), 不能强制改变交易之间的退出方法 (例如,随机改变获利/止损比例), 交易本身不能过于频繁等等。这些条件的大致实现可以通过在理论上检查或者使用蒙特卡洛方法在计算机上建模。
收益分布. 概述
我们首先对分布的一般形式作了讨论,无论何时引入概率分布函数的概念,离散型和连续型通常都是隐含的。事实证明,除此之外,它们的混合也是可能的。也就是说,离散函数的形式为 P(x)=γcPc(x)+γdPd(x) 也是可能的, 其中 γc≥0, γd≥0, γc+γd=1, while Pc(x) and Pd(x) 是相应的连续型 (具有密度) 和离散型(分步)分布函数。
作为例子,让我们考虑一个简单的退出方法 — 以固定的止损和获利比例 k , 加上仓位持有的时间 t 来做退出。简单地说,基于获利/止损的交易具有离散分布,而根据时间退出的交易具有连续分布,总体的分布是它们的混合。当然,这样的复杂性会再做讨论。让我们做一个简单化的假设: 假设t退出足够大了,以至于γc可以忽略不计。假设 P(x)=Pd(x).
使用固定的跟踪止损是一个 γd=0 情况的实例,也可能 γd≠0 并且同时 γс≠0。例如,这可以是所讨论的两个例子的组合,使用这种方法,止损在交易开始的一段时间是不可移动的,而一旦满足的某个条件,它就可以像跟踪止损一样开始移动。
让我们具体化例子例来探讨上述风险理论(组合将不予考虑)。为每种特定的收益分布来计算最优风险值 ropt 的脚本程序将在下面提供,但是有时还有一些其它有趣的任务。例如,设置了风险,就有必要来计算 δ — 对应的可靠性水平(或者把最大平均收益 G0 作为选项). 在这种情况下,就有必要或者修改脚本程序,或者使用不同的输入数据来运行它,来取得想要的风险值。
固定止损和获利
就像上面提到的,分布将会被当成离散的,交易的收益可以从两个数值中取得: -1 金额 k, 而相应的概率为 P-1 和 Pk。而总的概率公式是, P-1+Pk=1。分布函数是分步的,有两个跳空,位于-1 和 k, 级数为 P-1 和 Pk. 分布的期望值是 M=-1*P-1+k*Pk。引入了变量 θ=Pk, 使得 P-1=1-θ, M=(1+k)θ-1。这样,我们就是处理着由参数 k>0 和 0≤θ≤1 定义的参数家族分布。在对称随机游走的情况下,M=0, 会使得 θ=θ0=1/(1+k).
会有一个i — n 个交易的收益, 每个等于 -1, 或者 k。
- 计算期待值的估算 M≈Mapr=(a1+a2+...+an)/n=(1+k)nk/n-1, 其中 nk 是获利交易的数量。如果 Mapr≤0, 就否定这个交易系统,因为它是亏损的。没有风险管理技巧可以把亏损的系统转化为获利。如果 Mapr>0, 就继续进行下一步。
- 有必要显示出交易不是在对称随机游走中交易的结果,为此,估计的 Mapr 必须显著大于0 (可靠性 δ). 要确认 M=0 为原假设。测试统计将是变量 S=n(Mapr+1)/(1+k)=nk, 当满足原假设时它有标准的二项分布 B(n,θ0)。使用 P(x) 表示其分布函数。为了达成原假设, 需要确认 P(S)>P(nθ0)+δ/2. 如果这一步成功,就继续到下一步,否则,排除此交易系统。
- 检验对于选择的最小平均收益G0是否满足所需条件。为此, G0 应当大于 δ- qδ 的分位数的随机变量分布 Λ, 这是在第一部分中引入的 (收益的算术平均值). 变量 Λ 与 Mapr一致, 通过 S 表示。现在,变量S是根据二项规则使用参数 n 和 θapr=nk/n 来分布的。如果满足条件,就继续下一步。如果不满足,确定需要满足条件的交易数的最小值n=nmin (使用固定的 θapr 逐步增加n,直到满足所需不等值达到要求)。
- 使用蒙特卡洛方法,取得经验分布 ρopt. 为此,需要模拟大数量的集合,其中每个都有 n 个交易收益。每个收益等于 k 的概率是 Pk, 并且等于 -1 的概率为 1-Pk。对于每个集合,使用在第一部分介绍的方法来确定数值 ropt,i,它们在总体上确定随机变量 ρopt 的经验分布。为了估算风险 ropt, 使用这个分布的分位数样本 δ。
#include <Math\Stat\Binomial.mqh> #property script_show_inputs input uint na=50; // 序列中的交易数量 input double kt=3; // 获利对止损的比例 input double pk=0.5; // 获利的概率 #define NX 300 // 序列中的最大交易数量 (用于搜索 nmin) #define NB 10000 //为蒙特卡洛方法生成的样本数量 #define NR 1000 // 风险的间隔分区数 double G0=0.15; // 最低平均收益 double D0=0.9; // 最低最小增益 double dlt=0.05; // 显著性水平 void OnStart() { if (D0<=0||D0>=1) {Print("D0 必须是正的并且小于1"); return;} double m=(1+kt)*pk-1; // 期望值 if(m<=0) {Print("期望值必须为正"); return;} double s=na*pk; // 统计 (获利交易平均数量) double s0=na/(1+kt); // 在0期望值时的获利交易平均数量 int ner; double p=MathCumulativeDistributionBinomial(s,na,1/(1+kt),ner); if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) 错误 ",ner); return;} double p0=MathCumulativeDistributionBinomial(s0,na,1/(1+kt),ner); if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) 错误 ",ner); return;} if(p<=p0+dlt/2) {Print("期望值近似于0"); return;} double q=MathQuantileBinomial(dlt,na,pk,ner),q0=na*(G0+1)/(kt+1); if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) 错误 ",ner); return;} if(q0>q) { Print("G0 大于收益算数平均值的分值 dlt "); uint nmin=na+1; for(;nmin<=NX;++nmin) { q=MathQuantileBinomial(dlt,nmin,pk,ner); q0=nmin*(G0+1)/(kt+1); if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) 错误 ",ner); return;} if(q0<=q) break; } if(nmin<=NX) Print("nmin = ",nmin); else Print("nmin 大于 ",NX); return; } // 蒙特卡洛方法 MathSrand(GetTickCount()); double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR; uint ir; ArrayResize(a,na); ArrayResize(c,na); for(uint ib=0; ib<NB;++ib) { for(uint i=0; i<na;++i) if(MathRandomNonZero()<=pk) a[i]=kt; else a[i]=-1; A=MathMean(a); A0=a[ArrayMinimum(a)]; if(A<G0) {ropt[ib]=0; continue;} if(A0>0) {ropt[ib]=1-stp; continue;} cn1=1; for(ir=1;ir<NR;++ir) { r=ir*stp; cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i]; if(cn2<cn1) {ropt[ib]=r-stp; break;} cn1=cn2; g=(MathPow(cn2,1.0/na)-1)/r; if(g<G0) {ropt[ib]=r-stp; break;} c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]); d=dcalc(c); if(d<D0) {ropt[ib]=r-stp; break;} } } ArraySort(ropt); uint nr=(uint)(dlt*NB); Print("ropt = ",ropt[nr]); } // dcalc() 函数接受 c1, c2, ... cN 数组值而且 // 返回最小收益 d. Assume that c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(uint i=1; i<na;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; } //+------------------------------------------------------------------+
使用默认参数,这个脚本程序计算以下的风险值:
- ropt = 0.011
这对应着每个交易使用系统 1.1% 的资产。
固定的跟踪止损
假定有一个买入交易 (将会隐含用于卖出交易的修改). 使用 Δp=penter-pstop 来表示进场价格和初始止损的差距。当价格达到数值 pmax-Δp 时交易将会被关闭,其中 pmax 是交易开启后的最高价格。如果价格序列是使用连续的时间和线性偏移的随机游走来建模的,收益分布可以使用明确的形式获得,它将是与左边偏移1的指数分布。分布函数可以更准确地使用公式 P(x)=1-exp(-θ(x+1)) 如果 x≥-1, 以及 P(x)=0 如果 x<-1 来表示。使用正的偏移(上升趋势),参数 θ 满足不等式 0<θ<1, 使用负的偏移 (下跌趋势): θ>1 ,还有为0 (平盘): θ=1. 期望值是由公式 M=1/θ-1 定义的。
因为我们假定,真实价格与随机游走很接近,序列中交易收益的分布也将会这样考虑,使用某个数值的 θ 参数。这就给出了一个单个参数族的连续分布。在趋势中的 θ 参数的特定值依赖于趋势的强度和跟踪止损的比例。让我们用指数统计的方法来计算现有交易历史的指数分布 (在这种情况下,使用最大似然估计)。对于进一步的计算,很重要的是确定数量的这样的变量的综合(以及算术平均)具有良好的可研究的伽玛分布。
让这里有一个ai — n个交易的收益, 每个交易满足 ai>-1 (为此,忽略滑点). 与前一章一样,提出了进一步行动的计划。
- 计算期望值的估算值 M≈Mapr=(a1+a2+...+an)/n,如果 Mapr≤0, 则否定此交易系统,它无法获利。如果 Mapr>0, 就进行下一步。
- 尝试反驳 M=0 假设。测试统计变量 S=Mapr+1, 它的伽玛分布 Γ(n,1/n) (如果满足 M=0 的原假设),使用 P(x) 表示它的分布。然后,为了同意另外的假设, 必须实现 P(S)≥P(1)+δ/2 的不等式。如果成功否定了原假设,就进行下一步,如果不是 - 就排除该系统。
- 检查 G0 的基本条件。首先,需要取得参数 θ=θapr 的估算值,使用最大似然估计,我们得到 θapr=1/(1+Mapr)。Λ 的值将根据伽玛分布 Γ(n,θapr/n) 来进行分布,向左偏移1。如果这个伽玛分布的 δ 分值不小于 G0+1,所需的条件就能被满足。如果满足条件,就继续下一步,如果没有满足,就可能需要确定满足此条件的最小交易数量。为此,要逐步增加 n 的值并把 nmin 设置为等于1,来看是否满足需要的条件。
-
它的执行方式和本文的前一章中是相同的。变化只涉及随机产生收益的分布。这一次我们使用指数分布,把参数设为 θ=θapr 向左偏移1。MQL5 中的统计库使用的是略有不同的参数形式用于指数分布的 — 参数 μ (期望值), 通过 θ 或者 M 作为 μ=1/θ 或者 μ=M+1 来表达。
#include <Math\Stat\Gamma.mqh> #include <Math\Stat\Exponential.mqh> #property script_show_inputs input uint na=50; // 序列中的交易数量 input double tht=0.65; // 指数分布参数 0<tht<1 #define NX 300 // 序列中交易的最大数量 (用于搜索 nmin) #define NB 10000 // 用于蒙特卡洛方法生成样本的数量 #define NR 1000 // 风险间隔分区的数量 double G0=0.15; // 最小平均收益 double D0=0.9; // 最小最低收益 double dlt=0.05; // 显著性水平 void OnStart() { if(D0<=0 || D0>=1) {Print("D0 必须为正且小于1"); return;} double m=1/tht-1; // 期望值 if(m<=0) {Print("期望值必须为正"); return;} int ner; double p=MathCumulativeDistributionGamma(m+1,na,1.0/na,ner); if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;} double p0=MathCumulativeDistributionGamma(1,na,1.0/na,ner); if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;} if(p<=p0+dlt/2) {Print("expected value is close to zero"); return;} double q=MathQuantileGamma(dlt,na,1/tht/na,ner),q0=G0+1; if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) 错误 ",ner); return;} if(q0>q) { Print("G0 大于 dlt 收益算数平均分值"); uint nmin=na+1; for(;nmin<=NX;++nmin) { q=MathQuantileGamma(dlt,nmin,1/tht/nmin,ner); q0=G0+1; if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) 错误 ",ner); return;} if(q0<=q) break; } if(nmin<=NX) Print("nmin = ",nmin); else Print("nmin 大于 ",NX); return; } // 蒙特卡洛方法 MathSrand(GetTickCount()); double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR; uint ir; ArrayResize(a,na); ArrayResize(c,na); for(uint ib=0; ib<NB;++ib) { for(uint i=0; i<na;++i) { a[i]=MathRandomExponential(m+1,ner); if(!MathIsValidNumber(a[i])) {Print("MathRandomExponential() 错误",ner); return;} a[i]-=1.0; } A=MathMean(a); A0=a[ArrayMinimum(a)]; if(A<G0) {ropt[ib]=0; continue;} if(A0>0) {ropt[ib]=1-stp; continue;} cn1=1; for(ir=1;ir<NR;++ir) { r=ir*stp; cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i]; if(cn2<cn1) {ropt[ib]=r-stp; break;} cn1=cn2; g=(MathPow(cn2,1.0/na)-1)/r; if(g<G0) {ropt[ib]=r-stp; break;} c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]); d=dcalc(c); if(d<D0) {ropt[ib]=r-stp; break;} } } ArraySort(ropt); uint nr=(uint)(dlt*NB); Print("ropt = ",ropt[nr]); } // dcalc() 函数接受 c1, c2, ... cN 数组值而且 // 返回最小收益 d. Assume that c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(uint i=1; i<na;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; } //+------------------------------------------------------------------+
使用默认参数,可以取得下面的风险值:
- ropt = 0.015
这对应着每个交易使用系统 1.1% 的资产。
在 前一部份 讨论过的三十个交易的序列作为例子,得到了根据跟踪止损退出的系统,所以,我们的方法可以用在它上面。与之前探讨的方法类似,它显示出这个序列不适合于在给定条件 (n, δ, G0, D0) 下进行交易。这个结果就算是在去除点差的的情况下也不会改变,在所有的 ai 上加上一个小的正数, 这样所有的 i=1,...,n 条件 ai>-1 都将能够满足。
注意: 如果脚本程序对于默认参数生成了错误编号 4 ,表明终端需要进行必要的更新。在这种情况下,脚本中的一部分 (从21行到42行) 要被注释掉。这个部分包含有关于伽玛分布的计算,对于它们,您可以在R中使用下面的脚本。
na=50; tht=0.65; dlt=0.05; G0=0.15; nx=300 m=1/tht-1; l1=l2=l3=FALSE l1 = m > 0 if (l1) l2 = pgamma(m+1,na,scale = 1/na) > pgamma(1,na,scale = 1/na)+dlt/2 if (l2) l3 = G0+1 <= qgamma(dlt,na,scale = 1/tht/na) if(!l1) cat("m 必须大于 0\n") if(l1 & l3) cat("G0 和 na 是可以的\n") else cat("na 太小或者 G0 太大了\n") if(l1 & l2 & !l3) {for (nmin in (na+1):(nx+1)) {if(G0+1 <= qgamma(dlt,nmin,scale = 1/tht/nmin)) break()} if (nmin<=nx) {cat("nmin =",nmin)} else {cat("nmin >",nx)} }
下一步怎样做?
很明显,上面的方法不能认为是完整和最终的,为了简单性,交易被当作是独立并且相同分布的。但是这需要进一步的研究并且证明不是这样的。这可能是有用的分布收益率属于或接近一个特定的参数族,但是这个成员可能也需要另外的研究。
我们解决了分布参数的点估计,并没有寻求它们的置信区间。但是一旦它们被构建出来,系统的盈利稳定性问题就会随着这些参数的波动而出现。
当然,多种可能的方法并不意味着它们需要不断地使用,而且必须同时使用。但最好是了解他们,并能够在必要时使用它们,而不是“被随机愚弄”。
应用概率论的其他一些可能的方向将在文章的其余部分简要地概述。
统计和跳空
跳空是指两个连续的柱的收盘价和开盘之间有很大的跳跃。这些柱在它们之间也需要有很大的时间间隔,通常相信,“跳空总会被回补”,回补跳空的意思是,在出现跳空之后,价格最终总会回到跳空之前柱的收盘价,有的时候,交易者会尝试根据这个常见现象来构建一个交易系统。是否有可能呢?
直线上的对称随机游动理论指出,任何价格值都会在足够大的时间内到达,概率几乎等于一。也就是说,在这种情况下,“跳空总是被回填”几乎是肯定的。但是,正如我们所知道的那样,对称随机游动是不可能赚钱的。这是否意味着基于跳空的系统没有存在的可能性?
并非如此。不仅跳空缩小的事实是重要的,而且跳空填补的方式也很重要。这并不是指每一个具体的跳空,而是它们的某些集合。然后可以考虑与它们相关联的随机变量的经验概率分布。实际价格与对称随机游走模型之间可能存在差异。这种差别可能相差很大,这可能是由于跳空方向运动不足,直到闭合时间小于随机游走时,以及更多只有用概率论和数理统计的方法才能确定这些偏差的存在和意义。在核实这些偏差之后,交易系统可以建立在它们的基础上。你也可以试着检验一个分类差距的理论。
让我们考虑最简单的版本来寻找随机游走的偏差。这将是衡量价格在跳空方向上移动多少,直到它被回填为止。还可以通过价格历史得到该变量的经验分布,并与理论值进行比较。利用拟合优度准则可以较好地比较这两种分布。
考虑离散时间对称随机游动的模型。让大跳空在其中(如在实际价格)是罕见的,并让该模型接近于连续的时间间隔的步行(维纳过程)在调控之间的时间间隔。符号介绍: g — 跳空的大小, m — 在跳空回填之前,在跳空方向上的最大移动。然后随机变量 x=m/g 将有一个分布函数,近似于函数 P(x) — 如果 x≥1 则P(x)=1-1/x, 而如果x<1则 P(x)=0。下图展示了介绍的数值:
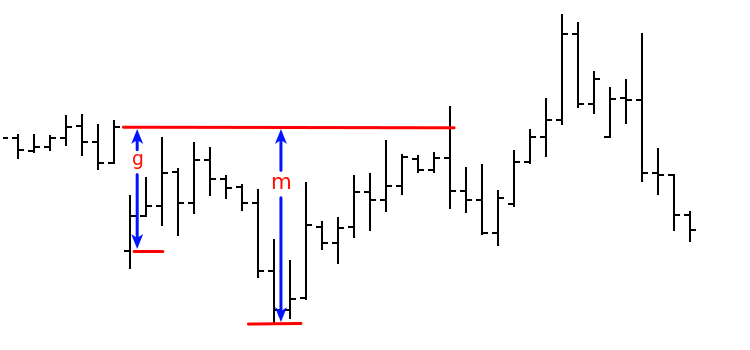
这个提出的课题需要更详细、更广泛的研究。因此,我们仅限于以下几点:
- 跳空研究的问题在于它们的稀有性。在研究与它们相关的分布时,这一点尤其正确,这取决于它们的参数(类似于下一章中描述的方式)。
- 为了检验跳空分类的理论(例如,在这里),需要建立一个更复杂的模型,它不仅考虑到价格的跳空,直到填补它,而且还要考虑以前和以后的差距。这将导致所考虑的随机变量的数目增加。反过来,由于缺少上面指定的数据,这可能导致问题。
统计学机器学习
考虑交易系统的方案。每一笔交易,一组参数h是已知的,它的值必须唯一确定的交易量和现有的算法(不是价格!)。h的值必须在入场时间上确定知道,它可以是一些技术指标值,等等。在机器学习术语中,h是一个特性集合。
以防万一,做下面的精炼。一般来说,当谈到一个交易系统时,不是一个特定的系统,而是它们的参数族。测试和优化的任务是通过确定和确定一个特定的参数值来从这个家庭中选择一个特定的系统。为了不复杂的演示文稿(不要混淆h参数定义从家庭系统的选择),本章考虑一个特定的系统,而不是他们的家族。优化的问题将在下一章中简要讨论。
固定一个特定的h值后,获得进入/退出市场的一个固定的算法。这给出了概率的固定分布。请注意,对于相同的h,可能有不同的收益。收益分布是固定的,而不是它们的特定值。
这给我们带来了恢复收益分布规律的特点在h的依赖问题。初始数据是一系列参数值和相应的收益率的历史记录(hi,ai)。这些问题都是用统计机器学习的方法解决的。事实证明,在解决确定性(非随机)依赖问题时,这些方法与机器学习中使用的方法没有根本区别。
让我们稍微澄清一下这个问题的提法,假设收益率的分步属于某一家庭,给出了一系列 (hi,ai) 对,收益分布 ai 属于依赖于参数θ的参数化分布家族,就有必要恢复依赖 θ(h)。在任意函数中不寻求这种依赖关系——初始数据不足以满足这个要求。通常在函数的参数族中求它: θ(h)=θ(h,β), 其中参数 β 由一系列 (hi,ai) 对确定, 要考虑到一些优化需求。寻找函数的依赖关系、参数的最优性条件和寻找该最优值的方法的广泛的函数族定义了机器学习方法的巨大变化。
从这几种方法中,有必要从交易者的观点中选择有意义的方法(例如,有助于增加利润或减少收益)。在选择参数β的最优性条件时,这一点尤其重要。当这个条件改变时,结果依赖 θ(h,β) 可能会有很大变化。
假设给定的参数族的收益分布 ai, 风险估计问题与上述两种情况类似。因为已经构建了 θ=θ(h) 的依赖, 并且知道对于每个给定的θ如何选择风险值 ropt, 依赖 ropt=ropt(h) 也就知道了。该系统的建设可以认为是完整的。
交易系统的统计和优化
考虑以下简单的优化变体。运行N次系统,每次有n个交易,从它们的结果中选择一个小的数值 εN(拥有最高的平均收益), 其中 0<ε<<1,使用 mopt 表示所选运行中的最小平均值, 而且把它作为优化系统将好到什么程度的指标,
现在让我们考虑一个系统,它将作为一个例子,优化结果应该谨慎对待。这个例子虽然是人为的,但足以说明问题的实质。考虑一个具有零期望收益率和随机依赖于参数的系统,
该系统将在固定时间随机输入条目,将使用相同概率的随机数发生器来选择方向。每个测试运行前该生成器的种子值将由参数的函数定义。因此,每一组参数都会得到相同的序列,而改变这些参数将以完全随机的、不可预知的方式改变序列。市场退出将根据固定的止损/获利水平比例,以常量比例 k 来执行,另外,认为测试时间段没有趋势,
显然,缺乏趋势将导致该系统收益率的预期值接近于零(考虑到价差的小负值)。使用n表示交易的数量,则收益的算术平均 m 在n个交易的序列中将是一个随机变量,它使用随机变量 nk 表示 — 序列中获利交易的数量: m=(1+k)nk/n-1. 变量nk 拥有二项分布,参数为 1/(1+k) 和 n。
在 N 足够大时, 数值 mopt 将接近于 (1-ε) m变量分布的分值,我们可以发现,尽管这个"交易系统" (因为0期望值)明显没有什么用, mopt的值将非常高。为了更加清晰, 设置: k=3, n=50, ε=0.1 就能得到 mopt=2.52。
很明显,在实际测试中,一切都是不同的,在实际的、有意义的系统中要复杂得多。然而,在这种情况下,有可能并有必要了解优化系统的优点是否随机。
附件
| No. | 名称 | 类型 | 描述 |
|---|---|---|---|
| 1 | bn.mq5 | 脚本程序 | 固定止损和获利的风险计算 |
| 2 | exp.mq5 | 脚本程序 | 固定跟踪止损的风险计算 |