单一资产交易顺序中的风险评估
Aleksey Nikolayev | 17 十月, 2017
前言
在这篇文章中, 我们将借鉴拉尔夫·文斯 (Ralph Vince) 管理仓位的思路 (在这一点上, 回忆 凯利 (Kelly) 公式 也是有用的)。这也被称为最佳 f。在该理论中, f 是每笔交易中部分资金所要承担的风险。根据文森 (Vince), f 根据盈利的最优化条件 (最大化) 来选择。在交易中使用这种理论时, 出现了两个问题。它们是:
- 帐户回撤太大。
- f 只有在成交历史中才能知道。
尝试解决这些问题只是本文的目标之一。另一个问题是还要尝试将概率理论和数学统计引入交易系统分析当中。这会导致偶尔偏离主题。我不会从基础知识说起。如果有必要, 读者可以参考 "技术分析的数学: 应用统计进行股票、期权和期货交易"。
本文提供了示例。它们只是本文中所研究理论的一个例证, 因此, 不推荐在实际交易中使用它们。
引言。缺乏不确定性
为了简单起见, 我们假设资产价格是按照资本的单位, 以其单位价值表达, 且无其它近似方式。最小交易量增量是资产单位当中的固定值。交易的最小非零交易量等于此增量。我们将使用一个简单的交易模型。
每笔交易均定义为, 类型 (买入/卖出), 交易量 v, 其中入场价格, 止损和离场价格与 penter, pstop 和 pexit 相对应。
明显的限制:
- 非零交易量 v≥0
- 离场价格必须低于买入时的入场价格: pstop<penter
- 离场价格必须高于卖出时的入场价格: pstop>penter。
我们来介绍一下以下的符号:
- C0 — 入场交易前的资本;
- C1 — 交易离场后的资本;
- Cs — 止损被触发后的资本;
- r — 止损触发时初始资本损失的份额,
就是 C0−Cs=rC0。
对于买入类型的交易: C1=C0+v(pexit−penter) 和 Cs=C0−v(penter−pstop)。
同样对于卖出类型的交易: C1=C0+v(penter−pexit) 和 Cs=C0−v(pstop−penter)。
经过简单的重新排列, 我们会达致 C1=C0(1+ra) 其中 a=(pexit−penter)/(penter−pstop)。这些表达式对于买卖两种类型的交易均是真实的。我们把 r 值成为 交易风险 且 a 值 称为交易的收益。
我们来申明对于我们的模式其管理风险的问题。我们假设我们有 n 笔交易收益为 ai 其中 i=1..n,。我们想评估风险 ri。应考虑到这一点 ri 只能取决于入场交易时的已知值。通常认为风险是相等的 ri=r 其中 0≤r<1。r=rmax 是最大盈利 Cn=C0(1+ra1)(1+ra2)…(1+ran) 的值。
我们有一个类似的方法, 但略有差异。我们会考虑到一些限制。这些是一系列交易中的最大回撤和平均收益。我们来介绍一下以下的符号:
- A0 是全部 ai 中最少的,
- A=(a1+a2+…+an)/n 是它们的算术平均数。
A0≤A 一直为 true, 且仅当所有 ai=A0 时才能实现平等。我们更详细地研究对 r 的限制。
- Cn=Cn(r)>0 自其之后 1+rA0>0。如果 A0≥−1 则对于所有 0≤r<1 皆为 true。当情况为 A0<−1 时我们收到 0≤r<−1/A0。我们可以看到, 仅当交易止损离场时伴随滑点, 才会出现针对 r 的额外限制。结果就是, 限制将被写为 0≤r<rc 此处 rc=1, 如果 A0≥−1, 以及 rc=−1/A0 如果 A0<−1。
-
于是我们将平均收益 g 定义为 Cn=C0(1+gr)^n。
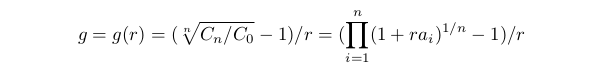
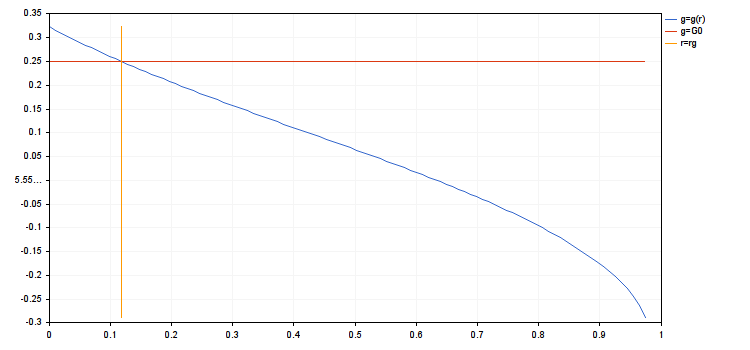
换言之, g 可称为一系列有关承受风险交易的平均收益率。g(r) 函数在执行前一点的限制时定义。它有一个可移动的奇点 r=0: 如果 r→0 则 g(r)→A, 并且我们可接受 g(0)=A。仅在如果所有 ai=A, 它也许被显示为 g(r)≡A。如果其中 ai 有所不同, 则当 r 增加时, g(r) 减少。限制将如下所示 g(r)≥G0>0。常数 G0 取决于许多事物 - 交易条件, 交易者的偏好等等。在当前的模型中, 可以说, 如果 G0>A, 那么满足不等式的一组 r 将为空。如果 G0≤A, 则我们的限制就像这样 0≤r≤rg 此处 rg 是方程式 g(rg)=G0 的解。如果这个方程式没有解的话, 则 rg=1。
-
为了评估最大回撤, 我们来考虑其相反值:
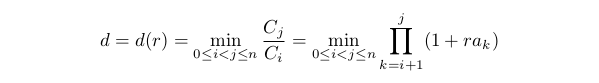
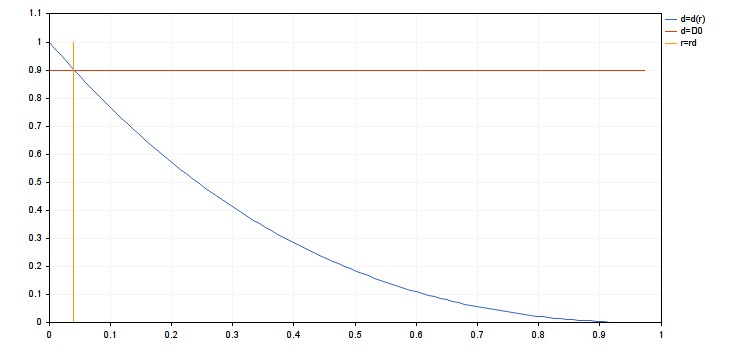
该值可以称为最小增益。这很便利, 因为当第一点规定的限制被满足时, 它始终是正数值且有限。很明显 d(0)=1。如果 A0<0, 则在第一点限制的区域内, 当 r 增加时, d(r) 减少。限制将会写为 d(r)≥D0 此处 0<D0<1。D0 越大, 允许的回撤越小。我们重写我们的限定 0≤r≤rd 此处 rd 是方程式 d(rd)=D0 的解 (如果此方程式没有解, 则 rd=1)。
-
当交易入场时, 交易量 v 不能是任意值。必须除以某个数值 Δv>0 就是 v=kΔv 其中整数 k≥0。那么, 对于第 i 笔交易:
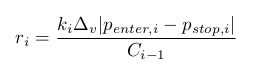
显然, 所有 ri 重合是极其不可能的。因此, 上述问题确实有一个精确解。我们将寻找一个近似解。我们仅限于计算这样一个最小的 rv 以便 ri 可在 [0,rv] 之内至少取得一个非零值。
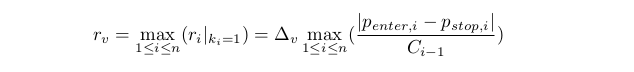
我们还要确定一个粗略的评估 rvr≥rv。自前一点实现的限制之后 Ci≥D0C0>0。那么它之后 (请注意 d0 和 D0 意思相同):
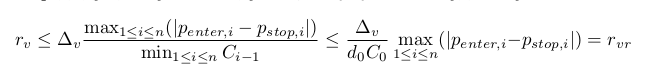
这种评估极其方便, 因为它与资本有更简单的关系。它只取决于资本的初始值。
我们假设满足前三条限制的集合是非空的。然后它将看起来像间隔 [0,ra] 此处 ra=min(rc,rg,rd)。
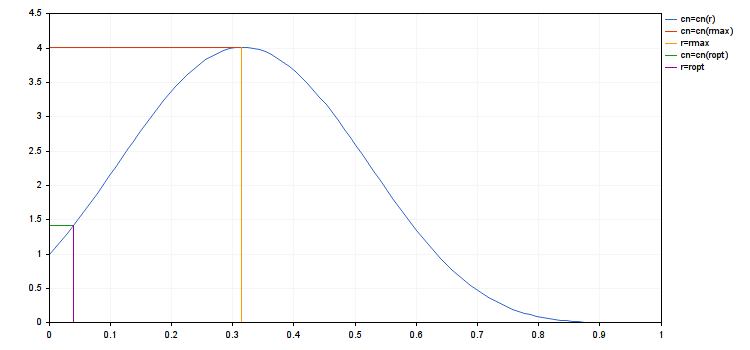
我们还假定第四条限制也是满足的。这就要求 ra≥rv。我们将考虑一个最大化的问题 Cn=Cn(r)。在重大情况下, A>0 和 A0<0。该函数在间隔 [0,rmax] 上递增, 并且在间隔 [rmax,rc] 上递减。在此 rmax 是一阶导数 dCn(r)/dr=0 的平稳点。
我们可以轻松发现 ropt 即在间隔 [0,ra] 上的最大化 Cn(r): ropt=min(ra,rmax)。还剩下两种情况: 1) A0≤A≤0 以及 2) 0≤A0≤A。在第一种情况下, ropt=rmax=0, , 以及在第二种情况下 rmax=rс 且 ropt=ra 。
现在, 我们将研究集合由限制定义的情况, 为空。仅在两种情况下是可能的: 1) G0>A 或 2) ra<rv。我们只需假设 ropt=0。
现在, 我们要考虑交易量的离散性质来搜索值 ri。令 Ri 作为间隔 [0,ra] 上一个非空有限集合, 适合第 i 笔交易的风险 ri。选择 ropt,i 即在 Ri 上的最大值 Cn(r)。如果 ropt∈Ri 则 ropt,i=ropt。如果 ropt∉Ri, 则有两种情形是可能的: 1) 所有点 Ri 属于 ropt 的一侧, 以及 2) 点 Ri 属于 ropt 的一侧。在第一种情况下, ropt,i 将为来自 Ri 的点, 靠近 ropt。在第二种情况下, Ri 将是靠近 ropt 每一侧的两个点。ropt,i 将是 Cn(r) 更大的那个点。
不确定。引入示例
我们令引言中研究的模型更加复杂。我们假设我们知道 ai 的数量 n, 但我们不知道它们的顺序。这样, 它们的随机排列是允许的。我们看看上面得到的结果会有什么变化。在前两点中, ai 的随机排列不会改变任何东西。如果使用更粗略的评估 rvr, 则第四点不会有任何变化。
在第三点可能有变化。实际上, 如果已按某种方式排序, 那么在负值之间没有正值, 则回撤将会最大。相反, 正数和负数均匀混合将降低回撤。一般情况下的排列总数等于 n!。若 n 在数十的范围内, 这是一个非常大的数字。理论上, 我们可以解决在引言中的来自顺序 ai 中 j=1..n! 个排列的问题集合, 并获得 rd,j 的集合。然而, 这是一个持续存在的问题。我们不知道要选择什么排列。为了应对这种不确定性, 我们需要部署概率论和数学统计学的概念和方法。
我们考虑一组数字 rd,j 作为取决于排列的 ρd=ρd(j)=rd,j 函数值。就概率论而言, ρd 是等效于一组 n 个排列的一组基本事件的随机变量。即使某些 ai 相同, 我们也会将它们视为不同。
我们还假定所有 n 个排列同等可能。那么它们当中每一个的概率是 1/n!。这违背了基本事件集上的概率测度。现在, 我们可以定义概率的分布 ρρd(x)=n(x)/n! 对于 Pd 此处 n(x) 是 rd,j<x 的 n 个排列的数量。在这一点上, 必须为回撤指定限制资格。最小允许 D0 当中, 我们必须指定可接受的明显等级 0<δ<<1。δ 指出哪些超过阈值概率的回撤我们是可忽略的。之后, 我们可以定义 rd(δ) 作为分布 Pρd(x) 的 四分位 δ。为了找到这个问题的近似解, 我们将随机生成大量的 nt, 此处 1<<nt<<n!, n 个排列。让我们为它们中的每一个找到值 r d, j , 其中1≤j≤nt 。然后, 对于 rd(δ) 进行评估, 我们可以采集 rd,j 群体的样本四分位 δ。
虽然这种模型有点人为制造, 但它有其用途。例如, 我们可以取 rd, 计算初始交易序列, 并找到概率 pd=Pρd(rd)。显然, 0≤pd≤1 不等式是有效的。pd 接近零表示由相互靠近的亏损交易造成的大幅缩水。接近一的 pd 表明盈利和亏损交易是均匀相混的。这种方式不仅能发现一连串交易中的一系列亏损 (例如, 在 Z 分值方法中), 而且还对回撤有一定程度上的影响。其它指数的生成可以依赖于 Pρd() 或是 rd。
不确定。一般情况
我们假设有一系列的收益交易 ai, 1≤i≤n。我们还假设该序列是群体中独立序列的实现, 并且具有相同分布的随机变量 λi。我们把它们的概率分布函数写成 Pλ(x)。它应该具有以下属性:
- 正面的数学期望 Mλ
- 来自下面的限制。这个数字 λmin≤−1, 当 x<λmin 时 Pλ(x)=0, 而当 x>λ0 时 Pλ(x)>0。
这些条件意味着平均收益率为正。尽管, 很可能有亏损交易, 但通过限制风险, 总不会在一笔交易中损失所有资本。
我们来陈述识别风险量级的问题。类似于前一部分的例子, 我们应该研究随机变量 ρopt 替代引言中计算的 ropt。然后, 设定了明显等级 δ, 我们来计算 ropt=ropt(δ) 其中 δ 是一个 Pρopt(x) 分布的四分位。具有这种风险的系统可以使用, 直至遇到回撤, 且平均收益在设定范围内。当它们超出范围边界时, 该系统应该被舍弃。误差概率不应超过 δ。
应该强调 δ 越小的重要性。当 δ 若是很大时, 使用得到的标准没有任何意义。只有在 δ 很小的情况下才能相信这两个事件相互联系: 1) 由于行情的变化, 系统不起作用, 2) 回撤太大或收益太小。除了已经讨论的错误, 还可以考虑另一个错误。当出现这种错误时, 我们不会注意到影响我们系统的回撤和收益的行情变化。没有必要讨论这个错误, 因为它不会影响系统的收益。
在我们的理论中, 它体现了一个事实, 即 Pλ(x) 和 Pρopt(x) 分布的变化对于我们来说不重要。唯一重要的是 δ 四分位 Pρopt(x) 的变化。特别地, 这意味着对于收益序列没有 平稳性 需求。说到这一点, 我们将需要平静性来恢复最终样本的收益分布规律 ai, 1≤i≤n。在此, 分布没有明显变化的需求替代绝对的平稳性也许就足够了。
在末尾, ρopt 可以借助 λi 表达, 虽然这个关系很复杂 (它通过其它随机中间变量表达)。这就要求研究由 λi 函数定义的随机变量, 并构建它们的分布。为此, 我们需要知道 Pλ(x)。我们来列出三个变体的有关分布信息哪些我们可以有。
- 有一个确切的Pλ(x) 表达, 或有一种方式可令被分析的交易系统进行任意近似。通常, 仅当针对资产价格行为创立假设时才有可能。举例来说, 我们可以考虑 随机游走假说 是真的。在交易中使用这些信息是太不可能的。这样得出的结论是不切实际的, 通常否认集体盈利的可能性。这可以区别对待。使用这个假设, 我们可以构建 空假设。然后, 使用经验数据和 一致性测试, 我们即可以放弃假设, 亦或承认我们在用我们的数据时不能丢弃它。在我们的例子中, 这样的经验数据就是序列 ai, 1≤i≤n。
- Pλ(x) 已知属于或接近分布的一些 参数族。从前一点来看, 有关资产价格的假设并不遥远, 这是可能的。当然. 分布类型家族也由交易系统的算法定义。分布参数精确值的计算使用序列 ai, 1≤i≤n 及 参数统计 方法。
- 在序列 ai, 1≤i≤n 当中, 一些 Pλ(x) 的常用属性是已知的 (或假设的)。例如, 这也许是关于存在的有限期望和分散的假设。在这种情况下, 我们会用一个 样本分布函数 作为 Pλ(x) 的近似。我们将基于相同的顺序 ai, 1≤i≤n 构建它。使用样本分布函数替代精确值的方法称为 自举。在某些情况下, 没有必要知道 Pλ(x)。举例来说, 随机变量 (λ1+λ2+…+λn)/n 当 n 很大时可作为正常分布 (有限的分散 λi)。
本文将继续使用第三个变体中描述的假设。前两个变体将会进一步描述。
我们将研究在引言中进行的计算如何变化。替代绝对数字 A0 和 A, 我们用同样的方式处理通过 λi 表达的随机变量: Λ0=min(λ1, λ2, …, λn) and Λ=(λ1+λ2+…+λn)/n。
我们看看在 n 不受限制地增长时它们的渐近行为。在这种情况下, 总是为真 Λ0→λmin。我们假设 λi 有限的分散 Dλ。则 Λ→Mλ。如上所述, 我们可以精准地认为 Λ 按预期 Mλ 正常分布, 以及分散 Dλ/n。如果 Mλ 和 Dλ 的确切值未知, 则可以使用 ai 计算样本模拟。Λ0 和 Λ 的经验分布也可以用来构建自举。
通过自举方法计算 ropt(δ) 之前, 我们应该考虑以下几点, 有关引言中的计算如何变化:
- 在第一点中, 由于Λ0 的渐近行为, 评估可以粗略转化为 rc=−1/λmin 的值。对于采样分布, λmin 与 А0 一致, 所以, 在这一点上的一切都保持不变。
- 重要的是确保条件 G0≤Λ 被破坏的概率不大于 δ。为此, Λ 的四分位 δ 必须不得小于 G0。为了近似计算该分位数, 我们将使用 Λ 的正态近似分布。结果就是, 我们将获得 nmin — 以下来自交易数量的评估需要分析。可以调整标准自举方法, 并且可以构建长度增长的样本集, 以便查找 nmin。从理论的角度来看, 我们或多或少与近似的正态分布相同。
- 在第四点, 与之前一样, 我们将对 rvr 进行粗略评估。
我们来设置 nb — 将产生的收益序列的数量。在执行自举的循环中, 我们将遍历每个 j=1..nb 的风险大小限制。考虑到以上几点, 我们只需要计算 rg(j), rd(j), rmax(j) 和 ropt(j)。如果在某个 j 处的的集合为空, 则假设 ropt(j)=0。
在自举结束时, 我们将有一个数值数组 ropt[]。依此数组计算出的样本 δ 分位数, 将其视为问题的解。结论
上面所写只是主题的开始。我将简要提及以下文章将致力于哪些内容。
- 为了使用交易模型作为独立分步的序列, 我们应该对资产价格和交易算法做出一些假设和推测。
- 这一理论对于某些交易离场的具体方法必须加以指定, 例如固定止损/止盈和固定尾随停止。
- 还有必要展示这种理论如何用于建立交易系统。我们将研究如何利用概率论构建缺口系统。我们还将触及机器学习的使用。
引言的附录
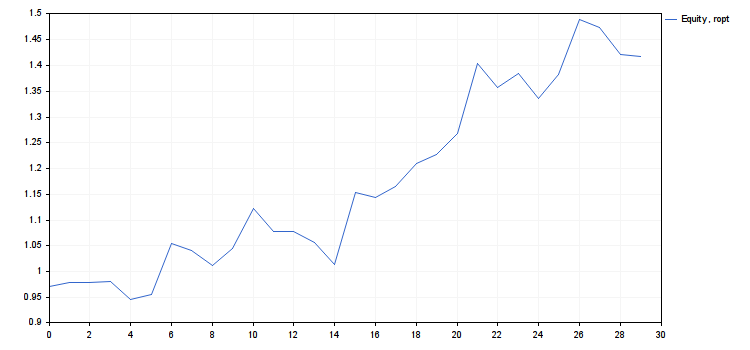
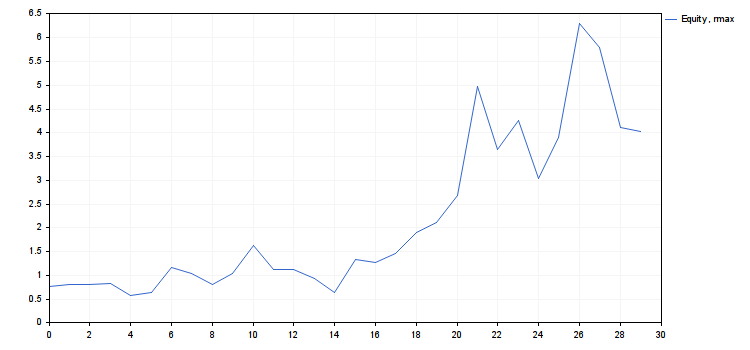
以下是 r_intro.mq5 脚本的代码, 其在图表上工作的数值结果
#include <Graphics\Graphic.mqh> #define N 30 #define NR 100 #property script_show_inputs input int ngr=0; // 显示的图表数量 double G0=0.25; // 最低平均收益 double D0=0.9; // 最低最小增益 // 初始资本 c0 被假定为等于 1 void OnStart() { double A0,A,rc,rg,rd,ra,rmax,ropt,r[NR],g[NR],d[NR],cn[NR],a[N]= { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // 交易收益率 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; A0=a[ArrayMinimum(a)]; A=0; for(int i=0; i<N;++i) A+=a[i]; A/=N; rc=1; if(A0<-1) rc=-1/A0; double c[N]; r[0]=0; cn[0]=1; g[0]=A; d[0]=1; for(int i=1; i<NR;++i) { r[i]=i*rc/NR; cn[i]=1; for(int j=0; j<N;++j) cn[i]*=1+r[i]*a[j]; g[i]=(MathPow(cn[i],1.0/N)-1)/r[i]; c[0]=1+r[i]*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+r[i]*a[j]); d[i]=dcalc(c); } int nrg,nrd,nra,nrmax,nropt; double b[NR]; for(int i=0; i<NR;++i) b[i]=MathAbs(g[i]-G0); nrg=ArrayMinimum(b); rg=r[nrg]; for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0); nrd=ArrayMinimum(b); rd=r[nrd]; nra=MathMin(nrg,nrd); ra=r[nra]; nrmax=ArrayMaximum(cn); rmax=r[nrmax]; nropt=MathMin(nra,nrmax); ropt=r[nropt]; Print("rc = ",rc,"\nrg = ",rg,"\nrd = ",rd,"\nra = ",ra,"\nrmax = ",rmax,"\nropt = ",ropt, "\ng(rmax) = ",g[nrmax],", g(ropt) = ",g[nropt], "\nd(rmax) = ",d[nrmax],", d(ropt) = ",d[nropt], "\ncn(rmax) = ",cn[nrmax],", cn(ropt) = ",cn[nropt]); if(ngr<1 || ngr>5) return; ChartSetInteger(0,CHART_SHOW,false); CGraphic graphic; graphic.Create(0,"G",0,0,0,750,350); double x[2],y[2]; switch(ngr) { case 1: graphic.CurveAdd(r,g,CURVE_LINES,"g=g(r)"); x[0]=0; x[1]=r[NR-1]; y[0]=G0; y[1]=G0; graphic.CurveAdd(x,y,CURVE_LINES,"g=G0"); x[0]=rg; x[1]=rg; y[0]=g[0]; y[1]=g[NR-1]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rg"); break; case 2: graphic.CurveAdd(r,d,CURVE_LINES,"d=d(r)"); x[0]=0; x[1]=r[NR-1]; y[0]=D0; y[1]=D0; graphic.CurveAdd(x,y,CURVE_LINES,"d=D0"); x[0]=rd; x[1]=rd; y[0]=d[0]; y[1]=d[NR-1]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rd"); break; case 3: graphic.CurveAdd(r,cn,CURVE_LINES,"cn=cn(r)"); x[0]=0; x[1]=rmax; y[0]=cn[nrmax]; y[1]=cn[nrmax]; graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(rmax)"); x[0]=rmax; x[1]=rmax; y[0]=cn[NR-1]; y[1]=cn[nrmax]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rmax"); x[0]=0; x[1]=ropt; y[0]=cn[nropt]; y[1]=cn[nropt]; graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(ropt)"); x[0]=ropt; x[1]=ropt; y[0]=cn[NR-1]; y[1]=cn[nropt]; graphic.CurveAdd(x,y,CURVE_LINES,"r=ropt"); break; case 4: c[0]=1+ropt*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+ropt*a[j]); graphic.CurveAdd(c,CURVE_LINES,"Equity, ropt"); break; case 5: c[0]=1+rmax*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+rmax*a[j]); graphic.CurveAdd(c,CURVE_LINES,"Equity, rmax"); break; } graphic.CurvePlotAll(); graphic.Update(); Sleep(30000); ChartSetInteger(0,CHART_SHOW,true); graphic.Destroy(); } // 函数 dcalc() 接收 c1, c2, ... cN 数值数组, 并 // 返回最小增益 d。Assume that c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(int i=1; i<N;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; }
- rc = 0.9839614287119945
- rg = 0.1180753714454393
- rd = 0.03935845714847978
- ra = 0.03935845714847978
- rmax = 0.3148676571878383
- ropt = 0.03935845714847978
- g(rmax) = 0.1507064833125653, g(ropt) = 0.2967587621877231
- d(rmax) = 0.3925358395456308, d(ropt) = 0.9037200051227304
- cn(rmax) = 4.018198063206267, cn(ropt) = 1.416754202013712
- 使用 ropt 作为该系统的风险值。
- 在这个 rmax−ropt 上释放的风险可以用于增加新的系统 (多样化)。
附录是概述的示例
下面是 r_exmp.mq5 脚本的代码, 及其工作的数值结果。
#include <Math\Stat\Uniform.mqh> #define N 30 // 交易系列长度 #define NR 500 // 按间隔分割的段落进入 [0,rc] #define NT 500 // 产生的排列数量 double D0=0.9; // 最低最小增益 double dlt=0.05; // 显著等级 void OnStart() { double A0,rc,r[NR],d[NR],rd[NT],a[N]=//A,rg,ra,rmax,ropt,g[NR],cn[NR], { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,// 交易收益 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; A0=a[ArrayMinimum(a)]; rc=1; if(A0<-1) rc=-1/A0; for(int i=0; i<NR;++i) r[i]=i*rc/NR; double b[NR],c[N]; int nrd; MathSrand(GetTickCount()); for(int j=0; j<NT;++j) { trps(a,N); for(int i=1; i<NR;++i) { c[0]=1+r[i]*a[0]; for(int k=1; k<N;++k) c[k]=c[k-1]*(1+r[i]*a[k]); d[i]=dcalc(c); } for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0); nrd=ArrayMinimum(b); rd[j]=r[nrd]; } double p[1],q[1]; p[0]=dlt; if(!MathQuantile(rd,p,q)) {Print("MathQuantile() 错误"); return;} PrintFormat("样本 %f-quantile rd[] 等于 %f",p[0],q[0]); double rd0=0.03935845714847978; // 引言中获得的 rd 值 double pd0=0; // pd 的对应值 for(int j=0; j<NT;++j) if(rd[j]<rd0) ++pd0; pd0/=NT; PrintFormat("对于 rd = %f 值 pd = %f",rd0,pd0); } // 函数 dcalc() 接收 c1, c2, ... cN 数值数组, 并 // 返回最小增益 d。Assume that c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(int i=1; i<N;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; } // 随机排列的第一个不大于 min(n,ArraySize(b)) // b[] 数组的元素 // 可以使用函数库 MathSample() 代替 trps() void trps(double &b[],int n) { if(n<=1) return; int sz=ArraySize(b); if(sz<=1) return; if(sz<n) n=sz; int ner; double dnc=MathRandomUniform(0,n,ner); if(!MathIsValidNumber(dnc)) {Print("错误 ",ner); ExpertRemove();} int nc=(int)dnc; if(nc>=0 && nc<n-1) { double tmp=b[n-1]; b[n-1]=b[nc]; b[nc]=tmp;} trps(b,n-1); }
- 样本 0.05 四分位 rd[] 等于 0.021647
- 对于 rd = 0.039358 pd = 0.584
第一行结果告诉我们, 与引言中获得的结果相比, 我们必须将风险减半。在此情况下, 如果回撤超过目标 (10%), 则意味着该系统可能存在缺陷, 不应用于交易。在这种情况下, 错误概率 (工作系统遭拒) 将是 δ (0.05 or 5%)。结果的第二行表示, 初始交易序列中的回撤幅度较小, 可能处于平均水平。应该注意的是, 30 笔交易可能不足以对这个系统进行评估。因此, 对大量交易进行详细分析将会是有用的, 并看看它如何影响结果。
一般情况的附录
下面是 r_cmn.mq5 脚本, 我们正在尝试评估来自下面的 nmin 值和脚本的工作结果:
#include <Math\Stat\Normal.mqh> #include <Math\Stat\Uniform.mqh> #include <Graphics\Graphic.mqh> #define N 30 // 交易系列长度 #define NB 10000 // 为自举生成的样本数 double G0=0.25; // 最低平均收益 double dlt=0.05; // 显著等级 void OnStart() { double a[N]= { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // 交易收益 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; double A=MathMean(a); double S2=MathVariance(a); double Sk=MathSkewness(a); double Md=MathMedian(a); Print("样本分布参数:"); PrintFormat("平均: %f, 分散: %f, 非对称: %f, 中位数: %f",A,S2,Sk,Md); PrintFormat("交易数量: %d, dlt 值: %f, G0 值: %f",N,dlt,G0); // 通过正态分布近似 Print("通过正态分布近似:"); double q0, p0; int ner; q0=MathQuantileNormal(dlt,A,MathSqrt(S2/N),ner); if(!MathIsValidNumber(q0)) {Print("错误 ",ner); return;} Print("dlt 四分位: ",q0); p0=MathCumulativeDistributionNormal(G0,A,MathSqrt(S2/N),ner); if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) 错误 ",ner); return;} Print("G0 的显著等级: ",p0); // 自举 MathSrand(GetTickCount()); double b[N],s[NB]; p0=0; for(int i=0;i<NB;++i) { sample(a,b); s[i]=MathMean(b); if(s[i]<G0) ++p0; } p0/=NB; double p[1],q[1]; p[0]=dlt; if(!MathQuantile(s,p,q)) {Print("MathQuantile() 错误"); return;} Print("自举近似"); Print("dlt 四分位: ",q[0]); Print("G0 的显著等级: ",p0); // 近似值 nmin (通过正态分布近似) int nmin; for(nmin=1; nmin<1000;++nmin) { q0=MathQuantileNormal(dlt,A,MathSqrt(S2/nmin),ner); if(!MathIsValidNumber(q0)) {Print("错误 ",ner); return;} if(q0>G0) break; } Print("最小交易数 nmin (通过正态分布近似)):"); PrintFormat("不小于 %d, dlt 四分位的值: %f",nmin,q0); } void sample(double &a[],double &b[]) { int ner; double dnc; for(int i=0; i<N;++i) { dnc=MathRandomUniform(0,N,ner); if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) 错误 ",ner); ExpertRemove();} int nc=(int)dnc; if(nc==N) nc=N-1; b[i]=a[nc]; } }
样本分布参数:
- 平均: 0.322655
- 分散: 1.419552
- 非对称: 0.990362
- 中位数: 0.023030
- 交易数量: 30
- dlt 值: 0.050000
- G0 值: 0.250000.
通过正态分布近似:
- dlt 四分位: -0.03514631247305994;
- G0 的显著等级: 0.3691880511783918.
自举近似:
- dlt 四分位: -0.0136361;
- G0 的显著等级: 0.3727.
- 最小交易数 nmin (通过正态分布近似): 不小于 728
- dlt 四分位的值: 0.250022。
从这些结果可以看出 ropt(δ)=0。这意味着我们的准则禁止使用此系统进行交易, 因为数据或需要更长时间的交易历史。即使在第一个附录中有漂亮的图表。自举产生与正态分布近似的相同结果。这提示了两个问题。1. 为什么结果如此糟糕?以及 2。我们如何改进这个系统?我们来尝试回答它们。
- 原因在于使用的标准以及系统本身。我们的标准太普通了。一方面, 这很好, 因为我们可以在大多数情况下使用它。另一方面, 它不仅考虑到所问题中的系统, 而且还有我们研究的所有系统。举例来说, 我们所有的系统都产生一个左切的分布, 其中一些在理论上可以有无限期望。这就是为什么作为一条规则, 所有分布都具有正确的偏度, 它们的平均值非常缓慢地收敛到对称的正态分布。我们示例中的系统有这样的偏度分布。这是由偏度比率, 或预期由中值向右偏转来指出的。来自系统的预期遵循 "砍掉亏损, 让利润奔跑"。
- 我们需要一些标准来使用关于某个交易系统和资产价格序列的信息。所以, 不推测价格是不可能完成的。这些推测不应该扭曲真实情况。这意味着我们应处在 "一般情况" 部分伊始讨论的三个变体中的第二个变体情形。这就是为什么我们应该把重点放在参数化方法上。从计算的角度来看, 它们更难, 更不普遍, 但在各种特定情况下都更精确。
到目前为止, 我们可以得出以下结论。亏损不仅是由资产价格行为出乎预料的变化 (例如趋势的变化) 所导致。还可能是由它们的噪音或波动性导致的。我们所研究的只不过是尝试分离这些原因, 并减少其影响力的方法之一。如果交易系统不能完成此任务, 则不建议使用此类系统。