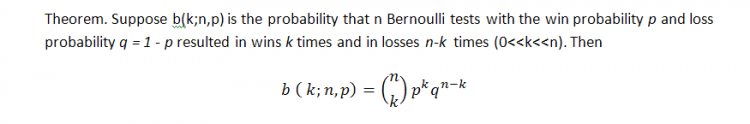谬误，第 2 部分统计学是一门伪科学，亦或是一部记录艰难生计的编年史

Sceptic Philozoff | 18 三月, 2016

简介

本文开头的第一个部分引述自 SergNF 于 2008 年 4 月 17 日 14:04 发布的帖子，网址为https://www.mql5.com/ru/forum/108164.即便是最精确的数学，如果使用它的人是一位专注于漂亮的公式而忽略任何实际应用的“研究人员”，最终也会变成一门伪科学。

即便加上了三个“笑脸”，引文作者的怀疑态度仍昭然若揭。原因非常明显：无数次将统计方法应用于客观现实（即金融序列）的尝试在流程的非稳定性、伴随概率分布的肥尾效应和金融数据量不足等障碍前撞得头破血流。现有市场模型没有一个被大众认可为足以胜任实际应用的模型。即使我们设法找出一些统计规律，但这些规律的应用结果与学习它们所花费的精力看上去似乎不成比例。

本文中，我将尝试不去探讨金融序列本身，而是探讨其主观呈现 - 在这种情况下，就是探讨交易者尝试控制序列（即交易系统）的方式。介绍交易结果流程的统计规律是个相当有意思的任务。在某些情况下，我们可以对此流程的模型下一个非常正确的结论，这些结论可以应用于交易系统。

我为本文的复杂性向平时对数学敬而远之的读者表示歉意，但很明显，这是本文不可或缺的一部分内容。看起来，我上篇文章结尾处所做的承诺并没有兑现。那么，让我们开始我们的探索之旅吧。

在本文中，我们设法构建一个人工示例，生动地显示使用资金管理 (MM) 规则“手数 = 0.1”时的可获利策略在使用几何 MM 时变成了亏损策略。这里的获利交易和亏损交易有非常规律的序列，现实世界是很难遇到这种情况的：P L P L P L P L P L P L ...第一个问题是：我为何要分析这种“有规律的”序列？

亏损系列：总览

原因很简单；文章我的第一个“圣杯”中就已经提到过：

因此，从最小亏损（和最大回收系数）角度来看，获利和亏损交易的“有规律”交替是最理想的状态。像上一篇文章中那样，如果我们能够设法证明即便在这种理想情况下（获利和亏损交易交替进行），系统在采用相同的获利和亏损交易的数学期望值时，一旦使用几何 MM 最终也会产生亏损，则可以确定在交易结果分布不规律时，情况甚至会变得更糟。

注意：假设获利交易与亏损交易之比等于 14:9。我们应该如何按顺序分布交易，以实现最低亏损？这不是件容易的事，即便我们使用 MM 规则“手数 = 0.1”并试着证明此系列是最佳的。有一点基本上是清晰的：亏损在系列中应“均匀”分布 - 即如以下方式：

PLPLP PLP PLP PLPLPLP PLP PL...

这是包含 23 个交易的“基本系列”，其中 14 个是可获利的。之后，此系列重复进行。很明显，此类系列在两种 MM 类型下的亏损都比以下这类系列的低得多：

P P P P P P P P P P P P P PL L L L L L L L L…

使用几何 MM 时情况尤为明显（原因在本文中已做说明）。但是，即使这种亏损系列（“亏损群集”）也不是极限。要理解这一点，让我们温习一下概率论的基础知识。但首先让我们定义一些术语。

术语

本文包含大量与可视化各种概率分布的柏努利级数和直方图相关的术语。为了避免混淆，让我们定义术语。因此：

1. 文中将把一个完整的交易系列简称为一个系列。此术语同时可指处理单个实际测试结果时获得的系列以及生成对应柏努利级数时获得的综合性系列。如果需要指定系列长度，我们将以如下方式指定：3457 系列（一个包含 3457 个交易的系列）。
2. 文中将把一个系列内带同样信号的一系列连续交易（获利或亏损交易，或是“成功”或“失败”）称为一个群集。如果应指定长度，则可称为 7 - 群集（长度为 7 的群集）。
3. 众多系列（在此上下文中，我们将主要讨论合成系列）将被称为一个系列数组。还可指定数量：65000 个 5049 -系列的数组（65000 个柏努利级数，每个的长度为 5049 个交易）。
4. 构建直方图时，我们有时需要考虑那些不但属于一些特定系列，同时还属于整个系列数组的群集。直方图名称与参数对应，其分布被可视化。我们不会写“长度 4 的群集在 5000 个系列（每个系列有 3174 个交易）的数组中的分布直方图”，而是会写：“5000 个 3174 -系列的数组中的 4 群集”。

伯努利方案：基础知识

很多包含一连串事件的实际任务经常可以简化成以下方案：

• 各个事件仅有两个结果 -“成功”和“失败”（“赢”和“输”）。“成功”的概率为 p，“失败”的概率为 q = 1-p。
• 事件结果的概率并不取决于该事件之前的事件历史记录。
  

这称为伯努利方案（或伯努利试验）。如果我们确定使用上述的第二个定义标准，那么我们的彩色编码序列可以被视为一个伯努利方案。

作者认为这对大部分交易系统来说都是正确的。以下是一些间接证明：

• 根据尝试将 Z 帐户系统应用于 MM 优化的人的观点，在尝试计算特定交易的概率时，任何关于 Z 帐户系统的信息似乎都是无用的 - 即便盈利的概率超过 90%；
• 各种鞅方案的效率显然也等于 0 甚至是负值，而这会导致不可接受的亏损。

因此，现在逻辑上可以接受的一点是，对于大部分交易系统，一系列连续交易与伯努利方案的标准是对应的。这样的假说导致了非常深远的影响。

在伯努利方案的 n 次测试系列中，k 次获利概率的经典公式（顺便提一下，这里也称亏损交易！）如下（获利的几率等于p）：

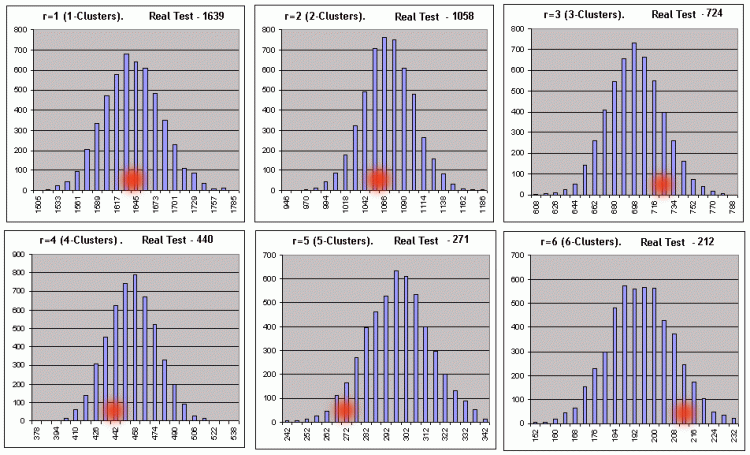
此公式显示此系列的一些综合参数、获利交易数，但不说明这些获利交易数的分布情况，即我们不知道可能群集的长度。搜索柏努利级数中可能亏损群集的长度是一项困难得多的任务；其解决方案已由 Feller [1] 提供。以下是测试系列长度的数学期望值及其在参数设置为 p（获利概率）、q（亏损概率）、r（获利群集长度）时的离散度的相关公式 - 假设我们有个与柏努利方案匹配的测试系列：r 长度的获利系列的回报时间的数学期望值和离散度相应地等于

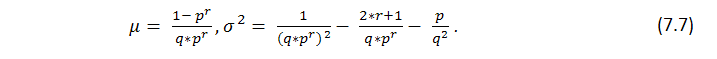
它遵循的定理是，n较大时，在 n 次测试中获得的 个 r 长度系列有一个近似的正态分布，即不等式的概率趋于固定的

。

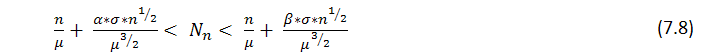
此表包含大量典型回报时间的数学期望值。

系列长度，r	p = 0.6	p=0.5（硬币）	p=1/6（骰子）
5	30.7 秒	1 分钟	2.6 小时
10	6.9 分钟	34.1 分钟	28.0 个月
15	1.5 小时	18.2 小时	18 098 年
20	19 小时	25.3 天	140.7 百万年

表 1.获利系列的平均回报时间（执行每秒一次的测试）。

后果 1：如果我们现在将 (7.7) 应用于亏损，并从第一个公式表示 r，由于测试系列的长度是无限的，我们会获得最长的亏损群集，因为它需要遵守对数定律！由于剥头皮策略的一些特征，此类策略的后果尤为严重（文中有进一步的说明）。

后果 2：从取决于测试系列长度的亏损群集的限制、大量减少或大量增加中，我们可以得出一个结论，即交易系统并不满足伯努利方案的要求。例如，如果使用预先指定的

n，p，qn、p、q，亏损的实际最大群集长度为 5 个项目，且根据“伯努利方案” 假说计算的相同长度为 15，我们可以认真地认为其是一个非伯努利方案，因为交易结果可表现为 相关事件。

后果 3：如果“伯努利方案”假说为真，此类策略与抛不对称硬币的方案并没有什么不同，对应的概率等于 p，q = 1-p（或抛带黄油的三明治）。

现在让我们从这个角度分析几个“有趣的”策略。

剥头皮：“Lucky”，第 1 部分

所有或几乎所有剥头皮系统都有很多共同特征：

• SL 远大于 TP（典型值 - 20 和 2；点值对应于 EURUSD 的 4 位报价）；
• P 远大于 q（获利交易的概率超过 80%，有时甚至达 99%）；
• 交易数量极大，1 年时间内数量可能成千上万。

我们不再详述第三点 - 这种方法在交易中心是否可行。这个话题在上述 SK.，文章以及论坛中都已讨论过。我们应假设交易中心内没有重新报价、滑点、增大 MODE_STOPLEVEL 等情况来阻碍我们的交易员。

创建了剥头皮交易系统 (TS) 的交易者经常会弄错亏损交易的频率。这种幻觉的根源可以追溯到有关收盘价流程的 Wiener 特性以及爱因斯坦公式针对布朗运动的真实特征的观点：“如果我们设置SL=20,TP=2，触发止损位的概率比达到 TP 的概率小 (20/2)^2=100 倍；因此，这种 TS 必然获利”。此概念的欺骗性在于，此流程不是 Wiener 流程，并且实际对应的概率差距远远小于 100 倍！

确实，这种情况下“伯努利方案”假说是相当可能的 - 这只是因为剥头皮交易策略通常试着使用流程及其在某些特定交易中心允许的过滤的随机特性。

现在让我们采用我们已知的交易策略“Lucky”的参数(https://www.mql5.com/zh/code/7464)。在其原始形态中（在同一部分中，即 Lucky_new.mq4），此 EA 仅仅是一个玩具，因为基本不会有交易中心会接受每天进行数百次交易，且其中的可获利交易的数学期望值约为 1 到 2 点的做法。但是，如果我们可以略微修改一下代码，并对 TP 位设置更严格的要求，有时还是能获得相当令人满意的余额/权益曲线。本文随附了修改后的 EA 代码（考虑了同时打开的交易数限制，在这种情况下等于 1；见下文说明）。

此 EA 的主要优势是它执行了大量交易，并提供了丰富的统计材料 - 这一点我们会进一步提供证明。现在我们的目标只是找出证据来确认或反驳此假说：“交易结果符合伯努利方案的理论”。对于想要对市场走势的非随机特征辩论一番的人，我要说：报价走势并不始终是随机的，我并不怀疑这一点。我不会把市场（真实的市场！）比作抛硬币；我只对交易结果的统计感兴趣，除此无它。此外，你会看到我们故意将一些外部参数集选择为“亏损”参数，这仅仅是为了检查所述的假说。

以下是第一次测试结果：

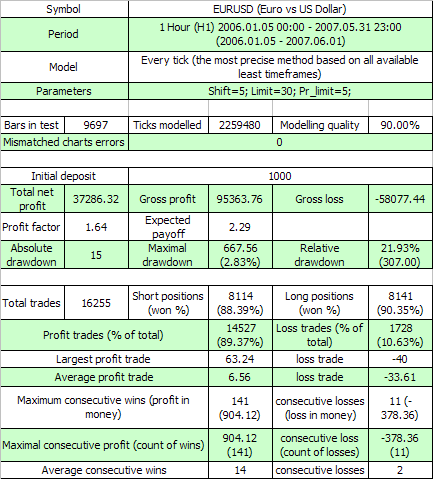
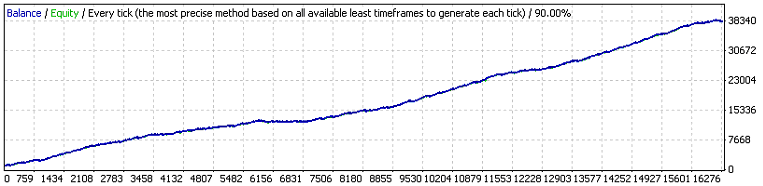
两个第一个外部变量的含义与原始代码中相同，第三个是订单发起获利事件所需超过的盈利点值。让我们根据 (7.7) 评估满足 11 - 群集亏损所需的最小测试系列的数学期望值p=0.8937,q=0.1063,r_loss=11):

N_loss= 1 / (p*q^r_loss) – 1 /p~ 57 140 275 804

以下是针对满足可获利 141 - 群集所需的测试系列长度的数学期望值的类似评估：

N_profit= 1 / (q*p^r_profit) – 1 /q~ 71 685 085

好吧...众所周知，系列的实际长度仅等于 16255 个交易，而不是几百亿或几千万个。超出实际系列长度这么多，说明对于此 TS，伯努利方案假说基本对其不产生直接的作用。也许还有一个我们没有考虑到的因素影响？

伯努利方案：有趣的结果

有一个这样的因素：一个 EA 可以一次性打开多个交易：在第二个 100 次交易中（订单 158 - 163），它连续打开了 6 个交易（并且在“峰值”处平仓）！此“倍增系数”可能就是群集长度大大高于期望值的原因：如果市场在交易量很大的情况下仍然很平缓，则 EA 开始几乎在每次价格变动时都打开大量交易。但是，考虑到其工作性质，由于平市和小规模获利与止损之间的对比，大部分交易（即便不是全部）也将获利平仓。另一方面，如果开始出现一个强大的定向变动，此 EA 将在市场变动的相反方向打开很多单向交易 - 最终大部分交易将“大规模”亏损平仓。

让我们进行简单的计算。我们使用两种针对上一段落中的完整测试系列长度的数学期望值的公式。此处，r_loss_real，r_profit_real是对应的最大亏损和最大获利群集的实际长度。而获得的N_xxxx 值相当大，如果我们将这些等式相互间逐项相除，砍掉第二项（1/p和 1/q）几乎也不会出错：

N_loss / N_profit = q * p ^ r_profit_real / ( p * q ^ r_loss_real)=

p ^ ( r_profit_real – 1) / q ^ (r_loss_real – 1)

让我们找出对数并简化：

ln( N_loss / N_profit ) = ( r_profit_real – 1 ) * ln( p ) - ( r_loss_real – 1 ) * ln( q )

现在让我们记住，如果测试遵循的是伯努利方案，且最长群集的长度以及 p 和 q 的概率并不是很小，N_loss和N_profit 值应基本相等。因此我们获得了一个有趣的近似关联：

(r_profit_real– 1 ) / (r_loss_real– 1 ) *ln(p) /ln(q) ~ 1 (*)

如果我们用另一种方式重新编写这个近似关联，则为：

p ^ ( r_profit_real – 1 ) ~ q ^ ( r_loss_real – 1 )

关联 (*) 的含义变得很清晰：在伯努利 TS 中（测试系列相当长，且 p 和 q 概率不是很小时），两个最大长度的群集（“赢”和“输”）的概率几乎是相等的。实际上，这个原理也适用于任何其他非伯努利 TS，但 (*) 关联形式是伯努利方案所特有。此关联可以说是一个针对“伯努利性”的 TS 粗略测试。

剥头皮：“Lucky”，第 2 部分

让我们排除倍增系数：将同时打开的订单数限制设置为 1。同一时间段内的订单数量已减少了几倍，我们将扩展测试范围，将其设置为从 2004 年 1 月 1 日到 2008 年 4 月 4 日。以下是结果和一些计算值的表格（BS 是“伯努利方案”的缩写形式（见下文分析）；第一个“+”表示获利群集对伯努利方案的良好响应，第二个针对亏损群集，“-”则是驳斥了“此系统满足 BS”假说，“0”表示其正确性尚存疑问）：

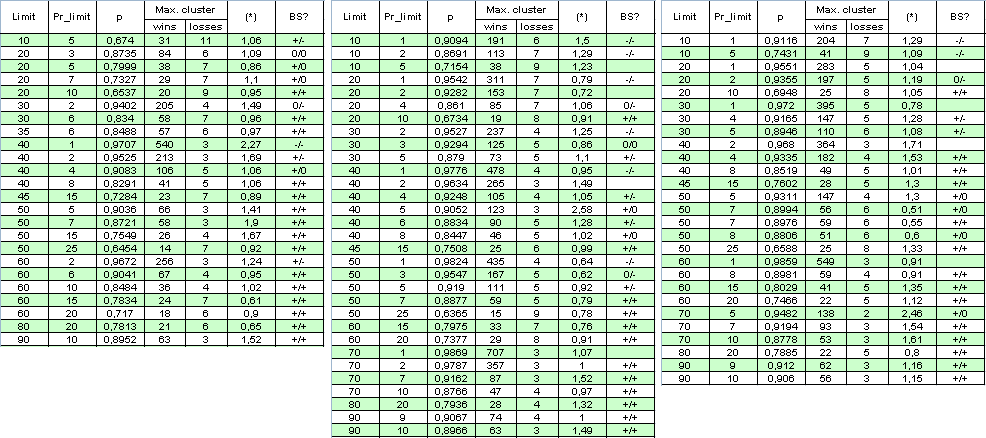
此表格的完整图片的尺寸很大，作者深感抱歉。参数 (*) 看上去不足以用于确定系统的“伯努利性”，因为有时即便它接近 1，系统也很难被称为伯努利方案。

附言：即使事实是 (*) 中的倍数有时偏离 1 很远，(*) 值仍然接近 1。例如，如果第二列中 Limit = 40 且 Pr_limit = 1，我们将得出：

( * ) = ( 478 - 1 ) / ( 4 - 1 ) * ln( 0.9776 ) / ln( 0.0224 ) ~

477 / 3 * ( -0.02265 ) / ( - 3.7987 ) ~ 0.95

这个事实又证明了另一个猜想：即使先不考虑系统伯努利性假说，此处的交易相关性对于获利和亏损交易来说“几乎是相同的”。

交易系统与伯努利方案的对应标准。

脚本运行的说明

我们如何将更可靠的测试结果划分为两组 - 伯努利方案和“非伯努利方案”？我们可以尝试多个方法，但我认为最简单的方法是：如果系统有“伯努利性”，当我们使用与测试期间实际检测到的系列对应的参数来生成大量伯努利级数，群集长度的概率分布函数 (p.d.f.) 应基本保持不变。这一事实显然源于有关获利概率的不变性和交易独立性的假设。

遗憾的是，根据获利/亏损群集的长度，这些群集的理论分布函数对我来说是未知的。上文中我介绍了一些公式，用于根据测试系列中获利群集的长度和获利概率（见上文 (7.8)）评估这些群集数的数学期望值。为此，Feller ([1]) 根据群集所属的复发事件理论推断出一种特殊的方法。第一眼看去，此方法并不完全符合交易者对“获利系列”术语的理解，但此方法大大简化了理论本身，使“r 群集注册”事件的识别不再依赖于未来的情况（[1]，第 302 页）：

另一方面，对于交易者来说，指示行 (WWWWLWWWWWW) 中的获利群集（Feller 的“赢系列”）的数量将如下：前 4 群集为获利群集，然后是 1 个亏损群集，后跟 6 群集为获利群集。对交易者来说，没有长度 1、2、3 和 5 的“已完成”群集，但据 Feller 所称是有的。此处发布这段来自 [1] 的摘录，仅用于表明问题的难度。因此，我们将仅生成大量伯努利系列并检测其中的系列，这与交易者对它们的理解相对应（一行中 15 个获利系列，最后是 1 个亏损系列，根据 Feller 的说法，这不是 15 次 1 群集的注册，或 5 次 3 群集的注册，仅仅是 1 次“真正”15 群集的注册）。要检查“伯努利性”的系列，1000 个伯努利系列已足够。

根据此观点，首先编写了一个脚本以允许将实际交易结果序列上传到一个数组，然后获取数据以在 MS Excel 中绘制使用群集长度的直方图。此脚本还包含一些用于生成伯努利系列的函数，并准备好数据以在 MS Excel中绘制使用群集长度的直方图。我不想把脚本代码插入到本文中；我会给出该代码的一般注释。脚本附于下方。测试程序报告文件应先放到目录experts\files\Sequences下，且其名称应移至外部脚本参数中。

开始时，根据测试程序报告文件，在 readIntoArray() 函数的帮助下，将交易（1 或 -1）的二进制结果输入到全局数组res[]中。要理解此操作，让我们使用一个小数组来进行说明。例如，此函数的操作最终产生以下数组 _res[]（交易数量，即系列长度为 50）：

1,1,-1,-1,1,1,1,1,1,-1,1,1,1,1,1,1,1,-1,1,1,-1,-1,-1,-1,1,1,1,-1,1,1,1,1,-1,1,-1,1,-1,-1,-1,1, 1,-1,1,1,1,1,1,1,1,1

之后，函数 formClustersArray( int results[], int& sequences[], int& h, int nr ) 计算群集长度，然后根据全局参数_what（用于定义我们针对的目标 - 盈利还是亏损），将系列长度写入数组 sequences[] 中（实际上是写入全局数组_seq[])。让我们计算此数组中的群集数量：

2,-2,5,-1,7,-1,2,-4,3,-1,4,-1,1,-1,1,-3,2,-1,8

负值指亏损群集。很明显，所有数量的绝对值的总和等于系列长度 50。假设我们对亏损感兴趣，即 _what = -1。然后，数组 _seq[] 将仅存储负值，但使用“＋”号。

2,1,1,4,1,1,1,3,1

之后，对数组_seq[] 进行处理，目的是构建数组 _histogramReal[]。现在我们仅需要计算 1-、2-、3- 等群集的数量，并将它们按顺序写入到数组中。结果，数组_histogramReal[] 将包含以下值：

6,1,1,1

这意味着我们的系列包含 6 个亏损的 1 群集，1 个亏损的 2 群集，1 个亏损的 3 群集，和 1 个亏损的 4 群集。后面的数组被写入到输出文件中。文件未关闭，因为我们需要根据伯努利方案将合成测试系列的相似“直方图”写入到该文件中。

组成“合成”系列时，根据伯努利方案，主要函数是单个测试的发生器。尽管代码很简单，但它能够很好地工作：未在 [0, 32767] 段中观察到会导致常规结果分布发生扭曲的“边缘效应”。

// generates a single Bernoulli test (+-1 with different probabilities)
int genBernTest( double probab )
{
   int rnd = MathRand();
   if( rnd < probab * 32767 ) return(  _what );
   else                       return( -_what );
}

在调用一次 MathSrand(GetTickCount() )后，此函数就相当于被调用了很多次，因为测试期间有真实交易 (_testsTotal)。然后，当我们获得生成的伯努利系列时，结果会相应地由群集计数和“直方图”构造函数进行处理。这些操作用于创建一个对应于一个测试的直方图（函数 genSynthHistogr( int& h, int nr ) ）。最终，在循环中调用最后一个函数，以在结果中生成伯努利系列的数组，组成相关的直方图，并将它们写入到输出文件。

现在我们可以在MS Excel 中打开此文件，构建必要的图，并得出有关系统与伯努利方案的对应性的结论。文件行中的数字具有以下含义（截取了表格的一部分，此处未显示有关 5 群集和以上的相关数据）：

测试系列的数量	最大群集长度	1 群集的数量	2 群集的数量	3 群集的数量	4 群集的数量
1	9	1639	1058	724	440
0	11	1649	1044	688	478
1	8	1681	1093	675	458
2	13	1628	1067	701	461
3	7	1616	1039	726	474
4	12	1601	1054	699	465

文件的第一行（绿色）显示实际测试结果，以下各行对应于合成测试系列，编号从 0 开始。

最终，也是最后一个阶段 - 评估实际测试结果以了解与伯努利方案的对应性：从合成伯努利系列中选择对应的列，以构建必要长度的群集的直方图。例如，要构建获利 1 群集数量分布的直方图，我们应取第三列 (1649, 1681, 1628, 1616, 1601….)；此类数字的总数等于合成伯努利系列的数量）。对于获利的 2 群集，我们取第四列 (1044, 1093, 1067, 1039, 1054…) 等等。

此类直方图是根据 Bulashev [7] 所述方法构建的，然后我们检查有关实际测试中数字的相等性的零假设，以评估合成系列中的平均值。假设零“实际数量等于合成平均数”的重要性的预接受水平等于 0.05（它表示大约 2 个标准偏差）。

第一个结果

让我们使用参数 3、20、10 针对 Lucky 测试结果启动脚本。脚本参数：_what = 1（获利群集），_globalSeriesQty= 5000.大表格中的参数 (*) 等于 1，即我们可以预期脚本运行结果应显示与伯努利方案的对应性。这里我们仅显示群集长度 1-6 的对应于零假设的直接检查的文件记录（它们在表格形式中略有修改，以便理解）：

// The first line of the file is results of the real test made in the tester.前两个数字是系列数量和最大群集的长度。

1,20,1639,1058,724,440,271,212,137,91,62,30,26,22,5,7,1,4,1,0,1,1,

…

// End of file (partially):

6 个两行式表格中，每个表格的上行对应于左侧的直方图间隔值，下行对应于伯努利系列的数量（最大 5000），在这些系列中，给定长度的群集的数量在这些间隔中。以下是上述情况的可视化视图（伯努利系列中的获利 r 群集的数量是以系列总数等于 5000 为基础的）：

红点的横坐标对应于实际测试中获取的群集数量。使用相同参数时，亏损群集 (_what = -1) 的相同脚本还会提供相当良好的情况 - 扣掉亏损群集的合理长度后：一旦根据 [7] 中的建议计算出的间隔数开始超过合成中的数据扩展，在使用设定的间隔数时，直方图的结构是不可能实现的。不过，不要被脚本报告中的形式零吓到，因为所有必要参数都可以在没有直方图的情况下计算出来。使用预设参数时，仅对 3 群集和 7 群集才拒绝零假设。选择了一个非常可疑的模糊型标准作为测试系统参照伯努利系统的主要标准。让我们以亏损群集的脚本运行结果为例来考虑决策原则：

实际测试与平均值估计之间的差值 = -0.37 SD（标准离差指标）

实际测试与平均值估计之间的差值 = 0.95SD

实际测试与平均值估计之间的差值=-2.04 SD

实际测试与平均值估计之间的差值= -0.45SD

实际测试与平均值估计之间的差值= 0.36SD

实际测试与平均值估计之间的差值= 1.13SD

实际测试与平均值估计之间的差值=3.27 SD

实际测试与平均值估计之间的差值= 0.11SD

实际测试与平均值估计之间的差值= 0.46SD

实际测试与平均值估计之间的差值= -0.47SD

所以，以下是主要标准：

• 如果图形模块的平均值未超过 1.5（此处为 0.96），
• 则数字平均值不会比模块大 1.2 以上。
• 最外层的数量（此处风险较大，对应的差值超过了 2 SD）不超过其总数的 20%，

系统被视为“一定是努利性系统”。如果对应的“关键”数字为 2、1.5 和 30%，则系统“可能是努利性系统”。如果数字超过这些界限，则假设不成立。我认为第二点是合理的，因为偏差不应只有一个主要标志。

伯努利方案对应性的统计标准对我来说是未知的，这就是我必须想出一个此类标准的原因。脚本运行报告文件中提供了这样一个临时性的决定性标准的结果。感兴趣的读者可以提供更合理的决定性标准。

对于这种情况，我们可以“得出肯定的结论”，即使用参数 3、20、10 的Lucky_系统确实符合伯努利方案，即使用随机抛黄油面包的方案。

现在让我们取一个“最差”案例，并在伯努利系列数等于 1000 时执行相同的计算；Lucky 的参数为 5、10、1。让我们考虑获利 1 群集：

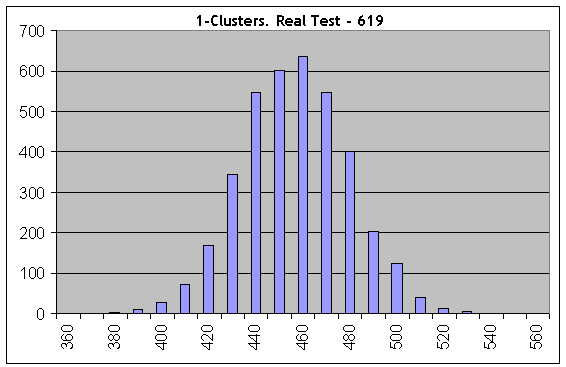
即使在第一个直方图上，所有东西也都是完全不同的：使用相同长度的测试系列和相同的获利概率时，实际测试结果（619 个 1 群集）不符合“合成”。因此，交易不是独立的。。

注意，使用大表格的很多其他参数集的类似评估测试可以得出结论，即伯努利方案（“抛黄油面包”）更像是一个规则，而不是一种例外情况。此外，还有一个满足伯努利方案的交易组（例如“获利交易”），和另一个不满足伯努利方案的交易组。这并不妨碍使用此模型，至少可部分用于获取有用信息，本文稍后会讨论这一点。最后一件事：由于统计数据量不足，决定性标准对于亏损群集并不那么可靠，但我还是对它们应用了此脚本 - 只是为了获取完整的情况。

“宇宙”系统：还是伯努利方案！

现在让我们使用完全不同的系统进行我们的研究 -“宇宙”系统；其源代码的帖子的网址为 https://www.mql5.com/zh/code/7999.作者主张此系统在形成的柱上进行操作，因此“所有价格变动”测试是不必要的。系统收集 2000.01.01 - 2008.04.04 期间内的交易统计数据时，初始余额约为 $10M。第一个打开的手数为 0.1。实际上发生变化的三个参数是p，tp，sl。不存在倍增，因此研究很简单：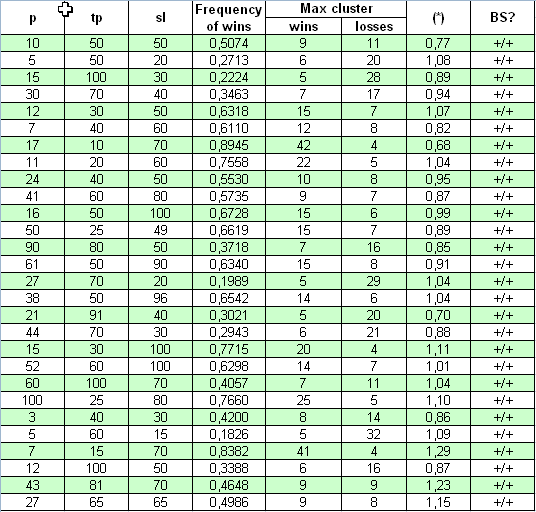

看，此处 (*) 参数为 1 时的符合性比上一种情况要好得多：(*) 值与 1 略有偏差。检查决定性标准时，结果也表明，在所有情况下，使用很广泛的参数范围时，此 TS 符合伯努利方案。

初步结论

Ralph Vince 在 [4] 中提供了另一个测试系列程序，用于检查伯努利方案的对应性。这是针对特殊关联（源行和旁边一行的自动关联）计算Z-分数 和测试交易结果。我并不觉得他的程序提供的结果比上述程序（其中，群集数量）更有意义（检查实际系列中不同长度的群集数量与模型系列的偏差）。实际上，提供的决定性标准更自由，需要更多证明。此外，正如我前面提到的，当最大群集的长度较短时，此检查的可靠性不高（对于Lucky_，这些通常是亏损系列测试）。但是，在我看来，尽管这个决定性标准需要更广泛的计算，但最好还是在符合伯努利方案的背景下包含测试系列的特定性状。此问题需要进一步研究，当然，目前还没有答案。

然而，以下预期已被证明：在大部分情况下，使用截然不同的外部参数集时，交易系列确实与伯努利方案相对应，与伯努利方案的偏差几乎始终源于规律的系统性利用，这些规律具有报价过滤流程的特性，更多时候是使用较小 Pr_limit 值的系统所固有的特性。这一点在包含 Lucky_ check 结果的大表格中尤其明显。

Vince 注意到，如果系列关联或 Z 分数测试的实证检验揭示了交易之间的依赖性，则此系统是次佳系统，且此依赖性应明确包括在 TS 中，在测试结果中降低它，并提高 TS 的优化程度。因此，抛开两个系统的测试结果不提，我们应该承认，“宇宙”系统通常比“Lucky”系统更佳。但是，这并不能证明宇宙系统中所用 MM 的合理性。

如何才能使用系统的伯努利性？

1.现在我们学到了什么？

我们已经知道，至少在某些情况下，交易结果序列为 1（“成功”，即获利）和 -1（“失败”，即亏损）的系统是伯努利系统，我们获得的此流程的模型已足够。现在我们已足够了解此流程，因为实际上这是对带偏移的常见布朗运动的修改版。P. Samuelson 已在金融理论与实践 ([6]) 中引入了几何（或是他所谓的经济）布朗运动：

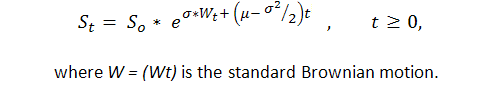
因此，我们可以将标准布朗运动的可靠理论研究结果（例如反正弦定律）应用于余额曲线。但是，布朗运动理论相当复杂，仅有很少在随机积分上有深厚数学知识的人才能理解。

第二种方法是拒绝高度理论性的计算，直接生成长伯努利系列的项目，然后将它们转换成余额曲线以“测试 0.1 手 MM”。这样我们只需要了解获利和亏损交易的平均值以及获利频率 p。即使是好几百个这种系列（例如，1000 个伯努利系列的数组）也能让我们相当了解符合伯努利方案的策略拥有的功能。

务必要明白，此类合成测试是令人厌烦的 Pardo 测试 ([5]) 的良好替代品：如果我们能够真正的证明零假设（“连续交易是伯努利交易”不被驳倒），它能够为我们提供有关与 [5] 中所述推进分析提供的系统大不相同的系统的足够信息。当然，余额曲线可能与实际测试中获得的曲线有很大不同。

***********

一般来说，没有什么会阻碍此类方法的实施，因为这种测试会在计算机上执行数分钟时间；结果，我们获得大量可用于深入分析的信息。遗憾的是，篇幅所限，本文无法贴出所有结果。在表中的同一测试周期内使用参数4、70、10 时，Lucky_ 的数个图表如下所示。生成合成伯努利方案的任务远比用上述脚本执行的任务简单；因此，。MS Excel的方法就完全够用了

对 0.1 的实际测试：

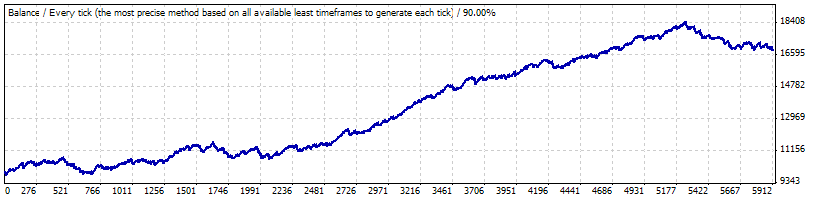
以下来自报告的参数对我们很重要；我们将在生成伯努利系列以及将系列转换成余额变化曲线时设置它们：

获利交易的频率 (p)	0.8765
平均获利交易	11.71
平均亏损交易	-73.73
交易总数	5904

基于伯努利系列的余额变化合成曲线：

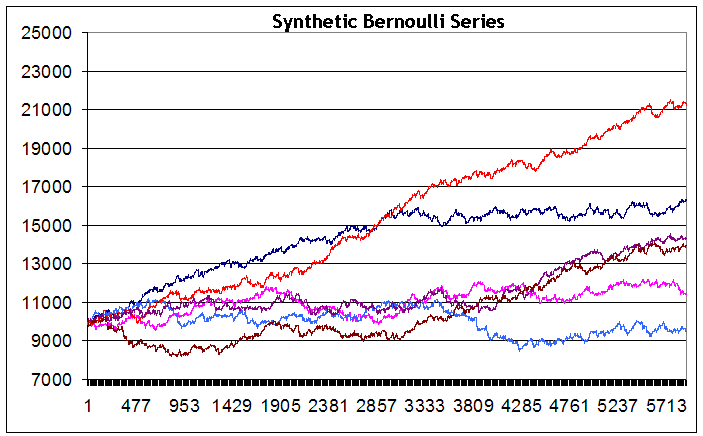
我们看到，尽管系列是使用完全相同的输入数据生成的，但测试结束时的整体余额结果从小规模亏损（蓝线）到大规模获利（红线），相互之间都有很大的不同。我必须承认，我并未设法生成一个余额明显下跌的系列（尽管如此，我还是想实现这种图表，并做了大约 200 次尝试）。也许使用大量系列时能够实现这一点。但这种情况似乎并不是此策略的典型情况。此外，我没有在任何系列中看到超过 2500 个点的跌幅。

现在让我们考虑几个孤立结果，它们与一个符合伯努利方案的策略的某些参数的评估相关。

2.超出报告值的最大亏损群集（“黑天鹅”）的评估

我们已经获得了系统伯努利性的证据，可以现实地评估亏损群集的最大长度，即在实际测试的相同交易次数中可等待的长度。在这里，我们可以生成大量伯努利系列，然后评估实际“黑天鹅”的几率（见 [2，3]），“黑天鹅”即我们无法仅基于测试结果评估概率的事件，因为这些事件在测试期间尚未出现过。它就是概率理论模型，我们可以在任何需要的交易量中收集需要的统计数据。

我们来使用同一个Lucky_ 系统用参数 4、50、7 时的交易结果：

根据报告，最大亏损群集的长度等于 5。现在，我们设置一个非常大的伯努利系列即 65000 个，使用等于 -1 的 _what参数（亏损群集），然后将我们的脚本应用于测试程序报告。我们来找到最长的一行（第一个数字为伯努利系列的数量，第二个数字为最大群集的长度，然后是每个长度的群集的数量）：

26001 9 1030 136 13 4 0 0 0 0 1

可以看出，最大亏损群集的长度比 5 大得多（它在这里为 9）！这可能是极罕见的事件？这种事件确实很罕见：在 65,000 个系列中仅遇到一次这种情况，因此它在实际测试中的出现概率可被视为几乎不存在（考虑到“遍历性假设”（稍后可以看到））。然而，此频率评估很不可靠；因此，不能依赖于它：例如，它可能仅在 20 个伯努利系列中出现。因此，如果我们不知道可靠性评估的统计标准，我们会错误地认为此估计有很高的概率。

在我提供的版本中，“遍历性假设”如下：事件在“合成测试空间”中发生的概率（基于事件的适当模型）约等于此事件在时间空间（即实际交易）中发生的概率 - 如果实际测试中的交易次数等于模型测试中的交易次数。当然会认为，交易结果在实际测试中的序列是稳定的，如同伯努利方案。。在大量交易中，这种说法与真实情况相差不大，因为在这里，非稳定性的唯一来源可能是所谓的“盈利偏移”，它们按照正态律分布，下文有介绍。

以下是 65000 个伯努利系列数组中的亏损群集数字表。

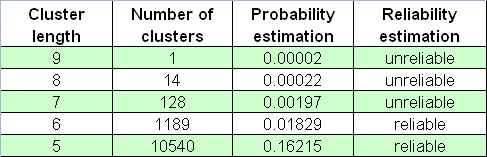
我们不应忘记那些完全在我们的预料之外发生的“黑天鹅”事件。

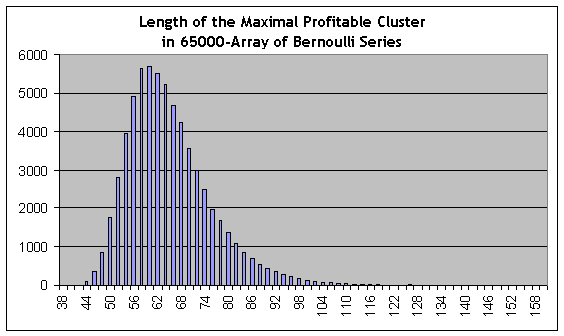
与上述计算相反，我们可以使用具有相反特性的的“黑天鹅”的估算，即长度增大的可获利群集。。我们记得实际测试显示，最大可获利群集的长度等于 59。对 65,000 个模型系列执行模拟建模，我们再次在脚本报告中找到最长的一行：

44118 153 115 117 111 87 70 71 52 51 50 40 36 42 42 34 20 32 15 20 20 13 10 11 12 8 5 7 3 5 4 2 2 6 7 0 2 1 2 1 1 5 0 0 1 0 0 0 0 0 0 1 0 0 2 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

这是模型系列 #44118，最大可获利群集长度等于 153 次交易（列表中的第 2 个数字），约比实际测试中的最大群集长 2.6 倍！然而，可从长度约为 80 （此系列的概率估计值为 0.0088）或者更短的位置处获得有统计意义的群集频率估值，而 80 比 59 高很多。可获利群集的 ½ 分位数（积分分布函数获得值 0.5 时的群集长度值，概率密度分布函数根据此值将分布划分为两个面积相同的部分）约为 62，即稍大于 59。这里包括了伯努利系列数组上的最大群集长度分布的直方图：

当然，在这里“黑天鹅”一词的使用不是很谨慎，因为根据 Taleb ，这似乎是一个无法计算其概率的事件。然而，我们可能会注意到，仅根据经验数据（测试报告）判断而不使用理论模型，我们很难针对亏损的 6 个群集或可获利的 80 个群集（即我们在报告中未碰到的事件）得出任何在统计上值得信赖的结论。

3.“失败偏移”：失败概率相对经验频率的不利偏离。
接近工具，第 1 次尝试

在根据伯努利方案对系列执行的大量测试中（大约数千次），失败频率 f 与失败概率 q 略有不同，基本遵循“正确的”正态分布，稍有差异：大数定律（这里为拉普拉斯定理）仍有效。不过，f 也可发生偏移，如果具有极少的数学期望值的交易采用超短期策略，偏移可能会很严重，能够在整个测试时间间隔内将系统转为亏损系统。我们现在有足够的工具来对发生这种偏移的概率进行统计估计 - 如果有证据显示伯努利方案在这种情况下可行。

遗憾的是，EALucky_ 甚至限值了其概率，直至某个交易在固定时间内提供了大量统计数据。

对于一个严肃的策略制定者，这是一个例外情况而不仅仅是一项规则，因为通常需要基于包括几百次甚至几十次交易的测试结果得出综合结论（见下文解释）。增加统计数量会适当地减小高斯分布的宽度，同时会明显减少显著偏离中心值的几率。

举个例子，基于手数 0.1 规则，我们来看看 Lucky_ 使用对 EA 不是很有利的参数：4、80、20。我们首先在从 2004 年 1 月 1 日到 2008 年 4 月 4 日的整个时间间隔（“时间间隔 A”）内对其执行测试 (EURUSD H1)。下面是报告给出的余额图表：

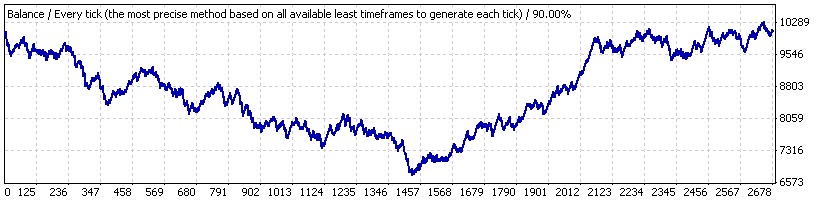
我们看到与想象的相差很远。在通过脚本查看交易序列后（基于 1000 个模型伯努利系列），我们发现，整个交易系列可视为对应于伯努利方案 - 同时适用于可获利和亏损群集。

我们来看看平均交易的参数：

平均获利交易

21.71

亏损交易

-83.32

现在，假设我们仅在从 2005.10.21 到 2007.06.07（“时间间隔 B”） 的较短时段（期间策略表明增长稳定）内测试了 EA。图表如下：

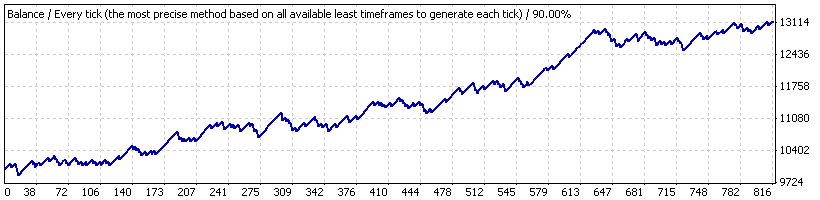
以下是平均交易的结果：

平均获利交易

21.69

亏损交易

-82.94

平均来说，交易的变化非常细微；因此，它们可被视为基本上保持不变，而与测试期间的策略盈利能力无关。。实际上，考虑到交易仅在达到由精确外部参数设置的某个获利位/亏损位之后才进行交易，我们可以更早了解这一点。

再次快速检查伯努利性（1000 个模型系列）确认其是否符合伯努利方案。现在，我们来将包含大量伯努利系列 (65000) 的脚本应用于较短测试时间（时间间隔 B）的结果中，然后将 65000 个伯努利模型系列的结果导入到 MS Excel 中，以建立一个有关可获利交易比率的分布的直方图：

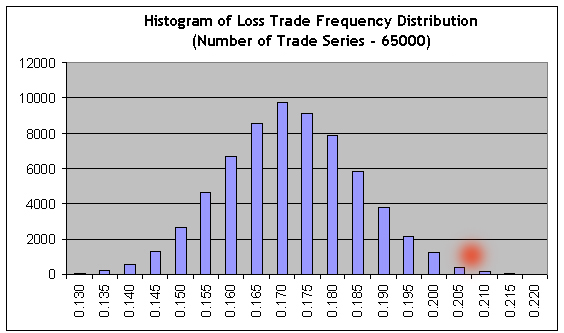
很显然，要实现不获利，获利和亏损的频率应与它们的平均值的比率反向关联：r= 21.69/82.94 = 0.2615.因此，亏损交易的频率应等于f=r/ ( 1+r= 0.2073。) ~ 0.2073我们可以看到，此值（见红色斑点）位于右侧尾部区域的较远处，其中右侧的条柱总数约占到所有直方图条柱总数的 0.3%，即出现非获利/亏损的概率约为 0.003。此值与直接使用拉普拉斯定理所获得的值基本相同。

在 Danish Kingdom 中一些内容是错误的：有关时间间隔 A 的报告数据告诉我们，在 A 的上半部分中，在此增长间隔之前的余额几乎以相同的速度快速下跌，至于交易次数，下跌时段并不比 B 短。如果我们基于时间间隔 B 的测试数据估计下跌余额（稳定亏损）出现大致相同间隔的概率，它将会消失（因为边界频率 f 甚至还会向右侧偏移），这似乎与试验数据相矛盾。

问题可能是，这种与时间间隔 B 相对应的可获利长系列交易有很大的偏差：从 1999 年 1 月到 2008 年 5 月初的测试显示，此策略既不会获利，也不会亏损：

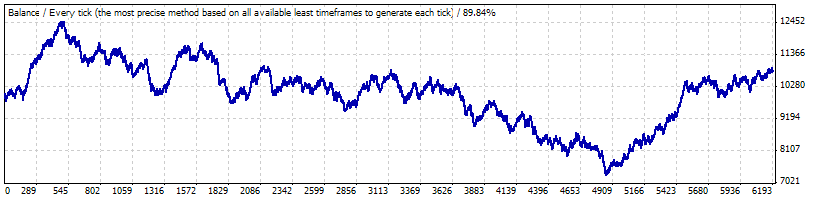
交易的数学期望值仅为 0.17，亏损交易的“自然”频率约等于之前计算的f(0.2073)，为 0.2054。

很显然，基于罕见事件的统计数据的概率估值（时间间隔 B 上的亏损交易的频率等于 0.1706，在大约 2.8 个“sigma”时，它与有利方向上的“自然”频率不同）不够可靠。但是，我们无法确切地掌握“真实”频率。“失败偏移”概念仍能给我们带来好处吗？

4.“失败偏移”：短期急剧下跌的概率评估。
接近工具，第 2 次尝试

显然，我们可以 - 如果我们设置了合理而非极端的目标来对应分布的尾部。我们来这样设置任务：假设我们有时间间隔 B 的测试结果。我们相信，这是伯努利方案，而且盈利交易和亏损交易的数学期望值实际上并不取决于余额的变化情况。基于对亏损概率非常乐观（实际上是错误的！）的评估，我们来尝试评估出现短暂而剧烈的下跌的几率。正是这些下跌会对交易者的心理造成最具破坏力的影响，因为在此之后交易者将开始发表神秘的言论，类似于“市场已发生改变”甚至于“已变成了命令市场”。

在这里，我应补充的是，拉普拉斯定理在这里没有很大帮助，因为此公式中包含的值 n*p*q 很小，大概等于 10 或者更小（这大约对应于几十个交易）。基于此计算得出的主要观点是，在很短的交易系列中，亏损的频率完全不同于“真实”交易，即概率不同：由于测试数量小，因此亏损频率的分布很广泛。

请注意，短期下跌的评估在很大程度上不同于亏损群集的最大长度的评估，因为下跌不一定仅包含亏损交易。我们来使用脚本生成 65000 个长度为 40 的系列，其中 0.1706 的亏损频率非常有利（“时间间隔 B”），然后构建一个类似于“接近工具，第一次尝试”中的直方图：

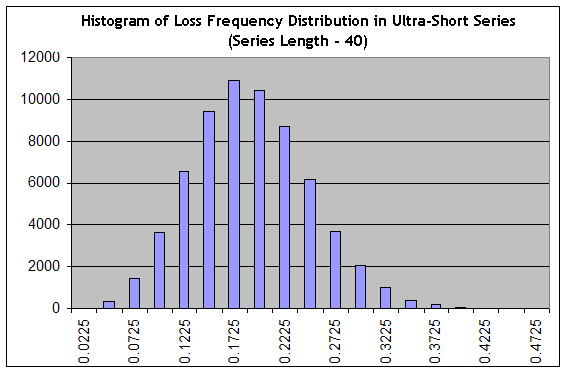
我们看到，设置已经发生了重大改变：分布已经从急剧转变为平稳，即“相对宽度”增大。在长度为 40 的系列中，包括几乎没有获利的交易（即亏损交易的频率等于 0.1975，平均交易产生 0.25 个点）到急剧亏损的交易（即亏损交易的频率为 0.3000，在此系列中，交易数学表达式的估值等于 0.7*20-0.3*80=-10 个点），我们实现这些交易的概率等于从“0.2225”列到其右侧列的列的总和，这在所有列 (65000) 的总数约占到 34%。同时，这是乐观估计，因为分布峰值的频率为乐观的 0.1706！

想起遍历性假说，该假说在概率分布与交易空间（即实际时间空间）之间构建一座桥梁，我们得出，平均来说，系统至少将在 34% 的交易时间内没有盈利或者出现亏损。这一数字与 [4] 中的数据有很好的对应关系，根据这些数据，伯努利系统将在大约 35% 到 55% 的所有交易时间内保持下跌状态。

请注意，符合急剧下跌的实际概率并不在很大程度上取决于最初“有利的”频率，与频率是否具有吸引力无关。这就是此系统的特性，它与伯努利性相关，而且只有提高获利交易与亏损交易的平均结果的比率，才能改善这种情况。

顺便说一下，这些基于生成超短系列的评估，往往能够很可靠地筛选出极具盈利能力的系统在测试时间间隔中的数十个交易的测试结果：尽管交易的“数学期望值”很乐观，然而交易数量非常少，即便系统具有“伯努利性”，“急剧”下跌也不可避免。

总结

尽管我们希望构建逻辑结构，自豪地宣称它们为“机械交易系统”，但是，我们往往没有认识到它们包含多少随机性 - 包括我们在测试结果中没有遇到的随机性（“黑天鹅”）。

由于使用二进制记数法表示的连续交易结果（“成功”或“失败”）往往遵循伯努利方案，因此，它们与通过抛掷黄油面包的做法没有任何明显不同。当然，这并不意味着无法实现可获利的系统：即使在原则上遵循伯努利方案，策略也可具有良好的获利性。这明显是源于以下观念：如果获利交易的概率和数学表达式持续高于亏损交易的概率和数学表达式，则策略显然具有盈利能力。

相对而言，对于至少有时能与数学“沟通”的读者，应该相当了解模型的优点 - 即便它们还远谈不上具有决定性。足以适用于实际统计现象的模型的主要价值在于，使用它们能够获得有关总体的宝贵知识 - 即无法从有限的试验数据中获得的信息。在这种情况下，由于极易生成性以及在关键概率分布中肥尾效果的缺位，因此，伯努利方案的价值相当高。

我们以一个很棘手的问题来结束这篇文章：或许，大多数 TS 的分析部分都没有用处，主要精力都集中在有充分依据的高效资金管理方法上（“分析方法不重要，资金管理才是最重要的！”），不是吗？