Комбинаторика и теория вероятностей для трейдинга (Часть II): Универсальный фрактал
Evgeniy Ilin | 23 июня, 2021
Содержание
- Введение
- Оценка возможностей применения фракталов в трейдинге
- Теоретические основы построения универсального фрактала
- Пишем код для реализации универсального фрактала
- Выводим первую формулу на основе симметричного фрактала
- Оценка работоспособности выведенной формулы для всех положительных и действительных аргументов
- Продвинутый фрактал как следствие универсального фрактала
- Обобщение результатов
- Заключение
- Ссылки
Введение
В прошлой статье мы познакомились с основами теории вероятностей, которая поможет нам более глубоко понять особенности применения фрактальных функций для задач трейдинга. Продолжая тему, начатую в прошлой статье, я покажу несколько самодостаточных фрактальных функций, которые способны описать все необходимые нам процессы ценообразования, которые мы в итоге сможем обобщить, упростить и даже составить некоторые формулы, которые помогут нам в поиске ответов на самые различные вопросы, в которых так не хватает четких количественных оценок и однозначных ответов.
Оценка возможностей применения фракталов в трейдинге
Продолжу свою мысль с обобщения результатов предыдущей статьи и сведения материала в нечто более компактное и универсальное. Если взять пример построения фрактала из прошлой статьи, понятно, что такой фрактал мало чем будет нам полезен в практическом плане, но нам не столько важен сам фрактал, как то, какие правила для построения данных структур мы смогли определить. Как оказалось, данные правила практически неизменны для трех типов фракталов:
- Фрактал с симметричными границами
- Фрактал с ассиметричными границами
- Фрактал с верхней либо нижней границей
Если поразмышлять, то становится понятно, что такие фракталы могут быть применимы для описания следующих процессов:
- Ускоренная имитация торговли с возможностью оценки вероятностей различных сценариев, учитывая наличие ограничений по депозиту (так как нижняя граница может символизировать уровень депозита при котором дальнейшая торговля будет невозможной, что можно еще назвать "полным сливом")
- Оценка среднего количества шагов внутри фрактала (например, можно оценить сколько в среднем ордеров произойдет до того, как мы получим либо желаемую прибыль, либо убыток)
- Оценка суммарных средних величин для каждого шага (например, можно посчитать среднее время которое будет висеть позиция, основываясь на статистике для более маленькой позиции (в качестве размера имеется в виду размер ее стопов в пунктах или разнице цен), так же возможен обратный процесс)
- Оценка прибыльности опционов на основе фрактала с единственной границей
- Неучтенные возможности
Теоретические основы построения универсального фрактала
Начнем мы с того, что возьмем те правила построения, что я получил в предыдущей статье, и дополним, для того чтобы иметь полное понимание того как строится фрактал. Кроме того, я нашел небольшую помарку в своих формулах, которая не давала осуществлять асимметрию границ как вверх, так и вниз. Оказалось, что формулы я вывел абсолютно верно, и они работают для абсолютно любого фрактала. Фактически получилась функция для реализации абсолютно любого фрактала. Все возможные фракталы являются частным случаем общего фрактала. Если взять три вида фрактала, которые я определил выше, то получится, что условия общего фрактала для реализации этих трех частных случаев примут вид:
- m = n & [ m > s & n > s ]
- ( m > n || n > m ) & [ m > s & n > s ]
- ( m > S && n <= S ) || ( n > S && m <= S )
Схематично эти три вида фрактала будут выглядеть так:
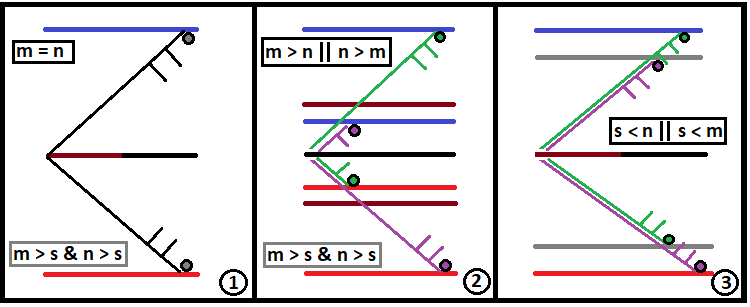
В идеале конечно же "S" должно стремиться к бесконечности. Следующие переменные я не описал в предыдущей статье, но опишу здесь, для того чтобы сложилась полная картина, как использовать общую формулу для получения частных случаев. Фрактал представляет собой функцию, работающую по принципу цепной реакции, как в атомной бомбе. Если задать слишком большую глубину цепной реакции, то компьютер может и не справиться с такими вычислениями, в не особо критичных случаях он просто будет очень долго считать, где-то минуты, где-то часы, а где-то и сутки. Для того чтобы правильно запустить цепную реакцию во фрактале, необходимо найти две основополагающие величины:
- Half - половина ширины канала
- Middle - величина "U" которая соответствует средней линии
Величина "Half" для всех трех случаев, которые мы определили в предыдущей статье, вычисляется очень просто, это среднее арифметическое "m" и "n":
- Half = ( n + m ) / 2
Для реализации второй величины уже как раз понадобится три варианта логики, но первый и второй варианты можно объединить в один, и тогда получится, что нам нужно рассмотреть всего два варианта:
- n >= m
- n < m
Далее, учитывая, что ось "U" у нас направлена "вверх" и величина "n" я вляется тоже верхней частью канала, а величина "m" - нижней, то получаем два соотношения для обоих возможных случаев задания "m" и "n":
- Middle = Half - m
- Middle = - ( Half - n )
Данные величины будут переданы в саму фрактальную функцию для внутреннего использования, потому что без них невозможна реализация внутренней логики ветвления, которую я описал в предыдущей статье. Прототип данной функции будет иметь такой вид:
- double Fractal(double Half, double Middle, int m, int n, int s,double p,int S, int U, double P)
Как видно для, корректного запуска фрактала, необходимо передать пять обязательных величин:
- Half - половина ширины канала
- Middle - величина "U" которая соответствует средней линии
- m - количество шагов до нижней границы
- n - количество шагов до верхней границы
- s - максимально допустимое количество шагов в любую сторону для отдельно взятой цепочки
Остальные величины названы заглавными буквами, для того чтобы было понятно, что эти величины динамические и будут абсолютно разными на каждом отдельном фрактальном уровне. Сначала я их определю:
- S - количество шагов которое набралось в текущей цепочке вероятностей, для передачи в следующий фрактальный уровень
- U - текущее удаление конца цепочки от точки старта цепочки, для передачи в следующий фрактальный уровень
- P - собранное произведение вероятностей всей цепочки на основе схемы Бернулли, для передачи в следующий фрактальный уровень
Из этого становится понятно, что для запуска фрактала нужно будет передать правильные значения в функцию:
- S = 0 (так как это старт и шагов еще не было)
- U = 0 (по той же причине, ведь мы находимся на старте цепочки)
- P = 1 (так как это нулевое звено и все цепи которые из него выходят должны составлять полную группу)
Закончим построение общих правил для фракталов, имитирующих ценообразование или торговлю, тем, что кратко перепишем те правила, которые были получены в предыдущей статье. Эти правила нужны для внутренностей фрактала. Правила базируются на нескольких основных формулах для одинаковых шагов:
- f = u + d — данная величина в данном случае является количеством шагов будущего дерева сочетаний (размер обусловлен расстоянием до ближайшей границы коридора фрактала)
- s = u - d — количество итоговых шагов вверх, выраженное через падающие и растущие сегменты
Мы определили, что мы будем итерироваться в цикле по "u". Кроме того, мы будем использовать величину "s" в роли нового "U", который мы передадим в следующий фрактальный уровень, если количество оставшихся шагов позволяет нам это сделать. Для этого мы должны будем определить формулу для "u", которая не содержит "d". Это сделать легко, выразив из первого уравнения "d" и подставив во второе:
- s = 2*u - f
Но это число можно было бы принять как новое значение "U" для передачи дальше если бы текущее "U" было равно нулю, поэтому данное "s" нужно прибавить к "U", так и получим новое значение для передачи дальше:
- NewU = s + U - наше новое "U" для передачи в следующий фрактальный уровень
Как уже было определено в прошлой статье, данное выражение принимает три возможных значения, исходя из трех возможных значений числа "f". Я взял диаграмму из прошлой статьи и переработал ее, чтобы ни у кого больше не осталось вопросов:
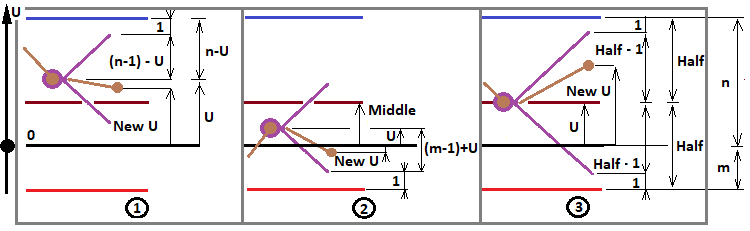
Данная диаграмма здесь очень к месту, так как сейчас мы занимаемся тем, что определяем все возможные фрактальные конфигурации, которые могут нам пригодиться для решения большинства задач. Исходя из данной диаграммы и определяем три случая для "f":
- f = ( n - 1 ) - U
- f = ( m - 1 ) + U
- f = Half - 1
Эти три случая появляются при выполнении соответствующих условий:
- U > Middle
- U < Middle
- U = Middle
Остается только описать последние две величины для передачи в следующий фрактальный уровень и отдельно осветить вопросы сбора чисел во фрактале. Две оставшиеся величины считаются так:
- NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) — наша новая вероятность цепочки "P" для передачи в следующий фрактальный уровень
- NewS = S + f = S + (floor(Mid) - 1) — наше новое "S" для передачи в следующий фрактальный уровень
Перед тем как начать сбор чисел в общую переменную, нужно понять, что сбор чисел должен происходить в похожем блоке, но с тем лишь отличием, что делаем только один шаг и, соответственно, схема Бернулли уже не нужна. Порядок операторов не важен, они просто должны находиться в одном блоке. Сбор чисел возможен только в ситуациях "1" и "2", но с некоторыми уточнениями:
- U = n - 1
- U = - ( m - 1 )
Для первого случая предыдущие три величины будут вычисляться гораздо легче, так как делаем всего один шаг:
- NewU = U - 1
- NewP = P * p
- NewS = S + 1
Для второго случая, конечно, же все похоже, с небольшими отличиями:
- NewU = U + 1
- NewP = P * ( 1 - p )
- NewS = S + 1
Еще очень важно сказать, что по итогу обобщения всех фракталов каждый из таких фракталов делится на 2 типа:
- Фрактал вычисления полной вероятности пересечения верхней границы коридора
- Фрактал вычисления полной вероятности пересечения нижней границы коридора
В свою очередь, каждому из этих типов соответствует еще по одному типу фрактала, которые идут в связке с исходным:
- Фрактал вычисления среднего количества шагов для пересечения верхней границы
- Фрактал вычисления среднего количества шагов для пересечения нижней границы
Все эти четыре типа фракталов на самом деле отличаются только видом суммируемых чисел. В случае сбора вероятностей, суммируемым числом могут являться только "P*p" и "P*(1-p)". Для рассмотрения остальных двух фракталов нам потребуются дополнительные переменные для передачи в следующие фрактальные уровни. Все дело в том, что в таких фракталах мы используем шаги одинаковые по величине, но противоположные по направлению, и их вероятности равны либо "p" либо "1-p" в силу полноты группы. Но в тех случаях когда "p" не равно "0.5", данный факт автоматически означает, что это два совершенно разных события, которые могут иметь совершенно отличные друг от друга характеристики. Под характеристиками я понимаю набор некоторых случайных величин, которые соответствуют данному событию. Одной из таких величин как раз и является "время жизни позиции". Таких величин может быть столько, сколько нам нужно, и при необходимости мы можем их рассматривать так же, как и время. Самое интересное то, что рассмотрение всех данных величин может быть упрощено после рассмотрения простого количества шагов. В данном случае суммируемые числа примут вид:
- P * p * NewS
- P * ( 1 - p ) * NewS
Видно, что вероятности просто домножены на само количество шагов в данной окончившейся цепочке шагов, только это формула для случаев, когда шаги вверх и вниз равновероятны. В альтернативных случаях придется описывать шаги вверх и шаги вниз двумя разными фракталами, либо предусматривать структуру для хранения обоих чисел внутри. Во втором случае фрактальная функция будет возвращать не число, а контейнер с данными. Контейнер самодостаточен и не требует расширения. Я пошел немного дальше и предусмотрел такой контейнер, который позволяет хранить все необходимые параметры, которые могут нам понадобиться, и в связи с этим нам не нужно будет описывать несколько функций с однотипным кодом. Вместо этого я соединил все эти функции в единую функцию, которая способна описать все параметры, которые нам могут понадобиться. Вид фрактала и задача которую он решает, будет напрямую зависеть от входных параметров функции. Для расширения концепции нам потребуется заменить переменную "S" и эквивалентную ей "NewS" на следующие величины:
- SU - итоговые шаги вверх из выбранной вероятностной цепочки
- SD - итоговые шаги вниз из выбранной вероятностной цепочки
- NewSU и NewSD - для передачи в следующий фрактальный уровень
- SU + SD = S
Данные величины необходимо определить, также как мы определяли "S". Для случая, когда "U > Middle":
- NewSU = SU
- NewSD = SD + 1
Для случая когда "U < Middle":
- NewSU = SU + 1
- NewSD = SD
Кроме того, для окончательного апгрейда самого фрактала нам потребуются шесть величин:
- UpperMidSDown - суммарное средневероятностное количество шагов вниз до достижения верхней границы
- UpperMidSUp - суммарное средневероятностное количество шагов вверх до достижения верхней границы
- UpperSummProbability - вероятность пересечения верхней границы
- LowerMidSDown - суммарное средневероятностное количество шагов вниз до достижения нижней границы
- LowerMidSUp - суммарное средневероятностное количество шагов вверх до достижения нижней границы
- LowerSummProbability - вероятность пересечения нижней границы
Величины "1","2","4","5" отображают сумму произведений соответствующего количества шагов на их вероятность. Данные величины сами по себе бессмысленны, но они являются составляющими формул именно тех более полезных величин, о которых речь пойдет дальше. Величины "3","6" являются вероятностями гипотез пересечения двух границ, которые образуют полную группу. Вместе все эти величины позволяют определить очень многие вещи.
Пишем код для реализации универсального фрактала
Для корректного запуска фрактала нам понадобится функция, которая производит все подготовительные операции перед запуском фрактала, и после чего правильно запускает сам фрактал на основании правил, которые были определены. Я сделал реализацию данного алгоритма в стиле MQL5:
Container StartFractal(int m, int n, int s,double p)//подготовка всех переменных и старт фрактала { int Minimum; if ( m <= n ) Minimum=m; else Minimum=n; double Middle; if ( n >= m ) Middle = (m+n)/2.0 - Minimum; else Middle = -((m+n)/2.0 - Minimum); double Half = (m+n)/2.0; return Fractal(Half,Middle,m,n,s,p,0,0,0,1.0); }
После вычисления фрактала функция возвращает наш контейнер со всеми данными, которые нам могут понадобиться:
struct Container//контейнер для сборки всех необходимых данных о фрактале { //суммируемые величины для верхней границы double UpperMidSUp;//сумма вероятностей, помноженных на количество шагов вверх конкретной цепочки (для пересечения верхней границы) double UpperMidSDown;//сумма вероятностей, помноженных на количество шагов вниз конкретной цепочки (для пересечения верхней границы) double UpperSummProbability;//сумма вероятностей (для пересечения верхней границы) //суммируемые величины для нижней границы double LowerMidSUp;//сумма вероятностей, помноженных на количество шагов вверх конкретной цепочки (для пересечения нижней границы) double LowerMidSDown;//сумма вероятностей, помноженных на количество шагов вниз конкретной цепочки (для пересечения нижней границы) double LowerSummProbability;//сумма вероятностей (для пересечения нижней границы) Container()//конструктор по умолчанию { UpperMidSUp=0.0; UpperMidSDown=0.0; UpperSummProbability=0.0; LowerMidSUp=0.0; LowerMidSDown=0.0; LowerSummProbability=0.0; } // void Summ(Container &c0,const Container &c1) const//полная сумма для перегрузки оператора { c0.UpperMidSUp=c0.UpperMidSUp+c1.UpperMidSUp; c0.UpperMidSDown=c0.UpperMidSDown+c1.UpperMidSDown; c0.UpperSummProbability=c0.UpperSummProbability+c1.UpperSummProbability; c0.LowerMidSUp=c0.LowerMidSUp+c1.LowerMidSUp; c0.LowerMidSDown=c0.LowerMidSDown+c1.LowerMidSDown; c0.LowerSummProbability=c0.LowerSummProbability+c1.LowerSummProbability; } void operator+=(Container &c) { Summ(this,c); }//перегрузка оператора += };
В данном контейнере предусмотрена перегрузка оператора "+=" для слияния двух одинаковых структур, это нам пригодится для основной функции. Ну и сама фрактальная функция:
Container Fractal(double Half, double Middle, int m, int n, int s,double p,int SU,int SD, int U, double P)//фрактал { Container C; ///для передачи в следующий фрактальный уровнь int NewU; int NewSU; int NewSD; double NewP; /// if ( U > Middle && SU + SD < s )//1 случай { if ( (n-1) - U > 0 ) { for ( int u=0 ; u <= (n-1) - U; u++ ) { NewU = -(n-1) + 2*u + 2*U; NewP = P * (Factorial((n-1) - U)/(Factorial(u)*Factorial((n-1) - U - u))) * pow(p,u)*pow(1.0-p,(n-1) - U - u); NewSU = SU + u; NewSD = SD + ((n-1) - U - u); C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP); } } if ( (n-1) - U == 0 ) { NewU = U - 1; NewP = P * (1.0 - p); NewSU = SU; NewSD = SD + 1; Container ct; ct.UpperMidSDown=P*p*SD; ct.UpperMidSUp=P*p*(SU+1); ct.UpperSummProbability=P*p; C+=ct; C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP); } } if ( U < Middle && SU + SD < s )//2 случай { if ( (m-1) + U > 0 ) { for ( int u=0 ; u <= (m-1) + U; u++ ) { NewU = -(m-1) + 2*u; NewP = P * (Factorial((m-1) + U)/(Factorial(u)*Factorial((m-1) + U - u))) * pow(p,u)*pow(1.0-p,(m-1) + U - u); NewSU = SU + u; NewSD = SD + ((m-1) + U - u); C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP); } } if ( (m-1) + U == 0 ) { NewU = U + 1; NewP = P * p; NewSU = SU + 1; NewSD = SD; Container ct; ct.LowerMidSDown=P*(1.0 - p)*(SD+1); ct.LowerMidSUp=P*(1.0 - p)*SU; ct.LowerSummProbability=P*(1.0 - p); C+=ct; C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP); } } if ( U == Middle && SU + SD < s )//3 случай { if ( int(MathFloor(Half))-1 > 0 ) { for ( int u=0 ; u <= int(MathFloor(Half))-1; u++ ) { NewU = -(int(MathFloor(Half))-1) + 2*u + U; NewP = P * (Factorial(int(MathFloor(Half))-1)/(Factorial(u)*Factorial(int(MathFloor(Half))-1 - u))) * pow(p,u)*pow(1.0-p,int(MathFloor(Half))-1 - u); NewSU = SU + u; NewSD = SD + (int(MathFloor(Half))-1 - u); C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP); } } } return C; }
Код был проверен в MetaTrader 5 и прекрасно работает. Данную логику при желании можно расширить, тут еще очень много дополнительных возможностей, но в данном случае я не стал плодить входные параметры данной функции, потому что пока для моих целей подобного кода хватает. Внимательно изучите ее код, и вы увидите полное соответствие математическим принципам, которые были изложены выше. Как видно, даже такой небольшой кусочек кода способен сотворить чудеса. Я всегда придерживаюсь того, что код должен содержать максимум логики и математики, это именно то, что нам пригодится в итоге, просто код ради кода не имеет никакого смысла, даже красивый код бесполезен, если нельзя его использовать по прямому назначению. Для нас прямое назначение - это полезности для торговли. В качестве доказательства я покажу лог:
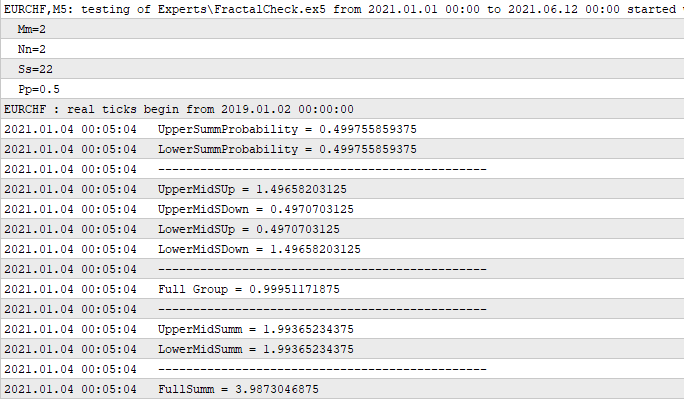
В данном случае видно, что я создал простенького эксперта, который на первом поступившем тике вычисляет весь фрактал, это происходит всего один раз, так как повторные вычисления нам не требуются, в виду того, что они дадут тот же результат. Первые шесть чисел являются частью контейнера, а все остальные являются их производными. Не все производные я вывел, а лишь самые важные, которые пригодятся для понимания того, что с помощью этих шести переменных можно получить все остальные данные, которые нам будут интересны. Например, разберем "Full Group". Не зря она так названа, потому что сумма вероятностей двух несовместных гипотез пересечения одной из границ по нашим предыдущим выкладкам должна быть равна единице, что наш код с успехом подтверждает. Далее идут два идентичных числа, которые являются суммой "1","2" и "3","4". А последнее число уже является суммой предпоследних двух чисел и представляет собой среднее количество шагов, которое пройдет цепь. Я не зря задал именно такие входные параметры стартовой функции, где "m" и "n" равны друг другу и симметричны, а зачем станет понятно ниже.
Выводим первую формулу на основе симметричного фрактала
Если внимательно посмотреть на результат лога, то видно, что среднее количество шагов, которое пройдет цепочка, стремится к числу "4". При этом понятно, что коридор мы увеличили в 2 раза относительно единичного шага. Единичный шаг будет если мы "n" и "m" зададим равными единице. Иначе говоря, если мы хотим посчитать среднее количество шагов в коридоре, который составлен из более мелких коридоров, таких, что в новом коридоре умещается целое количество более мелких коридоров и новый коридор так же симметричен, то можно считать, что:
- P[n] = P[n-1] * 2 - рекурсивное выражение для ширины в шагах, нового коридора, основываясь на ширине старого более мелкого коридора из которого составлен новый коридор
- S[n] = S[n-1] * 4 - рекурсивное выражение для вычисления среднего количества шагов нового коридора, выраженное через среднее количество шагов более мелкого коридора
Если принять "P[0]=1" и "S[0]=1", и соответственно начать нумерацию этой рекурсии с индекса "0", то несложно догадаться, что данная рекурсия может быть представлена в виде двух очень похожих рядов:
- P[n] = 2^n , n = 0 ... + infinity
- S[n] = 4^n = (2^2)^n = (2^n)^2 = P[n]^2
Если внимательно посмотреть на первый ряд и правильно преобразовать второй ряд, то окажется, что второй ряд можно выразить через элементы первого. Иначе говоря, вырисовывается зависимость S = S(P) = P^2. Данная зависимость пока что выполняется только для рекурсивного удвоения ширины коридора. Лично у меня, когда я увидел эту формулу сразу возникла мысль, проверить данную формулу на предмет ее важности для любого, сколь угодно большого числа "n" и "m". Это логично вторым шагом принять, что "n=3","m=3" и вычислить те же самые величины. При проверке данного факта оказалось, что для данных входных параметров получится, что среднее количество шагов стремится уже к числу "9". Кстати говоря, вы так же самостоятельно сможете все это проверить, используя либо код, который я приводил выше, либо MathCad 15 программки, которые я также приложу к статье. Несложно догадаться, что можно составить точно такие же ряды для данных параметров и проделать те же самые манипуляции:
- P[n] = 3^n , n = 0 ... + infinity
- S[n] = 9^n = (3^2)^n = (3^n)^2 = P[n]^2
Как видно по результатам, мы получили ту же самую зависимость "S=S(P)=P^2". Можно, конечно, проделать те же самые вещи для всех остальных возможных сценариев дробления интервала, но в этом нет необходимости. Данный факт означает, что если нам известно, например, среднее время существования цены внутри какого-либо симметричного коридора, то мы можем вычислить среднее время существования цены в любом ином коридоре. Вычислить можно так:
- S = S0 * K^2 - среднее количество шагов нового коридора
- T = S * T0 - среднее время существования нового коридора
- T = T0 * K^2- среднее время существования нового коридора выраженное через среднее время другого коридора (получаем принимая S0 = 1)
- S0 - среднее количество шагов старого коридора
- T0 - среднее время одного шага старого коридора
- P = K * P0 --> K = P/P0 - во сколько раз новый коридор больше старого
- P - ширина нового коридора
- P0 - ширина старого коридора
Теперь можно проверить данную гипотезу, используя используя MathCad 15. Сначала проверим наши предположения относительно квадратичной зависимости:
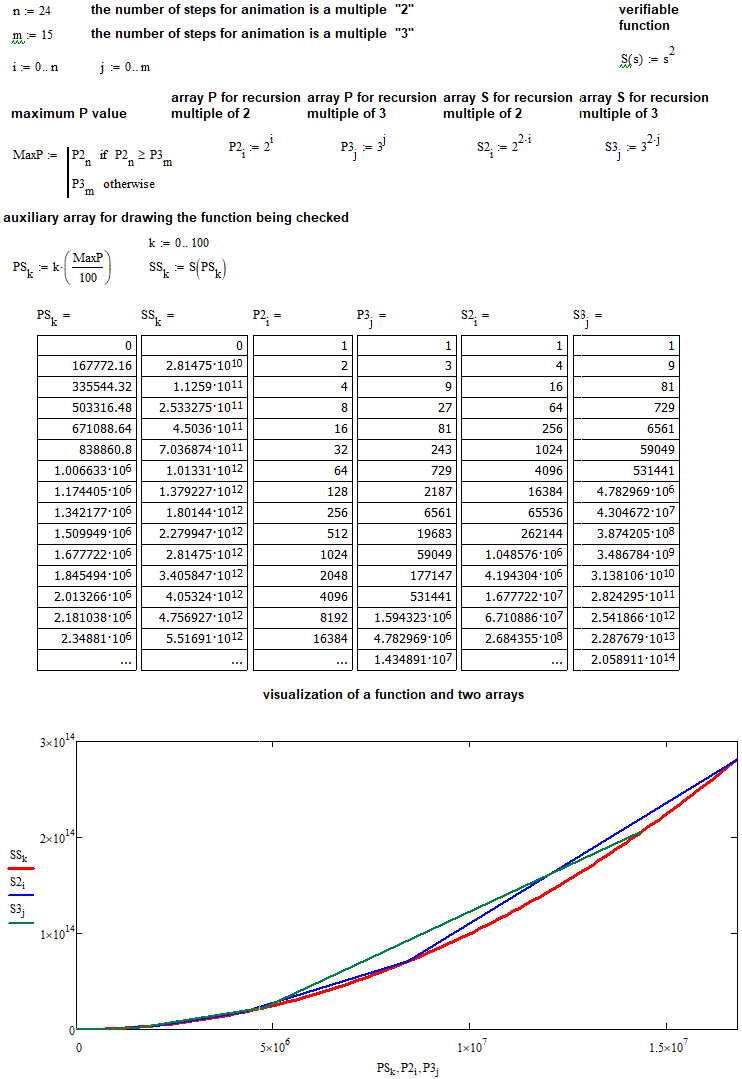
Теперь, я думаю, все предельно наглядно и понятно.
Оценка работоспособности выведенной формулы для всех положительных и действительных аргументов
Получается, что формула работает для всех целых "P", но неясно, можно ли ее использовать для случая дробного "K"? Чтобы обеспечить дробное "K", мы должны придумать кое-какую хитрость. Представим, что у нас есть ценовой коридор с известным средним временем его существования, и, скажем, есть коридор, в который "N" раз укладывается в нашем коридоре, но среднее время его существования пока нам неизвестно. Но чуть ниже мы сможем его найти, используя ту же самую формулу. По этой логике получается, что:
- T = T0 * N^2 ---> T0 = T / N^2
- T - время нашего коридора, среднее время которого известно
- T0 - среднее время более маленького коридора, из которого составлен наш коридор
То есть получается, что мы можем найти и время более маленького коридора, оно нам понадобится для вычисления времени третьего коридора с дробным коэффициентом увеличения. Раз мы нашли среднее время самого маленького коридора, то теперь можно найти его ширину в пунктах:
- d = P / N
После чего мы можем найти сколько таких целых коридоров укладывается в увеличенном коридоре используя следующее соотношение:
- Smin = MathFloor( K * P / d ) = MathFloor( K * N )
- Lim( N --> +infinity ) [ K * N/MathFloor( K * N ) ] = 1
Видно, что ширина коридора сокращается и она не влияет на результат. Второй строчкой написано очень важное соотношение, которое позволит понять, что же делать дальше. Оно говорит о том, что при дроблении исходного коридора на как можно большее число сегментов, можно пренебречь той дробной частью, которая отбрасывается в результате выполнения функции "MathFloor". Предел, стремящийся к единице, как раз и говорит нам об этом. Если уж нас смущает эта неточность, то можно найти еще одну величину:
- Smax = MathFloor( K * P / d ) + 1 = MathFloor( K * N ) + 1 = Smin + 1
Теперь понятно, что истинная величина "K * N" лежит как раз между величинами "Smin" и "Smax", и при стремлении величины "N" к бесконечности мы получим два максимально похожих коридора, и среднее время их тоже будет стремиться друг к другу, так как их размеры отличаются всего на 1 сегмент. Из чего выходит, что среднее время того коридора, которое нам нужно, будет более точно определяться средним арифметическим среднего времени этих коридоров:
- T1 =( T0 * Smin^2 + T0 * Smax^2 ) / 2 = T0 *( Smin^2 + Smax^2 ) / 2
- T1 - среднее время коридора которое нам нужно определить
Для сопровождения размышлений я создал следующую графическую иллюстрацию:
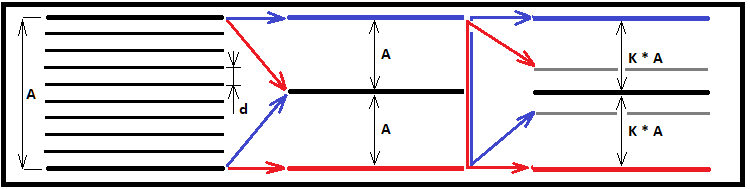
Теперь, вычислив альтернативное выражение для вычисления времени существования коридора, можно сравнить его результат со значением функции для целых "K", подставив туда дробное "K". В случае совпадения чисел на выходе двух выражений, мы сделаем вывод о том, что найденная функция для целых "K" абсолютно работоспособна для абсолютно любых целых и дробных чисел в диапазоне "0 ... +infinity". Первую проверку произведем с "N = 1000", я думаю, данного дробления будет вполне достаточно, для того чтобы увидеть идентичность двух чисел, если это так:

Как видно, два числа практически идентичны, и эта идентичность по идее должна быть тем больше, чем более большое значение "N" мы используем. Это тоже можно доказать, предположив следующее:
- Lim( N --> +infinity ) [ (T0 *( Smin^2 + Smax^2 ) / 2) / ( T * K^2 ) ] = 1
В числителе данного предела наше приближенное выражение для вычисления среднего времени нового коридора, а в знаменателе - выражение, которое предположительно абсолютно точно описывает ту же самую величину. Я сделал простую функцию, которая производит все те же вычисления, которые были проделаны на предыдущем скриншоте, только для всего диапазона числа "N", начиная с числа "1". Теперь можно посмотреть на результат работы данной программки:
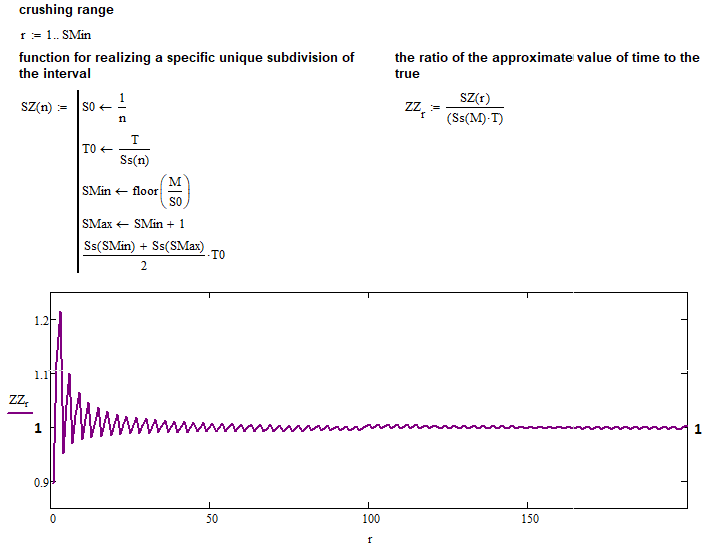
Как видно, все предположения полностью подтверждаются, и функция, которую мы нашли для целых "K", абсолютно работоспособна для любого положительного "K". Теперь у нас есть всего единственная, но очень полезная формула, на которой можно построить очень много всего, в том числе дальнейшую математику для полного описания всего универсального фрактала.
Продвинутый фрактал как следствие универсального фрактала
В качестве полезного и дополнительного примера дальнейшего применения универсального фрактала можно взять фрактал только с одной границей, взяв скажем "n=1", "m ---> +infinity", "s = m+1", "p=0.5". Пока что мы рассматриваем фракталы с равновероятностными шагами в обоих направлениях, что применимо только к случайному блужданию, но в данном фрактале предусмотрены все возможност. Просто для того чтобы переходить к более глубокому анализу подобной сложной структуры, нужно сначала рассмотреть основы, которые помогут нам с более глубоким его анализом, кроме того уже на этом этапе мы получаем очень полезные и интересные формулы и фундаментальные выводы касаемо данных фрактальных процессов. Прогнав данный фрактал с разными значениями "s", я получил следующие данные:
- s = 22 , FullSumm = 2.868 , UpperSummProbability = 0.831
- s = 32 , FullSumm = 3.618 , UpperSummProbability = 0.860
- s = 42 , FullSumm = 4.262 , UpperSummProbability = 0.877
- s = 45 , FullSumm = 4.499 , UpperSummProbability = 0.882
Дальнейшее увеличение количества допустимых шагов приводит к сингулярности времени вычисления, иначе говоря время вычисления настолько лавинообразно возрастает, что ждать можно часами и днями, это конечно неудивительно, но если посмотреть на то, с какой скоростью увеличивается средневероятностная сумма, то можно увидеть, что оценить сходимость данного ряда не представляется возможным, используя данную разновидность фрактала. Но оказывается, что на основе той формулы, что мы вывели выше, можно уже будет оценить эту сходимость, используя совершенно иной, но очень полезный вид фрактала, который даст нам ответ на этот вопрос. Кроме того, как вы увидите, данный вид фрактала способен будет помочь нам с просчетом времени для одной очень знакомой всем прибыльной стратегии "Carry trade". Сначала я покажу графическую иллюстрацию, а потом расскажу, что на ней:
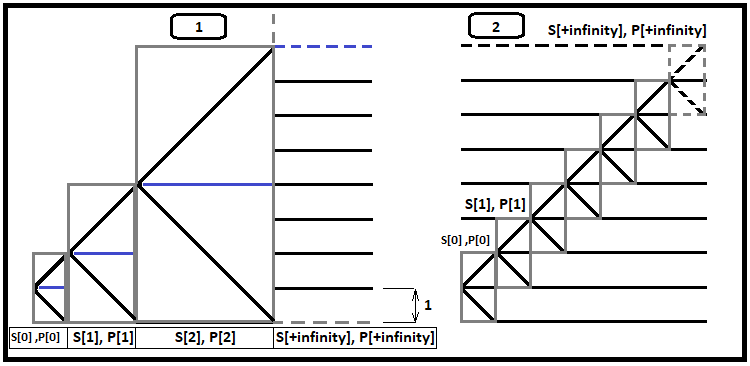
Представьте, что процесс ценообразования начинается в одном шаге от границы, и неважно, где находится эта граница, вверху или внизу. На рисунке я взял пример с нижней границей, потому что он лучше воспринимается. Посмотрим внимательно на первый фрактал. В каждом сером прямоугольнике находится два сценария развития событий:
- Достижение верхней границы прямоугольника
- Достижение нижней границы прямоугольника
Так же видно, что при достижении верхней границы коридора, у нас автоматически в этой же точке начинается новый более большой фрактал, и так далее до бесконечности. Если рассматривать данный процесс так же, как в универсальном фрактале, мы увидим не что иное, как те же цепочки вероятностей, но теперь у нас есть формула, которая говорит о том какое среднее количество шагов произойдет в том или ином симметричном коридоре основываясь на том, сколько шагов укладывается в нем (теперь то мы понимаем, что шагом мы считаем исключительно более маленький коридор, который можно вложить в исходный).
Получается, теперь нам не нужно рассматривать полностью весь фрактал для вычисления среднего количества шагов, а лишь нужно применить выведенную формулу к каждому из данных фракталов и считать уже шагом не одинаковую величину, а достижение верхней либо нижней границы очередного вложенного фрактала. На этой основе можно составить вероятностные цепочки, которые будут очень просты. Вероятность достижения границы на самом первом фрактале "P[0]" будет равна "0.5", думаю, это всем очевидно, но это значит, что есть и второй случай, где пришлось создать следующий фрактал, и так же надеяться, что цена достигнет границы. Видно, что эти события вложены друг в друга, и все такие цепочки так же образуют полную группу.
Получается, вероятность достижения границы на втором фрактале "P[1]" равна предыдущей, но домноженной на те же "0.5", выходит, что этот процесс можно продолжать бесконечно, и, конечно же, можно так же определить среднее количество исходных шагов, основываясь на выведенной формуле и вероятностях данных цепочек. Для этого сначала определим формулу для вероятности каждой отдельной цепочки, принимая во внимание, что среднее количество шагов для пересечения как верхней, так и нижней границы фрактала идентично. Выходит, что:
- PUp = PDown = P - соотношение которое показывает, что вероятность касания верхних и нижних границ фрактала равновероятны для всех границ всех вложенных фракталов
- P[j] = 0.5^(j+1) , j = 0 ... + infinity- вероятность того, что произойдет именно цепочка "j"
- S[i] = S[i-1] + P[i] * ( S[i-1]/P[i-1] + F(D[i]) ), i = 1... + infinity - рекуррентная формула для вычисления суммарного средневероятностного количества шагов для всех фрактальных уровней (при этом S[0] = 1*0.5 = 0.5)
- F(K) = K^2 - наша выведенная формула для вычисления среднего количества шагов
- D(i) = 2^i - количество шагов которое умещается в очередном фрактальном уровне
- S[i-1]/P[i-1] - среднее количество шагов в оставшейся неучтенной ветке, при условии, что текущая ветка произошла (ведь мы обязаны учитывать и те шаги, что были до этого, помимо текщего вложенного фрактала)
Второй фрактал на самом деле идентичен первому, в том плане, что идентичны вероятности их цепей, иначе говоря массив "P[]". Да и зачем он нужен? Представьте, что у нас есть стратегия "Carry Trade". Выходит, что для оценки прибыльности нам требуется понять, что у нас есть два счета, один своповый, а другой безсвоповый для локирования позиции с положительным свопом. Кроме того, нам понадобится формула для вычисления среднего времени удержания прибыльной позиции, а это среднее время является прямым следствием формулы среднего количества шагов. Я не буду освещать этот вопрос слишком глубоко в данной статье, но просто хочу, чтобы хотя бы немногие начали понимать всю важность этой математики. Подробно этот вопрос я буду освещать в своей ветке со свопами чуть позже. А сейчас определим формулу средневероятностных шагов для второго фрактала:
- S[j] = S[j-1] + P[j] * ( S[i-1]/P[i-1] + F(1) ) - рекуррентная формула для вычисления суммарного средневероятностного количества шагов для всех фрактальных уровней (при этом S[0] = 1*0.5 = 0.5)
В данном случае эта формула является лишь частным случаем предыдущей, потому что во втором фрактале "K=1" абсолютно всегда, для всех фрактальных уровней. Выясним, чему равны пределы сумм этих величин для обоих фракталов:

Как видно, первый ряд расходится, говоря нам о том, что при отсутствии верхней границы, при бесконечной торговле, мы получим среднее время равное той же самой бесконечности, а вот во втором случае мы получаем четкий предел, равный "2". Что означает, что если открыть позицию с положительным свопом, то в среднем нам придется закрыть эту позицию после двух шагов (соответственно, среднее время удержания одной позиции будет равно 2*T, где "T" - среднее время удержания, при условии что мы закрываем позицию когда она достигнет одной из границ). Во втором и самом простом случае мы просто закрываем обе позиции на обоих счетах, даже если на счете со свопами плюс. Понятно, что первый вариант куда привлекательнее, но для его реализации потребуется быстрый и беспрепятственный вывод и ввод средств на оба счета. В случае, если такая опция отсутствует, то нам придется воспользоваться классическим вариантом, который не такой прибыльный, но зато стабильный.
Обобщение результатов
Во второй части цикла мы достигли очень интересных результатов, в том числе для практического применения в трейдинге, но что самое главное, стало понятно, что это еще далеко не все, что можно сделать, применяя фракталы. Если определять четко, что было сделано в данной статье:
- Определены четкие математические правила для построения универсального фрактала
- Создан работающий код в стиле MQL5 на основе заявленных математических принципов
- Благодаря двум разным платформам MetaTrader 5 и MathCad 15 все заявленные математические принципы были успешно проверены
- Благодаря полученным алгоритмам получена первая формула для вычисления времени существования произвольного коридора
- Формула была проверена и подтверждена с применением программирования для всех возможных случаев
- На основе полученной формулы был получен новый вид более быстродейственного фрактала
- Полученный фрактал позволил ускорить вычисления и определить то, что было не под силу универсальному фракталу
- Поверхностно рассмотрен частный случай применения продвинутого фрактала для задач своповой тороговли
- Получены инструменты для дальнейшего развития теории
Кроме того, хочу отметить, что мой инструментарий сильно расширился, и теперь можно приступать к анализу фракталов с разновероятностными шагами (трендовые ситуации и ситуации, связанные с анализом торговой статистики). Еще раз хочу уточнить, что в данной статье исследовались только случаи когда "p = 1 - p = q = 0.5". Данное допущение означает, что все выкладки пока применимы только к ситуациям, описывающим случайное блуждание, но, я думаю, вы понимаете, что возможностей здесь еще очень много и это даже не половина.
Отдельно хочу еще раз просто и быстро показать ту формулу, которая была получена в результате исследования фрактала. Подозреваю, что многие, возможно, не поняли этого, и во избежание этого кратко еще раз опишу что и зачем:
- S = K^2 - среднее количество шагов нового коридора, основываясь на том, что шагом является другой коридор
- T = S * T0 = T0 * K^2- среднее время существования неизвестного коридора
- T0 - среднее время существования известного коридора
- P = K * P0 --> K = P/P0 - во сколько раз известный коридор больше неизвестного
- P - ширина коридора, среднее время существования которого неизвестно
- P0 - ширина известного коридора
Подставив "4" в "1", можно выразить среднее количество шагов, которое будет в неизвестном коридоре через известные нам величины, а подставив "1" в "2" мы получаем среднее время существования данного коридора которое вычисляется исходя из известных величин:
- T0, P0, P
Хочу еще добавить ответ на вопрос, который я думаю многих начал волновать в процессе прочтения данной статьи:
- Зачем нам использовать какие-то формулы, если можно набрать торговую статистику в тестере стратегий MetaTrader 5?
Ответ:
- Да можно так поступить, но не везде есть возможность набрать эту статистику в виду того, что не по всем инструментам имеется история торгов в достаточном количестве для того, чтобы набрать сколь угодно значимое количество данных для подобных оценок. Для больших коридоров это сделать будет невозможно, так как можно выбрать такой коридор, который за всю историю ни разу не пересек свои границы, а используя коридоры меньшей ширины, можно используя данную формулу получить те данные, которые невозможно будет получить из статистики. Кроме того, подобная математика дает непревзойденную точность и гибкость использования. Это далеко не все плюсы.
Заключение
В данной статье я старался описать всю логику размышлений, на которой можно строить дальнейшие исследования процессов ценообразования. Да, пока что для практического применения этого маловато, но я на сто процентов уверен, что можно исследовать все разновидности универсального фрактала и получить на их основе все возможные формулы для описания, в том числе, ассиметричных ценовых коридоров и коридоров с одной свободной границей. В следующей статье я продолжу исследования универсального фрактала и постараюсь свести все результаты в простые формулы, а также будет новая очень интересная математика, которая позволит использовать полученные формулы не только для процессов ценнобразования, а также для описания бектестов и торговых сигналов. Благодяря этому мы сможем абсолютно точно проанализировать любую стратетию на предмет времени и вероятностей, а ведь это, в конечном итоге, все, что может нас волновать применительно к торговле.
Ссылки