Нейросети — это просто (Часть 2): Обучение и тестирование сети

Содержание

• Введение
• 1. Постановка задачи
• 2. Проектирование модели нейронной сети
• 2.1. Определение количества нейронов входного слоя
• 2.2. Проектирование скрытых слоев
• 2.3. Определение количества нейронов выходного слоя
• 3. Программирование
• 3.1. Подготовительная работа
• 3.2. Инициализация классов
• 3.3. Обучение нейронной сети
• 3.4. Доработка метода расчета градиента
• 4.Тестирование
• Заключение
• Программы, используемые в статье

Введение

В предыдущей статье "Нейросети — это просто" рассказано о принципах построения класса CNet для работы с полносвязными нейронными сетями средствами MQL5. В данной статье я хочу продемонстрировать пример применения данного класса в советнике и оценить работоспособность нашего класса в "полевых условиях".

1. Постановка задачи

Прежде чем приступить к построению нашего советника, мы должны определиться с целями и задачами, которые мы поставим перед нашей новой нейронной сетью. Несомненно, общей целью любого советника на финансовых рынках является получение прибыли. Однако, это довольно обобщенная цель. Мы же должны конкретизировать задачи для нейронной сети. Более того, мы должны понимать, как будем оценивать результаты работы нейронной сети.

И еще один аспект: ранее созданный класс CNet построен по принципам обучения с учителем, что предполагает наличие размеченных данных для обучающей выборки.

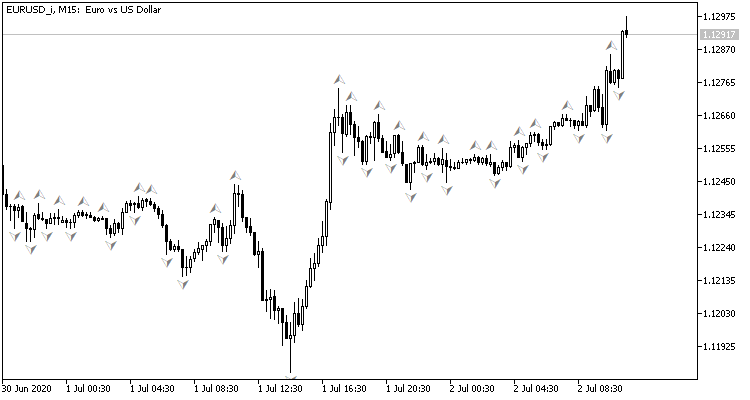
Глядя на график валютной пары, естественным желанием является совершать торговые операции на пиках, которые нам легко помечает стандартный индикатор фракталов Билла Вильямса. Но есть один нюанс, индикатор определяет пики по 3-м свечам и всегда дает сигнал с опозданием на 1 свечу, на которой часто может в последующем сформироваться обратный сигнал. А что, если поставить перед нейронной сетью задачу определять точки разворота до формирования третьей свечи? Данный подход нам даст как минимум одну свечу движения в направлении сделки.

Таким образом мы решаем вопрос с обучающей выборкой:

• Для прямого прохода на вход нейронной сети будем подавать текущую рыночную ситуацию, а на выходе оценку вероятности формирования пика на последней закрытой свече.
• Для обратного прохода после формирования очередной свечи проверяем наличие фрактала на предыдущей свече и подаем результат для корректировки весов. 

Для оценки результатов работы сети можно использовать среднеквадратичную ошибку предсказания, процент правильного предсказания фракталов, процент пропущенных фракталов.

Теперь осталось решить вопрос, какие же исходные данные будем подавать на вход нашей нейронной сети. И тут давайте вспомним, что мы делаем сами, когда пытаемся оценить рыночную ситуацию по графику.

Первое, что советуют начинающему трейдеру — визуально оценить направление тренда по графику. Следовательно, мы должны оцифровать и передать на вход нейронной сети информацию о ценовых движениях. Я предлагаю передавать информацию о ценах открытия и закрытия, максимальной и минимальной цене, объемах и времени формирования. 

Еще одним, наверное, самым популярным способом определения тренда и его силы являются индикаторы-осцилляторы. Применение таких индикаторов удобно еще и тем, что выходные данные индикаторов являются нормализованными. Недолго думая, для эксперимента я взял 4 стандартных индикатора RCI, CCI, ATR и MACD со стандартными параметрами. Я не проводил никакого дополнительного анализа по выбору индикаторов и подбора их параметров.

Возможно, кто-то скажет, что применение индикаторов бессмысленно, так как их данные строятся из пересчета ценовых данных свечей, которые мы уже передали на вход нейронной сети. Но все не совсем так. Значения индикаторов определяются из расчета данных нескольких свечей, что позволяет несколько расширить анализируемую выборку. Задачу же "определить их влияние на результат" мы возлагаем на процесс обучения нейронной сети.

Для возможности оценки динамики рынка будем подавать на вход нейронной сети всю информацию за некий исторический период.

2. Проектирование модели нейронной сети

2.1. Определение количества нейронов входного слоя

Приступая к проектированию самой нейронной сети, надо понимать количество нейронов во входном слое. Для этого мы оцениваем исходную информацию на каждой свече и умножаем на глубину анализируемой истории.

Предварительно обрабатывать данные индикаторов нет необходимости, они нормализованы и их количество индикаторных буферов известно (4 вышеупомянутых индикатора в сумме дают 5 значений). Следовательно, для приема данных индикаторов во входном слое необходимо создать 5 нейронов на каждую анализируемую свечу.

С ценовыми данными свечей ситуация немного другая. Визуально определяя тренд и его силу на графике, мы прежде всего смотрим направление свечей и их размер. И только потом, определяя начало тренда и вероятные точки разворота, обращаем внимание на уровень цены анализируемого инструмента. Следовательно, до подачи данных на вход нейронной сети мы должны их как-то нормализовать. Для себя я решил данную задачу в подаче на вход нейронной сети разности цен закрытия, максимума и минимума от цены открытия описываемой свечи. При таком подходе для описания свечи достаточно 3-х нейронов, а знак первого значения покажет направление свечи.

В различной литературе можно встретить описание влияния различных временных факторов на волатильность валют: сезонность, различия в динамике по дням недели, а также европейская, американская и азиатская торговые сессии по-разному влияют на курсы валют. Для анализа подобных факторов на вход нейронной сети подадим месяц, час и день недели формирования свечи. Я намеренно разбил время и дату образования свечи на составляющие, чтобы дать возможность нейронной сети обобщить и найти зависимости.

Дополнительно добавим информацию об объемах. Если ваш брокер предоставляет данные о реальных объемах, то укажем их, в противном случае укажем тиковые объемы.

Таким образом, для описания каждой свечи нам потребуется 12 нейронов. Умножив это количество на глубину анализируемой истории, получаем размер входного слоя нейронной сети.

2.2. Проектирование скрытых слоев

Следующим шагом нам предстоит спроектировать скрытые слои нашей нейронной сети. Выбор структуры сети (количество слоев и нейронов) является одной из наиболее сложных задач. Однослойный перцептрон хорошо справляется с линейным разделением классов. Двухслойные сети могут повторять извилистые нелинейные границы. Трёхслойные сети позволяют описать сложные многосвязные области. С ростом количества слоёв шире класс функций, которые реализует сеть, но при этом ухудшается ее сходимость и растут затраты на её обучение. Количество нейронов в каждом слое должно удовлетворять ожидаемой вариативности функций. На практике слишком простые сети неспособны в реальных условиях моделировать поведение с достаточной точностью, а слишком сложные сети обучаются на повторение не только целевой функции, но и шума.

В первой статье упоминался метод "5-почему" и я предлагаю продолжить данный эксперимент и создать сеть с 4-мя скрытыми слоями. Количество нейронов в первом скрытом слое я поставил равным 1000, но вполне допускаю и настраивание некой зависимости от глубины анализируемого периода. Воспользовавшись правилом Парето, будем уменьшать количество нейронов в каждом последующем слое на 70%. К вышесказанному добавим ограничение по количеству нейронов в скрытом слое не менее 20.

2.3. Определение количества нейронов выходного слоя

Количество нейронов выходного слоя зависит от поставленной задачи и подхода к ее решению. Для решения задач регрессии достаточно одного нейрона, который будет выдавать ожидаемое значение. Для решения задач классификации потребуется количество нейронов, равное ожидаемому количеству классов, каждый из которых будет выдавать вероятность отнесения исходного объекта к каждому классу. На практике класс объекта определяется по максимальной вероятности.

Для решения нашей задачи я предлагаю создать 2 варианта нейронных сетей и на практике оценить их применимость для решения задачи. В первом случае в выходном слое будет один нейрон. Значения в диапазоне 0.5...1.0 будут соответствовать фракталу на покупку, -0.5...-1.0 - сигналу на продажу, а в диапазоне -0.5...0.5 - отсутствию сигнала. Напомню, в предложенном решении в качестве функции активации используется гиперболический тангенс, выходные значения которого возможны в диапазоне от -1.0 до +1.0.

Во втором случае, в выходном слое создадим 3 нейрона (покупка, продажа, отсутствие сигнала). В данном варианте будем обучать нейронную сеть на получение результата в диапазоне 0.0 ... 1.0, с получением в качестве результата вероятность появления фрактала. Определять сигнал будем по максимальной вероятности, а его направление по индексу нейрона с максимальной вероятностью.

3. Программирование

3.1. Подготовительная работа

Приступая к программированию, вначале добавим необходимые библиотеки:

• NeuroNet.mqh — библиотека для создания нейронной сети из предыдущей статьи;
• SymbolInfo.mqh — стандартная библиотека для получения информации об инструменте;
• TimeSeries.mqh — стандартная библиотека для работы с тайм-сериями;
• Volumes.mqh — стандартная библиотека для получения информации об объемах;
• Oscilators.mqh — стандартная библиотека с классами индикаторов-осцилляторов.

#include "NeuroNet.mqh"
#include <Trade\SymbolInfo.mqh>
#include <Indicators\TimeSeries.mqh>
#include <Indicators\Volumes.mqh>
#include <Indicators\Oscilators.mqh>

Следующим шагом пропишем параметры нашей программы, с помощью которых мы будем задавать параметры нейронной сети и индикаторов.

//+------------------------------------------------------------------+
//|   input parameters                                               |
//+------------------------------------------------------------------+
input int                  StudyPeriod =  10;            //Study period, years
input uint                 HistoryBars =  20;            //Depth of history
ENUM_TIMEFRAMES            TimeFrame   =  PERIOD_CURRENT;
//---
input group                "---- RSI ----"
input int                  RSIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   RSIPrice    =  PRICE_CLOSE;   //Applied price
//---
input group                "---- CCI ----"
input int                  CCIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   CCIPrice    =  PRICE_TYPICAL; //Applied price
//---
input group                "---- ATR ----"
input int                  ATRPeriod   =  14;            //Period
//---
input group                "---- MACD ----"
input int                  FastPeriod  =  12;            //Fast
input int                  SlowPeriod  =  26;            //Slow
input int                  SignalPeriod=  9;             //Signal
input ENUM_APPLIED_PRICE   MACDPrice   =  PRICE_CLOSE;   //Applied price

И объявим глобальные переменные, о функционале которых я расскажу по мере их использования.

CSymbolInfo         *Symb;
CiOpen              *Open;
CiClose             *Close;
CiHigh              *High;
CiLow               *Low;
CiVolumes           *Volumes;
CiTime              *Time;
CNet                *Net;
CArrayDouble        *TempData;
CiRSI               *RSI;
CiCCI               *CCI;
CiATR               *ATR;
CiMACD              *MACD;
//---
double               dError;
double               dUndefine;
double               dForecast;
double               dPrevSignal;
datetime             dtStudied;
bool                 bEventStudy;

На этом подготовительная работа закончена и приступаем к инициализации классов.

3.2 Инициализация классов

Непосредственно инициализацию классов будем осуществлять в функции OnInit. Сначала создадим экземпляр класса работы с инструментами CSymbolInfo и обновим данные об инструменте графика.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   Symb=new CSymbolInfo();
   if(CheckPointer(Symb)==POINTER_INVALID || !Symb.Name(_Symbol))
      return INIT_FAILED;
   Symb.Refresh();

Затем создадим экземпляры тайм-серий. Каждый раз, создавая экземпляр очередного класса, проверяем успешность его создания и инициализируем. В случае ошибки выходим из функции с результатом INIT_FAILED.

   Open=new CiOpen();
   if(CheckPointer(Open)==POINTER_INVALID || !Open.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Close=new CiClose();
   if(CheckPointer(Close)==POINTER_INVALID || !Close.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   High=new CiHigh();
   if(CheckPointer(High)==POINTER_INVALID || !High.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Low=new CiLow();
   if(CheckPointer(Low)==POINTER_INVALID || !Low.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Volumes=new CiVolumes();
   if(CheckPointer(Volumes)==POINTER_INVALID || !Volumes.Create(Symb.Name(),TimeFrame,VOLUME_TICK))
      return INIT_FAILED;
//---
   Time=new CiTime();
   if(CheckPointer(Time)==POINTER_INVALID || !Time.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;

В представленном примере взяты тиковые объемы. Если же вы хотите использовать реальные объемы, то при вызове метода Volumes.Creare нужно будет заменить "VOLUME_TICK" на "VOLUME_REAL".

После объявления тайм-серий аналогичным способом создадим экземпляры классов для работы с индикаторами.

   RSI=new CiRSI();      
   if(CheckPointer(RSI)==POINTER_INVALID || !RSI.Create(Symb.Name(),TimeFrame,RSIPeriod,RSIPrice))
      return INIT_FAILED;
//---
   CCI=new CiCCI();      
   if(CheckPointer(CCI)==POINTER_INVALID || !CCI.Create(Symb.Name(),TimeFrame,CCIPeriod,CCIPrice))
      return INIT_FAILED;
//---
   ATR=new CiATR();      
   if(CheckPointer(ATR)==POINTER_INVALID || !ATR.Create(Symb.Name(),TimeFrame,ATRPeriod))
      return INIT_FAILED;
//---
   MACD=new CiMACD();      
   if(CheckPointer(MACD)==POINTER_INVALID || !MACD.Create(Symb.Name(),TimeFrame,FastPeriod,SlowPeriod,SignalPeriod,MACDPrice))
      return INIT_FAILED;

Следующим шагом приступим к работе непосредственно с классом нейронной сети. Вначале нам нужно создать экземпляр класса. При инициализации класса CNet в параметрах конструктора передается ссылка на массив с указанием структуры сети. Здесь хочется сказать, что обучение нейронной сети процесс довольно трудозатратный как по вычислительным ресурсам, так и по времени. Поэтому, было бы, наверно, неправильно каждый раз при перезапуске программы обучать нашу нейронную сеть заново. И я применил небольшую хитрость, вначале объявляем экземпляр сети без указания структуры и пытаемся загрузить предварительно обученную сеть с локального хранилища (имя файла я вынес в #define).

#define FileName        Symb.Name()+"_"+EnumToString((ENUM_TIMEFRAMES)Period())+"_"+IntegerToString(HistoryBars,3)+"fr_ea"
...
...
...
...
   Net=new CNet(NULL);
   ResetLastError();
   if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false))
     {
      printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError());

Если не удалось загрузить данные предварительно обученной сети, то выводим в журнал сообщение с указанием кода ошибки и приступаем к созданию новой необученной сети. Вначале объявляем экземпляр класса CArrayInt, в котором укажем структуру нейронной сети, количество элементов указывает на количество слоев нейронной сети, а значение элементов указывает на количество нейронов в соответствующем слое.

      CArrayInt *Topology=new CArrayInt();
      if(CheckPointer(Topology)==POINTER_INVALID)
         return INIT_FAILED;

Как уже говорилось выше, во входном слое нам требуется 12 нейронов для описание каждой свечи. Поэтому, в первый элемент массива запишем произведение 12 на глубину анализируемой истории.

      if(!Topology.Add(HistoryBars*12))
         return INIT_FAILED;

Далее опишем скрытые слоя. Мы определили, что у нас будет 4 скрытых слоя с 1000 нейронов в первом скрытом слое и уменьшением числа нейронов на 70% в каждом последующем слое, но не менее 20 нейронов в одном слое. Внесение данных в массив организуем в цикле.

      int n=1000;
      bool result=true;
      for(int i=0;(i<4 && result);i++)
        {
         result=(Topology.Add(n) && result);
         n=(int)MathMax(n*0.3,20);
        }
      if(!result)
        {
         delete Topology;
         return INIT_FAILED;
        }

В выходном слое для построения модели регрессии укажем 1 нейрон.

      if(!Topology.Add(1))
         return INIT_FAILED;

Для модели классификации в нашем случае потребовалось бы указать значение 3 для выходного нейрона.

Далее удалим ранее созданный экземпляр класса CNet и создадим новый с указанием структуры создаваемой нейронной сети. После создания нового экземпляра нейронной сети удалим класс структуры сети, так как далее он больше не используется.

      delete Net;
      Net=new CNet(Topology);
      delete Topology;
      if(CheckPointer(Net)==POINTER_INVALID)
         return INIT_FAILED;

И зададим начальные значения переменных для сбора статистических данных:

• dError — среднеквадратичное отклонение (ошибка)
• dUndefine — процент ненайденных фракталов
• dForecast — процент правильно предсказанных фракталов
• dtStudied — дата свечи последнего обучения.

      dError=-1;
      dUndefine=0;
      dForecast=0;
      dtStudied=0;
     }

Напомню, задание структуры нейронной сети, создание нового экземпляра класса нейронной сети и инициализация статистических переменных осуществляется только если не была загружена предварительно обученная нейронная сеть из локального хранилища.
В заключение функции OnInit создадим экземпляр класса CArrayDouble(), который будем использовать для обмена информацией с нейронной сетью и запустим процесс обучения нейронной сети.

И здесь делюсь еще одним решением. В MQL5 нет асинхронного вызова функций. И если мы явно вызовем функцию обучения из функции OnInit, то терминал будет считать незавершенным процесс инициализации программы до момента завершения обучения. Поэтому, вместо прямого вызова функции мы создаем пользовательское событие, а непосредственно вызов функции обучения осуществляется из функции OnChartEvent. При создании события в параметре lparam укажем дату для начала обучения. Такой подход позволяет нам осуществить вызов функции и при этом завершить функцию OnInit.

   TempData=new CArrayDouble();
   if(CheckPointer(TempData)==POINTER_INVALID)
      return INIT_FAILED;
//---
   bEventStudy=EventChartCustom(ChartID(),1,(long)MathMax(0,MathMin(iTime(Symb.Name(),PERIOD_CURRENT,(int)(100*Net.recentAverageSmoothingFactor*(dForecast>=70 ? 1 : 10))),dtStudied)),0,"Init");
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| ChartEvent function                                              |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,
                  const long &lparam,
                  const double &dparam,
                  const string &sparam)
  {
//---
   if(id==1001)
     {
      Train(lparam);
      bEventStudy=false;
      OnTick();
     }
  }

И не забываем произвести очистку памяти в функции OnDeinit.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   if(CheckPointer(Symb)!=POINTER_INVALID)
      delete Symb;
//---
   if(CheckPointer(Open)!=POINTER_INVALID)
      delete Open;
//---
   if(CheckPointer(Close)!=POINTER_INVALID)
      delete Close;
//---
   if(CheckPointer(High)!=POINTER_INVALID)
      delete High;
//---
   if(CheckPointer(Low)!=POINTER_INVALID)
      delete Low;
//---
   if(CheckPointer(Time)!=POINTER_INVALID)
      delete Time;
//---
   if(CheckPointer(Volumes)!=POINTER_INVALID)
      delete Volumes;
//---
   if(CheckPointer(RSI)!=POINTER_INVALID)
      delete RSI;
//---
   if(CheckPointer(CCI)!=POINTER_INVALID)
      delete CCI;
//---
   if(CheckPointer(ATR)!=POINTER_INVALID)
      delete ATR;
//---
   if(CheckPointer(MACD)!=POINTER_INVALID)
      delete MACD;
//---
   if(CheckPointer(Net)!=POINTER_INVALID)
      delete Net;
   if(CheckPointer(TempData)!=POINTER_INVALID)
      delete TempData;
  }

3.3. Обучение нейронной сети

Для обучения нейронной сети создадим функцию Train, в параметры функции будем передавать дату начала периода обучения.

void Train(datetime StartTrainBar=0)

В начале функции объявим локальные переменные:

• count  — подсчет эпох обучения;
• prev_un  — процент не распознанных фракталов за предыдущую эпоху;
• prev_for  — процент правильных "предсказаний" фракталов в предыдущую эпоху;
• prev_er  — ошибка предыдущей эпохи;
• bar_time  — дата бара пересчета;
• stop  — флаг для отслеживания вызова принудительного завершения программы.

   int count=0;
   double prev_up=-1;
   double prev_for=-1;
   double prev_er=-1;
   datetime bar_time=0;
   bool stop=IsStopped();
   MqlDateTime sTime;

Далее, проверим, не выходит ли полученная в параметрах функции дата за пределы изначально заданного периода обучения.

   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year-=StudyPeriod;
   if(start_time.year<=0)
      start_time.year=1900;
   datetime st_time=StructToTime(start_time);
   dtStudied=MathMax(StartTrainBar,st_time);

Непосредственно обучение нейронной сети организуем в цикле do-while. В начале цикла пересчитаем количество исторических баров для обучения нейронной сети и сохраним статистические данные предыдущего прохода.

   do
     {
      int bars=(int)MathMin(Bars(Symb.Name(),TimeFrame,dtStudied,TimeCurrent())+HistoryBars,Bars(Symb.Name(),TimeFrame));
      prev_un=dUndefine;
      prev_for=dForecast;
      prev_er=dError;
      ENUM_SIGNAL bar=Undefine;

Затем скорректируем размер буферов и загрузим необходимые исторические данные.

      if(!Open.BufferResize(bars) || !Close.BufferResize(bars) || !High.BufferResize(bars) || !Low.BufferResize(bars) || !Time.BufferResize(bars) ||
         !RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars) || !Volumes.BufferResize(bars))
         break;
      Open.Refresh(OBJ_ALL_PERIODS);
      Close.Refresh(OBJ_ALL_PERIODS);
      High.Refresh(OBJ_ALL_PERIODS);
      Low.Refresh(OBJ_ALL_PERIODS);
      Volumes.Refresh(OBJ_ALL_PERIODS);
      Time.Refresh(OBJ_ALL_PERIODS);
      RSI.Refresh(OBJ_ALL_PERIODS);
      CCI.Refresh(OBJ_ALL_PERIODS);
      ATR.Refresh(OBJ_ALL_PERIODS);
      MACD.Refresh(OBJ_ALL_PERIODS);

Актуализируем флаг отслеживания принудительного завершения программы и объявим новый флаг, сигнализирующей о прохождении эпохи обучения (add_loop).

      stop=IsStopped();
      bool add_loop=false;

И организуем вложенный цикл обучения с перебором всех исторических данных. В начале цикла проверим достижения конца перебора исторических данных и при необходимости изменим флаг add_loop. А также выведем на график через функционал комментариев текущее состояние обучения нейронной сети. Таким образом мы сможем наблюдать за процессом обучения.

      for(int i=(int)(bars-MathMax(HistoryBars,0)-1); i>=0 && !stop; i--)
        {
         if(i==0)
            add_loop=true;
         string s=StringFormat("Study -> Era %d -> %.2f -> Undefine %.2f%% foracast %.2f%%\n %d of %d -> %.2f%% \nError %.2f\n%s -> %.2f",count,dError,dUndefine,dForecast,bars-i+1,bars,(double)(bars-i+1.0)/bars*100,Net.getRecentAverageError(),EnumToString(DoubleToSignal(dPrevSignal)),dPrevSignal);
         Comment(s);

Затем проверим, было ли просчитано прогнозное состояние системы на предыдущем шаге цикла. Если да, то проведем корректировку весов в направлении правильного значения. Для этого очистим содержимое массива TempData, проверим сформировался ли фрактал на предыдущей свече и внесем правильное значение в массив TempData (ниже приведен код для нейронной сети регрессии с одним нейроном в выходном слое). После чего вызовем метод backProp нашей нейронной сети с передачей ссылки на массив TempData в качестве параметра. И актуализируем статистические данные в переменных dForecast (процент правильно предсказанных фракталов) и dUndefine (процент пропущенных фракталов).

         if(i<(int)(bars-MathMax(HistoryBars,0)-1) && i>1 && Time.GetData(i)>dtStudied && dPrevSignal!=-2)
           {
            TempData.Clear();
            bool sell=(High.GetData(i+2)<High.GetData(i+1) && High.GetData(i)<High.GetData(i+1));
            bool buy=(Low.GetData(i+2)<Low.GetData(i+1) && Low.GetData(i)<Low.GetData(i+1));
            TempData.Add(buy && !sell ? 1 : !buy && sell ? -1 : 0);
            Net.backProp(TempData);
            if(DoubleToSignal(dPrevSignal)!=Undefine)
              {
               if(DoubleToSignal(dPrevSignal)==DoubleToSignal(TempData.At(0)))
                  dForecast+=(100-dForecast)/Net.recentAverageSmoothingFactor;
               else
                  dForecast-=dForecast/Net.recentAverageSmoothingFactor;
               dUndefine-=dUndefine/Net.recentAverageSmoothingFactor;
              }
            else
              {
               if(sell || buy)
                  dUndefine+=(100-dUndefine)/Net.recentAverageSmoothingFactor;
              }
           }

После корректировки весовых коэффициентов нейронной сети посчитаем вероятность появления фрактала на текущем историческом баре (при i равном "0" посчитается вероятность формирования фрактала на текущем баре). Для этого очистим  массив TempData и внесем в него текущие данные для входного слоя нейронной сети. При ошибке добавления данных или недостатке введенных данных выходим из цикла.

         TempData.Clear();
         int r=i+(int)HistoryBars;
         if(r>bars)
            continue;
//---
         for(int b=0; b<(int)HistoryBars; b++)
           {
            int bar_t=r+b;
            double open=Open.GetData(bar_t);
            TimeToStruct(Time.GetData(bar_t),sTime);
            if(open==EMPTY_VALUE || !TempData.Add(Close.GetData(bar_t)-open) || !TempData.Add(High.GetData(bar_t)-open) || !TempData.Add(Low.GetData(bar_t)-open) ||
               !TempData.Add(Volumes.Main(bar_t)/1000) || !TempData.Add(sTime.mon) || !TempData.Add(sTime.hour) || !TempData.Add(sTime.day_of_week) ||
               !TempData.Add(RSI.Main(bar_t)) ||
               !TempData.Add(CCI.Main(bar_t)) || !TempData.Add(ATR.Main(bar_t)) || !TempData.Add(MACD.Main(bar_t)) || !TempData.Add(MACD.Signal(bar_t)))
                  break;
           }
         if(TempData.Total()<(int)HistoryBars*12)
            break;

После подготовки исходных данных запускаем метод feedForward и результаты работы нейронной сети записываем в переменную dPrevSignal. Ниже приведен код для нейронной сети регрессии с одним нейроном в выходном слое. С кодом для нейронной сети классификации с 3-мя нейронами в выходном слое можно ознакомиться во вложении к статье.

         Net.feedForward(TempData);
         Net.getResults(TempData);
         dPrevSignal=TempData[0];

Для визуализации работы нейронной сети на графике выведем метки прогнозных фракталов для последних 200 свечей.

         bar_time=Time.GetData(i);
         if(i<200)
           {
            if(DoubleToSignal(dPrevSignal)==Undefine)
               DeleteObject(bar_time);
            else
               DrawObject(bar_time,dPrevSignal,High.GetData(i),Low.GetData(i));
           }

И в заключении цикла перебора исторических данных актуализируем флаг принудительного завершения программы.

         stop=IsStopped();
        }

После обучения нейронной сети на всем объеме исторических данных увеличим счетчик эпох обучения и сохраним текущее состояние нейронной сети в локальный файл для возможности последующей загрузке при перезапуске программы.

      if(add_loop)
         count++;
      if(!stop)
        {
         dError=Net.getRecentAverageError();
         if(add_loop)
           {
            Net.Save(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false);
            printf("Era %d -> error %.2f %% forecast %.2f",count,dError,dForecast);
           }
         }

В заключении укажем условия выхода из цикла обучения. Это может быть получение сигнала с вероятностью достижения цели выше заранее заданного  уровня, достижение целевого параметра ошибки, или же когда после очередной эпохи обучения статистические данные не изменяются или их изменение незначительное (обучение остановилось в локальном минимуме). Или же вы можете определить свои критерии выхода из процесса обучения. 

     }
   while((!(DoubleToSignal(dPrevSignal)!=Undefine || dForecast>70) || !(dError<0.1 && MathAbs(dError-prev_er)<0.01 && MathAbs(dUndefine-prev_up)<0.1 && MathAbs(dForecast-prev_for)<0.1)) && !stop);

И перед выходом из функции обучения сохраним время последней свечи обучения.

   if(count>0)
     {
      dtStudied=bar_time;
     }
  }

3.4. Доработка метода расчета градиента.

Хочется обратить внимание на один момент, который был обнаружен в процессе тестирования. При обучении нейронной сети в некоторых случаях возникала ситуация с неконтролируемым ростом весовых коэффициентов нейронов скрытых слоев, что приводило к превышению максимально допустимых значений переменных и, как следствие, параличу всей нейронной сети. Такая ситуация складывалась в случаях, когда ошибка последующего слоя требовала с выхода нейронов значений, выходящих за пределы возможных значений функции активации. Решение было найдено в нормализации целевых значений нейронов. Скорректированный код метода расчета градиента приведен ниже.

void CNeuron::calcOutputGradients(double targetVals)
  {
   double delta=(targetVals>1 ? 1 : targetVals<-1 ? -1 : targetVals)-outputVal;
   gradient=(delta!=0 ? delta*CNeuron::activationFunctionDerivative(targetVals) : 0);
  }

С полным кодом всех методов и функции можно ознакомиться во вложении.

4.Тестирование

Тестовое обучение нейронной сети проводилось по паре EURUSD на таймфрейме H1. На вход нейронной сети подавались данные за 20 свечей. Обучение проводилось за период в 2 последних года. Для чистоты эксперимента на двух графиках одного терминала были запущены оба советника: с нейронными сетями регрессии (Fractal — с 1-м нейроном в выходном слое) и классификации (Fractal_2  — с 3-мя нейронами в выходном слое).

Первая эпоха обучения на 12432 барах потребовала 2 часа 20 минут. Оба советника показали схожие результаты с уровнем попадания чуть более 6%.

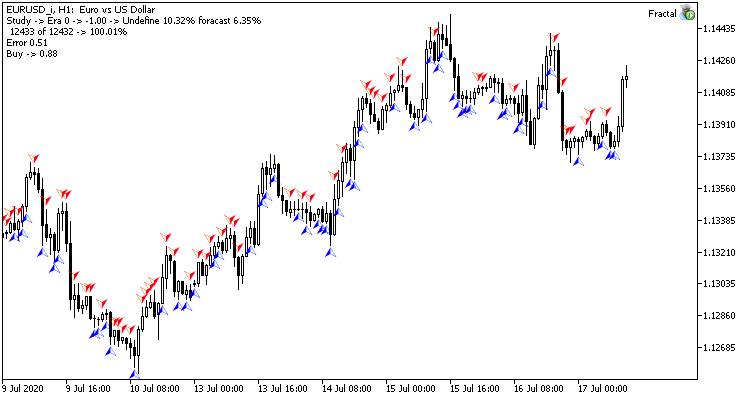
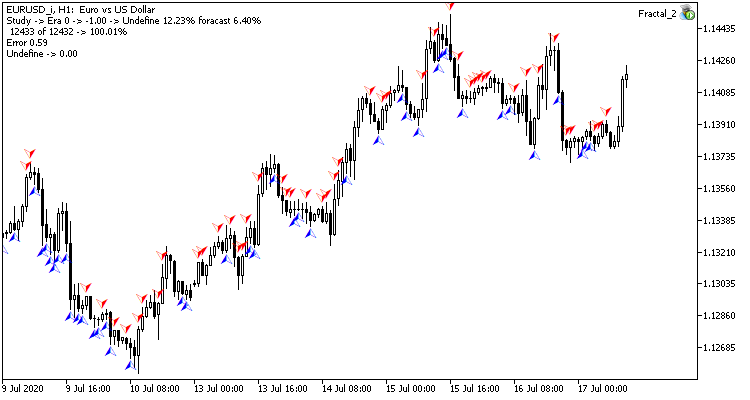
Первая эпоха максимально зависима от случайно выбранных на начальном этапе весовых коэффициентов нейронной сети.

После 35 эпох обучения разрыв в статистических показателях немного увеличился в пользу регрессионной модели нейронной сети:

Показатель	Нейронная сеть регрессии	Нейронная сеть классификации
Среднеквадратичная ошибка	0.68	0.78
Процент "попадания"	12.68%	11.22%
"Пропущенных" фракталов	20.22%	24.65%

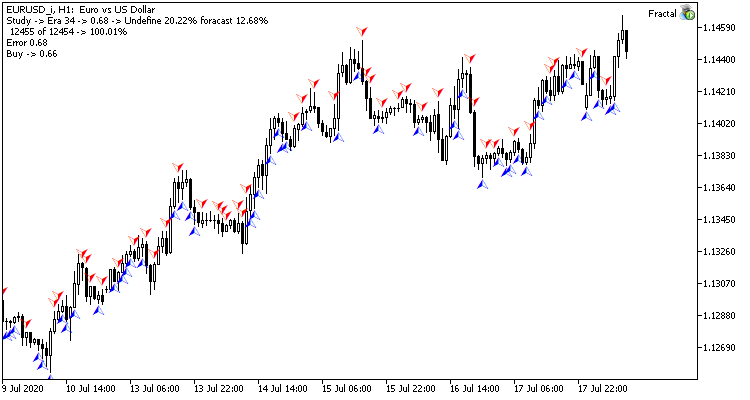
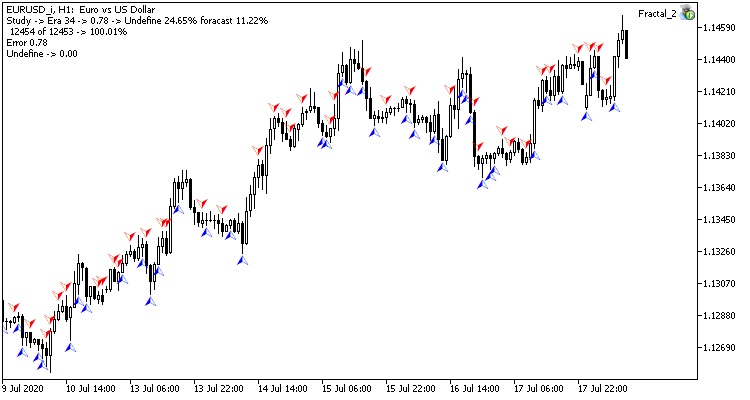
Результаты тестирования показывают, что оба варианта организации нейронной сети дают схожие результаты как по времени обучения, так и по точности предсказания. В тоже время полученные показатели говорят о необходимости дополнительных затрат времени и ресурсов на обучение. Желающие проанализировать динамику обучения нейронных сетей могут ознакомиться со скриншотами каждой эпохи обучения во вложении.

Заключение

В данной статье мы рассмотрели процесс построения, обучения и тестирования нейронной сети. Полученные результате говорят о существующем потенциале использования данной технологии. Однако процесс обучения нейронных сетей довольно затратный как по вычислительным ресурсам, так и по времени.

Программы, используемые в статье

#	Имя	Тип	Описание
	Experts\NeuroNet_DNG\
1	Fractal.mq5	Советник	Советник с нейронной сетью регрессии (1 нейрон в выходном слое)
2	Fractal_2.mq5	Советник	Советник с нейронной сетью классификации(3 нейрона в выходном слое)
3	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети (перцетрона)
	Files\
4	Fractal	Директория	Содержит скриншоты тестирования нейронной сети регрессии
5	Fractal_2	Директория	Содержит скриншоты тестирования нейронной сети классификации