Оценка риска в последовательности сделок с одним активом

Aleksey Nikolayev | 28 августа, 2017

Предисловие

Будем опираться на идею Ральфа Винса по управлению объёмом позиций (полезно также вспомнить в этом свете формулу Келли). Она известна под названием "оптимальное f". В этой теории f — доля капитала, которой рискуют в каждой сделке. По Винсу, f выбирается исходя из условия оптимизации (максимизации) прибыли. При использовании этой теории в торговле возникают две проблемы:

Слишком большая просадка счета.
f известно только на истории сделок.

Попытка решения этих проблем — лишь одна из задач этой статьи. Другая, не менее важная, — очередная попытка ввести теорию вероятностей и математической статистики в процесс анализа торговых систем. Поэтому периодически мы будем немного отклоняться от основной темы. Я воздержусь от систематического изложения основ: при необходимости пользователь может обратиться, например, к этой книге: "Статистика для трейдера".

В конце статьи приведены примеры. Их задача — проиллюстрировать изложенную теорию, поэтому их не рекомендуется применять на практике.

Введение. Отсутствие неопределённости

Для простоты предположим, что цена актива выражает стоимость его единицы в единицах капитала, а не наоборот. Минимальный шаг объема сделки — фиксированная величина в единицах актива. Минимальный ненулевой объём сделки равен этому же шагу. Будем использовать простую модель сделки.

Для каждой сделки определены её тип buy/sell, объём v и цены входа, стоп-лосса и выхода: penter, pstop и pexit, соответственно.

Очевидные ограничения:

ненулевой объем v≥0
цена выхода должна быть меньше цены входа для покупки: pstop<penter
цена выхода должна быть больше цены входа для продажи: pstop>penter.

Введем следующие обозначения:

C0 — капитал перед входом в сделку;
C1 — капитал после выхода из сделки;
Cs — капитал после точного срабатывания стоп-лосса;
r — доля начального капитала, теряемая при точном срабатывании стоп-лосса,

то есть C0−Cs=rC0.

Для сделки типа buy: C1=C0+v(pexit−penter) и Cs=C0−v(penter−pstop).

То же самое для сделки типа sell: C1=C0+v(penter−pexit) и Cs=C0−v(pstop−penter).

После несложных преобразований получим C1=C0(1+ra), где a=(pexit−penter)/(penter−pstop). Эти выражения верны для сделок обоих типов — buy и sell. Назовём величину r риском сделки, а величину a — её доходностью.

Сформулируем задачу управления риском для нашей модели. Пусть у нас имеется n сделок с доходностями ai, где i=1..n, и требуется определить риски ri. Нужно учесть, что ri могут зависеть только от величин, известных на момент входа в сделку. Обычно полагают, что все риски равны между собою ri=r, где 0≤r<1, и находят такое r=rmax, которое максимизирует величину прибыли Cn=C0(1+ra1)(1+ra2)…(1+ran).

Мы поступим схожим образом, но с некоторыми отличиями — при максимизации учтем некоторые ограничения. Например, это ограничения по максимальной просадке и средней доходности в серии сделок. Введем следующие обозначения:

A0 — наименьшее из всех ai,
A=(a1+a2+…+an)/n — их среднее арифметическое.

Верно, что всегда A0≤A и равенство достигается только если все ai=A0. Рассмотрим ограничения на r более подробно.

Cn=Cn(r)>0, откуда следует, что 1+rA0>0. Если A0≥−1, то это верно для всех 0≤r<1. В том случае, когда A0<−1 — получаем, что 0≤r<−1/A0. Мы видим, что дополнительное ограничение на r появляется, только если есть сделки, выход из которых произошел по стоп-лоссу с проскальзыванием. В итоге ограничение примет вид 0≤r<rc, где rc=1, если A0≥−1, и rc=−1/A0 — если A0<−1.
Определим среднюю доходность g следующим образом: Cn=C0(1+gr)^n, откуда:

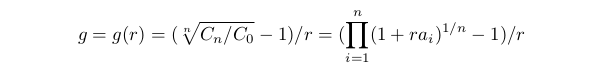
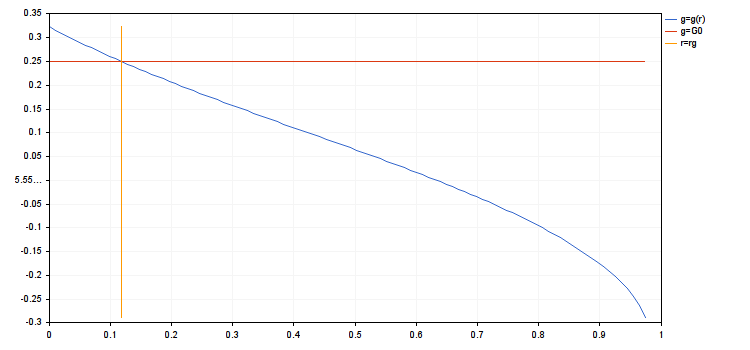
По-другому g можно назвать средней прибылью сделки в серии в отношении к принятому риску. Функция g(r) определена при выполнении ограничений предыдущего пункта. Она имеет устранимую особенность в точке r=0: если r→0, то g(r)→A, и мы можем считать, что g(0)=A. Можно показать, что g(r)≡A, только если все ai=A. В том же случае, если среди ai есть различные, то g(r) убывает при росте r. Ограничение будет иметь вид g(r)≥G0>0. Константа G0 зависит от многих вещей — условий торговли, предпочтений трейдера и т.д. В рамках данной модели можно сказать, что если взять G0>A, то множество r, удовлетворяющих неравенству, будет пустым. Если же G0≤A, то наше ограничение примет вид 0≤r≤rg, где rg — это решение уравнения g(rg)=G0. Если это уравнение не имеет решений, то rg=1.
Для оценки максимальной просадки рассмотрим противоположную ей величину:

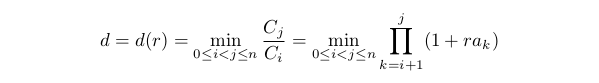
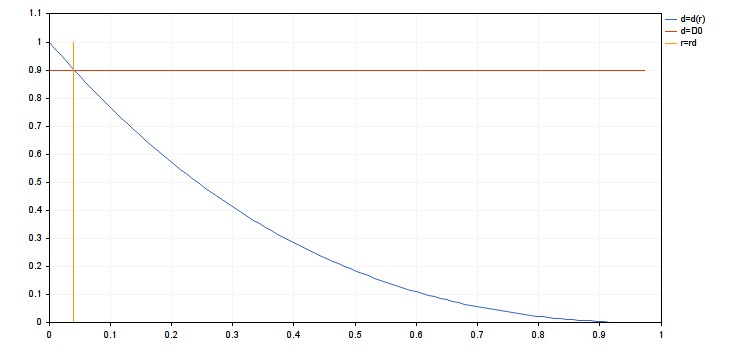
Можно назвать эту величину минимальным приростом. Она более удобна, поскольку всегда положительна и конечна при выполнении ограничения, указанного в первом пункте. Очевидно, что d(0)=1. Если A0<0, то d(r) убывает при росте r в области, ограниченной первым пунктом. Ограничение будет иметь вид d(r)≥D0, где 0<D0<1. Чем больше D0, тем меньшая просадка допустима. Перепишем наше ограничение в следующем виде: 0≤r≤rd, где rd — это решение уравнения d(rd)=D0 (если это уравнение не имеет решений, то rd=1).
При входе в сделку объём v не может принимать произвольное значение. Он должен быть кратным некоторому значению Δv>0, то есть v=kΔv при некотором целом k≥0. Далее, для i-й сделки:

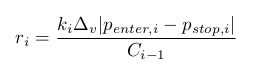
Очевидно, что совпадение всех ri крайне маловероятно. Таким образом оказывается, что точно решить поставленную выше задачу невозможно. Поэтому будем искать решение приближённо. Ограничимся сейчас лишь вычислением такого минимального rv, чтобы каждое ri могло принимать хотя бы одно ненулевое значение на отрезке [0,rv]

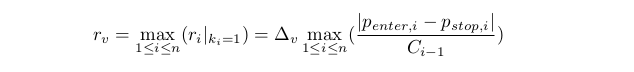
Выведем также более грубую оценку rvr≥rv. Из выполнения ограничения в предыдущем пункте следует Ci≥D0C0>0. Откуда получаем (примечание: d0 и D0 означают одно и то же):

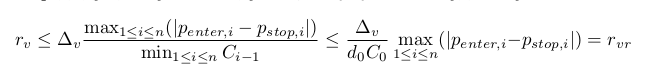
Эта оценка удобна тем, что зависит от капитала более простым образом — только от его начального значения.

Предполагаем, что множество, удовлетворяющее первым трём ограничениям, не пустое. Тогда оно имеет вид отрезка [0,ra], где ra=min(rc,rg,rd).

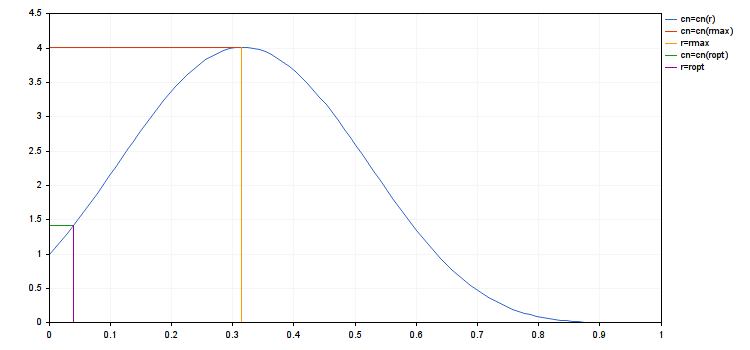
Также предположим, что выполняется и четвертое ограничение, которое требует ra≥rv. Рассмотрим теперь задачу максимизации Cn=Cn(r). В содержательном для нас случае: A>0 и A0<0 эта функция растет на отрезке [0,rmax] и убывает на отрезке [rmax,rc]. Здесь rmax — точка обнуления первой производной: dCn(r)/dr=0.

Теперь легко найти ropt, максимизирующий Cn(r) на отрезке [0,ra]: ropt=min(ra,rmax). Осталось два случая: 1) A0≤A≤0 и 2) 0≤A0≤A. В первом случае ropt=rmax=0, а во втором rmax=rс и ropt=ra .

Далее рассмотрим случай, когда множество, задаваемое ограничениями, оказывается пустым. Это возможно только в двух случаях: 1) G0>A либо 2) ra<rv. Здесь нам остается только принять, что ropt=0.

Теперь найдем приближенные значения ri с учетом дискретности объёмов сделок. Пусть Ri — непустое конечное множество чисел на отрезке [0,ra], подходящих для значения риска ri в i-й сделке. Выберем из них ropt,i , максимизирующее Cn(r) на Ri. Если ropt∈Ri, то ropt,i=ropt. Если ropt∉Ri, то возможны две ситуации: 1) все точки Ri лежат по одну сторону от ropt и 2) точки Ri лежат по обе стороны от ropt. В случае (1) в качестве ropt,i берем из Ri точку, ближайшую к ropt. В случае (2) берем из Ri две точки, ближайшие к ropt с каждой из сторон, и в качестве ropt,i выбираем ту из них, в которой значение Cn(r) больше.

Неопределенность. Вводный пример

Немного усложним модель, рассмотренную во введении. Пусть нам известны n чисел ai, но неизвестен их порядок. Таким образом, допускается их произвольная перестановка. Посмотрим, что поменяется в результатах, полученных выше. В первых двух пунктах произвольная перестановка ai ничего не поменяет. В четвертом пункте тоже не будет перемен, если использовать более грубую оценку rvr.

В третьем же пункте изменения вполне возможны. Действительно, можно составить последовательность так, что между отрицательными числами не будет положительных, и тогда просадка будет максимальной. И наоборот, можно равномерно перемешать положительные числа с отрицательными, и это уменьшит просадку. Общее число перестановок в общем случае n!. Это очень большое число уже при n в пределах нескольких десятков. Теоретически, мы можем решить задачу, поставленную во введении для каждой из j=1..n! перестановок последовательности ai и получить набор чисел rd,j. Но даже тогда остается вопрос о том, какую именно перестановку выбрать. Чтобы содержательно работать с подобной неопределенностью, необходимы понятия и методы теории вероятности и математической статистики.

Рассмотрим набор чисел rd,j как значения функции ρd=ρd(j)=rd,j зависящей от перестановки. То есть, говоря языком теории вероятностей, ρd — случайная величина, множеством элементарных событий для которой будет множество n-перестановок. Будем считать их все различными, даже если некоторые ai совпадают.

Также будем считать все n-перестановки равновероятными. Тогда вероятность каждой из них будет равна 1/n! — это задает вероятностную меру на множестве элементарных событий. Теперь мы можем определить для ρd распределение вероятностей Pρd(x)=n(x)/n!, где n(x) — количество n-перестановок, для которых rd,j<x. Теперь мы должны уточнить условие ограничения просадки. Помимо минимального допустимого D0 , мы должны указать устраивающий нас уровень значимости 0<δ<<1. Величина δ показывает, какую вероятность превышения просадки выше пороговой мы считаем пренебрежимо малой. Тогда мы можем определить rd(δ) как δ-квантиль распределения Pρd(x). Чтобы приближенно решить эту задачу, сгенерируем случайным образом достаточно большое количество nt, где 1<<nt<<n!, n-перестановок. Найдем для каждой из них значение rd,j, где 1≤j≤nt. Затем, в качестве оценки для rd(δ) можно взять выборочный δ-квантиль совокупности этих rd,j.

Несмотря на некоторую искусственность данной модели, ей вполне можно найти применение. Например, можно взять rd, посчитанное для исходной серии сделок, и определить величину вероятности pd=Pρd(rd). Очевидно, выполняется неравенство 0≤pd≤1. Близкое к нулю pd означает большую просадку из-за собирания убыточных сделок близко друг к другу, а близкое к единице — очень равномерную перемешанность прибылей и убытков. Так мы определяем не просто наличие серийности убытков в последовательности сделок (как, например, в методе Z-счёта), а степень её влияния на просадку. Можно составить и другие показатели, зависящие либо только от Pρd(), либо ещё и от rd.

Неопределенность. Общий случай

Предположим, что имеется последовательность сделок с доходностями ai, 1≤i≤n. Предположим также, что эта последовательность — конкретная реализация последовательности независимых в совокупности и одинаково распределённых случайных величин λi. Обозначим их функцию распределения вероятностей через Pλ(x). Предполагается, что у нее есть такие свойства:

положительное матожидание Mλ
ограниченность снизу — существует число λmin≤−1, такое, что Pλ(x)=0 при x<λmin и Pλ(x)>0 при x>λ0.

Эти условия означают, что в среднем доходность положительна и, хотя убыточные сделки вероятны, всегда есть возможность не потерять весь капитал в единственной сделке, ограничив риск.

Сформулируем нашу задачу по определению величины риска. Аналогично примеру из предыдущей части, мы должны вместо числа ropt , вычисленного во введении, изучить случайную величину ρopt. Затем, задав уровень значимости δ, мы вычислим ropt=ropt(δ), как δ-квантиль распределения Pρopt(x). В будущем мы можем пользоваться нашей системой с этим риском, пока просадка и средняя доходность находятся в заданных пределах. При их выходе за эти пределы мы должны отвергнуть эту систему. Вероятность ошибки при этом будет не более δ.

Хочется акцентировать внимание на важности того, чтобы δ была малой. При большой δ теряется смысл использования полученного критерия. Только в случае малого значения есть основания считать связанными между собой два события: 1) система не работает в силу изменений рынка и 2) возникла слишком большая просадка или слишком маленькая доходность. Помимо той ошибки, про которую мы уже говорили, может быть рассмотрена ошибка другого рода. При ней мы не замечаем изменений рынка, которые не влияют на просадку и доходность нашей системы. С практической точки зрения такую ошибку, конечно же, нет смысла рассматривать, поскольку она не меняет прибыльность системы.

В нашей теории это выражается в том, что нам не важны изменения распределений Pλ(x) и Pρopt(x). Имеет значение лишь изменение δ-квантиля Pρopt(x). В частности, это означает отсутствие требования стационарности к последовательности доходностей. Хотя она нам все равно нужна для восстановления закона распределения доходностей по конечной выборке ai, 1≤i≤n. Но и здесь вместо точной стационарности может оказаться достаточным потребовать не слишком сильную изменчивость распределения.

В конечном итоге ρopt выражается через λi, хотя и довольно сложным образом (через другие промежуточные случайные величины). Потому нам потребуется изучать случайные величины, определяемые как функции от λi и строить их распределения. В свою очередь, для этого нам нужно знать Pλ(x). Обозначим три варианта того, какой информацией об этом распределении мы можем обладать.

Известно точное выражение для Pλ(x) или есть способ построить сколь угодно точное его приближение для анализируемой торговой системы. Как правило, такое возможно только при довольно сильных предположениях о поведении ряда цен актива. Например, мы можем считать верной гипотезу "случайного блуждания". Но использование этой информации непосредственно в торговле обычно вряд ли возможно. Выводы, полученные таким образом, всегда малореалистичны и зачастую в принципе отвергают возможность получения прибыли. Польза здесь в другом — на основе таких предположений строится, как говорят в математической статистике, нулевая гипотеза. Потом мы можем, используя эмпирические данные и критерии согласия, либо отвергнуть эту гипотезу, либо признать, что отвергнуть её с нашими данными невозможно. В нашем случае такими эмпирическими данными является последовательность ai, 1≤i≤n.
Известно, что Pλ(x) принадлежит или хорошо приближается к некоторому параметрическому семейству распределений. Например, это возможно при не слишком большом нарушении предположений о ценах актива из предыдущего пункта. Вид семейства распределений определяется, конечно, ещё и алгоритмом торговой системы. Конкретные значения для параметров распределения вычисляются с использованием последовательности ai, 1≤i≤n методами параметрической статистики.
Помимо последовательности ai, 1≤i≤n известны (или предполагаются) только некоторые общие свойства Pλ(x). Например, это может быть предположение о существовании конечных матожидания и дисперсии. В этом случае как приближение для Pλ(x) будем использовать выборочную функцию распределения. Её мы будем строить, исходя из той же последовательности ai, 1≤i≤n. Методы, использующие выборочную функцию распределения вместо точной, обычно называются бутстрэпом. В некоторых случаях знать Pλ(x) не обязательно. Например, случайную величину (λ1+λ2+…+λn)/n при больших n можно считать нормально распределённой (при конечной дисперсии λi).

С использованием предположений, описанных в третьем варианте, будет написано продолжение данной статьи. Первые два варианта будут описаны в дальнейшем.

Мы изучим, как изменятся расчеты, проведённые нами во введении. Вместо конкретных чисел A0 и A мы будем иметь дело со случайными величинами, выражающимися через λi тем же образом: Λ0=min(λ1, λ2, …, λn) и Λ=(λ1+λ2+…+λn)/n.

Рассмотрим их асимптотическое поведение при неограниченно растущем n. В этом случае всегда и с хорошей скоростью Λ0→λmin. Предположим, что у λi существует конечная дисперсия Dλ, тогда Λ→Mλ. При этом, как мы уже упоминали ранее, можно с хорошей точностью считать Λ нормально распределённой с матожиданием Mλ и дисперсией Dλ/n. Если точные значения Mλ и Dλ неизвестны, то можно воспользоваться их выборочными аналогами, посчитанными по ai. Также можно построить эмпирические распределения для Λ0 и Λ, используя бутстрэп.

Перед вычислением ropt(δ) методом бутстрепа учтем следующие замечания о том, как изменятся расчеты, проделанные во введении:

В первом пункте в силу асимптотического поведения Λ0 можно просто огрубить оценку до числа rc=−1/λmin. Но для выборочного распределения значение λmin совпадает с А0 и, следовательно, в этом пункте всё останется без изменений.
Необходимо убедиться в том, что условие G0≤Λ нарушается с вероятностью не больше δ. Для этого δ-квантиль Λ должен быть не меньше, чем G0. Для приближенного вычисления этого квантиля воспользуемся нормальным приближением распределения Λ. В результате этого мы получим nmin — оценку снизу необходимого для анализа количества сделок. Также можно немного подправить стандартный метод бутстрепа и строить наборы выборок растущей длины и по ним искать nmin. Но с точки зрения теории, получится примерно то же, что и для приближения нормальным распределением.
В четвертом пункте, как и ранее, возьмем более грубую оценку rvr.

Зададим nb — количество последовательностей доходностей, которое будет сгенерировано. В цикле выполнения бутстрэпа мы должны для каждой j=1..nb, пройтись по ограничениям на величину риска, перечисленным нами во введении. В силу написанного выше нам остаётся при этом вычислить rg(j), rd(j), rmax(j) и, наконец, ropt(j). Если множество для r при каком-то j оказывается пустым, то полагаем ropt(j)=0.

По завершению работы бутстрепа мы будем иметь массив значений ropt[]. Вычислив по этому массиву выборочную δ-квантиль возьмем ее в качестве решения поставленной задачи.

Вместо заключения

Можно сказать, что написанное выше — только начало темы. Вкратце перечислю то, чему будут посвящены следующие статьи.

Для использования модели сделок как последовательности независимых одинаково распределений мы должны сделать некоторые предположения и допущения о ценах актива и торговом алгоритме.
Нужно конкретизировать теорию для некоторых частных способов выхода из сделок: 1) фиксированные stop-loss/take-profit, 2) фиксированный трейлинг-стоп.
Необходимо продемонстрировать, как использовать излагаемую теорию для построения торговых систем. Рассмотрим, как можно использовать теорию вероятностей при построении системы на гэпах. Коснемся темы использования машинного обучения.

Приложение к введению

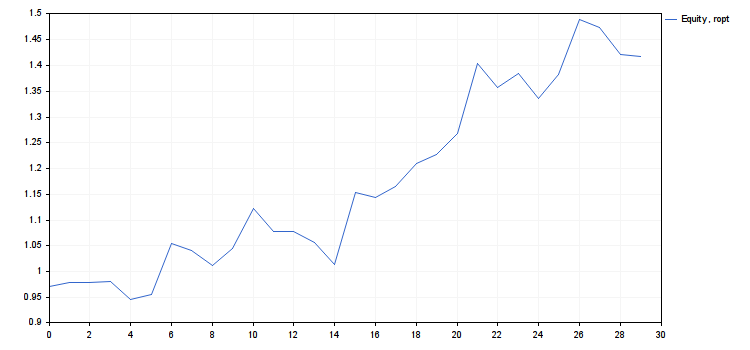
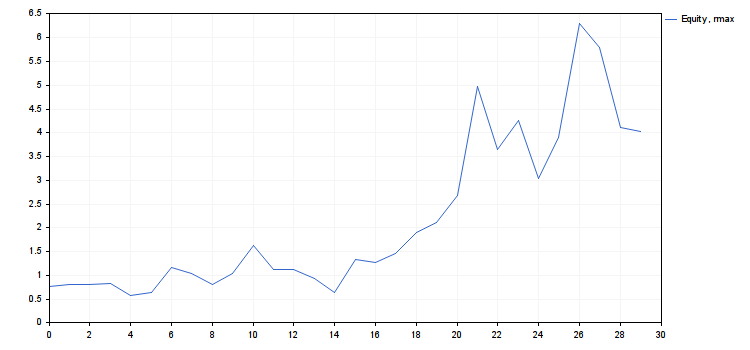
Ниже приведен текст скрипта r_intro.mq5 и результаты его работы — в виде графиков и численные.

#include <Graphics\Graphic.mqh>
#define N 30
#define NR 100
#property script_show_inputs
input int ngr=0;    // номер графика, выводимого на экран
double G0=0.25;     // наименьшая средняя доходность
double D0=0.9;      // наименьший минимальный прирост
                    // начальный капитал c0 полагаем равным 1


void OnStart()
  {
   double A0,A,rc,rg,rd,ra,rmax,ropt,r[NR],g[NR],d[NR],cn[NR],a[N]=
     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // доходности сделок
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   A0=a[ArrayMinimum(a)];
   A=0; for(int i=0; i<N;++i) A+=a[i]; A/=N;
   rc=1; if(A0<-1) rc=-1/A0;
   double c[N];
   r[0]=0; cn[0]=1; g[0]=A; d[0]=1;
   for(int i=1; i<NR;++i)
     {
      r[i]=i*rc/NR;
      cn[i]=1; for(int j=0; j<N;++j) cn[i]*=1+r[i]*a[j];
      g[i]=(MathPow(cn[i],1.0/N)-1)/r[i];
      c[0]=1+r[i]*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+r[i]*a[j]); d[i]=dcalc(c);
     }
   int nrg,nrd,nra,nrmax,nropt;
   double b[NR];
   for(int i=0; i<NR;++i) b[i]=MathAbs(g[i]-G0);
   nrg=ArrayMinimum(b); rg=r[nrg];
   for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0);
   nrd=ArrayMinimum(b); rd=r[nrd];
   nra=MathMin(nrg,nrd); ra=r[nra];
   nrmax=ArrayMaximum(cn); rmax=r[nrmax];
   nropt=MathMin(nra,nrmax); ropt=r[nropt];
   Print("rc = ",rc,"\nrg = ",rg,"\nrd = ",rd,"\nra = ",ra,"\nrmax = ",rmax,"\nropt = ",ropt,
         "\ng(rmax) = ",g[nrmax],", g(ropt) = ",g[nropt],
         "\nd(rmax) = ",d[nrmax],", d(ropt) = ",d[nropt],
         "\ncn(rmax) = ",cn[nrmax],", cn(ropt) = ",cn[nropt]);
   if(ngr<1 || ngr>5) return;
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   graphic.Create(0,"G",0,0,0,750,350);
   double x[2],y[2];
   switch(ngr)
     {
      case 1: graphic.CurveAdd(r,g,CURVE_LINES,"g=g(r)");
      x[0]=0; x[1]=r[NR-1]; y[0]=G0; y[1]=G0;
      graphic.CurveAdd(x,y,CURVE_LINES,"g=G0");
      x[0]=rg; x[1]=rg; y[0]=g[0]; y[1]=g[NR-1];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rg");
      break;
      case 2: graphic.CurveAdd(r,d,CURVE_LINES,"d=d(r)");
      x[0]=0; x[1]=r[NR-1]; y[0]=D0; y[1]=D0;
      graphic.CurveAdd(x,y,CURVE_LINES,"d=D0");
      x[0]=rd; x[1]=rd; y[0]=d[0]; y[1]=d[NR-1];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rd");
      break;
      case 3: graphic.CurveAdd(r,cn,CURVE_LINES,"cn=cn(r)");
      x[0]=0; x[1]=rmax; y[0]=cn[nrmax]; y[1]=cn[nrmax];
      graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(rmax)");
      x[0]=rmax; x[1]=rmax; y[0]=cn[NR-1]; y[1]=cn[nrmax];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rmax");
      x[0]=0; x[1]=ropt; y[0]=cn[nropt]; y[1]=cn[nropt];
      graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(ropt)");
      x[0]=ropt; x[1]=ropt; y[0]=cn[NR-1]; y[1]=cn[nropt];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=ropt");
      break;
      case 4: c[0]=1+ropt*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+ropt*a[j]);
      graphic.CurveAdd(c,CURVE_LINES,"Equity, ropt");
      break;
      case 5: c[0]=1+rmax*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+rmax*a[j]);
      graphic.CurveAdd(c,CURVE_LINES,"Equity, rmax");
      break;
     }
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(30000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
  }

// функция dcalc() принимает массив из значений c1, c2, ... cN и
// возвращает минимальный прирост d. Полагаем c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(int i=1; i<N;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }

средняя доходность

минимальный прирост

конечный капитал Cn

рост капитала при меньшем риске r=ropt

рост капитала при большем риске r=rmax

rc = 0.9839614287119945
rg = 0.1180753714454393
rd = 0.03935845714847978
ra = 0.03935845714847978
rmax = 0.3148676571878383
ropt = 0.03935845714847978
g(rmax) = 0.1507064833125653, g(ropt) = 0.2967587621877231
d(rmax) = 0.3925358395456308, d(ropt) = 0.9037200051227304
cn(rmax) = 4.018198063206267, cn(ropt) = 1.416754202013712

Как видим, используя rmax в качестве значения для риска, мы получаем гораздо большую прибыль (300% вместо 40%). Но достигается это путем гораздо большей просадки (более 60% вместо 10%). Также следует учесть разницу почти в два раза у средней доходности. Если она меньше, то при увеличении трансакционных издержек прибыль упадет сильнее. По этим причинам напрашиваются следующие выводы:

Использовать ropt в качестве значения для риска у этой системы.
"Высвободившийся" при этом риск rmax−ropt можно использовать для добавления новых систем (диверсификация).

Приложение к вводному примеру

Ниже приведен текст скрипта r_exmp.mq5 и численные результаты его работы.

#include <Math\Stat\Uniform.mqh>
#define N 30      // длина серии сделок
#define NR 500    // количество интервалов разбиения отрезка [0,rc]
#define NT 500    // количество генерируемых перестановок
double D0=0.9;    // наименьший минимальный прирост
double dlt=0.05;  // уровень значимости

void OnStart()
  {
   double A0,rc,r[NR],d[NR],rd[NT],a[N]=//A,rg,ra,rmax,ropt,g[NR],cn[NR],
     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,// доходности сделок
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   A0=a[ArrayMinimum(a)];
   rc=1; if(A0<-1) rc=-1/A0;
   for(int i=0; i<NR;++i) r[i]=i*rc/NR;
   double b[NR],c[N];
   int nrd;
   MathSrand(GetTickCount());
   for(int j=0; j<NT;++j)
     {
      trps(a,N);
      for(int i=1; i<NR;++i)
        {
         c[0]=1+r[i]*a[0];
         for(int k=1; k<N;++k) c[k]=c[k-1]*(1+r[i]*a[k]);
         d[i]=dcalc(c);
        }
      for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0);
      nrd=ArrayMinimum(b); rd[j]=r[nrd];
     }
   double p[1],q[1]; p[0]=dlt;
   if(!MathQuantile(rd,p,q)) {Print("MathQuantile() error"); return;}
   PrintFormat("выборочная %f-квантиль rd[] равна %f",p[0],q[0]);
   double rd0=0.03935845714847978;   // значение rd, полученное во Введении
   double pd0=0;                     // соответствующее ему значение pd
   for(int j=0; j<NT;++j) if(rd[j]<rd0) ++pd0; pd0/=NT;
   PrintFormat("для rd = %f значение pd = %f",rd0,pd0);
  }
// функция dcalc() принимает массив из значений c1, c2, ... cN и
// возвращает минимальный прирост d. Полагаем c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(int i=1; i<N;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
// случайная перестановка первых не более чем min(n,ArraySize(b))
// элементов массива b[]
// вместо trps() можно использовать библиотечную MathSample()
void trps(double &b[],int n)
  {
   if(n<=1) return;
   int sz=ArraySize(b);
   if(sz<=1) return;
   if(sz<n) n=sz;
   int ner;
   double dnc=MathRandomUniform(0,n,ner);
   if(!MathIsValidNumber(dnc)) {Print("Error ",ner); ExpertRemove();}
   int nc=(int)dnc;
   if(nc>=0 && nc<n-1)
     { double tmp=b[n-1]; b[n-1]=b[nc]; b[nc]=tmp;}
   trps(b,n-1);
  }

выборочная 0.05-квантиль rd[] равна 0.021647
для rd = 0.039358 значение pd = 0.584

Первая строка результатов говорит нам, что мы должны уменьшить риск еще почти в два раза в сравнении с результатом, полученным во Введении. В этом случае превышение просадки выше целевой (10%) в будущем будет означать, скорее всего, что система не работает должным образом, и торговать по ней нужно прекратить. Вероятность ошибки (отвергнута работающая система) при данном решении составит δ (0.05 или 5%). Вторая строка результата говорит о том, что просадка в исходной серии сделок чуть меньше, чем могла быть в среднем. Вполне возможно, что 30 сделок недостаточно для оценки данной системы. Поэтому было бы полезно провести подобный анализ для большего их количества и посмотреть, как при этом меняются результаты.

Приложение к общему случаю

Ниже приведен скрипт r_cmn.mq5, в котором мы пытаемся оценить снизу величину nmin и результаты его работы:

#include <Math\Stat\Normal.mqh>
#include <Math\Stat\Uniform.mqh>
#include <Graphics\Graphic.mqh>
#define N 30        // длина серии сделок
#define NB 10000    // количество генерируемых выборок для бутстрепа
double G0=0.25;     // наименьшая средняя доходность
double dlt=0.05;    // уровень значимости

void OnStart()
  {
   double a[N]=
     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,   // доходности сделок
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   double A=MathMean(a);
   double S2=MathVariance(a);
   double Sk=MathSkewness(a);
   double Md=MathMedian(a);
   Print("выборочные параметры распределения:");
   PrintFormat("среднее: %f, дисперсия: %f, асимметрия: %f, медиана: %f",A,S2,Sk,Md);
   PrintFormat("число сделок: %d, величина dlt: %f, величина G0: %f",N,dlt,G0);
// приближение нормальным распределением
   Print("приближение нормальным распределением:");
   double q0, p0;
   int ner;
   q0=MathQuantileNormal(dlt,A,MathSqrt(S2/N),ner);
   if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;}
   Print("dlt-квантиль: ",q0);
   p0=MathCumulativeDistributionNormal(G0,A,MathSqrt(S2/N),ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   Print("уровень значимости для G0: ",p0);
// бутстреп
   MathSrand(GetTickCount());
   double b[N],s[NB];
   p0=0;
   for(int i=0;i<NB;++i)
     {
      sample(a,b);
      s[i]=MathMean(b);
      if(s[i]<G0) ++p0;
     }
   p0/=NB;
   double p[1],q[1];
   p[0]=dlt;
   if(!MathQuantile(s,p,q)) {Print("MathQuantile() error"); return;}
   Print("приближение бутстрепом");
   Print("dlt-квантиль: ",q[0]);
   Print("уровень значимости для G0: ",p0);
// определение nmin (приближение нормальным распределением)
   int nmin;
   for(nmin=1; nmin<1000;++nmin)
     {
      q0=MathQuantileNormal(dlt,A,MathSqrt(S2/nmin),ner);
      if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;}
      if(q0>G0) break;
     }
   Print("Минимальное количество сделок nmin (приближение нормальным распределением):");
   PrintFormat("не менее %d, значение dlt-квантиля: %f",nmin,q0);
  }
  
void sample(double &a[],double &b[])
  {
   int ner;
   double dnc;
   for(int i=0; i<N;++i)
     {
      dnc=MathRandomUniform(0,N,ner);
      if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();}
      int nc=(int)dnc;
      if(nc==N) nc=N-1;
      b[i]=a[nc];
     }
  }

Выборочные параметры распределения:

среднее: 0.322655
дисперсия: 1.419552
асимметрия: 0.990362
медиана: 0.023030
число сделок: 30
величина dlt: 0.050000
величина G0: 0.250000.

Приближение нормальным распределением:

dlt-квантиль: -0.03514631247305994;
уровень значимости для G0: 0.3691880511783918.

Приближение бутстрепом:

dlt-квантиль: -0.0136361;
уровень значимости для G0: 0.3727.
минимальное количество сделок nmin (приближение нормальным распределением): не менее 728
значение dlt-квантиля: 0.250022.

Из этих результатов сразу же следует что ropt(δ)=0. То есть, наш критерий запрещает торговлю по этой системе при таких данных или требует историю сделок гораздо большей длины. И это — несмотря на замечательные графики капитала в первом приложении. Причем бутстреп дает практически те же результаты, что и приближение нормальным распределением. Естественно, возникают вопросы: 1) почему всё так плохо? и 2) как сделать лучше? Попробуем на них ответить.

Причины лежат как в используемом критерии, так и в самой системе. Наш критерий слишком универсальен. С одной стороны это хорошо — им просто и удобно пользоваться в большом числе случаев. С другой — он не учитывает особенности не то что конкретной системы, а вообще всех, рассматриваемых нами. Например, все наши системы дают распределения с "обрезанным" левым хвостом, а некоторые теоретически могут иметь бесконечное матожидание. Поэтому, как правило, все распределения скошены вправо и их среднее слишком медленно сходится к симметричному нормальному распределению. У системы в нашем примере именно такое скошенное распределение и есть, судя по коэффициенту асимметрии или по смещению матожидания вправо от медианы. В принципе, именно такого поведения и следует ожидать от системы, следующей правилу "обрезай убытки, позволяй прибыли расти".
Нужны критерии, полнее использующие информацию о конкретной торговой системе и о ряде цен актива. То есть, совсем без предположений о ценах не обойтись. Но эти предположения не должны слишком искажать реальную картину. Это значит, что мы должны оказаться в ситуации второго варианта из трех пунктов, приведенных в начале главы "Общий случай". Именно поэтому мы должны далее заняться параметрическими методами. С вычислительной точки зрения они более сложны и менее универсальны, но могут быть более точными в конкретном случае.

Можно сделать следующий вывод. Источниками убытков являются не только неожиданные изменения в поведении цен актива (например, смена тренда). Это может быть и всегда присущая им неопределённость (волатильность, шум). Методы, рассматриваемые нами — один из способов попытаться разделить эти причины и уменьшить влияние второй. Если же для торговой системы не удается сделать этого, то она не рекомендуется к использованию.