Анализ основных характеристик временных рядов
Victor | 3 июня, 2011
Введение
Анализ процессов, представленных ценовыми рядами, является достаточно сложной задачей, зачастую требующей существенных затрат усилий и времени. Это связано и с особенностями исследуемых последовательностей, и с тем, что, несмотря на большое количество различного рода публикаций, бывает трудно подобрать для той или иной задачи подходящее программное решение.
Даже если найден подходящий скрипт или индикатор, то это не означает, что не придется адаптировать его исходный код под текущую задачу.
Кроме того, зачастую даже для решения простых задач эти программы могут потребовать использования входных параметров, смысл которых хорошо известен разработчикам, но не всегда полностью понятен стороннему пользователю.
Конечно, при проведении серьезных исследований эти трудности не могут являться непреодолимым препятствием, но если возникло желание проверить какое-либо предположение или просто удовлетворить свое любопытство, то чаще всего это любопытство так и остается неудовлетворенным. Именно поэтому возникла идея создания универсального программного инструмента, позволяющего легко производить предварительный анализ основных характеристик и параметров входной последовательности.
Такой инструмент должен быть предельно прост в установке и для максимального упрощения его использования не должен требовать никаких входных параметров. В тоже время оцениваемые параметры и характеристики должны достаточно полно и наглядно отображать характер исследуемой последовательности.
Предварительная оценка характеристик могла бы помочь определить пути дальнейшего углубленного исследования или отвергнуть на начальном этапе то или иное предположение и предотвратить потерю времени на дальнейшее их изучение.
Хорошо известно, что универсальное программное обеспечение чаще всего проигрывает по своим характеристикам специализированному. Это обычная плата за универсальность, которая почти всегда достигается за счет целой системы компромиссов. Тем не менее, в данной статье представлена попытка создания именно универсального инструмента, позволяющего максимально облегчить процесс предварительного анализа характеристик последовательностей.
Инсталляция и возможности
Файл TSAnalysis.zip, размещенный в конце статьи, включает в себя каталог \TSAnalysis, в котором содержатся все необходимые для работы файлы. После раскрытия архива этот каталог со всем его содержимым (не переименовывая его) необходимо скопировать в каталог \MQL5\Scripts. В скопированном каталоге \TSAnalysis содержится тестовый скрипт TSAexample.mq5, который после компиляции можно запустить на исполнение.
Этот скрипт, используя класс TSAnalysis, должен подготовить данные и для их отображения вызвать браузер, установленный по умолчанию. Необходимо учесть, что для нормальной работы класса TSAnalysis в терминале должно быть разрешено использование внешних DLL. Для деинсталляции достаточно просто удалить каталог \TSAnalysis.
Весь исходный код, используемый для анализа последовательностей, реализован в виде класса TSAnalysis и размещен в единственном файле TSAnalysis.mqh.
При использовании этого класса для входной последовательности оценивается и может быть отображена следующая информация:
- Количество элементов последовательности;
- Максимальное и минимальное значение последовательности (max, min);
- Медиана (median);
- Среднее значение (mean);
- Дисперсия (variance);
- Стандартное отклонение (standard deviation);
- Несмещенная оценка дисперсии (unbiased variance);
- Несмещенная оценка стандартного отклонения (unbiased standard deviation);
- Коэффициент асимметрии (skewness);
- Коэффициент эксцесса (kurtosis);
- Коэффициент эксцесса (excess kurtosis);
- Тест Жака-Бера (Jarque-Bera test);
- p-значение теста Жака-Бера (JB test p-value);
- Скорректированный тест Жака-Бера (Adjusted Jarque-Bera test);
- p-значение скорректированного теста Жака-Бера (AJB test p-values);
- Границы для значений, не принадлежащих данной последовательности (outliers);
- Данные гистограммы (histogram);
- Данные графика со шкалой нормального распределения (Normal Probability Plot);
- Данные графика функции автокорреляции (correlogram);
- Значения 95% доверительного интервала для функции автокорреляции;
- Данные графика спектра, построенного по функции автокорреляции;
- Данные графика частной автокорреляционной функции;
- Данные графика спектральной оценки, произведенной методом максимальной энтропии.
В рассматриваемом классе TSAnalysis для визуализации полученных результатов используется виртуальный метод show, который отвечает только за способ отображения предварительно подготовленной информации.
Поэтому переопределив данный метод в потомках класса TSAnalysis, можно организовать вывод результатов любым доступным способом, а не только через HTML-файл, как это сделано в базовом классе, где после формирования файла с данными для отображения графиков вызывается интернет-браузер.
Прежде чем перейти к рассмотрению класса TSAnalysis, проиллюстрируем результат его использования на тестовой последовательности данных. На рисунке показан результат работы скрипта TSAexample.mq5.
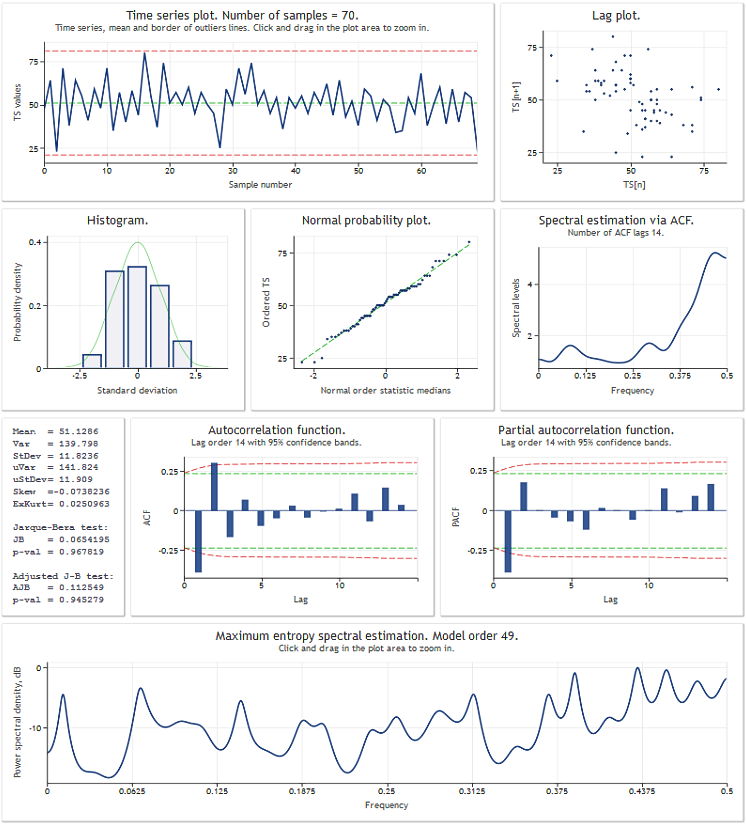
Рисунок 1. Результат работы скрипта TSAexample.mq5
Предварительно ознакомившись с возможностями класса TSAnalysis, перейдем к более подробному его рассмотрению.
Класс TSAnalysis
Класс TSAnalysis (см. файл TSAnalysis.mqh) включат в себя только один доступный (public) метод Calc, в котором производятся все необходимые вычисления и после этого происходит вызов виртуального метода show. Метод show будет кратко рассмотрен позже, а сейчас перейдем к поэтапному пояснению сути производимых вычислений.
При использовании класса TSAnalysis на исследуемую входную последовательность накладываются некоторые ограничения.
Во-первых, последовательность должна содержать не менее восьми элементов. Скорее всего, такое ограничение не является слишком жестким, так как для практических целей вряд ли может возникнуть необходимость в исследовании таких коротких последовательностей.
Кроме ограничения на минимальную длину последовательности необходимо, чтобы величина дисперсии входной последовательности не была близкой к нулю. Это требование вызвано тем, что значение дисперсии используется в дальнейших вычислениях и для получения устойчивого результата должно быть не менее некоторой величины.
Последовательности с дисперсией, имеющей очень маленькую величину, встречаются не так часто, поэтому и это ограничение, наверное, не будет являться серьезным недостатком. И в случае слишком короткой последовательности, и в случае близкой к нулю дисперсии, выполнение вычислений будет прервано и в журнале появится соответствующее сообщение об ошибке.
Существует еще одно неявное ограничение, связанное с максимально допустимой длиной входной последовательности. Это ограничение не задано явным образом, оно зависит от производительности используемого компьютера и количества установленной на нем памяти и определяется чисто субъективно по времени выполнения скрипта и скорости отрисовки результатов в Web-браузере. Предполагается, что обработка последовательностей, содержащих 2-3 тысячи элементов не должна вызывать серьезных затруднений.
В качестве основы для вычисления статистических параметров последовательности служит приведенный ниже фрагмент исходного кода метода Calc (см. файл TSAnalysis.mqh).
Описание используемого алгоритма можно найти по ссылке "Алгоритм вычисления дисперсии".
. . . Mean=0; sum2=0; sum3=0; sum4=0; for(i=0;i<NumTS;i++) { n=i+1; delta=TS[i]-Mean; a=delta/n; Mean+=a; // Mean (average) sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // sum of fourth degree b=TS[i]-Mean; sum3+=a*(b*delta*(n-2.0)-3.0*sum2); // sum of third degree sum2+=delta*b; // sum of second degree } . . .
В результате исполнения этого фрагмента вычисляются значения
![]()
где n = NumTS – количество элементов в последовательности.
Используя полученные значения, вычисляются следующие параметры.
Дисперсия и стандартное отклонение:
![]()
Несмещенная оценка дисперсии и стандартного отклонения:
![]()
Коэффициент асимметрии:
![]()
Коэффициент эксцесса (kurtosis). Минимальное значение коэффициента равно 1, значение для последовательности с нормальным законом распределения будет равно 3.
![]()
Коэффициент эксцесса (excess kurtosis):
![]()
В этом случае минимальное значение коэффициента равно -2, а его значение для последовательности с нормальным законом распределения будет равно 0.
Традиционно для первого предварительного теста на нормальность закона распределения последовательности используется критерий Жака-Бера, который легко вычисляется по известным значениям асимметрии и эксцесса. Для критерия Жака-Бера величина статистической значимости (p-значение) при увеличении длины последовательности асимптотически стремится к обратной функции распределения хи-квадрат с двумя степенями свободы.
Таким образом,
![]()
Для коротких последовательностей полученное таким образом р-значение обязательно будет иметь весьма ощутимую погрешность. Несмотря на это, очень часто используют именно такой вариант вычислений. Трудно сказать, с чем это связано, может быть, привлекает простота и ясность используемых выражений, или может быть, это связано с тем фактом, что сам по себе критерий Жака-Бера не является идеальным тестом на нормальность и поэтому не имеет смысла производить более точные вычисления.
В нашем случае в методе Calc (файл TSAnalysis.mqh) вычисление критерия Жака-Бера и его р-значения производятся в соответствии с приведенными выше выражениями.
Кроме того, дополнительно вычисляется скорректированный тест Жака-Бера:
![]()
где
![]()
Скорректированный вариант теста Жака-Бера для коротких последовательностей снижает погрешность найденного указанным способом р-значения, но полностью эту погрешность не устраняет.
Предполагается, что конечный результат анализа будет включать в себя график входной последовательности, на котором будет отображена линия, соответствующая среднему значению и линии, определяющие границы, при выходе за которые значения могут считаться ошибочными, не принадлежащими данной последовательности (outliers).
Эти границы в данном случае рассчитываются следующим образом:
![]()
![]()
Это выражение приведено в книге С.В. Булашева "Статистика для трейдеров" со ссылкой на книгу П.В. Новицкого и И.А. Зографа "Оценка погрешностей результатов измерений". После нахождения границ, никакой обработки входной последовательности не предусматривается, предполагается отображать эти границы только в качестве информации.
Кроме графика входной функции предполагается отображать гистограмму с эмпирической оценкой закона распределения входной последовательности. Количество интервалов при построении гистограммы определяется следующим образом (С.В. Булашев, Статистика для трейдеров):
![]()
Результат округляется до ближайшего меньшего целого нечетного значения. Если полученное значение меньше пяти, то используется значение 5.
Количество элементов в массивах с данными для шкалы X и шкалы Y гистограммы соответствует найденному количеству интервалов плюс два, так как слева и справа к гистограмме принудительно добавляются по одному столбцу с нулевым значением.
Ниже приведен фрагмент кода (см. файл TSAnalysis.mqh), подготавливающий данные для построения гистограммы.
. . . n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0); if((n&0x01)==0)n--; if(n<5)n=5; // Number of bins ArrayResize(XHist,n); ArrayResize(YHist,n); ArrayInitialize(YHist,0.0); a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean); if(a<b)a=b; v=Mean-a; delta=2.0*a/n; for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // Histogram. X-axis for(i=0;i<NumTS;i++) { k=(int)((TS[i]-v)/delta); if(k>(n-1))k=n-1; YHist[k]++; } for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev; // Histogram. Y-axis . . .
В приведенном коде:
- NumTS – количество элементов последовательности,
- XHist[] и YHist[] – массивы содержащие значения для шкалы X и Y соответственно,
- TSort[] – массив содержащий отсортированную входную последовательность.
При таком способе вычислений значения шкалы X будут выражены в единицах стандартного отклонения, а значения шкалы Y будут соответствовать плотности вероятности.
Для построения графика со шкалой нормального распределения в качестве значений для шкалы Y используется отсортированная по возрастанию входная последовательность. Количество значений по шкале Y и шкале X предполагается равным.Для вычисления значений шкалы X сначала находятся значения медиан как для случая равномерного закона распределения:
![]()
![]()
![]()
Далее из них вычисляются значения шкалы X при помощи обратной функции нормального распределения (см. метод ndtri).
Для построения графика автокорреляционной функции (АКФ), графика частной автокорреляционной функции (ЧАКФ) и вычисления спектральной оценки по методу максимальной энтропии для входной последовательности должны быть найдены значения функции автокорреляции.
Количество значений, которые предполагается отображать на графиках АКФ и ЧАКФ, определим следующим образом:
![]()
![]()
![]()
Найденное таким образом количество значений будет вполне достаточным для отображения автокорреляционной функции на графике, но для дальнейшего вычисления авторегрессионной спектральной оценки желательно иметь значительно большее количество вычисленных значений АКФ, которое в нашем случае будет равно порядку используемой модели авторегрессии.
Порядок модели IP будем определять по найденному значению NLags:
![]()
![]()
Формализовать процесс определения оптимального порядка модели для спектральной оценки достаточно сложно. При низком порядке модели будут получены излишне сглаженные результаты, а при завышенном порядке, скорее всего, будет получена неустойчивая спектральная оценка, имеющая большой разброс значений.
Кроме того, на порядок модели оказывает влияние и характер входной последовательности, поэтому порядок IP, определенный по приведенному выше выражению, в некоторых случаях будет оказываться завышенным, а в некоторых случаях заниженным. К сожалению, эффективного подхода, к определению требуемого порядка модели найти не удалось.
Таким образом, для входной последовательности должно быть определено количество значений АКФ, равное порядку модели IP, используемому при спектральной оценке последовательности.
. . . ArrayResize(cor,IP); a=0; for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i]; for(i=1;i<=IP;i++) { c=0; for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i]; cor[i-1]=c/a; // Autocorrelation } . . .
Данный фрагмент исходного кода (см. файл TSAnalysis.mqh) иллюстрирует процесс вычисления функции автокорреляции (АКФ). Результат вычисления размещается в массиве cor[]. Как видим, сначала вычисляется значение нулевого коэффициента автокорреляции, а затем в цикле происходит вычисление и нормирование остальных коэффициентов. При таком нормировании нулевой коэффициент всегда будет равен единице, поэтому нет необходимости сохранять его в массиве cor[].
Этот массив содержит количество коэффициентов, равное IP, начиная с первого. При вычислении АКФ используется массив TSCenter[], содержащий входную последовательность, из всех элементов которой было вычтено среднее значение.
Для сокращения времени, требуемого для вычисления АКФ, можно воспользоваться методами, использующими алгоритмы быстрого преобразования, например, FFT. Но в данном случае время, затрачиваемое на вычисление АКФ, оказывается вполне приемлемым, поэтому в усложнении программного кода, скорее всего, нет необходимости.
Используя найденные значения коэффициентов корреляции, нетрудно построить график АКФ (correlogram). Для того чтобы на этом графике можно было отображать границы 95% доверительного интервала (confidence bands), по приведенным ниже выражениям вычисляются их значения.
Для интервала, используемого при тестировании на случайность:
![]()
Для интервала, используемого при определении порядка ARIMA модели
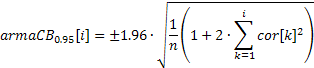
В первом случае доверительный интервал имеет постоянное значение, а во втором он будет увеличиваться с увеличением номера коэффициента автокорреляции.
Иногда может представлять интерес сильно сглаженная частотная характеристика входной последовательности, отображающая только общую тенденцию распределения частот. Например, существенный подъем в области нижних или верхних частот, преобладание в области средних частот и так далее.
Отображать такую частотную характеристику желательно в линейном масштабе, для того чтобы сильнее подчеркнуть преобладающие частотные области. Такая АЧХ может быть построена по найденным ранее коэффициентам автокорреляции. Для вычисления АЧХ будем использовать количество коэффициентов, равное количеству, отображаемому на графике АКФ.
Учитывая, что это количество невелико, в результате должны получаться достаточно гладкие спектральные оценки.
В этом случае частотная характеристика последовательности может быть выражена через коэффициенты автокорреляции следующим образом:
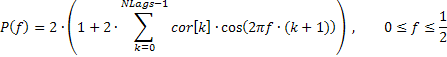
Ниже приведен фрагмент кода (см. файл TSAnalysis.mqh), используемый для вычисления АЧХ по приведенному выражению
. . . n=320; // Number of X-points ArrayResize(Spect,n); v=M_PI/n; for(i=0;i<n;i++) { a=i*v; b=0; for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1)); Spect[i]=2.0*(1+2*b); // Spectrum Y-axis } . . .
Необходимо отметить, что в приведенном коде для дополнительного сглаживания значения коэффициентов корреляции умножаются на треугольную оконную функцию.
Для более детального спектрального анализа в качестве очередного компромисса был выбран метод максимальной энтропии. Выбрать универсальный метод спектральной оценки достаточно сложно. Недостатки, связанные с классическими непараметрическими методами спектрального анализа хорошо известны.
В качестве таких методов можно упомянуть метод периодограмм и метод коррелограмм, которые легко реализуются при помощи алгоритмов быстрого преобразования Фурье. Но, несмотря на высокую стабильность результатов, для получения достаточно хорошей разрешающей способности эти методы требуют слишком длинных входных последовательностей. В отличие от них, параметрические методы спектральной оценки (например, авторегрессионные методы) для коротких последовательностей могут обеспечить значительно более высокое разрешение.
К сожалению, при их использовании необходимо учитывать не только особенности конкретной реализации этих методов, но и характер входной последовательности. При этом достаточно сложно определить оптимальный порядок авторегрессионной модели, с ростом которого возрастает разрешающая способность, но увеличивается разброс полученных результатов. Если использовать сильно завышенные значения порядка модели, то эти методы начинают давать неустойчивые результаты.
Сравнительные характеристики различных алгоритмов спектрального оценивания можно найти в книге С.Л. Марпл "Цифровой спектральный анализ и его приложения". Как уже упоминалось, в данном случае был выбран метод максимальной энтропии. Этот метод обеспечивает, наверное, самую низкую разрешающую способность по сравнению с другими авторегрессионными методами, но выбор остановился именно на нем в надежде получить более стабильные спектральные оценки.
Рассмотрим порядок вычислений авторегрессионной спектральной оценки. Про выбор порядка модели ранее уже упоминалось, поэтому будем считать, что порядок модели уже выбран и равен IP, и уже вычислены IP коэффициентов автокорреляции cor[].
Для нахождения коэффициентов авторегрессии по известным коэффициентам автокорреляции используется рекурсивный алгоритм Левинсона-Дарбина (Levinson-Durbin), реализованный в виде метода LevinsonRecursion.
//----------------------------------------------------------------------------------- // Calculate the Levinson-Durbin recursion for the autocorrelation sequence R[] // and return the autoregression coefficients A[] and partial autocorrelation // coefficients K[] //----------------------------------------------------------------------------------- void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[]) { int p,i,m; double km,Em,Am1[],err; p=ArraySize(R); ArrayResize(Am1,p); ArrayInitialize(Am1,0); ArrayInitialize(A,0); ArrayInitialize(K,0); km=0; Em=1; for(m=0;m<p;m++) { err=0; for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1]; km=(R[m]-err)/Em; K[m]=km; A[m]=km; for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]); Em=(1-km*km)*Em; ArrayCopy(Am1,A); } return; }
Метод имеет три входных параметра. Все три параметра являются ссылками на массивы. при обращении к данному методу в первом массиве R[] должны располагаться входные коэффициенты автокорреляции. В процессе вычислений эти значения не подвергаются никаким изменениям.
Найденные коэффициенты автокорреляции будут размещены в массиве A[]. Кроме того, в массиве K[] будут располагаться значения частной автокорреляционной функции, которые равны коэффициентам отражения авторегрессионной модели, взятым с обратным знаком. Порядок модели в качестве входного параметра не передается, предполагается, что он равен количеству элементов во входном массиве R[].
Поэтому необходимо, чтобы размеры выходных массивов были не меньше чем размер входного массива, внутри функции это условие не проверяется. По завершению вычислений нулевой коэффициент авторегрессии и нулевой коэффициент частной автокорреляционной функции в массивах A[] и K[] не сохраняются.
Предполагается, что они всегда равны единице. Таким образом, как и для входной последовательности, в выходных массивах будут располагаться коэффициенты с индексами от 1 до IP (не следует путать с индексами самих массивов, которые начинаются с нуля).
Найденные значения частной автокорреляционной функции в дальнейшем используются только для отображения на соответствующем графике, а по коэффициентам авторегрессии вычисляется оценка частотной характеристики, которая определяется следующим выражением:
![]()
Вычисление частотной характеристики производится для 4096-и значений нормированной частоты в диапазоне от 0 до 0.5. При прямом вычислении значений АЧХ по приведенной формуле затрачивается слишком большое время, которое можно существенно сократить, используя для нахождения суммы комплексных экспонент алгоритм быстрого преобразования Фурье.
В методе Calc для этого используется не быстрое преобразование Фурье, а быстрое преобразование Хартли (Fast Hartley transform, FHT).
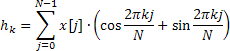
Преобразование Хартли не использует комплексных операций, и входная, и выходная последовательность являются действительными. Обратное преобразование Хартли вычисляется по той же формуле, требуя лишь дополнительного множителя 1/N.
Для действительной входной последовательности коэффициенты этого преобразования имеют простую связь с коэффициентами преобразования Фурье
![]()
Информацию об алгоритмах быстрого преобразования Хартли можно найти по ссылкам "FXT algorithm library" и "Дискретные преобразования Фурье, Хартли".
В данной реализации функция быстрого преобразования Хартли оформлена в виде метода fht.
//----------------------------------------------------------------------------------- // Radix-2 decimation in frequency (DIF) fast Hartley transform (FHT). // Length is N = 2 ** ldn //----------------------------------------------------------------------------------- void TSAnalysis::fht(double &f[], ulong ldn) { const ulong n = ((ulong)1<<ldn); for (ulong ldm=ldn; ldm>=1; --ldm) { const ulong m = ((ulong)1<<ldm); const ulong mh = (m>>1); const ulong m4 = (mh>>1); const double phi0 = M_PI / (double)mh; for (ulong r=0; r<n; r+=m) { for (ulong j=0; j<mh; ++j) { ulong t1 = r+j; ulong t2 = t1+mh; double u = f[t1]; double v = f[t2]; f[t1] = u + v; f[t2] = u - v; } double ph = 0.0; for (ulong j=1; j<m4; ++j) { ulong k = mh-j; ph += phi0; double s=MathSin(ph); double c=MathCos(ph); ulong t1 = r+mh+j; ulong t2 = r+mh+k; double pj = f[t1]; double pk = f[t2]; f[t1] = pj * c + pk * s; f[t2] = pj * s - pk * c; } } } if(n>2) { ulong r = 0; for (ulong i=1; i<n; i++) { ulong k = n; do {k = k>>1; r = r^k;} while ((r & k)==0); if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;} } } }
При обращении к этому методу ему на вход передается ссылка на массив с входными данными f[] и беззнаковое целое ldn, определяющее длину преобразования N = 2 ** ldn. Размер массива f[] должен быть не меньше длины преобразования N. Нужно иметь в виду, что внутри функции никаких проверок по этому поводу не производится. Не следует также забывать и о том, что результат преобразования располагается в том же массиве, в котором были размещены входные данные.
Сами входные данные в результате преобразования не сохраняются. В рассматриваемом методе Calc для нахождения 4096 значений АЧХ используется преобразование размером N=8192. После вычисления квадрата модулей результата преобразования и взятия обратной величины, полученный результат нормируется к своему максимальному значению и приводится к логарифмическому масштабу.
В остальном никаких серьезных особенностей метод Calc не содержит, в случае необходимости с его реализацией можно ближе познакомиться, обратившись к файлу TSAnalysis.mqh.
Все найденные и подготовленные к отображению величины в результате вычислений сохраняются в переменных, являющихся членами класса TSAnalysis. Поэтому, при обращении к виртуальному методу show для отображения результатов, передавать их в качестве аргументов не приходится.
Визуализация
Уже упоминалось о том, что метод show объявлен как виртуальный. Поэтому, переопределив его, можно реализовать необходимый метод отображения результатов вычислений, отличный от предлагаемого. В предлагаемом классе TSAnalysis визуализация производится путем подготовки файла с данными и вызова Web-браузера для их отображения.
Для того чтобы Web-браузер мог отобразить эти данные используется файл TSA.htm, расположенный в том же каталоге, что и все остальные файлы данного проекта. Такой способ отображения графической информации ранее был описан в статье "Графики и диаграммы в формате HTML".
В методе show класса TSAnalysis производится форматирование и сохранение в переменной типа string всех предназначенных для отображения результатов вычислений (см. файл TSAnalysis.mqh). Сформированная таким образом длинная строка одним приемом записывается в файл TSDat.txt. Создание этого файла и запись в него производится штатными средствами MQL5, поэтому файл создается в каталоге \MQL5\Files.
Далее при помощи вызова внешних системных функций этот файл перемещается в каталог данного проекта. Затем вызывается Web-браузер, отображающий файл TSA.htm, который использует данные из TSDat.txt. Так как в методе show производятся вызовы системных функций, то для работы с классом TSAnalysis в терминале должно быть разрешено использование внешних DLL.
Примеры
Файл TSAexample.mq5, включеный в архив TSAnalysis.zip, является примером использования класса TSAnalysis.
//----------------------------------------------------------------------------------- // TSAexample.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "TSAnalysis.mqh" //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50, 60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52, 38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23}; TSAnalysis *tsa=new TSAnalysis; tsa.Calc(bd); delete tsa; }
Как видим, обращение к классу производится достаточно просто, если подготовлен массив, содержащий входную последовательность, то не представляет никакого труда передать его методу Calc для анализа. При этом не следует забывать освобождать память вызовом delete. Результат выполнения этого скрипта уже был приведен в начале статьи.
Для того чтобы продемонстрировать эффективность производимых спектральных оценок, обратимся к дополнительным примерам, в которых будем использовать сгенерированные последовательности.
Для начала используем последовательность, состоящую из двух синусоид.
int i,n; double a,x[]; n=400; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);
На рисунке приведена оценка частотной характеристики этой последовательности.
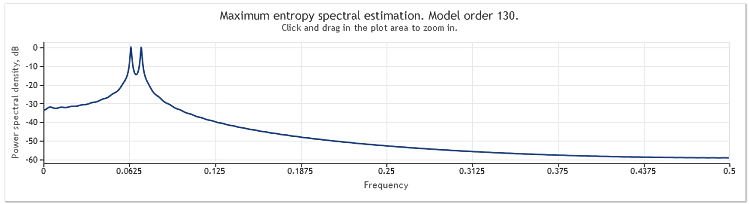
Рисунок 2. Спектральная оценка. Две синусоиды
Несмотря на то, что обе частоты хорошо различимы, при увеличении интересующего нас участка графика было обнаружено, что пики расположены на частотах 0.0637 и 0.0712. То есть несколько отличаются от истинных значений. В случае, когда последовательность состоит только из одной синусоиды, такое смещение оценки не наблюдается. Отнесем это явление за счет особенностей выбранного метода спектрального анализа.
Далее усложним задачу, добавив к нашей последовательности случайную составляющую. Для этого используем генератор псевдослучайной последовательности, реализованный в виде класса RNDXor128, который размещен в конце статьи в архиве RNDXor128.zip.
Для формирования тестового сигнала использовался следующий фрагмент кода.
int i,n; double a,x[]; RNDXor128 *rnd=new RNDXor128; n=800; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm(); delete rnd;
В этом примере к двум синусоидам добавлен случайный сигнал с нормальным законом распределения и единичной дисперсией.
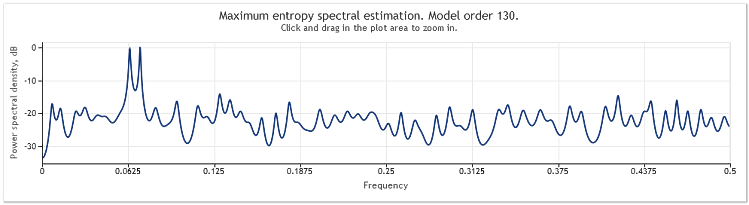
Рисунок 3. Спектральная оценка. Две синусоиды плюс случайный сигнал
При этом синусоидальные компоненты остаются хорошо различимыми.
После пятикратного увеличения амплитуды случайной компоненты, синусоиды оказываются серьезно замаскированными.
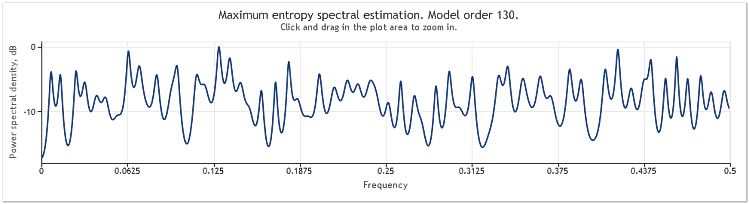
Рисунок 4. Спектральная оценка. Две синусоиды плюс случайный сигнал большей величины
При увеличении длины последовательности от 400 до 800 элементов, синусоиды вновь становятся хорошо различимыми.
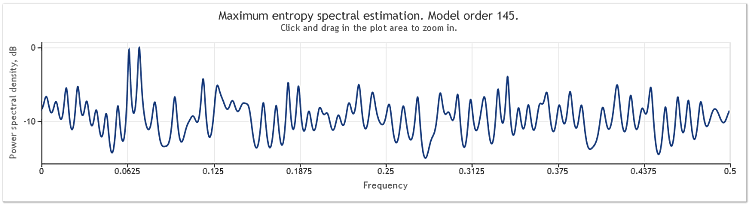
Рисунок 5. Две синусоиды плюс случайный сигнал большей величины. N=800
При этом порядок авторегрессионной модели возрос от 130 до 145. Увеличение длины последовательности привело к росту порядка модели, и как следствие, при этом увеличилась разрешающая способность спектральной оценки, пики на графике стали заметно острее.
Спектральная оценка котировок валютной пары EURUSD, D1 за два года (2009 и 2010) выглядит следующим образом.

Рисунок 6. Котировки EURUSD. 2009, 2010 год. Период D1
Входная последовательность содержала 519 значений, порядок модели, как следует из приведенного рисунка, оказался равным 135.
Как видим, эта спектральная оценка содержит целый ряд ярко выраженных пиков. Но для того, чтобы определить, действительно ли эти пики являются периодическими компонентами котировок, одной этой оценки недостаточно.
Возникновение пиков на частотной характеристике может быть вызвано наличием в котировках случайной компоненты достаточно большого уровня или явной нестационарностью рассматриваемой последовательности.
Поэтому, прежде чем сделать окончательный вывод о наличии периодической компоненты, всегда желательно подтвердить полученный результат по данным с другого фрагмента последовательности или другого таймфрейма. Кроме того, при исследовании цикличности вместо самой последовательности можно попробовать использовать ее разности.
Заключение
Так как используемый в статье метод спектральных оценок базируется на коэффициентах автокорреляции, то при его применении из входной последовательности всегда оказывается удалено ее среднее значение. Зачастую удаление из входной последовательности постоянной составляющей является просто необходимым, но при использовании авторегрессивных методов ее удаление в некоторых случаях может вызвать искажения спектральной оценки в низкочастотной области.
Пример таких искажений приведен в конце главы "Краткая сводка результатов по спектральным оценкам" в книге С. Л. Марпл "Цифровой спектральный анализ и его приложения". В нашем случае используемый метод спектрального анализа не оставляет нам выбора, поэтому необходимо просто помнить о том, что спектральная оценка всегда производится для последовательности с удаленным среднем значением.
Ссылки
- Wuertz, Diethelm and Katzgraber, Helmut (2009): Precise finite-sample quantiles of the Jarque-Bera adjusted Lagrange multiplier test, Swiss Federal Institute of Technology, Zurich,2009.
- Tanweer-ul-Islam, Asad Zaman, Normality Testing - A new Direction, IIE, International Islamic University, Islamabad, Pakistan, 2008.
- Carlos M. Urzua, Portable and powerful tests for normality, Tecnologico de Monterrey, Campus Ciudad de Mexico, 2007.
- Comparison of Common Tests for Normality
- Булашев С.В. Статистика для трейдеров. - М.: Компания Спутник +, 2003. - 245 с.
- Новицкий П.В., Зограф И.А., Оценка погрешностей результатов измерений, Энергоатомиздат, 1991.
- С. Л. Марпл-мл., Цифровой спектральный анализ и его приложения. Москва: Мир, 1990.
- David J. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures, Chapman and Hall/CRC.