Фрактальный анализ совместного движения валют
Руслан | 25 августа, 2010
Введение
Довольно часто приходится слышать разговоры о связи между различными валютами на рынке Форекс.
Основное обсуждение при этом обычно сводится к фундаментальным факторам, практическому опыту или просто домыслам, обусловленными личными стереотипами говорящего. Как
крайний случай, выступает гипотеза одной или нескольких «мировых» валют, которые «тянут» за собой все остальные.
Действительно, какова связь между различными котировками? Движутся ли они согласованно или информация о направлении движения одной валюты ничего не скажет о движении другой? В этой статье предпринята попытка разобраться в этом вопросе, используя методы нелинейной динамики и фрактальной геометрии.
1. Теоретическая часть
1.1. Зависимые и независимые переменные
Рассмотрим две переменные (котировки) x и y. В любой момент времени, мгновенные значения этих переменных определяют точку на плоскости XY (рис. 1). Движение точки с течением времени образует траекторию. Форма и тип этой траектории будут определяться типом связи между переменными.
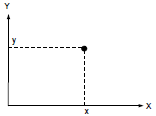
Рисунок 1. Точка на плоскости
Например, если переменная x никак не связана с переменной y, то мы не увидим никакой регулярной структуры: при достаточном количестве точек, они равномерно заполнят плоскость XY (рис.2).
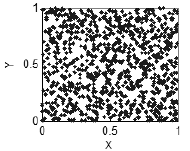
Рисунок 2. Отсутствие корреляций - равномерное заполнение плоскости
Если же зависимость между x и y существует, то будет видна некоторая регулярная структура: в простейшем случае это будет кривая (рис. 3),
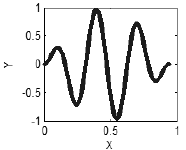
Рисунок 3. Наличие корреляций - кривая
хотя может быть и более сложная структура (рис. 4).
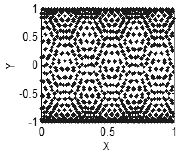
Рисунок 4. Наличие корреляций - структура на плоскости
То же самое характерно для трех- и более -мерного пространства: если между всеми переменными есть связь или зависимость, то точки будут образовывать кривую (рис. 5), если в наборе присутствуют две независимые переменные, то точки образуют поверхность (рис. 6), если три — то точки заполнят трехмерное пространство и т.д.
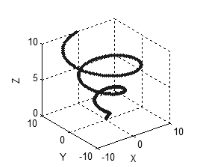
Рисунок 5. Кривая в трехмерном пространстве
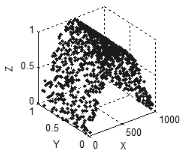
Рисунок 6. Поверхность в трехмерном пространстве
Если связи между переменными нет, то точки равномерно распределятся по всем доступным измерениям (рис. 7). Таким образом, мы можем судить о характере связи между переменными, определяя, каким образом точки заполняют пространство.
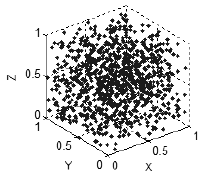
Рисунок 7. Отсутствие корреляций - равномерное распределение точек в пространстве
Причем форма получившейся структуры (линии, поверхности, объемной фигуры и т.д.), в данном случае, не имеет значения.
Важна фрактальная размерность этой структуры: линия имеет размерность равную 1, поверхность — 2, объемная структура — 3 и т.д. Обычно можно считать, что значение фрактальной размерности соответствует количеству независимых переменных в наборе данных.
Также мы можем встретиться с дробной размерностью, например, 1.61 или 2.68. Такое может произойти, если получившаяся структура окажется фракталом — самоподобным множеством с нецелой размерностью. Пример фрактала приведен на рисунке 8, его размерность приблизительно равна 1.89, т.е. это уже не линия (размерность равна 1), но еще не поверхность (размерность равна 2).

Рисунок 8. Ковер Серпинского
Фрактальная размерность может быть разной для одного и того же множества на разных масштабах.
Например, если смотреть на множество, изображенное на рисунке 9 «издалека», то ясно видно, что это линия, т.е. фрактальная размерность этого множества равна единице. Если же посмотреть на это же множество «вблизи», то увидим что это совсем не линия, а «расплывчатая труба» - точки не образуют четкую линию, но случайным образом собраны вокруг нее. Фрактальная размерность этой «трубы» должна быть равна размерности пространства, в котором мы рассматриваем нашу структуру, т.к. точки в «трубе» равномерно заполнят все доступные измерения.
Увеличение фрактальной размерности на малых масштабах дает возможность определить размер, при котором связи между переменными становится неразличимы из-за присутствующего в системе случайного шума.
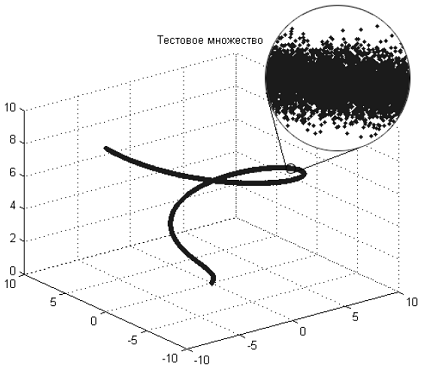
Рисунок 9. Пример фрактальной "трубы"
1.2. Определение фрактальной размерности
Для определения фрактальной размерности можно использовать box-counting алгоритм, основанный на исследовании зависимости количества кубиков, содержащих точки
множества, от размера ребра кубика (здесь имеются ввиду не обязательно трехмерные кубики: в одномерном пространстве «кубиком» будет отрезок, в двумерном — квадрат и т.д.).
Теоретически, эта зависимость имеет вид N(ε)~1/εD, где D – фрактальная размерность множества, ε — размер ребра кубика, N(ε) – количество кубиков, содержащих точки множества при размере кубика ε. Это позволяет определить фрактальную размерность
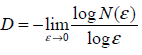
Не вдаваясь в детали алгоритма, его работу можно описать следующим образом:
Исследуемое множество точек разбивается на кубики размера ε и считается количество кубиков N, содержащих хотя бы одну точку множества.
Для разных ε определяется соответствующее значение N, т.е. накапливаются данные для построения зависимости N(ε).
Зависимость N(ε) строится в двойных логарифмических координатах и определяется угол ее наклона, который и будет значением фрактальной размерности.
Например, на рисунке 10 изображены два множества: плоская фигура (а) и линия (б). Ячейки содержащие точки множества окрашены серым цветом. Подсчитывая, количество «серых» ячеек при разных размерах ячеек, получаем зависимости изображенные на рисунке 11. Определяя наклон прямых, аппроксимирующих эти зависимости, находим фрактальные размерности: Dа≈2,Dб≈1.
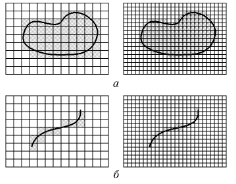
Рисунок 10. Измерение множеств
На практике для определения фрактальной размерности обычно используют не box-counting, а алгоритм Грассберга-Прокаччиа, т.к. он дает более точные результаты в пространствах высокой размерности. Идея алгоритма заключается в получении зависимости С(ε) — вероятности попадания двух точек множества в ячейку размера ε от размера ячейки и определении наклона линейного участка этой зависимости.
К сожалению, рассмотрение всех аспектов определения размерности невозможно в рамках данной статьи. При желании, вы сможете найти необходимую информацию в специальной литературе.
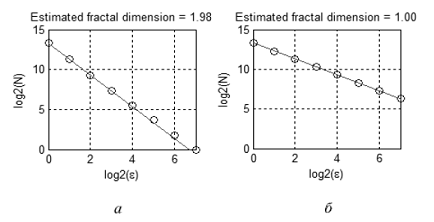
Рисунок 11. Оценка фрактальной размерности множеств
1.3. Пример определения фрактальной размерности
Чтобы убедится в работоспособности предложенной методики, попробуем определить уровень шума и количество независимых переменных для множества изображенного на рисунке 9. Это трехмерное множество состоит из 3000 точек и представляет из себя линию (одна независимая переменная) с наложенным на нее шумом. Шум имеет нормальное распределение при СКО равном 0.01.
На рисунке 12 показана зависимость С(ε) в логарифмическом масштабе. На ней мы видим два линейных участка, пересекающихся при ε≈2-4.6≈0.04. Наклон первой прямой ≈2.6, а второй ≈1.0.
Полученные результаты означают, что тестовое множество имеет одну независимую переменную на масштабе большем 0.0 и «почти три» независимые переменные или наложенный шум на масштабе меньшем 0.04. Это хорошо согласуется с исходными данными: согласно правилу «трех сигм», 99.7% точек образуют «трубу» диаметром 2*3*0.01≈0.06.
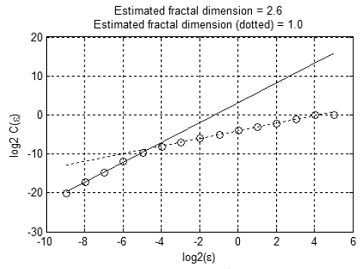
Рисунок 12. Зависимость C(e) в логарифмическом масштабе
2. Практическая часть
2.1. Исходные данные
Для изучения фрактальных свойств рынка Форекс, были использованы общедоступные данные, охватывающие период с 2000 по 2009 год включительно. Исследование проводилось на ценах закрытия семи основных валютных пар: EURUSD, USDJPY, GBPUSD, AUDUSD, USDCHF, USDCAD, NZDUSD.
2.2. Реализация
Алгоритмы определения фрактальной размерности реализованы в виде функций среды MATLAB на базе разработок профессора Майкла Смолла (Dr Michael Small http://www.eie.polyu.edu.hk/~ensmall/matlab/). Функции с примерами использования доступны в архиве frac.rar приложенном к данной статье.
Для ускорения вычислений, наиболее трудоемкий этап выполнен на языке Си. Перед началом использования, вам необходимо скомпилировать Си-функцию "interbin.c" с помощью команды MATLAB "mex interbin.c".
2.3. Результаты исследования
На рисунке 13 показано совместное движение котировок EURUSD и GBPUSD с 2000 по 2010 год. Сами значения котировок показаны на рисунках 14 и 15.
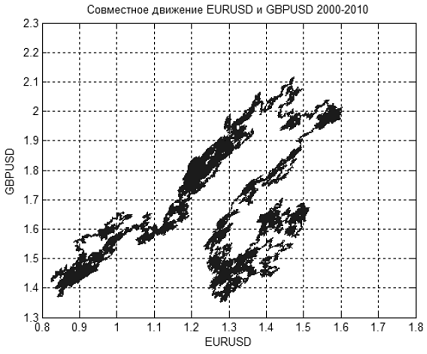
Рисунок 13. Совместное движение котировок EURUSD и GBPUSD с 2000 по 2010 год
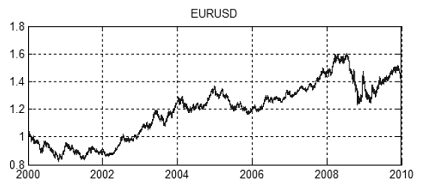
Рисунок 14. График котировок EURUSD с 2000 по 2010 год
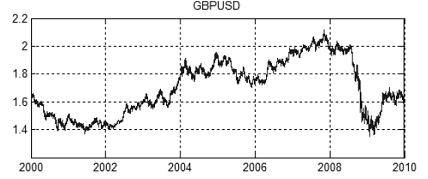
Рисунок 15. График котировок GBPUSD с 2000 по 2010 год
Фрактальная размерность множества, изображенного на рисунке 13, приблизительно равна 1.7 (рис. 16). Это означает, что движение EURUSD + GBPUSD не образует «чистого» случайного блуждания, иначе размерность была бы равна 2 (размерность случайного блуждания, в двух- и более мерных пространствах всегда равна 2).
Тем не менее, так как движение котировок очень похоже на случайное блуждание, то мы не можем изучать непосредственно сами значения котировок — при добавлении новых валютных пар, фрактальная размерность изменяется незначительно (табл. 1) и никаких выводов сделать не удастся.
| Валютные пары |
EURUSD GBPUSD |
+USDJPY |
+AUDUSD |
+USDCHF | +USDCAD |
+NZDUSD |
|---|---|---|---|---|---|---|
| Размерность | 1.7 | 1.9 | 1.9 | 1.9 | 1.9 | 1.9 |
Таблица 1. Изменение размерности при увеличении числа валют
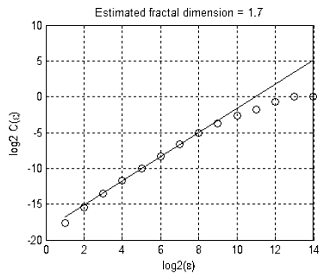
Рисунок 16. Оценка фрактальной размерности
Чтобы получить более интересные результаты, следует перейти от самих котировок, к их изменениям.
В таблице 2 приведены значения размерности для разных интервалов приращений и разного количества валютных пар.
| Даты |
Количество точек |
EURUSD GBPUSD |
+USDJPY |
+AUDUSD |
+USDCHF |
+USDCAD |
+NZDUSD |
|
|---|---|---|---|---|---|---|---|---|
| M5 | 14 Aug 2008 — 31 Dec 2009 | 100000 | 1.9 | 2.8 | 3.7 | 4.4 | 5.3 | 6.2 |
| M15 | 18 Nov 2005 — 31 Dec 2009 | 100000 | 2 | 2.8 | 3.7 | 4.5 | 5.9 | 6.7 |
| M30 | 16 Nov 2001 — 31 Dec 2009 | 100000 | 2 | 2.8 | 3.7 | 4.5 | 5.7 | 6.8 |
| H1 | 03 Jan 2000 — 31 Dec 2009 | 61765 | 2 | 2.9 | 3.8 | 4.6 | 5.6 | 6.5 |
| H4 | 03 Jan 2000 — 31 Dec 2009 | 15558 | 2 | 3 | 4 | 4.8 | 5.9 | 6.3 |
| D1 | 03 Jan 2000 — 31 Dec 2009 | 2601 | 2 | 3 | 4 | 5.1 | 5.7 | 6.5 |
Таблица 2. Изменение размерности при разных интервалах приращений
Если валюты связаны между собой, то при добавлении каждой новой валютной пары, фрактальная размерность должна увеличиваться все меньше и меньше и, в итоге, должна сойтись к некоторому значению, которое покажет количество «свободных переменных» на валютном рынке.
Также, если предположить, что на котировки накладывается «рыночный шум», то на малых интервалах (М5, М15, М30) возможно заполнение всех доступных измерений шумом и этот эффект должен ослабевать на больших таймфреймах «обнажая» зависимости между котировками (аналогично как в тестовом примере).
Как видно из таблицы 2, эта гипотеза не нашла подтверждения на реальных данных: на всех таймфремах множество заполняет все доступные измерения, т.е. все валюты независимы друг от друга.
Это несколько противоречит интуитивным убеждениям о связи валют. Кажется, что близкие валюты, например GBP и CHF или AUD и NZD должны показывать схожую динамику. Например, на рисунке 17 показаны зависимости приращений NZDUSD от AUDUSD для пятиминутных (коэффициент корреляции 0.54) и дневных (коэффициент корреляции 0.84) интервалов.
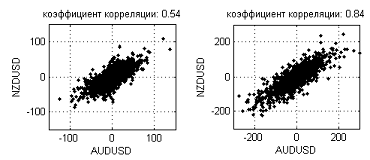
Рисунок 17. Зависимости приращений NZDUSD от AUDUSD для M5 (0.54) и D1 (0.84) интервалов
Из этого рисунка видно, что при увеличении интервала, зависимость все больше вытягивается по диагонали и коэффициент корреляции увеличивается. Но, с «точки зрения» фрактальной размерности, уровень шума слишком высок, чтобы считать эту зависимость одномерной линией. Возможно, на более длительных интервалах (недели, месяцы) фрактальные
размерности сойдутся к некоторому значению, но у нас нет возможности это проверить — слишком мало точек для определения размерности.
Заключение
Конечно, интереснее было бы свести движение валют к одной или нескольким независимым переменным — это серьёзно бы упростило задачу восстановления рыночного аттрактора и прогнозирования котировок. Но рынок показывает другой результат: зависимости слабо выражены и «хорошо спрятаны» в большом количестве шума. В этом плане, рынок очень эффективен.
Методы нелинейной динамики, стабильно показывающие хороший результат в других областях: медицине, физике, химии, биологии и пр, при анализе рыночных котировок требуют особого внимания и аккуратной интерпретации результатов.
Полученные результаты, не позволяют однозначно утверждать о наличии или отсутствии связи между валютами. Можно лишь сказать, что на рассматриваемых таймфреймах уровень шума сопоставим с «силой» связи, поэтому вопрос о связи между валютами остается открытым.