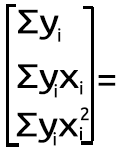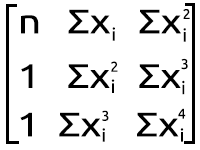Машинное обучение и Data Science (Часть 07): Полиномиальная регрессия
Omega J Msigwa | 6 декабря, 2022
Содержание:
- Введение
- Вспоминаем многочлены
- Порядок многочленов
- Полиномиальная регрессия
- Когда их использовать?
- Байесовский информационный критерий
- Находим коэффициенты модели
- Находим лучшую модель
- Масштабирование признаков
- Плюсы и минусы полиномиальной регрессии
- Заключительные мысли
Введение
Мы еще не закончили с регрессионными моделями. Надо вернуться к ним на секундочку. Как мы говорили в первой статье из этой серии, базовая линейная регрессия служит основой для многих моделей машинного обучения. Сегодня мы пойдем немного дальше линейной регрессии и познакомимся с полиномиальной. Машинное обучение сильно изменило наш мир во многих отношениях — доступны различные методы обучения для задач классификации и регрессии, таких как линейная и логистическая регрессия, метод опорных векторов, полиномиальная регрессия и многие другие методы. Отдельно можно выделить параметрические методы, такие как полиномиальная регрессия и методы опорных векторов, за их универсальность.
Они создают простые границы для простых задач и нелинейные границы для сложных.
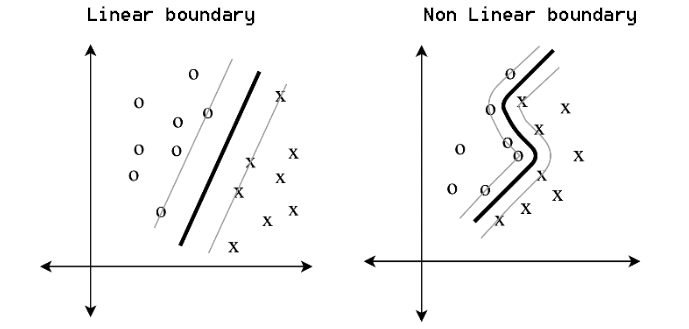
Вспоминаем многочлены
Многочлен (или полином) — это любое математическое выражение, которое выглядит так:
- полиномиальное уравнение 1
У нас есть данные x, которые возводятся в степень, а также коэффициенты, которые используются для масштабирования данных.
Вот другой пример полиномиальной регрессии:
- полиномиальное уравнение 2
5 соответствует ao, -7 соответствует a1, 4 соответствует a2, а 11.3 соответствует a3.
В многочлене не обязательно здесь должна быть все члены x, посмотрим на следующее уравнение:
- полиномиальное уравнение 3
Также можно представить как:
Порядок многочлена
В многочленах есть понятие, называемое порядком. Порядок многочлена обозначается буквой n. Это самый высокий коэффициент в математическом выражении. Например:- Полиномиальное уравнение 1 выше представляет собой n-ый порядок полиномиальной регрессии
- Полиномиальное уравнение 2 — полиномиальная регрессия третьего порядка/степени.
- Полиномиальное уравнение 03, приведенное выше, также является полиномиальной регрессией третьего порядка/степени.
Здесь можно запутаться, потому что во втором уравнении у нас есть 3 переменные, умноженные на x, и их коэффициенты расположены в порядке возрастания 1,2,3, тогда как во втором уравнении у нас только две переменные. Порядок полинома в первую очередь определяется старшим коэффициентом в выражении.
Полиномиальная регрессия
Полиномиальная регрессия — алгоритм машинного обучения, используемый для прогнозирования. Я слышал, что он широко использовался для прогнозирования скорости распространения COVID-19 и других инфекционных заболеваний. Давайте посмотрим, из чего состоит этот алгоритм.Посмотрим на простую линейную модель.
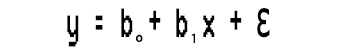
Заметили кое-что?
Эта простая линейная регрессия представляет собой не что иное, как полиномиальную регрессию первого порядка. В зависимости от полиномиальной регрессии, можно добавлять к ней переменные, например, полиномиальная регрессия второго порядка будет выглядеть так:
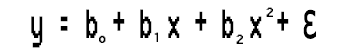
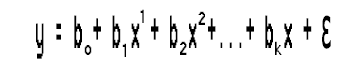
Что случилось с линейностью?
Не говорил ли я в предыдущих статьях, что любая регрессия связана с линейной моделью? Тогда как подогнать эту полиномиальную регрессию к линейности, когда у нас есть эти квадраты коэффициентов?
Все сводится к тому, что должно быть линейным, а что может быть нелинейным. Все коэффициенты/бета линейны, просто сами данные возводятся в более высокие степени.
Когда использовать полиномиальную регрессию?
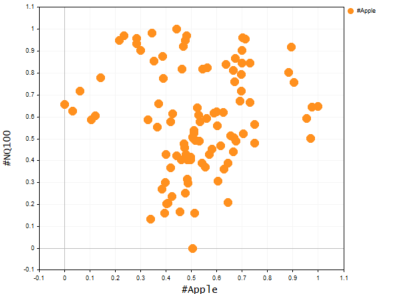
Как мы знаем, базовая линейная модель не подходит для сложных данных (нелинейных) или поиска сложных отношений в наборе данных. Для решения подобных задач используется полиномиальная регрессия. Представьте, что пытаетесь предсказать цену NASDAQ, используя цену акций APPLE. Apple — один из сильнейших факторов, влияющих на цену NASDAQ, и при этом взаимосвязь не является линейной. Поэтому для такого набора данных линейная модель будет недостаточно подходящей, чтобы ей можно было доверить принятие решений о будущих прогнозах. Посмотрим, как выглядит график этих двух символов на одной оси. Для этого используем диаграмму рассеяния, на которой представим ценовые значения.
Ниже представлена функция, которая создает диаграмму рассеяния в терминале, используя CGraphics (вероятно, я бы не узнал о такой возможности, не начни я писать эту статью).
bool ScatterPlot( string obj_name, vector &x, vector &y, string legend, string x_axis_label = "x-axis", string y_axis_label = "y-axis", color clr = clrDodgerBlue, bool points_fill = true ) { if (!graph.Create(0,obj_name,0,30,70,440,320)) { printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError()); return(false); } ChartSetInteger(0,CHART_SHOW,ChartShow); double x_arr[], y_arr[]; pol_reg.vectortoArray(x,x_arr); pol_reg.vectortoArray(y,y_arr); CCurve *curve = graph.CurveAdd(x_arr,y_arr,clr,CURVE_POINTS); curve.PointsSize(10); curve.PointsFill(points_fill); curve.Name(legend); graph.XAxis().Name(x_axis_label); graph.XAxis().NameSize(10); graph.YAxis().Name(y_axis_label); graph.YAxis().NameSize(10); graph.FontSet("Lucida Console",10); graph.CurvePlotAll(); graph.Update(); delete(curve); return(true); }
string plot_name = "x vs y"; ObjectDelete(0,plot_name); ScatterPlot(plot_name,x_v,y_v,X_symbol,X_symbol,Y_symol,clrOrange);
Выводимая информация:
Очевидно, линейная модель плохо справляется с такого рода задачами, поэтому давайте попробуем решить ее, используя полиномиальную регрессию. Здесь возникает вопрос, какой же порядок следует использовать для создания полиномиальной модели.
График Nasdaq и Apple
Взгляните на выражение модели:
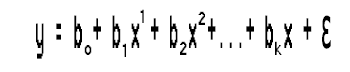
Поскольку у нас только одна независимая переменная, можно возвести ее в любую степень, которую захотим. Но откуда узнать, в какую степень нужно возвести эту единственную независимую переменную, другими словами, как мы узнаем, какого порядка должен быть полином? Чтобы понять это, давайте сначала разберемся с тем, что называется Байесовский информационный критерий (BIC).
Байесовский информационный критерий
Формула его такая:
BIC = n log(SSE) + k log (n)
n = количество точек данных
k = количество параметров
Но прежде, чем мы выясним, какая модель подходит лучше, создадим базовую полиномиальную регрессию и посмотрим, что заставляет ее работать. От этого оттолкнемся и перейдем к поиску подходящего порядка.
Находим коэффициенты модели
Есть уравнение
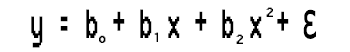
Решим эту задачу полиномиальной регрессии второй степени, найдя значения b0, b1 и b2.
Используем следующую систему уравнений:
n = количество точек данных
Для расчета значений будем использовать простой набор данных.
| X | y |
|---|---|
| 3 | 2.5 |
| 4 | 3.2 |
| 5 | 3.8 |
| 6 | 6.5 |
| 7 | 11.5 |
Итак, теперь мы имеем набор одновременных уравнений для задачи и простой набор данных, на котором можно строить расчеты. Можно легко подставить значения и найти коэффициенты в научном калькуляторе, Microsoft Excel или чем-то еще, в зависимости от ваших предпочтений. Получим такие значения:
- b0 = 12.4285714
- b1= -5.5128571
- b2 = 0.7642857
Но вообще-то это не дело, когда работаешь с MQL5. Поэтому давайте посмотрим, как добиться такого же результата в редакторе MetaEditor из набора приведенного выше одновременного уравнения. Преобразуем его в матричную форму. Теперь имеем следующее:
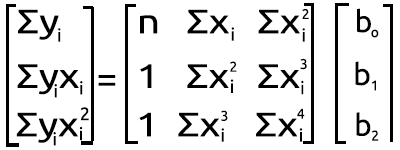Полиномиальная матричная фигура
Результат умножения возвращает нас к уравнению. Итак, математически все верно.
Перейдем к написанию кода.
Класс полиномиальной регрессии:
class CPolynomialRegression { private: ulong m_degree; //зависит от независимых переменных int n; //количество выборок в наборе данных vector x; vector y; matrix PolyNomialsXMatrix; //матрица x matrix PolynomialsYMatrix; //матрица y matrix Betas; double Betas_A[]; //коэффициенты модели, хранимые в массиве void Poly_model(vector &Predictions,ulong degree); public: CPolynomialRegression(vector& x_vector,vector &y_vector,int degree=2); ~CPolynomialRegression(void); double RSS(vector &Pred); //сумма квадратов остатков void BIC(ulong k, vector &bic,int &best_degree); //Байесовский информационный критерий void PolynomialRegressionfx(ulong degree, vector &Pred); double r_squared(vector &y,vector &y_predicted); void matrixtoArray(matrix &mat, double &Array[]); void vectortoArray(vector &v, double &Arr[]); void MinMaxScaler(vector &v); };
Наш класс достаточно прост, код его должен быть понятен. Если будут какие-либо изменения, я буду обновлять код в файлах, прикрепленных ниже, потому что код я пишу одновременно с написанием статьи.
Из нашего матричного выражения на рисунке полиномиальной матрицы выше видно, что в каждой точке много сложения, а затем возведение в экспоненту. Такое вычисление требуется почти для каждого элемента в первом массиве справа от знака равенства. Ниже приведен короткий пример кода, показывающий, как это сделать.
vector c; vector x_pow; for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++) for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) { if (i+j == 0) PolynomialsYMatrix[i][j] = y.Sum(); else { x_pow = MathPow(x,i); c = y*x_pow; //элементы вектора x возводим в степень i, получаемый вектор //затем умножаем на вектор значений y, результат сохраняем в векторе c PolynomialsYMatrix[i][j] = c.Sum(); //Наконец, сумму всех элементов вектора c сохраняем в матрице полиномов } }
Посмотрите на матрицу справа на рисунке полиномиальной матрицы выше. Можно заметить, что так есть функции Σxy и Σxy^2. Это немного другой подход, давайте также рассмотрим код, реализующий его.
double pow = 0; ZeroMemory(x_pow); for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++) for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++) { pow = (double)i+j; //Степень соответствует индексу доступа к строкам и столбцам i+j if (pow == 0) PolyNomialsXMatrix[i][j] = n; else { x_pow = MathPow(x,pow); //x_pow это вектор, в который сохраняем вектор x, возведенных в определенную степень PolyNomialsXMatrix[i][j] = x_pow.Sum(); //находим сумму вектора степени } }
Итак, у нас есть эти строки для нахождения сумм, которые так важны для полиномиальной регрессии. Теперь приступим к созданию матрицы, которая будет представлять эти значения, как вторая матрица на изображение фигуры полиномиальной матрицы.
Начнем с матрицы слева от знака равенства.
ulong order_size = degree+1; PolyNomialsXMatrix.Resize(order_size,order_size); PolynomialsYMatrix.Resize(order_size,1); vector c; vector x_pow; for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++) for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) { if (i+j == 0) PolynomialsYMatrix[i][j] = y.Sum(); else { x_pow = MathPow(x,i); c = y*x_pow; PolynomialsYMatrix[i][j] = c.Sum(); } } if (debug) Print("Polynomials y vector \n",PolynomialsYMatrix);
Просто взглянув на то, как расположены элементы внутри матрицы, можно понять, что первый элемент — единственный, который не умножается на значения x, а все остальные умножаются на значения x, увеличенный на индекс их местоположения в матрице.
Переключение массива на фокус уравнения
Мое первое наблюдение состоит в том, что этот размер массива Matrix равен квадратному размеру Y-матрицы/матрицы с левой стороны, которую мы вычислили ранее, а степень, в которую возводятся элементы x, зависит от того, где элемент расположен в матрице. Это зависит от строк и столбцов. Поскольку эта матрица является квадратной, построить ее можно, дважды пройдясь по ее столбцам в двух соответствующих циклах. Код представлен ниже.
ulong order_size = degree+1; PolyNomialsXMatrix.Resize(order_size,order_size); PolynomialsYMatrix.Resize(order_size,1); vector x_pow; //--- PolyNomialsXMatrix.Resize(order_size, order_size); double pow = 0; ZeroMemory(x_pow); //x_pow.Copy(x); for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++) for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++) { pow = (double)i+j; if (pow == 0) PolyNomialsXMatrix[i][j] = n; else { x_pow = MathPow(x,pow); PolyNomialsXMatrix[i][j] = x_pow.Sum(); } } //--- if (debug) Print("Polynomial x matrix\n",PolyNomialsXMatrix);
Что этот код выводит:
CS 0 02:10:15.429 polynomialReg test (#SP500,D1) Polynomials y vector CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [[27.5] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [158.8] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [966.2]] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) Polynomial x matrix CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [[5,25,135] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [25,135,775] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [135,775,4659]]
Вот тут-то и возникают сложности. Чтобы найти значения неизвестной матрицы бета-значений, нужно обратиться к определенным математическим операциям с матрицами.
Нахождение неизвестных значений умноженной матрицы:
Повторим ту же процедуру для наших матриц, значения которых мы только что получили выше.
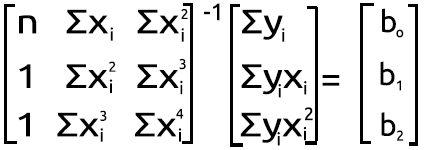
Процесс нахождения обратной матрицы относительно прост и занимает две, если не одну строку кода с использованием стандартной библиотеки матриц.
PolyNomialsXMatrix = PolyNomialsXMatrix.Inv(); //находим обратную матрицу и присваиваем ее исходной матрице Наконец, чтобы найти коэффициенты модели, нужно умножить обратную матрицу на матрицу с суммами значений y.
Betas = PolyNomialsXMatrix.MatMul(PolynomialsYMatrix);
Теперь время распечатать бета-матрицу, чтобы посмотреть, что мы получили в результате всех наших действий:
CS 0 02:10:15.429 polynomialReg test (#SP500,D1) Betas CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [[12.42857142857065] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [-5.512857142857115] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [0.7642857142856911]]
Отлично, это именно то, что мы искали. Теперь у нас есть коэффициенты полиномиальной регрессии 2-й степени, и мы можем построить модель на их основе.
void CPolynomialRegression::Poly_model(vector &Predictions, ulong degree) { ulong order_size = degree+1; Predictions.Resize(n); matrixtoArray(Betas,Betas_A); for (ulong i=0; i<(ulong)n; i++) { double sum = 0; for (ulong j=0; j<order_size; j++) { if (j == 0) sum += Betas_A[j]; else sum += Betas_A[j] * MathPow(x[i],j); } Predictions[i] = sum; } }
Каким бы простым ни казался код модели, он может обрабатывать столько степеней, сколько нужно по крайней мере на данный момент. Давайте построим прогнозы модели на одной оси значений x и y.
ObjectDelete(0,plot_name); plot_name = "x vs y"; ScatterCurvePlots(plot_name,x_v,y_v,Predictions,"Predictions","x","y",clrDeepPink); bool ScatterCurvePlots( string obj_name, vector &x, vector &y, vector &curveVector, string legend, string x_axis_label = "x-axis", string y_axis_label = "y-axis", color clr = clrDodgerBlue, bool points_fill = true ) { if (!graph.Create(0,obj_name,0,30,70,440,320)) { printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError()); return(false); } ChartSetInteger(0,CHART_SHOW,ChartShow); //--- дополнительные кривые double x_arr[], y_arr[]; pol_reg.vectortoArray(x,x_arr); pol_reg.vectortoArray(y,y_arr); double curveArray[]; //массив матрицы кривых pol_reg.vectortoArray(curveVector,curveArray); graph.CurveAdd(x_arr,y_arr,clrBlack,CURVE_POINTS,y_axis_label); graph.CurveAdd(x_arr,curveArray,clr,CURVE_POINTS_AND_LINES,legend); //--- graph.XAxis().Name(x_axis_label); graph.XAxis().NameSize(10); graph.YAxis().Name(y_axis_label); graph.YAxis().NameSize(10); graph.FontSet("Lucida Console",10); graph.CurvePlotAll(); graph.Update(); return(true); }
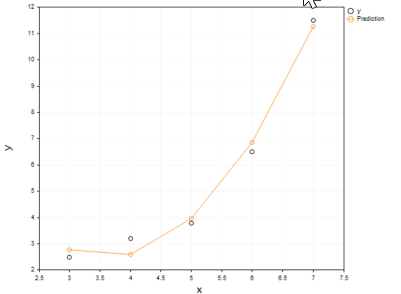
Выводимая информация:
Согласитесь, полиномиальная модель лучше подошла для наших данных и в этом может превзойти линейную модель при подборе данных.
Поиск лучшей степени полинома
Как выяснили ранее, Байесовский информационный критерий — алгоритм, который используется для поиска лучшей модели. Преобразуем формулу в код. Согласно BIC, модель с наименьшим значением BIC является лучшей моделью, потому что эта модель имеет наименьшую сумму остатков/ошибок.
void CPolynomialRegression::BIC(ulong k, vector &bic,int &best_degree) { vector Pred; bic.Resize(k-2); best_degree = 0; for (ulong i=2, counter = 0; i<k; i++) { PolynomialRegressionfx(i,Pred); bic[counter] = ( n * log(RSS(Pred)) ) + (i * log(n)); counter++; } //--- bool positive = false; for (ulong i=0; i<bic.Size(); i++) if (bic[i] > 0) { positive = true; break; } double low_bic = DBL_MAX; if (positive == true) for (ulong i=0; i<bic.Size(); i++) { if (bic[i] < low_bic && bic[i] > 0) low_bic = bic[i]; } else low_bic = bic.Min(); //bic[ best_degree = ArrayMinimum(bic) ]; printf("Best Polynomial Degree(s) is = %d with BIC = %.5f",best_degree = best_degree+2,low_bic); }
Функция RSS в коде — это остаточная сумма квадратов (Residual Sum of Squares). Эта функция находит сумму квадратов остатков.
double CPolynomialRegression::RSS(vector &Pred) { if (Pred.Size() != y.Size()) Print(__FUNCTION__," Predictions Array and Y matrix doesn't have the same size"); double sum =0; for (int i=0; i<(int)y.Size(); i++) sum += MathPow(y[i] - Pred[i],2); return(sum); }
Теперь запустим эту функцию, чтобы найти лучший полином среди 10 степеней.
vector bic_; //вектор для хранения значений BIC только для визуализации int best_order; //переменная для хранения лучшего порядка модели pol_reg.BIC(polynomia_degrees,bic_,best_order);
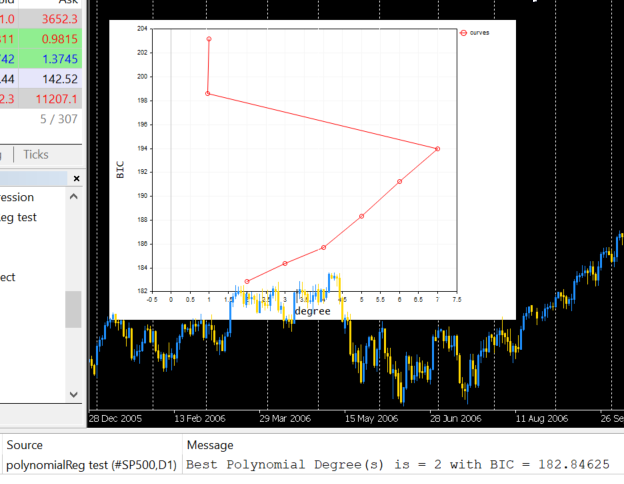
Результат работы в терминале будет таким:
Согласно этому коду, лучшая модель имеет степень полинома 2. Итак, для нашей простой выборки лучше всего подходит модель со степенью 2.
2022.09.22 20:58:21.540 polynomialReg test (#NQ100,D1) Best Polynomial Degree(s) is = 2 with BIC = 0.93358
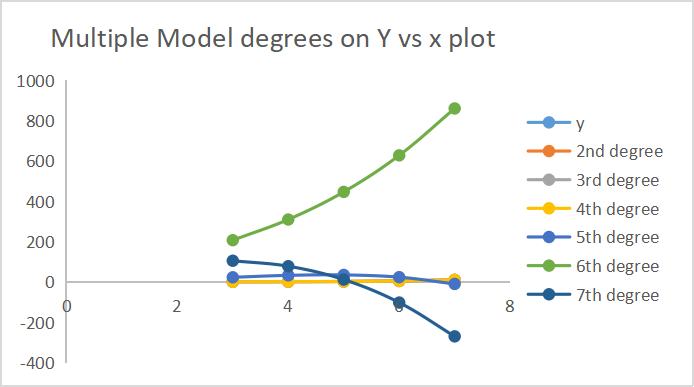
Ниже приведены результаты того, какие прогнозы делала каждая из моделей.
На оси нанесены 7 результатов в градусах.
Важное масштабирование признаков
Поскольку в полиномиальной регрессии есть только одна независимая переменная, которую можно возвести в любую степень, очень важной становится возможность масштабирования признаков, потому что если независимая переменная имеет признаки в диапазоне 100-1000, по второй степени эти признаки будут колебаться между значениями 10000 - 1000000, а в третьей — 10^6 - 10^9. Это очень много.
Существует много способов и алгоритмов для масштабирования набора данных, мы же будем использовать функцию масштабирования Min-Max для масштабирования векторов. Имейте в виду, что этот процесс следует выполнять до любых манипуляций с набором данных. Ниже приведен код функции, которая будет использоваться для масштабирования векторов из набора данных.
void MinMaxScaler(vector &v) { //Нормализация вектора с помощью Min-max double min, max, mean; min = v.Min(); max = v.Max(); mean = v.Mean(); for (int i=0; i<(int)v.Size(); i++) v[i] = (v[i] - min) / (max - min); }
Все, что нам нужно, готово. Пришло время построить модель на реальных рыночных данных — см. график Nasdaq vs Apple выше. Чтобы получить результаты, понадобится сделать несколько шагов.
Извлечение данных о рыночных ценах и масштабирование.
if (!SymbolSelect(X_symbol,true)) printf("%s not found on Market watch Err = %d",X_symbol,GetLastError()); if (!SymbolSelect(Y_symol,true)) printf("%s not found on Market watch Err = %d",Y_symol,GetLastError()); matrix rates(bars, 2); vector price_close; //--- vector x_v, y_v; price_close.CopyRates(X_symbol,PERIOD_H1,COPY_RATES_CLOSE,1,bars); //extracting prices rates.Col(price_close,0); x_v.Copy(price_close); //--- price_close.CopyRates(Y_symol,PERIOD_H1,COPY_RATES_CLOSE,1,bars); y_v.Copy(price_close); rates.Col(price_close,1); //--- MinMaxScaler(x_v); //масштабируем все цены закрытия MinMaxScaler(y_v); //масштабируем все цены закрытия //---
Ниже представлен результат, представленный на диаграмме рассеяния:
2. Находим лучшую модель
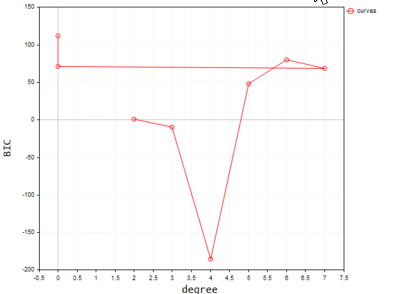
//--- Находим лучшую модель, используя BIC vector bic_; //вектор для хранения значений BIC только для визуализации int best_order; //переменная для хранения лучшего порядка модели pol_reg.BIC(polynomia_degrees,bic_,best_order); ulong bic_cols = polynomia_degrees-2; //2 - первый в полиномиальном порядке //--- Построим BIC в зависимости от степени модели vector x_bic; x_bic.Resize(bic_cols); for (ulong i=2,counter =0; i<bic_cols; i++) { x_bic[counter] = (double)i; counter++; } ObjectDelete(0,plot_name); plot_name = "curves"; ScatterCurvePlots(plot_name,x_bic,y_v,bic_,"curves","degree","BIC",clrBlue); Sleep(10000);
Результат будет таким:
И последнее.
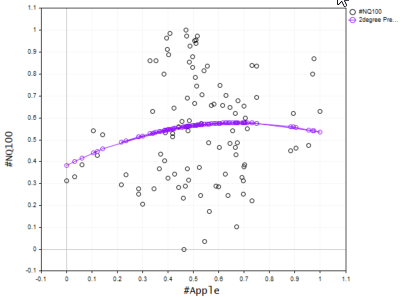
Теперь мы знаем, что лучший порядок модели — 2. Давайте создадим модель с 2 степенями, затем используем ее для прогнозирования значений и, наконец, выведем значения на график.
vector Predictions; pol_reg.PolynomialRegressionfx(best_order,Predictions); //Создаем модель с лучшим порядком, используем для прогнозирования ObjectDelete(0,plot_name); plot_name = "Actual vs predictions"; ScatterCurvePlots(plot_name,x_v,y_v,Predictions,string(best_order)+"degree Predictons",X_symbol,Y_symol,clrDeepPink);
Полученный график показан ниже:
Проверка точности модели
Несмотря на то, что мы нашли наилучшую степень для модели, мы все еще не знаем, как эта модель способна понять взаимосвязь в нашем наборе данных. Проверим точность ее прогнозирования.
Print("Model Accuracy = ",DoubleToString(pol_reg.r_squared(y,Predictions)*100,2),"%");
Журнал:
2022.09.30 16:19:31.735 polynomialReg test (#SP500,D1) Model Accuracy = 2.36%
Плохая новость заключается в том, мы получили плохую модель из числа худших моделей. Прежде чем принять решение об использовании полиномиальной регрессии для решения конкретной задачи, просто помните, что в основе полиномиальной регрессии лежит линейная модель, поэтому данные всегда должны быть коррелированы. Они не обязательно должны быть линейно коррелированы, но корреляция около 50% будет идеальной. Возвращаясь к набору данных NASDAQ и APPLE, проверяем корреляцию — я получил коэффициент корреляции менее 1%. Вероятно, поэтому мы не смогли получить хорошую модель из этого набора данных.
Print("correlation coefficient ",x_v.CorrCoef(y_v));
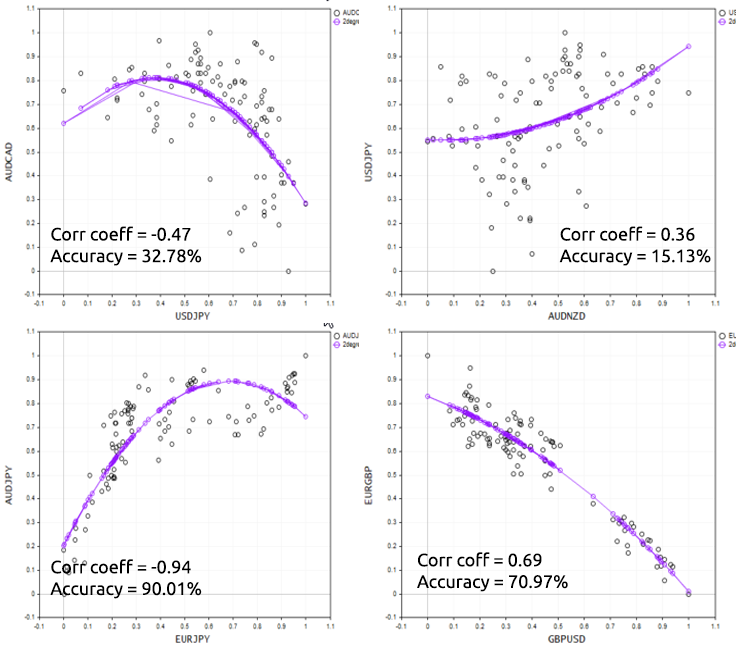
Чтобы хорошо продемонстрировать этот момент, давайте попробуем скрипт на разных форекс-инструментах.
Плюсы и минусы полиномиальной регрессии
Преимущества:
- Позволяет моделировать нелинейную связь между переменными
- Существует широкий спектр функций, которые модно использовать для настройки
- Подходит для исследовательских целей; можно протестировать различные полиномиальные порядки/степени, чтобы увидеть, какие из них лучше всего подходят для конкретного набора данных.
- Просто программировать и интерпретировать результаты, при этом мощный инструмент
Недостатки:
- Выбросы могут серьезно исказить результаты
- Модели полиномиальной регрессии склонны к переобучению
- Вследствие переобучения модель может не работать с данными вне выборки
Заключительные мысли
Полиномиальная регрессия — полезный методом машинного обучения во многих случаях, где ожидается, что связь между независимой переменной и зависимыми переменными нелинейна. Поэтому он дает больше свободы при работе с разными наборами данных. Позволяет заполнить пробелы линейной модели. Ее можно использовать для работы с данными, для которых не подходит линейная модель. При этом очень важно помнить о риске переобучения, потому что, поскольку эта параметрическая модель очень гибкая, она может очень плохо работать с необученными данными / данными тестирования. Возможно, лучше выбирать самые низкие порядки и оставить модели место для ошибок.
Спасибо за внимание!
Подробнее о матрицах: Матрицы и векторы
Дополнительная литература
- Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
- Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
- Глубокое обучение (серия «Адаптивные вычисления и машинное обучение»)
Статьи:
- Машинное обучение и Data Science (Часть 01): Линейная регрессия
- Машинное обучение и Data Science (Часть 02): Логистическая регрессия
- Машинное обучение и Data Science (Часть 03): Матричная регрессия
- Машинное обучение и Data Science (Часть 06): Градиентный спуск