Abordagem econométrica para a busca de padrões de mercado: Autocorrelação, Mapas de Calor e Gráficos de Dispersão

Uma breve revisão do material anterior e dos pré-requisitos para a criação de um novo modelo

No primeiro artigo, nós introduzimos o conceito de memória de mercado, que é determinado como uma dependência à longo prazo dos incrementos de preços de alguma ordem. Além disso, nós consideramos o conceito de "padrões sazonais" que existem nos mercados. Até agora, esses dois conceitos existiam separadamente. O objetivo do artigo é mostrar que a "memória de mercado" é de natureza sazonal, que é expressa através da correlação maximizada de incrementos de ordem aleatória para os intervalos de tempo mais próximos e através da correlação minimizada para intervalos de tempo mais distantes.

Vamos apresentar a seguinte hipótese:

A correlação dos incrementos de preços depende da presença de padrões sazonais, bem como do agrupamento dos incrementos mais próximos. 

Vamos tentar confirmar ou refutá-lo em um estilo livre, intuitivo e levemente matemático.

A abordagem econométrica clássica para identificar padrões nos incrementos de preços é a autocorrelação

De acordo com a abordagem clássica, a ausência de padrões nos incrementos de preços é determinada pela ausência de correlação em série. Se não houver autocorrelação, a série de incrementos é considerada aleatória e a busca desses padrões serão consideradas ineficazes. 

Vamos ver um exemplo da análise visual de incrementos do EURUSD usando a função de autocorrelação. Todos os exemplos serão realizados usando o IPython.

def standard_autocorrelation(symbol, lag):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 
    rates = rates.diff(lag).dropna()
    from pandas.plotting import autocorrelation_plot
    plt.figure(figsize=(10, 5))
    autocorrelation_plot(rates)

standard_autocorrelation('EURUSD', 50)

Essa função calcula a diferença dos preços de fechamento H1 em relação ao período especificado (é utilizado um atraso de 50) e exibe o gráfico de autocorrelação.

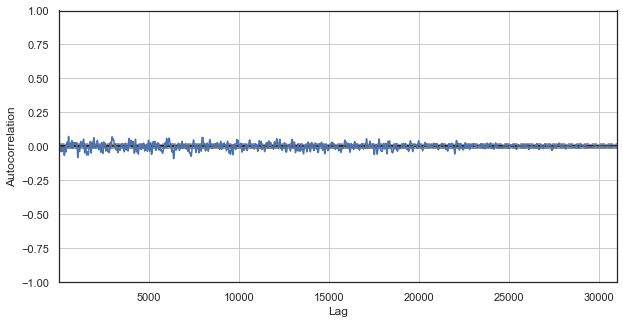
Fig. 1. Correlograma clássico dos incrementos de preços

O gráfico de correlação automático não revela nenhum padrão nos incrementos de preços. As correlações entre os incrementos adjacentes flutuam em torno de zero, o que aponta para a aleatoriedade da série temporal. Nós poderíamos terminar nossa análise econométrica aqui, concluindo que o mercado é aleatório. No entanto, eu sugiro revisar a função de autocorrelação de um ângulo diferente: no contexto dos padrões sazonais.

Eu assumi que a correlação dos incrementos de preços pudesse ser gerada pela presença dos padrões sazonais. Portanto, vamos excluir do exemplo todas as horas, exceto uma específica. Assim, nos criaremos uma nova série temporal, que terá suas próprias propriedades específicas. Vamos criar uma função de correlação automática para esta série:

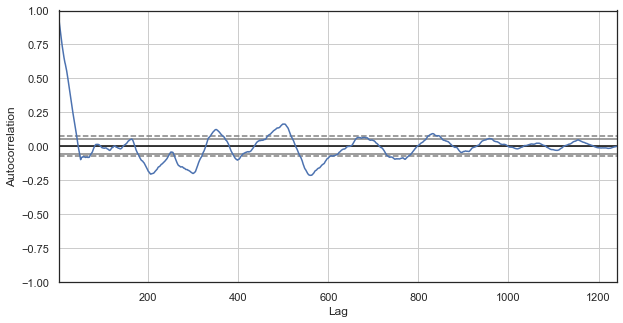
Fig. 2. Um correlograma dos incrementos de preços com as horas excluídas (apenas a primeira hora de cada dia)

O correlograma parece mais interessante para a nova série. Existe uma forte dependência dos incrementos atuais em relação aos anteriores. A dependência diminui quando o tempo delta entre os incrementos aumenta. Isso significa que o incremento atual da primeira hora do dia está fortemente correlacionado com o incremento da primeira hora do dia anterior e assim por diante. Esta informação muito importante indica a existência de padrões sazonais, ou seja, os incrementos possuem uma memória.

A abordagem personalizada para identificar os padrões dos incrementos de preços é a autocorrelação sazonal

Nós descobrimos que existe uma correlação entre o incremento da primeira hora do dia atual e os incrementos da primeira hora dos dias anteriores, que, no entanto, diminuem quando o delta aumenta (distância em dia). Agora vamos ver se há uma correlação entre as horas adjacentes. Para esse fim, vamos modificar o código:

def seasonal_autocorrelation(symbol, lag, hour1, hour2):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 
    rates = rates.drop(rates.index[~rates.index.hour.isin([hour1, hour2])]).diff(lag).dropna()
    from pandas.plotting import autocorrelation_plot
    plt.figure(figsize=(10, 5))
    autocorrelation_plot(rates)

seasonal_autocorrelation('EURUSD', 50, 1, 2)

Aqui, excluímos todas as horas, exceto a primeira e a segunda, calculamos as diferenças para as novas séries e criamos a função de autocorrelação:

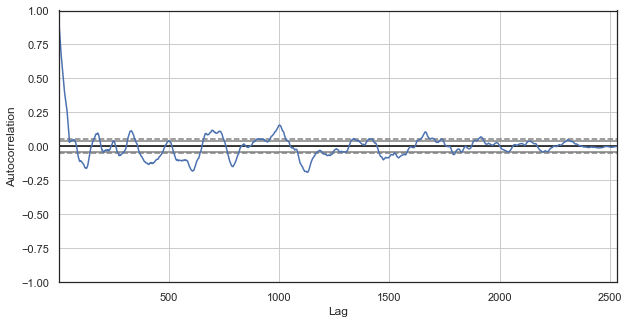
Fig. 3. Um correlograma de incrementos de preços com horas excluídas (com apenas a primeira e a segunda hora para cada dia)

Também se observa uma alta correlação para a série das horas mais próximas, o que indica sua correlação e influência mútua. Será que podemos obter uma pontuação relativa confiável para todos os pares de horas, não apenas para os selecionados? Para fazer isso, vamos usar os métodos descritos abaixo.

Mapa de calor de correlações sazonais para todas as horas

Vamos continuar a explorar o mercado e tentar confirmar a hipótese original. Vamos olhar para o quadro geral. A função abaixo remove sequencialmente as horas da série temporal, deixando apenas uma hora. Ele cria a diferença de preço para esta série e determina a correlação com a série criada por outras horas:

#calculate correlation heatmap between all hours
def correlation_heatmap(symbol, lag, corrthresh):
    out = pd.DataFrame()
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 

    for i in range(24):
        ratesH = None
        ratesH = rates.drop(rates.index[~rates.index.hour.isin([i])]).diff(lag).dropna()
        out[str(i)] = ratesH['close'].reset_index(drop=True)
    plt.figure(figsize=(10, 10))
    corr = out.corr()
    # Generate a mask for the upper triangle
    mask = np.zeros_like(corr, dtype=np.bool)
    mask[np.triu_indices_from(mask)] = True
    sns.heatmap(corr[corr >= corrthresh], mask=mask)
    return out

out = correlation_heatmap(symbol='EURUSD', lag=25, corrthresh=0.9)    

A função aceita a ordem do incremento (intervalo de tempo), bem como o limite de correlação para interromper as horas com uma baixa correlação. Aqui está o resultado:

Fig. 4. Mapa de calor das correlações entre os incrementos para as diferentes horas para o período 2015-2020.

Se vê claramente que os seguintes clusters possuem a correlação máxima nas seguintes horas do dia: 0-5 e 10-14 horas. No artigo anterior, nós criamos um sistema de negociação baseado no primeiro cluster, que foi descoberto de uma maneira diferente (usando o boxplot). Agora os padrões também são visíveis no mapa de calor. Agora vamos ver o segundo cluster interessante e analisá-lo. Aqui está o resumo das estatísticas para o cluster:

out[['10','11','12','13','14']].describe()

	10	11	12	13
count	1265.000000	1265.000000	1265.000000	1265.000000	1265.000000
mean	-0.001016	-0.001015	-0.001005	-0.000992	-0.000999
std	0.024613	0.024640	0.024578	0.024578	0.024511
min	-0.082850	-0.084550	-0.086880	-0.087510	-0.087350
25%	-0.014970	-0.015160	-0.014660	-0.014850	-0.014820
50%	-0.000900	-0.000860	-0.001210	-0.001350	-0.001280
75%	0.013460	0.013690	0.013760	0.014030	0.013690
max	0.082550	0.082920	0.085830	0.089030	0.086260

Os parâmetros para todas as horas do cluster são bastante próximos, porém seu valor médio para a amostra analisada é negativo (cerca de 100 pontos de cinco dígitos). Uma mudança nos incrementos médios indica que é mais provável que o mercado diminua durante essas horas do que cresça. Também é importante notar que um aumento nos incrementos de atraso leva a uma maior correlação entre as horas devido ao aparecimento de um componente de tendência, enquanto uma diminuição no atraso leva a valores mais baixos. No entanto, o arranjo relativo dos clusters é praticamente inalterado. 

Por exemplo, para um único atraso, os incrementos das horas 12, 13 e 14 ainda se correlacionam fortemente:

plt.figure(figsize=(10,5))
plt.plot(out[['12','13','14']])
plt.legend(out[['12','13','14']])
plt.show()

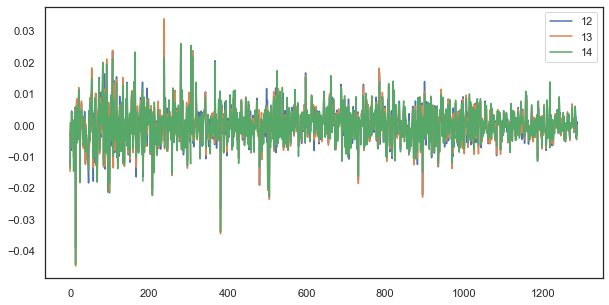
Fig. 5. A semelhança visual entre as séries de incrementos com um único atraso composto por diferentes horas

Fórmula da regularidade: simples, mas boa

Lembre-se da hipótese:

A correlação dos incrementos de preços depende da presença de padrões sazonais, bem como do agrupamento dos incrementos mais próximos. f

Nós vimos no diagrama de autocorrelação e no mapa de calor que existe uma dependência de incrementos por hora, tanto em valores passados quanto em incrementos das horas mais próximas. O primeiro fenômeno decorre da recorrência dos eventos em determinadas horas do dia. O segundo está relacionado ao agrupamento da volatilidade em determinados períodos de tempo. Ambos os fenômenos devem ser considerados separadamente e devem ser combinados, se possível. Neste artigo, nós realizaremos um estudo adicional da dependência dos incrementos de horas específicos (removendo todas as outras horas da série temporal) em relação aos valores anteriores. A parte mais interessante da pesquisa será realizada no próximo artigo.

# calculate joinplot between real and predicted returns
def hourly_signals_statistics(symbol, lag,  hour, hour2, rfilter):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
# price differences for every hour series   
    H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True).diff(lag).dropna()
    H2 = rates.drop(rates.index[~rates.index.hour.isin([hour2])]).reset_index(drop=True).diff(lag).dropna()
# current returns for both hours    
    HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True)     
# previous returns for both hours    
    HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True)  
    
# Basic equation:  ret[-1] = ret[0] - (ret[lag] - ret[lag-1])
# or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) 

    predicted = HF-(HF2-HL2)
    real = HL 
# correlation joinplot between two series    
    outcorr = pd.DataFrame()
    outcorr['Hour ' + str(hour)] = H['close']
    outcorr['Hour ' + str(hour2)] = H2['close']
# real VS predicted prices     
    out = pd.DataFrame()
    out['real'] = real['close']
    out['predicted'] = predicted['close']
    out = out.loc[((out['predicted'] >= rfilter) | (out['predicted'] <=- rfilter))]
# plptting results    
    from scipy import stats
    sns.jointplot(x='Hour ' + str(hour), y='Hour ' + str(hour2), data=outcorr, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) 
    sns.jointplot(x='real', y='predicted', data=out, kind="reg", height=7, ratio=6).annotate(stats.pearsonr)

hourly_signals_statistics('EURUSD', lag=25, hour=13, hour2=14, rfilter=0.00)

Aqui está uma explicação do que é feito na listagem acima. Existem duas séries formadas pela remoção das horas desnecessárias, com base nos incrementos de preço (sua diferença) calculados. As horas da série são determinadas nos parâmetros "hour" e "hour2". Em seguida, nós obtemos as sequências com um atraso de um para cada hora, ou seja, a série HF está à frente de HL por um valor igual a um — isso permite calcular o incremento real e o incremento previsto, bem como a diferença entre eles. Primeiro, vamos construir um gráfico de dispersão para os incrementos da primeira e da segunda hora:

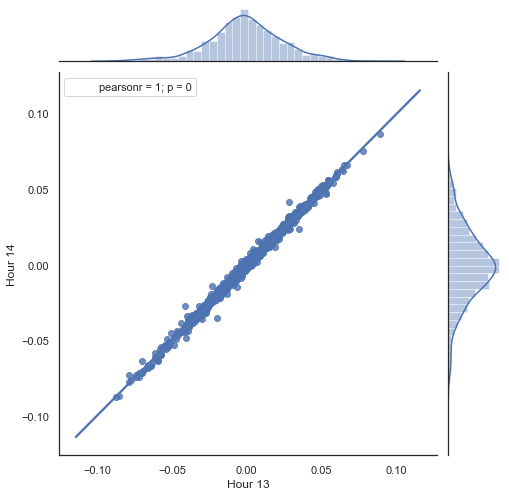
Figura 5. Gráfico de dispersão para incrementos das horas 13 e 14 para o período de 2015-2020.

Como esperado, os incrementos são altamente correlacionados. Agora vamos tentar prever o próximo incremento com base no anterior. Para fazer isso, aqui está uma fórmula simples, que pode prever o próximo valor:

Equação básica:  ret[-1] = ret[0] - (ret[lag] - ret[lag-1])

ou Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) 

Aqui está a explicação da fórmula resultante. Para prever o incremento futuro, nós estamos na barra zero. Prevemos o valor do próximo incremento ret[-1]. Para fazer isso, subtraímos a diferença do incremento anterior (com um 'atraso') e o próximo (lag-1) do incremento atual. Se a correlação dos incrementos entre as duas horas adjacentes for forte, pode-se esperar que o incremento previsto seja descrito por esta equação. Abaixo está uma explicação da equação para os preços de fechamento. Assim, a previsão futura é baseada em três incrementos. A segunda parte do código prevê os incrementos futuros e os compara aos reais. Aqui está um gráfico:

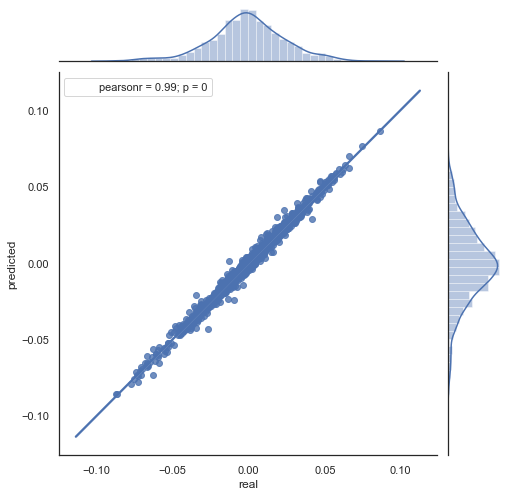
Figura 6. Gráfico de dispersão para os incrementos reais e os previstos para o período de 2015-2020.

Você pode ver que os gráficos nas figuras 5 e 6 são semelhantes. Isso significa que o método para determinar os padrões via correlação é adequado. Ao mesmo tempo, os valores estão espalhados pelo gráfico; eles não estão na mesma linha. Esses são erros de previsão que afetam negativamente a previsão. Eles devem ser tratados separadamente (o que está além do escopo deste artigo). A previsão em torno de zero não é realmente interessante: se a previsão para o próximo incremento de preço for igual à atual, você não poderá gerar lucro a partir dele. As previsões podem ser filtradas usando o parâmetro rfilter.

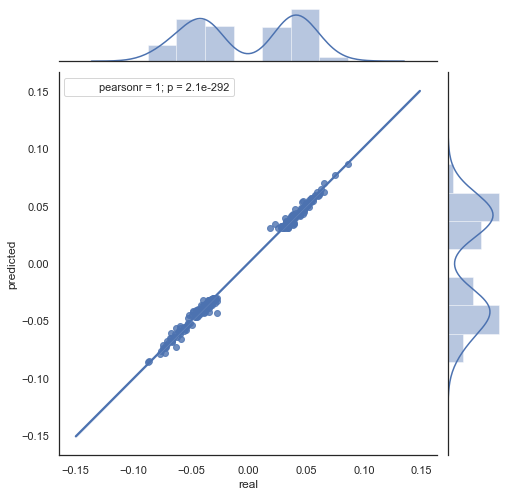
Figura 7. Gráfico de dispersão para os incrementos reais e os previstos com rfilter = 0.03 para o período de 2015-2020.

Observe que o mapa de calor foi criado usando os dados de 2015 até a data atual. Vamos mudar o dia inicial para 2000:

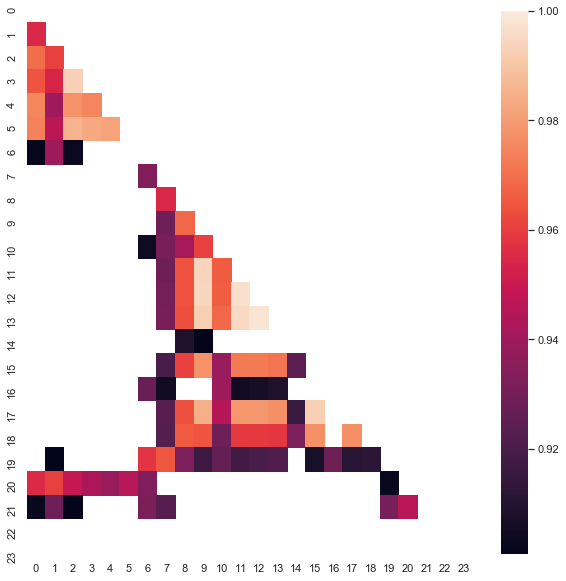
Fig. 8. Mapa de calor das correlações entre os incrementos para as diferentes horas no período de 2000-2020.

	10	11	12	13
count	5151.000000	5151.000000	5151.000000	5151.000000	5151.000000
mean	0.000470	0.000470	0.000472	0.000472	0.000478
std	0.037784	0.037774	0.037732	0.037693	0.037699
min	-0.221500	-0.227600	-0.222600	-0.221100	-0.216100
25%	-0.020500	-0.020705	-0.020800	-0.020655	-0.020600
50%	0.000100	0.000100	0.000150	0.000100	0.000250
75%	0.023500	0.023215	0.023500	0.023570	0.023420
max	0.213700	0.212200	0.210700	0.212600	0.208800

Podemos ver que o mapa de calor está um pouco mais fino, havendo uma diminuição na dependência entre as horas 13 e 14. Ao mesmo tempo, o valor médio dos incrementos é positivo, o que define uma prioridade mais alta para a compra. Uma mudança no valor médio não permitirá as negociações efetivas nos dois intervalos de tempo, portanto, você deve escolher.

Vejamos o gráfico de dispersão resultante para este período (aqui, eu apenas forneço o gráfico atual/previsto):

Fig. 9. Gráfico de dispersão para os incrementos reais e os previstos com rfilter = 0.03, para o período de 2000 a 2020.

O spread dos valores aumentou, o que é um fator negativo por um período tão longo.

Assim, nós obtivemos uma fórmula e uma ideia aproximada da distribuição dos incrementos reais e dos previstos por determinadas horas. Para uma maior clareza, as dependências podem ser visualizadas em 3D.

# calculate joinplot between real an predicted returns
def hourly_signals_statistics3D(symbol, lag,  hour, hour2, rfilter):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
    rates = pd.DataFrame(rates['close'].diff(lag)).dropna()
    
    out = pd.DataFrame();
    for i in range(hour, hour2):
        H = None; H2 = None; HF = None; HL = None; HF2 = None; HL2 = None; predicted = None; real = None;
        H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True)
        H2 = rates.drop(rates.index[~rates.index.hour.isin([i+1])]).reset_index(drop=True)
        HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True);     # current hours
        HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True)  # last day hours
    
        predicted = HF-(HF2-HL2)
        real = HL 
    
        out3D = pd.DataFrame()
        out3D['real'] = real['close']
        out3D['predicted'] = predicted['close']
        out3D['predictedABS'] = predicted['close'].abs()
        out3D['hour'] = i
        out3D = out3D.loc[((out3D['predicted'] >= rfilter) | (out3D['predicted'] <=- rfilter))]
        
        out = out.append(out3D)
        
    import plotly.express as px
    fig = px.scatter_3d(out, x='hour', y='predicted', z='real', size='predictedABS', color='hour', height=1000, width=1000)
    fig.show()

hourly_signals_statistics3D('EURUSD', lag=24, hour=10, hour2=23, rfilter=0.000)

Esta função usa a fórmula já conhecida para calcular os valores previstos e reais. Cada gráfico de dispersão separado mostra a dependência real/prevista para cada hora, como se um sinal tivesse sido gerado no incremento décima hora do dia anterior. São usadas como exemplo as horas de 10.00 até 23.00. A correlação entre as horas mais próximas é máxima. À medida que a distância aumenta, a correlação diminui (os gráficos de dispersão se tornam mais parecidos com círculos). A partir da hora 16, as horas adicionais dependem pouco da hora 10 do dia anterior. Usando o anexo, você pode girar o objeto 3D e selecionar os fragmentos para obter as informações mais detalhadas.

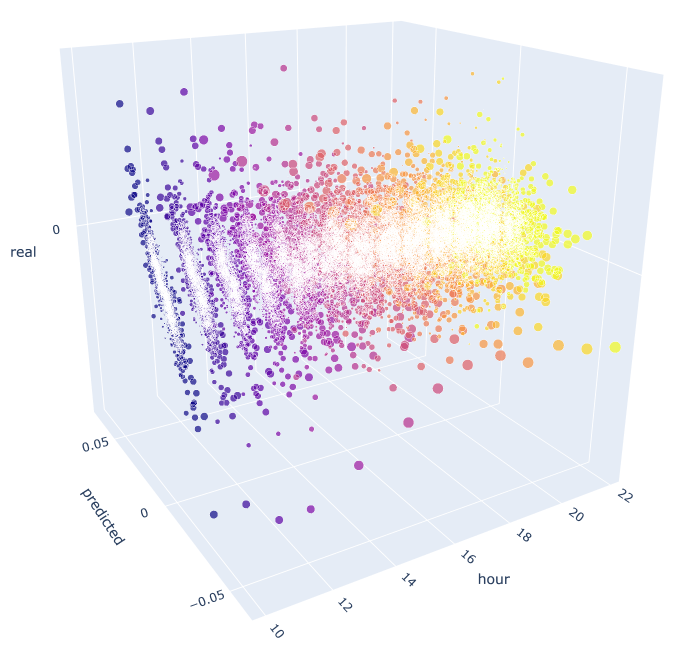
Fig. 10. Gráfico de dispersão 3D para os incrementos reais e previstos para 2015 até 2020.

Agora é hora de criar um Expert Advisor para ver como ele funciona.

Exemplo de um Expert Advisor negociando os padrões sazonais identificados

Da mesma forma que o exemplo do artigo anterior, o robô trocará um padrão sazonal que é baseado apenas na relação estatística entre o incremento atual e o anterior por uma hora específica. A diferença é que ele negociará em outras horas, utilizando um princípio baseado na fórmula proposta. 

Vamos considerar um exemplo de uso da fórmula resultante para negociação, com base no estudo estatístico:

input int OpenThreshold = 30;     //Open threshold
input int OpenThreshold1 = 30;    //Open threshold 1
input int OpenThreshold2 = 30;    //Open threshold 2
input int OpenThreshold3 = 30;    //Open threshold 3
input int OpenThreshold4 = 30;    //Open threshold 4
input int Lag = 10;
input int stoploss = 150;         //Stop loss
input int OrderMagic = 666;       //Orders magic
input double   MaximumRisk=0.01;  //Maximum risk
input double   CustomLot=0;       //Custom lot

O seguinte intervalo com os padrões foi determinado: {10, 11, 12, 13, 14}. Com base nele, o parâmetro "Open threshold" pode ser definido para cada hora individualmente. Estes parâmetros são semelhantes ao "rfilter" na fig. 9 A variável 'Lag' contém o valor do atraso para os incrementos (lembre-se, nós analisamos o atraso de 25 por padrão, ou seja, quase um dia para o período H1). Os atrasos podem ser definidos separadamente para cada hora, mas o mesmo valor para todas as horas é usado aqui para fins de simplicidade. O Stop Loss também é o mesmo para todas as posições. Todos esses parâmetros podem ser otimizados.

A lógica de negociação é a seguinte:

void OnTick() {
//---
   if(!isNewBar()) return;
   CopyClose(NULL, 0, 0, Lag*2+1, prArr);
   ArraySetAsSeries(prArr, true);
   const double pr = (prArr[1] - prArr[Lag]) - ((prArr[Lag] - prArr[Lag*2]) - (prArr[Lag-1] - prArr[Lag*2-1]));

   TimeToStruct(TimeCurrent(), hours);

   if(hours.hour >=10 && hours.hour <=14) {

      //if(countOrders(0)==0)
      //   if(pr >= signal && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY))
      //      OrderSend(Symbol(),OP_BUY,LotsOptimized(), Ask,0,Bid-stoploss*_Point,NormalizeDouble(Ask + signal, _Digits),NULL,OrderMagic,INT_MIN);

      if(CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_SELL)) {
         if(pr <= -signal && hours.hour==10)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal, _Digits),NULL,OrderMagic);
         if(pr <= -signal1 && hours.hour==11)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal1, _Digits),NULL,OrderMagic);
         if(pr <= -signal2 && hours.hour==12)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal2, _Digits),NULL,OrderMagic);
         if(pr <= -signal3 && hours.hour==13)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal3, _Digits),NULL,OrderMagic);
         if(pr <= -signal4 && hours.hour==14)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal4, _Digits),NULL,OrderMagic);
      }
   }
}

A constante 'pr' é calculada pela fórmula especificada acima. Essa fórmula prevê o aumento do preço na próxima barra. Então, a condição para cada hora é verificada. Se o incremento atingir o limite mínimo para a hora específica, uma negociação de venda será aberta. Nós já descobrimos que mudar os incrementos médios para a zona negativa torna as compras ineficazes no intervalo de 2015 a 2020, você pode verificar isso por conta própria.

Vamos iniciar a otimização genética com os parâmetros especificados na fig. 11 e ver o resultado:

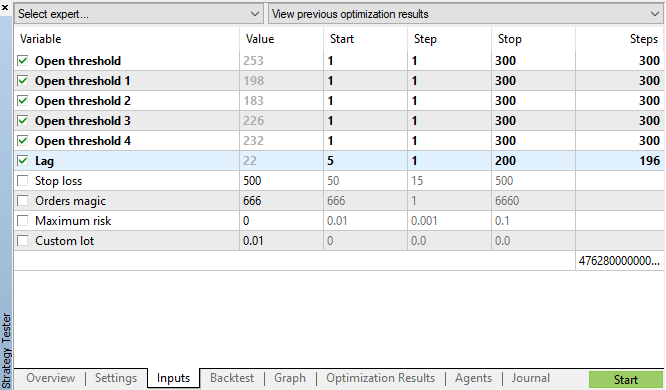
Fig. 11. A tabela de parâmetros da otimização genética

Vamos olhar para o gráfico de otimização. No intervalo otimizado, os valores de Lag mais eficientes estão localizados entre 17 e 30 horas, o que é muito próximo da nossa suposição sobre a dependência de incrementos de uma hora específica no dia atual na mesma hora do dia anterior:

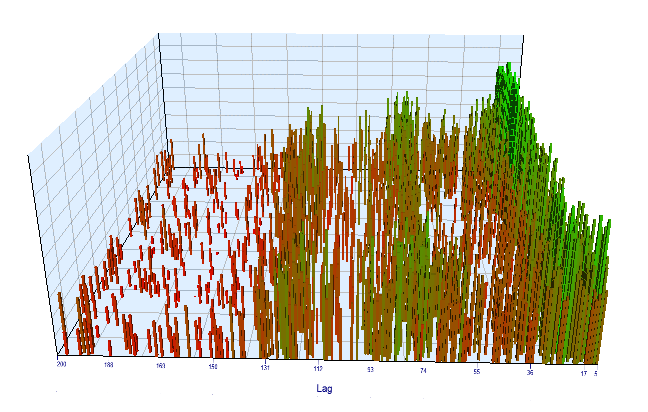
Fig. 12. Relação da variável 'Lag' com a variável 'Order threshold' no intervalo otimizado

O gráfico de forward é semelhante:

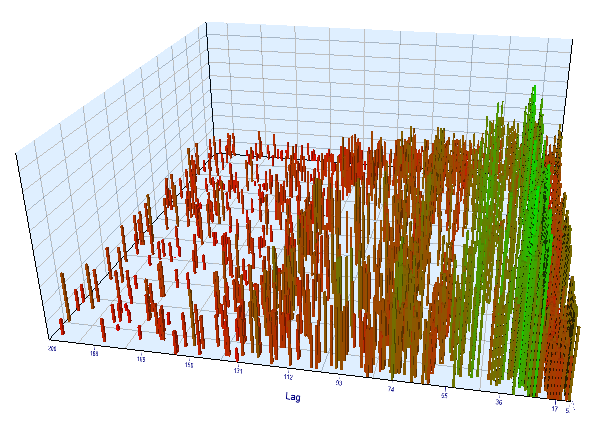
Fig. 13. Relação da variável 'Lag' com a variável 'Order threshold' no intervalo de forward

Aqui estão os melhores resultados das tabelas de backtest e dos forward tests:

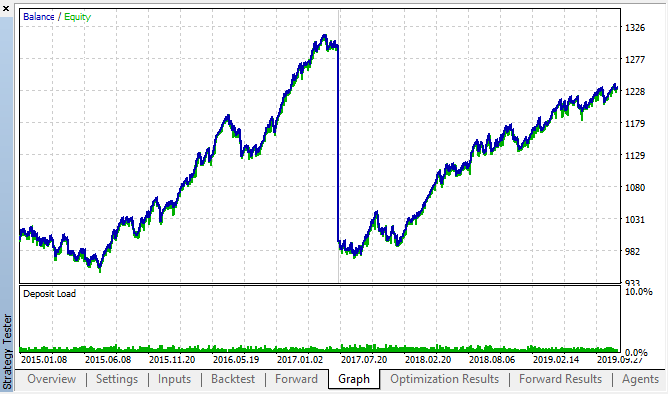
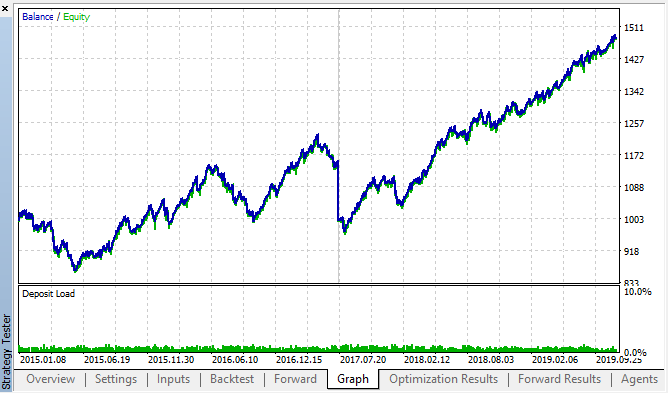
Fig. 14, 15. Gráficos de Backtest e forward.

Pode-se observar que o padrão persiste durante todo o intervalo de 2015-2020. Nós podemos assumir que a abordagem econométrica funcionou perfeitamente bem. Existem dependências entre os incrementos da mesma hora para os próximos dias da semana, com alguns agrupamentos (a dependência pode não estar na mesma hora, mas em uma hora próxima). No próximo artigo, nós analisaremos como usar o segundo padrão.

Verificar o período de incremento em outro período

Vamos fazer uma verificação adicional no período M15. Suponha que nós estamos procurando a mesma correlação entre a hora atual e a mesma hora do dia anterior. Nesse caso, o atraso efetivo deve ser 4 vezes maior e ser cerca de 24*4 = 96, porque cada hora contém quatro períodos M15. Eu otimizei o Expert Advisor com as mesmas configurações e com o período M15.

No intervalo otimizado, o atraso efetivo resultante é <60, o que é estranho. Provavelmente, o otimizador encontrou outro padrão, ou o EA foi super otimizado.

 

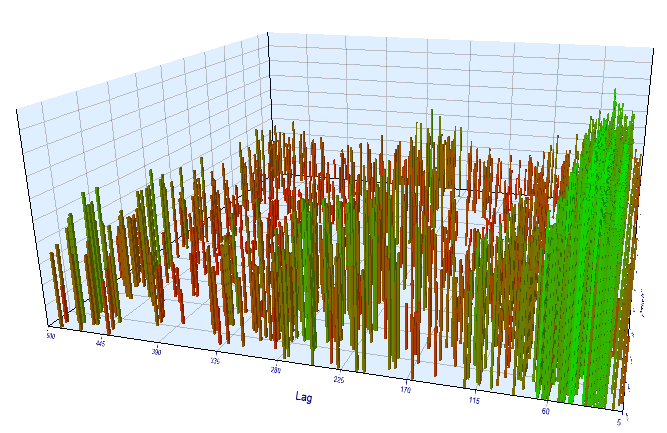
Fig. 16. Relação da variável 'Lag' com a variável 'Order threshold' no intervalo otimizado

Quanto aos resultados do forward test, o atraso efetivo é normal e corresponde a 100, o que confirma o padrão. 

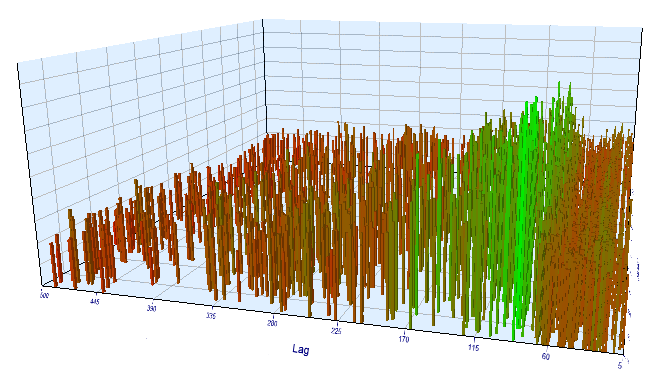
Fig. 17. Relação da variável 'Lag' com a variável 'Order threshold' no intervalo de forward

Vamos ver os melhores resultados do backtest e de forward:

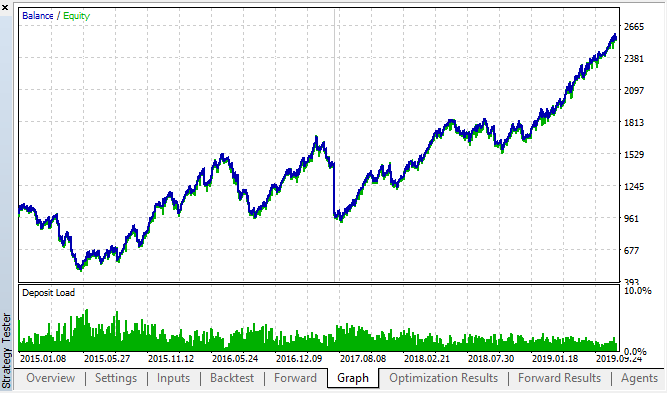
Fig. 18. Backtest e forward; o melhor passe do forward

A curva resultante é semelhante à curva do gráfico H1, com um aumento significativo no número de negócios. Provavelmente, a estratégia pode ser otimizada para períodos menores.

Conclusão

Neste artigo, nós apresentamos a seguinte hipótese:

A correlação dos incrementos de preços depende da presença de padrões sazonais, bem como do agrupamento dos incrementos mais próximos. 

A primeira parte foi totalmente confirmada: há correlação entre os incrementos horários de diferentes semanas. A segunda declaração foi confirmada implicitamente: a correlação tem agrupamentos, o que significa que os incrementos horários atuais também dependem dos incrementos das horas vizinhas.

Observe que o Expert Advisor proposto não é de forma alguma a única variante possível para negociar as correlações encontradas. A lógica proposta reflete a visão do autor sobre as correlações, enquanto a otimização do EA foi realizada apenas para confirmar adicionalmente os padrões encontrados na pesquisa estatística.

Como a segunda parte do nosso estudo requer uma pesquisa adicional substancial, nós usaremos um modelo simples de aprendizado de máquina no próximo artigo para confirmar ou refutar totalmente a segunda parte da hipótese. 

O anexo contém uma estrutura pronta para uso no formato do Jupyter notebook, que você pode usar para estudar outros instrumentos financeiros. Os resultados ainda podem ser testados usando o EA de teste anexado.