Fundamentos de estatística
QSer29 | 12 março, 2014
Introdução
O que é estatística? Aqui está a definição encontrada na Wikipédia: "Estatística é o estudo da coleta, organização, análise, interpretação e apresentação de dados". (Estatísticas). Esta definição sugere três componentes principais das estatísticas: coleta de dados, medidas e analises. A análise de dados parece ser especialmente útil para o negociador, como a informação recebida é fornecida pelo corretor, ou através de um terminal de negociação, e já é medida.
Os comerciantes modernos (principalmente) usam a análise técnica para decidir se querem comprar ou vender. Eles lidam com estatísticas em praticamente tudo o que fazem ao usar um determinado indicador ou ao tentar prever o nível de preços para o próximo período. Na verdade, o próprio gráfico de flutuação de preços representa certas estatísticas de uma ação ou moeda no tempo apropriado. Por isso é muito importante compreender os princípios básicos das estatísticas subjacentes à maioria dos mecanismos que facilitam o processo de tomada de decisão para um comerciante.
Teoria da probabilidade e estatísticas
Quaisquer estatísticas é o resultado da mudança nos estados do objeto que a gera. Vamos considerar uma tabela de preços EURUSD em prazos de horários:
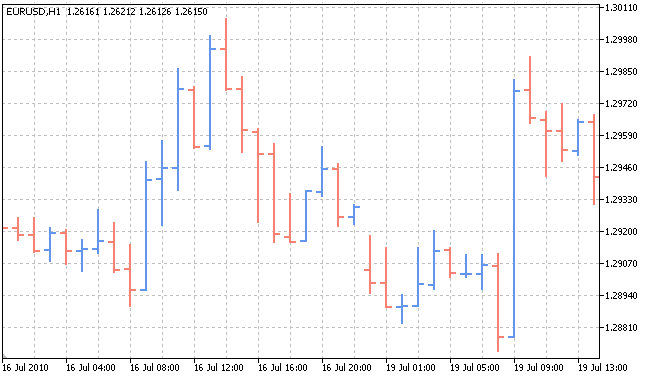
Neste caso, o objeto é a correlação entre duas moedas, enquanto que a estatística são seus preços em cada ponto de tempo. Como a correlação entre duas moedas afetam seus preços? Por que temos esta tabela de preços e não uma diferente em um determinado intervalo de tempo? Por que os preços atualmente diminuem e não crescem? A resposta a estas perguntas é a palavra "probabilidade". Cada objeto, dependendo da probabilidade, pode assumir um ou outro valor.
Vamos fazer um experimento simples: pegue uma moeda e lance-a um certo número de vezes, cada vez que ela cair grave o resultado que a mesma marcou. Suponha que temos uma moeda honesta. Em seguida, a tabela pode ser como se segue:
| Resultado | Probabilidade |
|---|---|
| Caras | 0,5 |
| Coroas | 0,5 |
A tabela sugere que a moeda tem a mesma probabilidade de dar cara ou coroa. Qualquer outro resultado não é possível aqui (a possibilidade de cair sobre a borda da moeda foi excluída antecipadamente) como a soma das probabilidades de todos os eventos possíveis será igual a um.
Lance a moeda 10 vezes. Agora vamos notar os resultados dos lances:
| Resultado | Número |
|---|---|
| Caras | 8 |
| Coroas | 2 |
Por que temos estes resultados se a moeda tem a mesma probabilidade de parar em qualquer um dos lados? A probabilidade de a moeda parar em qualquer um dos lados é de fato igual, o que no entanto, não significa que, depois de algumas jogadas a moeda parede um lado mais vezes que do outro. A probabilidade só mostra que nesta tentativa particular (lance), a moeda vai parar tanto em cara quanto em coroa e ambos os eventos sustentam chances iguais.
Vamos agora lançar a moeda 100 vezes. Obtivemos a nova tabela de resultados:
| Resultado | Número |
|---|---|
| Caras | 53 |
| Coroas | 47 |
Como pode ser visto, o número de resultados não são novamente iguais. No entanto, 53 a 47 é o resultado que demonstra os pressupostos da probabilidade inicial. A moeda caiu sobre cara quase tantas vezes quanto em coroa.
Agora vamos fazer o mesmo na ordem inversa. Suponha que temos uma moeda, mas a probabilidade de parar em um dos seus lados é desconhecida. Precisamos determinar se é uma moeda honesta, ou seja, se a moeda tem a mesma probabilidade de dar cara ou coroa.
Vamos pegar os dados do primeiro experimento. Dividir o número de resultados de cada lado pelo número total de resultados. Nós obtemos a seguinte probabilidade:
| Resultado | Probabilidade |
|---|---|
| Caras | 0,8 |
| Coroas | 0,2 |
Podemos ver que é muito difícil concluir a partir do primeiro experimento que a moeda é justa. Vamos fazer o mesmo para o segundo experimento:
| Resultado | Número |
|---|---|
| Caras | 0,53 |
| Coroas | 0,47 |
Tendo estes resultados em mãos, podemos dizer com um alto grau de precisão que se trata de uma moeda honesta.
Este simples exemplo nos permite tirar uma conclusão importante: quanto maior o número de experimentos, mais precisamente as propriedades do objeto são refletidas pelas estatísticas geradas pelo objeto.
Assim, estatística e probabilidade estão intimamente interligadas. As estatísticas representam os resultados experimentais com um objeto, e é diretamente dependente na probabilidade do estado do objeto. Por outro lado, a probabilidade dos estados do objeto pode ser estimada pela estatística. Aqui é onde o principal desafio para um negociador se encontra: dispor de dados sobre negociações durante um determinado período de tempo (estatísticas), para prever o comportamento dos preços para o seguinte período de tempo (de probabilidade) e com base nessas informações fazer uma decisão de compra ou venda.
Portanto, voltando aos pontos feitos na introdução, também é importante conhecer e entender a relação entre estatística e probabilidade, bem como ter conhecimento da avaliação de risco e situações de risco. Os dois últimos estão, porém, fora do escopo deste artigo.
Parâmetros estatísticos básicos
Vamos agora analisar os parâmetros estatísticos básicos. Suponha que temos dados sobre a altura em cm sobre 10 pessoas em um grupo:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Altura | 173 | 162 | 194 | 181 | 186 | 159 | 173 | 178 | 168 | 171 |
Os dados apresentados na tabela são chamados de amostra, enquanto que a quantidade de dados é o tamanho da amostra. Vamos dar uma olhada em alguns parâmetros do exemplo dado. Todos os parâmetros serão os parâmetros de amostra tal como resultam dos dados da amostra, ao invés de dados variáveis aleatórios.
1. Média amostral
A média amostral é o valor médio na amostra. No nosso caso, é a altura média das pessoas no grupo.
Para calcular a média, devemos:
- Somar todos os valores da amostra.
- Dividir o valor resultante pelo tamanho da amostra.
Fórmula:
![]()
Onde:
- M é a média amostral,
- a[i] é o elemento da amostra,
- n é o tamanho da amostra.
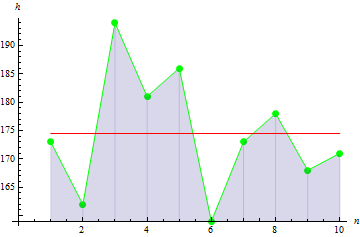
Após os cálculos, obtemos o valor médio de 174.5 cm.

2. Variância amostral
A variância amostral descreve o quão longe os valores da amostra se encontram a partir da média amostral. Quanto maior for o valor, mais amplamente os dados são propagados.
Para calcular a variância, devemos:
- Calcular a média amostral.
- Subtrair a média de cada elemento da amostra e elevar ao quadrado a diferença.
- Somar os valores resultantes obtidos acima.
- Dividir a soma pelo tamanho da amostra menos 1.
Fórmula:
![]()
Onde:
- D é a variância amostral,
- M é a média amostral,
- a[i] é o elemento da amostra,
- n é o tamanho da amostra.
A variância amostral em nosso caso é de 113.611.
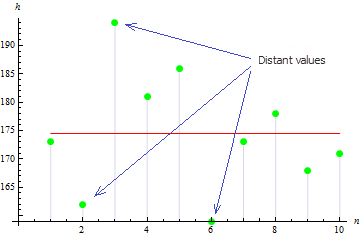
A figura 3 indica que os valores estão amplamente espalhados do meio que conduz ao valor de variação grande.
3. Simetria amostral
A simetria amostral é usada para descrever o grau de assimetria dos valores da amostra em torno da sua média. Quanto mais próximo ao zero o valor da simetria está, mais simétricos são os valores da amostra.
Para calcular a simetria, devemos:
- Calcular a média amostral.
- Calcular a variância amostral.
- Adicionar diferenças ao cubo de cada elemento da amostra e da média.
- Dividir a resposta pelo valor de variância elevado à potência de 2/3.
- Multiplicar a resposta pelo coeficiente igual ao tamanho da amostra dividido pelo produto do tamanho da amostra menos 1 e pelo tamanho da amostra menos de 2.
Fórmula:
![]()
Onde:
- A é a simetria amostral,
- D é a variância amostral,
- M é a média amostral,
- a[i] é o elemento da amostra,
- n é o tamanho da amostra.
Obtivemos um valor muito pequeno de simetria para este exemplo: 0,372981. Isto é devido ao fato de que os valores divergentes compensam uns aos outros.
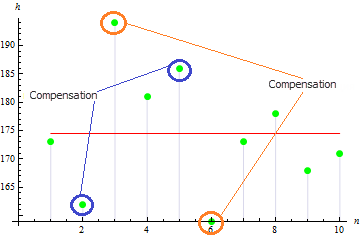
O valor será maior para a amostra assimétrica. Por exemplo o valor para os dados como abaixo será de 1.384651.
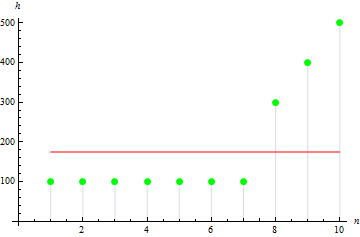
4. Curtose amostral
A curtose amostral descreve o pico da amostra.
Para calcular a curtose, devemos:
- Calcular a média amostral.
- Calcular a variância amostral.
- Somar as diferenças na quarta potência de cada elemento da amostra e da média.
- Dividir a resposta pela variância ao quadrado.
- Multiplicar o valor resultante pelo coeficiente igual ao produto do tamanho da amostra e o tamanho da amostra mais 1, dividido pelo produto do tamanho da amostra menos 1, menos 2 e menos 3.
- Subtrair do valor resultante o produto de 3 e a diferença ao quadrado do tamanho da amostra e 1, dividido pelo produto do tamanho da amostra menos 1 e menos 2.
Fórmula:
![]()
Onde:
- E é a curtose amostral,
- D é a variância amostral,
- M é a média amostral,
- a[i] é o elemento da amostra,
- n é o tamanho da amostra.
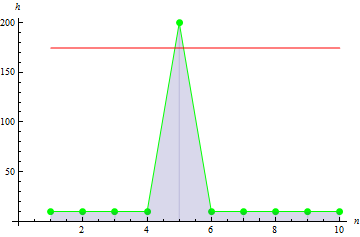
Para dados de altura dados, obtemos um valor de -0.1442285.
Para dados de pico mais distintos, obtemos um valor maior: 10.
5. Covariância amostral
A covariância amostral é uma medida que indica o grau de dependência linear entre duas amostras de dados. A covariância entre os dados independentes linearmente será 0.
Para ilustrar este parâmetro, adicionaremos dados de peso a cada uma das 10 pessoas:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Peso | 65 | 70 | 83 | 60 | 105 | 58 | 69 | 90 | 78 | 65 |
Para calcular a covariância de duas amostras, devemos:
- Calcular a média da primeira amostra.
- Calcular a média da segunda amostra.
- Adicionar todos os produtos de duas diferenças: a primeira diferença - um elemento da primeira amostra menos a média da primeira amostra, a segunda diferença - um elemento da segunda amostra (correspondente ao elemento da primeira amostra), menos a média da a segunda amostra.
- Dividir a resposta pelo tamanho da amostra menos 1.
Fórmula:
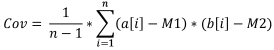
Onde:
- Cov é a covariância amostral,
- a[i] é o elemento da primeira amostra,
- b[i] é o elemento da segunda amostra,
- M1 é a média amostral da primeira amostra,
- M2 a média amostral da segunda amostra,
- n é o tamanho da amostra.
Deixe-nos calcular o valor da covariância das duas amostras: 91,2778. A dependência existente pode ser mostrada no gráfico combinado:
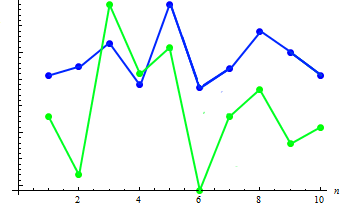
Como pode ser visto, o aumento da altura (em regra) corresponde à redução do peso, e vice-versa.
6. Correlação amostral
A correlação amostral também é usada para descrever o grau de dependência linear entre duas amostras de dados, mas o seu valor sempre se encontra dentro da gama de -1 a 1.
Para calcular a correlação de duas amostras, devemos:
- Calcular a variância da primeira amostra.
- Calcular a variância da segunda amostra.
- Calcular a covariância destas amostras.
- Dividir a covariância pela raiz quadrada do produto das variâncias.
Fórmula:
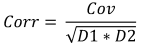
Onde:
- Corr é a correlação amostral,
- Cov é a covariância amostral,
- D1 é a variância amostral da primeira amostra,
- D2 é a variância amostral da segunda amostra,
Para uma dada altura e peso de dados, a correlação será igual a 0.579098.
Como usar estatísticas em negociação
O exemplo simples o qual ilustra a utilização de parâmetros estatísticos em negociações é o indicador MovingAverage. Seu cálculo exige dados em um determinado período de tempo e dá o valor da média aritmética do preço:
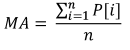
Onde:
- MA é o valor do indicador,
- P[i] é o preço,
- n é o período de medição de MA
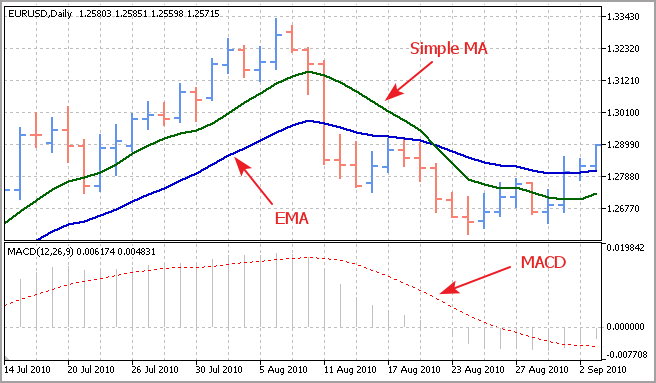
Podemos ver que o indicador é um análogo completo da média amostral. Apesar da sua simplicidade, este indicador é utilizado para o cálculo de EMA, a média móvel exponencial, que, por sua vez, é um elemento básico necessário para o indicador MACD - uma ferramenta clássica para a força e direção da tendência.
Estatísticas em MQL5
Consideramos a implementação de MQL5 dos parâmetros estatísticos básicos descritos acima. Os métodos estatísticos analisadosacima (e muito mais) são implementados nas funções de estatística na biblioteca statistics.mqh. Vamos rever seus códigos.
1. Média amostral
A função da biblioteca do cálculo da média da amostra é chamada média:

Dados de entrada: amostra de dados. Dados de saída: média.
2. Variância amostral
A função da biblioteca do cálculo da variância amostral é chamada variância:
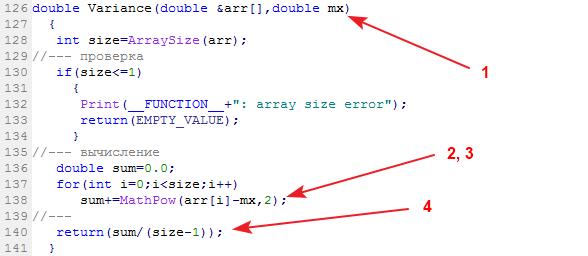
Dados de entrada: amostra de dados e sua média. Dados de saída: variância.
3. Simetria amostral
A função da biblioteca do cálculo da variância amostral é chamada assimetria:
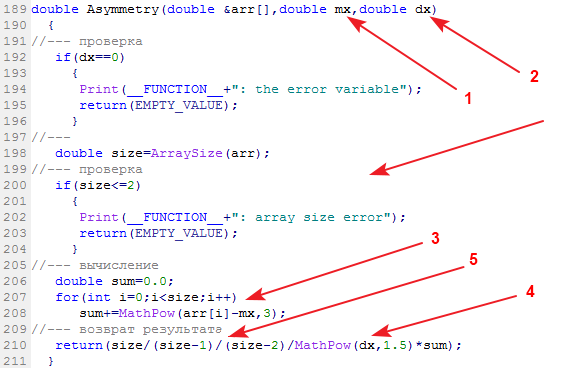
Dados de entrada: amostra de dados, sua média e variância. Dados de saída: simetria.
4. Curtose amostral
A função da biblioteca do cálculo da curtose amostral é chamada excesso (excesso 2):
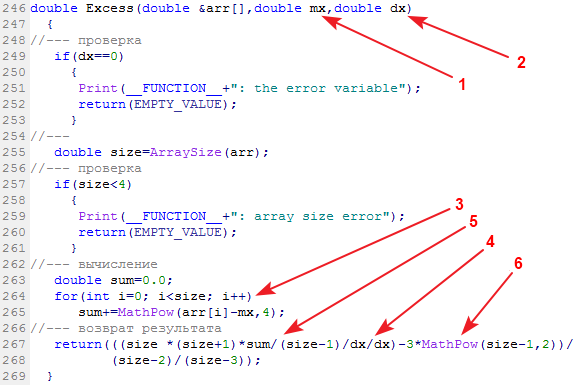
Dados de entrada: amostra de dados, sua média e variância. Dados de saída: curtose.
5. Covariância amostral
A função da biblioteca do cálculo da covariância amostral é chamada Cov:
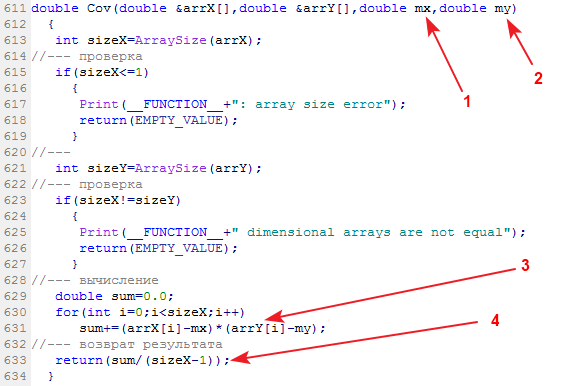
Dados de entrada: duas amostras de dados e suas respectivas médias. Dados de saída: covariância.
6. Correlação amostral
A função da biblioteca do cálculo da correlação amostral é chamada Corr:

Dados de entrada: covariância de duas amostras, variância da primeira e segunda amostras. Dados de saída: correlação.
Agora, deixe-nos inserir dados da amostra de altura e peso e processá-los usando a biblioteca.#include <Statistics.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- specify two data samples. double arrX[10]={173,162,194,181,186,159,173,178,168,171}; double arrY[10]={65,70,83,60,105,58,69,90,78,65}; //--- calculate the mean double mx=Average(arrX); double my=Average(arrY); //--- to calculate the variance, use the mean value double dx=Variance(arrX,mx); double dy=Variance(arrY,my); //--- skewness and kurtosis values double as=Asymmetry(arrX,mx,dx); double exc=Excess(arrX,mx,dx); //--- covariance and correlation values double cov=Cov(arrX,arrY,mx,my); double corr=Corr(cov,dx,dy); //--- print results in the log file PrintFormat("mx=%.6e",mx); PrintFormat("dx=%.6e",dx); PrintFormat("as=%.6e",as); PrintFormat("exc=%.6e",exc); PrintFormat("cov=%.6e",cov); PrintFormat("corr=%.6e",corr); }
Depois de executar o script, o terminal irá produzir os resultados da seguinte forma:
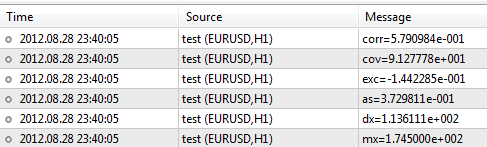
A biblioteca contém muito mais funções de descrições as quais podem ser encontrados em CodeBase - https://www.mql5.com/pt/code/866.
Conclusão
Algumas conclusões já foram tiradas no final da seção da "Teoria da probabilidade e estatística". Além do referido, vale a pena mencionar que as estatísticas, tal como qualquer outro ramo da ciência, serão estudadas começando com os seus ABCs. Até mesmo os seus elementos básicos podem facilitar a compreensão de uma grande quantidade de coisas, mecanismos complexos e padrões que, no final do dia, podem ser extremamente necessários no trabalho de um negociante.