価格系列の離散化、ランダム成分とノイズ

Maxim Romanov | 26 11月, 2020

イントロダクション

価格シリーズを時間間隔（タイムフレーム）で表現する古典的な方法は、はるか昔、コンピュータがなく、実相場でトレードされていた金融相場が形成され始めた頃に登場しました。 これらを1日の間に価格が変わるたびに保管するのは大変でしました。 しかも値段がすぐに変わらないので無駄でした。 そのため、一定の時間間隔で価格の値を登録することが自明の解決策でした。 これは一見論理的です："今日の小麦は90セントですが、昨日は80セントだった。" すべてはっきりしています。需要が増え、価格が上昇しました。 今の相場のトレードに比べてトレードが少なかったので、価格が再定義されることはほとんどありませんでした。

価格行動をより良く予測することを目的とした価格データ分析の登場と発展、トレードオペレーションの増加に伴い、ある期間の高値と安値がどちらなのかを把握することが重要になってきました。 つまり、昨日の80セントと今日の90セントの情報は、もはや十分ではなかったのです。 人々は、指定された期間内にどの高値と安値に到達したかを知りたいと思っていました。 よく知られているローソク足やバーが発明されたのもその頃です。

トレード回数の増加に伴い、価格系列の離散化が進んでいましたが、価格系列の離散化の精度が向上していました。 さて、すでに分単位の離散化を使っていますが、時には1秒や10秒など、もっと小さなフレームを使うこともあります。

価格系列を時間的に離散化することの主な利点は以下の通りです。

信号の離散化の特徴

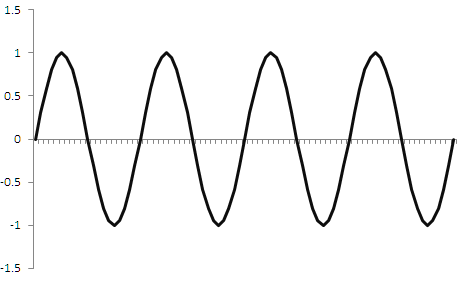
データの離散化は、トレードだけでなく、多くの信号処理分野で必要とされています。 例えば音楽では、元々連続していた信号をデジタル化します。 時間離散化を用いて符号化します。 一定時間間隔の信号振幅値をメモリに書き込みます。 この信号は、その後、特定の操作を用いて連続した信号に変換することができます。 連続的な信号の離散化はよく研究された分野です。 例えば、コテルニコフ（ナイキスト・シャノン）／Kotelnikov (Nyquist-Shannon) 定理から続くルールは次のように述べています。"離散化周波数が信号周波数の２倍以上であれば、信号は完全に復元できる" つまり、信号周波数が１ヘルツであれば、その振幅値は１秒間に２回以上（つまり、２ヘルツの周波数で）読み込まれなければならない。 この場合に限り、離散化後の原形を得ることができます。 図1は、1ヘルツの正弦波を2ヘルツのサンプルレートで離散化するとどうなるかを示しています。 信号を緑で示し、離散化の結果を赤で示します。

Sinus

図1.

離散化後、正弦波は三角波に変換されます。 もちろん多少の誤差はありますが、この三角信号はローパスフィルタを使って正弦波に戻すことができます。 多少の誤差はあるもの、信号のアイデア、周期、振幅を維持したまま、信号を復元することができることを意味します。 このような歪みは音楽では致命的とされていますが、トレードではあまり関係ありません。 しかし、離散化率が元の信号率よりも低い場合はどうでしょうか？ その一例を下図２に示します。

サイナスアナログ---->>

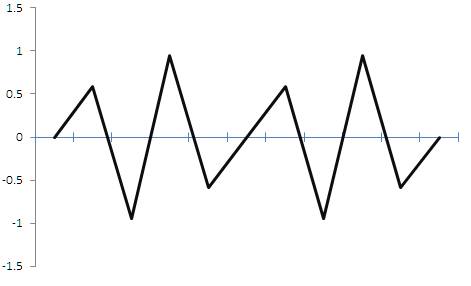
図2.

図に示すように、離散化周波数が２倍信号の周波数よりも小さい場合には、結果として得られる信号が大きく歪んでしまい、実際には元の信号とは関係のないランダムな信号を受信していることがわかります。 トレードに適用すると、最初のケースでは、高値を見つけたら売り、安値を見たら買うことができるようになります。 また、この場合は周波数がわかります。 離散化を誤ると、振幅と信号周波数の情報が失われます。 特性が既知の決定論的な周期信号は、離散化率の選択を誤ったために、特性が未知のランダムな非周期信号に変化しました。

上記の知識から、2つの論理的な疑問が生じます。"価格系列を離散化するときに間違っているのではないか？"と "価格系列は離散的なのか連続的な信号なのか、そしてそのパラメータは何なのか？"です。 

答えはそんなシンプルなものではなく、とても重要なものです。

価格系列は離散的か連続的か？

相場形成のメカニズムがわかれば、その疑問は解消されます。 この解説は「モスクワ取引所のデリバティブ市場を例にした取引所価格決定の原則」の記事にありますので、ここでは詳しくは説明しません。 参加者の中には、マーケットデプスにオーダーを出す人もいれば、必要な量を必要な価格で買う人もいます。 値動きチャートが形成されるとこうなります。 レベルは離散的で、つまり、1、2、3などの価格で、一定の精度でオーダーを出すことが可能です。 Bidで設定された数量と、買った数量は、1個、2個、3個以上の買いが可能なので、離散的なものでもあります。 下の図3は、マーケットデプスの例を示します。価格とボリュームが離散的な値があることがわかります。 

図3.

したがって、価格シリーズチャートは離散的な性質があると結論づけることができます。 参加者が離散的な数量の買いを入れた後、離散的な水準に沿って相場が動きます。 

価格とは何かの関数

価格系列自体は離散的であることがわかりましたが、価格の変化はどのパラメータの関数なのでしょうか？

オーディオ信号は時間の経過とともに変化する関数であるため、オーディオ信号を一定の間隔で離散化することは、許容される解決策です。 信号自体は時間に依存する振幅です。 この信号特性は基本的なものです。 よって、ここでは何の問題もありません。

価格シリーズは異なる性質があります。 ここでは、振幅（価格）は時間の経過とともに変化しますが、時間の経過が価格の変化の理由ではありません。 価格変更の理由を探ろうとすると、そうシンプルな問題ではありません。 いくつかの仮定があります。

  1. トレードの関数としての価格。 トレード操作によって価格が動くため、実行されたトレードに応じて価格が変化します。 しかし、トレードオペレーションが価格変動につながらない場合があります。 例えば、10銘柄が1ドルで買います。 参加者が4銘柄を買い、同じ価格で6銘柄が残ります。 ということで、売買操作が行われましたが、価格は変わっていません。 しかし、この価格で利用可能なボリュームが減少しているため、次の参加者が全量買いした場合には、さらに価格が変化する可能性があります。 1ドルで買える銘柄の量が足りず、需要をカバーできずに全額買われてしまった場合にのみ価格が変動します。 この場合、ASK価格は1.1米ドルまで動きます。 しかし、他の参加者はまだ1米ドルでオーダーを出し、アスクの価格を戻すことができます。
  2. 相場のすべてのトレード操作の機能としての価格。 参加者が一定のレベルでボリュームを買い切る場合だけでなく、オーダーをキャンセルしたり、他のレベルに移動させたりする場合にも価格は変化します。 このように、トレード操作は行われませんが、BIDとASKの価格は動きます。
  3. 「利益」の機能としての価格。 参加者が自分に資産価値を再定義するので、価格が変わることがあります。 資産価値を再定義する理由は全く異なる場合があります。 いずれにしても、資産価値の再定義は、参加者の利益と密接に関係しています。 理論的には、確立された価格は、買い手と売り手を含む参加者のセット全体にとって最も有益なものです（たとえこの利益がマイナスであっても）。 もともと相場は利益を最大化するために作られたもので、買う側も売る側も納得できる最適な均衡価格を決めるために作られたものです。 この恩恵は、特定の資産とは関係がない場合があります。 例えば、投資ファンドは資産を緊急売りする必要があります。 この操作を実行することで、別の資産を買いしたり、顧客に利益を出すことができるようになるなど、他にも何らかの利益を得ることができるかもしれないので、たとえ損失が出たとしても、実行する準備ができています。 この恩恵の性質が異なる場合があります。 このような場合、価格は、各参加者の利益の各再定義の役割です。
  4. それ自体の役割としての価格。 明らかに、すべての価格の変更は、相場参加者の利益の変化につながります。 価格が変わらなくても利益は変わりますが、価格が変わると参加者の利益が変わります。 価格の変化を正確に説明するものではありませんが、理想のモデルに大まかに近づけることができ、将来的には結果に大きな影響を与えないような想定をすることができるようになります。 基本的には価格変動でトレードをします。 配当戦略を選択（価格無視）しても、配当金の支払いが最終的には価格の変動につながります。 この場合、値動きはチャートを左にシフトさせるための信号です。 価格が1ポイント動いたときだけ価格が変わることを登録します。 好みのスケールに応じて任意のステップを使用することができます：nポイント上または下に移動するたびに価格値を登録することができます。 

価格は利益の再定義の機能であると述べ、第３の選択肢が最も可能性が高いと考えています。 しかし、このシリーズを離散化するためには、各参加者の利益を計算することは不可能です。 前者の2つのケースでは、為替相場における売買オペレーションと非売買オペレーションを計算することは可能ですが、難しいこともあります。 例えば、資産は2つ以上の異なるトレード所でトレードすることができます。 先物やオプションのように資産のデリバティブが存在する場合、間接的に資産と結びついている操作を計算する必要があるのでしょうか。 この質問には、別途大規模な研究が必要です。 いずれにしても、4つのケースはいずれも間接的に関係します。 第４の選択肢は、価格がそれ自体の関数である場合、大まかなモデルであると仮定すれば、さらに研究を進めることができます。

資産価格の変動率は、トレード数に依存します。 売買オペが多ければ多いほど、価格変動の頻度が高くなるので、直接的な相関関係があるということになります。 したがって、相場参加者が多ければ、トレード操作が多くなり、参加者ごとの利益の再定義がより頻繁に行われることになります。 そのため、どの参加者もより頻繁に価格を再定義しようとし、トレード回数の増加につながり、資産価格の変化の頻度が高くなります。

時間間隔とランダム成分による価格系列離散化の特徴

ラフモデルによれば、価格はそれ自体の関数であり、価格が一定のポイント数だけ変化した場合にのみ、価格を離散化します。 仮にこれが全く正しくなくても、この前提があれば、最終的な結果に影響を与えることなく、トピックをより深く理解することができます。 さらに、利益を出すためには、価格が変わったことを知る必要があります。 さらに、パターンを検索するためには、どのように変化してきたかを知る必要があります。 

1ポイントの価格変化（ここでは1ポイントが最小の価格変化）は、1ステップに相当します。 このような系列を時間的に離散化するとどうなるかを見てみましょう。 明らかに、時間単位で価格が通過するポイントの数は、トレードの動きに依存します。 トレード活動（トレードを行った回数）が多いほど、最終的には価格のステップ数が多くなります。 トレード活動は値動きとは直接関係ありませんが、値動きはトレード活動に依存しており、トレード活動が高ければ高いほど値動きは大きくなります。 依存関係は間接的ですが、相関関係は正です。 1ステップが10ポイントだとします。 一時間ローソク足は例のものを使用します。 下の2つの図は、価格をボックとして表したものです。 ブロックはレンコ足に似ていますが、少し違う原理で作られています。 クラシックローソク足の高値・安値を利用して、ブロック形成時間の高値・安値を表示します。 ローソク足と同様に、ブロックにも4つの特徴があります。「始値」「高値」「安値」「終値」です。 ローソク足との差は、始値と終値の距離が常に固定されており、ポイントで表現されていることです。 価格が垂直にNポイントを上に通過すると、ブロックは閉じます。 例えば、ブロックサイズは１０点とします。 価格が10ポイント上下に動くと、ブロックが閉じて新しいブロックが始まります。

ロウソク足で25ブロック

ロウソク足で53ブロック

図4.

1ブロックがN点の1ステップに等しい場合、1時間ローソク足の中で何が起こるかを見てみましょう。 図4は、1時間足ローソク足の形成中に起こった動きを示します。 上図では、1時間で10ブロックを縦に通過しました。 ブロックサイズを10ポイントとすると、ローソク足サイズは100ポイントとなります。 全体では、ローソク足形成時間全体で25ブロック形成されており、25ステップに相当します。 別の例として下の図のように、ローソク足形成時間中に0ブロックまたは0ポイントの値動きをした例があります。 合計すると、価格形成時間内に40ブロック、つまり40ステップで価格が動いたことになります。 では、このようなローソク足で構成されたチャートを見てみましょう。 図５に示します。 ローソク足は1時間に1度閉じ、価格シリーズは間違いなく時間の関数ではありません。 簡略化すると、通過したポイント数と正の相関関係を持つトレード操作の関数です。 ポイントをブロックに換算したので、ブロック数はトレード数と正の相関があります。 実際には、各ローソク足は（1時間と仮定して）ブロックの乱数、またはステップNポイントごとに持っていることが判明しました。 さらに、これがなぜ重要なのかを見ていきましょう。 ローソク足は、相場で行われているプロセスそれにも関わらず、特定の時間後に閉じるためです。 時間は、価格に関連するプロセスとはほとんど関係のない外部パラメータです。 つまり、1時間が経過したから価格が変わるのではなく、何らかの理由で価格が変わるのであって、そのうちの1つが経過時間であってもよいのです。

ロウソク足

図5.

トレード活動は時間の経過とともに大きく変化することがあります。 さらに、異なるトレード商品のトレード活動は異なります。 アルゴトレードの発展は、時間単位あたりの操作数の増加とトレード回転率の増加をもたらします。つまり、2010年と2020年の間のローソク足の直接比較は、それぞれに異なる操作数が含まれているため、間違っていることになります。

さて、もう一つシンプル化して、ランダムウォークの相場を見てみましょう。 もちろん、相場は行き当たりばったりのランダムウォークではありませんが、こうするとわかりやすくなります。 その後、現実の相場に戻ります。

中心極限定理は、ほぼ同じ尺度を持つ（いずれの項も支配しないか、または和に決定的な寄与をしない）弱く従属性のあるランダム変数の十分に大きな数の和が、ほぼ正規分布であることを述べています。 この定理から、今回のケースに適用すると、平均して、ランダムプロセスはNステップの間、ステップ数の平方根にほぼ垂直に比例する距離を通過すると結論づけることができます。 1ブロックが1段だとすると、100ブロックでは100^0.5=10ブロック、平均して縦に価格が通ることになります。 孤立した場合は多かれ少なかれありますが、平均的には乱数系列は正規分布のルールに従います。 このランダムシリーズのステップ数は、時間の経過とともに大きく変化することがある価格活動によって生成されるため、時間によって若干異なります。

したがって、このようなランダムな価格シリーズの1時間足のローソク足の大きさは、平均してN^0.5に比例します。 つまり、1時間足のローソク足のサイズが正規分布の法則の対象になるということです。 さらに、ローソク足の中に乱数のステップが存在することを考慮すると、ローソク足の大きさも正規分布の法則に従うと結論づけることができます。 つまり、ローソク足のサイズは、このローソク足内のステップ数の平方根です。 この主張を確認してみましょう。 今回は、2020.05.18から2020.07.03までの期間、GBPUSDの1分足ローソク足50,000本を使ってみます。

  1. 1 分間のローソク足の平均サイズのモジュロ値を見つけましょう - ステップサイズになります。 これを行うには、次のローソク足の終値から前のローソク足の終値を差し引き、モジュロ値を取ります。 GBPUSDの1分足ローソク足の平均サイズ＝0.000170を取得しました。
  2. では、同じ期間の1時間ローソク足の平均サイズを求めてみましょう（1時間ローソク足には1分足のローソク足が60本入っています）。 これを行うには、次の1時間ローソク足の終値から前の1時間ローソク足の終値を差し引き、モデューロ値を取ります。 GBPUSDの1時間ローソク足の平均サイズを取得しました＝0.001117
  3. ここで、価格系列がランダムウォークだと仮定した場合、1時間あたりの価格が平均してどれくらい通過するかを求めてみましょう。 これを求めるには、1分足のローソク足の平均サイズにステップ数の平方根をかけて、平均ステップサイズを乗算します。 60 => 0.000170*(60^0.5) = 0.001315.となります。 1時間ローソク足の大きさは、元の系列が正規分布の法則に従っている場合、この平均的な大きさになるトレンドがあります。
  4. 実物ローソク足とランダムウォークローソク足の平均サイズ（実0.001117）≒（理論0.001315）を比較してみましょう。 その差はわずか0.0002. ローソク足のサイズが正規分布の法則に従うという仮定が真であり、実際のシンボル相場のデータによって確認されていると結論付けることができます。 0.0002の差は有意ではありません。

さらに、得られた1時間ローソク足を用いて、正規分布則に従った振幅を持つ価格系列の特定のセグメントのシーケンスを実際に組み合わせて分析します。 当然のことながら、より高い時間枠に移動すると、すべて同じローソク足が得られ、その大きさは段数の平方根に比例します。 系列が正しく離散化されていない場合、結果としてランダムな系列が出力されます。 実際には、時間離散化を利用して、価格系列をランダムな系列に変換します。 まあ、相場はランダムなシーケンスではなく、時間に間接的に依存しているので、時間離散化されたシーケンスは、まだパターンを持つことができますが、そのようなシリーズを分析し、パターンを識別することははるかに困難になります。 いわゆる「ノイズ」と価格シリーズの非定常性につながる時間的離散化である-よく考察されるが、ノイズがどこから来るのかは誰も説明していません。 さて、ノイズとは、信号が離散化されたときに現れる離散化ノイズだけでなく、自体が離散的な価格系列の離散化パラメータが正しくないために現れるランダム成分も含まれています。

1時間のローソク足で得られた結果が偶然の偶然の一致ではないことを確認するために、日のローソク足についても同じ処理を繰り返してみましょう。 一日に24時間あります。 通貨ペアは24時間トレードされているので、1日のローソク足には1440本の1分足ローソク足が含まれていると仮定してみましょう。 H1で使用したのと同じ1分間隔のデータをサンプリングしてみましょう。 今回は便宜上、該当データを表形式で表現します。

M1ローソク足の平均サイズ
H1ローソク足の平均サイズ
次の値で計算されたH1ローソク足の理論的な大きさ
。 0.000117*(60^0.5)
D1ローソク足の平均実寸
D1ローソク足の理論サイズは、
のように計算されます。 0.00017*(1440^0.5)
0.000170
 0.001117
 0.001315
 0.006547
 0.006442

ご覧のように、日足ローソク足の実質平均サイズは、実際の相場ではなく、ランダムウォークであれば、理論的に予測されたサイズとあまり変わらないでしょう。 過去のデータと計算結果をまとめたExcelファイルを以下に添付します。

上位のタイムフレームのローソク足の平均サイズを算出するために、1分足のタイムフレームデータを使用しました。 しかし、もし、より低い枠からティックデータを取得した場合はどうなるのでしょうか - 異なる結果をもたらすでしょうか？ 今やろうとしていること

  1. 同期間の1分足ローソク足のティックボリュームデータ（実際の口座から）を取り、1分足ローソク足の平均ティック数を計算してみましょう-平均は1分足59.99ティックです。 
  2. ティックデータを読み込んで平均ティックサイズを求めると、0.000014378になります。 
  3. 1分足ローソク足の理論サイズを(59.99^0.5)*0.00014378=0.000111363として計算します。
  4. 1時間足のローソク足の理論的なサイズを計算する ((59.99*60)^0.5)* 0.000014378= 0.00086
平均ティックサイズ 実質M1ローソク足の平均サイズ M1ローソク足の理論サイズは、(59.99^0.5)*0.000014378として計算されます。 H1ローソク足の平均サイズ
H1ローソク足の理論サイズの計算 ((59.99*60)^0.5)*0.000014378
0.000014378 0.00017 0.000111363 0.001117 0.00086

ご覧のように、M1とH1のローソク足の平均サイズは、価格シリーズがランダムウォークであれば持っているであろう理論上のサイズとあまり差がありません。 このように、何らかの理由で価格シリーズがランダムウォークのように振る舞うのは、時間間隔の離散化が正しくないためではないかと結論づけられます。

価格系列の増加分の分布密度

量的評価により、価格シリーズのローソク足の大きさがランダムウォークのローソク足の大きさにどのように対応しているかを大まかに見積もることができました。 価格系列の増分の分布密度をプロットすると、ランダムウォークの増分の分布密度との類似点や相違点を視覚的に評価することができ、より興味深いです。

分析の重要な部分はデータの準備です。 インクリメント密度は、60分（1時間）で価格が動くポイント数、つまり60段階で計算されます。 ここでは、1分足ローソク足の平均サイズと歩数（1分足ローソク足の1分足の数）を知る必要があります。 すでに1分間のローソク足の平均サイズを計算しました - これは、0.000170に等しいです。 1分足のローソク足の本数は60本です。 つまり、価格は1時間に60歩、1歩ごとに0.000170歩を稼ぐことができるということです。 このように、極端なケースとしては、起点から60ポイント上昇した場合と60ポイント下降した場合のどちらかが継続的に値動きすることになります。 そこで、-0.00017*60=-0.0102と0.00017*60=0.0102の範囲で分布密度を推定することになります。 つまり、価格が0.00017ステップで上昇するだけであれば、60ステップ（1時間）で最大0.0102に到達することがわかっています。 さらに、60ステップでは、価格は離散的なレベル0、0.00034、0.00068、0.00102 ...しか取ることができません。0.0102と同様の負の値を取ることができます。 図6は、価格が正確にレベルを取る理由を示します。

探査距離

図6.

ある離散関数がゼロ点から始まり、そのステップが1に等しく、6ステップを踏む場合、最終的には垂直方向に6、4、2、または0のセグメントを移動することができ、2倍のステップサイズを持つ離散値しか取ることができません。 今回のケースも同様です：1分足のローソク足の平均サイズが0.00017であれば、価格はローソク足のサイズの2倍の間隔で離散的なレベルを取ることができます。 現実にローソク足は0.00017に限らず、大きさが違うこともありますから、中間値を取ることもあります。 したがって、分析に、2倍の平均的なローソク足のサイズで、間隔内に落ちるイベントの数をカウントします。 価格系列の結果の分布の差を求めるために、ランダムウォークの分布と比較します。 ランダムウォークの特徴は、次のステップごとの方向転換ストキャスティクスが５０％であり、メモリがないことです。 図7は、価格系列のストキャスティクス密度分布を黒で、ランダムウォークのストキャスティクス密度分布を赤で示したものです。

図7.

図７から、価格系列ストキャスティクス分布の密度がランダムウォークストキャスティクス分布の密度とほぼ一致していることがわかります。 価格系列ストキャスティクス分布の密度は、ランダムウォーク分布の密度と比較して、天井がやや高く、幅がやや狭く、やや右にずれています。 価格シリーズの次のステップの各段階での反転のストキャスティクスが50％よりもやや高いことを示唆しており、小さな上昇トレンドはあるが、差は大きくはない。 この偏差で利益を得ることは、ほど難しいことではないように思えるかもしれませんが、ついては次回の記事で考えてみます。 ここでは、十分に大きなサンプルを持つ理想的なランダム変数を扱います。 ランダムウォークのストキャスティクス密度分布のチャートを表を用いてプロットし、その一部を図８に示します。

参照表

図8

このストキャスティクス密度分布チャートは、ローソク足の大きさ（この場合はH1ローソク足）が、価格系列がランダムウォークである場合のローソク足の大きさに傾いているという以前の結論を確認させてくれます。 また、この事実を視覚的に、より正確に評価することができます。

この記事で言及されているすべてのデータと計算は、以下のxlsxファイルに添付されています。

高値・安値 ボラティリティーエリア

注意深いトレーダーは、相場のローソク足は慣習的に「大」と「小」の大きさのローソク足のグループに分けられていることに気づくかもしれません（価格レートが高いエリアと価格レートのボラティリティが低いエリア）、つまりチャートがランダムウォークではなく、パターンがあることを意味します。 もし時間離散化が強い歪みをもたらすならば、この効果は観測されないでしょう。 しかし、この特徴は、ローソク足のサイズが、このローソク足の内部で実行されたトレード操作の回数に依存することで説明できます。 どのようにして確認できるのでしょうか？ ティックのあるチャートを見ることができます - "小さなローソク足 "の期間は、安値のティックのボリュームを伴い、"大きなローソク足 "の期間は、高値のティックのボリュームの期間と一緒に来ます。 1ティックを1ステップと仮定すると、「大きなローソク足」の期間中に価格はより多くのステップを行いますが、ローソク足のサイズは、ステップ数の平方根に平均ステップサイズを乗じた値に比例したままです（図9の例）。 ティックボリュームは、順番に、トレード活動と直接相関しています：トレード活動が高いほど、単位時間あたりのティック数が多くなります。 トレード相場は、ティックのボリュームが強くまたティックの数とトレード活動の強度の間の関係を示し、実際のボリュームと相関していることを見ることができ、実際のボリュームのヒストリーを提供します。

図9

このことは、時間離散化が結果として生じる価格系列の形に強い歪みをもたらし、価格分析を困難にすることを証明します。 この歪みが原因で、いわゆる「ナイトスキャルピング」と呼ばれるトレードシステムの別カテゴリーが登場してきました。 利益が出ないと言っているわけではありませんが、このようなシステムを開発する際には、価格シリーズの提示の特殊性を考慮し、以下の疑問に答えるための追加研究を行う必要があります。"このようなシステムは、このパターンに基づいているので、「トレンドが継続する確率よりも、反転する確率の方が高いのか」、「これらの統計的特性は利益を生み出すことができるのか」という疑問に答えるために、さらに研究を重ねる必要があります。 

代替価格系列離散化

上記の分析のシンプルな結論からすると、ティックデータは価格系列の離散化誤差を回避できるため、処理や分析に適していると考えられます。 もっと大きなスケールが必要な場合は、10ティックや100ティックのブロックを使うことになります。 しかし、ティック自体が離散化の手法でもあることが問題です。 この方法は広く使われていますが、価格は受信したティックの関数ではないため、プロセスに歪みを導入することができます。 価格は少なくとも実行されたトレードの関数であり、トレードは常にティックを生成するとは限りません。 トレード所のティックは、何らかの形で実際のトレードにつながっています。 しかし、外国為替相場では、どの会社もティック数をいくらでも用意していて、どれが正しいのかわかりづらいです。 したがって、価格がトレードの関数であると仮定しても、ティックは価格シリーズを歪め、誤差をもたらすランダムな成分を導入することが明らかになります。

適切な離散化の問題は、データ分析の重要な部分です。 例えば、図10は、ビットコインの対ドル価格の2つのチャートを示します。 上のチャートは通常の週足ローソク足チャートで、下のチャートはN点のブロックで離散化します。 同じ期間、同じブロック数/ロウソク足切であるが、離散化の方法が異なります。 同じ資産でもチャートが違うことがわかります。 ここで自然な疑問が生じます。"この2つの主張のどちらが正しいのか？"

BTCUSD

図10

私は価格シリーズの不一致の性質を考慮した表示が正しいという結論に至りました。 しかし、離散性の本質は不明のままなので、自分も他の相場参加者も損益の発生を反映できるような離散化手法を採用した方が「より正しい」ということになります。 そのため、収益が形成されているデータを元に分析した方が良いでしょう。 つまり、時間的な値動きを考慮するのではなく、価格がどれだけ動いたかだけを考慮するべきなのです。

時間離散化の代替として、価格が自体の関数であると仮定して、固定振幅離散化を行うことができます。 先ほど説明したブロックです。 N点のブロックは、価格がN点を上下に移動した後に決済されたとみなされます。 最善のアプローチではないかもしれませんが、生み出す利益や損失に影響するため、価格が何ポイントを通過したかということに興味があります。 さらに、価格が垂直方向にN点を通過した直後に、各参加者の利益が変化します。 価格が自体の関数であるモデルが最も現実のトレードに近いということです。 図１１は、固定サイズのブロックで離散化された正弦波を示します。 形状は失われていますが、周期や振幅などの主要な特徴は保存されています。

サインスモールブロック

図11

離散化パラメータが正しく設定されていない場合でも、振幅と周期の値は保持されます。 図１２は、ブロックサイズが大きすぎるとどうなるかの一例を示す図です。 ブロック内にある情報の一部が失われるため、精度が悪くなる（データ圧縮では避けられない）が、振幅や周期に関する情報は保存されています。 ブロックサイズが価格シリーズの振幅より大きい場合、ブロックは表示されません。 したがって、図２とは対照的に、不正確な離散化パラメータが選択された場合には、元の決定論的な信号はランダムな信号にはならない。

サインビッグブロック

図12

これより、時間離散化された価格系列によって導入されたランダム成分を除去することができ、ソース系列がどのパラメータの関数であるかが不明な場合には、そのような状況を解消することができます。 この方法は、時間離散化よりも優れた働きをし、1ポイントまでのスケーリング変化精度でチャートのスケーリングを便利に行うことができます。


結論