取引における相関の実用化

MetaTrader 5 — 統計と分析 | 13 5月 2019, 09:25

1 419

概論

あらゆる取引の本質は、何らかの形で、市場のさらなる発展を予測することが必要であり、潜在的な利益は予測の成功に強く依存するという事実に帰着します。価格変動の方向とスピードに基づいた取引アイデアの記事の冒頭で、私はあらゆる動きは方向、加速度、スピードという特性を持っているという考えを説明しました。これは外国為替やその他の市場での価格変動にも当てはまります。

どのような動きでも、動きの始まり、一定のスピード、慣性、そして終わりという兆候があります。可能な限り早く動きの開始をキャッチし、市場に参入するだけでなく、その終了を明確に識別する取引戦略が成功戦略となります。しかし、絶対的な確率でエントリーポイントとイグジットポイントを決定することはできません。ここでは、私達は有益なチャンスと可能性についてだけいうことができます。したがって、この記事では、確率論のツールの1つである相関関係について検討します。これを金融市場の枠組みに適用します。

相関の概念

相関関係とは、2つ以上の確率変数（またはある程度許容できる精度でそのように考えることができる値）間の統計的関係です。この時、これらの値の1つまたはいくつかの値の変化は、別または他の値の系統的な変化を伴います。2つの確率変数の相関の数学的尺度が相関係数です。ある確率変数の変化が別の確率変数の規則的な変化をもたらさず、この確率変数の別の統計的特性の変化をもたらす場合、そのような関係は統計的ではあるが相関とは見なされません。

相関係数は-1から+1までの値を取ります。相関値が1に近いほど、研究された値の間の相互関係はより高いです。そして、値が1になる傾向がある場合、その関係は正と見なされ、-1は負と見なされます。正の相関プロセスでは、変数の1つの増加は2番目の変数の増加をもたらし、負の相関の場合は1つの値の増加は2番目の値の減少をもたらします。

言い換えれば、相関関係は、利用可能なデータに基づいて、ある変数の第2の変数への依存関係を判断するのに役立ちます。この関連性は金融市場取引においてどのような助けとなるでしょうか？

図1と下降トレンドの領域を見てみましょう。

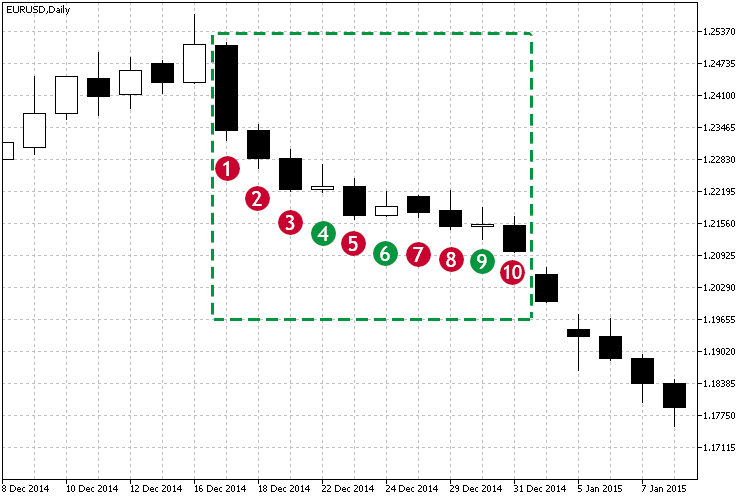
図1.下降トレンドの例

ローソク足1から始まる印の付いた領域からわかるように、ほとんどの終値は始値より低く、各終値は前の終値より低くなっています。したがって、価格は下落しています。視覚的には、これは減少傾向です。しかし、依存関係が強いかどうかをどのように理解したらよいでしょうか？さらに、この傾向は完全ではなく、ローソクの4、6、および9で小さい上昇がありました。関連性はどのように役立つでしょうか？この場合、相関係数は現在の変化の強さを示します。相関係数の経時的観察に基づいて、以下の結論を引き出すことができます。

現在のトレンドの強さ。現在値への直接相関。
トレンドの期間。選択したしきい値の時間内の観測。たとえば、しきい値が0.75を超えていて、3〜4ローソクの範囲内ではない。

相関の種類

調べた変数間の関係を判断する、相関のタイプは次のようになります。

線形および非線形。線形相関とは、ある値が増減し、それに応じて2番目の値が変化する相関を指します。非線形相関では、1つの変数が変化しても別の変数は直接変化しませんが、他の関数で表すことができます。
正と負の相関は依存の性質と呼ばれます。正の相関の場合、一方の変数の増加は他方の変数の増加につながります。

図1に線形負相関の例を示します。次に、2つの変数の相互依存関係を判断するためのさまざまな種類の計算と方法を検討します。

線形相関係数（ピアソン相関係数）

この計算により、変数間の直接の関係を変数の絶対値に基づいて決定することができます。数値間の関係が線形の場合、ピアソン係数が表示されるように計算が整理されています。金融市場の文脈では、この関係は時間がどちらかの方向に流れることを意味します。ピアソン相関係数は次のように計算されます。

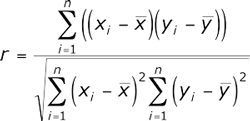
ここで、図1に示すデータのピアソン相関係数を計算し、終値の経時的依存性を測定しましょう。これを行うために、フォームにデータを入力しましょう。

終値	ローソク番号
1,23406	1
1,22856	2
1,22224	3
1,22285	4
1,21721	5
1,21891	6
1,21773	7
1,21500	8
1,21546	9
1,20995	10

全体の計算は次の図に示されています。

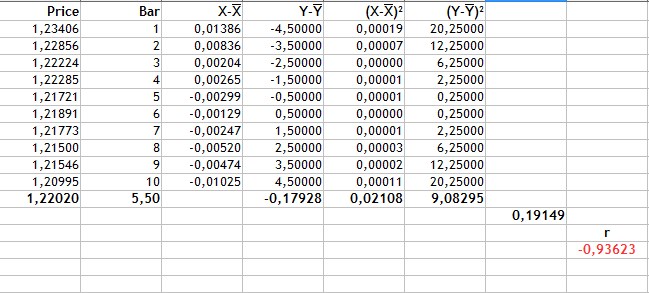
図2. ピアソン相関係数の計算

計算の順序は以下のとおりです。

価格とローソク足数の平均値を計算します。これは1.22020と5.5となります。
変数の種類ごとに平均からの偏差がわかります（列3〜4）。
値-0.17928 は、価格偏差と式の分子であるローソク足数の積です。これは式の分子です。
5列目と6列目は偏差の2乗です。0.02108と9.08295の値は偏差の二乗和の平方根です。
式の分母または偏差の二乗和の積は、0.19149です。
この場合、ピアソンの相関係数は-0.93623となります。

これらの結果は、強い線形の負の依存性があることを示しています。

スピアマンの順位相関係数

この計算方法では、確率変数間に線形関係を確立できます。評価は分析要素の値ではなく、対応するレベルに基づいています。その値もスピアマン係数と同様に-1から1まで変化します。絶対値は相互接続の近さを表し、符号は2つの要素間のこの接続の方向を表します。次の式を使って計算されます。

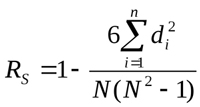
Diは、調査対象の機能のグレード差です。図1に示すデータレベルの相関を計算する例を考えて、新しい表に値を入力します。

終値	ローソク番号	終値ランク	ローソク足数ランク
1,23406	1	10	1
1,22856	2	9	2
1,22224	3	7	3
1,22285	4	8	4
1,21721	5	4	5
1,21891	6	6	6
1,21773	7	5	7
1,21500	8	2	8
1,21546	9	3	9
1,20995	10	1	10

表からわかるように、終値の値をランク付けし、ランク1を最低値に割り当てます。この式を用いて、調べた特性のDランクの差を計算し、得られた値を式に代入します。

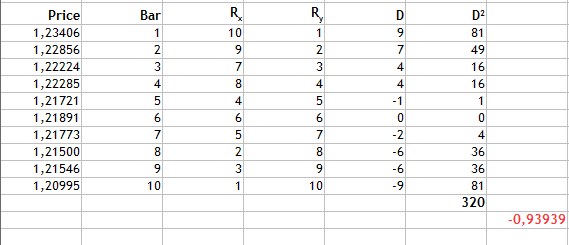
図3. スピアマン順位相関係数の計算

図3からわかるように、ランクの差を見つけ、それから結果の差の2乗の合計を求めると320となります。得られた値を式に代入すると、結果は-0.93939となります。

得られた相関係数の値に基づいて、同じ結論を得ることができます。これは、強い線形の負の関係です。この場合、関係の近さはピアソンの相関係数に匹敵することがわかったが、この方法の計算には1つの欠点があるという事実を考慮に入れる必要があります。この計算方法は１つの欠点があり、比較できない差の値は、同じランクの差の値に対応します。たとえば、価格の変動はかなり小さく、1000分の1だけ異なりますが、価格ランクの値は均一ではありませんが、バーランクは同等です。したがって、この計算方法はこの場合に適しています。

ケンドール順位相関係数

スピアマンの係数と同様に、ケンドール順位相関係数は、確率変数間の線形関係の尺度です。計算方法は異なりますが、分析要素の値の順序は似ています。ここでは、以下の係数計算式を使用します。

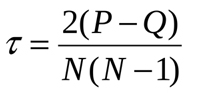
ここで、Pは一致の合計、Qは反転の合計です。上記の意味を理解するために、図1の例を見てみましょう。まず、表のデータを次のようにソートしましょう。

終値	ローソク番号	終値ランク	ローソク足数ランク
1,20995	10	1	10
1,21500	8	2	8
1,21546	9	3	9
1,21721	5	4	5
1,21773	7	5	7
1,21891	6	6	6
1,22224	3	7	3
1,22285	4	8	4
1,22856	2	9	2
1,23406	1	10	1

ご覧のとおり、表は終値のランク列でソートされています。次に、ローソク番号のRank列の最初の行から始めて、現在のランクより上のランク数を決定します。最初の値は10なので、それを確認すると、それ以上のランクはありません。次に、8を見て、より高いレベルの9を見つけます。これらはPと一致します。

それから私達はより低いランクを計算します。10は最高のものであるため、10の場合9つの低いランクが、8の場合、5、7、6、3、4、2、1と7つ低いランクがあることになります。これらはQ反転です結果の値を表に追加して係数を計算しましょう。

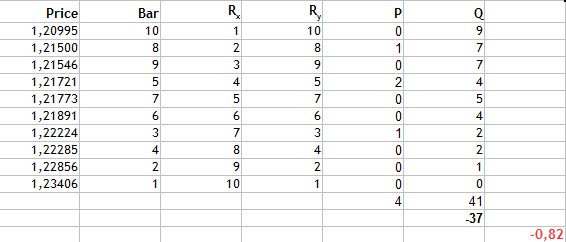
図4. ケンドール順位相関係数の計算

次に、結果のマッチング値と反転値を合計します。それらの違いは-37に等しく、この値を式に挿入すると、ケンドール係数は-0.82になります。これはもう一つの強い負の相関ですが、結果は、絶対値がより小さいので、この方法が最初の2つの方法よりも選択的であることを示しています。

フェヒナー符号相関係数

この方法は、平均値の偏差の方向における一貫性の程度の評価、およびその値に対応する偏差の符号の計算に基づいています。計算式はとても簡単です。

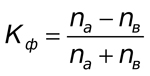
Naは符号で表される一致数、Nbは一致数です。より明確に理解するために、図1から、この例の相関係数も計算します。

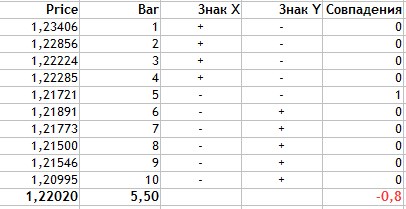
図5. フェヒナーの相関係数の計算

計算を詳しく見てみましょう。

2つの方法でデータの平均値を見つけます。これは、価格が1.2202、ローソク足数が5.5です。
記号Xの列に、Price属性の現在の値が平均値を上回る場合はプラスを、小さい場合はマイナスを付けます。
同様にローソク足の数値についても同じことを行います。
次に、2つの特性（価格とローソク足の数）の一致する符号を計算します。
表から分かるように、値は一度だけ一致し、したがってNa = 1であり、Nb = 9です。
得られた値を式に代入します。

ご覧のとおり、Fechner相関係数の計算方法は非常に簡単で、この値は-0.8となります。これは、前の方法と同様に、終値がローソクの数または時間内に強い線形の負の相関があることを示しています。

指標の実装

それでは、MQL5を使用して相関を計算するためのすべての方法を実装しましょう。

ピアソン相関係数

この計算方法は優れた公式を持っているので、計算ステップのより良い可視化と理解のために、これを分子と分母の計算の2つの計算ステップに分けました。

//+------------------------------------------------------------------+
//| 式の分子を計算する                                                  |
//+------------------------------------------------------------------+
double Numerator(double &Ranks[],int N)
  {
//----
   double Y[],dx[],dy[],mx=0.0,my=0.0,sum=0.0,sm=0.0;
   ArrayResize(Y,N);
   ArrayResize(dx,N);
   ArrayResize(dy,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0;j<N;j++)
     {
      dx[j]=Y[j]-mx;
      dy[j]=Ranks[j]-my;
      sm+=dx[j]*dy[j];
     }
   return sm;
  }
//+------------------------------------------------------------------+
//| 式の分母を計算する                                                  |
//+------------------------------------------------------------------+
double Denominator(double &Ranks[],int N)
  {
//----
   double Y[],dx2[],dy2[],mx=0.0,my=0.0,sum=0.0,smx2=0.0,smy2=0.0;
   ArrayResize(Y,N);
   ArrayResize(dx2,N);
   ArrayResize(dy2,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0;j<N;j++)
     {
      dx2[j]=MathPow(Y[j]-mx,2);
      dy2[j]=MathPow(Ranks[j]-my,2);
      smx2+=dx2[j];
      smy2+=dy2[j];
     }
   return(MathSqrt(smx2*smy2));
  }

指標の可視化を計算するための最終的な計算方法とロジックは以下のとおりです。

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // number of bars in history at the current tick
                const int prev_calculated,// number of bars calculated at previous call
                const int begin,          // bars reliable counting beginning index
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=PearsonCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }

//+------------------------------------------------------------------+
//| ピアソン相関係数の計算                                               |
//+------------------------------------------------------------------+
double PearsonCalc(double &Ranks[],int N)
  {
   double ch,zn;
   ch=Numerator(Ranks,N);
   zn=Denominator(Ranks,N);
   return (ch/zn);
  }

スピアマンの順位相関係数

この計算方法に基づく指標については、ここで利用可能な既存の解決策のいくつかを使用しました。

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // number of bars in history at the current tick
                const int prev_calculated,// number of bars calculated at previous call
                const int begin,          // bars reliable counting beginning index
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=limit; i>=0; i--)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=int(price[i+k]*multiply);

      RankPrices(TrueRanks,PriceInt);
      ExtLineBuffer[i]=SpearmanCalc(R2,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| スピアマン相関係数の計算　　　　　　　　　                             |
//+------------------------------------------------------------------+
double SpearmanCalc(double &Ranks[],int N)
  {
//----
   double sumd2=0.0;

   for(int i=0; i<N; i++)
      sumd2+=MathPow(Ranks[i]-i-1,2);

   return(1-6*sumd2/(N*(MathPow(N,2)-1)));
  }

ケンドール順位相関係数

このメソッドの計算には、mql5自体の内部予約を使用します。つまり、組み込みの統計ライブラリを使用して計算に適用します。

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // number of bars in history at the current tick
                const int prev_calculated,// number of bars calculated at previous call
                const int begin,          // bars reliable counting beginning index
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;

      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=KendallCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| ケンドール相関係数の計算                                             |
//+------------------------------------------------------------------+
double KendallCalc(double &Ranks[],int N)
  {
   double Y[],t;
   ArrayResize(Y,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }
   MathCorrelationKendall(Ranks,Y,t);
   return (t);
  }
//+------------------------------------------------------------------+

フェヒナー符号相関係数

この計算方法は、平均からの偏差一致符号の計算に基づいています。そして、一致する符号がカウントされます。

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // number of bars in history at the current tick
                const int prev_calculated,// number of bars calculated at previous call
                const int begin,          // bars reliable counting beginning index
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);
   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=FechnerCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| フェヒナーの相関係数の計算                                           |
//+------------------------------------------------------------------+
double FechnerCalc(double &Ranks[],int N)
  {
   double Y[],res,mx,my,sum=0.0,markx[],marky[];
   double Na=0.0,Nb=0.0;
   ArrayResize(Y,N);
   ArrayResize(markx,N);
   ArrayResize(marky,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0; j<N; j++)
     {
      markx[j]=(Y[j]>mx)?1:-1;
      marky[j]=(Ranks[j]>my)?1:-1;
      if(markx[j]==marky[j])
         Na++;
      else
         Nb++;
     }

   res=(Na-Nb)/(Na+Nb);
   return (res);
  }

図6は、ローソクの終値と時間の相関関係を計算するための4つの方法すべての操作を示しています。すべての指標は10の期間を持っているので、明らかに同じ条件でそれらの仕事を見ることができます。

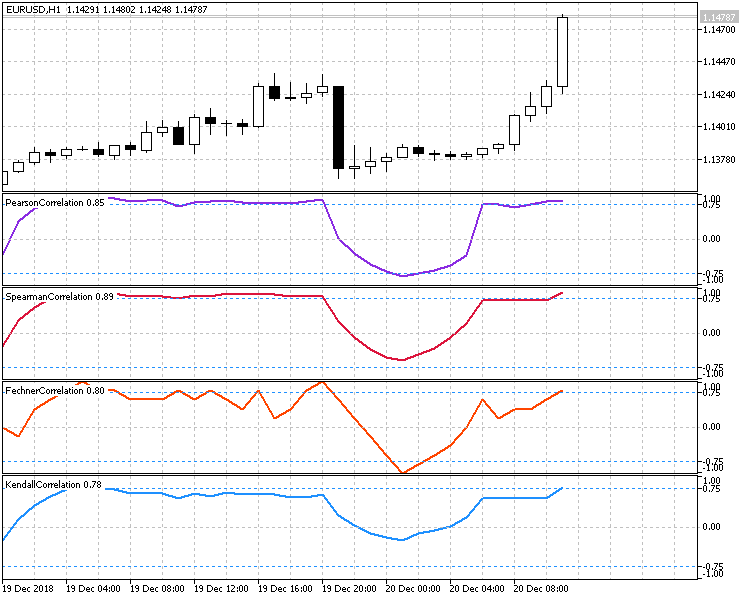
図6. 全ての計算方法の比較図

相関をベースにした取引システム

相関関係に基づいて取引戦略を作成するときは、インディケータと計算方法の詳細を慎重に検討し、市場に参入するために起こりうる悪条件または危険な状況を特定する必要があります。

インディケータは遅れを取るので、大きな期間の使用はほとんどすべてのインディケータで推奨されません。また急激な逆転の場合には弱い相関を示すことがあります。インディケータが完了した逆方向運動の値を考慮に入れるためです。

インディケータは現在の価格ではなく、ある期間にわたる複数の値の合計を分析するので、現在の相関値は絶対推定値と見なされるべきではありませんが、関連するダイナミクスは分析されるべきです。これは相関係数の現在および以前の値を利用する振動指標を使用して達成することができます。

したがって、相関係数のオシレーターの動作の性質に基づいて戦略を構築することにしました。つまり、いくつかの事前に確立されたレベルを突破する時です。次の2つの選択肢があります。

係数の低下。正の係数が定義済みのキーレベルを下回り、突破したときに売り、負の係数が成長し、正の領域に設定された対称レベルを突破するときに買います。
係数の増加。係数が負の領域に入り、事前定義されたレベルを突破したときに売り、係数が大きくなり対称的な正のレベルを突破したときに買います。

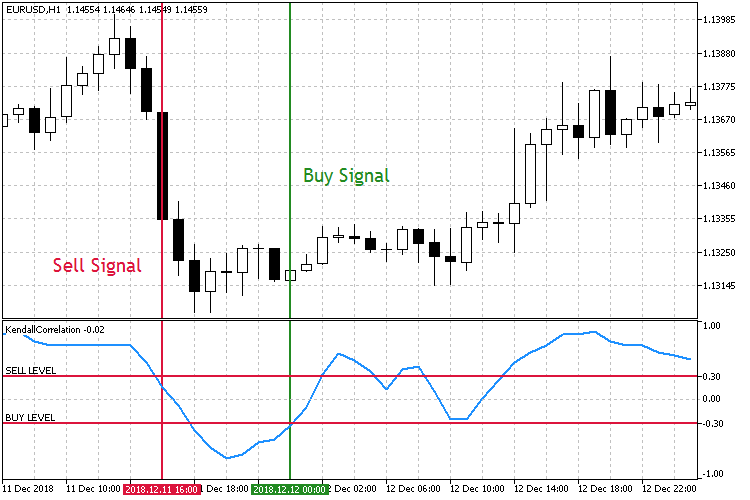
わかりやすくするために、潜在的なエントリポイントは、以下のスクリーンショットに表示します。

図7. 相関係数の低下に基づく取引

スクリーンショットでわかるように、相関係数Sell Level 0.3とBuy Level -0.3の2つの確立された対称レベルがあります。売りレベルが上から下に割れている場合は売り注文を開き、買いレベルが壊れている場合は下から上に買い注文を出します。

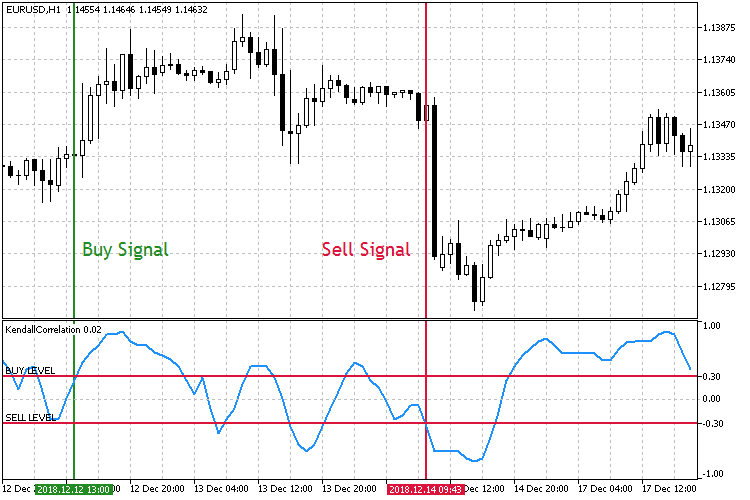
図8. 相関係数の増加に基づく取引

図８に示す第２の取引モードでは、主要市場参入レベルは反対です。今度は、買いレベルが上向きになると、買い注文を開き、売りレベルが下向きになると売り注文を開きます。

エキスパートアドバイザーを実装するためには、上記の戦略を提供し、適切な相関計算方法を選択する必要があります。

//+------------------------------------------------------------------+
//| 動作モードの列挙                                                    |
//+------------------------------------------------------------------+
enum Strategy_type
  {
   DECREASE = 1,           //On Decrease       
   INCREASE                //On Increase
  };
//+------------------------------------------------------------------+
//| 相関を測定する方法の列挙                                             |
//+------------------------------------------------------------------+
enum Corr_method
  {
   PEARSON = 1,            //Pearson       
   SPEARMAN,               //Spearman
   KENDALL,                //Kendall
   FECHNER                 //Fechner
  };

入力パラメータでは、アドバイザのパラメータに加えて、計算方法、戦略タイプ、キーレベル、および作業時間枠のカスタム選択の選択を追加します。

//+------------------------------------------------------------------+
// | エキスパートアドバイザの入力パラメータ                                 |
//+------------------------------------------------------------------+
input    string               Inp_EaComment="Correlation Strategy";        //EA Comment
input    double               Inp_Lot=0.01;                                //Lot
input    MarginMode           Inp_MMode=LOT;                               //MM

//--- 相関の計算方法と戦略の種類の選択　
input    Corr_method          Inp_Corr_method=1;                           //Correlation Method
input    Strategy_type        Inp_Strategy_type=1;                         //Strategy type

//--- エキスパートアドバイザのパラメータ
input    string               Inp_Str_label="===EA parameters===";         //Label
input    int                  Inp_MagicNum=1111;                           //Magic number
input    int                  Inp_StopLoss=40;                             //Stop Loss(points)
input    int                  Inp_TakeProfit=60;                           //Take Profit(points)
//--- インディケータのパラメータ 
input    int                  Inp_RangeN=10;                               //Rang Calculation
input    double               Inp_KeyLevel=0.2;                            //Key Level    
input    ENUM_TIMEFRAMES      Inp_Timeframe=PERIOD_CURRENT;                //Working Timeframe

エキスパートアドバイザの初期化中に、正当性のチェック、すなわち0から1の範囲でキーレベルを見つけるためのキーレベルのチェックを追加します。キーレベルについては、絶対値を使用します。

//--- キーレベルの正当性のチェック
   if(Inp_KeyLevel>1 || Inp_KeyLevel<0)
     {
      Print(Inp_EaComment,": Incorrect key level!");
      return(INIT_FAILED);
     }

次に、設定で選択した相関計算方法を選択します。

//--- 
   switch(Inp_Corr_method)
     {
      case 1:
         ind_type="Correlation\\PearsonCorrelation";
         break;
      case 2:
         ind_type="Correlation\\SpearmanCorrelation";
         break;
      case 3:
         ind_type="Correlation\\KendallCorrelation";
         break;
      case 4:
         ind_type="Correlation\\FechnerCorrelation";
         break;
      default:
         break;
     }
//--- インディケータのハンドルの取得 
   InpInd_Handle=iCustom(Symbol(),Inp_Timeframe,ind_type,Inp_RangeN);
   if(InpInd_Handle==INVALID_HANDLE)
     {
      Print(Inp_EaComment,": Failed to get indicator handle");
      Print("Handle = ",InpInd_Handle,"  error = ",GetLastError());
      return(INIT_FAILED);
     }

その後、参入条件とエキスパートアドバイザのロジックを設定します。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
// --- 計算用データを取得する

   if(!GetIndValue())
      return;

   if(!Trade.IsOpenedByMagic(Inp_MagicNum))
     {
      // --- 買いシグナルで注文をする
      if(BuySignal())
         Trade.BuyPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment);
      // --- 売りシグナルで注文をする
      if(SellSignal())
         Trade.SellPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment);
     }
  }
//+------------------------------------------------------------------+
// | 買いの条件                                                        |
//+------------------------------------------------------------------+
bool BuySignal()
  {
   bool res=false;
   if(Inp_Strategy_type==1)
      res=(corr[1]>Inp_KeyLevel && corr[0]<Inp_KeyLevel)?true:false;
   else if(Inp_Strategy_type==2)
      res=(corr[0]>Inp_KeyLevel && corr[1]<Inp_KeyLevel)?true:false;
   return res;
  }
//+------------------------------------------------------------------+
// | 売りの条件                                                        |
//+------------------------------------------------------------------+
bool SellSignal()
  {
   bool res=false;
   if(Inp_Strategy_type==1)
      res=(corr[1]<-Inp_KeyLevel && corr[0]>-Inp_KeyLevel)?true:false;
   else if(Inp_Strategy_type==2)
      res=(corr[0]<-Inp_KeyLevel && corr[1]>-Inp_KeyLevel)?true:false;
   return res;
  }

テスト

出来上がったエキスパートアドバイザをテストするには、初期のプリセットを選択します。

インターバル：Uptrendモード用01/01/2015 - 01/12/2018。
通貨ペア：EURUSD。
取引モード：遅延なし。提示された戦略は高周波のものを参照していないので、遅延の影響は非常に小さいでしょう。
テスト：M1のOHLC。実際のティックでの予備テストは、このモードとほとんど区別がつかないことがわかりました。
初回デポジット：1000ドル。
レバレッジ：1：500。
サーバー：MetaQuotes-Demo。
引用符：5桁。

また、テストおよび最適化されるパラメータも決定します。

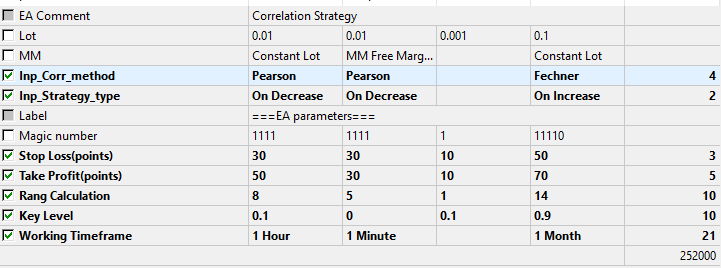
図9. 最適化されたパラメータ

最適化の結果をみると、どの計算方法および戦略の種類がより好ましいかが判明しました。テストと最適化の結果は次のようになります。

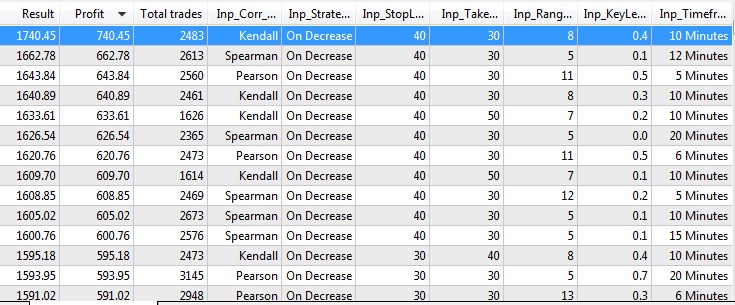
図10. テストと最適化の結果

最も良い最適化パラメータもテストします。

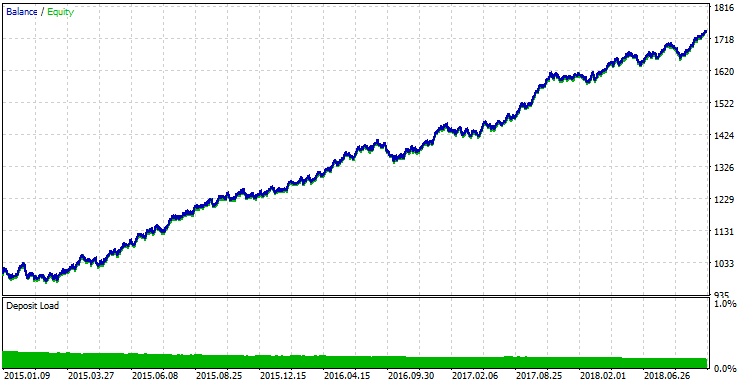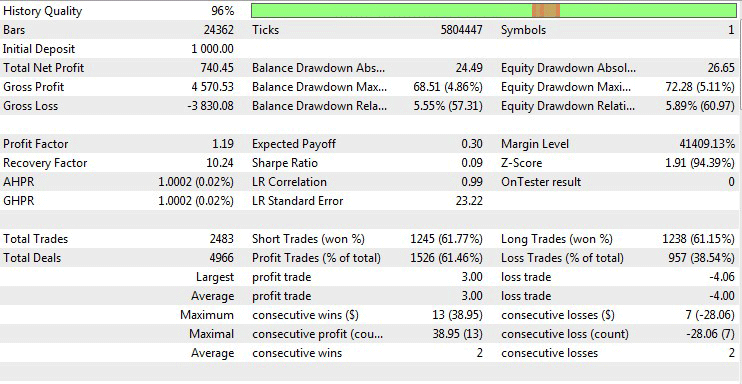
図11. 最良のパラメータをテストした結果

まとめ

得られた結果に基づいて、以下の観察を行うことができます。

On Decreaseモードの相関係数低下戦略で最良の結果が得られる。この結果は、係数が低下すると、オシレータが市場の動きにより早く反応するという事実によってのみ説明できます。上述のように、相関係数に基づくオシレータ、特に大きな周期のオシレータは著しく遅延しています。
フェヒナーによる相関係数の最も単純な計算が、上位20の結果の中にないことは驚くべきことです。この方法で一番良いのは99位です。
最良の結果は、小さなテイクプロフィットとストップロスの少ない期間で得られました。
選択された期間および事前に設定されたキーレベルに対する利益率の依存性は見つかりませんでしたが、特に、期間5の最適化範囲の下限が常に最良の結果となります。これは、相関ベースのインディケータが長い期間では大きな遅れを持ち、より悪い結果をもたらすことを示唆しています。

まとめ

この記事の最後に、リストアップしたすべてのファイルを含むアーカイブがフォルダごとにソートされて添付されています。正しく動作させるためには、MQL5フォルダを端末のルートディレクトリに保存する必要があります。

記事で使用されているプログラム：

#	名前	タイプ	説明
1	Correlation.mq5	EA	相関関係を計算する4つの方法とそれらに基づく2つの戦略を含むエキスパートアドバイザ。
2	Trade.mqh	ライブラリ	取引関数のクラス
3	FechnerCorrelation.mq5	インディケータ	フェヒナー相関係数計算指標
4	KendallCorrelation.mq5	インディケータ	ケンドール相関係数計算指標
5	PearsonCorrelation.mq5	インディケータ	ピアソン相関係数を計算するための指標
6	SpearmanCorrelation.mq5	インディケータ	スピアマンの相関係数指標

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/5481

添付されたファイル |

ZIPをダウンロード

MQL5.zip (807.75 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

MQLによるMQLの構文解析

本稿では、MQLに基づいたソースコードの解析に使用されるプリプロセッサ、スキャナ、パーサについて説明します。MQLの実装が添付されています。

トレード戦略の色の最適化

この記事では、ある実験をします。つまり、色の最適化の結果を行います。色は、赤、緑、青 (RGB) のレベルの3つのパラメータによって決まります。他にも3つのパラメータを使用した色分け方法があります。したがって、3つのテストパラメータを1つの色に変換して、値を視覚的に表すことができます。この記事を読んで、このような表現が役立つかどうかを確認してください。

MetaTrader5 での MATLAB 2018 計算関数の使用

2015年にMATLAB パッケージがアップグレードされた後、DLL ライブラリを作成する最新のメソッドを検討する必要がありました。この記事では、サンプルの予測インジケータを使用して、現代の64ビットバージョンのプラットフォームを使用して MetaTrader5 と MATLAB をリンクするメソッドを説明します。 MATLAB の接続シーケンス全体を考慮することにより、MQL5 開発者は速く高度な計算機能があるアプリケーションを作成し、«落とし穴»を回避することができます。

MetaTrader5 と Python インテグレーション: データの受信と送信

包括的なデータ処理には広範なツールが必要であり、多くの場合、1つのアプリケーションのサンドボックスの範疇を超えています。専門のプログラミング言語は、データ、統計、機械学習の処理と分析に使用されます。データ処理の主要なプログラミング言語の1つは Python です。この記事では、ソケットを使用して MetaTrader5 と Python を接続する方法、およびターミナル API を介してクオートを受け取る方法について説明します。

目次

概論

相関の概念

相関の種類

指標の実装

相関をベースにした取引システム

テスト

まとめ

まとめ

この著者による他の記事