ビンスによる資金管理 MQL5 ウィザードのモジュールとしての実装
Dmitrii Troshin | 9 4月, 2018
イントロダクション
金融相場が動いている間、絶えず利益を取るシステムを誰もが模索しています。 もちろん、そのシステムを安定させ、最小限のリスクを維持することを望んでいます。 このような戦略を見つけるために、最適なエントリーと決済を検索する別のトレーディングシステムが開発されています。 このようなシステムには、買いや売りの助言をするテクニカルインジケーターやトレードシグナルがあります。 テクニカル分析の価格パターンの全体的なシステムがあります。 同時に、ラルフ·ヴィンスは、彼の本 "Mathematics of Money Management" "で、トレードを実行するために使用する資本金の量はあまり重要ではないことを示しています。 利益を最適化し、資産を保護するには、ロットサイズを決定する必要があります。
また、ヴィンスは "偽の概念 "について反証しています。 たとえば、このような概念の1つには、次のようなものがありみあす。 "リスクが高いほど、利益が大きい ":
潜在的な利益は潜在的なリスクの線形関数です。 これは、真実ではありません!
次の "偽の概念 " は "多様化は損失を減少させる " です。 これも間違っています。 ヴィンスは言及しています:
多様化は損失を減らすことができますが、特定の場合にのみ当てはまり、ほとんどのトレーダーが想像しているよりもはるかに少ないと考えています。
ファンダメンタルズ
わかりやすくするために、基本的な考え方を例を通して説明します。 2つのトレードが条件付きシステムを持っていると仮定します。 最初のトレードは 50%勝ち、2番目で40% 負けます。再トレードしない場合は、 10% の利益になります。 再トレードすれば、トレードの同じシーケンスは、損失の 10% につながります。 (P&L=Profit or Loss).
| トレード番号 | 再トレードなしの損益 | 資産合計 | 再トレードによる損益 | 資産合計 | |
|---|---|---|---|---|---|
| 100 | 100 | ||||
| 1 | +50 | 150 | +50 | 150 | |
| 2 | -40 | 110 | -60 | 90 |
利益の再投資は勝利システムに負けをもたらしました。 ここでは、トレードの順序は重要ではありません。 この例では、再投資時の戦略が、固定ロットのトレードと異なることを示しています。 したがって、再投資時に最適なロットサイズを検索することは、ビンスの資金の管理メソッドの基礎となります。
簡単なことから始めて、複雑なものに移りましょう。 よって、コインフリップを開始します。 勝利の場合には2ドルを取得し、損失の場合には1ドルを失う仮定します。 負けるか勝つかの確率は1/2。 100ドルを持っていると仮定します。 その後、100ドルを賭ける場合、潜在的な利益は200ドルになります。 しかし、損失の場合には、すべての資金を失うことになると、ゲームを継続することはできません。 最適化のターゲットである無限のゲーム中に、間違いなく失うことになる。
一度にすべての資金を賭けていない場合、そして一部を、例えば20ドルを使用して、ゲームを続けるために資金を持っているでしょう。 トレードごとの資本の異なるシェアで可能なトレードのシーケンスを検討してみましょう。 最初の資本金は100ドルです。
| トレード | P&L if K=0.1 | 資本 | P&L if K=0.2 | 資本 | P&L if K=0.5 | 資本 | P&L if K=0.7 | 資本 | P&L if K=1 | 資本 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 100 | 100 | 100 | 100 | ||||||||||
| +2 | 20 | 120 | 40 | 140 | 100 | 200 | 140 | 240 | 200 | 300 | ||||
| -1 | -12 | 108 | -28 | 112 | -100 | 100 | -168 | 72 | -300 | 0 | ||||
| +2 | 21.6 | 129.6 | 44.8 | 156.8 | 100 | 200 | 100.8 | 172.8 | 0 | 0 | ||||
| -1 | -12.96 | 116.64 | -31.36 | 125.44 | -100 | 100 | -120.96 | 51.84 | 0 | 0 | ||||
| +2 | 23.33 | 139.97 | 50.18 | 175.62 | 100 | 200 | 72.58 | 124.42 | 0 | 0 | ||||
| -1 | -14 | 125.97 | -35.12 | 140.5 | -100 | 100 | -87.09 | 37.32 | 0 | 0 | ||||
| Total | 126 | 141 | 100 | 37 | 0 |
上述したように、損益はトレードの順序に依存しません。 なので、利益と損失の入れ替えが正解です。
利益が最大になる最適な係数 (除数) がなければなりません。 シンプルなケースでは、勝利の確率と損益率が一定である場合、この係数は、ケリーの式にあります。
f=((B+1)*P-1)/B
fは、最適化で固定であり、検索対象となります。
Pが勝つ確率
Bは勝利/損失の率
便宜上、 fを係数と呼びましょう。
実際には、サイズと勝利の確率は常に変化するので、ケリーの式は適用されません。 したがって、経験的データの f 係数は数値解法によって発見されます。 システムの収益性は、トレードの任意の経験的フローに最適化されます。 トレード利益に、ビンスは HPR (保持期間のリターン) という語を使用します。 トレードは 10% の利益をした場合は、HPR = 1 + 0.1 = 1.1。 従って、トレードごとの計算は次のとおりである: HPR =1+f*リターン/(最大想定損失)、リターンは利益または損失であるかどうかによってプラスまたはマイナスの符号を持つことができます。 実際にfは、可能な最大ドローダウンの係数です。 最適なf値を見つけるには、すべてのトレードのmax(HPR1 * HPR2 * ... *HPRn).のプロダクトの最大限を見つける必要があります。
任意のデータ配列のfを検索するためのプログラムを作成してみましょう。
プログラム 1. 最適なfを検索します。
double PL[]={9,18,7,1,10,-5,-3,-17,-7}; //利益/損失の配列 double Arr[]={2,-1}; void OnStart() { SearchMaxFactor(Arr); //または PL およびその他の配列 } void SearchMaxFactor(double &arr[]) { double MaxProfit=0,K=0; //最大利益 //利益に対応する比率 for(int i=1;i<=100;i++) { double k,profit,min; min =MathAbs(arr[ArrayMinimum(arr)]); //配列内の最大損失の検出 k =i*0.01; profit =1; //セット係数によるリターンの検索 for(int j=0;j<ArraySize(arr);j++) { profit =profit*(1+k*arr[j]/min); } //最大利益との比較 if(profit>MaxProfit) { MaxProfit =profit; K=k; } } Print("Optimal K ",K," Profit ",NormalizeDouble(MaxProfit,2)); }
ケース + 2、-1、+ 2、-1 など f はケリーの数式を使用して得たものと等しくなることを確認することができます。
最適化は、収益性の高いシステム、すなわちポジティブな数学的期待 (平均利益) を持つシステムに理にかなっていることに注意してください。 負けのための最適なf= 0。 ロットサイズ管理は、負けシステムを作るのに役立ちません。 逆に、フローに損失がない場合、すなわち、すべての損益 > 0 の場合、最適化も意味をなさない: f= 1 であり、最大ロットを交換する必要があります。
MQL5 のグラフィカル性を利用してf の最大値を見つけるとともに、 fに応じて利益配分の全体曲線を表示することができます。 以下のプログラムは、 f係数に応じた利益チャートを描画します。
プログラム 2. fに応じた利益のチャート。
//+------------------------------------------------------------------+ //| Graphic.mq5 | //| Orangetree | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Orangetree" #property link "https://www.mql5.com" #property version "1.00" #include<Graphics\Graphic.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ //double PL[]={9,18,7,1,10,-5,-3,-17,-7}; // An array of profits/losses from the book double PL[]={2,-1}; void OnStart() { double X[100]={0}; for(int i=1;i<=100;i++) X[i-1]=i*0.01; double Y[100]; double min =PL[ArrayMinimum(PL)]; if(min>=0){Comment("f=1");return;} min =MathAbs(min); int n = ArraySize(X); double maxX[1]= {0}; double maxY[1] ={0}; for(int j=0;j<n;j++) { double k =X[j]; double profit =1; for(int i=0;i<ArraySize(PL);i++) { profit =profit*(1+k*PL[i]/min); } Y[j] =profit; if(maxY[0]<profit) { maxY[0] =profit; maxX[0] =k; } } CGraphic Graphic; Graphic.Create(0,"Graphic",0,30,30,630,330); CCurve *Curve=Graphic.CurveAdd(X,Y,ColorToARGB(clrBlue,255),CURVE_LINES,"Profit"); Curve.LinesStyle(STYLE_DOT); //必要に応じて、チャートを平滑化することができます /*Curve.LinesSmooth(true); Curve.LinesSmoothTension(0.8); Curve.LinesSmoothStep(0.2);*/CCurve *MAX =Graphic.CurveAdd(maxX,maxY,ColorToARGB(clrBlue,255),CURVE_POINTS,"Maximum"); MAX.PointsSize(8); MAX.PointsFill(true); MAX.PointsColor(ColorToARGB(clrRed,255)); Graphic.XAxis().MaxLabels(100); Graphic.TextAdd(30,30,"Text",255); Graphic.CurvePlotAll(); Graphic.Update(); Print("Max factor f = ", maxX[0]); }
{+ 2,-1} のチャートは次のようになります。
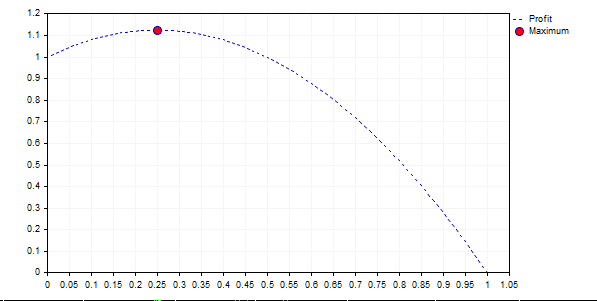
このチャートは、次の法則性が間違っていることを示しています: "リスクが高いほど、利益が大きい "。 いずれの場合も、曲線が 1 (f> 0.5) を下回ると、最終的には損失が発生し、無限のゲームではアカウントに0が付きます。
ここには1つの興味深い矛盾があります。 利益の数学的期待が高く、システムが安定しているほど、 f係数が大きくなります。 たとえば、フロー {-1, 1, 1, 1, 1, 1, 1, 1, 1, 1} の場合、係数は0.8 に等しくなります。 これは夢のシステムのように見えます。 しかし、0.8 の係数は、最大許容損失が 80% に等しいことを意味し、一度でアカウントの 80% を失う可能性があります! 数学的統計の観点からバランスを最大化するための最適なロットサイズですが、そのような損失の準備ができていますか?
多様化に関する言葉
たとえば、2つのトレード戦略A と 戦略Bがあるとします: 同じ利益/損失で、例として (+ 2、-1)としましょう。 最適なfは0.25 に等しくなります。 システムに1.0 と-1 の相関関係がある場合を考えてみましょう。 アカウント残高は、システム間で均等に分割されます。
Correlation 1, f=0.25
| システム A | トレード損益 | システム B | トレード損益 | 複合アカウント | ||
|---|---|---|---|---|---|---|
| 50 | 50 | 100 | ||||
| 2 | 25 | 2 | 25 | 150 | ||
| -1 | -18.75 | -1 | -18.75 | 112.5 | ||
| 2 | 28.13 | 2 | 28.13 | 168.75 | ||
| -1 | -21.09 | -1 | -21.09 | 126.56 | ||
| 利益26.56 |
このバリアントは、資本全体を使用して1つの戦略に基づいてトレードした場合と変わりません。 次に、0と等しい相関関係を見てみましょう。
Correlation 0, f=0.25
| システム A | トレード損益 | システム B | トレード損益 | 複合アカウント |
|---|---|---|---|---|
| 50 | 50 | 100 | ||
| 2 | 25 | 2 | 25 | 150 |
| 2 | 37.5 | -1 | -18.75 | 168.75 |
| -1 | -21.1 | 2 | 42.19 | 189.85 |
| -1 | -23.73 | -1 | -23.73 | 142.39 |
| 利益42.39 |
この利益ははるかに高いです。 そして、最後に、相関関係は-1 と等しくなります。
Correlation -1, f=0.25
| システム A | トレード損益 | システム B | トレード損益 | 複合アカウント |
|---|---|---|---|---|
| 50 | 50 | 100 | ||
| 2 | 25 | -1 | -12.5 | 112.5 |
| -1 | -14.08 | 2 | 28.12 | 126.56 |
| 2 | 31.64 | -1 | -15 | 142.38 |
| -1 | 17.8 | 2 | 35.59 | 160.18 |
| 利益 60.18 |
この場合、利益は最高になります。 この例だけでなく、同様のものが利益再投資の多様化の場合にはより良い結果を与えることを示しています。 しかし、システムの相関関係が-1 の場合、バリアントを除いて、最悪のケース (最大の損失は、バランスサイズのf= 0.25) が排除されないことは明らかです。 実際には、-1 の相関関係を持つシステムは存在しません。 異なる方向に対し同じシンボルで両建てするのに似ています。 そのような考察に基づいて、ヴィンスは次の結論に至りました。 彼の本からの引用です:
多様化は、適切に行われた場合、リターンを増加させる技術です。 必ずしも最大ドローダウンを減らすことにはつながりません。 有名な概念には反しています。
相関とその他の統計
f係数を求めるパラメトリックメソッドに進む前に、利益と損失のストリームのより多くの特性を考慮してみましょう。 相互に関連する一連の結果を得ることができます。 有益なトレードは、収益性の高いものに続き、負けトレードは、収益性の低いものによって続いています。 このような依存関係を特定するには、次の2つのメソッドを検討します。シリーズとシリアルテストの自己相関を検索します。
シリアルテストは、 "Z スコア " という値の計算です。 コンテンツの面では、Z スコアは、データが正規分布の平均から離れている標準偏差の数です。 負の Z スコアは、通常の分布よりも少ない縞 (連続した利益/損失シリーズ) があることを示しているため、利益は損失とその逆が続く可能性があります。 Z スコアの計算式:
Z=(N(R-0.5)-Х)/((Х(Х-N))/(N-1))^(1/2)
or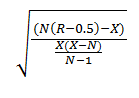
ただし:
- N は、トレードの合計数です
- R はシリーズの合計数です
- X=2*W*L, where
- W = シーケンス内の獲得トレードの合計数
- L = シーケンス内の損失トレードの合計数
プログラム 3. Z スコア。
double Z(double &arr[]) { int n =ArraySize(arr); int W,L,X,R=1; if(arr[0]>0) { W=1; L=0; } else { W=0; L=1; } for(int i=1;i<n;i++) { if(arr[i]>0) { W++; if(arr[i-1]<=0){R++;} } else { L++; if(arr[i-1]>0){R++;} } } X =2*W*L; double x=(n*(R-0.5)-X); double y =X*(X-n); y=y/(n-1); double Z=(n*(R-0.5)-X)/pow(y,0.5); Print(Z); return Z; }
z スコアは、バックレポートの "z スコア " と呼ばれ、ストラテジーテスターによって計算されます。
シリアル相関は、シフトで使用される1つの系列の値のシーケンス間の静的な関係です。 シリーズ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} は、{1, 2, 3, 4, 5, 6, 7, 8, 9} と {2, 3, 4, 5, 6, 7, 8, 9, 10} の間の相関関係です。 シリアル相関を見つけるためのプログラムです。
プログラム 4. シリアル相関。
double AutoCorr(double &arr[]) { int n =ArraySize(arr); double avr0 =0; for(int i=0;i<n-1;i++) { avr0=avr0+arr[i]; } avr0=avr0/(n-1); double avr1 =0; for(int i=1;i<n;i++) { avr1=avr1+arr[i]; } avr1=avr1/(n-1); double D0 =0; double sum =0.0; for(int i=0;i<n-1;i++) { sum =sum+(arr[i]-avr0)*(arr[i]-avr0); } D0 =MathSqrt(sum); double D1 =0; sum =0.0; for(int i=1;i<n;i++) { sum =sum+(arr[i]-avr1)*(arr[i]-avr1); } D1 =MathSqrt(sum); sum =0.0; for(int i=0;i<n-1;i++) { sum =sum +(arr[i]-avr0)*(arr[i+1]-avr1); } if(D0==0||D1==0) return 1; double k=sum/(D0*D1); return k; }
トレードの結果が相互に関連している場合は、トレード戦略を調整することができます。 利益と損失に2つの異なる係数 f1 と f2 を使用する場合、より良い結果が得られます。 この場合、MQL5 に個別の資金管理モジュールを作成します。
パラメトリックメソッド
システムのパラメータを最適化する場合、2つの方法を使用できます。 最初のアプローチは実験データに直接基づいていた経験的な方法です。 この場合、特定の結果のパラメータを最適化します。 2番目の方法はパラメトリックです。 関数または静的依存関係に基づいています。 パラメトリックメソッドの例では、ケリーの数式から最適な係数を見つけることです。
ビンスは、最適な係数を見つけるために得られたリターンの分布を使用して示唆しています。 最初、ビンスは最も人気のあり、最もよく研究されている正規分布を考慮しました。 次に、一般化された分布を構築します。
問題は以下のように定式化されます。 利益/損失は、通常の (または他の) 分布に応じていると仮定します。 この分布の最適なf係数を見つけてみましょう。 通常の分布の場合、PL (損益) ストリームと標準偏差の平均値を見つけるために実験データを使用することができます。 2つのパラメータは、正規分布を完全に特徴付けるものです。
正規分布密度の数式は次のとおりです。
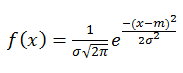
ただし
- σ は標準 偏差を表します。
- m は数学的な期待 (平均) です。
この考えが好きでした。 損益分布の性質は、経験的データを使用して見つけることができます。 その後、結果が求めるこの関数を使用することができます。 残念ながら、実際にはそう簡単ではありません。 最初から始めましょう。 まず、そのメソッドについて考察します。
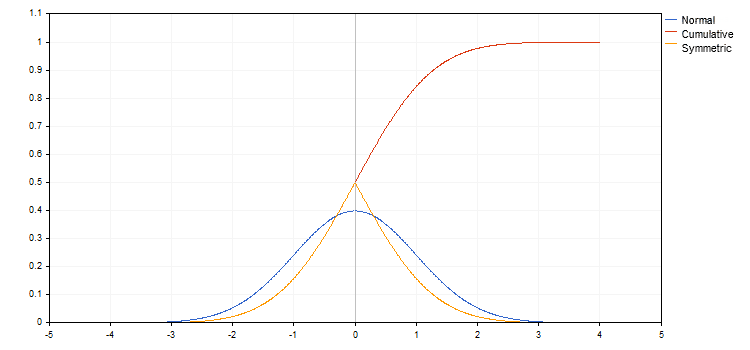
このチャートでは、通常の分布密度のチャートが青色でプロットされています。 平均値は0に等しく、標準偏差は1に等しくなります。 赤い色は、この関数の積分を示しています。 累積確率 (つまり、値が指定された X より小さいか等しい確率) です。通常はF (x)として表されます。 オレンジ色のチャートには、xがゼロかx<0である確率を表します。また、xが0以上か x=>0 (F(x)' =1-F(x)である確率を表します。 この関数はすべてよく知られており、その値は取得できます。
トレードの最大の幾何学的な平均は、このルールに従って分布を見つける必要があります。 ここでは、ヴィンスは、次のアクションを示唆しています。
まず、分布の特性、すなわち平均と標準偏差を見つけます。 次に、標準偏差で表される "信頼区間 " またはカットオフ幅を選択します。 3σが通常選択されます。 3σより大きい値はカットオフされます。 その後、間隔が分割され、利益/損失 (PL) の関連付けられた値が検出されます。 たとえば、σ = 1 と m = 0 の場合、間隔の境界における関連するPLsの値は、m +-3 = + 3 と-3 です。 長さ0.1 σの bin に間隔を分割する場合は、関連付けられたPLs -3, -2.9, -2.8 ... 0 ... 2.8, 2,9, 3.になります。 このPLのストリームに最適なfを見つけます。
PLの異なる値には異なる確率があるため、それぞれの値について、個々の "関連する確率 " Pが検出されます。 その後、最大値が見つかりました:
HPR = (1 +PL* f/maxLoss) ^ P, 、 ただし、maxLoss は最大損失 (剰余).
ヴィンスは、関連する確率として累積確率を使用することを示唆しています。 累積確率は、チャートF ' (x)のオレンジ色で表示されます。
論理的には、累積確率は極端な値に対してのみ取得する必要がありますが、その他の値はP = f ' (x)-f ' (y)、x と y は間隔の境界でF (x)の値です。
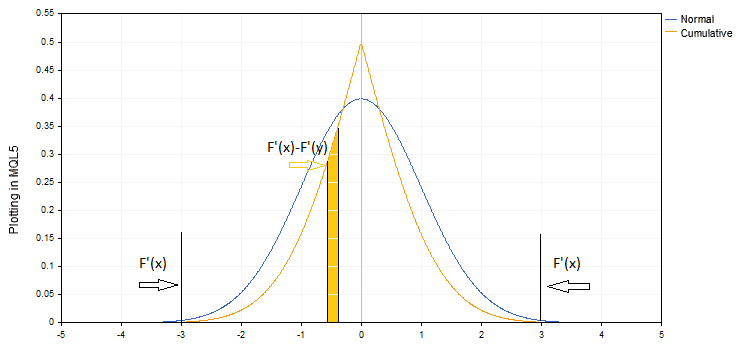
その後、ファクター HPR = (1 +PL* f/maxLoss) ^ P は、確率加重値の一種になります。 予想通り、値の合計確率は1に等しくなります。 ビンスは、この方法で得られた結果は、実際のデータで得られた結果と一致しないことを彼の本で認めています。 彼は、サンプリングの限られた性質と、通常のものから実際の分布の差とそのような結果をバインドしています。 その分布は、通常の法則によると、最適なf係数のパラメトリックと実際の値が一致することになっています。
ビンスのメソッドで分析した例では、合計確率は7.9 に等しくなります。 ヴィンスは、結果の7.9 度のルートを取ることによって幾何学的な意味を見つけました。 どうやら、このようなアプローチの厳密な数学的正当性がある必要があります。
MQL5 ツールを使用すると、上記を確認することができます。 この目的のために、<MathStatNormal.mqh>にあるNormal.mqh ライブラリを使用します。
実験の2つのバージョンを作成しています。:一つは ヴィンス、一つは上記のものです。 ライブラリ関数 MathCumulativeDistributionNormal(PL,mean,stand,ProbCum) は、関連する確率を見つけるために使用されます。
プログラム 5. 正規分布 (ビンス) で最適なfを検索します。
//+------------------------------------------------------------------+ //| Vince.mq5 | //| Copyright 2017, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2017, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include<Math\Stat\Math.mqh> #include<Math\Stat\Normal.mqh> input double N=3; //標準偏差のカットオフ間隔 input int M=60; //セグメント数 //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { double arr[10000]; bool ch =MathRandomNormal(1,8,10000,arr); double mean =MathMean(arr); double stand =MathStandardDeviation(arr); double PL[]; // "関連する利益 " の配列 ArrayResize(PL,M+1); //配列のエントリー for(int i=0;i<M+1;i++) { double nn =-N+2.0*i*N/M; PL[i] =stand*nn+mean; } //............................. "関連する確率 " の配列 double ProbCum[]; ArrayResize(ProbCum,M+1); //............................. Filling the array.................. ch =MathCumulativeDistributionNormal(PL,mean,stand,ProbCum); //F'(x)= 1-F(x) при х>0 for(int i=0,j=0;i<M+1;i++) { if(i<=M/2)continue; else j=M-i; ProbCum[i] =ProbCum[j]; } double SumProb=0; for(int i=0;i<M+1;i++) { SumProb =SumProb+ProbCum[i]; } Print("SumProb ",SumProb); double MinPL =PL[ArrayMinimum(PL)]; double min =arr[ArrayMinimum(arr)]; double f=0.01,HPR=1,profit=1; double MaxProfit=1,MaxF=0; for(int k=0;k<1000;k++) { f=k*0.001; profit =1; for(int i=0;i<M+1;i++) { HPR=pow((1-PL[i]/MinPL*f),ProbCum[i]); profit =HPR*profit; } if(MaxProfit<profit) { MaxF =f; MaxProfit =profit; } } Print("Profit Vince"); Print(MaxF," ",pow(MaxProfit,1/SumProb)," ",Profit(MaxF,min,arr)); //... 比較のため、実際のデータを使用して最大の利益を探してみましょう MaxF =0; MaxProfit =1; for(int k=0;k<1000;k++) { f=k*0.001; profit =Profit(f,min,arr); if(MaxProfit<profit) { MaxF =f; MaxProfit =profit; } } Print("------MaxProfit-------"); Print(MaxF," ",MaxProfit); } //実際のデータを使用して利益を見つけるためのプログラム // of the arr[] array with the minimum value 'min' // and a specified f value double Profit(double f,double min, double &arr[]) { if(min>=0) { return 1.0; Alert("min>=0"); } double profit =1; int n =ArraySize(arr); for(int i=0;i<n;i++) { profit =profit*(1-arr[i]*f/min); } return profit; }
プログラムコードは、Vince.mq5 ファイルで入手できます。
このプログラムは、正規分布からの係数とし、実際のデータからしています。 2番目のバリアントは、 "関連 " 確率と PL の配列でのみ異なります。
プログラム 6.
............................................. double ProbDiff[]; ArrayResize(ProbDiff,M+2); double PLMean[]; ArrayResize(PLMean,M+2); ProbDiff[0]=ProbCum[0]; ProbDiff[M+1]=ProbCum[M]; PLMean[0]=PL[0]; PLMean[M+1]=PL[M]; for(int i=1;i<M+1;i++) { ProbDiff[i] =MathAbs(ProbCum[i]-ProbCum[i-1]); PLMean[i] =(PL[i]+PL[i-1])/2; } ..............................................
プログラムコードは、Vince_2.mq5 ファイルで使用できます。
ここでPLMean [i] = (pl [i] + pl [i-1])/2;は、bin の PL の平均値であり、 ProbDiff []は、指定された間隔で値が見つかる確率です。 境界の値は (おそらくストップロスまたはテイクプロフィット) 断ち切られ、従って境界の確率は累積確率と等しい。
2つのプログラムはほぼ同じ方法で動作し、ほぼ同じ結果を生成します。 応答が大幅にカットオフ幅 N (いわゆる信頼区間) に依存していることが判明しました。 最も残念な事実は、N が増加すると、正規分布から得られた f 係数が1になる傾向があるということです。 理論的には、信頼区間が広いほど、より正確な結果が得られるはずです。 しかし、実際には発生しません。
これは累積エラーによって発生する可能性があります。 指数関数は、高速に減少し、小さな値に対処する必要があります:HPR=pow((1-PL[i]/MinPL*f),ProbCum[i]). メソッド自体にもエラーが含まれている可能性があります。 しかし、実用的な使用に際し重要ではありません。 いずれにしても、N 個のパラメータを "調整 " して、結果に強く影響させる必要があります。
もちろん、任意の PL ストリームは、通常の分布とは異なります。 よって、ビンスは、任意のランダムな分布の特性をエミュレートするパラメータを使用して一般化分布を作成しました。 分布の異なるモーメントを設定するパラメータ (平均、尖、幅、歪) が追加されます。 次に, 数値解法を用いて経験的データのパラメータを検索し, PL ストリーム分布関数を作成します。
正規分布の実験結果が気に入らなかったので、一般化分布を用いて数値計算を行わないことにしました。 ここでの疑問を説明するのは別の引数です。
ビンスは、パラメトリックメソッドは、はるかに強力であると主張しています。 実験の数が増えるにつれて、サンプルから得られる係数は、限られたサンプリングで不正確であるため、データは理論的な結果になりがちです。 ただし、正規分布のパラメータ (平均値と標準偏差) は、同じ制限されたサンプルから取得されます。 分配特性の計算の不正確さは全く同じです。 誤差は蓄積されたエラーにより、さらに計算が増え続けます。 そして、実用的な実装の結果もカットオフ幅に依存することが判明しました。 分布は実際には正常ではないので、1つ以上の要素 (同じ経験的最終データに基づく分布関数の検索) を追加します。 追加の要素は、追加のエラーにつながります。
ここで謙虚な意見です。 パラメトリックなアプローチは、理論的によく似合うアイデアは、常に実際にはとても良い見ていないという事実を示しています。
ヴィンスの本の概要
MQL5 ウィザードモジュール
モジュールの実装は、使用可能な標準モジュール MoneyFixedRisk に似ていますが、ロットサイズは構成されたストップロスの値に基づいて計算されます。 デモンストレーションとして、ストップロスは独立したままにし、インプットパラメータによってf係数と最大損失を明示的に設定します。
まず、Include/Expert ディレクトリ (MyMoney) にモジュール用の新しいフォルダを作成します。 次に、このフォルダに MoneyF1.mql ファイルを作成します。
すべてのトレーディングモジュールは、標準部品のセットで構成されています: トレーディングモジュールクラスとその特別な説明。
通常、クラスには次の要素が含まれます。
- コンストラクタ
- デストラクタ
- インプットパラメータ設定関数
- 関数の ValidationSettings (void) を検証するパラメータ
- ポジションボリュームを決定するためのメソッド CheckOpenLong(double price,double sl) と CheckOpenShort(double price,double sl)
このクラス CMoneyFactor を呼びましょう
class CMoneyFactor : public CExpertMoney { protected: //---インプットパラメータ double m_factor; //最大損失係数 f double m_max_loss; //ポイントの最大損失 public: CMoneyFactor(void); ~CMoneyFactor(void); //--- void Factor(double f) { m_factor=f;} void MaxLoss(double point) { m_max_loss=point;} virtual bool ValidationSettings(void); //--- virtual double CheckOpenLong(double price,double sl); virtual double CheckOpenShort(double price,double sl); }; //+------------------------------------------------------------------+ //|コンストラクタ | //+------------------------------------------------------------------+ void CMoneyFactor::CMoneyFactor(void) : m_factor(0.1), m_max_loss(100) { } //+------------------------------------------------------------------+ //|デストラクタ | //+------------------------------------------------------------------+ void CMoneyFactor::~CMoneyFactor(void) { }
ポイントの最大損失は、標準モジュールに合わせて double 型として設定されます。 パッケージのストップロスおよびテイクプロフィットレベルで利用可能な他の標準モジュールでは、ExpertBase.mqh 基本クラスで定義されたポイントに設定されます。
ExpertBase.mqh int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1; m_adjusted_point=m_symbol.Point()*digits_adjust;
1つのポイントは 10*Point() で、 小数点以下3と5でクオートに等しいことを意味します。 Point() の105ポイントは、標準の MQL5 モジュールでは10.5 と等しくなります。
Factor(double f)とMaxLoss(double point) 関数は、インプットパラメータを設定し、モジュール記述子に記述されているように、同じメソッドで名前を指定する必要があります。
インプットパラメータを検証する関数:
boolCMoneyFactor:: ValidationSettings (void) { if(!CExpertMoney::ValidationSettings()) return(false); //---初期データチェック if(m_factor<0||m_factor>1) { Print(__FUNCTION__+"The coefficient value must be between 0 and 1"); return false; } return true; }
係数の値が0から1の間であることを確認します。
最後に、ポジションのボリュームを決定する関数です。 ロングポジションを開く:
double CMoneyFactor::CheckOpenLong(double price,double sl) { if(m_symbol==NULL) return(0.0); //ロットサイズの決定 double lot; /* ExpertBase.mqh int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1; m_adjusted_point=m_symbol.Point()*digits_adjust; */ double loss; if(price==0.0)price =m_symbol.Ask(); loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor/loss/stepvol)*stepvol; double minvol=m_symbol.LotsMin(); //最小ロットのチェック if(lot<minvol) lot=minvol; //最大ロットのチェック double maxvol=m_symbol.LotsMax(); if(lot>maxvol) lot=maxvol; //--- return trading volume return(lot); }
ここでは、最大ロットは、ライブラリから CAccountInf クラスの OrderProfitCheck() メソッドを使用して発見されます。 次に、ロットのコンプライアンスを、最小値と最大数の制限にチェックします。
各モジュールは、モジュールを認識するためにコンパイラが必要とする記述子で始まります。
//ウィザードの説明の開始 //+------------------------------------------------------------------+ //|クラスの説明 | //| Title=Trading with the optimal f coefficient | //| Type=Money | //| Name=FixedPart | //| Class=CMoneyFactor | //| Page= ? | //| Parameter=Factor,double,0.1,Optimum fixed share | //| Parameter=MaxLoss,double,50,Maximum loss in points | //+------------------------------------------------------------------+ // wizard description end
テストとして、このモジュールを既存のシグナルモジュールでコンパイルすることができます。 選択されたトレードシグナルモジュールは、固定ロットに基づいた資金管理のモジュールを使用してコンパイルすることもできます。 得られた結果は、最大損失と PL ストリームを見つけるために使用されます。 次に、プログラム1を結果に適用して、最適なf係数を見つけます。 したがって、実験データを使用して、最適なf値を見つけることができます。 もう1つの方法は、最適化によって得られたEAから最適なfを直接見つけることです。 +/-0.01 として少し結果の差がありました。 この差は計算エラーによるもので、丸めたことによって発生することがあります。
モジュールコードは、MoneyF1.mqh ファイルで使用できます。
利益/損失の流れは、重要なシリアル相関関係を持っていることが判明することがあります。 Z スコアとシリアル相関を計算するために、上記のプログラムを使用して見つけることができます。 次に、2つの係数を指定することができます: f1 と f2。 最初の1つは、収益性の高いトレード後に適用され、2番目のトレードを失った後に使用されます。 この戦略の2番目の資金管理モジュールを書いてみましょう。 係数は、最適化を使用して、または固定ロットと同じ戦略の利益/損失ストリームのデータから直接見つけることができます。
プログラム 7. PL ストリームに基づいて最適な f1 と f2 を決定します。
void OptimumF1F2(double &arr[]) { double f1,f2; double profit=1; double MaxProfit =0; double MaxF1 =0,MaxF2 =0; double min =MathAbs(arr[ArrayMinimum(arr)]); for(int i=1;i<=100;i++) { f1 =i*0.01; for(int j=1;j<=100;i++) { f2 =j*0.01; profit =profit*(1+f1*arr[0]/min); for(int n=1;n<ArraySize(arr);n++) { if(arr[n-1]>0){profit =profit*(1+f1*arr[n]/min);} else{profit =profit*(1+f2*arr[n]/min);} } if(MaxProfit<profit) { MaxProfit=profit; MaxF1 =i;MaxF2 =j; } } }
また、MQL5 ウィザードの 資金管理モジュールの基本的な関数を調整する必要もあります。 まず、別の f2 パラメータとこのパラメータのチェックを追加します。 次に、CheckOpenLong () と CheckOpenShort () 関数を変更します。 また、前のトレードの結果を決定するために CheckLoss () を追加します。
//+------------------------------------------------------------------+ //| Checks the result of the previous trade | //+------------------------------------------------------------------+ double CMoneyTwoFact:: CheckLoss() { double lot=0.0; HistorySelect(0,TimeCurrent()); int deals=HistoryDealsTotal(); //ヒストリーのトレードの数 CDealInfo deal; //以前のトレードを検索 if(deals==1) return 1; for(int i=deals-1;i>=0;i--) { if(!deal.SelectByIndex(i)) { printf(__FUNCTION__+": Failed to select a trade with the specified index"); break; } //シンボルまたはその他のパラメータに基づいてトレードを選択 if(deal.Symbol()!=m_symbol.Name()) continue; //トレード結果を返す lot=deal.Profit(); break; } return(lot); }
Functions CheckOpenLong() and CheckOpenShort():
double CMoneyTwoFact::CheckOpenLong(double price,double sl) { double lot=0.0; double p=CheckLoss(); /* ExpertBase.mqh int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1; m_adjusted_point=m_symbol.Point()*digits_adjust; */ double loss; if(price==0.0)price =m_symbol.Ask(); if(p>0) { loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor1/loss/stepvol)*stepvol; } if(p<0) { loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor2/loss/stepvol)*stepvol; } return(lot); } //+------------------------------------------------------------------+ double CMoneyTwoFact::CheckOpenShort(double price,double sl) { double lot=0.0; double p=CheckLoss(); /* int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1; m_adjusted_point=m_symbol.Point()*digits_adjust;*/ double loss; if(price==0.0)price =m_symbol.Ask(); if(p>0) { loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_SELL,1.0,price,price+m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor1/loss/stepvol)*stepvol; } if(p<0) { loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_SELL,1.0,price,price+m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor2/loss/stepvol)*stepvol; } return(lot); }
モジュールの完全なコードは、MoneyF1F2.mqhで入手できます。
前述したように、資金管理のビンスの概念は、基本的に最適な f 係数によってもたらされます。 したがって、2つのモジュールは、この例では十分です。 ただし、追加のバリエーションを実装することができます。 たとえば、ゲール要素です。
添付
Programs.mq5 ファイルには、この記事で使用されているプログラムコードがあります。 oid ReadFile(string file,double &arr[]) からデータを読み取るためのプログラムも以下に添付されています。 このプログラムは、ストラテジーテスターからの PL ストリームに基づいて f 係数を見つけることができます。 誰かがレポートを解析するためにクラス全体を記述する場合は、 「Resolving Entries into Indicators」を参照してください。 しかし、独自のクラスとは別のプログラムになります。
簡単な方法を提案します。 ストラテジーテスターで固定ロットと戦略を実行します。 テスターレポートを Open XML (MS Office Excel) として保存します。 利益列にスワップとコミッションを追加して、PL ストリームを取得します。 この列をテキストまたは csv ファイルに保存します。 従って、各トレードの別の結果から成っているラインのセットを得ることができます。 ReadFile() 関数は、結果を arr[] 配列に読み込みます。 したがって、固定ロットを持つ任意の戦略のデータに基づいて最適なf係数を見つけることができます。
Vince.mq5 と Vince_2.mq5のファイルは、この記事に記載されている最適な係数を見つけるためのパラメトリックメソッドのソースコードです。
MoneyF1.mqh と MoneyF1F2.mqh には、資金管理モジュールのソースコードがあります。
添付 zip フォルダ内のファイルは、メタエディタ ディレクトリに従って配置されます。