非加法的統計分布構造解析への固有座標法の応用

MetaQuotes | 27 10月, 2015

はじめに

1988年コンスタンツィーノ・ツァリスが Boltzmann-Gibbs-Shannon 統計力学[1]の一般化を提案しました。そこで彼は非加法エントロピーの考え方を紹介しました。

エントロピーの一般化の重要な結果は新しい統計力学（Q指数およびQガウス分布）での主要な役割を演じる新たな統計タイプ[2] に見られます。

こういった分布タイプは長期メモリを伴うシステム、遠距離力を伴うシステム、強い相関関係のあるシステムにおいて多くの実験データを類型化するのに使用可能であることがわかりました。

エントロピーは情報に強く関連しています [7]。情報理論に基づく統計力学の一般化は [8-9] に述べられています。新しい非加法統計力学は計量経済学にとってひじょうに有用であると証明されました [10-17]。たとえばQガウス分布は金融商品のクオート（q～1.5）のインクリメント分布の広いウィング（テール）をよく説明します。ファイナンシャルの時系列インクリメント分布の多くは、より大きい基準（月、年）において正規分布（q=1）に転換するというものです。 [10]

このような統計力学の一般化が結果として q ガウス分布に対する中心極限定理の類似体になることは当然ながら予測されました。しかしこれは [18] で誤りであることが示されました。- 強い相関のあるランダム変数の合計の極限分布は q ガウスとは分析的に異なるのです。

ただし、別の問題が浮上しました。というのも発見される厳密解の数値は Qガウス（「数値的に近いが、分析的に異なる」）にひじょうに近いのです。関数間の差を分析し Qガウス分布の最良パラメータを取得するのに[18]では級数展開が使用されました。これら関数の関係によりシステムの非拡張程度を特徴づける q パラメータにおけるべき級数展開に至りました。

応用統計学の主な問題は受け入れる統計仮説の問題です。それは近代的な応用統計学手法を用いることで、可能なこと以上のものを見極めることができるようになる特別なツール（電子顕微鏡のようなもの）を要求するため、長い間解決は不可能だと考えられていました。[19-20]

[21] で紹介されている固有座標法により、より深いレベルに到達することができます。- 関数関係の構造的プロパティ分析です。このひじょうにすぐれた手法は多様な問題を解決するのに利用可能です。上の非加法的分布に対応する関数の演算子展開は [22]で示されています。

本稿は固有座標法とその実用例を取り上げます。そこには、この手法の基礎を理解するのにたいへん重要な式が多く含まれています。計算をすべて繰り返したら、ご自身が興味を感じる関数に対して展開関数をプロットできるようになっていることでしょう。

1. 計量経済学におけるQガウス分布

Qガウス分布は計量経済学においてひじょうに重要な役割を果たします[4,10-17]。

現在の調査レベルで一般的な理解を得るために、クラウディオ・アントニー二博士の "q-Gaussians in Finance" [23] および "The Use of the q-Gaussian Distribution in Finance" [24]を参照することができます。

主な結果を簡潔に概説します。

図1　科学的方法論（"The Use of the q-Gaussian Distribution in Finance"スライドNo.4 ）

金融の時系列の主要な事項は図2で説明されています。

図2　金融時系列プロパティ（"The Use of the q-Gaussian Distribution in Finance"スライドNo.3）

金融時系列を述べるために使用される多くの理論モデルは Qガウス分布につながります。

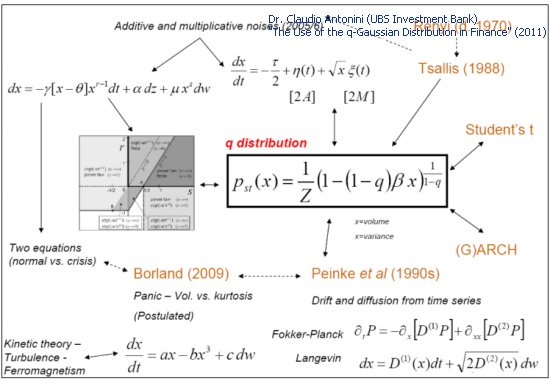
図3　理論モデルと Qガウス分布（"The Use of the q-Gaussian Distribution in Finance" スライドNo.27）

The Qガウス分布はクオート分布の現象論的記述にも利用されます。

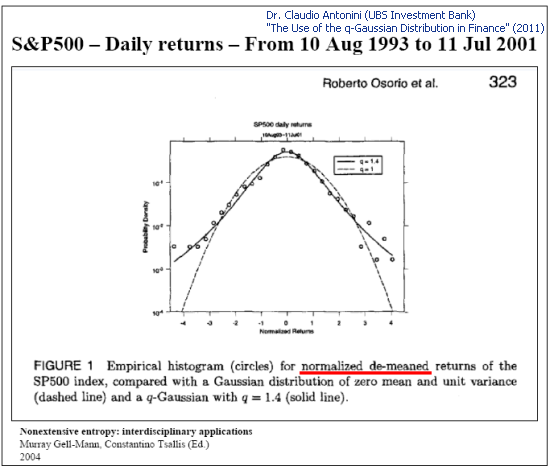
図4　S&P 500 前日比のサンプル分析（"The Use of the q-Gaussian Distribution in Finance" スライドNo.8）

実データで作業することは関数特定問題を poses

図5　分布関数特定の問題（"q-Gaussians in Finance"のスライドNo.14）

クラウディオ・アントニーニ博士の両論文では、物理的プロセスの適切なモデルを構築するための関数を正しく特定することの重要性が強調されています。

図6　"q-Gaussians in Finance" および "The Use of the q-Gaussian Distribution in Finance" (Dr. Claudio Antonini, 2010, 2011)で導かれる結論

金融における q ガウス分布の使用例（ワークシート+ MathCad ファイル）

q-Gaussian Stock Price Dynamics, (Michael English, 2008)
q-Gaussian European Options (Michael English, 2008)
q-Gaussian Random Deviates & Distribution, (Michael English, 2008)
q-Gaussian Portfolios (Michael English, 2008)
q-Gaussian Risk Measures (Michael English, 2008)
Expected Value & Value at Risk for Lognormal Asset (Michael English, 2008)

2. 固有座標

以下は固有座標展開です。

ここで C1…CN は定数。そして X1(t),..,XN(t) は『固有座標』です。

そのような線展開はひじょうに便利でデータ分析によく使用されます。たとえば、対数尺度における指数関数は直線になります（傾斜は線形回帰を利用して簡単に計算できます）。よって関数パラメータを決定するための非線形最適化（フィッティング）は不要です。

ただし対数尺度は、関数が直線を表さない、より複雑な関数（たとえば2つの指数合計）を扱う場合はほとんど役に立ちません。また非線形最適化は関数係数を決めるために必要となります。

実験的データが複数の関数を用いて等しくよく説明される場合があります。それら関数はすべて物理的プロセスの異なるモデルに対応します。どの関数をえらべばよいか？実験データ外でより適切な現状を提供するのはどれでしょうか？

現時点での関数同定は複合システム（金融時系列など）分析にとっては重要です。- 各分布は特定の物理プロセスに対応しており、適切なモデル選択により力学および複合システムの一般的プロパティをよりよく理解することができます。

応用統計学 [19, 20] は誤った統計的仮説を却下する基準がないことを述べています。固有座標法はこの問題（仮説受け入れ）に新たな光を投げかけてくれます。

実験的データの記述に使用される関数は特定の微分程式に対する解とみなすことができます。その形式は固有座標展開のストラクチャを決定します。

固有座標展開の特殊な性質は関数 Y(t) によって生成されるデータがすべて関数 Y(t)の固有座標 X1(t)..XN(t) に基づくストラクチャで線形であることです。その他あらゆる関数 F(t) によって生成されるデータはこの原理においてもはや直線とはなりません（それらは関数 F(t) の固有座標に基づき線に見えます）。

これにより関数を正確に同定することができ、よって統計的仮説の作業が大きく進むこととなります。

2.1. 固有座標法

この手法の背後にあるコンセプトは関数 Y(t)を基にしたオペレータ内の固有座標 Xk(t) を構築することです。

それは固有座標 Xk(t) が畳み込み積分の形を取り、展開が関数 Y(t) によって満たされる微分方程式のストラクチャが決定する数学的分析を用いて行うことができます。そののち、係数 C1.. CN を決める問題が発生します。

直交基底展開（フーリエ変換係数を決定する場合など）では、展開係数は基底のベクトルを予測することで計算されます。望む結果は基底関数の直交性によって取得されます。

しかしこれはわれわれの場合には当てはまりません。なぜなら X1(t)… XN(t)の直交性に関して情報がまったくないからです。

2.2. 最小二乗法を用いた展開係数の計算

係数 Ck は最小二乗法を用いて計算することができます。この問題は連立一次方程式を解く量を減らします。

以下であったとします。

実質的に各の測定にあたりエラーがあるとすると

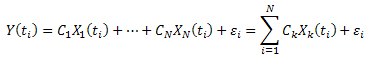
偏差平方和を最小化します。

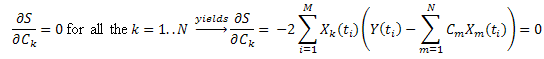
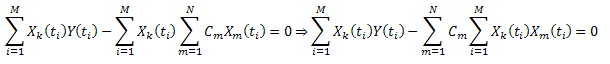
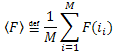を取り入れると、以下のように書くことができます。

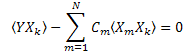
よって、C1...CN (k=1..N)に連立一次方程式を得ます。

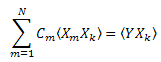
『相関』行列は対称です。

固有座標展開が整形式であればより都合よい場合もあります。

これはエラー（平均化による）の影響を軽減しますが、追加の計算が必要となります。

2.3. R(x) 関数展開例

以下の関数についての固有座標展開を見ていきます。

この関数は複数の統計分布を生成します [21]。

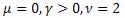- 正規（ガウス）分布
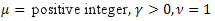- ポワソン分布
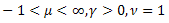- ガンマ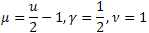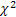分布
- 分布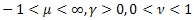
- 特殊なケースとしてのワイブル分布を含むシュタウファーの分布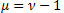

また、それは緩和過程を説明するのに適しています。

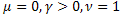- 通常型指数関数
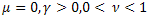- 引き延ばされた指数関数
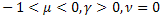- べき緩和関数

x に対して R(x) を微分すると、以下を得ます。

両辺を x で掛けます。

を変換します。

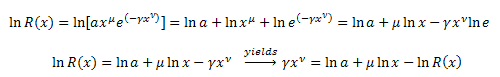
式に代入します。

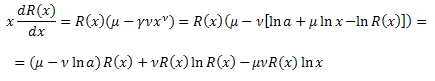
関数 R(x) に対して微分方程式を得ます。

区間 [xm,x]で x に対し両辺を積分します。

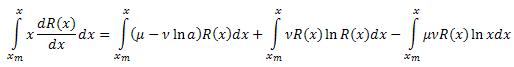
左辺を部分積分します。

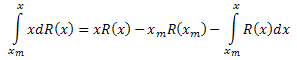
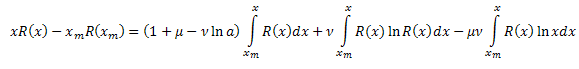
結果、次を得ます。

ここで

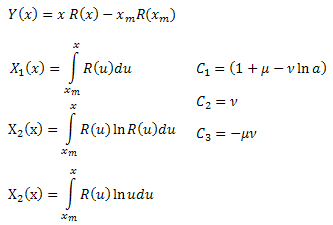
係数を計算することで関数パラメータを決めます。4番目のパラメータは R(x) に対する式から得ます。

2.4. 実装

展開係数の計算には連立一次方程式を解くことが必要です。行列作業がやりやすいように、個別のクラス CMatrix （CMatrix.mqh ファイル）とすることもできます。このクラスのメソッドを使用すると、行列パラメータ、行列エレメント値を設定し、ガウス手法を採用して連立一次方程式を解くことができます。

//+------------------------------------------------------------------+
//| CMatrix class                                                    |
//+------------------------------------------------------------------+
class CMatrix
  {
   double            m_matrix[];
   int               m_rows;
   int               m_columns;
public:
   void              SetSize(int nrows,int ncolumns);
   double            Get(int i,int j);
   void              Set(int i,int j,double val);
   void              GaussSolve(double &v[]);
   void              Test();
  };

固有座標と関数 R(x) のパラメータを計算するスクリプト例（EC_Example1.mq5）を挙げます。

//+------------------------------------------------------------------+
//|                                                  EC_Example1.mq5 |
//|                        Copyright 2012, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <CMatrix.mqh>
//+------------------------------------------------------------------+
//| CECCalculator                                                    |
//+------------------------------------------------------------------+
class CECCalculator
  {
protected:
   int               m_size;
   //--- x[i]
   double            m_x[];
   //--- y[i]
   double            m_y[];
   //--- matrix
   CMatrix           m_matrix;
   //--- Y[i]
   double            m_ec_y[];
   //--- eigen-coordinates X1[i],X2[i],X3[i]
   double            m_ec_x1[];
   double            m_ec_x2[];
   double            m_ec_x3[];
   //--- coefficients C1,C2,C3
   double            m_ec_coefs[];
   //--- function f1=Y-C2*X2-C3*X3
   double            m_f1[];
   //--- function f2=Y-C1*X1-C3*X3
   double            m_f2[];
   //--- function f3=Y-C1*X1-C2*X2
   double            m_f3[];
private:
   //--- function for data generation
   double            R(double x,double a,double mu,double gamma,double nu);
   //--- calculation of the integral
   double            Integrate(double &x[],double &y[],int ind);
   //--- calculation of the function Y(x)
   void              CalcY(double &y[]);
   //--- calculation of the function X1(x)
   void              CalcX1(double &x1[]);
   //--- calculation of the function X2(x)
   void              CalcX2(double &x2[]);
   //--- calculation of the function X3(x)
   void              CalcX3(double &x3[]);
   //--- calculation of the correlator
   double            Correlator(int ind1,int ind2);
public:
   //--- method for generating the test function data set x[i],y[i]
   void              GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu);
   //--- loading data from the file
   bool              LoadData(string filename);
   //--- saving data into the file
   bool              SaveData(string filename);
   //--- saving the calculation results
   void              SaveResults(string filename);
   //--- calculation of the eigen-coordinates
   void              CalcEigenCoordinates();
   //--- calculation of the linear expansion coefficients
   void              CalcEigenCoefficients();
   //--- calculation of the function parameters
   void              CalculateParameters();
   //--- calculation of the functions f1,f2,f3
   void              CalculatePlotFunctions();
  };
//+------------------------------------------------------------------+
//| Function R(x)                                                    |
//+------------------------------------------------------------------+
double CECCalculator::R(double x,double a,double mu,double gamma,double nu)
  {
   return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x)))));
  }
//+-----------------------------------------------------------------------+
//| Method for generating the data set x[i],y[i] of the test function R(x)|
//+-----------------------------------------------------------------------+
void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu)
  {
   if(size<=0) return;
   if(x1>=x2) return;
   m_size=size;
   ArrayResize(m_x,m_size);
   ArrayResize(m_y,m_size);
   double delta=(x2-x1)/(m_size-1);
//---
   for(int i=0; i<m_size; i++)
     {
      m_x[i]=x1+i*delta;
      m_y[i]=R(m_x[i],a,mu,gamma,nu);
     }
  };
//+------------------------------------------------------------------+
//| Method for loading data from the .CSV file                       |
//+------------------------------------------------------------------+
bool CECCalculator::LoadData(string filename)
  {
   int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   m_size=0;
   while(!FileIsEnding(filehandle))
     {
      string str=FileReadString(filehandle);
      if(str!="")
        {
         string astr[];
         StringSplit(str,';',astr);
         if(ArraySize(astr)==2)
           {
            ArrayResize(m_x,m_size+1);
            ArrayResize(m_y,m_size+1);
            m_x[m_size]=StringToDouble(astr[0]);
            m_y[m_size]=StringToDouble(astr[1]);
            m_size++;
           }
         else
           {
            m_size=0;
            return(false);
           }
        }
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for saving data into the .CSV file                        |
//+------------------------------------------------------------------+
bool CECCalculator::SaveData(string filename)
  {
   if(m_size==0) return(false);
   if(ArraySize(m_x)!=ArraySize(m_y)) return(false);
   if(ArraySize(m_x)==0) return(false);
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   for(int i=0; i<ArraySize(m_x); i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the integral                       |
//+------------------------------------------------------------------+
double CECCalculator::Integrate(double &x[],double &y[],int ind)
  {
   double sum=0;
   for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5;
   return(sum);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function Y(x)                  |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the function X1(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X2(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i]));
   ArrayResize(x2,m_size);
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X3(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i]));
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the eigen-coordinates              |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoordinates()
  {
   CalcY(m_ec_y);
   CalcX1(m_ec_x1);
   CalcX2(m_ec_x2);
   CalcX3(m_ec_x3);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the correlator                     |
//+------------------------------------------------------------------+
double CECCalculator::Correlator(int ind1,int ind2)
  {
   if(m_size==0) return(0);
   if(ind1<=0 || ind1>4) return(0);
   if(ind2<=0 || ind2>4) return(0);
//---
   double arr1[];
   double arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
//---
   switch(ind1)
     {
      case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
   switch(ind2)
     {
      case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
//---
   double sum=0;
   for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i];  }
   sum=sum/m_size;
   return(sum);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the linear expansion coefficients  |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoefficients()
  {
//--- setting the matrix size 3x4
   m_matrix.SetSize(3,4);
//--- calculation of the correlation matrix 
   for(int i=3; i>=1; i--)
     {
      string s="";
      for(int j=1; j<=4; j++)
        {
         double corr=Correlator(i,j);
         m_matrix.Set(i,j,corr);
         s=s+" "+DoubleToString(m_matrix.Get(i,j));
        }
      Print(i," ",s);
     }
//--- solving the system of the linear equations
   m_matrix.GaussSolve(m_ec_coefs);
//--- displaying the solution - the obtained coefficients C1,..CN 
   for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]);
  };
//+--------------------------------------------------------------------+
//| Method for the calculation of the function parameters a,mu,nu,gamma|
//+--------------------------------------------------------------------+
void CECCalculator::CalculateParameters()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//--- calculate a
   double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1]));
//--- calculate mu
   double mu=-m_ec_coefs[2]/m_ec_coefs[1];
//--- calculate nu
   double nu=m_ec_coefs[1];
//--- calculate gamma
   double arr1[],arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
   double corr1=0;
   double corr2=0;
   for(int i=0; i<m_size; i++)
     {
      arr1[i]=MathPow(m_x[i],nu);
      arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]);
      corr1+=arr1[i]*arr2[i];
      corr2+=arr1[i]*arr1[i];
     }
   double gamma=-corr1/corr2;
//---
   Print("a=",a);
   Print("mu=",mu);
   Print("nu=",nu);
   Print("gamma=",gamma);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the functions                      |
//| f1=Y-C2*X2-C3*X3                                                 |
//| f2=Y-C1*X1-C3*X3                                                 |
//| f3=Y-C1*X1-C2*X2                                                 |
//+------------------------------------------------------------------+
void CECCalculator::CalculatePlotFunctions()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//---
   ArrayResize(m_f1,m_size);
   ArrayResize(m_f2,m_size);
   ArrayResize(m_f3,m_size);
//---
   for(int i=0; i<m_size; i++)
     {
      //--- plot function f1=Y-C2*X2-C3*X3
      m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f2=Y-C1*X1-C3*X3
      m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f3=Y-C1*X1-C2*X2
      m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i];
     }
  }
//+------------------------------------------------------------------+
//| Method for saving the calculation results                        |
//+------------------------------------------------------------------+
void CECCalculator::SaveResults(string filename)
  {
   if(m_size==0) return;
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI);
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename," for writing, error",GetLastError());
      return;
     }
   for(int i=0; i<m_size; i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+=DoubleToString(m_ec_y[i],8)+";";
      s+=DoubleToString(m_ec_x1[i],8)+";";
      s+=DoubleToString(m_f1[i],8)+";";
      s+=DoubleToString(m_ec_x2[i],8)+";";
      s+=DoubleToString(m_f2[i],8)+";";
      s+=DoubleToString(m_ec_x3[i],8)+";";
      s+=DoubleToString(m_f3[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CECCalculator ec;
//--- model function data preparation
   ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3);
//--- saving into the file
   ec.SaveData("ex1.csv");
//--- calculation of the eigen-coordinates
   ec.CalcEigenCoordinates();
//--- calculation of the coefficients
   ec.CalcEigenCoefficients();
//--- calculation of the parameters
   ec.CalculateParameters();
//--- calculation of the functions f1,f2,f3
   ec.CalculatePlotFunctions();
//--- saving the results into the file
   ec.SaveResults("ex1-results.csv");
  }

2.5. R(x) モデル関数計算結果

モデルデータとして区間 [0.25,15.25] でR(x)関数の値を100生成します。

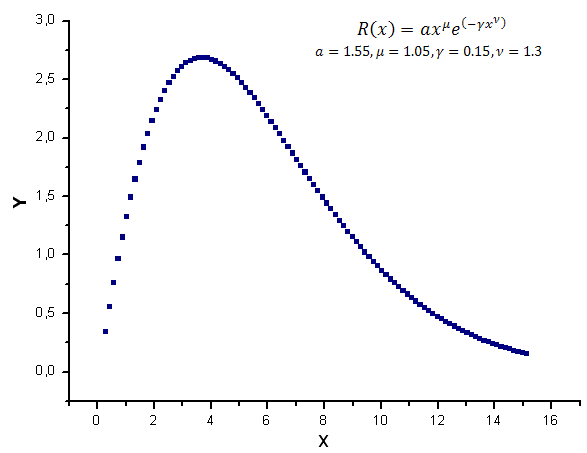
図7　計算に使用されるモデル関数

これらデータは関数 Y(x) と関数 X1(x), X2(x) および X3(x) におけるその展開を描く基礎を提供します。

図8では関数 Y(x) とその『固有座標』X1(x)、 X2(x)、 X3(x)が示されています。

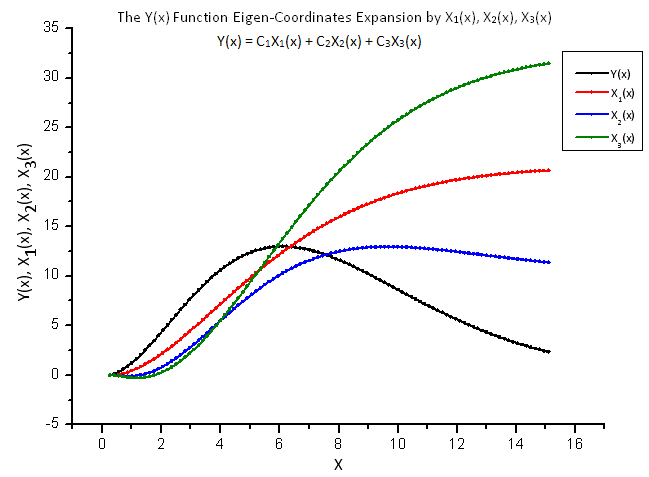
図8　関数 Y(x) および固有座標 X1(x)、X2(x)、 X3(x)の一般形式

オペレータ X1(x)、 X2(x) 、 X3(x) の積分性質の結果をもたらす関数の平滑度に注意が必要です。

関数 Y(x)、X1(x)、X2(x)、X3(x) の計算に続き、相関行列が作成され、係数 C1、C2、 C3に対する式が解かれ、取得された値を基にR(x) 関数パラメータが計算されます。

2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1  221.03637620 148.53278281 305.48547011 101.93843241
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2  148.53278281 101.63995012 202.85142688 74.19784681
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3  305.48547011 202.85142688 429.09345292 127.82779760

ここで計算された展開の線形性を確認します。このためには3つの関数を計算する必要があります。

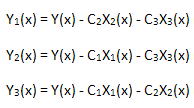
それはどれも固有座標 X1(x)、X2(x)、 X3(x)の基底について予測されます。

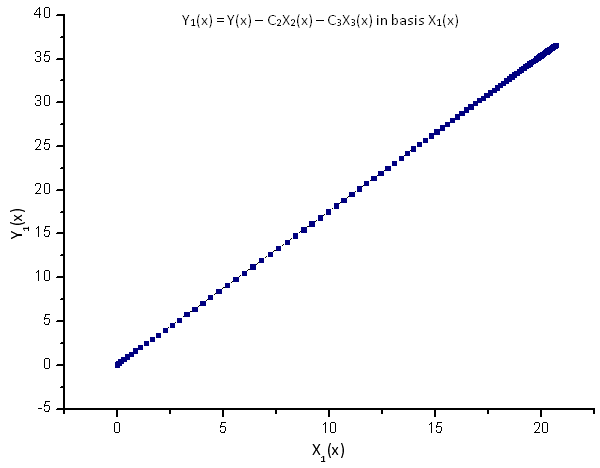
図9　基底 X1(x) における関数 Y1(x) の描写

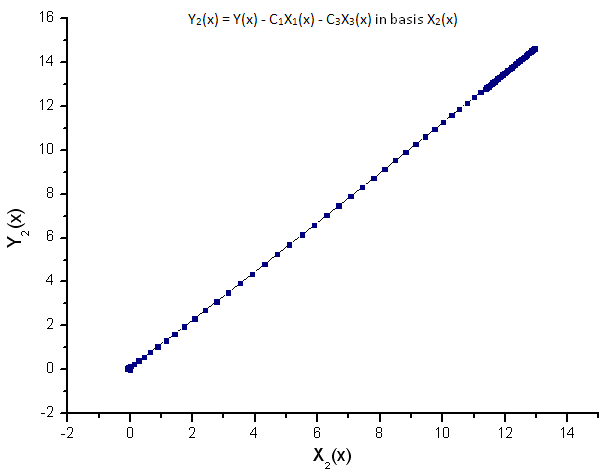
図10　基底X2(x) における関数 Y2(x) の描写

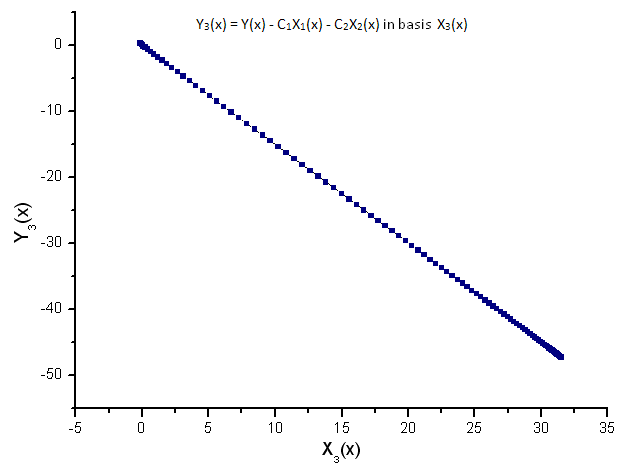
図11　基底X3(x) における関数 Y3(x) の描写

プロットされた関数の線依存性は図7のデータ系列が関数R(x)に正確に対応していることを意味しています。

R(x) 固有座標で表されるその他あらゆる関数（形は似通っていても）はもはや線形ではありません。このことにより関数の同定が可能となるのです。

ポイントの数値が10000まで増えれば（同一区間を保持している間）モデル関数パラメータの計算精度は改善することができます。

2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1  225.47846911 151.22066473 311.86134419 104.65062550
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2  151.22066473 103.30005101 206.66297964 76.03285182
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3  311.86134419 206.66297964 438.35625824 131.91955339

この場合、関数パラメータはより正確に計算されています。

2.6. ノイズ効果

実際の実験データには必ずノイズが含まれています。

ECCCalculatorクラスの GenerateData() メソッド内の次を

m_y[i]=R(m_x[i],a,mu,gamma,nu);

以下と置き換えます。

m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;

その際ランダムノイズを加え、それを最大関数値の約 10% にします。

以下は EC_Example1-noise.mq5 スクリプトの結果です。

2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1  254.45082565 185.19087989 354.25574000 125.17343164
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2  185.19087989 136.81028987 254.92996885 97.14705491
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3  354.25574000 254.92996885 501.76021715 159.49440494

ランダムノイズを伴うモデル関数グラフは図12に示しています。

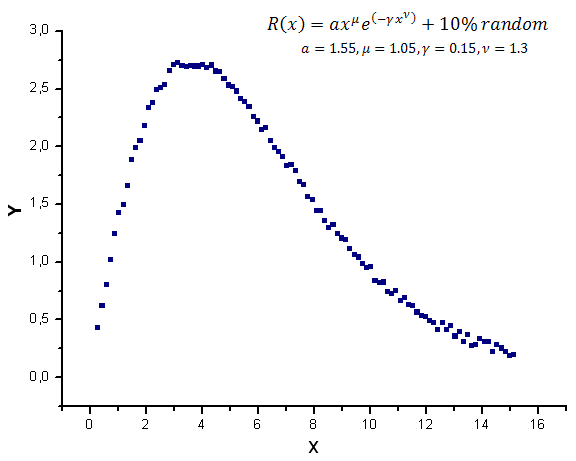
図12　計算に使用されるノイズを含んだモデル関数

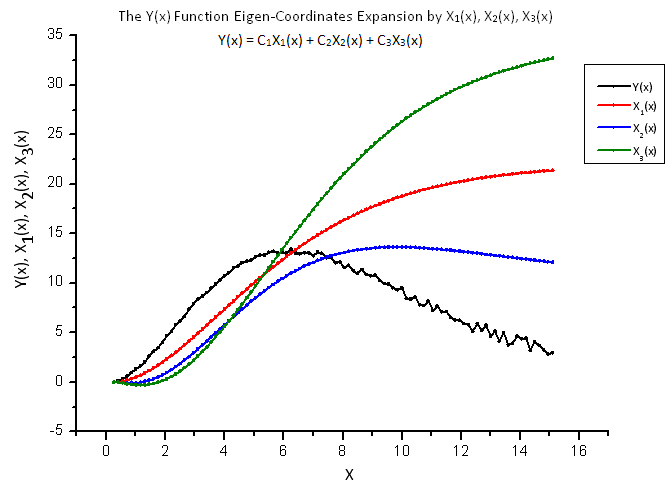
図13　関数 Y(x) および固有座標 X1(x)、X2(x)、 X3(x)の一般形式

固有座標としての関数 X1(x)、X2(x)、X3(x) はまだ似通って見えますが、線形コンビネーションとしてプロットされている Y(x) は異なって見えます（図13）。

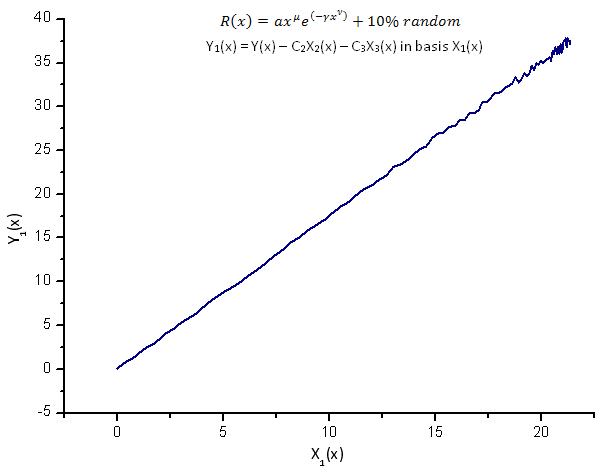
図14　基底 X1(x) における関数 Y1(x) の描写

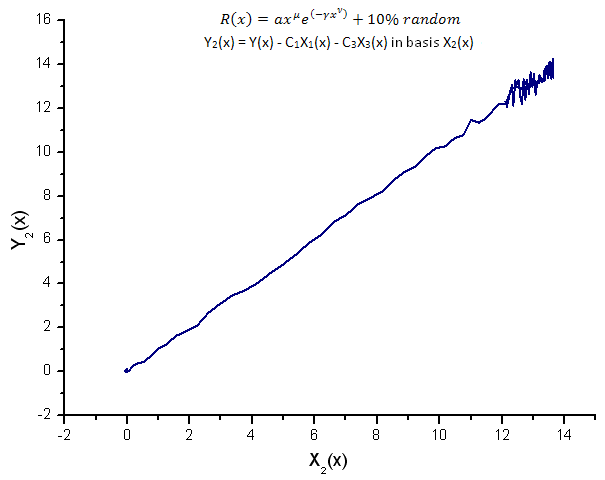
図15　基底X2(x) における関数 Y2(x) の描写

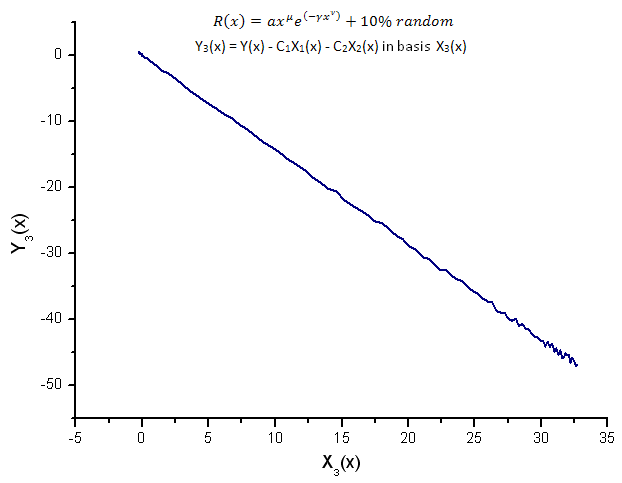
図16　基底X3(x) における関数 Y3(x) の描写

固有座標（図8～10）を基にした関数 Y1(x)、Y2(x)、Y3(x) はまだ線形をしていますが、ノイズのおかげで直線にぶれがあるのがわかります。シグナル／ノイズが最小になる場所で X が大きくなるに従いそれがはっきりと判ります。

ここではノイズ構成は直線の両側にあり、この場合このことで積分固有座標展開を使用するのが便利です（2.2項）。

3. 非加法確率分布

統計力学を一般化することで分布につながります。[2, 22]

ここで、

q ガウス分布は関数 P2(x)の特殊な場合です。

3.1. P1(x) 関数固有座標展開

P1(x)を微分します。

以下が結果としての微分方程式です。

期間 [xm,x]について積分します。

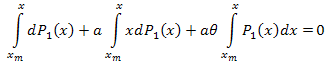
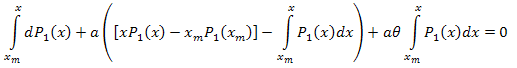
そうすると

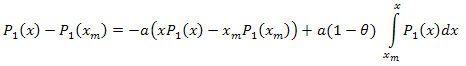
以下は固有座標展開です。

ここで

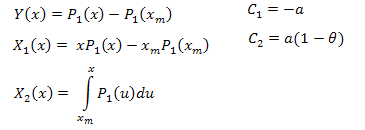
計算用の関数は以下(EC_Example2.mq5)に説明されています。

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
//--- Y=P(x)-P(xm)
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
//--- X1=x*P(x)-xm*P(xm)
   for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
//--- X2=Integrate(P1(x)) 
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i);
  }

今回、相関行列サイズは 2x3、パラメータ値は a で P1(x) 関数の θ は係数 С1 および C2を基に決められます。パラメータ B の数値は正規化要件から取得可能です。

以下は区間 x [0,10] についての P1(x,1,0.5,2) モデル関数計算結果で、使用されているポイント数は 1000です。

2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1  0.15420524 0.48808959 -0.32145543
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2  0.48808959 1.79668322 -1.14307410

関数 P1(x) およびその固有座標展開は図17～20に示されています。

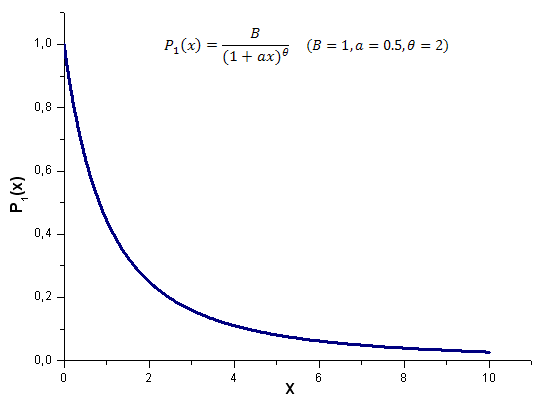
図17　計算に使用されたモデル関数 P1(x, 1, 0.5, 2) 、ポイント数 1000

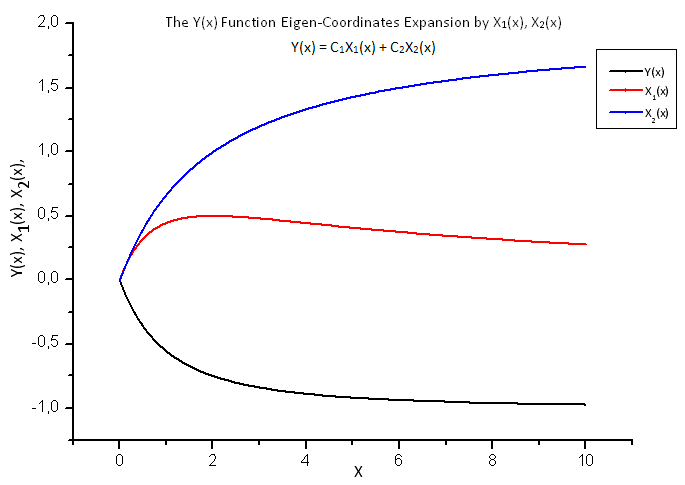
図18　関数 Y(x) と固有座標 X1(x) および X2(x)の一般形態

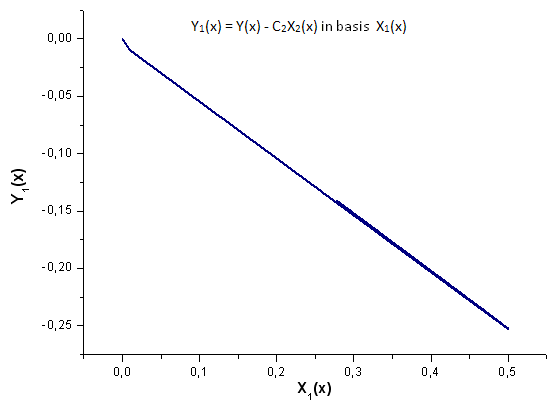
図19　基底 X1(x) における関数 Y1(x) の描写

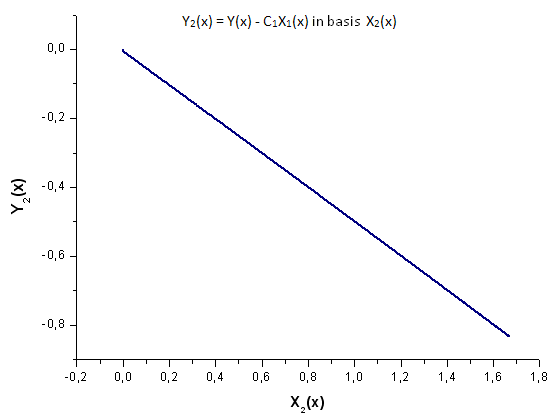
図20　基底X2(x) における関数 Y2(x) の描写

図19をよく見てみます。グラフのごく最初と3分の2の部分にわずかに線のゆがみがあります。

これは計算された展開の特殊性に関連しています。 - X1(x) は積分特質ではありません。

3.2. P2(x) 関数固有座標展開

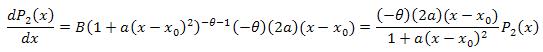
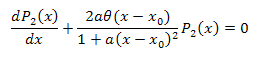
微分方程式

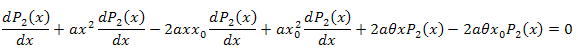
期間 [xm,x]で x に対して積分します。

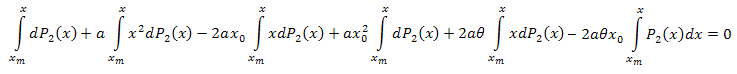
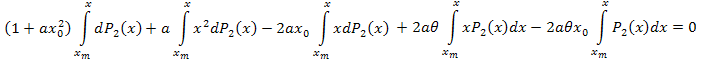
部分積分をすると、以下を得ます。

簡約します。

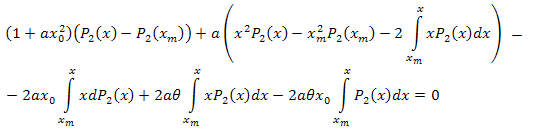
代数操作のあと、次のようになります。

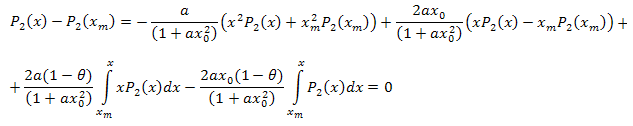
よって結果の展開は以下です。

ここで

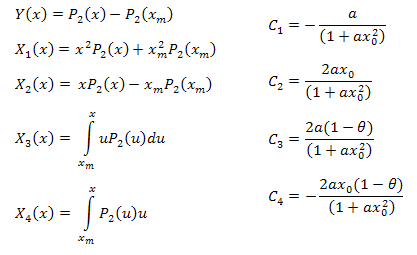
下の式を利用して関数パラメータが計算できます。

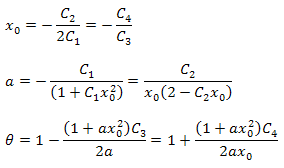
結果として得た展開のパラメータ間には別の関係があることに注意が必要です。このことは分析するために選択される関数の正確性を検証するのに使用することができます。こういった関係はつねに関数 P2(x)に正確に対応しているデータに対して真です。

パラメータ B の数値は正規化要件から取得可能です。

固有座標の計算用関数は以下です。 (EC_Example3.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm)
   for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
   //--- X2=(x)*P2(x)-(xm)*P2(xm)
   for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX3                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i];
   //--- X3=Integrate(X*P2(x)) 
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);  
  }
//+------------------------------------------------------------------+
//| CalcX4                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX4(double &x4[])
  {
   if(m_size==0) return;
   //--- X4=Integrate(P2(x))
   ArrayResize(x4,m_size);
   for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i);
  }

下記はモデル関数 P2(x) の計算結果です(B=1, a=0.5, theta=2, x0=1)。使用されているポイント数は 1000です。

2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1  1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2  0.60684314 0.37995888 0.55974145 0.58899739 0.06731011
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3  1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4  1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168

関数 P2(x) およびその固定座標展開は図21～26に示されています。

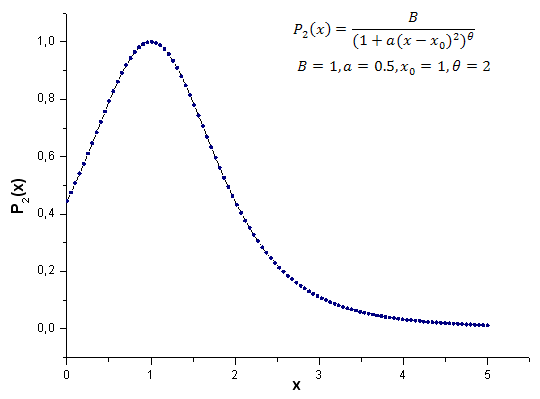
図21　計算に使用されたモデル関数 P2(x,1,0.5,2,1) 、ポイント数は 100

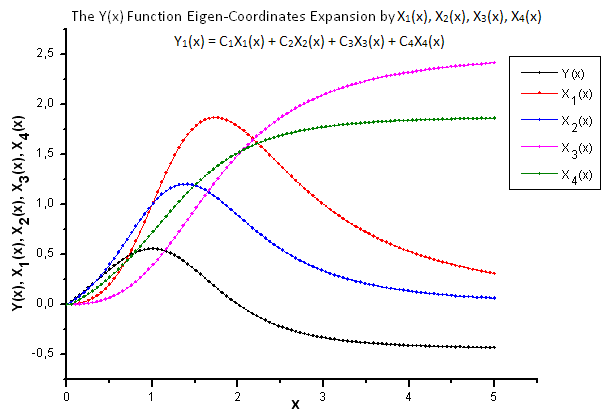
図22　関数 Y(x) および固有座標 X1(x)、X2(x)、 X3(x)、X4(x) の一般形式

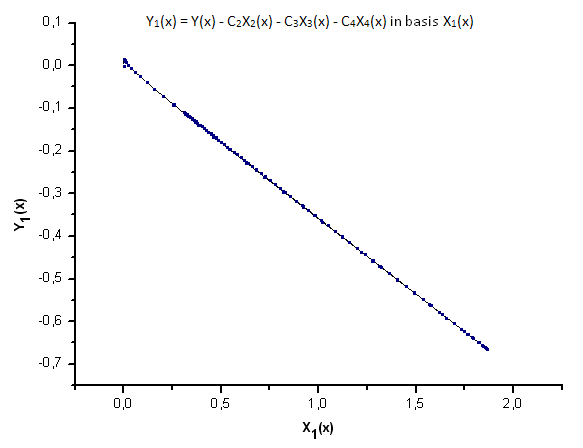
図23　基底 X1(x) における関数 Y1(x) の描写

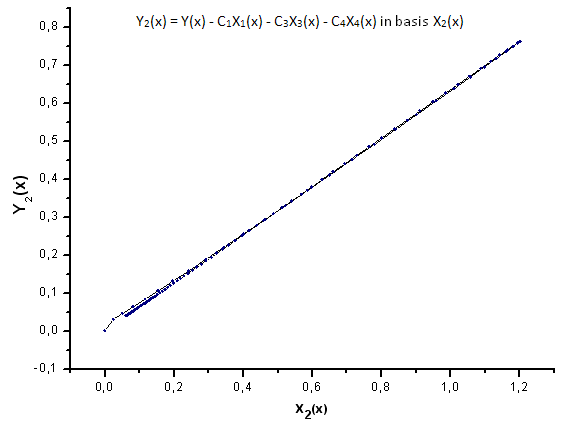
図24　基底X2(x) における関数 Y2(x) の描写

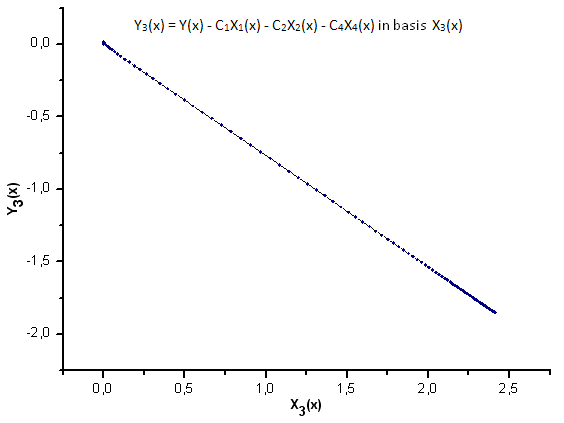
図25　基底X3(x) における関数 Y3(x) の描写

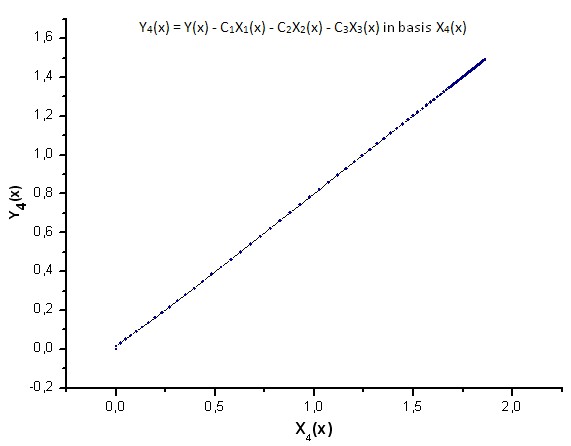
図26　基底X4(x)における関数 Y4(x) の描写

4. 似て非なるもの

qガウス分布族は非加法的統計力学のちょうど中心に位置し、そのためそれが一般化された中心極限定理に現れるであろうと予想するのは当然でした。自身で主要引数としての役目をするエントロピーの考察 [26]

ただし、記事 [18、プレゼンテーション] は qガウス分布のような分布は汎用的ではなく、そのため限定的分布としての特殊な役割に疑問を投げかけているということを示しました。

たとえば、関数（問題の一つに対する分析的解決）

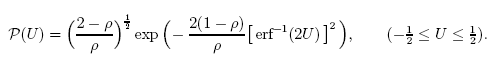
はqガウス分布を用いるとひじょうに正確に表現できます。

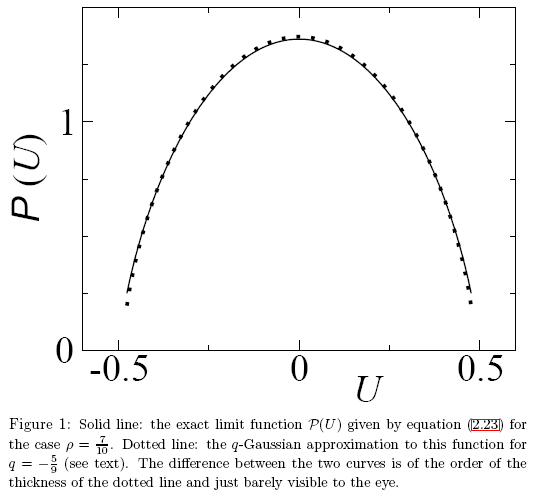
図27　記事 "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics" からの一例

この場合、分析的に異なる関数は似た数値を持ち、そのため違いを目で確認するのはかなり困難です。正確な関数同定手法が必要です。この問題は固有座標法を使うことでうまく解決することができます。

P(U) 関数固有座標展開例を振り返り、qガウス分布との違いを決定づけているものは何か示します。関数は見た目にはひじょうに似ています（図27）。

シグナル（P(U) 関数の100個の値）を作成し、3.2.項で描いたP2(x) 関数の固有座標システムにおいてその信号を『予測』します。

Hilhorst-Schehr-problem.mq5 スクリプトにより P(U) 関数を計算し、MQL5\Files\test-data.csv ファイルに保存するデータ系列を構築します。これらデータは EC_Example3_Test.mq5により分析されます。

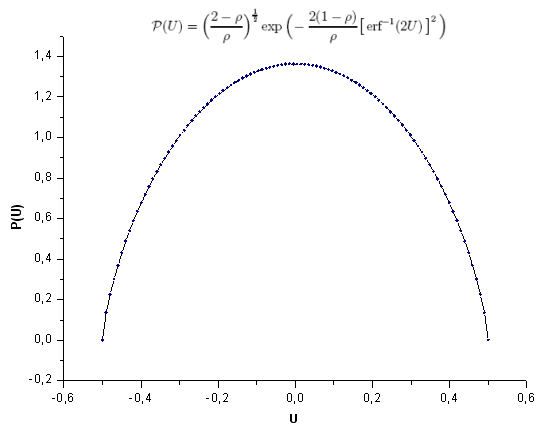
図28　モデル関数 P(U)、ポイント数 100

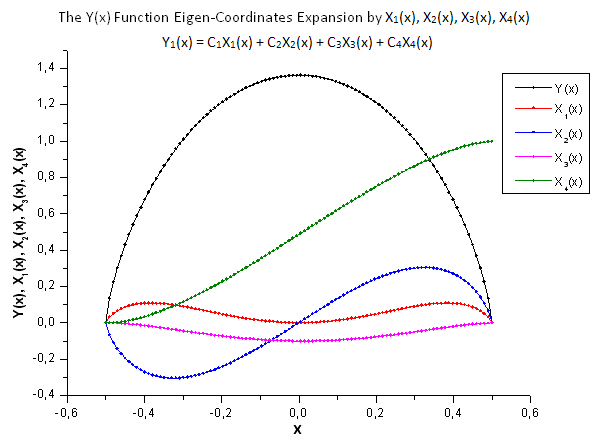
図29　関数 Y(x) および固有座標 X1(x)、X2(x)、 X3(x)、X4(x) の一般形式

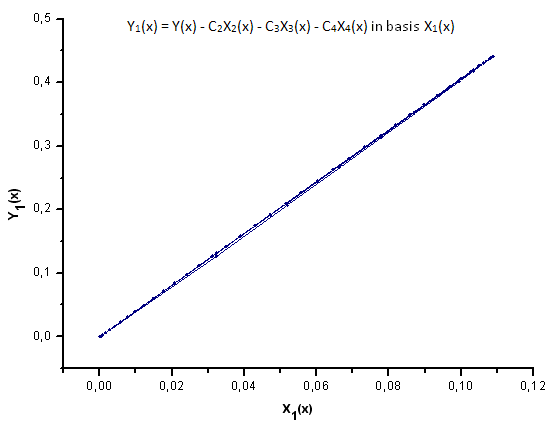
図30　基底 X1(x) における関数 Y1(x) の描写

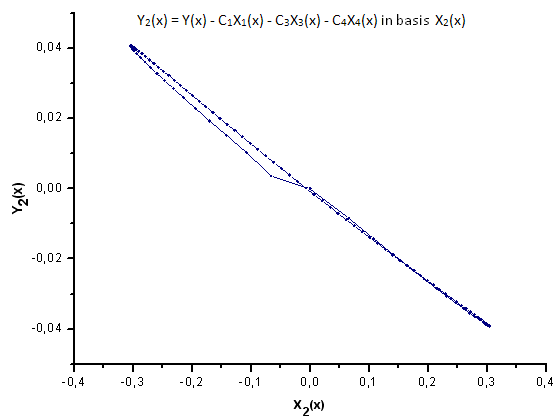
図31　基底X2(x) における関数 Y2(x) の描写

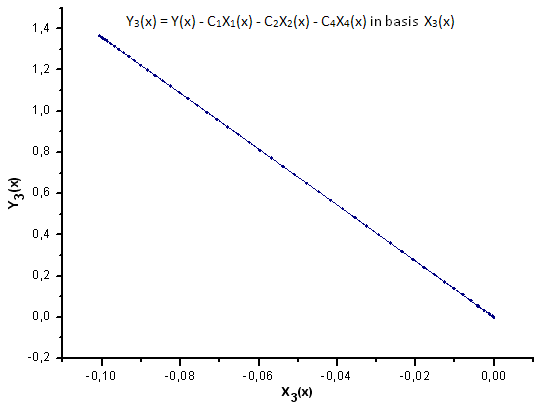
図32　基底X3(x) における関数 Y3(x) の描写

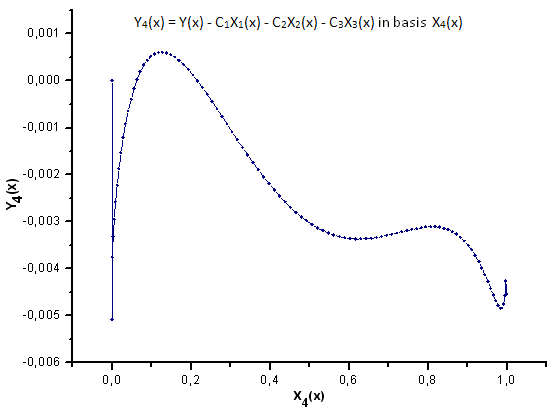
図33　基底X4(x)における関数 Y4(x) の描写

図30～33が示すように、関数 P2(x) および P(U) は座標 X1(x)、X2(x)、 X3(x) に関してはひじょうに似ています。- Xi(x) と Yi(x)の間によい線形の依存性が観測されます。大きな違いは X4(x) コンポーネントに見ることができます（図33）。

X4(x) コンポーネントに線形の依存性がないことは qガウス分布に似て見えるにもかかわらず、P(U) によって作成されたデータは実際には q ガウス分布ではないことを証明しています。

Xi(x) と Yi(x) を一緒にプロットすることで関数に対して別の見かたをすることができます（図34～図37）。

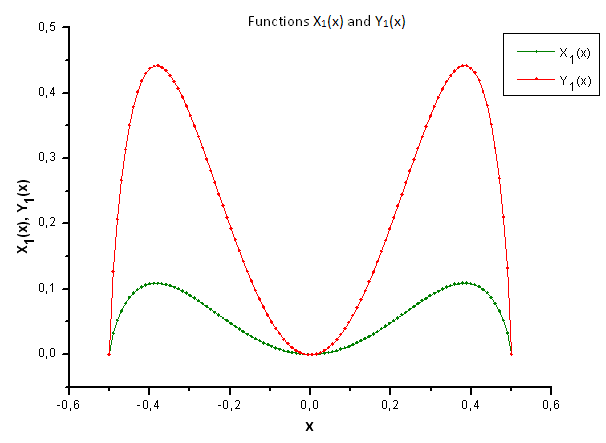
図34　関数 X1(x) および Y1(x)の一般形態

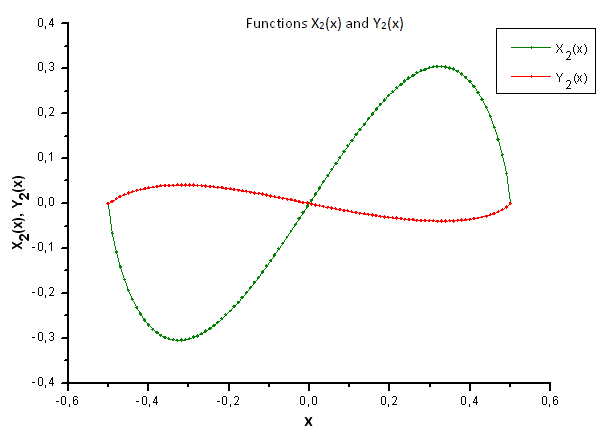
図35　関数 X2(x) および Y2(x)の一般形態

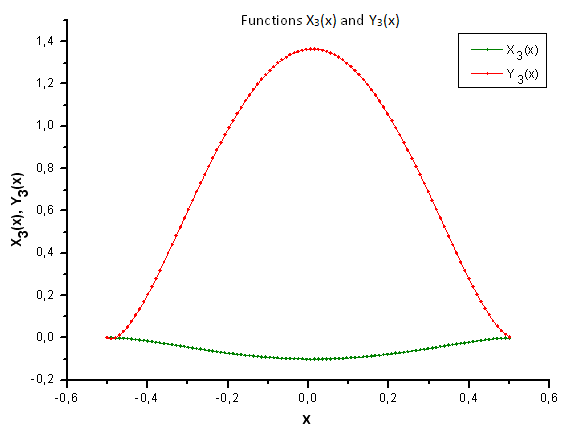
図36　関数 X3(x) および Y3(x)の一般形態

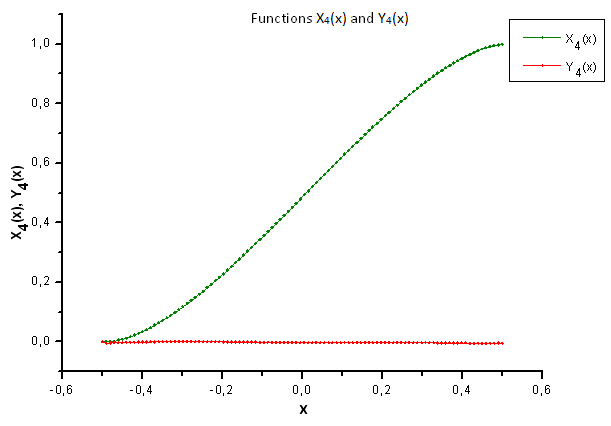
図37　関数 X4(x) および Y4(x)の一般形態

図37が示すように、 P2(x) 関数の固有座標においてP(U) 関数によって作成されるデータを予測するとき、X4(x) コンポーネントにおける構造が異なるのは明らかです。よって実験データは P2(x) 関数に対応していないことが明確に言えます。

以下に記述されている計算(EC_Example3_test) はこれを裏づけています。

2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1  0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2  0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3  -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4  0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994

それはまたパラメータ間の関係も低下させます。

おわりに

固有座標法は関数の関係についての構造的プロパティを分析するのに優れたツールであり、それにより分析とデータ解釈を大幅に簡素化することができます。

この手法の背後にあるコンセプトは実験的データセット {xi,yi} を使用して、提案のモデルに対欧する新しい関数をｐ構築することです。オペレータ展開形式はデータ記述のための『候補』の役目をする関数が成立させる微分方程式のストラクチャによって決定されます。関数がネイティブであれば、データ {xi,yi}を使用して計算される関数展開は、固有座標の基底において線形を取ります。『候補関数』の固有座標基底における線形性の偏差はデータ{xi,yi} が既定の関数から生成されたものではないかもしれないこと、そして構築されるモデルは適切ではないことを示します。

複雑なケースでは、候補者関数とネイティブ関数はひじょうに似通って見え、計算された展開の大きな部分は線形であることがわかります。そればかりか、固有座標法により低下された展開の線形性によってあることが判るこういった関数間の違いを特定することができます。 - Hilhorst と Schehr の例は X4(x)を予測する際、最後の展開メンバーに置いて違いが明らかになっていることを説明する役割を担いました。

この情報は関数P2(x)によって成立する微分方程式（3.2.項）を使うのにも有用です。 - 問題のメンバーは P2(x)に関して線形部分に対応します。実験的データの現象論的記述の場合はそれほど興味を引かれるものではないかもしれません（"we are looking for a solution in the form of the q-Gaussian"）。とはいうものの、モデルが異なる式（図3）を基にしているなら、物理的プロセスのモデルを考慮するそれぞれのメカニズムの役割は理解しやすいかもしれません。

参照資料

C. Tsallis, "Possible Generalization of Boltzmann-Gibbs Statistics", Journal of Statistical Physics, Vol. 52, Nos. 1/2, 1988.
C. Tsallis, "Nonextensive Statistics: Theoretical, Experimental and Computational Evidences and Connections". Brazilian Journal of Physics, (1999) vol. 29. p.1.
C. Tsallis, "Some Comments on Boltzmann-Gibbs Statistical Mechanics", Chaos, Solitons & Fractals Volume 6, 1995, pp. 539–559.
Europhysics News "Special Issue: Nonextensive Statistical Mechanics: New Trends, New Perspectives", Vol. 36 No. 6 (November-December 2005).
M. Gell-Mann, C. Tsallis, "Nonextensive Entropy: Interdisciplinary Applications", Oxford University Press, 15.04.2004, 422 p.
Constantino Tsallis, the Official Website Nonextensive Statistical Mechanics and Thermodynamics.
Chumak, O.V. "Entropy and Fractals in Data Analysis", М.-Izhevsk: RDC "Regular and Chaotic Dynamics", Institute for Computer Research, 2011. - 164 p.
Qiuping A. Wang, "Incomplete Statistics and Nonextensive Generalizations of Statistical Mechanics", Chaos, Solitons and Fractals, 12(2001)1431-1437.
Qiuping A. Wang, "Extensive Generalization of Statistical Mechanics Based on Incomplete Information Theory", Entropy, 5(2003).
Lisa Borland, "Long-Range Memory and Nonextensivity in Financial Markets", Europhysics News 36, 228-231 (2005)
T. S. Biró, R. Rosenfeld, "Microscopic Origin of Non-Gaussian Distributions of Financial Returns", Physica A: Statistical Mechanics and its Applications, Vol. 387, Nr. 7 (Mar 1, 2008) , p. 1603-1612 (preprint).
S. M. D. Queiros, C. Anteneodo, C. Tsallis, "Power-Law Distributions in Economics: A Nonextensive Statistical Approach", Proceedings of SPIE (2005) Volume: 5848, Publisher: SPIE, Pages: 151-164, (preprint)
R Hanel, S Thurner, "Derivation of Power-Law Distributions within Standard Statistical Mechanics", Physica A: Statistical Mechanics and its Applications (2005), Volume: 351, Issue: 2-4, Publisher: Elsevier, Pages: 260-268. (preprint)
A K Rajagopal, Sumiyoshi Abe, "Statistical Mechanical Foundations of Power-Law Distributions", Physica D: Nonlinear Phenomena (2003), Volume: 193, Issue: 1-4, Pages: 19 (preprint)
T. Kaizoji, "An Interacting-Agent Model of Financial Markets from the Viewpoint of Nonextensive Statistical Mechanics", Physica A: Statistical Mechanics and its Applications, Vol. 370, N. 1 (Oct 1, 2006) , p. 109-113. (preprint)
V. Gontis, J. Ruseckas, A. Kononovičius, "A Long-Range Memory Stochastic Model of the Return in Financial Markets", Physica A: Statistical Mechanics and its Applications 389 (2010) 100-106. (preprint)
H.E. Roman, M. Porto, "Self-Generated Power-Law Tails in Probability Distributions", Physical Review E - Statistical, Nonlinear and Soft Matter Physics (2001), Volume: 63, Issue: 3 Pt 2, Pages: 036-128.
H. J. Hilhorst, G. Schehr, "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics" (2007, preprint, presentation).
D. J. Hudson, "Lectures on Elementary Statistics and Probability", CERN-63-29, Geneva : CERN, 1963. - 101 p.
D. J. Hudson, "Statistics Lectures II : Maximum Likelihood and Least Squares Theory", CERN-64-18. - Geneva : CERN, 1964. - 115 p.
R. R. Nigmatullin, "Eigen-Coordinates: New Method of Analytical Functions Identification in Experimental Measurements", Applied Magnetic Resonance Volume 14, Number 4 (1998), 601-633.
R.R. Nigmatullin, "Recognition of Nonextensive Statistical Distributions by the Eigencoordinates Method", Physica A: Statistical Mechanics and its Applications Volume 285, Issues 3–4, 1 October 2000, pp. 547–565.
C. Antonini "q-Gaussians in Finance" (2010).
C. Antonini, "The Use of the q-Gaussian Distribution in Finance" (2011).
L. G. Moyano, C. Tsallis, M. Gell-Mann, "Numerical Indications of a q-Generalised Central Limit Theorem", Europhysics Letters 73, 813-819, 2006, (preprint).
T. Dauxois, "Non-Gaussian Distributions under Scrutiny", J. Stat. Mech. (2007) N08001. (preprint)

付録Qガウス分布によるSP500前日比分析

SP500 前日比率(P2(x) function)に対するqガウス分布法のよくある成功例（図4）を考察します。

http://wikiposit.org/w?filter=Finance/Futures/Indices/S__and__P%20500/から日次データを利用しました。

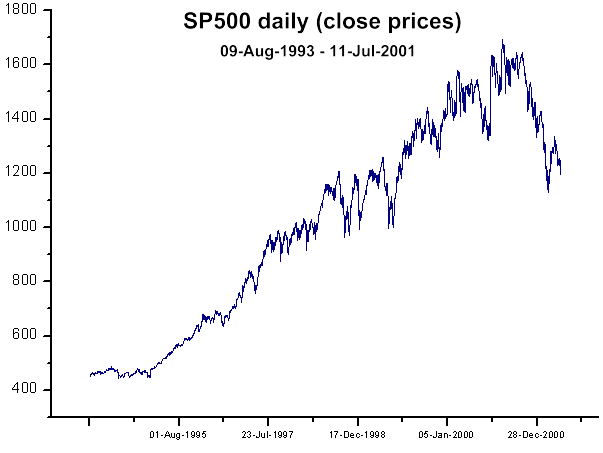
図38　SP500 終値（日次）

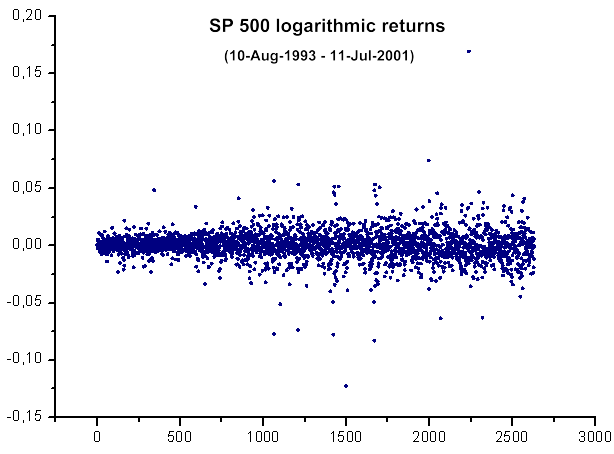
図39　SP500 対数利益率

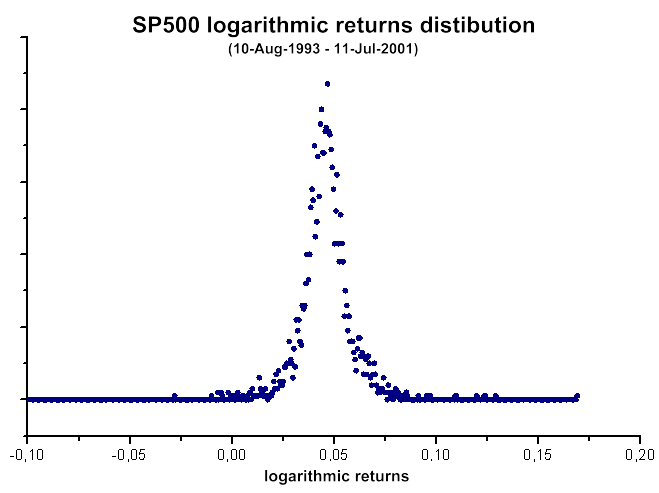
図40　SP500 対数利益率分布

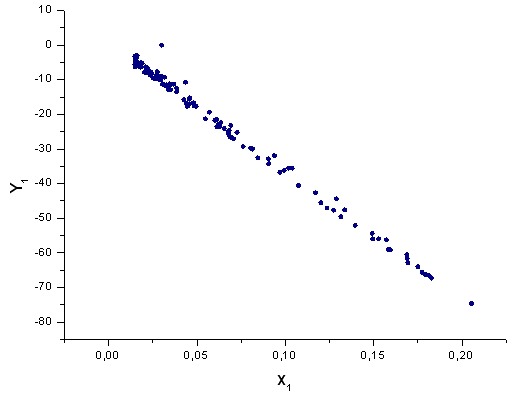
図41　基底 X1(x) における関数 Y1(x)

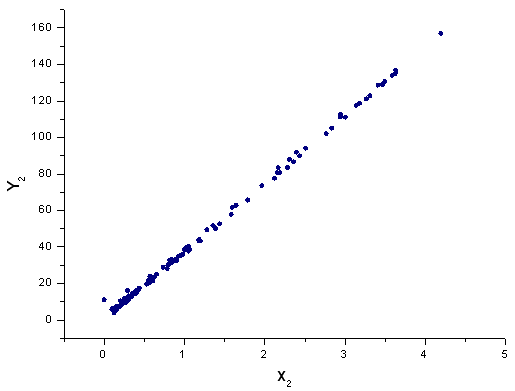
図42　基底 X2(x) における関数 Y2(x)

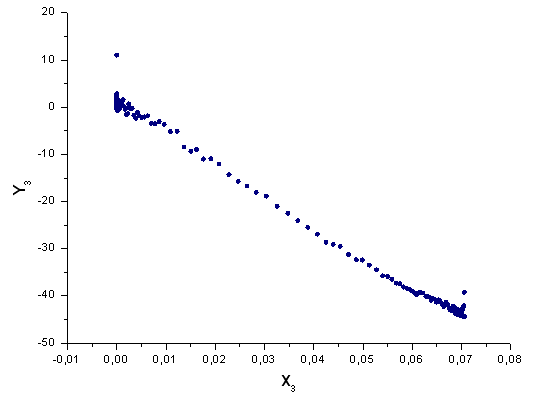
図43　基底 X3(x) における関数 Y3(x)

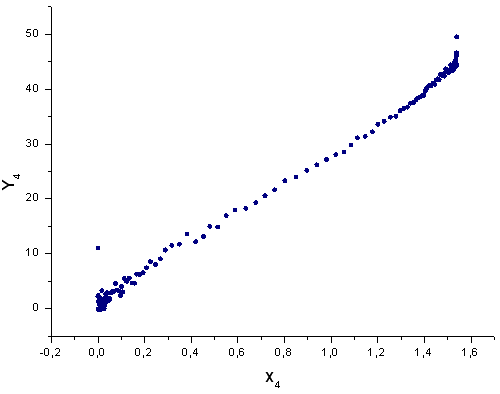
図44　基底 X4(x) における関数 Y4(x)

ご自身のターミナルで分析を行うには、ファイル SP500-data.csv must be placed to \Files\ folderを参照ください。

その後、スクリプトを2つ導入する必要があります。

CalcDistr_SP500.mq5 （分布を計算します。）
q-gaussian-SP500.mq5 （固有座標分析）

以下が結果です。

2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: theta=1.770125768485269
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: theta=1.864132228192338
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: a=2798.166930885822
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: a=8676.207867097581
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: x0=0.04567518783335043
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: x0=0.0512505923716428
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C1=-364.7131366394939
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C2=37.38352859698793
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C3=-630.3207508306047
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C4=28.79001868944634
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1  0.00177913 0.03169294 0.00089521 0.02099064 0.57597695
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2  0.03169294 0.59791579 0.01177430 0.28437712 11.55900584
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    3  0.00089521 0.01177430 0.00193200 0.04269286 0.12501732
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    4  0.02099064 0.28437712 0.04269286 0.94465120 3.26179090
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    checking distibution cnt=2632.0 n=2632
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    Min=-0.1229089015984444 Max=0.1690557338964631 range=0.2919646354949075 size=2632
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    Total data=2633

qの推定値。固有座標法により得られます。(q=1+1/theta): q～1.55

値は本に報告されています（図4）q～1.4。

結論：一般的にこれらデータは qガウス関数によって記述することができるのは判ります。qガウス分布を用いてうまく説明をしているのは本に報告されているとおりです。