一連の取引に対するリスク評価

Aleksey Nikolayev | 25 10月, 2017


序章

この記事では、ポジションのボリュームを管理する上でラルフ·ヴィンスのアイデアをなぞります。 (同様にケリー式を使います) これは最適な f とも呼ばれます。 この理論では、f はあらゆる取引のリスクにさらされる資金の一部分です。 ビンスによると、f は利益の最適化 (最大化) の条件に応じて選択されます。 トレーディングでこの理論を使用する場合、2つの問題があります。 これらは:

  1. 大きすぎるアカウントのドローダウン。
  2. fは取引のヒストリーで知られます。

問題を解決する試みは、この記事の目的の1つにすぎません。 もう一つの問題は、トレードシステムの分析に確率と数学的な統計の理論を導入することです。 主なトピックから時折偏差が発生します。 基本の講釈は省きます。 必要性であれば「The Mathematics of Technical Analysis: Applying Statistics to Trading Stocks, Options and Futures」参照してください。

この記事では、例を特筆します。 その記事の理論の実例です。従って、実際のトレードで使用することは推薦されません。

イントロダクション. 不確実性の欠如

シンプルにするため、資産の価格は資本の単位ではなく、他のメソッドラウンドでその単位の値を表現すると仮定しましょう。 最小ボリュームステップは、資産の単位の固定値です。 トレードの最小のゼロ以外のボリュームは、これに等しくなります。 シンプルなトレードモデルを使用します。

定義される各取引タイプ (買いまたは売り)、記入項目の価格とボリュームv 、ストップロスおよび決済p エントリー、 pストップおよびp 決済。

明白な制約があります:

  • ゼロ以上のボリュームv ≥ 0
  • ストップ価格は、買いのエントリー価格より低くする必要があります: pstop< penter
  • ストップ価格は、売りのエントリー価格よりも大きくする必要があります: pstop> penter

次の表記法をしましょう:

  • C0 —トレードに入る前の資金;
  • C1 -トレードを決済した後の資本金;
  • C -ストップロスが発生した後の資本金。
  • r —ストップロスが発生したときに失われた初期資本のシェア

これはC0− Cs= rC0です。

買いのタイプの取引C1=C0+v(pexit−penter) and Cs=C0−v(penter−pstop)。

売りのタイプの取引: C1=C0+v(penter−pexit) and Cs=C0−v(pstop−penter)。

調整するとこうなります。 C1=C0(1+ra) ただし、 a=(pexit−penter)/(penter−pstop). この式は、両方の売買タイプに当てはまります。 rの値をコントラクトのリスクとし、aを コントラクト上の利回りとしましょう。

モデルのリスクを管理する問題を明白にしましょう。 >i=1..n,のとき、利回りは、aで nの取引を持っていると仮定してみます。 リスクriを評価しようとしています。 r は、トレードのエントリー時に知られている値にのみ依存することを考慮に入れておく必要があります。 リスクは通常、 0 ≤ r < 1のときri= rと見なされます。 r=rmaxは、 Cn=C0(1+ra1)(1+ra2)…(1+ran)の利益の最大値です。

これと同様のアプローチを持つことになります。 制限を考慮に入れます。 最大ドローダウンと情報のシリーズの平均利回りです。 次の表記法をしましょう:

  • A0 は、すべてのiの最小値です。
  • a = (1+ a2+n)/nは、その算術平均です。

常にA0≤A が達成されるのは、すべて のaiが=A0の場合に限られます。 詳細については、 rを検討してみましょう。

  1. Cn= Cn(r) > 0ここでは、 1 + rA0> 0に従います。 A0≥− 1の場合、すべて0 ≤ r < 1に当てはまります。 、A0<−1の場合は、 0 ≤ r−1/A0を受け取ります。 rに対する追加制限は、遅延によるストップロスによって決済したトレードがある場合にのみ表示されます。 その結果、制限は、 A0<1の場合、rc= 1かつA0≥− 1かつrc= − 1/A 0のとき0 ≤ rc として書き込まれます。

  2. 平均利回りgをCn= C0(1 + gr) ^ nとして定義します。

    average yield

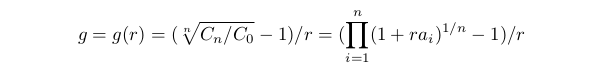
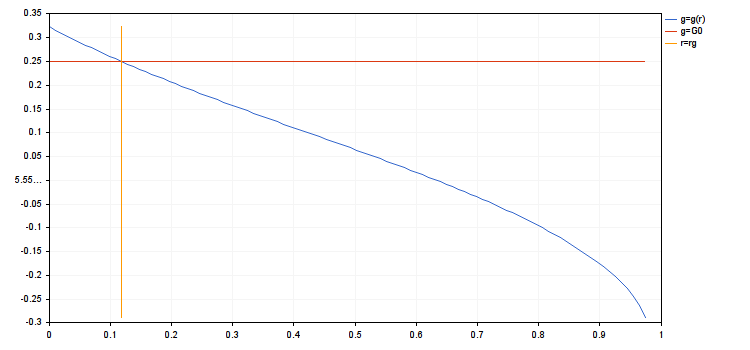
    言い換えれば、 gは、受け入れられたリスクに関連する一連のトレードの平均利回りです。 g (r)関数は、前の点の制約を実行するときに定義されます。 ポイントr = 0で取り外し可能な特異性を持っています: r → 0次にg (r) → Aとそのg (0) = Aを受け入れることができます。 全てのai=A である場合にのみg (r)≡Aを示すことができます。 aiの中で、rが増加しているときに、 g (r)が減少している別のがあります。 この制限は、 g (r) ≥ G0> 0のようになります。 定数G は0 は多くの-トレードの条件、トレーダーの好みなどに依存します。 現在のモデルでは、 G0> Aの場合、不等式を満たすrのセットが空になります。 g0≤ Aの場合、制限は、 0 ≤ r ≤ rg のようになりますが、 rg は式 g (rg) = g0. の解です。この式に解がない場合は、 g= 1となります。

  3. 最大ドローダウンを評価するには、その逆の値を考慮してみましょう:

    minimal gain

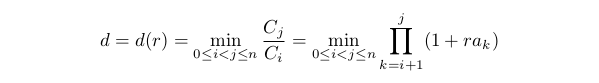
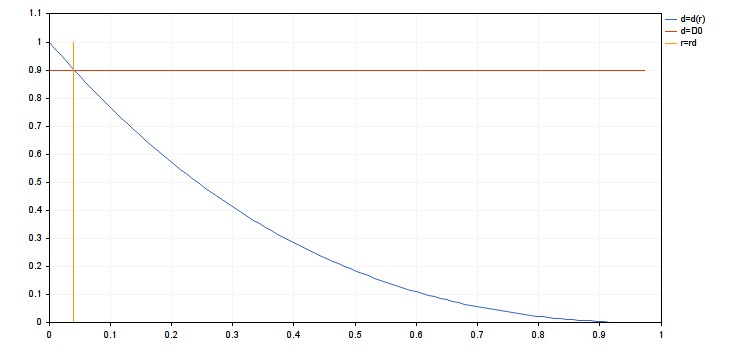
    この値は、最小ゲインと呼ぶことができます。 最初の点で指定された制限が満たされている場合は、常に正で有限であるため便利です。 d (0) = 1であることは明らかです。 A0<0の場合、最初の点で制限されている領域でrが増加すると、 d (r)が減少します。 この制限は、 d (r) ≥ D0 として書き込まれます。 ただし、0 < D0< 1. D0が大きいほど、ドローダウンのサイズが小さくなります。 rd が方程式の解d(rd) = D0 (この方程式が解を持たない場合は、 0 ≤ r ≤ rd として制限を書き換えましょう。その後、 rd= 1)。

  4. トレードがされると、ボリューム v は任意の値を持つことができません。 整数k ≥ 0の値がv = ekv であるΔv> 0によって割り切れるようにしなければなりません。 次に、 i番目のトレードについてです:

    許容リスク

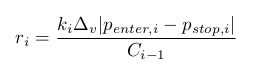
    どうやら、すべてのri の偶然の一致は非常に低い出来事です。 したがって、上記の問題は、正確な解を持っていません。 おおよその解決策を探します。 このような最小のrv を計算するために、 ri は少なくとも1つのゼロ以外の値を[0, rv]で取ることができるように制限します。

    最小限のリスクの評価

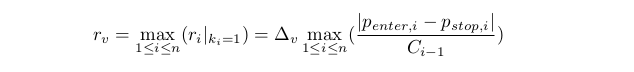
    また、大まかな評価rvr≥rvを決定してみましょう。 前の点の制限を満たすことから続くCi≥ D0C0> 0. そこからは、次のようになります ( d0 とD0 は同じことを意味します)。

    最小限のリスクの大まかな評価

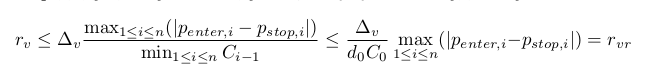
    資本とのより簡単な関係を持っているので、この評価は便利です。 資本の初期値にのみ依存します。

最初の3つの制約を満たすセットが空ではないと仮定します。 次に、[0, ra]という間隔になります。ただし、r a= min (rc、rg、rd)。

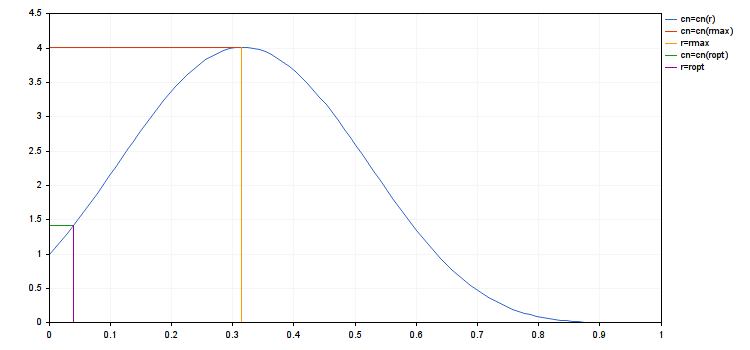
また、4番目の制限も満たされていると仮定します。 、ra≥ rvが必要です。 最大化の問題を考慮するつもりです。Cn= Cn(r). 重要なケースでは、 A > 0かつA0< 0. この関数は、インターバル[0, rmax]で増加し、間隔[rmax, rc]で減少します。 ここでrmax は、1次微分dCn(r)/dr = 0の静止点です。

Cn(r)を最大化するropt を見つけることができます。 間隔[0, ra]: ropt= 最小 (ra, rmax). 残りの2つのケースがあります: 1) A0 ≤A≤0および 2) 0 ≤A0≤ A。 最初のケースでは、 ropt=rmax=0, で、二番目のケースはrmax=rс と ropt=ra です。

ここで、制約によって定義されたセットが空である場合を考慮します。 2つのケースでのみ可能です: 1) G0> Aまたは 2) ra<rv. ropt=0と仮定する必要があります。

トレード量の離散的な性質を考慮に入れてri を見つけます。 i番目のトレードにおけるリスクriの値に適した間隔[0, ra]上の数値の非空の有限集合をRi にしてみましょう。 roptを選択して、これはCnを最大化する (r) のRiです。 ropt∈Ri の場合 ropt,i=roptです。 ropt∉ Riの場合は、次に2つの状況が可能です: 1) すべてのポイントRiはropt から1つの側に属していると 2) ポイントRi の2つの側面に属するroptです. 最初のケースでは、 ropt、iは r からのポイントになります。Riは、 roptに最も近い。 2番目のケースでは、 Ri は各側のropt に最も近い2つのポイントになります。 ropt は、 Cn(r)が大きい点になる。

不確実性 入門例

モデルをより複雑に考慮してみましょう。 aiのn個の数字を知っていると仮定してみましょう。 この方法では、ランダムな順列が許可されます。 上記の結果に変更されるものを見てみましょう。 最初の2つの点では、 ai のランダム置換は何も変更されません。 さらに大まかな評価rvr が使用されている場合は、この点に変更はありません。

3点目で変更が可能です。 実際には、シーケンスは、負の値の間に正の値がないように配置されている場合、ドローダウンは最大になります。 逆に、正と負の値が混ざっている場合は、ドローダウンを減します。 一般的な場合、順列の合計数は、 n!に等しくなります。 数十の範囲にあるnを持つ非常に大きな数値です。 理論的には、各j = 1...n!の導入で設定された問題を解決することができます。 ai からの順列は、一連の番号rd, jを取得します。 しかし、永続性の問題があります。 どの順列を選択するかはわかりません。 この不確実性を回避するには、概念と確率と数学的統計の理論を展開する必要があります。

rd,jの集合を、永続性に依存する関数ρd=ρd(j)=rd,jとして扱ってみましょう。 確率論の観点から、 ρd は、一連の基本イベントが一連のn順列に等しいランダム変数です。 ai が同じであっても、すべて別のものとして扱います。

また、すべてのnの順列が等しく可能性があると仮定します。 その後、それぞれの確率は1/n!です。 これは、初等事象の集合の確率的な尺度を覆す。 Pdにおける確率 ρρd(x)=n(x)/n!を定義できます。 ただしn (x)は、 rd、j< xのn個の順列の数です。 この時点で、ドローダウンの制限条件を指定する必要があります。 許可されている最小限のD0と共に、許容される有意レベル (< 0 < δ < 1) を指定する必要があります。 δは、無視できると考えられる、しきい値ドローダウンを超える確率を示します。 そして、分布Pρd(x)のδとしてrd(δ)を定義することができる。 この問題のおおよその解決法を見つけるために、大量のntをランダムに生成します (ここでは1<< n t<< n! n個の順列を指定します。) 1 ≤ j ≤ ntのそれぞれについて、値rd, j を見つけてみましょう。 そして、 rd(δ)に対する評価のために、 rd、j の母集団のサンプルδを取ることができます。

このモデルは人工的ですが、用途があります。 例えば、取引の最初のシリーズのために計算し、確率pd= pρd(rd)rdを取ることができる。 明らかに、 0 ≤ pd≤ 1の不等式は有効です。 pd をゼロに近づけると、損失を発生させるトレードによって引き起こされる大きなドローダウンが互いに接近していることを示します。 1に近い pd は、収益性と損失のトレードが均一に混合されたことを示しています。 (例えば、Z スコアのメソッド） だけでなく、ドローダウンにその度合いの一連の損失を発見する方法です。 Pρd()またはrd のいずれかに依存するその他のインデックスを生成できます。


不確実性 一般的なケース

利回りaiとのトレードのシーケンスがあることを仮定しましょう, 1 ≤ i ≤ n. また、このシーケンスは、母集団内で独立したシーケンスの実装であり、同じように分散されたランダム変数λと仮定します。 その確率分布関数をPλ(x)として記述してみましょう。 次のプロパティがあることになります。 

  • 正の数学的期待Mλ
  • 以下の制限。 x > λ0のとき、Pλ(x) = 0の数λmin≤− 1x < λmin およびPλ(x) > 0 。

この条件は平均利回りがポジティブであることを意味します。 損失のトレードの可能性がありますが、常にリスクを制限することにより、1つのトレードですべての資本を失うことはありません。

リスクの大きさを特定する問題を列挙しましょう。 前のパートの例と同様に、ランダムな変数を考察する必要があります。 roptの代わりに、ρopt で計算します。 その後、有意水準δを設定して、 δがPρopt(x)分布の変位量であるropt= r のopt(δ)を計算してみましょう。 リスクを持つこのシステムは、ドローダウンと平均利回りが設定範囲内になるまで使用することができます。 範囲の境界を超えると、このシステムは破棄されます。 エラーの確率はδを超えません。

δの重要性を強調する必要があります。 得られた基準を使用して、大きい場合、δを意味しません。 δが小さい場合にのみ2つのイベントは、お互いに接続されていると考えられることができます: 1) このシステムは、相場の変更に動作しません 2) ドローダウンが大きすぎるか、利回りが小さすぎる。 既に説明されているエラーと共に、別のエラーを考慮することができます。 そのエラーが存在する場合、ドローダウンとシステムの収率に影響を与える相場の変化に気付けません。 システムの利回りに影響しないため、このエラーについて説明する点はありません。

この理論では、 Pλ(x)とPρopt(x)の分布の変化が重要ではありません。 δの等量の変更であるPρopt(x)が問題です。 特に、利回りのシーケンスに定常要件がないことを意味します。 かと言って、最終的なサンプル aiの収率分布の法則を復元するための定常が必要になります。 1 ≤ i ≤ n。 ここで、分布が大きく変化しないという要件は、絶対的な定常の代わりに十分であるかもしれません。

複雑な関係ですが、最終的には、 ρopt は、 λiを通じて表現することができます (他のランダムな中間変数も表現されます)。 λi の関数として定義されたランダム変数を調査し、その分布を構築するために呼び出します。 Pλ (x)を知っておく必要があります。 この分布に関する情報の3つの亜種を列挙しましょう。

  1. Pλ (x)の厳密な式か、または分析中のトレードシステムに対して任意に近い近似を行う方法があります。 通常、資産価格の行動について仮定があるときだけ可能です。 例えば、ランダムウォーク仮説が真であると考えることができます。 トレードでこの情報を使用することはほとんど不可能です。 この方法は非現実的であり、通常、利益の可能性を否定します。 異なる方法で使用できます。 この仮説を使用して、 null 仮説を構築できます。 その後、経験的データと一致のテストを使用して、仮説を破棄するか、データで破棄できないことを認めます。 このような経験的データは、配列ai、 1 ≤≤ nです。
  2. Pλ (x)は、分布のパラメトリックファミリーに属しているか、近づいてくることが知られています。 前のポイントからの資産価格についての仮定が遠くないとき可能です。 もちろん、トレーディングシステムのアルゴリズムによっても定義されています。 分布パラメータの正確な値は、パラメトリック統計のメソッドによってai、 1 ≤ i ≤ nを使用して計算されます。
  3. 配列aiと共に、 1 ≤ i ≤ n Pλ (x)の一部の一般的な性質が知られている (または想定される)。 例では、既存の有限の期待と分散についての仮定かもしれません。 この場合、 Pλ (x)の近似としてサンプル分布関数を使用します。 1 ≤ i ≤ nと同じ配列aiに基づいてそれを構築します。 厳密な関数の代わりにサンプル配布関数は、ブートストラップと呼ばれます。 場合によっては、 Pλ (x)を知る必要はありません。 たとえば、ランダム変数(λ1+ λ2+ λn)/nは、 nが大きい場合には、通常の分散として扱うことができます (有限分散λi)。

この記事では、3番目のバリアントで説明されている仮定が使用されます。 最初の2つの亜種は、さらに説明されます。

イントロダクションで行われた計算がどのように変化するかを研究します。 絶対数値の代わりにA0 とA、同じようにλi を通して表現されたランダム変数に対処します: λ0= min (λ1、λ2,.., λn)とλ = (λ1+ λ2+ + λn)/n。

成長ñでの漸近的な様子を見てみましょう。 このような場合、常にλ0→λminが当てはまります。 λi が有限の分散 Dλを持っていると仮定しましょう。 Λ→Mλとなります。 前述したように、 λは通常、期待値Mλ および分散Dλ/nで分散されていることを考慮することができます。 Mλ とDλ の正確な値が不明な場合は、そのサンプルをi で計算して使用することができます。 λ0 およびλの Empiric 分布は、ブートストラップを使用して構築することもできます。

ブートストラップメソッドによってropt(δ)を計算する前に、イントロダクションで実行された計算がどのように変化するかについて、次の点を考慮してください。

  1. 最初の点では、 λ0 の漸近的な振る舞いにより、評価は値rc= − 1/λminに対して粗くすることができます。 サンプリング分布の場合、 λmin はА0と一致し、したがって、この点のすべてが同じままになります。
  2. 条件G0≤Λが、 δより大きくない確率で確認することが重要です。 Λのδの位小数をG0より小さくする必要があります。 この変位量の近似計算では、分布Λの法線近似を使用します。 結果として、分析に必要なトレード数の下からの推定値として、 nmin を取得します。 標準的なブートストラップメソッドを調整することができ、成長する長さのサンプルのセットは、 nminに構築することができます。 理論的な観点から、多かれ少なかれ通常の分布による近似と同じになります。
  3. これまでと同じように、 rvrについては、より粗い評価を受けます。

ここでは、生成される yield シーケンスの数を、 n に設定します。 ブートストラップを実行するサイクルでは、各j = 1...nbのリスクの大きさの制限を繰り返し処理します。 上記の点を考慮すると、r g(j)、 rd(j)、 rmax (j)、および ropt(j) を計算するだけですみます。 j の r のセットが空である場合は、 ropt (j)= 0と仮定します。

ブートストラップの終了時には、値の配列がropt[]になります。 この配列によって計算されたサンプルδ位の値は、セットの問題に対する解として扱われます。

結論

これらはすべて、上に書かれたテーマの始まりにすぎません。 次の記事により言及するつもりです。

  • トレードモデルを独立した分配のシーケンスとして使用するには、資産価格とトレードアルゴリズムについて仮定を行う必要があります。
  • この理論は、固定ストップロス/テイクプロフィットおよび固定トレーリングストップなどのトレードを決済する特定のメソッドに対して、より具体的なものにする必要があります。
  • また、この理論がどのようにトレーディングシステムを構築するために使用できるかを示す必要があります。 システム構築には確率論をどのように活用できるかを検討します。 機械学習の利用についても触れていきます。

付録の紹介

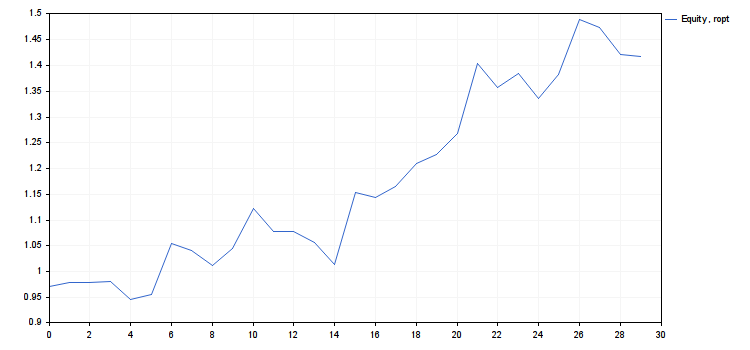
r_intro.mq5 スクリプトのテキストとチャートと数値結果におけるそのタスクの結果です。

#include<Graphics\Graphic.mqh>
#defineN 30
#defineNR 100
#propertyscript_show_inputs
input int ngr=0;    //表示されたチャートの数
double G0=0.25;     // lowest average yield
double D0=0.9;      //最低の最小ゲイン
                    //初期資本 c0 は1に等しいと仮定される


void OnStart()
  {
   double A0,A,rc,rg,rd,ra,rmax,ropt,r[NR],g[NR],d[NR],cn[NR],a[N]=
     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // deal yields
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   A0=a[ArrayMinimum(a)];
   A=0; for(int i=0; i<N;++i) A+=a[i]; A/=N;
   rc=1; if(A0<-1) rc=-1/A0;
   double c[N];
   r[0]=0; cn[0]=1; g[0]=A; d[0]=1;
   for(int i=1; i<NR;++i)
     {
      r[i]=i*rc/NR;
      cn[i]=1; for(int j=0; j<N;++j) cn[i]*=1+r[i]*a[j];
      g[i]=(MathPow(cn[i],1.0/N)-1)/r[i];
      c[0]=1+r[i]*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+r[i]*a[j]); d[i]=dcalc(c);
     }
   int nrg,nrd,nra,nrmax,nropt;
   double b[NR];
   for(int i=0; i<NR;++i) b[i]=MathAbs(g[i]-G0);
   nrg=ArrayMinimum(b); rg=r[nrg];
   for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0);
   nrd=ArrayMinimum(b); rd=r[nrd];
   nra=MathMin(nrg,nrd); ra=r[nra];
   nrmax=ArrayMaximum(cn); rmax=r[nrmax];
   nropt=MathMin(nra,nrmax); ropt=r[nropt];
   Print("rc = ",rc,"\nrg = ",rg,"\nrd = ",rd,"\nra = ",ra,"\nrmax = ",rmax,"\nropt = ",ropt,
         "\ng(rmax) = ",g[nrmax],", g(ropt) = ",g[nropt],
         "\nd(rmax) = ",d[nrmax],", d(ropt) = ",d[nropt],
         "\ncn(rmax) = ",cn[nrmax],", cn(ropt) = ",cn[nropt]);
   if(ngr<1 || ngr>5) return;
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   graphic.Create(0,"G",0,0,0,750,350);
   double x[2],y[2];
   switch(ngr)
     {
      case 1: graphic.CurveAdd(r,g,CURVE_LINES,"g=g(r)");
      x[0]=0; x[1]=r[NR-1]; y[0]=G0; y[1]=G0;
      graphic.CurveAdd(x,y,CURVE_LINES,"g=G0");
      x[0]=rg; x[1]=rg; y[0]=g[0]; y[1]=g[NR-1];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rg");
      break;
      case 2: graphic.CurveAdd(r,d,CURVE_LINES,"d=d(r)");
      x[0]=0; x[1]=r[NR-1]; y[0]=D0; y[1]=D0;
      graphic.CurveAdd(x,y,CURVE_LINES,"d=D0");
      x[0]=rd; x[1]=rd; y[0]=d[0]; y[1]=d[NR-1];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rd");
      break;
      case 3: graphic.CurveAdd(r,cn,CURVE_LINES,"cn=cn(r)");
      x[0]=0; x[1]=rmax; y[0]=cn[nrmax]; y[1]=cn[nrmax];
      graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(rmax)");
      x[0]=rmax; x[1]=rmax; y[0]=cn[NR-1]; y[1]=cn[nrmax];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rmax");
      x[0]=0; x[1]=ropt; y[0]=cn[nropt]; y[1]=cn[nropt];
      graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(ropt)");
      x[0]=ropt; x[1]=ropt; y[0]=cn[NR-1]; y[1]=cn[nropt];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=ropt");
      break;
      case 4: c[0]=1+ropt*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+ropt*a[j]);
      graphic.CurveAdd(c,CURVE_LINES,"Equity, ropt");
      break;
      case 5: c[0]=1+rmax*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+rmax*a[j]);
      graphic.CurveAdd(c,CURVE_LINES,"Equity, rmax");
      break;
     }
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(30000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
  }

//dcalc () 関数は、c1、c2、cN 値の配列を受け取り、
//最小ゲイン d を返します。 Assume that c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(int i=1; i<N;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }

average yield

minimal gain

final capital Cn

growth of capital at lower risk r=ropt

growth of capital at greater risk r=rmax

  • rc = 0.9839614287119945
  • rg = 0.1180753714454393
  • rd = 0.03935845714847978
  • ra = 0.03935845714847978
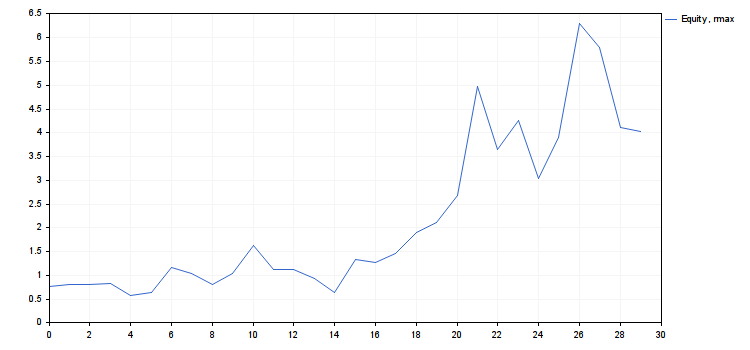
  • rmax = 0.3148676571878383
  • ropt = 0.03935845714847978
  • g(rmax) = 0.1507064833125653, g(ropt) = 0.2967587621877231
  • d(rmax) = 0.3925358395456308, d(ropt) = 0.9037200051227304
  • cn(rmax) = 4.018198063206267, cn(ropt) = 1.416754202013712
ご覧のように、リスク値としてrmax を使用すると、はるかに大きな利益 (40% の代わりに 300%) が保証されます。 はるかに大きなドローダウン (10% の代わりに60パーセントより大きい) によって達成されます。 平均利回りの値の変化も考慮する必要があります。 小さい場合は、トランザクションコストの増加は利益の低下につながります。 したがって、次の結論が得られます:

  1. このシステムのリスク値としてropt を使用します。
  2. このrmax− ropt でエントリーされたリスクは、新しいシステム (多様化) を追加するために使用することができます。

サンプルの付録

r_exmp の mq5 スクリプトとそのタスクの数値結果です。

#include<Math\Stat\Uniform.mqh>
#define N 30      // length of deal series
#define NR 500    // number of segments the interval is split into  [0,rc]
#define NT 500    // number of generated permutations
double D0=0.9;    // smallest minimal gain
double dlt=0.05;  // significance level

void OnStart()
  {
   double A0,rc,r[NR],d[NR],rd[NT],a[N]=//Japanese  English Chinese Simplified

     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,// deal yields
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   A0=a[ArrayMinimum(a)];
   rc=1; if(A0<-1) rc=-1/A0;
   for(int i=0; i<NR;++i) r[i]=i*rc/NR;
   double b[NR],c[N];
   int nrd;
   MathSrand(GetTickCount());
   for(int j=0; j<NT;++j)
     {
      trps(a,N);
      for(int i=1; i<NR;++i)
        {
         c[0]=1+r[i]*a[0];
         for(int k=1; k<N;++k) c[k]=c[k-1]*(1+r[i]*a[k]);
         d[i]=dcalc(c);
        }
      for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0);
      nrd=ArrayMinimum(b); rd[j]=r[nrd];
     }
   double p[1],q[1]; p[0]=dlt;
   if(!MathQuantile(rd,p,q)) {Print("MathQuantile() error"); return;}
   PrintFormat("sample %f-quantile rd[] equals %f",p[0],q[0]);
   double rd0=0.03935845714847978;   // value of rd obtained in the introduction
   double pd0=0;                     // correspondent value of pd
   for(int j=0; j<NT;++j) if(rd[j]<rd0) ++pd0; pd0/=NT;
   PrintFormat("for rd = %f value pd = %f",rd0,pd0);
  }
//dcalc () 関数は、c1、c2、cN 値の配列を受け取り、
//最小ゲイン d を返します。 Assume that c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(int i=1; i<N;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//最初の最小値のランダム順列 (n, ArraySize (b))
//b [] 配列の要素
//ライブラリ MathSample () は、trps () の代わりに使用することができます。
void trps(double &b[],int n)
  {
   if(n<=1) return;
   int sz=ArraySize(b);
   if(sz<=1) return;
   if(sz<n) n=sz;
   int ner;
   double dnc=MathRandomUniform(0,n,ner);
   if(!MathIsValidNumber(dnc)) {Print("Error ",ner); ExpertRemove();}
   int nc=(int)dnc;
   if(nc>=0 && nc<n-1)
     { double tmp=b[n-1]; b[n-1]=b[nc]; b[nc]=tmp;}
   trps(b,n-1);
  }
  • サンプル0.05 分位点 rd [] は0.021647 に等しくなります。
  • rd = 0.039358 pd = 0.584

結果の最初の行は、イントロダクションで得られた結果と比較してリスクを半減しなければならないことを教えてくれます。 この場合、ドローダウンが目標を超えた場合 (10%)、システムが欠陥を持っている可能性が高いことを意味し、トレードに使うべきではありません。 エラー確率 (タスクシステムは拒否) は、 δ (0.05 または 5%) になります。 結果の2番目の行、情報の最初のシリーズのドローダウンは、平均になる可能性が小さいです。 このシステムを評価するために30の取引が不十分であるかもしれないことに注意してください。 したがって、より多くのトレードの詳細な分析を実行し、結果にどのように影響するかを確認すると便利です。

一般的なケースへの付録

nmin の値の下から、スクリプトのタスクの結果を評価する r_cmn mq5 スクリプトです。

#include<Math\Stat\Normal.mqh>
#include<Math\Stat\Uniform.mqh>
#include<Graphics\Graphic.mqh>
#define N 30        // length of the deal series
#define NB 10000    // number of generated samples for bootstrap
double G0=0.25;     // lowest average yield
double dlt=0.05;    // significance level

void OnStart()
  {
   double a[N]=
     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,   // deal yields
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   double A=MathMean(a);
   double S2=MathVariance(a);
   double Sk=MathSkewness(a);
   double Md=MathMedian(a);
   Print("sample distribution parameters:");
   PrintFormat("average: %f, variance: %f, asymmetry: %f, median: %f",A,S2,Sk,Md);
   PrintFormat("number of deals: %d, dlt value??: %f, G0value??: %f",N,dlt,G0);
//正規分布による近似
   Print("approximation by normal distribution:");
   double q0, p0;
   int ner;
   q0=MathQuantileNormal(dlt,A,MathSqrt(S2/N),ner);
   if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;}
   Print("dlt quantile: ",q0);
   p0=MathCumulativeDistributionNormal(G0,A,MathSqrt(S2/N),ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   Print("level of significance for G0: ",p0);
//ブートストラップ
   MathSrand(GetTickCount());
   double b[N],s[NB];
   p0=0;
   for(int i=0;i<NB;++i)
     {
      sample(a,b);
      s[i]=MathMean(b);
      if(s[i]<G0) ++p0;
     }
   p0/=NB;
   double p[1],q[1];
   p[0]=dlt;
   if(!MathQuantile(s,p,q)) {Print("MathQuantile() error"); return;}
   Print("approximation by bootstrap");
   Print("dlt quantile: ",q[0]);
   Print("level of significance for G0: ",p0);
// approximation nmin (approximation by normal distribution)
   int nmin;
   for(nmin=1; nmin<1000;++nmin)
     {
      q0=MathQuantileNormal(dlt,A,MathSqrt(S2/nmin),ner);
      if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;}
      if(q0>G0) break;
     }
   Print("Minimal number of deals nmin (approximation by normal distribution):");
   PrintFormat("no less than %d, value of the dlt quantile: %f",nmin,q0);
  }
  
void sample(double &a[],double &b[])
  {
   int ner;
   double dnc;
   for(int i=0; i<N;++i)
     {
      dnc=MathRandomUniform(0,N,ner);
      if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();}
      int nc=(int)dnc;
      if(nc==N) nc=N-1;
      b[i]=a[nc];
     }
  }

サンプル分布パラメータ:

  • 平均: 0.322655
  • 差異: 1.419552
  • 非対称: 0.990362
  • 中央値: 0.023030
  • 数:30
  • dlt 値: 0.050000
  • G0 値: 0.250000。

正規分布による近似:

  • dlt quantile: -0.03514631247305994;
  • G0: 0.3691880511783918 の重要性のレベル。

ブートストラップによる近似:

  • dlt quantile: -0.0136361;
  • G0: 0.3727 の重要性のレベル。
  • 最小トレード数 nmin (正規分布による近似): 728 以下
  • dlt の分位点の値: 0.250022。


これらの結果から、 ropt(δ) = 0となります。 データにこのシステムを使用してトレードを禁止するか、より大きな長さのトレードのヒストリーを必要とすることを意味します。 最初の美しいチャートにもかかわらずです。 ブートストラップは、通常の分布による近似とほぼ同じ結果を生成します。 ここで2つの質問があります。 1. なぜ結果が悪いのでしょうか。 2. どうすればこのシステムを改善することができるでしょうか? 答えはあります。

  1. 理由は、使用される基準とシステム自体の両方です。 この規準は余りに普遍的です。 一方で、ほとんどの場合使用することができます。 また、問題のシステムだけでなく、すべてのシステムを考慮に入れていません。 例えば、すべてのシステムは、左側のカットとの分布を生成し、理論的にはいくつかは無限の期待値を持つことができます。 原則として、すべての分布が右歪を持っており、その平均は非常にゆっくりと対称正規分布に収束している理由です。 この例のシステムには、このような偏った分布があります。 歪比または中央値から右への期待値の変位によって示されます。 "損失をカットし、利益が実行させて" 次のシステムから期待されています。
  2. 特定のトレードシステムと資産価格のシーケンスについての情報を使用する基準が必要です。 よって、価格について仮定なしで行うことはできません。 これらの仮定は、事実を曲げない。 「一般ケース」の冒頭で論じた３つの点からなる第2の変形の状況にあるべきであることを意味します。 このため、今後のパラメトリックメソッドに専念する必要があります。 計算の観点から、普遍的ではないが、各特定の場合でより正確である場合もあります。

これまでのところ、次の結論を出すことができます。 損失は、資産価格の行動の予期しない変化 (例えば、トレンドの変化) によって引き起こされます。 ノイズやボラティリティの特性が原因で発生することもあります。 理由を分離し、その影響を減らすために試みる方法の一つです。 トレードシステムに対して実行できない場合、このようなシステムを使用することは推奨されません。