指数平滑化を利用した時系列予測(続編)

Victor | 30 11月, 2015

はじめに

記事 "Time Series Forecasting Using Exponential Smoothing" [1] は指数平滑化の概要を簡単に述べ、モデルパラメータの最適化の可能は方法を解説し、最終的には減衰を伴う線形成長モデルを基にした予測インディケータを提案しました。本稿はこの予測インディケータの精度をいくらか高める試みを紹介します。

通貨クオートを予想したり3～4ステップ前もって信頼性ある予測を得るのは簡単ではありません。それでもなお、そのような長いホライゾンラインについて満足な結果を得るのは不可能であることを明確に認識しつつこのシリーズの前回記事のように12ステップ先の予測をしていきます。もっとも狭い信頼区間を持つ予測の最初の数ステップに最大の注意が払われるべきです。

A 10～12ステップ先の予測は主に異なるモデルと予測手法の変動特徴を示します。どの場合においても、あらゆるホライズンに対し取得した予測の精度は信頼区間限度を用いて評価することができます。本稿は基本的に記事 [1]で作成済みのインディケータをグレードアップするのに役立ついくつかの手法を示すのが狙いです。

インディケータ作成に適用される複数変数の最低限の関数を見つけるアルゴリズムは前の記事で取り上げているのでここで繰り返し述べることはしません。記事の負荷を増やさないため理論的インプットは最小限に留めています。

1. 初期的インディケータ

IndicatorES.mq5 インディケータ（記事 [1]を参照ください）は開始ポイントとして使用されます。

インディケータを比較するために、IndicatorES.mq5, CIndicatorES.mqh および PowellsMethod.mqhが必要です。それらは両方同じディレクトリにあります。ファイルは本稿末尾のアーカイブ files2.zip で参照できます。

このインディケータ、減衰を伴う線形成長モデル、を開発する際使用された伴う指数平滑化モデルを定義づける式をリフレッシュします。

ここで

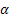- シーケンスレベル [0,1]に対する平滑化パラメータ
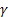- トレンド [0,1]に対する平滑化パラメータ
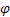- damping パラメータ [0,1];
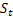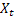- が観測された後時刻 t で計算されるシーケンスの平滑化されたレベル
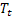- 時刻 tで計算される平滑化されたadditiveトレンド
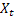- 時刻 tのシーケンス値
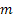- 予測されるのに先んじたステップ数
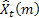- 時刻 tで行われるm-ステップ先の予測
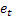- 時刻 tにおける1ステップ先の予測エラー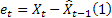

インディケータの唯一の入力パラメータはそれによってモデルパラメータが最適化され初期値（調査区間）が選択される区間長を決める値です。既定の区間と必要な計算における最適なモデルパラメータ値を決めたら、予測、信頼区間、1ステップ先の予測に応じたラインが作成されます。新規バーのたびにパラメータは最適化され予測が行われます。

問題のインディケータはグレードアップされるので、われわれが行う変化の効果は本稿末尾のアーカイブ Files2.zip からのテストシーケンスを用いて評価されます。アーカイブディレクトリ \Dataset2 には保存されたファイルにはクオート EURUSD、 USDCHF、USDJPYまたU.S.が含まれます。ドルインデックス DXY. これらそれぞれは3つの時間枠：M1、H1、D1で提供されます。ファイルに保存された「オープン」の値はファイルの最後で直近の値となるようセットされています。各ファイルには1200個のエレメントがあります。

予測エラーは "Mean Absolute Percentage Error" (MAPE) 係数の計算によって推定されます。

12のテストシーケンスをそれぞれ80エレメントを含む50の重複セクションに分け、ひとつずつに対して MAPE 値を計算します。取得される推測の平均値は比較するインディケータに関する予測エラー指数として使用されます。2または3ステップ先の予測エラーに対するMAPE 値も同じ方法で計算されます。そのような平均化された予測値はさらに以下のように記述されます。

MAPE1 – 1ステップ先の予測エラーの平均予測値
MAPE2 – 2ステップ先の予測エラーの平均予測値
MAPE3 – 3ステップ先の予測エラーの平均予測値
MAPE1-3 – 平均値 (MAPE1+MAPE2+MAPE3)/3

MAPE 値を計算するとき、絶対予測エラー値はシーケンスの現在値で割った毎ステップにあります。ゼロ除算または除算で負の値を得ることがないように、ここでの場合のように入力シーケンスはゼロでない正の数のみを取ります。

最初のインディケータ予測値は表1に示しています。

	MAPE1	MAPE2	MAPE3	MAPE1-3
IndicatorES	0.2099	0.2925	0.3564	0.2863

表1　初期インディケータ予測エラー推定

表1に示されるデータは Errors_IndicatorES.mq5 スクリプト（本稿末尾のアーカイブfiles2.zip ）を使用して取得されています。スクリプトをコンパイルし実行するには CIndicatorES.mqh および PowellsMethod.mqh が同じディレクトリ Errors_IndicatorES.mq5にセットされル必要があります。入力シーケンス Files\Dataset2\ ディレクトリにあります。

予測エラーの最初の推定値を得たら、検討中のインディケータグレードアップを進めていくことができます。

2. 最適化基準

記事"Time Series Forecasting Using Exponential Smoothing"に述べられている初期インディケータのモデルパラメータは1ステップ先の予測エラーの二乗合計を最小化することで決められています。 1ステップ先の予測に対する最適なモデルパラメータはより大きなステップ数先の予測に対して最小エラーを導かないであろというのは理論的に思えます。10～12ステップ先の予測エラーを最小限にするのは望ましいことですが、検討中のシーケンスに対して与えられた範囲での満足のいく予測結果を得ることは遂行不可能なミッションかもしれません。

現実的に考えると、モデルパラメータを最適化するとき、われわれのインディケータの最初のグレードアップとして1～3ステップ先の予測エラーを二乗した合計を使用します。エラーの平均数は予測の最初の3ステップの範囲では現象することが予想されます。

明らかにこのような初期インディケータのグレードアップはその主な構造原則には関与せず、ただパラメータ最適化基準を変更します。よって2～3ステップ先の予測エラーが少し減ったからと言って、予測精度が数倍あがることは期待できません。

予測結果を比較するために、変更オブジェクト関数funcと共に前稿で紹介したCIndicatorESクラスに似た CMod1 クラスを作成しました。

初期 CIndicatorES クラスのfunc関数

double CIndicatorES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}       // Alpha  > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}       // Alpha  < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}      // Gamma  > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}       // Gamma  < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }      // Phi    > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}       // Phi    < 0.05
  sse=0; 
  for(i=0;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(Dlen*MathLog(k1*k2*k3*sse));
  }

いくらか改良をしたあとにfunc 関数は以下のように表されます。

double CMod1::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,err,ae,pt,phi2,phi3,a;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;        // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}       // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}      // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}       // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }      // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}       // Phi     < 0.05
  phi2=phi+phi*phi; phi3=phi2+phi*phi*phi;
  err=0;
  for(i=0;i<Dlen-2;i++)
    {
    e=Dat[i]-(s+phi*t); err+=e*e;
    a=Dat[i+1]-(s+phi2*t); err+=a*a;
    a=Dat[i+2]-(s+phi3*t); err+=a*a;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  e=Dat[Dlen-2]-(s+phi*t); err+=e*e;
  a=Dat[Dlen-1]-(s+phi2*t); err+=a*a;
  ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
  a=Dat[Dlen-1]-(s+phi*t); err+=a*a;
  return(k1*k2*k3*err);
  }

ここで、目的関数を計算する際、1～3ステップ先の予測エラーの二乗合計を使用します。

のちにこのクラスを基に、すでに述べられているErrors_IndicatorES.mq5スクリプトのように予測エラーを推定することのできる Errors_Mod1.mq5 スクリプトが作成されます。CMod1.mqh および Errors_Mod1.mq5 は本稿末尾のアーカイブ files2.zip にあります。

表2は初期インディケータおよびグレードアップ版に対して予測エラー推定値を示しています。

	MAPE1	MAPE2	MAPE3	MAPE1-3
IndicatorES	0.2099	0.2925	0.3564	0.2863
Mod1	0.2144	0.2898	0.3486	0.2842

表2　予測エラー推定値比較

ご覧のようにエラー係数 MAPE2 および MAPE3 、平均値 MAPE1-3 は実際検討中のシーケンスに対してわずかに低い値を示しています。このバージョンを保存しわれわれのインディケータをさらに改良していきます。

3. 平滑化プロセスにおけるパラメータ調整

入力シーケンスの現在値に依存する平滑化パラメータを変更するという考えは新しくもなければ初めてのものでもなく、入力シーケンスの性質における既定のあらゆる変更が最適であり続けるよう平滑化係数を調整したいという願いから来ています。いくつかの平滑化係数の調整手法は文献 [2]、[3]に述べられています。

インディケータのさらなるグレードアップのために適応型指数平滑化モデルを使用することでわれわれのインディケータの予測精度が上がることを期待して動的変更平滑化係数を伴うモデルを使用します。

残念ながら、予測アルゴリズムで使用される場合、主要な適応型メソッドは必ずしも望ましい結果を生じるとは限りません。適切な適応型メソッドを選択することは面倒で、時間がかかりすぎるように思えます。そこでここの場合は、文献 [4] で提供されている研究結果を利用し、記事 [5]に記載のある"Smooth Transition Exponential Smoothing" (STES)手法を採用します。

この方法の基礎は指定の記事に解りやすく解説されているので、ここでは省き、適応型平滑化係数を考慮しつつわれわれのモデル（指定記事の初めを参照ください）についての式解説に進んでいきます。

ここで判るように、平滑化係数αはアルゴリズムの各段階で計算され、それは二乗された予測エラー値に依存します。係数 b および g の値はα値における予測エラーの影響を判断します。その他あらゆる点において採用されたモデルの式に変更は加えられません。STES 手法の利用に関するその他情報は記事 [6]にあります。

前バージョンでは既定の入力シーケンスへのα係数の最適値を決める必要がありましたが、今回は最適化を表す2つの適応型係数 b および g を決める必要があります。またα値は入力シーケンスを平滑化する過程で動的に決定されます。

グレードアップは CMod2 クラス形式で実装されます。主な変更（前回のように）はまず今では以下のように記述されるfunc 関数です。

double CMod2::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,sb,sg,k1,k2,e,err,ae,pt,phi2,phi3,a;
  
  s=p[0]; t=p[1]; gam=p[2]; phi=p[3]; sb=p[4]; sg=p[5]; k1=1; k2=1;
  if     (gam>0.95){k1+=(gam-0.95)*200; gam=0.95;}        // Gamma   > 0.95
  else if(gam<0.05){k1+=(0.05-gam)*200; gam=0.05;}        // Gamma   < 0.05
  if     (phi>1.0 ){k2+=(phi-1.0 )*200; phi=1.0; }       // Phi     > 1.0
  else if(phi<0.05){k2+=(0.05-phi)*200; phi=0.05;}        // Phi     < 0.05
  phi2=phi+phi*phi; phi3=phi2+phi*phi*phi;
  err=0;
  for(i=0;i<Dlen-2;i++)
    {
    e=Dat[i]-(s+phi*t); err+=e*e;
    a=Dat[i+1]-(s+phi2*t); err+=a*a;
    a=Dat[i+2]-(s+phi3*t); err+=a*a;
    alp=0.05+0.9/(1+MathExp(sb+sg*e*e));                  // 0.05 < Alpha < 0.95
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  e=Dat[Dlen-2]-(s+phi*t); err+=e*e;
  a=Dat[Dlen-1]-(s+phi2*t); err+=a*a;
  alp=0.05+0.9/(1+MathExp(sb+sg*e*e));                    // 0.05 < Alpha < 0.95
  ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
  a=Dat[Dlen-1]-(s+phi*t); err+=a*a;
  return(k1*k2*err);
  }

この関数を作成する際、α係数値を決める式はほんの少し変更されました。これはこの係数値の許容する最大最小限度ををれぞれ0.05、 0.95と設定するために行われました。

予測エラーを推定するには、以前に行ったとおり CMod2 クラスを基にErrors_Mod2.mq5スクリプトが書かれました。CMod2.mqh および Errors_Mod2.mq5 本稿末尾のアーカイブ files2.zip にあります。

スクリプトの結果は表3に示しています。

	MAPE1	MAPE2	MAPE3	MAPE1-3
IndicatorES	0.2099	0.2925	0.3564	0.2863
Mod1	0.2144	0.2898	0.3486	0.2842
Mod2	0.2145	0.2832	0.3413	0.2797

表3　予測エラー推定値比較

表3が示すように、適応型平滑化係数の使用によって、平均値においてわれわれの検証シーケンスに対して予測エラーがわずかに減っています。これにより2つのグレードアップ後エラー係数 MAPE1-3を約2%減らすことができました。の

かなり控えめたグレードアップの結果ではありますが、結果として出たバージョンに続けるし、これ以上のグレードアップは本稿では取り上げません。次のステップとして、 Box-Cox 変換を使用してみるのがおもしろいのではないでしょうか。この変換は主に初期シーケンス分布を正規分布に対して近似化するのに使用されます。

ここでの場合初期シーケンス変換、予測値計算、予測値の逆変換に使用可能であろうと思います。それをするために適用されている変換係数は結果としての予測エラーが最小限に留まるよう選択する必要があります。予測シーケンスにおける Box-Cox変換使用例は記事 [7]にあります。

4. 予測信頼区間

初期インディケータIndicatorES.mq5における予測信頼区間（前稿に記載があります。）は選択された指数平滑化モデルから派生した分析式に従って計算されました。 [8]ここで加えた変更により検討中モデルも変更されます。変数の平滑化係数により信頼区間を予測するために前述の分析式を使用するのは適切ではなくなります。

以前に使用された分析式は予測エラー分布が対象で正規分布であるという仮定に基づき作成されたことが、信頼区間推定方法を変更する別の理由となりえます。こういった要件はわれわれのシーケンスクラスでは満たされておらず、予測エラー分布は正規分布でも対称でもない可能性があります。

初期インディケータで信頼区間を推測するとき、1ステップ先の予測エラーバリアンスが入力シーケンスからまず計算されました。続いて分析式を用いて取得される1ステップ先の予測エラーバリアンスに基づき2ステップ、3ステップ、あるいはもっと多くのステップ数分先の予測バリアンスが計算されます。

分析式の使用を避けるため、1ステップ先の予測に対するバリアンス同様2ステップ、3ステップ、あるいはもっと多くのステップ数分先の予測に対してバリアンスが入力シーケンスから直接計算されます。ただしこの方法には大きな欠点があります。短い入力シーケンスにおいて、信頼区間推定値は広く分散しバリアンスおよび平均値二乗計算は期待されるエラーの正常化の制約を緩めないのです。

この解決方法はノンパラメトリックブートストラップ法（再サンプリング）の使用に見出すことが可能です。[9]その考え方の要点を簡単に述べます。：初期シーケンスからの置換を伴い無作為（一様分布）にサンプリングを行う場合、そのように生成される人工シーケンスの分布は最初のものと同じである。

仮にN メンバの入力シーケンスがあります。範囲 [0,N-1] について一様分布の疑似ランダムシーケンスを作成し初期配列からサンプリングをする際それを指数として使用することで、最初のものよりも長い形だけのシーケンスを作成することが可能であるとします。それの意味するところは、生成されたシーケンスは最初のシーケンスと同じ（ほとんど同じ）であるということです。

信頼区間推測のためのブートストラップ法手続きは以下です。

モデルパラメータの最適初期値、その係数、改良して得た指数平滑化モデルに対する入力シーケンスからの適応型係数を決めます。最適パラメータは前のように、パウエルの検索法を利用したアルゴリズムを使って決められます。
決定した最適モデルパラメータを使い、初期シーケンスを「通過」し、1ステップ先の予測エラーの配列を作成します。配列エレメント数は入力シーケンス長 Nに等しくなります。
平均値をエラー配列の各エレメントから引き算することでエラーを調整します。
疑似ランダムシーケンスジェネレータを使用し、[0,N-1] の範囲内に指数を作成し、9999 エレメント長の人口のエラーのシーケンスを作成します。（再サンプリング）
形だけ作成したエラー配列から値を現在使用のモデルを定義する式に挿入することで、疑似入力シーケンスの値を 9999 個持つ配列を作成します。言い方を変えると、以前、モデル式に入力シーケンスを挿入し予測エラーの計算をする必要がありましたが、今回は逆計算が行われます。配列の各エレメントに対してエラー値が挿入されインプット値が計算されます。結果として、入力シーケンスの分布と同じシーケンスを持つ 9999 エレメントの配列を得ます。同時にそれは信頼区間を直接予測するのに十分な長さです。

それから作成した適切な長さのシーケンスを使って信頼区間を推測します。このため、作成した予測エラー配列が昇順でソートされたら、249 と 9749 の指数を伴う配列セルは 9999 個の値を持つ配列に対して 95% 信頼区間の限度に対応する値を持ちます。 [10]

予想区間のより正確な推定のため、配列長は奇数である必要があります。ここでは、予測信頼区間の限界は以下のように推定されます。

以前に決定されたように最適モデルパラメータを使用し作成したシーケンスを通過」して9999 個の1ステップ先の予測エラーの配列を作成します。
結果配列のソート
ソートされたエラー配列から95% 信頼区間の限度を表す249 と 9749 の指数値を選択します。
2ステップ、3ステップ、またはより多くのステップ数分先の予測エラーに対して手順1～3を繰り返します。

この信頼区間予測方法にはメリットもデメリットもあります。

メリットの中には予測エラー分布の性質上仮説がないことが挙げられます。正規分布や対称分布である必要はないのです。また、この方法は使用のモデルに対して分析式ができない場合に有用です。

計算に要求されるスコープが劇的に増えることと、予測値が使用される疑似ランダムシーケンスジェネレータの質に依存することがデメリットとして考えられます。

再サンプリングと変位値を使用する信頼区間予測について提案されている方法はかなり原始的で改善の余地があります。ただこの場合の信頼区間は視覚的評価を目的としているため、上記の方法による精度は十分であると思われます。

5. インディケータの改良バージョン

本稿で紹介されているグレードアップを考慮して ForecastES.mq5 インディケータが開発されました。サンプリングのため、本稿で先に提案されている疑似ランダムシーケンスジェネレータを使用しました。 [11]標準的なジェネレータMathRand() はすこしお粗末な結果を生じました。おそらく[0,32767] を作成した値範囲が十分広くなかったためと思われます。

ForecastES.mq5 インディケータをコンパイルするとき、このインディケータと共に PowellsMethod.mqh、CForeES.mqh、 RNDXor128.mqh が同じディレクトリにセットされる必要があります。これらファイルはすべてアーカイブ fore.zip にあります。

以下はインディケータForecastES.mq5 のソースコードです。

//+------------------------------------------------------------------+
//|                                                   ForecastES.mq5 |
//|                                          Copyright 2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright   "2012, victorg."
#property link        "https://www.mql5.com"
#property version     "1.02"
#property description "Forecasting based on the exponential smoothing."

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"           // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "ConfUp"             // Confidence interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCrimson
#property indicator_style3  STYLE_DOT
#property indicator_width3  1
#property indicator_label4  "ConfDn"             // Confidence interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCrimson
#property indicator_style4  STYLE_DOT
#property indicator_width4  1

input int nHist=80; // History bars, nHist>=24

#include  "CForeES.mqh"
#include  "RNDXor128.mqh"

#define   NFORE 12
#define   NBOOT 9999

double    Hist[],Fore[],Conf1[],Conf2[];
double    Data[],Err[],BSDat[],Damp[NFORE],BSErr[NBOOT];
int       NDat;

CForeES   Es;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   NDat=nHist; if(NDat<24)NDat=24;
   MqlRates rates[];
   CopyRates(NULL,0,0,NDat,rates);                 // Load missing data
   ArrayResize(Data,NDat);
   ArrayResize(Err,NDat);
   ArrayResize(BSDat,NBOOT+NFORE);

   SetIndexBuffer(0,Hist,INDICATOR_DATA);
   PlotIndexSetString(0,PLOT_LABEL,"History");
   SetIndexBuffer(1,Fore,INDICATOR_DATA);
   PlotIndexSetString(1,PLOT_LABEL,"Forecast");
   PlotIndexSetInteger(1,PLOT_SHIFT,NFORE);
   SetIndexBuffer(2,Conf1,INDICATOR_DATA);         // Confidence interval
   PlotIndexSetString(2,PLOT_LABEL,"ConfUp");
   PlotIndexSetInteger(2,PLOT_SHIFT,NFORE);
   SetIndexBuffer(3,Conf2,INDICATOR_DATA);         // Confidence interval
   PlotIndexSetString(3,PLOT_LABEL,"ConfDN");
   PlotIndexSetInteger(3,PLOT_SHIFT,NFORE);
   IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int  &spread[])
  {
   int i,j,k,start;
   double s,t,alp,gam,phi,sb,sg,e,f,a,a1,a2;

   if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);}
   if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar
   start=rates_total-NDat;
//-----------------------
   PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat);
   PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE);
   PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE);
   PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE);

   for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data
   Es.CalcPar(Data);                                    // Optimization of parameters
   s=Es.GetPar(0); t=Es.GetPar(1); gam=Es.GetPar(2);
   phi=Es.GetPar(3); sb=Es.GetPar(4); sg=Es.GetPar(5);
//----
   a=phi; Damp[0]=phi;
   for(j=1;j<NFORE;j++){a=a*phi; Damp[j]=Damp[j-1]+a;}  // Phi table
//----
   f=s+phi*t;
   for(i=0;i<NDat;i++) // History
     {
      e=Data[i]-f; Err[i]=e;
      alp=0.05+0.9/(1+MathExp(sb+sg*e*e));               // 0.05 < Alpha < 0.95
      a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
      f=(s+phi*t); Hist[start+i]=f;                      // History
     }
   for(j=0;j<NFORE;j++)Fore[rates_total-NFORE+j]=s+Damp[j]*t;  // Forecast
//----
   a=0;
   for(i=0;i<NDat;i++)a+=Err[i];
   a/=NDat;
   for(i=0;i<NDat;i++)Err[i]-=a;                       // alignment of the array of errors
//----
   f=Es.GetPar(0)+phi*Es.GetPar(1);
   for(i=0;i<NBOOT+NFORE;i++) // Resampling
     {
      j=(int)(NDat*Rnd.Rand_01());
      if(j>NDat-1)j=NDat-1;
      e=Err[j];
      BSDat[i]=f+e;
      alp=0.05+0.9/(1+MathExp(sb+sg*e*e));               // 0.05 < Alpha < 0.95
      a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
      f=s+phi*t;
     }
//----
   for(j=0;j<NFORE;j++) // Prediction intervals
     {
      s=Es.GetPar(0); t=Es.GetPar(1);
      f=s+phi*t;
      for(i=0,k=0;i<NBOOT;i++,k++)
        {
         BSErr[i]=BSDat[i+j]-(s+Damp[j]*t);
         e=BSDat[i]-f;
         a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
         f=(s+phi*t);
        }
      ArraySort(BSErr);
      Conf1[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[249];
      Conf2[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[9749];
     }
   return(rates_total);
  }
//-----------------------------------------------------------------------------------

表示をよりよくするために、インディケータは実行され直線コードとして可能な限り拡張します。コード中、最適化は行われていません。

図1および図2は異なる2件のケースに関してインディケータが処理を行った結果を示しています。

ForecastES.mq5インディケータの最初の処理例

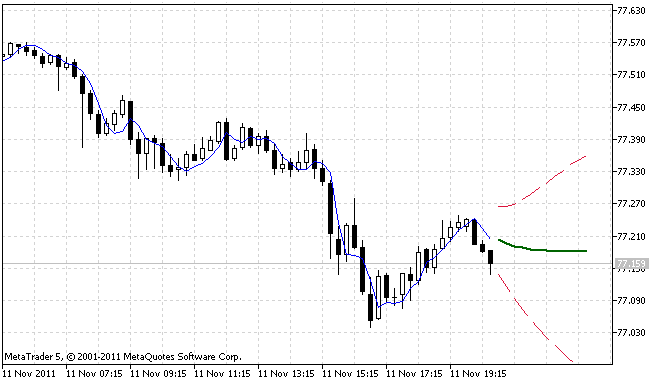
図1　ForecastES.mq5インディケータの最初の処理例

ForecastES.mq5インディケータの二度目の処理例

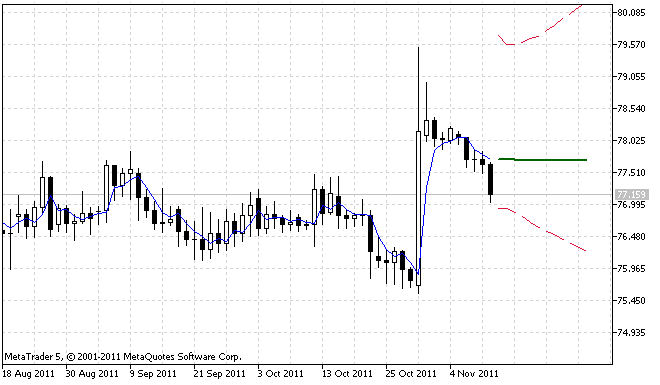
図2　ForecastES.mq5インディケータの二度目の処理例

図2は明らかに95%予測信頼区間は非対称であることを示しています。これは入力シーケンスには予測エラーの分布結果を非対称にする莫大な異常値が含まれているためです。

ウェブサイト www.mql4.com および www.mql5.com は早くに extrapolator インディケータを提供しました。これらの一つを見てみます。 - ar_extrapolator_of_price.mq5 そしてそのパラメータ値を図3にあるように設定し、結果をわれわれが作成したインディケータ使用の結果と比較します。

ar_extrapolator_of_price.mq5 インディケータ設定

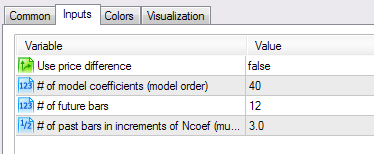
図3　ar_extrapolator_of_price.mq5 インディケータ設定

これら2つのインディケータ処理は EURUSD および USDCHFについて異なる時間枠で視覚的にされました。表面的にはどちらのインディケータによる予測も多くのケースで一致していることを指しています。ただし、より長く観測すると深刻な分散に遭遇するでしょう。それはar_extrapolator_of_price.mq5 は常により破壊された予測ラインを作ると言えます。

インディケータ ForecastES.mq5 およびar_extrapolator_of_price.mq5を連続して処理した結果が図4に示されています。

予測結果比較

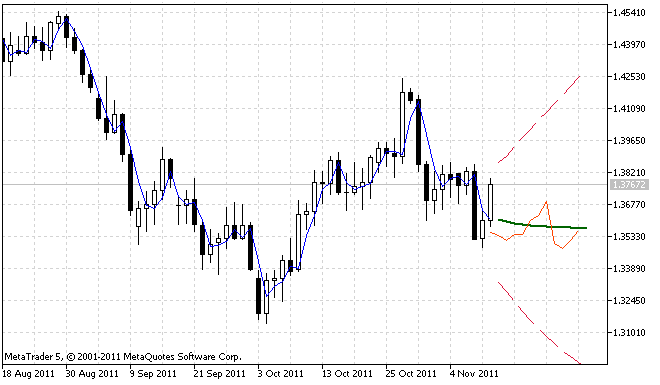
図4　予測結果比較

インディケータ ar_extrapolator_of_price.mq5 で行われた予測は図4に橙赤の実線で示されています。

おわりに

本稿および前稿に関する結果概要

時系列予測に使用される指数平滑化モデルが紹介されました。
モデル実装についてのプログラミングソル―ションが提案されました。
最適初期値およびモデルパラメータに関する問題の迅速な洞察
パウエルの検索法を使用した複数変数の最小関数を見つけるアルゴリズムの実装プログラミングが提供されました。
入力シーケンスを用いた予測モデルのパラメータ最適化に対するプログラミングソル―ションが提供されました。
推測アルゴリズムのシンプルなグレードアップ例が示されました。
ブートストラップ法および位相値を用いた信頼区間予測を推定方法が簡単に述べられました。
予測インディケータ ForecastES.mq5 が作成され、それは本稿で述べられているすべてのメソッドとアルゴリズムを含むものです。
本テーマに付随した記事、雑誌、書籍へのリンクが提供されました。

結果インディケータ ForecastES.mq5に関し、パウエル法を採用している最適化アルゴリズムは特定のケースでは所定の精度を持つ目的関数の最小値を判断することができないことに注意が必要です。反復の最大許容回数に到達した場合、それに関連するメッセージがログに表示されます。ただしこの状況は本稿で説明されるアルゴリズムセットを示すのに許容可能であるインディケータコードでは処理されません。ですが、本格的なアプリケーションに関してはそのようなインスタンスは監視されなんらかの方法で処理されます。

さらなる開発と予測インディケータの強化には、各ステップで同時にたとえば「赤池情報量規準」を用いてそのうちの一つを選択する目的で複数の異なる予測モデルを使用することを提案できるのではないでしょうか。または本質的に似た複数モデルを使用する場合は、予測結果値の加重平均の計算目的です。この場合の重み付け係数は各モデルの予測誤差係数に応じて選択されます。

予測時系列のテーマは広範に及ぶため残念ながら類似の記事ではかろうじて関連する問題の上っ面だけを論じるだけです。これら公表物が予測の問題とこの分野の今後の課題に対する読者の注意を引くのに役立つことを願っています。

参照資料

"Time Series Forecasting Using Exponential Smoothing".
Yu. P. Lukashin. Adaptive Methods for Short-Term Forecasting of Time Series: Textbook. - М.: Finansy i Statistika, 2003.-416 pp.
S.V. 実装します。Statistics for Traders. - М.: Kompania Sputnik +, 2003. - 245 pp.
Everette S. Gardner Jr., Exponential Smoothing: The State of the Art – Part II. June 3, 2005.
James W. Taylor, Smooth Transition Exponential Smoothing. Journal of Forecasting, 2004, Vol. 23, pp. 385-394.
James W. Taylor, Volatility Forecasting with Smooth Transition Exponential Smoothing. International Journal of Forecasting, 2004, Vol. 20, pp. 273-286.
Alysha M De Livera. Automatic Forecasting with a Modified Exponential Smoothing State Space Framework. 28 April 2010, Department of Econometrics and Business Statistics, Monash University, VIC 3800 Australia.
Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30 January 2003.
The Quantile Journal. issue No. 3, September 2007.
http://ru.wikipedia.org/wiki/Квантиль
"Analysis of the Main Characteristics of Time Series".