時系列の主要特性分析

Victor | 19 11月, 2015

はじめに

価格系列で代表される処理の分析はきわめて難しいがやりがいのある作業です。そこではしばしば多くの時間と多大な労力が必要となります。調査対象のシーケンスの特性、また事実としてあるのは膨大な数の出版物があるにもかかわらず時として特定の問題を解決するために適したプログラム手法を見つけるのは難しいということ関係があります。

適したスクリプトやインディケータを見つけても、それのソースコードが取り組んでいるタスクに対してそのまま使用できるとは限りません。

さらに簡単な問題の解決にすらこういったプログラムでは、開発者は心得ているがユーザーは必ずしもよく解っているとは言えないような入力パラメータを要求する可能性もあります。

本格的な調査においてはこういった問題が必ずしも克服できない障害になるものではありませんが、仮説を証明したり単純に好奇心を満たしたい場合、たいていそのような好奇心は満たされずに終わります。それが主要な特性や入力シーケンスのパラメータを前もって簡単に分析できるようにする汎用的プログラミングツールを作成しようと思った理由です。

そのようなツールは、使用を最大限シンプルにするために入力パラメータを要求することなく、インストールにおいて完全にシンプルである必要があります。また同時に推定されるパラメータや特性は検討中のシーケンスの性質を適切に明確に反映する必要があります。

特性の事前推定は今後の掘り下げた調査方法の判断、初期段階での仮説の取捨、のちの調査の時間ロス防止に役立ちます。

汎用ソフトウェアは特性に関してカスタムソフトウェアに比べると機能に乏しいとはよく知られたことです。これはほとんど常に妥協というものによって実現される汎用性にはつきものです。しかしながら本稿ではシーケンス特性の事前分析に最大限役に立つ汎用ツール作成する試みについて説明します。


インストールとキャパシティ

本稿末尾にあるファイルTSAnalysis.zip にインクルードされている \TSAnalysis ディレクトリには作業に必要なファイルがすべて含まれています。それを解凍したら、すべてのコンテンツと共にそのディレクトリを \MQL5\Scripts ディレクトリ内にコピーします（名前は付けなおさずに）。コピーしたディレクトリ \TSAnalysis にはコンパイル後実行するスクリプト TSAexample.mq5 が含まれています。

このスクリプトはデータを準備し、TSAnalysis クラスを用いてそれを表示するためのデフォルトブラウザを呼びます。外部 DLLの使用は TSAnalysis クラスの通常処理用「ターミナル」内で可能であることに注意が必要です。アンインストールするには \TSAnalysis ディレクトリを削除するだけです。

シーケンス分析に使用する全ソースコードは TSAnalysis クラスで表され、TSAnalysis.mqh ファイル内にのみ存在します。

入力シーケンスにこのクラスを使用する場合、それは以下の情報を判断し、また表示することが可能です。

検討中の TSAnalysis クラスに取得結果を視覚的に表示するためには、事前情報表示メソッドでしかない仮想表示メソッドが使用されます。

このメソッドを TSAnalysis 基本クラスで再定義することで、基本クラスではウェブブラウザが呼ばれるので、 チャート表示用データファイル作成において、HTML ファイルの使用だけで可能なあらゆる方法で結果の出力を整理することができます。

TSAnalysis クラスの概観に進む前にデータのテストシーケンスによる使用結果を解説します。下図は TSAexample.mq5 スクリプト処理結果を示しています。

図1　TSAexample.mq5 スクリプト処理結果

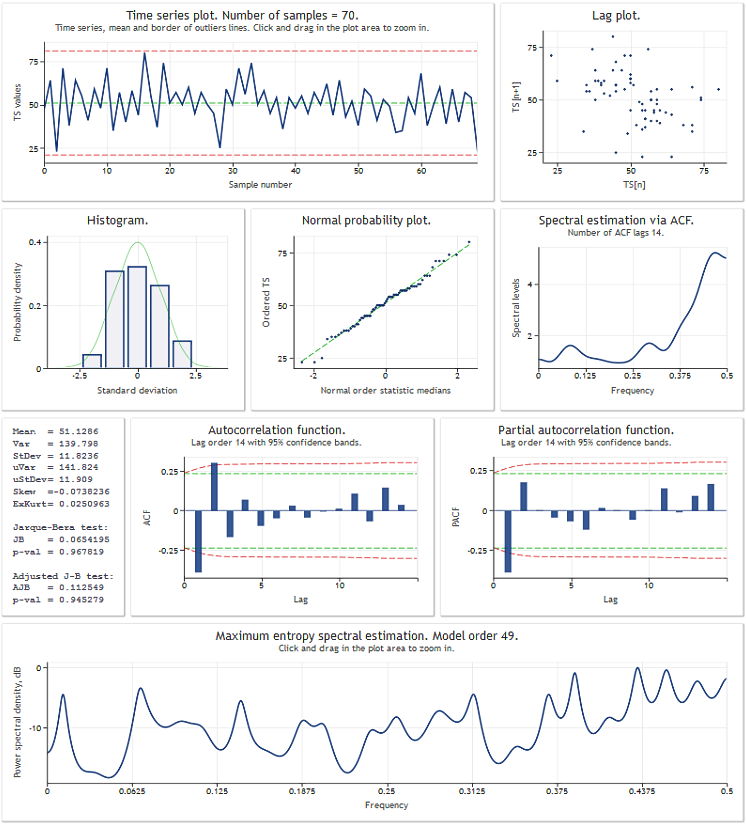
図1　TSAexample.mq5 スクリプト処理結果

TSAnalysis クラスのキャパシティについて簡単に理解したら、クラス自体を詳しく考察していきます。


TSAnalysis クラス

TSAnalysis クラス（TSAnalysis.mqh参照）仮想メソッドshow を呼ぶ前に必要な計算をすべて行う メソッド（パブリック）のみをインクルードします。show メソッドはあとで手短に考察しますが、ここでは行われる計算の要点を段階的に明確にしていきます。

TSAnalysis クラス使用の際、調査対象の入力シーケンスにはいくらか制約が加えられます。

まず、シーケンスには最低8個のエレメントが含まれなければなりません。実践的にはそのような短いシーケンスを調査する必要はほとんどないので、そのような制約はおそらく厳格に適用する必要はあまりありません。

また、最小シーケンス長制約のため、入力シーケンス分散値はゼロに近い値以外が要求されます。この要件は分散値がのちの計算に使われるため、安定した結果のためには一定の値より小さくてはいけないという事実によります。

低い分散値を伴うシーケンスはあまり一般的ではないので、この制約は深刻なデメリットにはなりえないはずです。シーケンスが短かすぎたり、ゼロに近い分散値がある場合、計算は中断されそれに応じたエラーメッセージがログに表示されます。

入力シーケンスの最大長に関する制約もあります。この制約は必ずしも設定されるものではなく、使用コンピュータのパフォーマンス、そのメモリキャパシティにより、スクリプトの実行に要求される時間、結果がウェブブラウザに描かれるスピードによって単純に主観的に判断されます。2,000～3,000エレメントで構成されるシーケンスの処理は深刻な問題を起こさないと考えられます。

シーケンスの統計パラメータ計算は以下のような Calc メソッドのソースコード（TSAnalysis.mqh参照）のフラグメントを基に行われます。

使用されるアルゴリズムの記述は次のリンク『バリアンス計算のためのアルゴリズム』で確認可能です。

. . .
Mean=0; sum2=0; sum3=0; sum4=0;
for(i=0;i<NumTS;i++)
  {
  n=i+1; delta=TS[i]-Mean;
  a=delta/n; Mean+=a;                                       // Mean (average)
  sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // sum of fourth degree
  b=TS[i]-Mean;
  sum3+=a*(b*delta*(n-2.0)-3.0*sum2);                       // sum of third degree
  sum2+=delta*b;                                            // sum of second degree
  }
. . .

このフラグメントの実行結果として以下の値が計算されます。

ここで n = NumTS はシーケンスのエレメント数です。

取得した値を使用し以下のパラメータを計算します。

分散と標準偏差：

不偏分散と標準分散：

歪度：

尖度 最小尖度は 1、正規分布シーケンスの尖度は 3です。

過剰尖度：

この場合、最小尖度は-2、 正規分布シーケンスの尖度は 0です。

従来シーケンス上で最初に予備適合度検定を行うとき、ジャック・ベラ統計が使われます。それは既知の歪度と尖度を使って簡単に計算されるものです。シーケンス長の増加に伴うジャック・ベラ統計の統計的有意性（p 値）は漸近的に2つの自由度を伴うカイ2乗分布 関数です。

よって

シーケンスが短ければ、この方法で取得される p 値はかなりのエラーを持つことになります。このまさに計算オプションはそれでもなおかなり頻繁に使われます。その理由は簡単ではありません。おそらく使用される単純明快な式に関係しているか、またはジャック・ベラ統計自体が理想的な適合度検定ではないためそれ以上の計算精度を求めることに意味がないからかもしれません。

ここでは、ジャック・ベラ統計と適切な p 値は前述の式に従い Calc メソッド(TSAnalysis.mqh)で計算されます。

また、調整されたジャック・ベラ検定は追加で計算されます。

ここで

短いシーケンス向けの調整済みのジャック・ベラ検定は指定された方法で計算される p 値のエラーを減らしますが、全くなくすわけではありません。

分析の最終結果は平均に対応する線および、その外側では値は無効と考えられ、既定のシーケンスに所属しない（異常値）限界を決める線を表示する入力シーケンスチャートをインクルードします。

こういった制限はこの場合次のように計算されます。

この式は S. V. Bulashevの著書 "Statistics for Traders" で提供されており、そこには P. V. Novitsky と I.A.Zograf著"Estimation of Error in Measurement Results"が参照として出ています。限界を決めたら、入力シーケンスの処理はしません。限界は情報としてのみ表示されるようになっています。

入力シーケンスチャートに加え、入力シーケンス分布の実験に基づいた評価を反映したヒストグラムが表示されます。ヒストグラム用区間数は次のように定義されます。（S. V. Bulashev著 "Statistics for Traders"）

結果は最も近い整数奇数値に切り捨てられます。取得値が5より小さければ、5が使用されます。

ヒストグラムの X 軸、 Y 軸のデータ配列内エレメント数は取得された区間数+2です。それはゼロ値ラインがヒストグラムの左右に足されるためです。

以下はヒストグラム構築のためにデータを準備するコード（TSAnalysis.mqh参照）のフラグメント説明です。

. . .
n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0);
if((n&0x01)==0)n--; if(n<5)n=5;                         // Number of bins
ArrayResize(XHist,n);
ArrayResize(YHist,n);
ArrayInitialize(YHist,0.0);
a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean);
if(a<b)a=b; v=Mean-a;
delta=2.0*a/n;
for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // Histogram. X-axis
for(i=0;i<NumTS;i++)
  {
  k=(int)((TS[i]-v)/delta);
  if(k>(n-1))k=n-1;
  YHist[k]++;
  }
for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev;   // Histogram. Y-axis
. . .

上記コードにて

この計算メソッドを使用し X 軸値は標準偏差単位で表現され、 Y 軸値は確立密度に相当します。

正規分布軸のチャートを構築するため、昇順にソートされた入力シーケンスは Y 軸値として使用されます。Y 軸、X 軸の値数は等しいはずです。X 軸値を計算するには、最初に一様分布の法則で中央値を探す必要があります。

それらはのちに逆正規分布関数によってX 軸値を計算するのに使用されます。（ndtri メソッド参照）

自己相関関数 (ACF) プロット、偏自己相関関数 (PACF) プロットを作成し、最大エントロピーメソッドを使ってスペクトル推定値を計算するには、入力シーケンスに対する自己相関関数値を求める必要があります。

ここではプロットACF および PACF で表示される値数を以下のように定義します。

指定方法で決定される値数はプロット上で自己相関関数の表示を行うには十分ですが、さらにスペクトル推定値の計算を行うにはこの場合、使用される自己回帰モデルの次数に等しい計算されたACF 値をより大きな数値にするのがよいでしょう。

IP モデル次数は取得した NLags 値によって決定されます。

スペクトル推定値を得るためのモデルの最適な次数を決めるプロセスを公式化するのは困難です。下位モデルは極端に平滑化された結果をもたらします。一方、高位モデルは値範囲の広い不安的なスペクトル推定値になるようです。

その上、モデル次数はまた入力シーケンスの性質によっても影響を受けるので、上記の式を使用して決められた IP 次数は高すぎたり低すぎたりします。残念ながら、要求されるモデル次数を決定する効果的な方法はまだ発見されていません。

このため、入力シーケンスに対しては、シーケンスのスペクトル推定に使用される IP モデル次数に等しいACF値数を判断する必要があります。

. . .
ArrayResize(cor,IP);
a=0;
for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i];    
for(i=1;i<=IP;i++)
  {  
  c=0;
  for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i];
  cor[i-1]=c/a;                                   // Autocorrelation
  }
. . .

ソースコードのこのフラグメント（TSAnalysis.mqh参照）は自己相関関数を説明します。 (ACF)の計算プロセスを表しています。計算結果は cor[] 配列にセットされます。ご覧のとおり、ゼロ自己相関係数がまず計算され、続いてループ内のその他係数の計算と正規化が行われます。そのような正規化において、ゼロ係数は常に1となり、そのため cor[] 配列に保存する必要はありません。

この配列には一番目のものから開始する IP に等しい係数数量が含まれます。ACF計算時には TSCenter[] 配列が使用されます。これには平均値が減算されるエレメントすべての入力シーケンスが含まれます。

ACF の計算時間を減らすため、高速変換アルゴリズムを採用したメソッドを使用することができます。たとえばFFTです。ただ、今回の場合ACF 計算に必要な時間は許容範囲なので、プログラミングコードを複雑にする必要はないと思われます。

ACF プロット（相関曲線）は取得した相関係数を用いて簡単に構築できます。このプロット上で 95% 信頼区間を表示するために下記の式を使ってその値を計算することができます。

無作為性を検証するのに使用される区間

ARIMA モデル次数を決めるために使用される区間

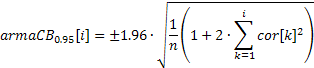
最初のケースで信頼区間の値は定数で、二番目のケースでの自己相関係数の増加に伴い増加します。

頻度分布の一般的トレンドのみを反映する入力シーケンスの平滑化された度数対応は時として興味深いものです。たとえば、低または高頻度レンジ、中央程度頻度の優位性がかなり上がるなど。

優勢頻度レンジを強く強調するた均等メモリで頻度応答を表示するとよいでしょう。そのような振幅応答（AFR）は前回取得した自己相関係数を基にプロットされます。AFR 計算のためには、ACF プロットに表示される数値に等しい係数数値を使用します。

この数値が大きくないと仮定すると、結果として取得するスペクトル推定値はかなりなめらかです。

この場合シーケンスの頻度応答は次のような自己相関係数の平均値によって表すことができます。

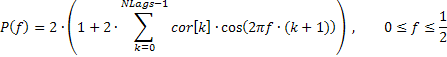
提供される式を基に AFR を計算するのに使用されるコードのフラグメント（TSAnalysis.mqh参照）は下記のように書かれます。

. . .
n=320;                                              // Number of X-points
ArrayResize(Spect,n);
v=M_PI/n;
for(i=0;i<n;i++)
  {
  a=i*v; b=0;
  for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1));
  Spect[i]=2.0*(1+2*b);                             // Spectrum Y-axis
  }
. . .

上記コードの相関係数値はのちの平滑化のために三角窓関数が掛けられていることに注意が必要です。

より詳細なスペクトル分析に対しては、別の妥協として最大エントロピーメソッドが選択されます。汎用スペクトル推定メソッドの選択はかなり困難なものです。スペクトル分析の従来タイプの非パラメータメソッドについてのデメリットはよく知られています。

ピリオドグラムと相関曲線メソッドは高速フーリエ変換アルゴリズムを用いて簡単に実装されるメソッド例です。ただ、結果が安定しているにもかかわらず、適切な分解能を獲得するにはこれらメソッドにはひじょうに長い入力シーケンスが必要です。逆に、スペクトル推定のパラメータを使用するメソッド（たとえば、自己回帰メソッド）は短いシーケンスで各段に高い解像度を保証します。

残念ながら、それらを使用する際、特定のこれらメソッド実装の特殊性のみならず、入力シーケンスの性質についても考慮に入れることが必要です。同時に、増加すると解像能は上がるが取得される結果は離散してしまうAR モデル次数を決めるのはひじょうに困難です。ひじょうに高次モデルが使用される場合、これらメソッドは不安定な結果を示し始めます。

異なるスペクトル推定アルゴリズムの特性はComparative S. L. Marple著の書物 "Digital Spectral Analysis with Applications"にかなり述べられています。すでにお話したとおり、最大エントロピーメソッドがこの場合に選択されました。このメソッドはおそらくその他の自己回帰メソッドに比べるともっとも低い解像能ですが、より安定したスペクトル推定値を取得する観点で選ばれました。

自己回帰スペクタル計算の次数を見ていきます。モデル次数の選択については以前に触れました。よってモデル次数はすでに選択され、それが IP に等しく IP 自己相関関数 cor[] は計算されているものとします。

既知の自己相関係数を使用して自己回帰係数を取得するために、 LevinsonRecursion メソッドとして実装されているレビンソン・ダービンアルゴリズムを使用します。

//-----------------------------------------------------------------------------------
// Calculate the Levinson-Durbin recursion for the autocorrelation sequence R[]
// and return the autoregression coefficients A[] and partial autocorrelation
// coefficients K[]
//-----------------------------------------------------------------------------------
void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[])
  {
  int p,i,m;
  double km,Em,Am1[],err;

  p=ArraySize(R);
  ArrayResize(Am1,p);
  ArrayInitialize(Am1,0);
  ArrayInitialize(A,0);
  ArrayInitialize(K,0);
  km=0;
  Em=1;
  for(m=0;m<p;m++)
    {
    err=0;
    for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1];
    km=(R[m]-err)/Em;
    K[m]=km; A[m]=km;
    for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]);
    Em=(1-km*km)*Em;
    ArrayCopy(Am1,A);
    }
  return;
  }

このメソッドには入力パラメータが3つあります。3つのパラメータはすべて配列に対する参照です。このメソッドを呼ぶとき、入力自己相関係数は最初の配列 R[] にセットする必要があります。計算過程でこれら値は変更されません。

取得された自己相関係数は配列 A[] に配置されます。その他、配列 K[] には反対符号で取られた自己回帰モデル反射係数に等しい偏己相関関数値が含まれます。モデル次数は入力パラメータとして渡されません。それは入力配列 R[] のエレメント数に等しいと考えられます。

アウトプット配列サイズはインプット配列サイズより大きいことが要求されます。この要件を満たされているかどうかは関数内部ではチェックされません。計算完了時、ゼロ自己回帰係数および偏自己相関関数のゼロ係数が配列 A[] と K[] に保存されます。

それらは常に1に等しいと考えられます。よってアウトプット配列には入力シーケンスのように 1 ～ IP （0から始まる配列指数 との混乱を避けるために）の指数を取る係数が含まれます。

取得された偏自己相関関数の値と以下の式で定義される頻度応答推定値計算を行うための基礎として提供する自己回帰係数はのちにそれぞれのプロットを表示するためだけに使用されます。

頻度応答は 0～ 0.5の範囲について4096個の正規化された頻度値に対して計算されます。上記の式を用いて AFR 値を直接計算するのは時間がかかりすぎますが、それは素数指数関数の合計を計算するためのフーリエ変換アルゴリズムを使うことで大幅に短縮することができます。

このために、Calc メソッドはフーリエ変換の代わりに高速ハートレー変換 (FHT) を採用します。

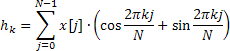
ハートレー変換には複雑な処理は含まれず、インプットおよびアウトプットシーケンスは有効です。逆 ハートレー変換は同じ式を使い計算されますが、別のファクター 1/Nを要求します。

有効な入力シーケンスではこの変換とフーリエ変換の間にシンプルな関連があります。

高速ハートレー変換アルゴリズムについては "FXT algorithm library" および "Discrete Fourier and Hartley Transforms"を参照ください。

既定の実装では高速ハートレー変換は関数 fht メソッドによって表されています。

//-----------------------------------------------------------------------------------
// Radix-2 decimation in frequency (DIF) fast Hartley transform (FHT).
// Length is N = 2 ** ldn
//-----------------------------------------------------------------------------------
void TSAnalysis::fht(double &f[], ulong ldn)
  {
  const ulong n = ((ulong)1<<ldn);
  for (ulong ldm=ldn; ldm>=1; --ldm)
    {
    const ulong m = ((ulong)1<<ldm);
    const ulong mh = (m>>1);
    const ulong m4 = (mh>>1);
    const double phi0 = M_PI / (double)mh;
    for (ulong r=0; r<n; r+=m)
      {
      for (ulong j=0; j<mh; ++j)
        {
        ulong t1 = r+j;
        ulong t2 = t1+mh;
        double u = f[t1];
        double v = f[t2];
        f[t1] = u + v;
        f[t2] = u - v;
        }
      double ph = 0.0;
      for (ulong j=1; j<m4; ++j)
        {
        ulong k = mh-j;
        ph += phi0;
        double s=MathSin(ph);
        double c=MathCos(ph);
        ulong t1 = r+mh+j;
        ulong t2 = r+mh+k;
        double pj = f[t1];
        double pk = f[t2];
        f[t1] = pj * c + pk * s;
        f[t2] = pj * s - pk * c;
        }
      }
    }
  if(n>2)
    {
    ulong r = 0;
    for (ulong i=1; i<n; i++)
      {
      ulong k = n;
      do {k = k>>1; r = r^k;} while ((r & k)==0);
      if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;}
      }
    }
  }

このメソッドを呼ぶとき、インプットデータ配列 f[] に対する参照と、変換長 N = 2 ** ldn を定義する符号なし整数がインプットで渡されます。配列 f[] のサイズは変換 Nより小さくなりません。関数内部ではこれをチェックしないことに注意が必要です。また、変換結果はインプットデータがセットされた配列に格納されることも覚えておきます。

変換のあと、インプットデータ自体は格納されません。検証対象の Calc メソッドでは4096 AFR 値を計算するために長さ N=8192 の変換が使用されます。二乗されたサイズの変換計算と逆数の取得に続いては取得された結果がその最大値と対数スケールに正規化されます。

それ以外にCalc メソッドには大きな特殊性はありません。必要であれば、TSAnalysis.mqhを参照してその実装をもっとよく見ることが可能です。

計算結果として表示のために取得され準備された値は TSAnalysis クラスのメンバである変数に保存されます。よってそれらは結果表示のために仮想メソッドshowを呼ぶとき渡される必要はありません。


視覚化

すでに述べたとおり、showメソッドは仮想メソッドとして宣言されます。それを再定義することで提案されているものとは異なる計算結果を表示するために要求されるメソッドを実装することができます。提案されている TSAnalysis クラスの可視化はデータファイル準備とデータ表示用ウェブブラウザ―を呼ぶことで実行します。

ウェブブラウザ―がそのようなデータを表示できるようにするには残りのプロジェクトファイルと同じディレクトリにセットされている TSA.htm ファイルが使用されます。グラフィック情報を表示するためのこのメソッドは記事『HTML形式でのグラフと図』で以前に述べられています。

表示メソッドのTSAnalysis クラスはフォーマットおよびstring-type変数（TSAnalysis.mqh参照）に表示するために計算結果をすべて格納します。この方法で作成された長い行は1ステップで TSDat.txt に保存されます。このファイルの作成とそこへのデータ保存は標準 MQL5ツールを用いて実行され、 \MQL5\Files ディレクトリにファイルが作成されます。

このファイルはその後外部システム関数を呼ぶことでこのプロジェクトのディレクトリに移動されます。これに続いてTSDat.txtからデータを使うTSA.htmを表示するウェブブラウザ―を呼びます。システム関数が表示メソッドで呼ばれるため、TSAnalysis クラスに連携するターミナル内で外部DLLの使用が可能となります。


例

TSAnalysis.zip アーカイブにインクルードされているTSAexample.mq5は TSAnalysis クラスを使う例です。

//-----------------------------------------------------------------------------------
//                                                                     TSAexample.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "TSAnalysis.mqh"
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50,
  60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52,
  38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23};

  TSAnalysis *tsa=new TSAnalysis;

  tsa.Calc(bd);

  delete tsa;

  }

ご覧のようにクラスへの参照はかなりシンプルなものです。入力シーケンスを含む準備された配列があれば、分析のためにそれを Calc メソッドに渡すのに労力はたいして必要ありません。またdeleteを呼ぶことでメモリ解放できることを思い出す必要があります。このスクリプトの実行結果はすでに本稿の冒頭で提供済みです。

結果としてのスペクトル推定の効率を示すために、作成されたシーケンスが使われる別の例を見ましょう。

まずは2本の正弦曲線で構成されるシーケンスを使用します。

int i,n;
double a,x[];
  
n=400;
ArrayResize(x,n);
a=2*M_PI;
for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);

下の図はこのシーケンスの頻度応答推定値です。

図2　

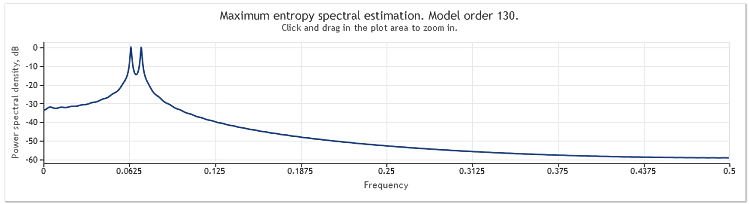
図2　スペクトル推定値2本の正弦曲線

どちらの正弦曲線もよく観測することができますが、興味を引かれるチャート領域を拡大することで最高値が頻度0.0637 ～ 0.0712に位置しているのが発見できました。別の言い方をすると、それらは真の値とはやや異なっています。シーケンスが単一の正弦曲線で構成されるとき、そのような推定のバイヤス は観測されません。スペクトル分析の選択したメソッドの効果としてこの事象を考察します。

あとでこのシーケンスに無作為なコンポーネントを加えてタスクを複雑にします。このために、本稿末尾のアーカイブRNDXor128.zipに見られるRNDXor128クラスによって表現される疑似ランダムシーケンスジェネレータが使用されます。

下記のコードの一部はテストシグナル作成に使用されました。

int i,n;
double a,x[];
  
RNDXor128 *rnd=new RNDXor128;
n=800;
ArrayResize(x,n);
a=2*M_PI;
for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm();
delete rnd;

この例では、正規分布とユニット分散を伴う不規則信号が2本の正弦曲線に追加されています。

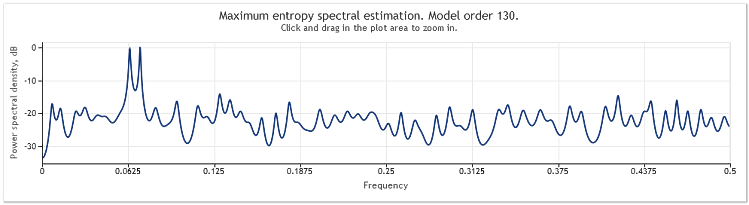
図3　スペクトル推定値2本の正弦曲線 + 不規則信号

この場合正弦曲線コンポーネントはよく識別できるままになっています。

ランダムコンポーネントの偏角が5倍増加していることで相当に マスクされた正弦曲線となっています。

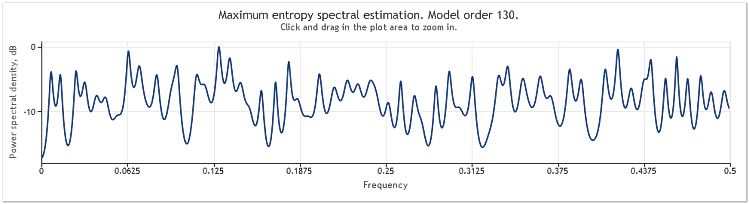
図4　スペクトル推定値2本の正弦曲線 +　大きい偏角を伴う不規則信号

シーケンス長が 400 から 800 エレメントまで増えるとき、正弦曲線は再びよく観測できるようになります。

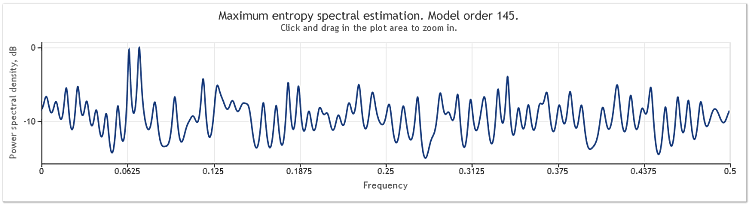
図5　2本の正弦曲線 + 大きい偏角を伴う不規則信号N=800

自己回帰モデル次数は130 から 145に増加しました。シーケンス長の増加によりモデルの高次数に導かれ、結果としてスぺクトル推定値の解像能は増しました。グラフの最高点が著しく鋭くなりました。

シンボル EURUSD、時間枠D1、 期間2年 (2009 および 2010) に対するクオートのスペクトル推定値は以下のように示されます。

図6　EURUSD クオート2009-2010. 期間 D1

値519で構成される入力シーケンスとモデル次数は、下図のように 135となるようです。

ご覧のようにこのスペクトル推定には多くの著しいピークがあります。ただ、この推定値だけではこういったピークがクオートの周期成分なのかどうか判断するのに十分ではありません。

頻度応答でのピーク発生はクオートに存在する高次ランダム成分または問題のシーケンスの明確定常性による可能性があります。

周期成分の存在について最終結論を出す前にシーケンスの別部分から採ったデータまたは別の時間枠を使用して取得された結果を検証することは常に奨励されます。それ以外にサイクル回帰を調査する際、シーケンス自体ではなくシーケンスの違いを使ってみることもできます。


おわりに

本稿で採用しているスペクトル推定メソッドは自己相関係数を基にしているため、入力シーケンスの平均はつねにメソッドの適用時にシーケンスから削除されてしまうようです。往々にして入力シーケンスから定数成分を削除する必要性がありますが、自己回帰手法を使用するとき、そのような削除は低頻度域においてスペクタル推定値のゆがみを招くこともあります。

そのようなゆがみの例は S. L. Marpleの著書"Digital Spectral Analysis with Applications"の "Summary of Results Regarding Spectral Estimates" 章に述べられています。本稿の場合で採用したスペクトル分析手法では、スペクトル推定はつねに削除される平均値を取るシーケンスに関して実行されることに留意するしかありません。


参照資料