Perceptrón Multicapa y Algoritmo de Retropropagación
Jonathan Pereira | 3 marzo, 2021
Introducción:
- Recientemente, al aumentar la popularidad de estos dos métodos, se han desarrollado tantas bibliotecas en Matlab, R, Python, C++, etc., que reciben el conjunto de entrenamiento como entrada y construyen automáticamente una red neuronal apropiada para el supuesto problema.
- Pero, al usar estas bibliotecas, a veces no entendemos exactamente qué sucede y cómo llegamos a la red optimizada. Conocer los fundamentos de una solución es muy importante para el desarrollo de métodos pasados. Así que, en este artículo, haremos una estructura muy simple del algoritmo de la red neuronal
- Vamos a entender cómo funciona un tipo básico de red neural -perceptrón de una sola neurona y perceptrón multicapa- y un fascinante algoritmo encargado del aprendizaje de la red, (gradiente descendente y retropropagación). Estos modelos de red servirán como base para los modelos más complejos que existen hoy en día.
Un breve paso por la historia:
- La primera red neuronal fue concebida por Warren McCulloch y Walter Pitts en 1943, que escribieron un artículo billante sobre cómo deberían funcionar las neuronas y, luego, modelaron sus ideas creando una red neuronal simple con circuitos eléctricos.
- Las investigaciones sobre IA se aceleraron rápidamente, siendo Kunihiko Fukushima la primera red neuronal multicapa de verdad en 1975.
- El objetivo original de una red neuronal era crear un sistema informático capaz de resolver problemas como un cerebro humano. Sin embargo, con el paso del tiempo, los investigadores cambiaron su enfoque y comenzaron a utilizar redes neuronales para resolver tareas específicas. Desde entonces, las redes neuronales han dado suporte a las más diversas tareas, incluyendo a la visión por computadora, reconocimiento de voz, traducción automática, filtrado de redes sociales, juegos de mesa o videojuegos, diagnóstico médico, pronóstico del tiempo, predicción de series de tiempo, reconocimiento de (imagen, texto, voz), etc.
Modelo informático de una neurona: el perceptrón
Perceptrón de una neurona:
El perceptrón se inspira en el procesamiento de información de una sola célula neural, la neurona. Una neurona acepta señales de entrada a través de sus dendritas, que pasan la señal eléctrica al cuerpo celular. Del mismo modo, el perceptrón recibe señales de entrada de ejemplos de datos de entrenamiento que hemos ponderado y combinado en una ecuación lineal llamada activación.
- z = sum(weight_i * x_i) + bias
Donde weight es un peso de red, x es una entrada, i es el índice de un peso o una entrada y bias es un peso especial que no tiene una entrada para multiplicar (o podemos pensar que en la entrada es siempre 1.0).
Luego, la activación se transforma en un valor de salida (predicción) utilizando una función de transferencia (función de activación).
- y = 1.0 se z >= 0.0 en caso contrario 0.0
De esta manera, el perceptrón es un algoritmo de clasificación para problemas con dos clases (clasificador binario) donde se puede utilizar una ecuación lineal para separar las dos clases.
Está estrechamente relacionado con la regresión lineal y la regresión logística que hacen predicciones de manera similar (por ejemplo, una suma ponderada de entradas).
El algoritmo perceptrón es el tipo más simple de red neuronal artificial. Es un modelo de neurona única que se puede utilizar en problemas de clasificación de dos clases y que proporciona la base para el desarrollo posterior de redes mucho más grandes.
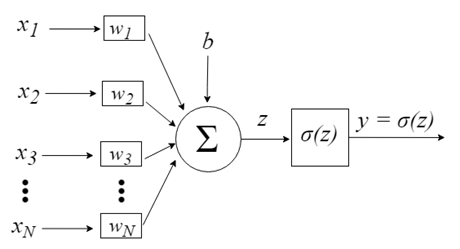
Las entradas a las neuronas están representadas por el vector x = [x1, x2, x3, …, xN], que puede corresponder, por ejemplo, a una serie de precios de cotización de un activo, a valores de indicadores técnicos, a una secuencia numérica, a píxeles de una imagen. Cuado ellas llegan a la neurona, se multiplican por los respectivos pesos sinápticos, que son los elementos del vector w = [w1, w2, w3, ..., wN], y, así, generan el valor z, comúnmente llamado potencial de activación, según la expresión:
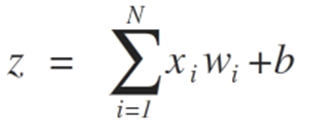
b proporciona un mayor grado de libertad y no se ve afectado por la entrada a esta expresión, que típicamente corresponde al bias (propensión). El valor z luego pasa a través de una función de activación σ, responsable de limitar este valor a un cierto intervalo (por ejemplo, 0 - 1), lo que produce el valor de salida final y de la neurona. Algunas funciones de activación utilizadas son paso, sigmoide, tangente hiperbólica, softmax y ReLU («rectified linear unit»).
Para ilustrar el proceso destinado a alcanzar el límite de la separabilidad de clases, presentamos a continuación dos situaciones que muestran su convergencia hacia la estabilización considerando solo dos entradas {x1 y x2}
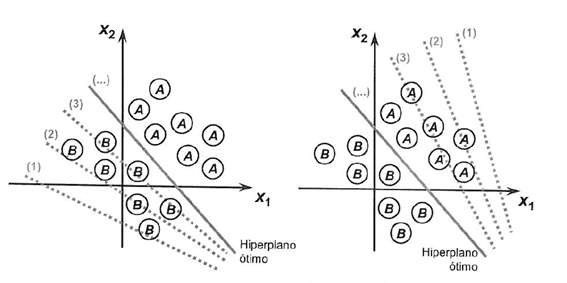
Los pesos del algoritmo perceptrón deben estimarse a partir de sus datos de entrenamiento mediante el descenso de gradiente estocástico.
Gradiente estocástico:
El descenso de gradientes es el proceso de minimizar una función siguiendo los gradientes de la función de costo.
Esto implica conocer la forma del costo, así como la derivada para que a partir de cierto punto conozcamos la pendiente y podamos movernos en tal dirección, por ejemplo, cuesta abajo hacia el valor mínimo.
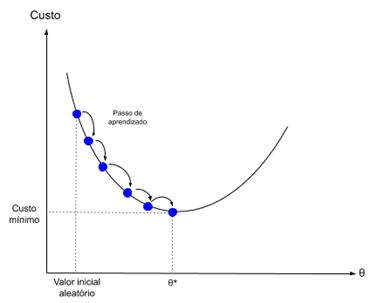
En el aprendizaje automático, podemos usar una técnica -que evalúa y actualiza los pesos para cada iteración- llamada descenso de gradiente estocástico, para minimizar el error de un modelo en nuestros datos de entrenamiento.
La forma en que funciona este algoritmo de optimización es que cada instancia de entrenamiento se muestra al modelo de una en una. El modelo hace una predicción para una instancia de entrenamiento, se calcula el error y el modelo se actualiza para reducir el error para la próxima predicción.
Este procedimiento se puede utilizar para encontrar el conjunto de pesos en un modelo que dé como resultado el menor error para el modelo dentro de los datos de entrenamiento.
Para el algoritmo perceptrón, a cada iteración los pesos w se actualizan utilizando la ecuación:
- w = w + learning_rate * (expected - predicted) * x
Donde w está siendo optimizado, learning_rate es una tasa de aprendizaje que debemos establecer (por ejemplo, 0,1), (expected - predicted) es el error de predicción para el modelo en los datos de entrenamiento atribuidos al peso y x es el valor de entrada.
El descenso del gradiente estocástico requiere dos parámetros:
- La tasa de aprendizaje: se utiliza para limitar la cantidad, cada peso se corrige cada vez que se actualiza.
- Épocas: la cantidad de veces que se deben ejecutar los datos de entrenamiento mientras se actualiza el peso.
Estos, junto con los datos de entrenamiento, serán los argumentos para la función.
Hay 3 bucles que debemos ejecutar en la función:
1. Bucle para cada época.
2. Bucle para cada línea en los datos de entrenamiento para una época.
3. Bucle para cada peso actualizándolo para una línea en una época.
Los pesos se actualizan en función del error cometido por el modelo. El error se calcula como la diferencia entre el valor real y la predicción realizada con los pesos.
Hay un peso para cada atributo de entrada, y estos se actualizan de forma coherente, por ejemplo:
- w(t+1)= w(t) + learning_rate * (expected(t) - predicted(t)) * x(t)
El bias se actualiza de manera similar, solo que sin una entrada, ya que no está asociado con un valor de entrada específico:
- bias(t+1) = bias(t) + learning_rate * (expected(t) - predicted(t)).
Ahora, pasemos a la aplicación práctica.
Este tutorial se divide en 2 partes:
1. Haciendo predicciones
2. Optimizando los pesos de la red
Estos pasos nos proporcionarán la base para poder implementar y aplicar el algoritmo perceptrón a otros problemas de clasificación.
Necesitamos definir el número de columnas en nuestro conjunto X, para eso definimos la constante
#define nINPUT 3
En MQL5, una matriz multidimensional puede ser estática o dinámica solo para la primera dimensión, y dado que todas las demás dimensiones serán estáticas, estamos obligados a definir el tamaño en la declaración de la matriz.
1. Haciendo predicciones
El primer paso es desarrollar una función que pueda hacer predicciones.
Esto será necesario tanto en la evaluación de los valores de pesos de los candidatos en el descenso del gradiente estocástico, como tras la finalización del modelo; además, queremos empezar a hacer predicciones sobre datos de prueba o datos nuevos.
A continuación se muestra una función llamada predict que predice un valor de salida para una línea, dado un conjunto de pesos.
El primer peso es siempre el bias, ya que es autónomo y no se encarga de un valor de entrada específico.
// Make a prediction with weights template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); }
Transferencia de neuronas:
Una vez que se activa una neurona, necesitamos transferir la activación para ver cuál es realmente la salida de la neurona.
//+------------------------------------------------------------------+ //| Transfer neuron activation | //+------------------------------------------------------------------+ double activation(const double activation) //# { return activation>=0.0?1.0:0.0; }
Recibimos como argumento en la función predict el conjunto de entrada X, la matriz con los pesos (W) y la línea a la que se le hace la predicción del conjunto de entrada X.
Podemos inventar un pequeño conjunto de datos para probar nuestra función de predicción.
También podemos usar pesos previamente preparados para hacer predicciones para este conjunto de datos.
double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
Después de ponerlo todo junto, podemos probar nuestra función de predicción a continuación.
#define nINPUT 3 //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- random.seed(42); double dataset[][nINPUT] = { //X1 //X2 //Y {2.7810836,2.550537003,0}, {1.465489372,2.362125076,0}, {3.396561688,4.400293529,0}, {1.38807019,1.850220317,0}, {3.06407232,3.005305973,0}, {7.627531214,2.759262235,1}, {5.332441248,2.088626775,1}, {6.922596716,1.77106367,1}, {8.675418651,-0.242068655,1}, {7.673756466,3.508563011,1} }; double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003}; for(int row=0; row<ArrayRange(dataset, 0); row++) { double predict = predict(dataset, weights, row); printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict); } } //+------------------------------------------------------------------+ // Make a prediction with weights template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); } //+------------------------------------------------------------------+ //| Transfer neuron activation | //+------------------------------------------------------------------+ double activation(const double activation) //# { return activation>=0.0?1.0:0.0; }
Existen dos valores de entrada (X1 y X2) y tres valores de peso (bias, w1 y w2). La ecuación de activación que modelamos para este problema es:
activation = (w1 * X1) + (w2 * X2) + b
O, con valores de peso específicos, elegimos manualmente como:
activation = (0.206 * X1) + (-0.234 * X2) + -0.1
Al ejecutar esta función, tenemos predicciones que corresponden a los valores de salida esperados y.
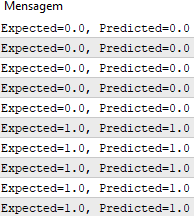
Ahora podemos implementar el descenso de gradiente estocástico para optimizar los valores de peso.
2. Optimizando los pesos de la red
Podemos estimar los valores de peso para nuestros datos de entrenamiento utilizando el descenso de gradiente estocástico, como se indicó anteriormente.
A continuación se muestra una función llamada train_weights() que calcula los valores de peso para un conjunto de datos de entrenamiento utilizando el descenso de gradiente estocástico.
En MQL5 no podemos tener un retorno de esta matriz con los datos de los pesos entrenados porque, a diferencia de las variables, las matrices solo se pueden pasar a una función por referencia. Esto significa que la función no crea su propia instancia de la matriz y, en cambio, trabaja directamente con la matriz que se le pasa. De ese modo, todos los cambios realizados en esta matriz dentro de la función hacen que la matriz original se vea afectada.
//+------------------------------------------------------------------+ //| Estimate Perceptron weights using stochastic gradient descent | //+------------------------------------------------------------------+ template <typename Array> void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5) { ArrayResize(weights, ArrayRange(X, 1)); for(int i=0; i<ArrayRange(X, 1); i++) { weights[i]=random.random(); } for(int epoch=0; epoch<n_epoch; epoch++) { double sum_error = 0.0; for(int row=0; row<ArrayRange(X, 0); row++) { double y = predict(X, weights, row); double error = X[row][nINPUT-1] - y; sum_error += pow(error, 2); weights[0] = weights[0] + l_rate * error; for(int i=0; i<ArrayRange(X, 1)-1; i++) { weights[i+1] = weights[i+1] + l_rate * error * X[row][i]; } } printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error); } }
Podemos ver que seguimos la suma del error cuadrado (un valor positivo) en cada época para rastrear la disminución del error, por lo que podemos ver en qué época el algoritmo pudo minimizar el error.
Luego, podemos probar nuestra función con el mismo conjunto de datos presentado anteriormente.
#define nINPUT 3 //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- random.seed(42); double dataset[][nINPUT] = { //X1 //X2 //Y {2.7810836,2.550537003,0}, {1.465489372,2.362125076,0}, {3.396561688,4.400293529,0}, {1.38807019,1.850220317,0}, {3.06407232,3.005305973,0}, {7.627531214,2.759262235,1}, {5.332441248,2.088626775,1}, {6.922596716,1.77106367,1}, {8.675418651,-0.242068655,1}, {7.673756466,3.508563011,1} }; double weights[]; train_weights(weights, dataset); ArrayPrint(weights, 20); for(int row=0; row<ArrayRange(dataset, 0); row++) { double predict = predict(dataset, weights, row); printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict); } } //+------------------------------------------------------------------+ // Make a prediction with weights template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); } //+------------------------------------------------------------------+ //| Transfer neuron activation | //+------------------------------------------------------------------+ double activation(const double activation) //# { return activation>=0.0?1.0:0.0; } //+------------------------------------------------------------------+ //| Estimate Perceptron weights using stochastic gradient descent | //+------------------------------------------------------------------+ template <typename Array> void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5) { ArrayResize(weights, ArrayRange(X, 1)); ArrayInitialize(weights, 0); for(int epoch=0; epoch<n_epoch; epoch++) { double sum_error = 0.0; for(int row=0; row<ArrayRange(X, 0); row++) { double y = predict(X, weights, row); double error = X[row][nINPUT-1] - y; sum_error += pow(error, 2); weights[0] = weights[0] + l_rate * error; for(int i=0; i<ArrayRange(X, 1)-1; i++) { weights[i+1] = weights[i+1] + l_rate * error * X[row][i]; } } printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error); } }
Usamos una tasa de aprendizaje de 0,1 y entrenamos el modelo por solo 5 épocas, o 5 exposiciones de los pesos para todo el conjunto de datos de entrenamiento.
Al ejecutar el ejemplo, se imprime un mensaje en cada época con la suma del error al cuadrado para tal época y el conjunto final de pesos.
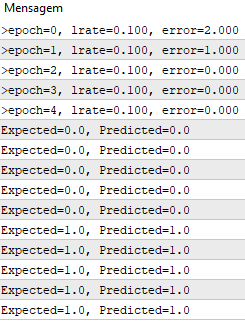
Podemos ver la rapidez con la que el algoritmo aprende el problema.
Esta prueba se puede encontrar en el archivo PerceptronScript.mq5.
Perceptrón multicapa:
- Combinando neuronas en capas
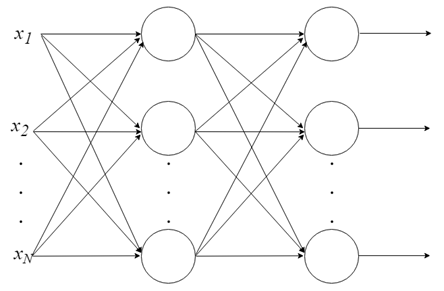
Con una sola neurona, no se puede hacer mucho, pero podemos combinarlas en una estructura en capas, cada una con un número diferente de neuronas, y formar una red neuronal llamada perceptrón multicapa («multi layer perceptron, MLP»). El vector de los valores de entrada X pasa por la capa inicial, cuyos valores de salida están vinculados a las entradas de la siguiente capa, y así sucesivamente, hasta que la red proporciona como resultado los valores de salida de la última capa. La red se puede organizar en varias capas, haciéndola profunda y capaz de aprender relaciones cada vez más complejas.
Entrenamiento un MLP:
Para que una red de este tipo funcione, debemos entrenarla. Es como enseñarle a un niño a leer. El entrenamiento de un MLP está en el contexto del aprendizaje automático supervisado, pero ¿cómo funciona?
Aprendizaje supervisado:
- Se nos da un conjunto de datos etiquetados para los cuales ya sabemos cuál es nuestra salida correcta y que debe ser similar al conjunto, teniendo la idea de que existe una relación entre la entrada y la salida.
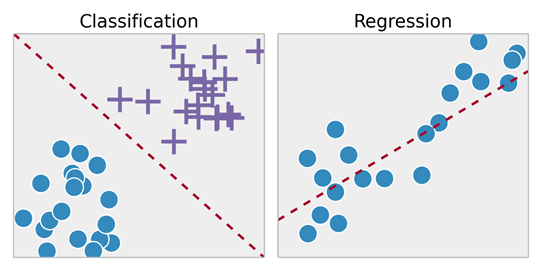
- Los problemas de aprendizaje supervisado se clasifican en problemas de "regresión" y "clasificación". En los de regresión, tratamos de predecir los resultados en una salida continua, lo que significa que estamos tratando de asignar variables de entrada a alguna función continua. En los de clasificación, intentamos predecir los resultados en una salida discreta. En otras palabras, tratamos de mapear variables de entrada en diferentes categorías.
Ejemplo 1:
- Dado un conjunto de datos sobre el tamaño de las casas en el mercado inmobiliario, intente predecir su precio. El precio en función del tamaño es una salida continua, por lo que este es un problema de regresión.
- También podríamos convertir este ejemplo en un problema de clasificación, en lugar de hacer nuestra producción sobre si la casa "se vende por más o menos que el precio de venta". Aquí clasificamos las viviendas según el precio en dos categorías distintas.
Retropropagación:
La retropropagación es, sin lugar a dudas, el algoritmo más importante en la historia de las redes neuronales; sin la retropropagación (eficiente), sería imposible entrenar redes de aprendizaje profundo como en la actualidad. La retropropagación puede considerarse la piedra angular de las redes neuronales modernas y del aprendizaje profundo.
¿No es cometiendo errores que se aprende?
La idea del algoritmo de retropropagación es, en función del cálculo del error ocurrido en la capa de salida de la red neuronal, volver a calcular el valor de los pesos del vector W de la última capa de neuronas y así proceder a las capas anteriores, de atrás hacia adelante, es decir, consiste en actualizar todos los pesos W de las capas, desde la última hasta llegar a la capa de entrada de la red, para hacerlo retropropagando el error obtenido por la red. En otras palabras, el error se calcula entre lo que predijo la red y lo que realmente fue (real 1, predicho 0; ¡tenemos aquí un error!), por lo que recalculamos el valor de todos los pesos, comenzando desde la última capa y yendo a la primera, siempre teniendo en cuenta disminuir ese error.
El algoritmo de retropropagación consta de dos fases:
1. El paso hacia adelante («forward pass»), en él nuestras entradas pasan a través de la red y se obtienen las predicciones de salida (este paso también se conoce como la fase de propagación).
2. El pase hacia atrás («backward pass»), en él calculamos el gradiente de la función de pérdida en la capa final (es decir, la capa de predicción) de la red y usamos este gradiente para aplicar recursivamente la regla de la cadena («chain rule») para actualizar los pesos en nuestra red (también conocida como etapa de actualización de peso o retropropagación).
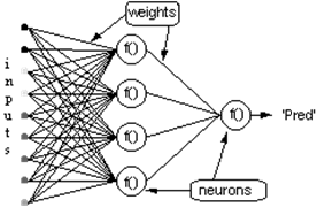
Consideremos la red anterior, con una capa de neuronas ocultas y una neurona de salida. Cuando un vector de entrada se propaga a través de la red, para el conjunto actual de pesos hay una salida Pred(y). El propósito del entrenamiento supervisado es ajustar los pesos para que la diferencia entre Pred(y) de la red y la salida requerida Req(y) esté reducida. Esto requiere un algoritmo que reduzca el error absoluto, que es lo mismo que reducir el error cuadrado, donde:
(1)
Error de la red = Pred - Req
= E
El algoritmo debe ajustar los pesos para minimizar E². La retropropagación es un algoritmo que realiza una minimización de gradiente descendente de E². Para minimizar E², se debe calcular su sensibilidad a cada uno de los pesos. En otras palabras, necesitamos saber qué efecto tendrá el cambio en cada uno de los pesos sobre E². Si se sabe eso, los pesos se pueden ajustar en la dirección que reduzca el error absoluto. La notación para la siguiente descripción de la regla de propagación inversa se basa en el diagrama a continuación.
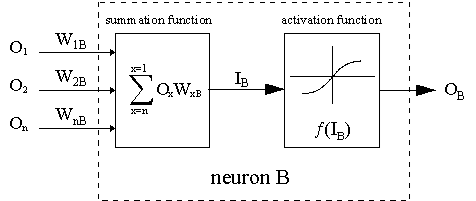
La línea discontinua representa una neurona B, que puede ser una neurona oculta o de salida. Las salidas de n neuronas (O 1 ... O n) en la capa anterior proporciona las entradas para la neurona B. Si la neurona B está en la capa oculta es porque se trata simplemente del vector de entrada. Estas salidas se multiplican por los respectivos pesos (W1B ... WnB), donde WnB es el peso que conecta la neurona n a la neurona B. La función de suma agrega todos estos productos para proporcionar la entrada, IB, que es procesada por la función de activación f(.) de la neurona B. f (IB) es la salida, OB, de la neurona B. Para el objetivo de esta ilustración, llamemos a la neurona 1 neurona A y luego consideremos el peso WAB conectando las dos neuronas. El enfoque utilizado para el cambio de peso viene dado por la regla delta:
(2)
![]()
donde ![]() es el parámetro de tasa de aprendizaje, que determina la velocidad de aprendizaje, y
es el parámetro de tasa de aprendizaje, que determina la velocidad de aprendizaje, y
![]()
es la sensibilidad del error, E², al peso WAB y determina la dirección de búsqueda en el espacio de peso para el nuevo peso WAB (nuevo) como se muestra en la figura a continuación.
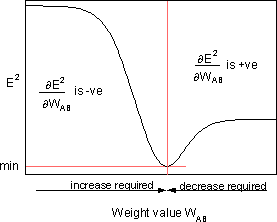
Para minimizar E², la regla delta proporciona la dirección del cambio de peso requerida
El concepto clave de la ecuación anterior es el cálculo de la expresión∂E² /∂WAB, que consiste en calcular las derivadas parciales de la función de error E² con relación a cada peso del vector W.
(3)
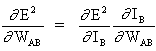
Y
(4)
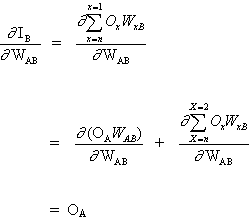
ya que el resto de las entradas a la neurona B no dependen del peso WAB. Así, partiendo de las ecuaciones (3) y (4), la ecuación (2) se convierte en
(5)
![]()
y el cambio de peso de WAB depende de la sensibilidad del error cuadrático, E², en la entrada, IB, unidad B y de la señal de entrada OA.
Hay dos posibles situaciones:
1. B es una neurona de salida;
2. B es una neurona oculta.
Considerando el primer caso:
Dado que B es la neurona de salida, el cambio en el error cuadrático debido a un ajuste de WAB es simplemente el cambio en el error cuadrático de la salida de B.
(6)
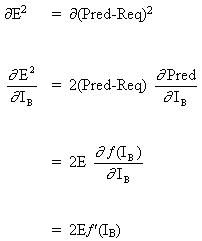
combinando la ecuación (5) con la (6) obtenemos:
(7)
![]()
la regla para modificar los pesos cuando la neurona B es una neurona de salida, si la función de activación de salida, f(.), es la función logística:
(8)
![]()
Diferenciando la ecuación (8) por su argumento x:
(9)
![]()
Pero,
(10)
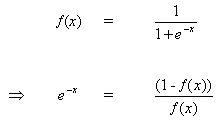
al insertar (10) en (9) da:
(11)
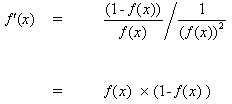
de la misma manera para la función tanh
![]()
o para la función lineal (identidad)
![]()
Esto da:
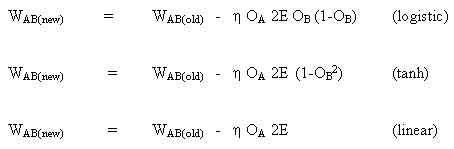
Considerando el segundo caso:
B es una neurona oculta
(12)
![]()
donde O representa la neurona de salida
(13)
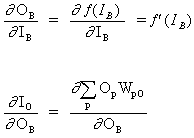
donde p es un índice que cubre todas las neuronas, incluida la neurona B, que proporciona señales de entrada a la neurona de salida. Expandiendo el lado derecho de la ecuación (13),
(14)
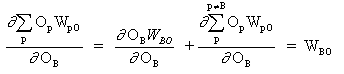
ya que los pesos de las otras neuronas, WpO (p! = B) no tienen dependencia de OB.
Al insertar (13) y (13) en (12):
(15)
![]()
Por lo tanto, ![]() ahora se expresa en función de
ahora se expresa en función de ![]() calculado como se describe en la ecuación (6).
calculado como se describe en la ecuación (6).
La regla completa para modificar el peso WAB entre una neurona A que envía una señal a una neurona B es
(16)
![]()
donde
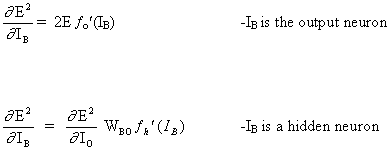
donde fo (.) y fh (.) son las funciones ocultas de activación y salida, respectivamente.
Ejemplo:
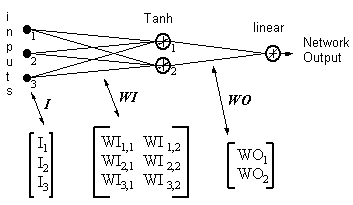
Salida de la red = [tanh(I T .WI)] . WO
HID = [Tanh(I T.WI)] T- las salidas de las neuronas ocultas
ERROR = (salida de red - salida necesaria)
LR = tasa de aprendizaje
Las actualizaciones de peso se vuelven
neurona de salida lineal
(17)
WO = WO - ( LR x ERROR x HID )
neurona oculta
(18)
WI = WI - { LR x [ERROR x WO x (1- HID 2)] . I T } T
Las ecuaciones 17 y 18 muestran que el cambio de peso es una señal de entrada multiplicada por un gradiente local. Esto proporciona una dirección que también tiene una magnitud dependiente de la magnitud del error. Si se toma la dirección sin magnitud, todos los cambios serán del mismo tamaño, lo que dependerá del ritmo de aprendizaje. El algoritmo anterior es una versión simplificada, ya que solo hay una neurona de salida. En el algoritmo original, se permite más de una salida y el descenso del gradiente minimiza el error cuadrático total de todas las salidas. Hay muchos algoritmos que han evolucionado a partir del algoritmo original para aumentar la velocidad de aprendizaje. Estos son resumidos en:
«Back Propagation family album" - Technical report C/TR96-05, Department of Computing, Macquarie University, NSW, Australia».
La retropropagación es un algoritmo elegante e ingenioso. Los modelos actuales de aprendizaje profundo como las redes neuronales convolucionales, aunque más refinados que el MLP, han demostrado ser muy superiores en tareas como la clasificación de imágenes y hacen uso de la retropropagación como método de aprendizaje, así como las llamadas redes neuronales recurrentes, en el procesamiento del lenguaje natural, también usan este algoritmo. Lo más increíble es que tales modelos logran encontrar patrones inobservables y confusos para nosotros los humanos, lo cual es fascinante y nos permite considerar que pronto contaremos con la ayuda del aprendizaje profundo para resolver muchos de los principales problemas que afligen a la humanidad.
Aplicación del modelo MLP:
Este tutorial se divide en 5 partes:
1. Inicialización de la red.
2. Propagación (FeedForward).
3. Retropropagación.
4. Entrenamiento de la red.
5. Predecir.
Para nuestro desarrollo haremos la implementación en MQL puro. Se sabe que existen bibliotecas en otros lenguajes que ya son mucho más sofisticadas y se recomienda encarecidamente utilizarlas, por razones prácticas y de rendimiento, pero, como se dijo al principio, es importante comprender el funcionamiento interno de tales bibliotecas para tener un mayor control de todo el proceso. Tampoco usamos POO en nuestra prueba, ya que, como es solo un algoritmo para ilustrar las ecuaciones anteriores, no es necesario, sin embargo, en casos del mundo real es mucho más práctico usar POO, porque aporta escalabilidad al proyecto.
1. Inicio de la red
Cada neurona tiene un conjunto de pesos que deben mantenerse. Un peso para cada conexión de entrada y un peso adicional para el bias.
Es una buena práctica inicializar los pesos de la red para números aleatorios pequeños. En este caso, usaremos números aleatorios en el rango de 0 a 1. Para ello creamos una función para la generación de números aleatorios.
double random(void) { return ((double)rand())/(double)SHORT_MAX; }
A continuación se muestra una función llamada initialize_network() que crea los pesos de nuestra red neuronal.
// Forward propagate input to a network output void forward_propagate(void) { //calculate the outputs of the hidden neurons //the hidden neurons are tanh int i = 0; for(i = 0; i<numHidden; i++) { hiddenVal[i] = 0.0; for(int j = 0; j<numInputs; j++) { hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]); } hiddenVal[i] = tanh(hiddenVal[i]); } //calculate the output of the network //the output neuron is linear outPred = 0.0; for(i = 0; i<numHidden; i++) { outPred += hiddenVal[i] * weightsHO[i]; } //calculate the error errThisPat = outPred - y[patNum]; }
3. Retropropagación
El algoritmo de retropropagación recibe su nombre de la forma en que se entrenan los pesos.
El error se calcula entre las salidas esperadas y las salidas de la red propagadas hacia adelante. Estos errores luego se propagan de regreso a través de la red desde la capa de salida a la capa oculta, atribuyendo la culpa por el error y actualizando los pesos a medida que estos avanzan.
La matemática del error de retropropagación se explicó anteriormente.
//+------------------------------------------------------------------+ //| Backpropagate error and change network weights | //+------------------------------------------------------------------+ void backward_propagate_error(void) { //adjust the weights hidden-output for(int k = 0; k<numHidden; k++) { double weightChange = LR_HO * errThisPat * hiddenVal[k]; weightsHO[k] -= weightChange; //regularisation on the output weights regularisationWeights(weightsHO[k]); } // adjust the weights input-hidden for(int i = 0; i<numHidden; i++) { for(int k = 0; k<numInputs; k++) { double x = 1 - pow(hiddenVal[i],2); x = x * weightsHO[i] * errThisPat * LR_IH; x = x * X[patNum][k]; double weightChange = x; weightsIH[k][i] -= weightChange; } } }
el método regularizationWeights se creó solo para regularizar pesos en un rango de -5 a 5.
//regularisation on the output weights void regularisationWeights(double &weight) { weight<-5?weight=-5:weight>5?weight=5:weight=weight; }
4. Entrenamiento de la red
La red se entrena mediante descenso de gradiente estocástico.
Esto implica varias iteraciones que exponen un conjunto de datos de entrenamiento a la red y para cada línea de datos hacia adelante propagando las entradas, retropropagando el error y actualizando los pesos de la red.
//# Train a network for a fixed number of epochs void train(void) { for(int j = 0; j <= numEpochs; j++) { for(int i = 0; i<numPatterns; i++) { //select a pattern at random patNum = rand()%numPatterns; //calculate the current network output //and error for this pattern forward_propagate(); backward_propagate_error(); } //display the overall network error //after each epoch calcOverallError(); printf("epoch = %d RMS Error = %f",j,RMSerror); } }
5. Predecir
Hacer predicciones con una red neuronal entrenada es bastante fácil.
Ya hemos visto cómo propagar un patrón de entrada para obtener una salida. Eso es todo lo que necesitamos hacer para hacer una predicción. Podemos usar los valores de salida directamente como la probabilidad de un patrón perteneciente a cada clase de salida.
// # Make a prediction with a network void predict(void) { for(int i = 0; i<numPatterns; i++) { patNum = i; forward_propagate(); printf("real = %d predict = %f",y[patNum],outPred); } }
El ejemplo completo se puede encontrar en el archivo MLP_Script.mq5
Conclusión:
Abordamos los cálculos involucrados en el proceso de desarrollo de una neurona perceptrón y también una red de neuronas perceptrón llamada «multi layer perceptron, MLP», en este proceso entendimos cómo se realiza el entrenamiento de este tipo de redes, utilizando retropropagación y descenso de gradiente.