Teoría de probabilidad y estadística matemática con ejemplos (Parte I): Fundamentos y teoría elemental

Aleksey Nikolayev | 3 noviembre, 2020

Índice

1. Introducción
2. Fundamentos de la teoría
3. Teoría elemental
• 3.1. Probabilidad combinatoria
• 3.2. Esquema de Bernoulli
4. Fundamentos de la estadística matemática
5. Ejemplos de aplicación de la estadística matemática en el marco de la teoría elemental
• 5.1. Estimación puntual del parámetro
• 5.2. Comprobación de hipótesis estadísticas
6. Conclusión
7. Archivos adjuntos
   

1.Introducción

El trading siempre ha estado relacionado con la toma de decisiones en condiciones de incertidumbre. Esto significa que los resultados de las decisiones tomadas no son totalmente obvios en el momento en que se toman. Por este motivo, resultan importantes los enfoques teóricos sobre la construcción de los modelos matemáticos que permiten describir estas situaciones ofreciendo información relevante e ilustrativa. Querría destacar dos enfoques de este tipo: la teoría de probabilidad y la teoría de juegos. A veces, se combinan juntas, denominando los métodos de probabilidad como teoría de "juegos con la naturaleza". Esto muestra bien la existencia de dos tipos diferentes de incertidumbre. El primero de ellos es de probabilidad, y normalmente está relacionado con fenómenos naturales. El segundo tiene que ver puramente con el juego, y se relaciona con la actividad de otros sujetos (personas o comunidades concretas). La incertidumbre del juego es significativamente más complicada para el análisis teórico. En ocasiones, estas incertidumbres incluso se conocen por "mala" y "buena". Con frecuencia, la evolución en el concepto de la incertidumbre de juego original se relaciona con la reducción de la misma a su forma de probabilidad.

En el caso del mercado, obviamente, es más importante la incertidumbre precisamente de carácter lúdico, dado que la actividad de la gente supone aquí el factor determinante. El paso a los modelos de probabilidad aquí tiene lugar, normalmente, debido al gran número de jugadores, que por separado no poseen una gran capacidad de influir en el cambio de los precios. En parte, se trata de un enfoque semejante al utilizado en la física estadística, lo cual provocó la aparición de un enfoque científico, llamado econofísica.

En la práctica, la cuestión sobre este paso es muy interesante, en absoluto trivial, y merece un análisis más detallado. Esperamos que los artículos dedicados a ello tengan cabida algún día en nuestro foro. En el presente artículo, no centraremos en el análisis de los propios fundamentos de la teoría de probabilidad y la estadística matemática.

2. Fundamentos de la teoría

La base de la teoría de probabilidad es un sistema formal conocido como Axiomas de probabilidad. No vamos a profundizar en aclaraciones sobre qué significa "sistema formal" y cómo entender correctamente el enfoque axiomático matemático: son cuestiones demasiado complejas de la lógica matemática. En lugar de ello, nos centraremos en el objeto básico de la teoría de probabilidad: el espacio de probabilidad (probability space). Este consta de un espacio muestral , un conjunto de eventos y la probabilidad de estos eventos. Más concretamente:

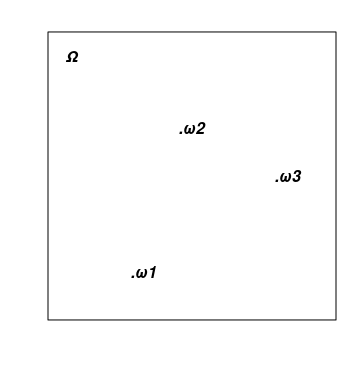
1) El espacio muestral (sample space) supone el conjunto de posibles resultados de un experimento aleatorio. Normalmente, se designa con una letra omega mayúscula − Ω y en las imágenes se representa con la forma de alguna figura. Los eventos elementales (elementary event, sample point) normalmente se marcan con una letra omega minúscula − ω, y en las imágenes se representa como puntos. El ejemplo estándar más sencillo para describir el resultado de una moneda lanzada al aire una única vez es: Ω={ω1, ω2}, donde ω1=H y ω2=T indican la caída de la cara y la cruz (heads y tails), mientras que los corchetes indican el conjunto establecido por una lista de elementos propios.

En la imagen de abajo se representa una cierta Ω abstracta en forma de rectángulo y varios puntos, es decir, los eventos elementales que les pertenecen:  ω1, ω2 y ω3.

2) Espacio de eventos aleatorios (event). Cada evento de este tipo constituye un conjunto de eventos elementales (subconjunto de todos los eventos elementales Ω). En el conjunto de eventos se incluyen el conjunto vacío ∅={} (evento que no sucederá nunca) y todo el conjunto Ω (evento que sucede siempre). La combinación (y cruzamiento) de dos eventos del conjunto deberá también pertenecer al conjunto. Este grupo de conjuntos se suele nombrar en matemáticas álgebra de conjuntos. En nuestro ejemplo, con la moneda suceden cuatro eventos: {}=∅,  {H}, {T} y {H,T}=Ω. (Pregunta de control: ¿puede ser un evento elemental un ejemplo de evento aleatorio?)

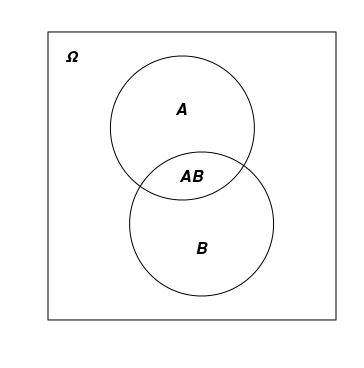
Se desginan los eventos aleatorios con letras latinas mayúsculas: A, B, C, ... y se representan en el dibujo en forma de figuras dentro de otra figura que representa Ω. La combinación y cruzamiento de eventos se designa de forma distinta. En ocasiones, se utiliza un registro similar a la suma y la multiplicación de las variables numéricas habituales: АВ y А+В, y a veces se utilizan los signos ∩ y ∪: А∩В y А∪В.

En el dibujo de abajo, se representa Ω en forma de rectángulo y dos eventos cruzados А y В.

3) Probabilidad: función de probabilidad (probability function) P=P(A), que opone a cada evento aleatorio A un número real en el segmento de 0 a 1. Además, P(Ω)=1 y P(∅)=0. Aparte de esto, se ejecuta una regla llamada adaptatividad: si el evento A supone la unión de los eventos no cruzados B y C, entonces P(A)=P(B)+P(C). Además del término "probabilidad", para la función P() se usan los términos "distribución de la probabilidad en Ω" o simplemente "distribución en Ω". Lo importante es no confundir el concepto con el concepto similar "función de distribución de una magnitud aleatoria". Aunque son de una misma familia, son distintos. El primero de ellos es una función que opone un número a un conjunto, mientras que el segundo es una función numérica normal que opone un número a otro.

No sabemos muy bien cómo representar la distribución de probabilidad con un dibujo, pero, a nivel intuitivo podemos imaginarla semejante a una masa única con volumen Ω. En este analogía, el evento es una parte del volumen, mientras que la probabilidad sería una fracción de la masa que ha resultado dentro de esta parte del volumen.

Todos los demás conceptos de la teoría de probabilidad son derivados de estos. Aquí, destacaremos un concepto muy importante de la dependencia (independencia) de probabilidad. Para ello, introduciremos una probabilidad condicional del evento А con la condición de que se cumpla el evento B, P(B)>0. Se desgina como P(A|B) y al determinarse P(A|B)=P(AB)/P(B) (recordemos que AB indica el cruzamiento de los eventos A y B). El evento A, por definición, se denomina independiente del evento B en el caso de que su probabilidad condicional, al darse el evento B, sea igual a su probabilidad: P(A|B)=P(A). Utilizando la expresión para la probabilidad condicional, esta definición de independencia se puede reescribir con el aspecto siguiente: P(A)P(B)=P(AB). Si esta igualdad no se cumple, diremos que el evento A depende del evento B.

Desde un punto de vista intuitivo, la independencia indica que el conocimiento de que haya sucedido el evento B no cambia la incertidumbre relacionada con el evento A. Y al contrario, la dependencia indica que la ejecución del evento B conlleva la información sobre el evento A. La expresión concreta de esta comprensión intuitiva se da en la teoría de la información de Claude Shannon.

La teoría de probabilidad se divide en elemental y no elemental. La diferencia de la teoría elemental respecto a la no elemental, reside en que en ella se analizan conjuntos de eventos elementales que constan de un número finito de elementos. Por consiguiente, también resultará finito el grupo de eventos aleatorios (pregunta de control: ¿por qué esto es cierto?). Esta teoría se desarrolló mucho antes de los axiomas de probabilidad de Kolmogórov, y no requería especialmente de estos. El resto del artículo se dedicará a esta parte de la teoría. La teoría no elemental se analizará en el próximo artículo.

3. Teoría elemental

Como el número de resultados elementales es finito, podemos simplemente establecer la probabilidad de eventos que contengan exactamente un evento elemental (conjunto de unidades) Solo tenemos que asegurarnos de que la suma de estas probabilidades sea igual a la unidad. La probabilidad de cualquier evento será igual a la suma de las probabilidades semejantes. Dichas probabilidades iniciales no son necesariamente iguales; no obstante, empezaremos con dichos modelos, generalmente conocidos por el nombre "probabilidad combinatoria".

3.1. Probabilidad combinatoria

Supongamos que Ω consta exactamente de N resultados elementales, entonces, la probabilidad de los eventos que los contienen en un número de m, será igual a m/N. Los cálculos de probabilidad aquí consisten en contar el número de variantes. Como norma general, se usan métodos combinatorios para esto, de ahí el nombre. Aquí hay unos ejemplos:

Ejemplo 1. Supongamos que tenemos n objetos diferentes. ¿Cuántas formas distintas de ordenarlos (ponerlos en una fila) tendremos? Respuesta: n!=1*2*3*....*(n-1)*n formas. Cada forma se llama permutación, y cada permutación es un evento elemental. Por lo tanto, N=n! y la probabilidad de un evento que consta de m permutaciones, será igual a m/n! (m/N=m/n!).

Como ejemplo, vamos a resolver un problema simple: deberemos encontrar la probabilidad de que un objeto dado se encuentre en la primera posición después de una permutación aleatoria. Si el primer lugar está ocupado por el primer elemento, los demás objetos n-1 se podrán distribuir por el resto de lugares n-1 con las formas (n-1)!. De esta manera, m=(n-1)! significará que la probabilidad buscada es igual a m/N=m/n!=(n-1)!/n!=1/n.

Ejemplo 2. También tenemos n objetos diferentes. ¿Cuántos grupos distintos de objetos k (k<=n) podemos seleccionar de ellos? Aquí hay dos opciones posibles, dependiendo de si consideramos dos grupos que solo se diferencian en el orden de los objetos. Si los diferenciamos, entonces la respuesta será: n!/(n-k)! grupos; si no diferenciamos, k! veces menos: n!/((n-k)!*k!). El grupo que considera el orden se llama asignación, el grupo que no lo hace, se llama combinación. La creación del número de asignación, también conocida como la fórmula del coeficiente binomial, aplica símbolos especiales; hay dos variantes, mostradas en la siguiente figura.

De esta forma, si en la tarea a resolver no importa el orden de los elementos a seleccionar, podremos utilizar para su solución la combinación como conjunto de eventos elementales. Si el orden es importante, deberemos utilizar las asignaciones.

Ejemplo 3. Vamos a analizar un ejemplo importante que provoca la distribución hipergeométrica. Vamos a imaginar ahora que cada uno de nuestros objetos n ha sido marcado con uno de los rótulos: "bueno" o "malo". Supongamos que b, b⋜n de los objetos son "malos", mientras que los demás n-b, al contrario, son "buenos". Seleccionamos un grupo de k elementos sin tener en cuenta el orden (combinación) en el mismo. ¿Cuál es la probabilidad de que nuestro grupo contenga exactamente x objetos "malos"? La tarea se resuleve calculando el número de combinaciones correspondiente. La respuesta resulta bastante voluminosa, y es mejor registrarla con la ayuda de desiganaciones para el número de combinaciones, como se muestra en la siguiente imagen, donde la probabilidad buscada se marca con p y se expresa con x, n, b y k.

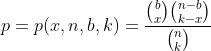
Este ejemplo es adecuado para comprender el sentido de la introducción del concepto "magnitud aleatoria" (del que hablaremos con detalle en el próximno artículo). Puede suceder perfectamente que para resolver una tarea concreta relacionada con el cálculo de probabilidades de eventos, resulte suficiente conocer los números x, n, b y k, siendo entonces innecesario poseer información completa sobre el grupo original de eventos. Entonces tendrá sentido simplificar el modelo original, descartando la información innecesaria. Vamos a actuar de la forma siguiente:

• Los números n, b y k se asumen como parámetros fijos.
• En lugar del espacio muestral Ω, construiremos un nuevo Ωх={0, 1, ..., k} sobre su base, utilizando los posibles valores para el número х.
• A cada evento {х} (que consta de un evento elemental) le opondremos la probabilidad mostrada en la imagen de arriba, usando la fórmula de la distribución hipergeométrica.

El objeto obtenido como resultado se llamará "magnitud aleatoria discreta", y tendrá una distribución hipergeométrica para sus posibles valores de Ωх.

3.2. Esquema de Bernoulli

Se trata de otro modelo bien conocido en el campo de la teoría de probabilidad elemental. Sus ejemplos generalmente implican la modelación de los resultados de los sucesivos lanzamientos de las monedas, no obstante, vamos a construir el esquema de una manera más formal.

Supongamos que tenemos un número entero positivo n y una pareja de números no negativos reales p y q, tales que p+q=1. El conjunto de eventos elementales Ω constará de palabras con una longitud igual a n, en las que solo se permitirán solo dos letras H y T (H de heads, cara, y T de tails, cruz). La probabilidad para un evento que conste de un evento elemental se establecerá con la fórmula pu({w})=p^nh*q^nt, donde w será la palabra, mientras que nh y nt, nh+nt=n, serán el número de letras H y T en ella, respectivamente.

No es complicado ver que, a diferencia de la probabilidad combinada, las probabilidades originales en general no son iguales entre sí (serán todas iguales solo si p=q=0.5).

Vamos a ver como ejemplo el caso n=2. En este caso, Ω={HH, HT, TH, TT}. El número de eventos elementales aquí es igual a 4, mientras que el número de eventos aleatorios es igual a 16. (Pregunta de control: mostrar para el esquema de Bernoulli el aspecto general de las fórmulas de dependencia de eventos elementales y los números de todos los eventos aleatorios de n).

Vamos a analizar el evento "en primer lugar se encuentra H"={HH, HT}. Su probabilidad es igual a pq+p^2=p. Los mismo es correcto para cualquier lugar, lo cual permite hablar del parámetro p, como de la "probablidad de que salga cruz en cada lanzamiento". Ahora, vamos a comprobar si se cumple la independencia del evento А="en el segundo lugar se encuentra H"={HH, TH} del evento В="en primer lugar se encuentra H"={HH, HT}. Utilizaremos la definición de independencia: el cruzamiento de АВ={HH}, P(A)=p, P(B)=p, P(AB)=p^2 y dado que P(A)P(B)=p*p=p^2=P(AB), los eventos resultan independientes.

Estas afirmaciones sobre la probabilidad del resultado de cada lanzamiento y su independencia también resultan ciertas para todos los n>2.

Podríamos haber especificado la probabilidad de una manera totalmente distinta, lo que podría conducir tanto a la ausencia de una probabilidad igual, como a la dependencia de los resultados de los lanzamientos. El asunto es que aquí el esquema de Bernoulli no es el único modelo válido que describe la secuencia de eventos, y no debemos limitarnos solo a él.

Ahora, vamos a calcular la probabilidad de un evento en el esquema de Bernoulli que conste de aquellas palabras en las que la letra H se encuentre exactamente k veces, o, de una manera menos formal: la probabilidad de que nos salga cara k veces al realizar n lanzamientos con la moneda. Podemos encontrar la respuesta a esta pregunta mediante la denominada ecuación de distribución binomial que se muestra en la siguiente figura. Con pb se designa la probabilidad buscada que depende de k, n, p y q.

Vamos a analizar otro ejemplo que muestra la relación de la distribución binomial con las hipergeométricas que hemos visto más arriba. Es importante tanto en sí misma, como en relación con sus aplicaciones a la estadística matemática (prueba exacta de Fisher). La cuestión es bastante compleja y significativa desde el punto de vista matemático. Detallaremos todo el razonamiento punto por punto.

• Usando el espacio muestral del esquema de Bernoulli Ω, construimos un nuevo Ω1, donde entrarán no solo las palabras en las que la letra H se encuentre exactamente b veces.
• Dado que cualquier evento A de Ω1 es un evento de Ω, para él se ha determinado una probabilidad de P(A). Sobre su base, introducimos las posibilidad P1 en Ω1 de acuerdo con la fórmula P1(A)=P(A)/Р(Ω1). En esencia, en este caso, se utiliza la fórmula de probabilidad condicional P1(A)=P(A|О1).
• Vamos a ver ahora la probabilidad P1() del evento "el sufijo de una palabra con una longitud k contiene exactamente x letras H" de Ω1. Resulta que esta probabilidad se ve determinada exactamente por la ecuación de distribución hipergeométrica ofrecida anteriormente. Aquí resulta peculiar el hecho de que la ecuación no muestra dependencia del parámetro p.

4. Fundamentos de la estadística matemática

La diferencia entre la estadística matemática y la teoría de la probabilidad normalmente se describe como una diferencia en los tipos de los problemas a resolver. En la teoría de la probabilidad, generalmente se asume que el modelo probabilístico se conoce por completo y se deben sacar algunas conclusiones basadas en este. En estadística matemática, nuestro conocimiento sobre el modelo no es completo, pero existe información adicional en forma de datos experimentales que ayudan a pulir el modelo. Por consiguiente, todas las cuestiones analizadas en el capítulo anterior constituyen problemas de la teoría de la probabilidad.

Podemos considerar la definición de matemática estadística que acabamos de ver como clásica. Existe otro enfoque más moderno sobre la definición de matemática estadística. En él, esta se define como parte de la teoría de la decisión (decision theory). En este enfoque, se hace hincapié en la construcción de reglas de decisión óptimas en el sentido de minimizar el coste medio de un error. Aquí se converge con mucha intensidad con los métodos de aprendizaje de máquinas. Una diferencia significativa de ellos estriba en el hecho de que, en la estadística matemática, el tipo de modelo matemático utilizado se define con bastante claridad (por ejemplo, con la precisión de un parámetro desconocido). En el aprendizaje de máquinas, la incertidumbre normalmente se extiende también al tipo de modelo.

Vamos a analizar ahora con ejemplos las tareas de la estadística matemática en su sentido convencional.

5. Ejemplos de aplicación de la estadística matemática en el marco de la teoría elemental

Podemos definir dos tipos de tareas: la valoración de un parámetro y la comprobación de hipótesis.

Empecemos por la valoración puntual de un parámetro. Esta presupone la presencia en el modelo probabilístico de cualquier variable numérica (no aleatoria, determinista). Respecto a ella, desconocemos su valor numérico exacto, pero podemos calcular su valor aproximado usando los datos obtenidos como resultado de un experimento aleatorio.

5.1. Estimación puntual del parámetro

El enfoque más general aquí consiste en utilizar el método de máxima verosimilitud. Si hemos realizado algún evento elemental ω como resultado de un experimento aleatorio, la función de verosimilitud será la probabilidad del evento {ω} (que consta únicamente de este evento elemental). Se denomina función en la medida en que depende del valor del parámetro del modelo. La estimación por máxima verosimilitud (abreviada como EMV) es el valor del parámetro con el que esta función alcanza su máximo.

Pueden existir diversas valoraciones de parámetros además de la EMV pero, como se muestra en las estadísticas matemáticas, la EMV es la mejor en cuanto a precisión. Dejaremos la explicación de lo que entendemos por "precisión" para el próximo artículo dedicado a las variables aleatorias. Sea como fuere, debemos considerar que la estimación estadística es casi siempre diferente del valor real del parámetro. Por consiguiente, es muy importante diferenciarlos. Por ejemplo, la probabilidad de un evento en el esquema de Bernoulli y su valoración como frecuencia.

Vamos a pasar al cálculo de la EMV con ejemplos.

Ejemplo 1. Estimación del parámetro b en una distribución hipergeométrica. Tenemos un lote de piezas de trabajo n=1000 uds. Tras comprobar k=20 de ellas, hemos detectado una pieza defectuosa: x=1. Estime la cantidad de piezas de trabajo defectuosas en todo el lote.

A continuación, mostramos el script hyperg_be.py escrito en Python, que resuelve este problema enumerando todas las opciones posibles para b. La respuesta será una estimación de be en la que el valor de probabilidad definido por la ecuación de distribución hipergeométrica será máximo.

from scipy.stats import hypergeom

n = 1000
k = 20
x = 1
lhx = 0.0
be = 0
for b in range(x, n - k + x):
    lh = hypergeom.pmf(x, n, b, k)
    if lh > lhx:
        be = b
        lhx = lh
        
print("be =",be)

Respuesta: be = 50, lo cual resulta totalmente esperado (cada 20-ésima pieza) 

Ejemplo 2 . Estimación del parámetro n en una distribución hipergeométrica. Debemos estimar la cantidad de peces en un estanque. Para ello, se capturan con una red b=50 peces, marcando y luego soltando estos de nuevo en el agua. A continuación, se capturan k=55 peces, de los cuales x=3 resultan marcados.

Después, se muestra el script hyperg_ne.py escrito en Python, que resuelve este problema enumerando las posibles opciones para n. La respuesta es una estimación ne con el mayor valor de probabilidad. Un pequeño detalle es que los posibles valores para n oscilan teóricamente entre 50+(55-3)=102 y el infinito. Esto podría conducir a un ciclo de iteración sin fin. Pero resulta que la función de verosimilitud aumenta hasta un valor n, y luego comienza a disminuir, tendiendo finalmente a cero. Como consecuencia, la respuesta será el primer valor ne en el que el valor de la función de verosimilitud sea mayor que su valor en ne+1.

from scipy.stats import hypergeom

b = 50
k = 55
x = 3
lh0 = 0.0
ne = b + k - x - 1
while True:
    lh = hypergeom.pmf(x, ne+1, b, k)
    if lh < lh0:
        break
    else:
        lh0 = lh
        ne += 1
        
print("ne =",ne)

Respuesta: ne = 916, lo cual resulta totalmente esperado (ne/b es aproximadamente igual a k/x, de donde resulta que ne es aproximadamente igual a b*k/x).

Todos los siguientes ejemplos se relacionan con el esquema de Bernoulli o sus modificaciones. La interpretación comercial convencional de este modelo conlleva su comparación con una versión discretizada del precio de un activo. Por ejemplo, para obtener dicha representación, podemos usar un gráfico renko o un gráfico de punto y figura.

Seguiremos con esta tradición. En lugar de palabras con las letras H y T, analizaremos una secuencia de números de 1 y -1, que, obviamente, se corresponden con los saltos discretos de precio hacia arriba y hacia abajo, respectivamente. En general, el salto del precio se puede definir como su superación de un nuevo nivel en una cuadrícula de precios. Estas cuadrículas de niveles normalmente se definen de forma que la diferencia o la relación entre cada nivel y el nivel inferior colindante permanezca igual: utilizaremos el segundo método. La desventaja de este método es que su aplicación resulta imposible para activos con precios negativos. Su ventaja más obvia es que no resulta necesario seleccionar individualmente el tamaño del salto para cada activo. Asimismo, muestra cierta arbitrariedad en la selección del nivel cero: su papel lo jugará el primer precio de los que se encuentran sujetos a discretización.

Ahora, mostraremos un script simple que discretiza el precio con un salto porcentual en un intervalo dado. El archivo Discr.mqh contiene solo la función setmv(), en la que realmente se produce la discretización de precios. Para simplificar, solo tomaremos como precios iniciales los precios abiertos de las barras de minutos.

// Constructing the array of discrete mv[] movements
// at a specified time interval and with a specified percentage step
void setmv(int& mv[], datetime t1, datetime t2, double dpr)
{
  int ND = 1000;
  ArrayResize(mv, 0, ND);
// Get price history
  double price[];
  int nprice = CopyOpen(Symbol(), PERIOD_M1, t1, t2, price);
  if(nprice < 2)
  {
    Print("not enough price history");
    return;
  }
// Construct mv[]
  int lvl = 0, dlvl, nmv = 0, dmv;
  double lp0 = log(price[0]), lstep = log(1 + 0.01 * dpr);
  for(int i = 1; i < nprice; ++i)
  {
    dlvl = (int)((log(price[i]) - lp0) / lstep - lvl);
    if(dlvl == 0) continue;
    lvl += dlvl;
    dmv = 1;
    if(dlvl < 0)
    {
      dmv = -1;
      dlvl = -dlvl;
    }
    ArrayResize(mv, nmv + dlvl, ND);
    for(int j = 0; j < dlvl; ++j) mv[nmv + j] = dmv;
    nmv += dlvl;
  }
}

El script discret_prices.mq5 muestra el resultado como una secuencia de 1, -1, y también como el gráfico de un análogo discreto del precio original.

#include <Discr.mqh>
#include <Graphics\Graphic.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // start of the considered time interval
input datetime tstop = D'2020.06.20 00:00';   // end of the considered time interval
input double   dprcnt = 0.5;                  // price discretization step in %
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[], nmv;
  setmv(mv, tstart, tstop, dprcnt);
  nmv = ArraySize(mv);
  if(nmv < 1)
  {
    Print("not enough moves");
    return;
  }
// Display mv[] as a sequence of 1 and -1
  string res = (string)mv[0];
  for(int i = 1; i < nmv; ++i) res += ", " + (string)mv[i];
  Print(res);
// Display the mv[] cumulative sum chart
  ChartSetInteger(0, CHART_SHOW, false);
  CGraphic graphic;
  graphic.Create(0, "G", 0, 0, 0, 750, 350);
  double x[], y[];
  ArrayResize(x, nmv + 1);
  ArrayResize(y, nmv + 1);
  x[0] = y[0] = 0.0;
  for(int i = 1; i <= nmv; ++i)
  {
    x[i] = i;
    y[i] = y[i-1] + mv[i-1];
  }
  ArrayPrint(x);
  ArrayPrint(y);
  graphic.CurveAdd(x, y, CURVE_LINES, "discret_prices");
  graphic.CurvePlotAll();
  graphic.Update();
  Sleep(30000);
  ChartSetInteger(0, CHART_SHOW, true);
  graphic.Destroy();
}

En todos los ejemplos posteriores se utilizarán los resultados de la discretización del precio de EURUSD con un salto de 0.5% en el periodo que va del 20 de mayo al 20 de junio de 2020. Como resultado, obtendremos la siguiente secuencia de saltos discretos: 1, -1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1. Para mayor claridad, también mostraremos abajo los gráficos del precio original y su análogo discreto.

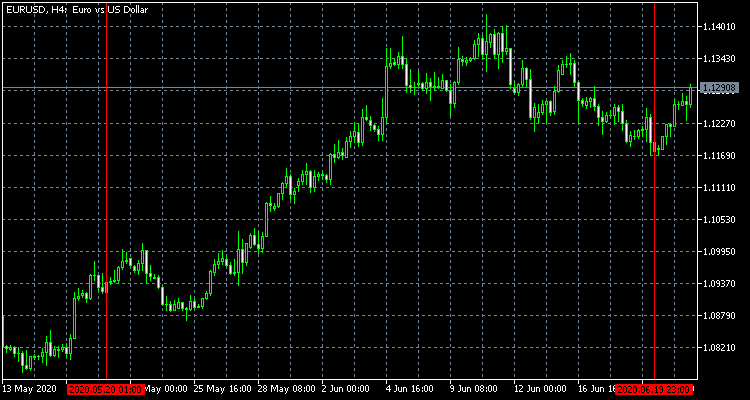
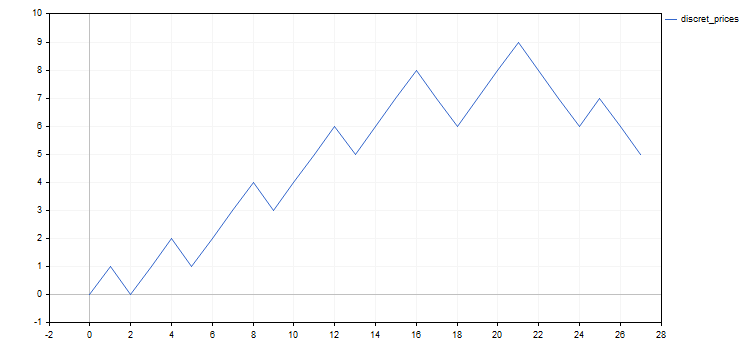
Además de analizar el comportamiento del precio discretizado, pueden existir otras maneras de aplicar el esquema de Bernoulli o sus modificaciones. Vamos a señalar dos de ellas relacionadas con el trading.

1. Los resultados del comercio en el que se realizan transacciones con stop loss, take profit y niveles de volumen fijos. Todos los beneficios en una serie de transacciones son más o menos similares, y lo mismo ocurre con las pérdidas. Por consiguiente, la probabilidad de lograr beneficios es un parámetro suficiente para describir el resultado comercial. Por ejemplo, podemos plantear si la probabilidad de obtener beneficios es lo suficientemente alta en una secuencia de transacciones existente. 
2. Selección de activos para inversión. Supongamos que tenemos un amplio abanico de métodos de inversión al comienzo de un periodo. Con cierta probabilidad, cualquiera de ellos puede provocar la pérdida total de los fondos invertidos. Si tenemos alguna manera de seleccionar los activos, entonces podremos plantearnos la diferencia en la probabilidad de quiebra entre los activos seleccionados, en comparación con la de los rechazados.
   

Volvamos al análisis de ejemplos.

Ejemplo 3. Estimación del parámetro p en el esquema de Bernoulli. Aquí vemos que se trata de una rara excepción en la que podemos resolver la tarea sobre el papel. La función de verosimilitud tiene la forma p^nup*(1-p)^ndn. Tomamos la derivada de p e igualando esta a cero, obtenemos el valor completamente esperado para la estimación de р en forma de frecuencia: pe=nup/(nup+ndn)=nup/nmv. Como suele ser habitual, a la hora de realizar la búsqueda, resulta más sencillo, en lugar de utilizar el máximo de la función de verosimilitud, usar su logaritmo. La respuesta será la misma, dado que el logaritmo es una función estrictamente creciente, y el máximo se alcanza con el mismo valor de parámetro. A continuación, mostramos el script p_model.mq5, que calcula esta estimación.

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // start of the considered time interval
input datetime tstop = D'2020.06.20 00:00';   // end of the considered time interval
input double   dprcnt = 0.5;                  // price discretization step in %
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 1)
  {
    Print("not enough moves");
    return;
  }
  double pe = calcpe(mv);
  Print("pe=", pe);
}
//+------------------------------------------------------------------+
// Calculate the probability estimation
double calcpe(int& mv[])
{
  int nmv = ArraySize(mv);
  if(nmv < 1) return 0.0;
  int nup = 0;
  for(int i = 0; i < nmv; ++i) if(mv[i] > 0) ++nup;
  return ((double)nup) / nmv;
}

Respuesta: pe = 0.59 (el número ha sido redondeado)

Ejemplo 4. Estimación del parámetro en el esquema de Bernoulli modificado. Como hemos escrito anteriormente, el esquema de Bernoulli se puede modificar perfectamente, si así lo necesitamos para nuestros propósitos de modelado. Vamos a considerar una posible opción de modificación.

Probablemente, la opción más fácil consista en dividir la secuencia de movimientos en dos más pequeños que vayan uno tras otro y que se corresponden con el esquema de Bernoulli con sus parámetros: n1, p1, n2=n-n1 y p2, donde n es la longitud de la secuencia cumulativa.
De esta forma, necesitamos estimar tres parámetros: n1, p1 y p2. Maximizando el logaritmo de la función de verosimilitud respecto a p1 y p2, podemos expresarlas de forma analítica mediante n1. La estimación de n1 deberemos encontrarla ya por búsqueda simple, sustituyendo las expresiones para p1 y p2 en la fórmula para el logaritmo de verosimilitud.
A continuación, mostramos el script p1p2_model.mq5, que calcula la estimación de los parámetros.

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // start of the considered time interval
input datetime tstop = D'2020.06.20 00:00';   // end of the considered time interval
input double   dprcnt = 0.5;                  // price discretization step in %
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 2)
  {
    Print("not enough moves");
    return;
  }
  double p1e, p2e;
  int n1e;
  calc_n1e_p1e_p2e(mv, n1e, p1e, p2e);
  Print("n1e=", n1e, " p1e=", p1e, " p2e=", p2e);
}
//+------------------------------------------------------------------+
// Calculate the probability estimation
void calc_n1e_p1e_p2e(int& mv[], int& n1e, double& p1e, double& p2e)
{
  n1e = 0;
  p1e = p2e = 0.0;
  int nmv = ArraySize(mv);
  if(nmv < 2) return;
  n1e = 1;
  double llhx = llhx_n1(mv, 1, p1e, p2e), llh, p1, p2;
  for(int n1 = 2; n1 < nmv; ++n1)
  {
    llh = llhx_n1(mv, n1, p1, p2);
    if(llh > llhx)
    {
      llhx = llh;
      n1e = n1;
      p1e = p1;
      p2e = p2;
    }
  }
}
//+------------------------------------------------------------------+
// log-likelihood function maximum depending on n1
double llhx_n1(int& mv[], int n1, double& p1, double& p2)
{
  p1 = p2 = 0.0;
  int nmv = ArraySize(mv);
  if(nmv < 2 || n1 < 1 || n1 >= nmv) return 0.0;
  int nu1 = 0, nu2 = 0;
  for(int i = 0; i < n1; ++i) if(mv[i] > 0) ++nu1;
  for(int i = n1; i < nmv; ++i) if(mv[i] > 0) ++nu2;
  double l = 0.0;
  if(nu1 > 0)
  {
    p1 = ((double)nu1) / n1;
    l += nu1 * log(p1);
  }
  if(nu1 < n1) l += (n1 - nu1) * log(((double)(n1 - nu1)) / n1);
  if(nu2 > 0)
  {
    p2 = ((double)nu2) / (nmv - n1);
    l += nu2 * log(p2);
  }
  if(nu2 < nmv - n1) l += (nmv - n1 - nu2) * log(((double)(nmv - n1 - nu2)) / (nmv - n1));
  return l;
}

Respuesta: n1e = 21; p1e = 0.71; p2e = 0.17 (los números han sido redondeados). Parece bastante obvio que nuestro modelo "ha visto" el cambio de dirección (o corrección) del movimiento de precio al final de su segmento. Esto nos indica que, en este caso, el paso a un modelo más complejo no se ha realizado en vano.

Ejemplo 5. En el ejemplo anterior, la probabilidad de movimiento hacia arriba dependía de su número (del tiempo). Vamos a analizar otra modificación del esquema de Bernoulli en el que esta probabilidad depende del propio movimiento anterior. Para ello, construiremos un modelo que constituya un ejemplo de la cadena de Márkov más simple con dos estados.

Supongamos que los movimientos están numerados de 0 a n. Para el movimiento cero, la probabilidad de un movimiento hacia arriba simplemente se establecerá en 0.5, ya que no existe un movimiento previo para ello. Para otras posiciones, la probabilidad de un movimiento ascendente será igual a p1, si fuera precedido por un movimiento ascendente, y p2, si fuera precedido por un movimiento descendente. En estos dos casos, las probabilidades de movimientos descendentes serán iguales a q1=1-p1 y q2=1-p2, respectivamente. Por ejemplo, la probabilidad de que haya un evento que tenga exactamente un evento elemental "abajo-arriba-arriba-abajo" es igual a 0.5*p2*p1*q1.

Hemos obtenido un modelo con dos parámetros que se pueden estimar utilizando el EMV. Una vez más, podemos realizar todos los cálculos nuevamente sobre papel, en especial si maximizamos la función logarítmica de verosimilitud. Al igual que en el esquema de Bernoulli, la respuesta se reduce a las frecuencias. Marcamos con nud el número de veces que ocurre el movimiento descendente después del ascendente (u − up, d − down). De forma similar, introducimos nuu, ndd y ndu. Las estimaciones para p1 y p2 las designamos mediante p1e y p2e. Entonces, estas estimaciones se encontrarán según las fórmulas p1e=nuu/(nuu+nud) y p2e=ndu/(ndu+ndd).

A continuación, mostramos el script markov_model.mq5, que calcula dichas estimaciones.

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // start of the considered time interval
input datetime tstop = D'2020.06.20 00:00';   // end of the considered time interval
input double   dprcnt = 0.5;                  // price discretization step in %
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 2)
  {
    Print("not enough moves");
    return;
  }
  double p1e, p2e;
  calcpes(mv, p1e, p2e);
  Print("p1e=", p1e, " p2e=", p2e);
}
//+------------------------------------------------------------------+
// Calculate probability estimations
void calcpes(int& mv[], double& p1e, double& p2e)
{
  p1e = p2e = 0;
  int nmv = ArraySize(mv);
  if(nmv < 2) return;
  int nuu = 0, nud = 0, ndu = 0, ndd = 0, nu, nd;
  for(int i = 0; i < nmv - 1; ++i)
    if(mv[i] > 0)
    {
      if(mv[i + 1] > 0) ++nuu;
      else ++nud;
    }
    else
    {
      if(mv[i + 1] > 0) ++ndu;
      else ++ndd;
    }
  nu = nuu + nud;
  nd = ndu + ndd;
  if(nu > 0) p1e = ((double)nuu) / nu;
  if(nd > 0) p2e = ((double)ndu) / nd;
}

Respuesta:  p1e = 0.56; p2e = 0.60 (los números han sido redondeados). El que ambas probabilidades sean prácticamente iguales entre sí, indica la ausencia de una dependencia entre los movimientos colindantes, mientras que el hecho de que ambas sean superiores a 0.5  indica la presencia de una tendencia ascendente. Asimismo, el hecho de que las estimaciones de las probabilidades se encuentren próximas a la probabilidad para un modelo más sencillo (el esquema simple de Bernoulli del tercer ejemplo), indica que el paso a este modelo complejo ha resultado innecesario en este caso concreto.

5.2. Comprobación de hipótesis estadísticas

Podemos establecer distribuciones de probabilidad distintas en el mismo espacio muestral. Una hipótesis es una declaración que especifica el tipo de distribución. Deberían existir varias hipótesis, al menos dos, dado que la solución se basa en la preferencia de una hipótesis sobre las otras. Entenderemos por simple una hipótesis si determina de forma única el tipo de distribución.

Vamos a mostrar varios ejemplos para el esquema de Bernoulli: la hipótesis de la igualdad del parámetro p con un cierto número  es una hipótesis simple (solo hay un valor de parámetro posible que defina de manera inequívoca la distribución), mientras que la hipótesis en la que el parámetro supera el número indicado es una hipótesis compleja (el número de posibles valores de parámetros es infinito).

A continuación, hablaremos sobre la selección de una de las dos hipótesis. Una de ellas se llama nula, y la otra, alternativa. La hipótesis se selecciona mediante un criterio estadístico. Básicamente, se trata solo de una función con los valores 0 y 1 dentro del espacio muestral, donde 0 indica que se acepta la hipótesis nula, mientras que 1 indica que se acepta la alternativa.

De esta forma, tenemos la posibilidad de aceptar la hipótesis nula o rechazarla. Por consiguiente, la hipótesis alternativa, al contrario, se rechaza o se acepta. Cada una de estas decisiones puede ser correcta o incorrecta. Así, tenemos cuatro posibles resultados derivados de la aceptación de la hipótesis, de los cuales dos son correctos y dos falsos.

1. Error de tipo 1: rechazo erróneo de una hipótesis nula.
2. Error de tipo 2: aceptación errónea de una hipótesis nula.

Las probabilidades de errores de tipo 1 y 2 se indican mediante a1 y a2. Obviamente, resultaría adecuado reducir estas probabilidades tanto como sea posible. Pero, desafortunadamente, esto es imposible. Además, si reducimos la probabilidad de obtener errores de cierto tipo, es más que posible que nos enfrentemos a un aumento de la probabilidad de obtener errores de otro tipo. Por ello, generalmente recurrimos a un cierto compromiso entre estos errores.

Con el número 1-a1, denominaremos el nivel de significación de la prueba, mientras que 1-a2 servirá para denominar la potencia. La potencia de la prueba puede ser difícil de calcular, especialmente para una hipótesis compleja. Por consiguiente, normalmente solo se usa el nivel de significación.

Por lo general, los criterios de prueba se basan en una función numérica (también definida en función de un espacio muestral) llamada estadística de prueba. Sus múltiples valores se dividen en dos áreas: una de ellas se corresponde con la aceptación de la hipótesis nula, mientras que la otra se corresponde con su rechazo. El área en la que se rechaza la hipótesis nula se denomina crítica.

A continuación, haremos una observación importante sobre la hipótesis "menos primero". Este término indica que debemos asegurarnos previamente de que se cumpla de forma obligatoria una de nuestras dos hipótesis. A grandes rasgos, si separamos a los chihuahuas de los perros de otras razas usando su peso como criterio, entonces deberemos asegurarnos de tener siempre un perro en la balanza (no un elefante, un ratón o un gato). En caso contrario, nuestra prueba no tendrá sentido. Este principio se ve quebrantado con mayor frecuencia cuando se aplican de manera inexacta los criterios estadísticos usados en econometría.

A continuación, mostramos varios ejemplos de hipótesis de prueba para el esquema de Bernoulli.

Ejemplo 1. Comprobación de la hipótesis nula p=p0 en el esquema de Bernoulli. Esta hipótesis es simple. La hipótesis alternativa podría ser una de las dos opciones siguientes (compleja, en ambos casos). El criterio estadístico en ambos casos será kup, el número de movimientos ascendentes en una secuencia, pero el área crítica se determinará de forma distinta.

1. p>p0, el área crítica está a la derecha kup⋝kr
2. p<p0, el área crítica está a la izquierda kup⋜kl

Los valores concretos para kr y kl se encuentran usando como base la condición de que la probabilidad de que las estadísticas entren en el área crítica no exceda la probabilidad de error de tipo 1 seleccionada por nosotros. Recordemos que todas estas probabilidades se calculan con la condición de que se ejecute la hipótesis nula, es decir, al darse una distribución de Bernoulli con el parámetro p=p0.

Vamos a comprobar esta hipótesis para p0=0.5 en la misma secuencia discretizada de precios. El valor para p0 es estupendo, porque se corresponde con la hipótesis del "paseo aleatorio" o, como se dice en ocasiones, de la "moneda justa".

Aquí tenemos el script p0_hypothesis.mq5, que comprueba esta hipótesis.

#include <Math\Stat\Binomial.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input int    nm = 27;          // total number of movements in the series
input int    kup = 16;         // number of upward movements
input double p0 = 0.5;         // checked probability value
input double alpha1 = 0.05;    // type 1 error probability
//+------------------------------------------------------------------+
void OnStart()
{
  int kl, kr, er;
  kr=(int)MathQuantileBinomial(1.0-alpha1,nm,p0,er);
  kl=(int)MathQuantileBinomial(alpha1,nm,p0,er);
  Print("kl=", kl, " kup=", kup, " kr=", kr);
  Print("kup<=kl = ", kup<=kl);
  Print("kup>=kr = ", kup>=kr);
}

Respuesta:

Ejemplo 2. Supongamos que tenemos dos secuencias con unas longitudes de n1 y n2 tomadas de dos esquemas de Bernoulli con parámetros p1 y p2. La hipótesis nula aquí consiste en afirmar la cumplimiento de la igualdad de p1=p2, mientras que las posibles alternativas contituyen diferentes tipos de su desigualdad, que aquí son también dos. El criterio estadístico en todos estos casos será k2, el número de movimientos ascendentes en la segunda secuencia de las dos, pero el área crítica se determinará de forma distinta.

• p2>p1, el área crítica está a la derecha k2⋝kr
• p2<p1, el área crítica está a la izquierda k2⋜kl

La diferencia más significativa respecto al ejemplo anterior reside en que aquí no estamos hablando de declaraciones relacionadas con valores precisos de p1 y p2, sino solo sobre su correspondencia. Las regiones críticas se determinan de la misma forma que en el ejemplo anterior, pero la distribución estadística con la hipótesis nula es hipergeométrica, no binomial. En estadística matemática, este criterio se conoce como prueba exacta de Fisher.

A continuación, mostramos el script p1p2_hypothesis.py en Python, capaz de resolver esta tarea para nuestro precio discretizado dividido en dos. Hemos usado la división obtenida en el cuarto ejemplo del párrafo anterior.

from scipy.stats import hypergeom

n1 = 21; n2 = 6
k1 = 15; k2 = 1
alpha1 = 0.05

kl = int(hypergeom.ppf(alpha1, n1 + n2, k1 + k2, n2))
kr = int(hypergeom.ppf(1.0 - alpha1, n1 + n2, k1 + k2, n2))

print("kl =", kl, " k2 =", k2, " kr =", kr)
print("k2<=kl =", k2<=kl)
print("k2>=kr =", k2>=kr)

 Respuesta:

• kl = 2;  k2 = 2;  kr = 6
• k2<=kl = True
• k2>=kr = False
  

6. Conclusión

En el artículo no hemos abarcado áreas tan importantes de la estadística matemática como la estadística descriptiva, la estimación de parámetros por intervalo, las estimaciones asintóticas y el enfoque bayesiano en estadística. La razón es que, para realizar análisis significativo de las mismas, aún necesitamos aclarar el concepto de variable aleatoria. Hemos decidido dedicarnos a ello en el próximo artículo, para así conseguir que el artículo actual sea lo suficientemente compacto.

7. Archivos adjuntos

#	nombre	tipo	descripción
1	hyperg_be.py	Script en Python	Cálculo de la estimación del parámetro b de una distribución hipergeométrica. Ejemplo 5.1.1
2	hyperg_ne.py	Script en Python	Cálculo de la estimación del parámetro n de una distribución hipergeométrica. Ejemplo 5.1.2
3	Discr.mqh	Archivo de encabezado MQL5	Archivo con la función setmv() utilizada en todos los ejemplos en MQL5 más abajo para discretizar el precio
4	discret_prices.mq5	Script en MQL5	Script para realizar la discretización del precio y mostrar el resultado como secuencia de 1 y -1 y como gráfico
5	p_model.mq5	Script en MQL5	Cálculo de la valoración del parámetro p en el esquema de Bernoulli. Ejemplo 5.1.3
6	p1p2_model.mq5	Script en MQL5	Cálculo de las estimaciones de los parámetros n1, p1 y p2 en el modelo de dos esquemas de Bernoulli. Ejemplo 5.1.4
7	markov_model.mq5	Script en MQL5	Cálculo de las estimaciones de los parámetros p1 y p2 de la cadena de Márkov. Ejemplo 5.1.5
8	p0_hypothesis.mq5	Script en MQL5	Comprobación de la hipótesis sobre la igualdad del parámetro del esquema de Bernoulli respecto al número indicado. Ejemplo 5.2.1
9	p1p2_hypothesis.py	Script en Python	Prueba exacta de Fisher. Ejemplo 5.2.2