Estimación del índice de fractalidad, exponente de Hurst y posibilidad de predecir series temporales financieras
Roman Korotchenko | 25 julio, 2019
Introducción
Actualmente, el mercado financiero es un ejemplo del sistema «natural» de equilibrio complejo. Por un lado, es bastante caótico, porque sus variaciones se determinan debido a la influencia de muchos participantes, por otro lado, en él operan los procesos estables que se determinan por las acciones de los participantes. Puesto que entre las tareas de la econofísica se encuentra la descripción de los procesos de interacciones sociales que forman la dinámica de precios observada en la bolsa, la definición y presentación de las propiedades especiales de series temporales financieras es muy deseable, porque va a diferenciar este tipo de datos de los demás procesos naturales. Hoy en día, ya se sabe que las series de precios representan los fractales de diferentes dimensiones (de minutos a una década).
Su comportamiento es mucho más complicado que el comportamiento de muchos procesos naturales y de modelo [3]. Para comprender en detalle este comportamiento, es deseable usar la herramienta del análisis numérica de las series con el fin de investigar su dinámica.Los algoritmos típicos de una estimación confiable de la dimensión fractal requieren unos conjuntos de datos voluminosos (alrededor de 10 000-100 000 informes), que caracterizan la serie durante un largo intervalo de tiempo, en el transcurso del cual el carácter del comportamiento puede variar, a veces, muchas veces. Con el fin de resolver los problemas reales del trading, son necesarios los métodos para determinar las características fractales locales de la serie. En este artículo, se discute y se muestra el modo de determinar la dimensión fractal de las series para las secuencias de precio descritas en los trabajos [1, 2], usando un método numérico.
Concepto de dimensión fractal y propiedades estáticas de las series temporales
La dimensión fractal estima como el conjunto de datos ocupa el espacio. Existen muchos métodos para estimar la dimensión fractal. La manera más común consiste en evaluar el volumen y el área en el espacio donde se encuentra este conjunto. Como ejemplo, usamos una serie temporal para un instrumento financiero compuesto de los precios de cierre {Close(t)}. Si los niveles de la serie {Close(t)} son independientes, su gráfico no tiene tendencias claramente expresadas, su comportamiento será semejante al «ruido blanco». En este caso, el valor de la dimensión fractal D se aproxima al tamaño de la dimensión topológica del plano, o sea, D->2. Si los valores de la serie {Close(t)} no son independientes, el valor D será sustancialmente menor que 2, lo que indica en la presencia de una «memoria» en la serie temporal, es decir, en algunos intervalos de tiempo, se observarán tanto las tendencias alcistas, como bajistas, que se alternan con los períodos de ambigüedad (Fig. 1).
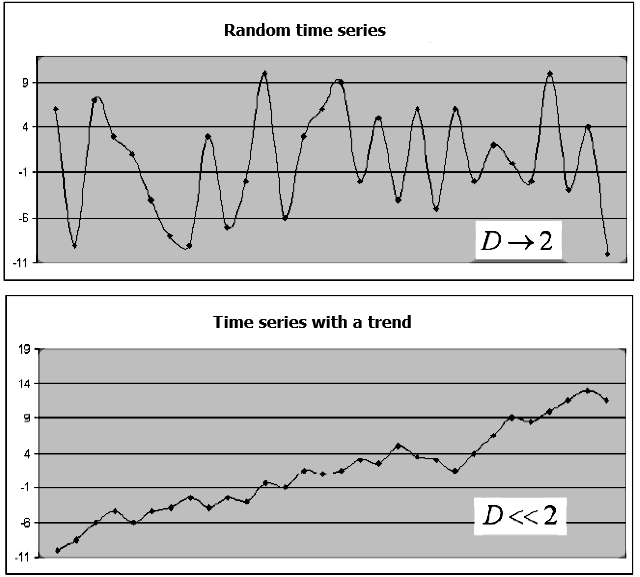
Fig. 1. Ejemplo de una serie aleatoria y una serie con tendencia, y la dimensión fractal correspondiente
Formas de estimar una dimensión fractal, sus particularidades
Hay varias maneras de calcular la dimensión fractal para una serie temporal. Discutamos el método de evaluación usando el exponente de Hurst.
El exponente de Hurst H se determina desde la suposición
![]() (1a)
(1a)
donde los paréntesis angulares indican en la promediación por el tiempo. La vinculación entre el exponente de Hurst y la dimensión fractal se obtene a través del método de la amplitud normalizada o el análisis R/S a base de de las expresiones
DH = 2-HH = log(R/ S) / log(N / 2) (1b)
donde R es max {Close(t)} - min {Close(t)}, i = 1..N amplitud de desviaciones de la serie Close(t), S es la desviación media cuadrática de los valores Close(t). Este método se considera más detalladamente en el artículo de Dmitry Piskarev « Cálculo del coeficiente de Hurst».
Si el exponente de Hurst para la serie temporal se encuentra en el rango 0.5-1, esta serie es persistente o resistente a la tendencia. Eso significa que la serie {Close(t)} no es aleatoria, contiene una tendencia, y es posible prever su comportamiento con una precisión suficiente. Cuanto más próximo sea el valor H a uno, más correlacionados serán los valores de la serie {Close(t)}.
La desventaja de este método consiste en que se requiere una cantidad de datos bastante grande (miles de valores de la serie de datos) para obtener una estimación confiable del exponente de Hurst, de lo contrario, las estimaciones obtenidas pueden ser incorrectas. Además de eso, los valores de la serie tienen que tener una ley de distribución normal, y eso no siempre es así. Puesto que, para un cálculo fiable (tanto de DH, como del exponente H), es necesaria una enorme escala representativa con una cantidad de datos grande, no es nada de extraño que, durante el proceso de negociación de una duración respectiva, la serie pueda cambiar su comportamiento varias veces. Para la vinculación entre la dinámica local del proceso estudiado y la dimensión fractal de la serie que se observa, hay que definir la dimensión D de manera local.
Estimación de la dimensión fractal a base del área mínima de cobertura
Durante la previsión de las series econométricas, el método más eficaz es el que se basa en el cálculo de la dimensión de la cobertura mínima
![]() [1, 2]. En el año
1919 Hausdorff propuso la siguiente fórmula para determinar la fractalidad:
[1, 2]. En el año
1919 Hausdorff propuso la siguiente fórmula para determinar la fractalidad:
![]()
donde
![]() es el número mínimo de las bolas de radio
es el número mínimo de las bolas de radio
![]() ,
que cubren este conjunto. Obsérvese que si el conjunto inicial se encuentra en el espacio euclidiano, entonces, en vez de cubrir el
conjunto con bolas, se puede usar cualquier otra figura simple (por ejemplo, células), para su aproximación con el factor
geométrico
,
que cubren este conjunto. Obsérvese que si el conjunto inicial se encuentra en el espacio euclidiano, entonces, en vez de cubrir el
conjunto con bolas, se puede usar cualquier otra figura simple (por ejemplo, células), para su aproximación con el factor
geométrico
![]() .
.
Supongamos que la función f(t) está definida en el intervalo [a, b]. Dividimos el intervalo wm =
[a=t0<t1<t2...tm=b], definiendo la escala de la división como
![]() Si para cubrir semejantes conjuntos, usamos, por ejemplo, las células de tamaño
Si para cubrir semejantes conjuntos, usamos, por ejemplo, las células de tamaño
![]() ,
entonces si el factor
,
entonces si el factor
![]() disminuye,
el número de las células
N aumentará de acuerdo con la ley potencial:
disminuye,
el número de las células
N aumentará de acuerdo con la ley potencial:
![]()
donde D es la dimensión fractal.
Al determinar la dimensión D usando el método de las células, la superficie donde se ubica el gráfico de la serie temporal se
divide en las células de tamaño
![]() ,
luego se cuenta el número de las células
N(
,
luego se cuenta el número de las células
N(
![]() ),
a las que pertenece por lo menos un punto de este gráfico. Después,
),
a las que pertenece por lo menos un punto de este gráfico. Después,
![]() se
altera y se construye el gráfico de la función
N(
se
altera y se construye el gráfico de la función
N(
![]() )
en la dimensión logarítmica doble. Luego, el conjunto de puntos obtenido se aproxima usando la línea del método de mínimos cuadrados (MMQ). D
se determina a base de la inclinación de esta línea.
)
en la dimensión logarítmica doble. Luego, el conjunto de puntos obtenido se aproxima usando la línea del método de mínimos cuadrados (MMQ). D
se determina a base de la inclinación de esta línea.
El área mínima de cobertura del gráfico de la función en esta dimensión, en el intervalo [a, b] será
igual a la suma de las áreas de rectángulos con base
![]() y
la altura igual a la variación
y
la altura igual a la variación
![]() —
la diferencia entre el máximo y el mínimo de la función
f(t) en cada intervalo[ti-1, ti]. Se puede usar la siguiente fórmula para encontrar el
área de la cobertura mínima
—
la diferencia entre el máximo y el mínimo de la función
f(t) en cada intervalo[ti-1, ti]. Se puede usar la siguiente fórmula para encontrar el
área de la cobertura mínima
![]() :
:
![]() (2)
(2)
donde
![]() es
la suma de las variaciones de amplitud de la la función
f(t) en el intervalo [a, b]. La estimación
es
la suma de las variaciones de amplitud de la la función
f(t) en el intervalo [a, b]. La estimación
![]() depende
de la magnitud seleccionada. Cuanto menos sea
depende
de la magnitud seleccionada. Cuanto menos sea
![]() ,
con mayor precisión será calculada
,
con mayor precisión será calculada
![]() .
En este caso, el valor
.
En este caso, el valor
![]() (cuando
se cambia
(cuando
se cambia
![]() )
cambia según la ley potencial:
)
cambia según la ley potencial:
![]() (3)
(3)
donde
![]() .
La magnitud
.
La magnitud
![]() se
llama «dimensión de cobertura mínima», y el índice
se
llama «dimensión de cobertura mínima», y el índice
![]() es
referido como «índice de fractalidad».
es
referido como «índice de fractalidad».
En la Fig. 2 se muestra la dependencia del área de cobertura mínima con diferentes valores
![]() para
una serie temporal compuesta de 32 observaciones.
para
una serie temporal compuesta de 32 observaciones.
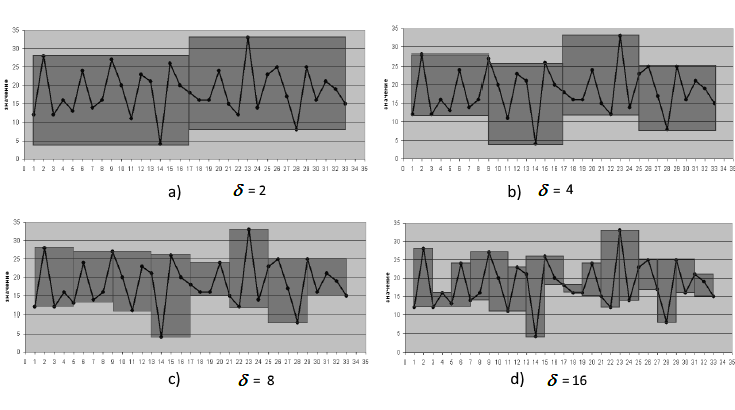
Fig. 2. Cálculo del área de cobertura con valores diferentes
![]()
En la referencia [2] se muestra que la dimensión fractal calculada usando la cobertura celular y la cobertura de rectángulos, a base de la variación de la función, coincide. Una propiedad importante del algoritmo que usa las variaciones de la función es su convergencia mucho más rápida, lo que permite determinar el valor de la dimensión fractal de la serie temporal de forma local, usando un pequeño conjunto de valores.
Aplicando el logaritmo para 3, obtenemos lo siguiente:
![]() (4)
(4)
Para determinar
![]() en
las coordenadas logarítmicas dobles a través del método de mínimos cuadrados (MMQ), se construye el gráfico de las dependencias
(3), luego, se determina la tangente del ángulo de inclinación de la recta. A base de la expresión (4), se calcula
en
las coordenadas logarítmicas dobles a través del método de mínimos cuadrados (MMQ), se construye el gráfico de las dependencias
(3), luego, se determina la tangente del ángulo de inclinación de la recta. A base de la expresión (4), se calcula
![]() (es
decir, el índice de la fractalidad que representa una característica local de la serie temporal). En [1] se muestra que la precisión de la
determinación de
(es
decir, el índice de la fractalidad que representa una característica local de la serie temporal). En [1] se muestra que la precisión de la
determinación de
![]() es mucho mayor que
la precisión de la determinación de otras características fractales, como la dimensión celular
es mucho mayor que
la precisión de la determinación de otras características fractales, como la dimensión celular
![]() o la dimensión
calculada a base del exponente de Hurst. Además, el método no tiene limitaciones respecto a la ley de la distribución de las series
o la dimensión
calculada a base del exponente de Hurst. Además, el método no tiene limitaciones respecto a la ley de la distribución de las series
![]() . En la
referencia [1] también se muestra que la serie temporal
. En la
referencia [1] también se muestra que la serie temporal
![]() debe incluir
como mínimo 32 observaciones para obtener una estimación fiable. En realidad las series temporales financieras tienen un historial mucho
más largo. Este enfoque ofrece la posibilidad de usar el índice de la fractalidad como una dependencia del tiempo
debe incluir
como mínimo 32 observaciones para obtener una estimación fiable. En realidad las series temporales financieras tienen un historial mucho
más largo. Este enfoque ofrece la posibilidad de usar el índice de la fractalidad como una dependencia del tiempo
![]() ,
donde cada valor se determina a base de 32 valores anteriores de la serie temporal
,
donde cada valor se determina a base de 32 valores anteriores de la serie temporal
![]() .
.
La Fig. 3 muestra un ejemplo del cálculo del índice de la fractalidad
![]() basándose
en el ángulo de la recta aproximada. Dea cuerdo de la imagen, el coeficiente de la determinación de la ecuación de la regresión
R
2 que aproxima la dependencia, es igual a 0.96, indicando que el índice de la fractalidad (que es igual a 0.4544) ha sido
calculado con bastante precisión para un fragmento de una serie de 32 puntos.
basándose
en el ángulo de la recta aproximada. Dea cuerdo de la imagen, el coeficiente de la determinación de la ecuación de la regresión
R
2 que aproxima la dependencia, es igual a 0.96, indicando que el índice de la fractalidad (que es igual a 0.4544) ha sido
calculado con bastante precisión para un fragmento de una serie de 32 puntos.
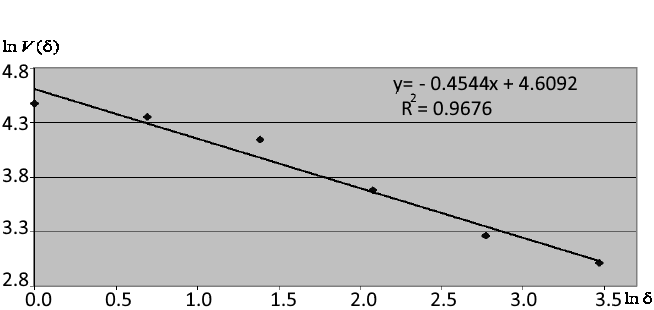
Fig. 3. Aproximación de la dependencia
![]() en
coordenadas logarítmicas dobles y determinación del índice de la fractalidad
en
coordenadas logarítmicas dobles y determinación del índice de la fractalidad
La estimación de la dimensión fractal puede realizarse a través del método de la dimensión celular, o bien, a través del exponente de Hurst. Como ejemplo, mostramos las cotizaciones de las acciones de Lukoil (MICEX) antes de la crisis al principio del siglo. Esta época puede considerarse como una tendencia estable con un aumento gradual (serie persistente). La figura 4 muestra los resultados de la estimación de la dimensión fractal en 1999.
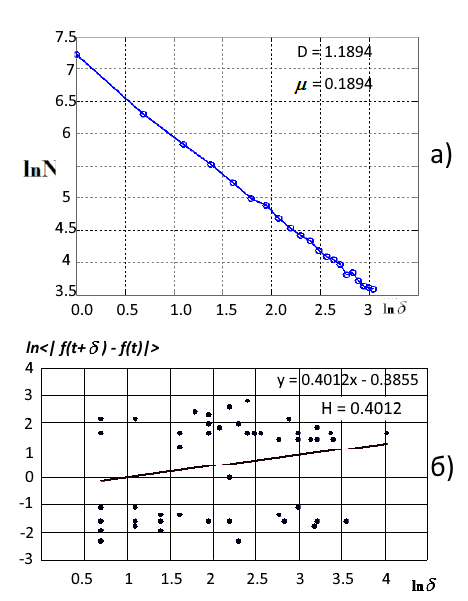
Fig. 4. a) aproximación de MMQde la medida fractal usando la cobertura celular (D=1.1894), b) Diagrama log-log de la estimación del parámetro de Hurst (D=1.6)
La dimensión fractal de la serie D = 1.18 indica en su carácter persistente resistente a la tendencia. Un valor próximo a uno indica en el fin pronto de la tendencia existente, lo que sucedió en los años 2000-2001. Valor del exponente de Hurst H=0.40. Por favor, preste atención en el coeficiente de determinación relativamente bajo R 2= 0.56 con el intervalo de confianza de 0.95. De acuerdo con las fórmulas (1), la dimensión fractal calculada por el exponente de Hurst es igual a D = 1.6, lo que indica en un comportamiento aleatorio de una serie con el aumento del nivel de estocasidad. No obstante, eso no se refiere al período de 1999 para las cotizaciones de Lukoil.
El trabajo [2] ofrece otro ejemplo interesante e ilustrativo de la precisión de la estimación del índice de fractalidad y del exponente de
Hurst, como indicadores locales de las series temporales . Esta evaluación de parámetros es más apropiada para las tareas comerciales
relacionadas con el análisis de mercado del comportamiento operacional cualitativo-cuantitativo de las series temporales. La serie de
precios inicial de Alcoa Inc., que incluye 8145 puntos, fue dividida en 8113 intervalos sobrepuestos de 32 días cada uno, desplazados a un
día en relación a otro. Como parámetros de la precisión de los cálculos, se usaban los siguientes: el ancho del intervalo de confianza es de
95% para
Н y
![]() ,
la estimación de la precisión de colocación de puntos reales en la recta teórica
K = 1- R
2 , donde R
2 es el coeficiente de de la determinación (si los puntos caen exactamente en la recta, entonces R
2=1 y К=0).
,
la estimación de la precisión de colocación de puntos reales en la recta teórica
K = 1- R
2 , donde R
2 es el coeficiente de de la determinación (si los puntos caen exactamente en la recta, entonces R
2=1 y К=0).
En cada uno de 8113 segmentos, han sido calculados:
- H — exponente de Hurst;
-
 —
índice de fractabilidad;
—
índice de fractabilidad; -
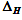 — ancho de
95 % del intevalo de confianza
H;
— ancho de
95 % del intevalo de confianza
H; -
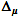 — ancho de
95 % del intevalo de confianza
— ancho de
95 % del intevalo de confianza
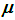 ;
; -
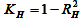 — precisión de
la correspondencia de los puntos experimentales de la recta obtenida para
H;
— precisión de
la correspondencia de los puntos experimentales de la recta obtenida para
H; -
 — precisión
de la correspondencia de los puntos experimentales de la recta obtenida para
— precisión
de la correspondencia de los puntos experimentales de la recta obtenida para
 .
.
Fragmentos típicos de los gráficos de las funciones
![]() ,
,
![]() y
y
![]() ,
,
![]() ,
construidos para los intervalos cuyo valor derecho coincide con el momento t, se muestran en las
imágenes 5a y 5b. Como se puede observar en estas imágenes, en la mayoría de los casos, el índice de
,
construidos para los intervalos cuyo valor derecho coincide con el momento t, se muestran en las
imágenes 5a y 5b. Como se puede observar en estas imágenes, en la mayoría de los casos, el índice de
![]() está
determinado mucho más exacto que H.
está
determinado mucho más exacto que H.
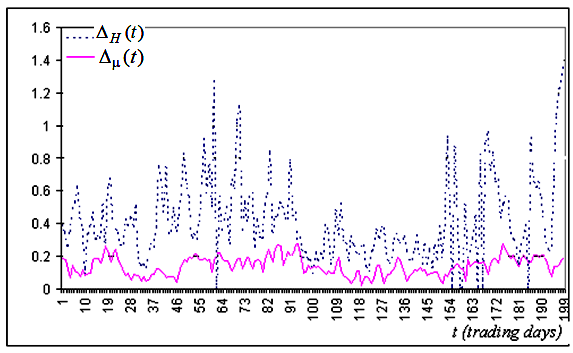
Fig. 5a. Los fragmentos típicos de la serie temporal del ancho de los intervalos de confianza creados a base de una serie de precios de cierre para Alcoa Inc.
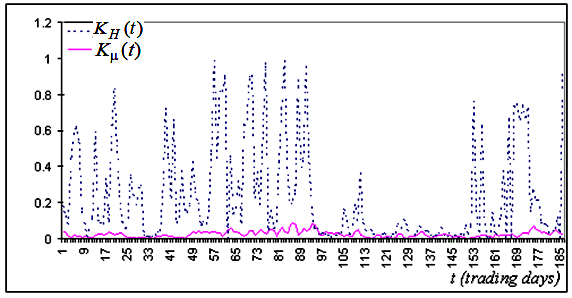
Fig. 5b. Fragmento correspondiente de la serie para los valores de la precisión de coincidencia de puntos experimentales en la línea teórica, construidos según el mismo principio
Estas imágenes permiten concluir que, en la mayoría de los casos, el índice de la fractalidad
![]() está
determinado con mucha más precisión que H.
está
determinado con mucha más precisión que H.
La principal ventaja del índice
![]() respecto
a otros indicadores fractales (en particular, exponente de Hurt) consiste en que el valor
respecto
a otros indicadores fractales (en particular, exponente de Hurt) consiste en que el valor
![]() correspondiente
entra rápidamente en el modo asintótico. Eso permite usar
correspondiente
entra rápidamente en el modo asintótico. Eso permite usar
![]() como
una característica local, determinando la dinámica del proceso inicial, puesto que la escala para su determinación confiable tiene la
misma orden que la escala principal de los estados determinantes del proceso. Estos estados incluyen los períodos de la calma relativa
(flat) y los períodos de un movimiento relativamente largo hacia arriba o hacia abajo (tendencias). Una solución conveniente para
vincular el valor
como
una característica local, determinando la dinámica del proceso inicial, puesto que la escala para su determinación confiable tiene la
misma orden que la escala principal de los estados determinantes del proceso. Estos estados incluyen los períodos de la calma relativa
(flat) y los períodos de un movimiento relativamente largo hacia arriba o hacia abajo (tendencias). Una solución conveniente para
vincular el valor
![]() con
el comportamiento de la serie es introducir la función
con
el comportamiento de la serie es introducir la función
![]() como valor
como valor
![]() que
se determina en el intervalo mínimo anterior
t, donde
que
se determina en el intervalo mínimo anterior
t, donde
![]() todavía
puede ser calculado con precisión aceptable.
todavía
puede ser calculado con precisión aceptable.
Correlación de la naturaleza de la serie temporal e índice de fractalidad
Para los usuarios del indicador basado en el índice de la fractalidad, será útil conocer algunas de sus características [2].
El comportamiento de la serie determina el valor
![]() ,
a saber:
,
a saber:
-
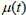 =
0.5 indica en un paseo aleatorio del precio (proceso de Wiener). Los inversores actúan independientemente y no hay ninguna
tendencia determinada en el comportamiento de los precios. En este caso, se puede decir que el precio tiene una estabilidad
«normal», porque el precio es poco dependiente de las influencias externas, no hay «feedback», no hay posibilidades de
arbitraje.
=
0.5 indica en un paseo aleatorio del precio (proceso de Wiener). Los inversores actúan independientemente y no hay ninguna
tendencia determinada en el comportamiento de los precios. En este caso, se puede decir que el precio tiene una estabilidad
«normal», porque el precio es poco dependiente de las influencias externas, no hay «feedback», no hay posibilidades de
arbitraje. -
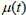 <
0.5 indica en la situación cuando el precio tiene una alta estabilidad contra las influencias externas, que puede estar
vinculada con la confianza elevada de los inversores en la estabilidad de dicha empresa y la ausencia de una nueva información
en el mercado. En este caso, los precios de las acciones fluctúan dentro de un rango de precios bastante estrecho. Hay un número
de vendedores cuando los precios suben, así como hay compradores cuando los precios bajan, ellos devuelven los precios en el
rango inicial con sus acciones. En este caso la «correlación» es negativa y afloja las variaciones de los precios,
manteniendo el comportamiento estable de los precios.
<
0.5 indica en la situación cuando el precio tiene una alta estabilidad contra las influencias externas, que puede estar
vinculada con la confianza elevada de los inversores en la estabilidad de dicha empresa y la ausencia de una nueva información
en el mercado. En este caso, los precios de las acciones fluctúan dentro de un rango de precios bastante estrecho. Hay un número
de vendedores cuando los precios suben, así como hay compradores cuando los precios bajan, ellos devuelven los precios en el
rango inicial con sus acciones. En este caso la «correlación» es negativa y afloja las variaciones de los precios,
manteniendo el comportamiento estable de los precios. -
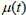 >
0.5 corresponde a la reducción de la estabilidad del precio. Eso puede indicar en la aparición de una nueva información y a la
reacción que provoca. Puesto que, con la primera aproximación se puede suponer que todos los participantes del mercado
evalúan la información recibida aproximadamente de la misma manera, entonces, surge una tendencia en el movimiento del
precio, que corresponde a la información obtenida. En algunas condiciones, esta situación puede causar una variaciones
bruscas del precio de la acción.
>
0.5 corresponde a la reducción de la estabilidad del precio. Eso puede indicar en la aparición de una nueva información y a la
reacción que provoca. Puesto que, con la primera aproximación se puede suponer que todos los participantes del mercado
evalúan la información recibida aproximadamente de la misma manera, entonces, surge una tendencia en el movimiento del
precio, que corresponde a la información obtenida. En algunas condiciones, esta situación puede causar una variaciones
bruscas del precio de la acción.
El índice de la fractalidad y el exponente de Hurst están vinculados con la relación
![]() =
1-H, lo que permite heredar las variantes de la clasificación desde las series temporales caóticas:
=
1-H, lo que permite heredar las variantes de la clasificación desde las series temporales caóticas:
- Cuando
 =
0.5, H = 0.5, la serie temporal es un proceso de Wiener (ruido «marrón»). La principal propiedad de este proceso es la ausencia de la
memoria, es decir, la evolución de la serie no está relacionada con los valores anteriores.
=
0.5, H = 0.5, la serie temporal es un proceso de Wiener (ruido «marrón»). La principal propiedad de este proceso es la ausencia de la
memoria, es decir, la evolución de la serie no está relacionada con los valores anteriores. - Cuando 0.5 <
 <= 1,
0 <= H < 0.5, el proceso se llama el ruido «rosado». Se caracteriza por la memoria «negativa», es decir, si antes se
registraba un incremento positivo, es muy probable, que será seguido por un incremento negativo, y viceversa.
<= 1,
0 <= H < 0.5, el proceso se llama el ruido «rosado». Se caracteriza por la memoria «negativa», es decir, si antes se
registraba un incremento positivo, es muy probable, que será seguido por un incremento negativo, y viceversa. - Cuando 0 <=
 <
0.5 , 0.5 < H <=1, la serie temporal es un ruido «negro» con memoria «positiva»: se antes había una
tendencia positiva, es muy probable que se mantendrá en el futuro, y viceversa.
<
0.5 , 0.5 < H <=1, la serie temporal es un ruido «negro» con memoria «positiva»: se antes había una
tendencia positiva, es muy probable que se mantendrá en el futuro, y viceversa.
Indicador para estimar el índice de la fractalidad y el exponente de Hurst
Una negociación exitosa, en una escala de días, semanas y un mes, está relacionada con la comprensión del estado caótico de las series temporales financieras. Una estimación estable de los indicadores fractales en los fragmentos de datos cortos permite desarrollar y usar un indicador para las acciones (cuya evolución se determina por la voluntad de muchas personas) que proporciona la posibilidad al trader de mejorar tanto la identificación, como la previsión de las series temporales financieras.
El indicador evalúa el índice de la fractalidad, el intervalo de confianza para él, los valores del coeficiente de la determinación
y el exponente de Hurt.
Los gráficos presentados muestran los gráficos de las funciones
![]() ,
,
![]() ,
y
,
y
![]() descritos
anteriormente.
descritos
anteriormente.
En el indicador, se puede especificar la longitud del segmento de una serie temporal, para la cual van a realizarse los cálculos y va a mostrarse la ventana de la evaluación de los parámetros. Al ejecutar el indicador, se realiza el cálculo a lo largo de la serie de los precios de cierre, mientras que la ventana se desplaza a una indicación. Puesto que la ventana (intervalo) de la estimación tiene la longitud igual a la potencia de dos, eso permite obtener un conjunto de valores y evaluar el índice de la fractalidad realizando la aproximación lineal del conjunto.
double CFractalIndexLine::CalculateFractalIndex(const double &series[],const int N0,const int N1, const double hourSampling,int CountFragmentScale=0) { //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // series[] - serie temporal // N0, N1 - puntos límite (izquierdo/derecho) en el array series[], por el que será estimado el índice de la fractalidad // hourSampling - digitalización entre los puntos EN HORAS // CountFragmentScale - número de escalas solicitadas para formar el conjunto de puntos para calcular el índice de la fractalidad // // RESULTADO // índice de la fractalidad (Mu), exponente de Hurst (Hurst), intervalo de confianza 95% (ConfInterval[2], // coeficiente de determinación (R2det) - cuanto más próximo sea a 1, con más precisión se colocan los puntos del cálculo sobre la recta aproximada // estabilidad de la determinación del coeficiente KR2 = 1-R2det. Cuanto más próximo a cero, más preciso será el valor Mu //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. Cargamos el fragmento interno con valores de la serie temporal LoadFragment(series,N0,N1,hourSampling); // 2. Determinamos el número de los ciclos para determinar los puntos de la recta de aproximación int nn2 = (int)floor(Nfrgm/2); // División límite, no menos de dos puntos int npow2 = (int)ipow2(nn2); // Número de la potencia de dos en la división límite posible; if(CountFragmentScale==0) CountFragmentScale=npow2; // por defecto int Count=fmin(CountFragmentScale,npow2); // Limitación del número de variantes de la división de los fragmentos de la serie int NumPartDivide; for(int i=0; i<=Count; i++) { NumPartDivide = (int)pow (2,i); // Número de las partes de división del fragmento de la serie CalcAmplVariation(NumPartDivide, i); // Cálculo del punto del modelo de la recta aproximada i=i; } // 4. Estimación del índice de la fractalidad y los límites de los intervalos de confianza del índice Mu=fCalculateConfidenceIntervalMU(LogDeltaScales,LogAmplVariations,Count,ConfInterval,R2det); Hurst=1-Mu; // Exponente de Hurst KR2=1-R2det; return Mu; } //----------------------------------------------------------------------------------------------------------------------------------
double CFractalIndexLine::CalcAmplVariation(const int NumPartDivide,int idxAmplVar=-1) { // Si idxAmplVar=-1, el índice se determina automáticamente en el array (por la contribución de la potencia de dos en NumPartDivide) // PREVIAMENTE: el fragmento está copiado, el tiempo de la digitalización está definido EN DÍAS // - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. DETERMINAMOS LOS LÍMITES DE LOS INTERVALOS CORRESPONDIENTES AL NÚMERO ESPECIFICADO DE LAS DIVISIONES int nCheckPoint=0,nIntervalPoints=0; // número de los puntos verificados en un subintervalo de la división double dayDeltaScales=BoundaryArray(NumPartDivide,fragment,0,Nfrgm-1,hSampling,Boundaries,nIntervalPoints); // 2. REPASO DE LOS INTERVALOS PARA DETERMINAR VALORES LÍMITE DE LOS VALORES DE LA FUNCIÓN Y VARIACIONES DE AMPLITUD int countInterval=Boundaries.CountNonEmty(); int maxFuncIdx=0,minFuncIdx=0; double A,V=0.; nCheckPoint=(int)(Boundaries.y[0]-Boundaries.x[0])+1; for(int i=0; i<countInterval; i++) { maxFuncIdx = ArrayMaximum(fragment,(int)Boundaries.x[i],nCheckPoint); // ÍNDICE CON VALOR MÁX. minFuncIdx = ArrayMinimum(fragment,(int)Boundaries.x[i],nCheckPoint); A = fragment[maxFuncIdx] - fragment[minFuncIdx]; V = V+A; i=i; } // 3. ACUMULACIÓN DE LOS RESULTADOS EN REPOSITORIO if(idxAmplVar==-1) idxAmplVar=ipow2(NumPartDivide); // índice en array de repositorio LogDeltaScales [idxAmplVar] = log(dayDeltaScales); // escala de log de la división actual LogAmplVariations[idxAmplVar] = log(V); // variación de amplitud log en la escala actual de divisiones return V; } //--------------------------------------------------------------------------------------------------------------------------------------
Los fragmentos del programa del archivo CFragmentIndexLine.mqh ejecutan los ciclos para calcular el área de cobertura, como se muestra en la Fig. 2. Los comentarios detallados en el texto del programa explican la secuencia de acciones.
Demostración del trabajo del indicador con datos reales
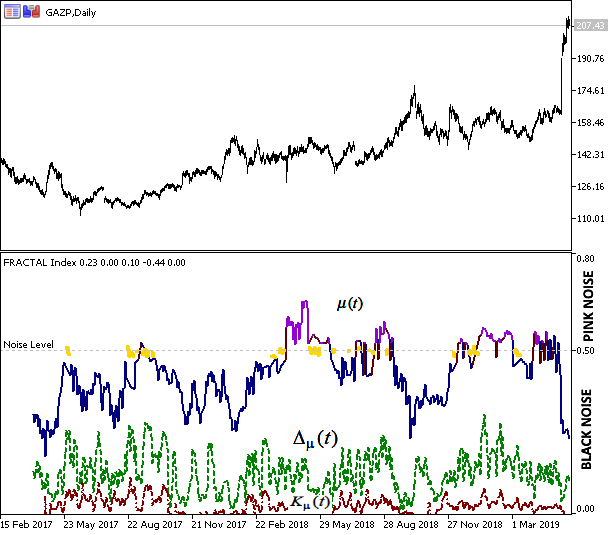
Fig. 6 Precios de cierre de Gazprom y resultados de la estimación del índice de la fractalidad
En la imagen se muestra la correlación de los valores del índice y el comportamiento de los precios. El color azul del gráfico del índice corresponde al estado tendencial del sistema, indica la estabilidad de la tendencia y la posibilidad de la predicción del comportamiento futuro. El color violeta indica en la antipersistencia del tipo «ruido rosado», lo que corresponde a la memoria «negativa» y a flat. El color amarillo corresponde al «movimiento browniano», o sea, el movimiento es aleatorio y no puede ser previsto.
Conclusiones
El análisis fractal local puede ser interesante en el trading según los siguientes puntos de vista:
- Determinación del desorden, es decir, el momento del cambio de las características estáticas de la serie temporal;
- Previsión de una serie temporal.
Hay que tener en cuenta que la escala de confianza para la determinación del índice
![]() con
una precisión apropiada, es en dos ordenes menor que la misma escala para calcular el exponente de Hurst H. Esta diferencia permite usar
el índice
con
una precisión apropiada, es en dos ordenes menor que la misma escala para calcular el exponente de Hurst H. Esta diferencia permite usar
el índice
![]() como
un índice fractal local. Por tanto, se puede considerar que el índice
como
un índice fractal local. Por tanto, se puede considerar que el índice
![]() describe
la estabilidad de la serie temporal. El caso
describe
la estabilidad de la serie temporal. El caso
![]() <0.5
puede ser interpretado como tendencia, y el caso
<0.5
puede ser interpretado como tendencia, y el caso
![]() >0.5
, como flat. El caso
>0.5
, como flat. El caso
![]() ~
0.5 corresponde al movimiento browniano. Así, usando la función
~
0.5 corresponde al movimiento browniano. Así, usando la función
![]() ,
se puede clasificar las series de precio iniciales y argumentar la previsión.
,
se puede clasificar las series de precio iniciales y argumentar la previsión.
Lista de referencias
- Dubovikov M.M., Starchenko N.V. Econophysics and fractal analysis of financial time series
- Dubovikov M.M., Starchenko N.V. Econophysics and fractal analysis of financial time series // Collected. «ECONOPHYSICS Modern Physics in search of economic theory»
- Peters. J. Chaos and Order in the Capital Markets. A New View of Cycles, Prices, and Market Volatility.
- Krivonosova E.K., Pervadchuk V.P., Krivonosova E.A. Comparison of fractal characteristics of time series of economic indicators.
- Starchenko N.V. Local fractal analysis in physical applications.