Comprendemos la "memoria" del mercado usando la diferenciación y el análisis entrópico
Maxim Dmitrievsky | 5 agosto, 2019
Motivación de la aplicación del enfoque y prehistoria breve
Se sabe que un gran número de los participantes en los mercados de liquidez que operan con diferentes horizontes de inversión producen mucho ruido de mercado. En otras palabras, los mercados tienen un ratio pequeño entre la señal y el ruido. La situación se redobla gracias a los intentos de la diferenciación entera de la serie temporal que borra los restos de la memoria convirtiendo las cotizaciones a una serie con propiedad estacionaria.
Las series de los precios tienen memoria, porque cada valor depende de una larga historia de los niveles de precios. Las transformaciones de una serie temporal, como logaritmo de incrementos, cortan la memoria porque se construyen a base de una longitud limitada de la ventana. Cuando las transformaciones a la estacionariedad eliminan la memoria de mercado, los estadísticos aplican unos métodos matemáticos complejos para extraer sus restos. No es asombroso que la aplicación de estos enfoques estadísticos clásicos en los mercados lleva a unas conclusiones falsas.
Concepto de la dependencia de largo alcance
La dependencia de largo alcance (LRD), también llamada la memoria a largo plazo o la persistencia a largo plazo, se observa durante el análisis de las series temporales financieras. Eso se expresa en la velocidad del decaimiento de la dependencia estadística entre dos precios, con el aumento del intervalo temporal (o la distancia entre ellos). Se considera que el fenómeno tiene una dependencia de largo alcance, cuando la dependencia se debilita más lentamente que la disminución exponencial. La dependencia de largo alcance también se asocia a menudo con los procesos autosimilares. Para más información sobre LRD (long-range dependence), consulte la Wikipedia.
Problema de estacionariedad y existencia de la memoria
La característica común de los diagramas de precios es la existencia de no estacionariedad, o sea, de una larga historia de los niveles de precios que desplazan el precio medio en el tiempo. Para realizar el análisis estadístico, los analistas tienen que trabajar con incrementos de los precios (o logaritmos de incrementos), cambios de la rentabilidad o de la volatilidad. Estas transformaciones hacen que la serie temporal sea estacionaria, eliminando toda la memoria de las secuencias de precios. A pesar de que la estacionariedad es una propiedad obligatoria para las conclusiones estadísticas, no siempre es necesario eliminar la memoria entera, porque es la base para las propiedades predictoras de los modelos. Por ejemplo, los modelos de equilibrio (estacionarios) tienen que contener un poco de memoria para evaluar hasta que grado el precio se ha alejado de su valor esperado.
El problema es que los incrementos de los precios son estacionarios, pero no contienen la memoria sobre el pasado, mientras que la serie de precios contiene el volumen completo de la memoria disponible pero no es estacionario. Surge la pregunta, ¿cómo es necesario diferenciar la serie temporal para que sea estacionario y, al mismo tiempo, contenga la memoria máxima posible? Por tanto, nos gustaría generalizar el concepto de los incrementos de precios para la consideración de las series estacionarias en las que no se borra toda la memoria. En este caso, los incrementos de precios no representan una solución óptima para la transformación de los precios, entre otros métodos disponibles.
De esta manera, vamos a introducir el concepto de la diferenciación fraccionada. Existe un amplio rango de posibilidades entre dos extremos: diferenciación unitaria y diferenciación cero. Los precios diferenciados completamente están por un lado, los no diferenciados están por otro.
El área de la aplicación de la diferenciación fraccionada es bastante amplia. Por ejemplo, los algoritmos del aprendizaje automático normalmente reciben una serie diferencial en la entrada. El problema es que es necesario mostrar los datos nuevos de acuerdo con la historia existente para que el modelo del aprendizaje automático pueda reconocerlos. En caso de una serie no estacionaria, los datos nuevos pueden estar fuera del rango de valores conocido, lo que llevará a un funcionamiento incorrecto del modelo.
Digresión histórica en la diferenciación fraccionada
Prácticamente, todos los métodos del análisis y previsión de las series temporales financieras descritos en los artículos científicos dan una idea sobre la diferenciación entera (integer).
Surge un par de preguntas:
- ¿Por qué la diferenciación entera (digamos, con un retardo unitario (lag) es óptima?
- ¿Será que esta hiperdiferenciación es una de las razones de que la teoría económica tienda tanto a la hipótesis de mercados eficientes?
El concepto de la diferenciación fraccionada, en aplicación al análisis y previsión de series temporales, asciende, por lo menos, a Hosking. En aquel artículo, la familia de los procesos ARIMA puede ser generalizada, permitiendo que el grado de la diferenciación reciba los valores fraccionados. Eso tenía sentido porque el proceso de la diferenciación fraccionada revelaba la persistencia a largo plazo o la antipersistencia, aumentando la capacidad predictora en comparación con ARIMA estándar. Este modelo fue llamado ARFIMA (autoregressive fractionally integrated moving average) o FARIMA. Después de este artículo, la diferenciación fraccionada a veces se mencionaba en los artículos de otros autores, respecto a la aceleración de los métodos de cálculos.
Estos modelos son útiles en modelación de las series temporales con una memoria larga, es decir, cuando las desviaciones de la media a largo plazo se debilitan más lentamente que la disminución exponencial.
Concepto de la diferenciación fraccionada
Vamos a considerar el operador de la desviación inversa (o operador retardo) B, que se aplica a la matriz de valores reales {Xt}, donde B^kXt = Xt−k, para cualquier entero k ≥ 0. Por ejemplo, (1 − B)^2 = 1 − 2B + B^2, donde B^2Xt = Xt−2, por tanto, (1 − B)^2Xt = Xt − 2Xt−1 + Xt−2.
Nótese que (x + y)^n = 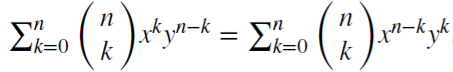 , para cada entero positivo n. Para el número real d,
, para cada entero positivo n. Para el número real d, 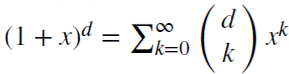 , es una serie binomial. En el modelo fraccionado, el indicador d puede ser un número real, con la siguiente extensión formal de la serie binomial:
, es una serie binomial. En el modelo fraccionado, el indicador d puede ser un número real, con la siguiente extensión formal de la serie binomial:
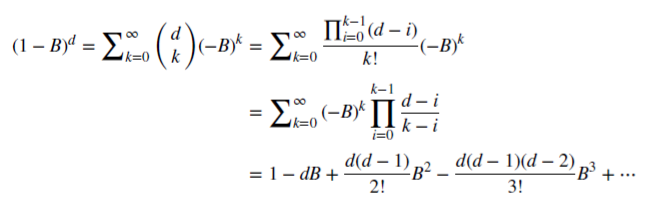
Guardando la memoria del mercado en caso de la diferenciación fraccionada
Vamos a ver cómo d no negativo racional guarda la memoria. Esta serie aritmética se compone de un producto escalar:
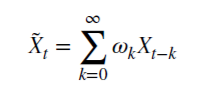
con pesos 𝜔
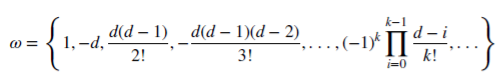
y variables Х
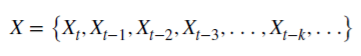
Cuando d es un entero positivo, 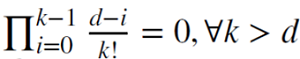 , la memoria se recorta en este caso.
, la memoria se recorta en este caso.
Por ejemplo, d = 1 se usa para calcular los incrementos, donde 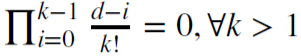 y 𝜔 = {1,−1, 0, 0,…}.
y 𝜔 = {1,−1, 0, 0,…}.
Diferenciación fraccionada para una ventana de observaciones fija
Habitualmente, la diferenciación fraccionada se aplica para la secuencia entera de la serie temporal. La complejidad es más alta en este caso, mientras que el desplazamiento de la serie transformada es negativo. En su libro "Advances in Financial Machine Learning", Marcos Lopez De Prado propuso el método de la ventana fija, en la que la secuencia de los coeficientes se descarta cuando su módulo (|𝜔k|) se hace menos del valor límite establecido (𝜏). Este procedimiento ofrece una ventaja ante el método clásico de la ventana de expansión, porque permite tener pesos iguales para cualquier secuencia de la serie original, reduce la complejidad computacional y libra del desplazamiento negativo. El resultado de esta transformación es el guardado de la memoria sobre los niveles de precios y el ruido. La distribución de esta transformación no es normal (Gaussian), debido a la presencia de la memoria, asimetría y el exceso demasiado, no obstante, puede ser estacionario.
Demostración del proceso de la diferenciación fraccionada
Vamos a escribir el script que permite evaluar visualmente el efecto obtenido de la diferenciación fraccionada de la serie temporal. Creamos dos funciones: para obtener los pesos 𝜔 y para calcular nuevos valores de la serie:
//+------------------------------------------------------------------+ void get_weight_ffd(double d, double thres, int lim, double &w[]) { ArrayResize(w,1); ArrayInitialize(w,1.0); ArraySetAsSeries(w,true); int k = 1; int ctr = 0; double w_ = 0; while (ctr != lim - 1) { w_ = -w[ctr] / k * (d - k + 1); if (MathAbs(w_) < thres) break; ArrayResize(w,ArraySize(w)+1); w[ctr+1] = w_; k += 1; ctr += 1; } } //+------------------------------------------------------------------+ void frac_diff_ffd(double &x[], double d, double thres, double &output[]) { double w[]; get_weight_ffd(d, thres, ArraySize(x), w); int width = ArraySize(w) - 1; ArrayResize(output, width); ArrayInitialize(output,0.0); ArraySetAsSeries(output,true); ArraySetAsSeries(x,true); ArraySetAsSeries(w,true); int o = 0; for(int i=width;i<ArraySize(x);i++) { ArrayResize(output,ArraySize(output)+1); for(int l=0;l<ArraySize(w);l++) output[o] += w[l]*x[i-width+l]; o++; } ArrayResize(output,ArraySize(output)-width); }
Vamos a mostrar el gráfico animado que se cambia dependiendo del parámetro 0<d<1:
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { for(double i=0.05; i<1.0; plotFFD(i+=0.05,1e-5)) } //+------------------------------------------------------------------+ void plotFFD(double fd, double thresh) { double prarr[], out[]; CopyClose(_Symbol, 0, 0, hist, prarr); for(int i=0; i < ArraySize(prarr); i++) prarr[i] = log(prarr[i]); frac_diff_ffd(prarr, fd, thresh, out); GraphPlot(out,1); Sleep(500); }
Veamos el resultado:
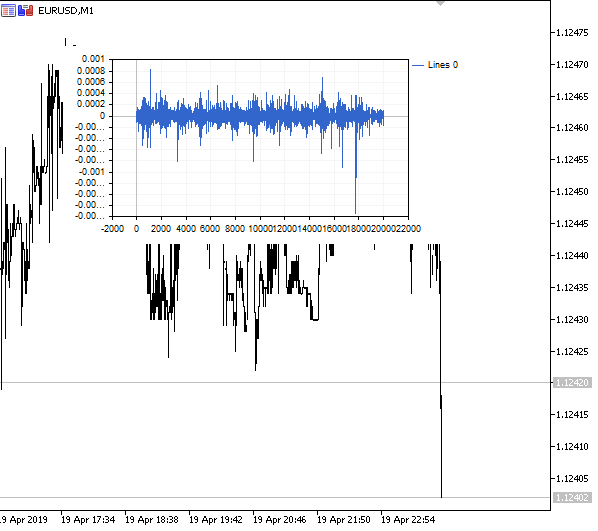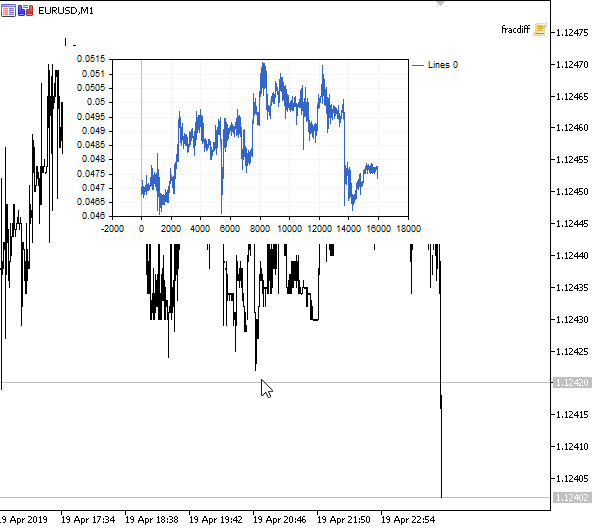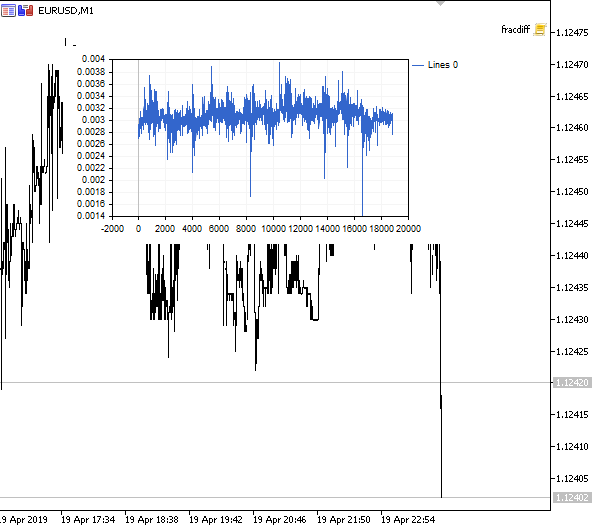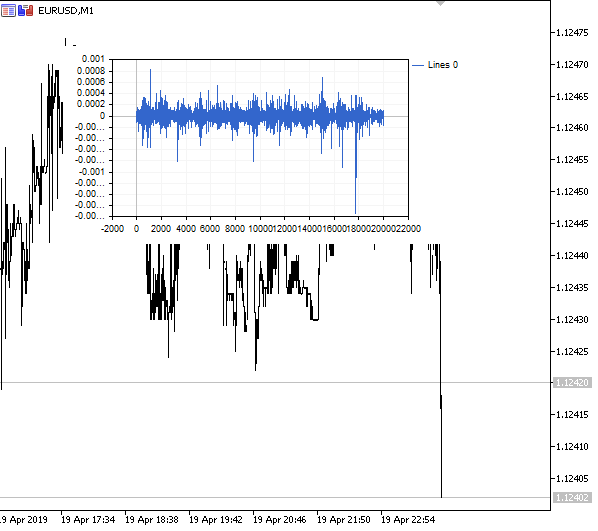
Fig. 1. Diferenciación fraccionada 0<d<1
Como se esperaba, al aumentar el grado de la diferenciación d, el gráfico se hacía más estacionario, perdiendo gradualmente la «memoria» sobre los niveles del pasado. Los pesos para la serie (funciones del resultado escalar de los pesos por los valores de precios) quedan inalterados para la secuencia entera y no necesitan el recálculo.
Creando un indicador a basa de la diferenciación fraccionada.
Para un uso conveniente en los EAs, escribimos un indicador que puede ser incluido especificando varias configuraciones: grado de la diferenciación, tamaño del umbral para recortar los pesos sobrantes y la profundidad del historial a mostrar. No voy a mostrar el código completo del indicador aquí, puede encontrarlo en el archivo de origen.
Sólo indicaré que la función del cálculo es la misma, para calcular el valor del búfer de indicador, se usa la siguiente función:
frac_diff_ffd(weights, price, ind_buffer, hist_display, prev_calculated !=0);
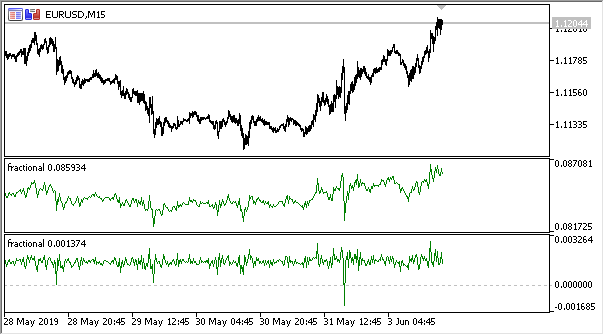
Fig. 2. Diferenciación fraccionada con potencias 0.3 y 0.9
Ahora tenemos un indicador que explica bastante exactamente la dinámica del cambio de la cantidad de la información en una serie temporal. Cuando se aumenta el grado de la diferenciación, la información se pierde y la serie obtiene un carácter más estacionario. No obstante, se pierde la información solamente sobre los niveles de precios, pero pueden quedarse los ciclos periódicos, siendo un punto de partida para la previsión. Así, nos aproximamos a los métodos de la teoría de la información, es decir, la entropía de la información, que ayudará a evaluar el volumen de datos.
Concepto de la entropía de la información
La entropía de la información es una concepción relacionada con la teoría de la información, que muestra cuánta información se contiene en un evento. En general, cuanto más especificado o determinado sea el evento, menos información va a contener. Para especificar mejor, la información está relacionada con el aumento de la incertidumbre. Esta concepción fue introducida por Claude Shannon.
Así, se puede determinar la entropía de un valor aleatorio, introduciendo el concepto de la distribución del valor X aleatorio, que obtiene un número final de valores:
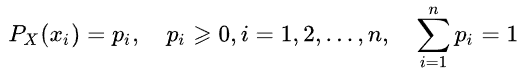
Entonces, la información especificada del evento (o serie temporal) se define como sigue:
![]()
La estimación de la entropía puede ser escrita así:
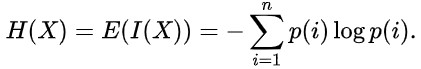
La unidad de la medición (por ejemplo, bit, nat, trit o hartley), del volumen de datos y de la entropía depende de la base del algoritmo.
No vamos a describir en detalles la entropía de Shannon. Sólo vamos a notar que este método conviene mal para estimar las series temporales cortas y de ruido. Así que Steve Pincus y Rudolf Kalman propusieron el método llamado " ApEn" (approximate entropy) en relación a las series temporales financieras, que fue descrito en detalle en el artículo "Irregularity, volatility, risk and financial market time series".
En este artículo, ellos proponen dos formas de la desviación de los precios de la constancia (descripción de la volatilidad), que son fundamentalmente diferentes:
- la primera describe una desviación grande estándar
- la segunda representa una extrema irregularidad e impredecibilidad
Son dos formas completamente diferentes y esta separación es necesaria: la desviación estándar sigue siendo una buena estimación de la desviación desde la medida de centralidad, mientras que ApEn ofrece la estimación de la irregularidad. Es más, el grado de la variabilidad no es tan crítica, mientras que la irregularidad e impredecibilidad suponen un problema.
Aquí tenemos un simple ejemplo con dos series temporales:
- serie (10,20,10,20,10,20,10,20,10,20,10,20...) con 10 y 20 alternados
- serie (10,10,20,10,20,20,20,10,10,20,10,20...) 10 y 20 se seleccionan de forma aleatoria, con probabilidad de 1/2
Los momentos de la estadística, como la media y la varianza, no mostrarán las diferencias entre dos series temporales. Al mismo tiempo, la primera serie es completamente regular, es decir, siempre se puede predecir el siguiente valor sabiendo el anterior. La segunda serie es absolutamente aleatoria y cualquier intento de previsión fracasará.
Joshua Richman y Randall Moorman sometieron a la crítica el método "ApEn" en su artículo "Physiological time-series analysis using approximate entropy and sample entropy", y propusieron un método mejorado "SampEn". En particular, criticaron la dependencia del valor de la entropía de la longitud de la muestra, así como, la inconsistencia de los valores para las series temporales diferentes pero relacionadas entre sí. Además, el nuevo método es menos complejo en cuanto a la computación. Nosotros vamos a usar este método y describiremos las particularidades de su aplicación.
Método Sample entropy para determinar la regularidad de los incrementos de precios
Pues bien, el método SampEn, siendo una modificación del método ApEn, se utiliza para estimar la complejidad (irregularidad) de la señal (serie temporal). Para el tamaño especificado de m puntos, la tolerancia r y el número de los valores calculados N, SampEn representa el algoritmo de la probabilidad de que si dos series de puntos simultáneos con la longitud m tienen la distancia < r, entonces dos series de puntos simultáneos con la longitud m + 1 también tienen la distancia < r.
Ahora, supongamos que tenemos un conjunto de datos de las series temporales de la longitud ![]() con un intervalo temporal constante. Vamos a definir la plantilla del vector de la longitud m como
con un intervalo temporal constante. Vamos a definir la plantilla del vector de la longitud m como ![]() y la función de la distancia
y la función de la distancia ![]() (i≠j) según Chebyshev, que es el máximo del módulo de la diferencia entre los componentes de estos vectores (pero puede ser otra función de distancia). Luego, definimos SampEn como sigue:
(i≠j) según Chebyshev, que es el máximo del módulo de la diferencia entre los componentes de estos vectores (pero puede ser otra función de distancia). Luego, definimos SampEn como sigue:
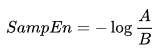
Aquí:
- A es el número de los pares de vectores de plantilla que tienen
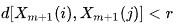
- B = es el número de los pares de vectores de plantilla que tienen
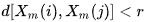
Está claro de lo expuesto que A siempre será <= B, por consiguiente, el valor de SampEn siempre será cero o positivo. Un valor menor también indica en una autosimilaridad más grande en el conjunto de datos o en menos ruido.
Normalmente, se usan los siguientes valores: m = 2 y r = 0.2 * std, donde std es la desviación estándar que debe usarse para un conjunto de datos muy grande.
He encontrado una implementación rápida del método propuesta en el código de abajo, y la he sobrescrito en MQL5:
double sample_entropy(double &data[], int m, double r, int N, double sd) { int Cm = 0, Cm1 = 0; double err = 0.0, sum = 0.0; err = sd * r; for (int i = 0; i < N - (m + 1) + 1; i++) { for (int j = i + 1; j < N - (m + 1) + 1; j++) { bool eq = true; //m - length series for (int k = 0; k < m; k++) { if (MathAbs(data[i+k] - data[j+k]) > err) { eq = false; break; } } if (eq) Cm++; //m+1 - length series int k = m; if (eq && MathAbs(data[i+k] - data[j+k]) <= err) Cm1++; } } if (Cm > 0 && Cm1 > 0) return log((double)Cm / (double)Cm1); else return 0.0; }
En adición, propongo una versión del cálculo de cross-sample entropy (cross-SampEn) para los casos cuando es necesario obtener una estimación de la entropía para dos series (dos vectores de entrada), pero también se puede usarlo para calcular sample entropy:
// Calculate the cross-sample entropy of 2 signals // u : signal 1 // v : signal 2 // m : length of the patterns that compared to each other // r : tolerance // return the cross-sample entropy value double cross_SampEn(double &u[], double &v[], int m, double r) { double B = 0.0; double A = 0.0; if (ArraySize(u) != ArraySize(v)) Print("Error : lenght of u different than lenght of v"); int N = ArraySize(u); for(int i=0;i<(N-m);i++) { for(int j=0;j<(N-m);j++) { double ins[]; ArrayResize(ins, m); double ins2[]; ArrayResize(ins2, m); ArrayCopy(ins, u, 0, i, m); ArrayCopy(ins2, v, 0, j, m); B += cross_match(ins, ins2, m, r) / (N - m); ArrayResize(ins, m+1); ArrayResize(ins2, m+1); ArrayCopy(ins, u, 0, i, m + 1); ArrayCopy(ins2, v, 0, j, m +1); A += cross_match(ins, ins2, m + 1, r) / (N - m); } } B /= N - m; A /= N - m; return -log(A / B); } // calculation of the matching number // it use in the cross-sample entropy calculation double cross_match(double &signal1[], double &signal2[], int m, double r) { // return 0 if not match and 1 if match double darr[]; for(int i=0; i<m; i++) { double ins[1]; ins[0] = MathAbs(signal1[i] - signal2[i]); ArrayInsert(darr, ins, 0, 0, 1); } if(darr[ArrayMaximum(darr)] <= r) return 1.0; else return 0.0; }
El primer método del cálculo será suficiente, por eso, vamos a usarlo.
Persistencia y modelo del movimiento browniano fraccionado
Si el valor del incremento de la serie de precios se aumenta en este momento, ¿cuál será la probabilidad de que también continuará creciendo en el siguiente momento? Así, hemos llegado a la comprensión de la persistencia (o estabilidad). La medición de la persistencia puede ser muy útil. En esta sección, vamos a considerar la aplicación del método SampEn a la estimación de la persistencia de incrementos en la ventana deslizante. Este método de evaluación fue propuesto en el artículo ya mencionado " Irregularity, volatility, risk and financial market time series".
Ya tenemos una serie diferenciada de acuerdo con la teoría del movimiento browniano fraccionado (el término «diferenciación fraccionada» procede de ella). Definimos una serie incremental binaria de grano grueso
BinInci:= +1, if di+1 – di > 0, –1. Por decir más simple, binarizamos los incrementos en el rango de +1, -1. Así, estimaremos directamente la distribución de cuatro posibles opciones del comportamiento de los incrementos:
- Arriba, Arriba
- Abajo, Abajo
- Arriba, Abajo
- Abajo, Arriba
La independencia de las estimaciones y la potencia estadística del método están relacionadas con la siguiente característica: prácticamente, todos los procesos tienen unos nivel extremadamente pequeños de los errores de SampEn para la serie Binlnci. Lo importante es que esta estimación no supone y no requiere que los datos sean de Markov y no exige los conocimientos a priori de algunas características, salvo la estacionariedad. Si los datos satisfacen la propiedad de Markov de la primera orden, entonces SampEn(1) = SampEn(2), lo cual permite sacar unas conclusiones adicionales.
El movimiento browniano fraccionado representa un buen modelo y se remonta a Benoit Mandelbrot, que modelaba los fenómenos que demostraban tanto una dependencia de largo alcance o la «memoria», como las «colas gordas» (heavy tails). Eso también llevó a la aparición de nuevas aplicaciones estadísticas, como el exponente de Hurst y el análisis R/S. Como ya sabemos, los incrementos de precios a veces demuestran una dependencia de largo alcance y las colas gordas,
De esta manera, podemos estimar directamente la persistencia de una serie temporal, donde los valores menores de SampEn van a corresponder a los valores mayores de la persistencia y viceversa.
Implementando la estimación de la persistencia para una serie diferencial
Vamos a rescribir nuestro indicador, o sea, añadimos la posibilidad de trabajar en modo de la estimación de persistencia. Puesto que la estimación de la entropía trabaja para los valores discretos, normalizamos los valores de los incrementos con precisión de hasta 2 dígitos.
La implementación completa está disponible en el indicador adjunto "fractional entropy". Aquí, describiré los ajustes del indicador:
input bool entropy_eval = true; // mostrar los valores de entropía o incremento input double diff_degree = 0.3; // grado de diferenciación de serie temporal input double treshhold = 1e-5; // umbral para cortar los pesos sobrantes (se puede establecer valores predefinidos) input int hist_display = 5000; // profundidad de historia visualizada input int entropy_window = 50; // ventana para estimar entropía del proceso
Como resultado, el indicador en dos modos se muestra a continuación (la parte de arriba muestra la entropía, la parte de abajo muestra los incrementos estándar):
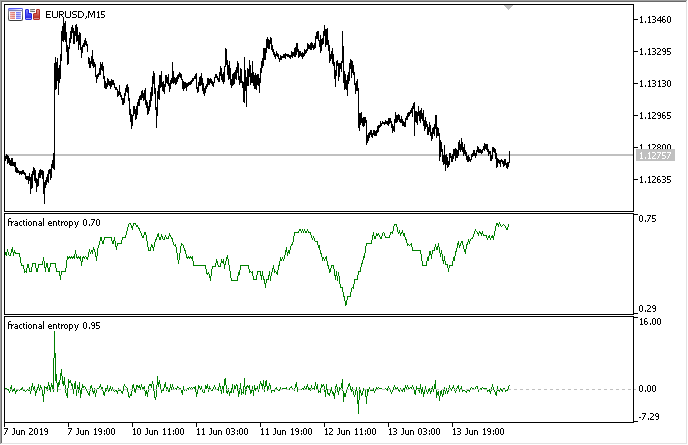
Fig. 3. Valores de la entropía para la ventana deslizante 50 (arriba) y diferenciación fraccionada con el grado de 0,8
Se puede observar que los valores de ambas estimaciones no se correlacionan, lo cual es una buena señal para el modelo del aprendizaje automático (falta de multicolinealidad) que será considerado en la siguiente sección.
Optimización del EA en tiempo real usando el aprendizaje automático: regresión logística
Pues bien, tenemos una serie temporal diferenciada apropiada, que se puede usar para obtener señales comerciales. Como ya ha sido mencionado antes, ella es más estacionaria y más conveniente para los modelos del aprendizaje automático. Además, tenemos la estimación de la pertinencia de la serie. Ahora, tenemos que elegir un modelo óptimo del aprendizaje automático. Puesto que el EA tiene que ser optimizado dentro de sí mismo, hay ciertos requerimientos para la velocidad del aprendizaje, es decir, tiene que ser muy rápido y tener los retardos mínimos. Por estas razones, he elegido la regresión logística.
La regresión logística se usa para predecir la probabilidad de algún evento basándose en los valores del conjunto de variables x1, x2, x3 ... xN,, que también se llaman predictores o regresores. En nuestro caso, las variables son los valores del indicador. Además, es necesario introducir una variable dependiente y, que habitualmente tiene uno de dos valores, 0 o 1. No es difícil de adivinar que puede tratarse de una señal de compra o de venta. Basándose en los valores de los regresores, se calcula la probabilidad de la pertenencia de la variable dependiente a una u otra clase.
Supongamos que la probabilidad del evento y = 1 es igual a: ![]() donde
donde ![]() son vectores de los valores de las variables dependientes 1, x1, x2 ... xN y coeficientes de regresión, respectivamente, y f(z) es una función logística o sigmoidea:
son vectores de los valores de las variables dependientes 1, x1, x2 ... xN y coeficientes de regresión, respectivamente, y f(z) es una función logística o sigmoidea: 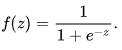 Como resultado, la función de distribución y con x especificada puede escribirse así:
Como resultado, la función de distribución y con x especificada puede escribirse así: ![]()
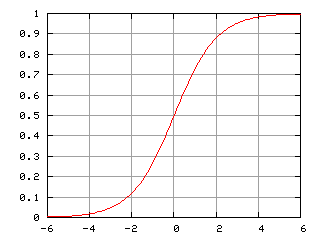
Fig. 4. Curva logística (sigmoidea). Fuente: Wikipedia.
No vamos a describir en detalle el algoritmo de la regresión logística, ya que es ampliamente conocido. Usaremos la clase hecha CLogitModel de la biblioteca Alglib.
Creando la clase del optimizador automático
Escribiremos la clase separada CAuto_optimizer que representará una combinación del Simulador de estrategias virtual simple y la regresión logística:
//+------------------------------------------------------------------+ //|Auto optimizer class | //+------------------------------------------------------------------+ class CAuto_optimizer { private: // Logit regression model ||||||||||||||| CMatrixDouble LRPM; CLogitModel Lmodel; CLogitModelShell Lshell; CMNLReport Lrep; int Linfo; double Lout[]; //|||||||||||||||||||||||||||||||||||||||| int number_of_samples, relearn_timout, relearnCounter; virtual void virtual_optimizer(); double lVector[][2]; int hnd, hnd1; public: CAuto_optimizer(int number_of_sampleS, int relearn_timeouT, double diff_degree, int entropy_window) { this.number_of_samples = number_of_sampleS; this.relearn_timout = relearn_timeouT; relearnCounter = 0; LRPM.Resize(this.number_of_samples, 5); hnd = iCustom(NULL, 0, "fractional entropy", false, diff_degree, 1e-05, number_of_sampleS, entropy_window); hnd1 = iCustom(NULL, 0, "fractional entropy", true, diff_degree, 1e-05, number_of_sampleS, entropy_window); } ~CAuto_optimizer() {}; double getTradeSignal(); };
Aquí, en la sección //Logit regression model// se crea una matriz para los valores x y y, el modelo logístico Lmodel y sus clases auxiliares. Después de entrenar el modelo, el array Lout[] va a recibir las probabilidades de la pertenencia de la señal a una de las clases, 0:1.
El constructor recibe el tamaño de la ventana del aprendizaje number_of_samples, el período pasado el cual el modelo será reoptimizado relearn_timout, y el grado del diferenciación diferenciada para el indicador diff_degree, así como, la ventana para calcular la entropía entropy_window.
Hablaremos sobre el método virtual_optimizer() con más detalle:
//+------------------------------------------------------------------+ //|Virtual tester | //+------------------------------------------------------------------+ CAuto_optimizer::virtual_optimizer(void) { double indarr[], indarr2[]; CopyBuffer(hnd, 0, 1, this.number_of_samples, indarr); CopyBuffer(hnd1, 0, 1, this.number_of_samples, indarr2); ArraySetAsSeries(indarr, true); ArraySetAsSeries(indarr2, true); for(int s=this.number_of_samples-1;s>=0;s--) { LRPM[s].Set(0, indarr[s]); LRPM[s].Set(1, indarr2[s]); LRPM[s].Set(2, s); if(iClose(NULL, 0, s) > iClose(NULL, 0, s+1)) { LRPM[s].Set(3, 0.0); LRPM[s].Set(4, 1.0); } else { LRPM[s].Set(3, 1.0); LRPM[s].Set(4, 0.0); } } CLogit::MNLTrainH(LRPM, LRPM.Size(), 3, 2, Linfo, Lmodel, Lrep); double profit[], out[], prof[1]; ArrayResize(profit,1); ArraySetAsSeries(profit, true); profit[0] = 0.0; int pos = 0, openpr = 0; for(int s=this.number_of_samples-1;s>=0;s--) { double in[3]; in[0] = indarr[s]; in[1] = indarr2[s]; in[2] = s; CLogit::MNLProcess(Lmodel, in, out); if(out[0] > 0.5 && !pos) {pos = 1; openpr = s;}; if(out[0] < 0.5 && !pos) {pos = -1; openpr = s;}; if(out[0] > 0.5 && pos == 1) continue; if(out[0] < 0.5 && pos == -1) continue; if(out[0] > 0.5 && pos == -1) { prof[0] = profit[0] + (iClose(NULL, 0, openpr) - iClose(NULL, 0, s)); ArrayInsert(profit, prof, 0, 0, 1); pos = 0; } if(out[0] < 0.5 && pos == 1) { prof[0] = profit[0] + (iClose(NULL, 0, s) - iClose(NULL, 0, openpr)); ArrayInsert(profit, prof, 0, 0, 1); pos = 0; } } GraphPlot(profit); }
Obviamente, es muy simple y, por eso, es rápido. La primera columna de la matriz LRPM se rellena cíclicamente con valores del indicador y valores de la tendencia lineal (ha sido añadido). En el siguiente ciclo, el precio de cierre actual se compara con el precio anterior para precisar la probabilidad de la transacción (compra o venta). Si el valor actual es más grande que el anterior, entonces, se trataba de una señal de compra, de lo contrario, era de venta. Por tanto, las siguientes columnas se rellenan con valores 0 y 1.
Así, es un Simulador muy simple, que no pretende a una selección óptima de señales, sino las lee en cada barra nueva. El simulador puede ser mejorado a través del método de sobrecarga, lo cual sale fuera de la consideración de este artículo.
Después de eso, se realza el entrenamiento de la regresión logística usando el método MNLTrain(), que recibe la matriz, su tamaño, el número de variables x (nosotros pasamos sólo una variable para cada caso específico), el objeto de la clase Lmodel para guardar el modelo entrenado, y las clases auxiliares.
Después del entrenamiento, el modelo se testea y se visualiza en la ventana del optimizador como gráfico del balance. Eso se hace con fines ilustrativos, para ver cómo el modelo ha sido entrenado en la muestra de aprendizaje, pero no se analiza desde el punto de vista algorítmico.
El optimizador virtual se invoca del siguiente método:
//+------------------------------------------------------------------+ //|Get trade signal | //+------------------------------------------------------------------+ double CAuto_optimizer::getTradeSignal() { if(this.relearnCounter==0) this.virtual_optimizer(); relearnCounter++; if(this.relearnCounter>=this.relearn_timout) this.relearnCounter=0; double in[], in1[]; CopyBuffer(hnd, 0, 0, 1, in); CopyBuffer(hnd1, 0, 0, 1, in1); double inn[3]; inn[0] = in[0]; inn[1] = in1[0]; inn[2] = relearnCounter + this.number_of_samples - 1; CLogit::MNLProcess(Lmodel, inn, Lout); return Lout[0]; }
Él comprueba el número de las barras pasadas desde el último entrenamiento. Si excede el límite especificado en los ajustes, el modelo vuelve a entrenarse. Después de eso, se copia el último valor de los indicadores y unidades de tiempo transcurridas después del último entrenamiento, y se pasa al modelo a través del método MNLProcess() que devuelve la pertinencia a una determinada clase 0:1, lo cual representa una señal comercial.
Creando el EA para comprobar el trabajo de la biblioteca
Ahora, necesitamos conectar la biblioteca al EA y añadir el manejador de señales:
#include <MT4Orders.mqh> #include <Math\Stat\Math.mqh> #include <Trade\AccountInfo.mqh> #include <Auto optimizer.mqh> input int History_depth = 1000; input double FracDiff = 0.5; input int Entropy_window = 50; input int Recalc_period = 100; sinput double MaximumRisk=0.01; sinput double CustomLot=0; input int Stop_loss = 500; //Stop loss, positions protection input int BreakEven = 300; //Break even sinput int OrderMagic=666; static datetime last_time=0; CAuto_optimizer *optimizer = new CAuto_optimizer(History_depth, Recalc_period, FracDiff, Entropy_window); double sig1;
Los ajustes del EA son muy simples e incluyen el tamaño de la ventana History_depth, o sea, el número de los ejemplos de entrenamiento para el optimizador automático. Además, es el grado de diferenciación FracDiff y el número de barras recibidas Recalc_period, después del cual el modelo será reentrenado. Además, hemos añadido el ajuste Entropy_window que permite ajustar la ventana para calcular la entropía.
La última función recibe una señal del modelo entrenado y realiza operaciones comerciales:
void placeOrders(){ if(countOrders(0)!=0 || countOrders(1)!=0) { for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true) { if(OrderType()==0 && sig1 < 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; if(OrderType()==1 && sig1 > 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; } } if(countOrders(0)!=0 || countOrders(1)!=0) return; if(sig1 > 0.5 && (OrderSend(Symbol(),OP_BUY,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN)>0)) { return; } if(sig1 < 0.5 && (OrderSend(Symbol(),OP_SELL,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,INT_MIN)>0)) {} }
Si la probabilidad de la compra es más de 0,5, es la señal de compra y/o la señal para cerrar una posición sell. Y viceversa.
Testeando el EA de optimización automática y conclusiones
Vamos a proceder a lo más interesante, es decir al testeo.
El EA fue iniciado con los hiperparámetros especificados sin optimización genética, es decir, prácticamente, a ojo, usando el par EURUSD, en M15, a base de los precios de apertura.
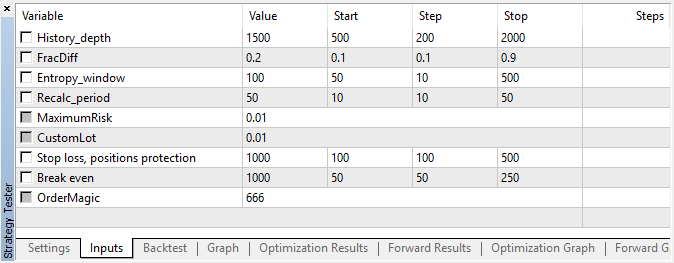
Fig. 5. Ajustes del EA
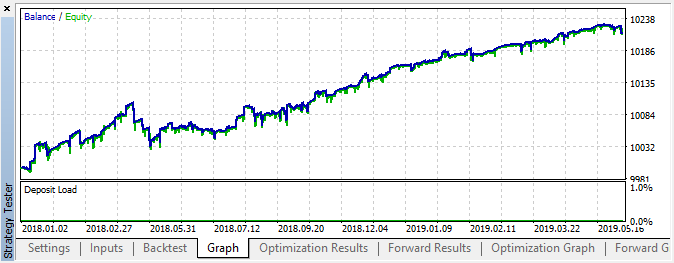
Fig. 6. Resultado del testeo con parámetros especificados
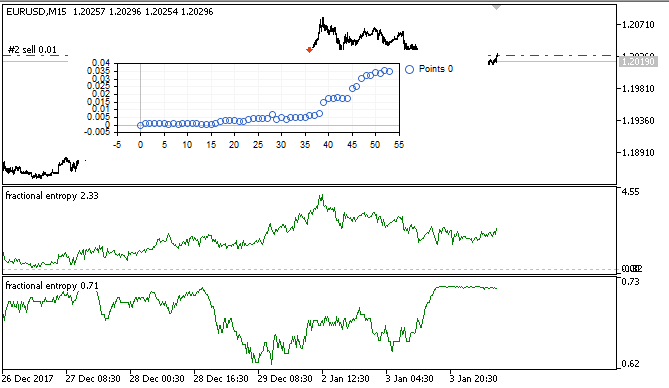
Fig. 7. Visualización de los resultados del Simulador virtual en la muestra de aprendizaje
En este intervalo, la implementación ha mostrado un crecimiento bastante estable. Eso quiere decir que el enfoque puede ser interesante para el futuro análisis.
Como resultado, hemos intentado matar tres pájaros de un tiro:
- hemos entendido la «memoria» de mercado,
- hemos aprendido estimarla en términos de la entropía,
- y desarrollar el EA auto-optimizable.