Neuroredes profundas (Parte III). Selección de ejemplos y reducción de dimensiones
Vladimir Perervenko | 31 octubre, 2017
Contenido
- Introducción
- 1 Selección de ejemplos
- 2. Reducción de las dimensiones
- 2.1. Análisis de los componentes principales (PCA)
- 2.2. Análisis de los componentes independientes (ICA)
- 2.3. Análisis probabilístico de los componentes principales (PPCA)
- 2.4. Autoencoder (PCA no lineal)
- 2.5. PCA no lineal inverso (NLPCA)
- 3. Dividiendo el conjunto en las muestras train/valid/test
- Conclusión
- Anexos
Introducción
Se trata del tercer (y último) artículo que describe la etapa más importante del trabajo con redes neuronales: la preparación de datos. Vamos a analizar dos métodos muy importantes para la preparación de datos: la eliminación de ruidos y la reducción de las dimensiones de las entradas. Ilustraremos la descripción de los métodos con ejemplos detallados y gráficos visuales.
1 Selección de ejemplos
En las tareas de clasificación, se considera como ruido el etiquetado incorrecto de los ejemplos de entrenamiento. Como ya sabemos, se trata de un peculiaridad bastante indeseable de los datos. Para resolver este problema, usaremos el paquete NoiseFilterR, en el que se han implementado en el lenguaje R los filtros clásicos y modernos de interferencias de ruido.
En los últimos años, el Data Mining (análisis de datos) topa con problemas más y más complejos desde el punto de vista del carácter de los datos disponibles. Esto se relaciona no solo con el volumen de los datos, sino también con su carácter imperfecto y con la diversidad de su forma, que suponen para los investigadores multitud de diferentes escenarios. Por consiguiente, el procesamiento preliminar de datos se ha convertido en una parte importante del proceso de KDD (Knowledge Discovery from Databases). A su vez, el desarrollo del software relacionado con el procesamiento preliminar de datos ofrece herramientas suficientes para el trabajo.
El procesamiento preliminar de los datos es un proceso necesario para que los consecuentes algoritmos de aprendizaje puedan extraer de la muestra el máximo de información. Este es uno de los pasos más laboriosos de todo el preceso de KDD. El procesamiento preliminar de los datos se divide en varias subtareas: por ejemplo, la selección de los predictores o la eliminación de los datos ausentes o los datos de ruido. La selección de los predictores busca extraer los atributos más importantes para la etapa del entrenamiento, lo que reduce la complejidad de los modelos y el tiempo de los cálculos. El procesamiento de los datos ausentes es necesario para guardar la mayor cantidad de datos posible. Y finalmente, los datos de ruido son, o bien incorrectos, o bien se salen enormemente de la distribución general del valor.
Para resolver estas tareas, ya tenemos software disponible. Por ejemplo, la herramienta KEEL (RKEEL) contiene un amplio conjunto de algoritmos para el procesamiento preliminar de datos, que abarca todos los temas mencionados anteriormente. También existen otras soluciones populares: tales como WEKA (RWEKA) o RapidMiner para seleccionar los predictores. Aparte de estos, tenemos una serie de complejos programáticos universales de Data Mining, tales como R, KNIME o Python.
En lo que respecta al software estadístico R, en el Repositorio de la voluminosa red de archivos (CRAN) hay multitud de paquetes para solucionar las tareas de procesamiento preliminar.
En los conjuntos de datos reales, normalmente existen imperfecciones y ruidos. Este ruido influye de forma negativa en el proceso de entrenamiento de los clasificadores, lo que, a su vez, reduce la precisión de los pronósticos, complica el modelo y aumenta el tiempo de los cálculos.
En la literatura especializada sobre clasificación, normalmente se destacan dos tipos diferentes de ruido: el ruido de los atributos y el ruido del etiquetado (se trata del ruido de la clase). El primero se relaciona con imperfecciones en los atributos de los conjuntos de datos de entrenamiento, el segundo, con errores en los métodos de clasificación. En el paquete NoiseFiltersR se presta atención principalmente al ruido de etiquetado, el más perjudicial, puesto que la calidad del etiquetado tiene mucha importancia para el entrenamiento de los clasificadores.
Se describen los dos enfoques principales para la solución del problema del ruido de etiquetado. Podrá familiarizarse con ellos en el reciente trabajo de Benoit Frenay y Michel Verleysen.
- Por una parte, este es un enfoque sobre el nivel del algoritmo, en el que el problema se soluciona mediante la creación de un algoritmo de clasificación fiable, en el que la presencia del ruido se refleja débilmente. Cada algoritmo, además, será una solución específica y no universal.
- Por otro lado, el enfoque del nivel de los datos (filtros), es un intento de desarrollar estrategias para limpiar el conjunto de datos, que se realizará antes del entrenamiento. El paquete NoiseFiltersR se ajusta al segundo enfoque, puesto que permite procesar de forma preliminar los datos solo una vez, y después cambiar los clasificadores para el procesamiento cuantas veces sea necesario.
De entre los clasificadores resistentes al ruido, podemos mencionar С4.5, J48 y Jrip (WEKA).
Vamos a realizar un experimento. Tomaremos tres conjuntos de datos: DT (un conjunto de datos brutos antes del procesamiento), DTn (solo un conjunto de datos brutos normalizados), DTTanh.n (sin valores atípicos, con datos transformados en tangente hiperbólica y normalizados) y, por supuesto, solo train. Los procesamos con la función ORBoostFilter(), que constituye un filtro para eliminar los valores atípicos. Veamos cómo ha cambiado la distribución después de este procesamiento.
evalq({
#-----DT---------------------
out11 <- ORBoostFilter(Class~., data = DT$train, N = 10, useDecisionStump = TRUE)
DT$train_clean1 <- out11$cleanData
#----------DTTanh.n------------------------
out1 <- ORBoostFilter(Class~., data = DTTanh.n$train, N = 10, useDecisionStump = TRUE)
DTTanh.n$train_clean1 <- out1$cleanData
#-----------DTn--------------------------------
out12 <- ORBoostFilter(Class~., data = DTn$train, N = 10, useDecisionStump = TRUE)
DTn$train_clean1 <- out12$cleanData
},
env)
#---Ris1-----------------
require(funModeling)
evalq({
par(mfrow = c(1,3))
par(las = 1)
boxplot(DT$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DT$train_clean1")
boxplot(DTn$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DTn$train_clean1")
boxplot(DTTanh.n$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DTTanh.n$train_clean1")
par(mfrow = c(1,1))
}, env)
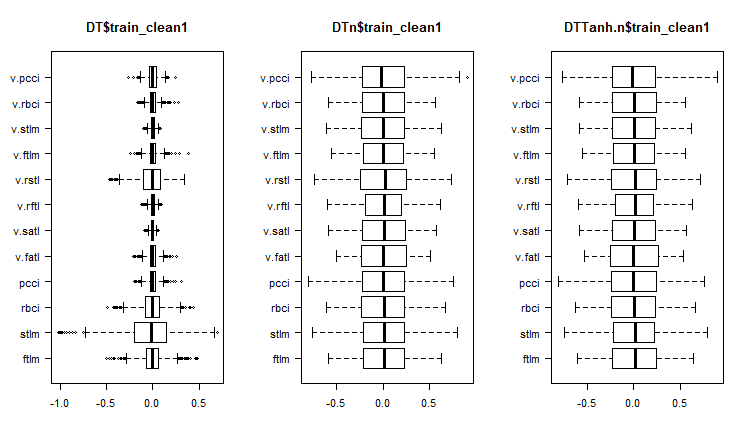
Fig. 1 Distribución de los predictores en los conjuntos tras eliminar los ejemplos de ruido
Vamos a ver la variación y la covariación de los predictores en estos conjuntos:
#----Ris2------------------ require(GGally) evalq(ggpairs(DT$train_clean1 %>% select(-Data), columns = c(1:6, 13), mapping = aes(color = Class), title = "DT$train_clean1/1"), env)
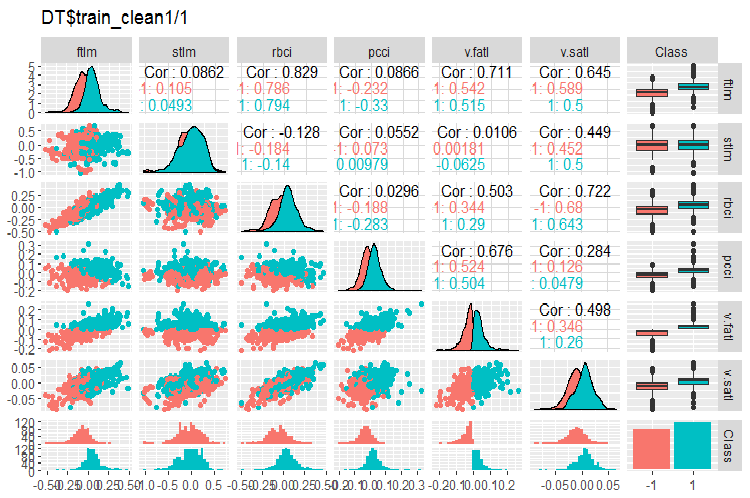
Fig. 2. Variación y covariación en el conjunto DT$train_clean1/1 tras eliminar los ejemplos de ruido
#-----Ris3--- evalq(ggpairs(DT$train_clean1 %>% select(-Data), columns = 7:13, mapping = aes(color = Class), title = "DT$train_clean1/2"), env)
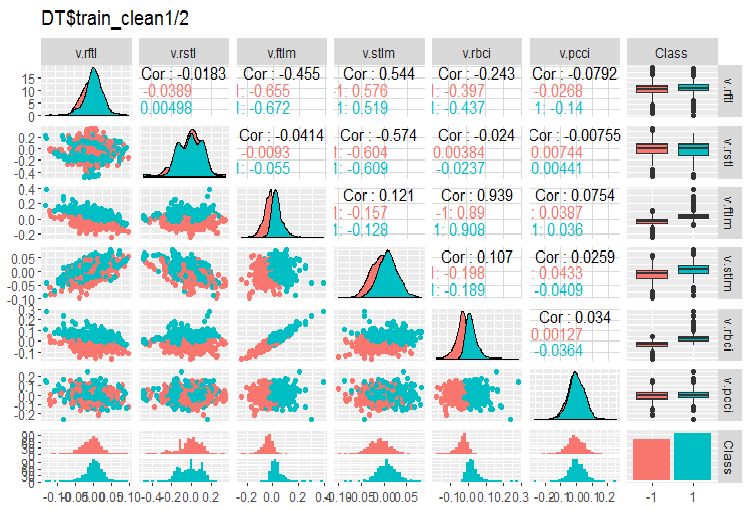
Fig. 3. Variación y covariación en el conjunto DT$train_clean1/2 tras eliminar los ejemplos de ruido
¿Cuántos eejmplos se han eliminado de DT$train?
> env$out11$remIdx %>% length()
[1] 658
Cerca del 30%. Tenemos dos opciones para continuar. La primera es eliminar las muestras de ruido del conjunto de entrenamiento y transmitir sus modelos para el entrenamiento. La segunda reorganizarlos con una nueva etiqueta de clase y entrenar el modelo con el conjunto train completo, pero con un nivel de objetivo adicional. Teniendo tanas muestras de ruido, la segunda variante podría ser preferible. Pero debemos comprobarlo con un experimento.
¿Qué vemos en los gráficos de distribución de las variables sin ruidos?
- Una división muy clara de la distribución de los predictores según la variable objetivo. Seguramente esto aumentará de forma significativa la precisón del modelo entrenado.
- Se han eliminado prácticamente todos los valores atípicos.
De la misma forma limpiaremos con el filtro los conjuntos DTn$train DTTanh.n$train. Aquí también podemos observar con sorpresa que hay casi tantas variables con ruido como en el primer caso.
c(env$out1$remIdx %>% length(), env$out12$remIdx %>% length())
[1] 652 653
Es decir, ¿ninguna transformación es capaz de hacer útiles las muestras de ruido? Esto es interesante.
Vamos a echar un vistazo a la variación y la covariación del conjunto DTTanh.n$train después de eliminar las variables de ruido.
#----Ris4----------------------- evalq(ggpairs(DTTanh.n$train_clean1, columns = 1:13, mapping = aes(color = Class), upper = "blank", title = "DTTanh.n$train_clean_all"), env)
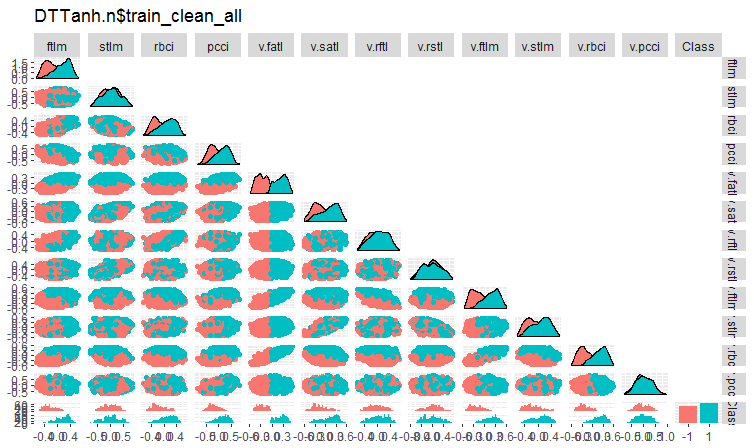
Fig. 4. Variación y covariación en el conjunto DTTanh.n$train_clean tras eliminar los ejemplos de ruido
Es muy interesante la covariación de todas las variables con la variable v.fatl. Visualmente, podemos definir de forma preliminar los predictores irrelevantes para la variable objetivo: se trata de stlm, v.rftl, v.rstl, v.pcci. A continuación, examinaremos este supuesto con otros métodos, y en otro conjunto.
El mismo gráfico para DTn$train_clean1:
#-------ris5---------- require(GGally) evalq(ggpairs(DTn$train_clean1 %>% select(-Data), columns = 1:13, mapping = aes(color = Class), upper = "blank", title = "DTn$train_clean1_all"), env)
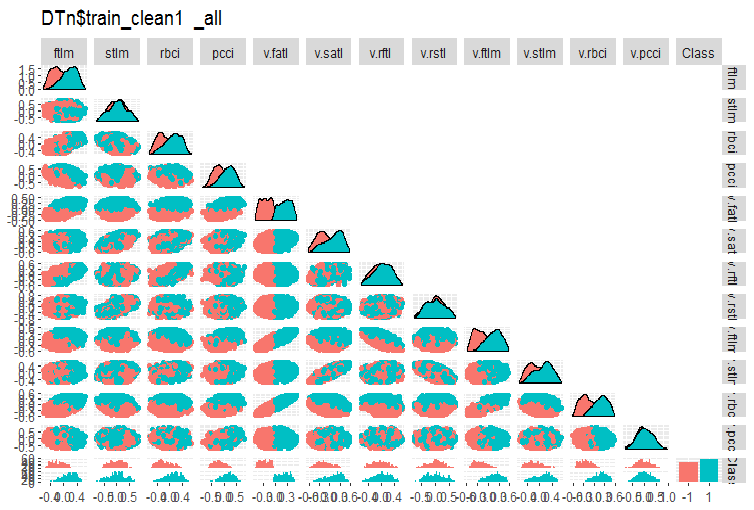
Fig. 5. Variación y covariación en el conjunto DTn$train_clean tras eliminar los ejemplos de ruido
Aquí podemos ver que la variación de los mismos predictores (stlm, v.rftl, v.rstl, v.pcci) no se divide conforme a los niveles de la variable objetivo. Depende del propio desarrollador decidir qué hacer con las variables de ruido, en función de los experimentos realizado con el entrenamiento de un modelo concreto.
Ahora vamos a ver cómo ha cambiado la importancia de los predictores en los conjutos después de eliminar las muestras de ruido.
#--------Ris6--------------------------- require(smbinning) par(mfrow = c(1,3)) evalq({ df <- renamepr(DT$train_clean1) %>% targ.int sumivt.dt = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.dt, cex = 0.8) rm(df) }, env) evalq({ df <- renamepr(DTTanh.n$train_clean1) %>% targ.int sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.8) rm(df) }, env) evalq({ df <- renamepr(DTn$train_clean1) %>% targ.int sumivt.dtn = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.dtn, cex = 0.8) rm(df) }, env) par(mfrow = c(1, 1))
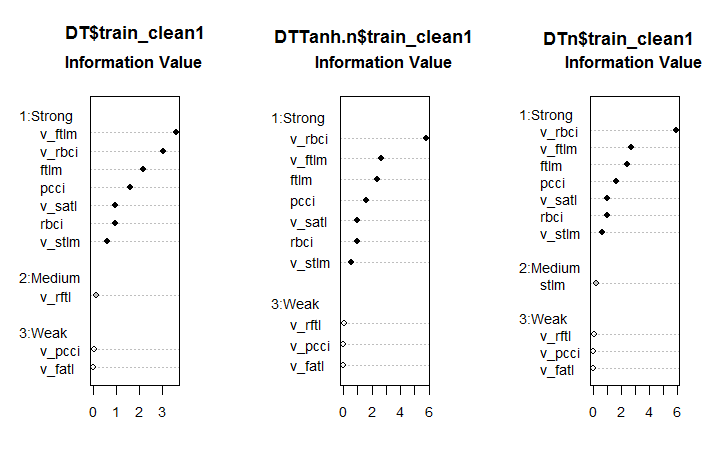
Fig. 6. Importancia de los predictores en los tres conjuntos
Hablando francamente, el resultado es inesperado. ¡La variable v.fatl es la más débil entre las débiles!
Siete predictores fuertes son iguales en todos los conjuntos. En el primero y el tercero aparece un indicador de fuerza media. Las variables (stlm, v.rftl, v.rstl, v.pcci), que habían sido definidas preliminarmente como irrelevantes, se confirman como tales con este cálculo. Todos esos cálculos deben ser comprobados usando experimentos con un modelo concreto.
En el paquete NoiseFilterR hay más de una decena de otros filtros para definir las muestras de ruido. ¡Experimente!
2. Reducción de las dimensiones
La disminución de las dimensiones constituye la transformación de los datos fuente de grandes dimensiones en una nueva representación de menores dimensiones que contenga la información principal. De una manera ideal, las dimensiones de la representacón transformada se corresponden con las dimensiones de los datos. Las dimesniones internas de los datos suponen el número mínimo de variables imprescindible para expresar todas las propiedades posibles de los datos. Tradicionalmente, para reducir las dimensiones se usan algoritmos tales como Principal Component Analisys (PCA), Independent Component Analisys (ICA), Singular Value Decomposition (SVD) y otros.
La reducción de las dimensiones ayuda a suavizar la influencia tanto de la así llamada maldición de la dimensionalidad, como de otras propiedades indeseables de los espacios de grandes dimensiones. En la tarea de descripción de los datos, esta persigue el siguiente objetivo.
- Reducir los gastos computacionales a la hora de procesar los datos
- Luchar contra el sobreentrenamiento. Cuanto menor sea el número de signos, menor será la necesidad de objetos que para restaurar las dependencias ocultas en los datos, y mayor será la calidad de la restauración de semejantes dependencias
- Compresión de datos para un almacenamiento de información más efectivo. En este caso, aparte de la transformación X → T, necesitaremos también la posibilidad de realizar la transformación opuesta T → X
- Visualización de datos. Proyectar una muestra en un espacio bi/tridimensional permite representar dicha muestra gráficamente
- Extracción de nuevos recursos. Los nuevos recursos obtenidos como resultado de la transformación X → T puede contribuir significativamente a la posterior solución de las tareas de reconocimiento (por ejemplo, como el método de los componenters principales)
Notemos que todos los métodos de reducción de las dimensiones descritos someramente a continuación se relacionan con la clase de métodos de entrenamiento no supervisado, es decir, en calidad de información original actúa solo la descripción de los recursos de los objetos X (predictores).
2.1. PCA, Análisis de componentes principales
El Análisis de componentes principales (Principal Component Analysis, PCA) es un método sencillísimo de reducción de las dimensiones de los datos. Sus ideas se expusieron ya en el siglo XIX. La idea del método consiste en encontrar un hiperplano de dimensiones definidas en el espacio original y proyectar la muestra en este hiperplano. En este caso, además, se elegirá el hiperplano con un error de proyección de datos mínimo, en el sentido de la suma de los cuadrados de las desviaciones.
Las dimensiones del espacio reducido d pueden ser establecidas por el usuario preliminarmente. Este valor es fácil de elegir si nuestra tarea es visualizar los datos (d = 2 o d = 3) o colocar la muestra en un volumen de memoria determinado. Sin embargo, en muchos otros casos, la selección de d no resulta obvia a partir de supuestos apriorísticos.
Existe un sencillo método eurístico de selección de la magnitud d para el método de componentes principales. Una de las peculiaridades del método de componentes principales es que todos los espacios reducidos para d = 1, 2, . . . están insertados unos en otros. Bien, calculando una vez todos los vectores propios y los propios valores de la matriz de covariación, obtenemos el espacio reducido para cualquier valor d. Por eso, para seleccionar el valor d, podemos representar en el gráfico nuestros propios valores en orden descendente y elegir el umbral de descarte, de tal forma que solo queden los valores que difieran apenas de cero. El otro método presupone la selección del umbral de tal forma que quede a la derecha un porcentaje determinado de la superficie total bajo la curva (por ejemplo, un 5% o un 1%).
Hablando en términos sencillos, el PCA se puede considerar como la supresión preliminar de los predictores de ruido en el caso de que sean numerosos (>50).
2.2. ICA, Análisis de Componentes Independientes
El Análisis de Componentes Independientes, a diferencia del PCA, es un objeto de estudio bastante reciente, pero que ha adquirido rápidamente popularidad en las diferentes esferas de investigación de datos.
El método de componentes independientes se ha difundido ampliamente al procesar las señales. Esta técnica intenta transformar de manera lineal los datos iniciales en nuevos componentes, que serán independientes al máximo los unos de los otros en el sentido estadístico. Los componentes independientes no son obligatoriamente ortogonales los unos con respecto a los otros, pero su independencia estadística es una regla aún más rigurosa que la ausencia de correlación estadística usada en PCA.
Los métodos PCA e ICA se han implementado en el paquete caret de la función preProcess(), en la que se puede indicar o bien un número concreto de componentes principales, o bien un porcentaje cumulativo de dispersión abarcado por PCA. Se ejecuta en dos etapas: primero en la muestra train se calculan los parámetros necesarios, y a continuación, usando predict(), ejecutan la transformación de las muestras train/val/test y todos los datos nuevos que lleguen después.
Recuadro 1. Características comparativas de PCA e ICA
| Método | Ventajas | Defectos | Particularidades | Resultado obtenido en general | Método de cálculo de los nuevos componentes principales |
|---|---|---|---|---|---|
| PCA | Sencillez de ejecución de los cálculos |
| Ausencia de unicidad de la solución (incerteza rotacional. Con cada cálculo nuevo basado en un conjunto de entrenamiento, obtendremos diferentes componentes principales. |
| Tnew = Xnew * P |
| ICA | Sencillez de ejecución de los cálculos |
| Si se da una gran diferencia entre las dimensiones del conjunto y los componentes independientes, aplican de forma secuencial PCA -> ICA. |
| Snew =scale( Xnew )* W * K |
Vamos a hacer un pequeño experimento. Cargamos en Rstudio la captura de los resultados de los scripts de la primera parte del artículo Part_1.Rda. Vamos a recordar el contenido del entorno env:
> ls(env) [1] "cap1" "cap2" "Close" "Data" "dataSet" [6] "dataSetCap" "dataSetClean" "dataSetOut" "High" "i" [11] "k" "k.cap" "k.out" "lof.x" "lof.x.cap" [16] "Low" "lower" "med" "Open" "out.ftlm" [21] "out.ftlm1" "pr" "pre.outl" "preProClean" "Rlof.x" [26] "Rlof.x.cap" "sk" "sk.cap" "sk.out" "test" [31] "test.out" "train" "train.out" "upper" "Volume" [36] "x" "x.cap" "x.out"Tomamos la muestra x.cap con valore atípicos imputdos y calculamos sus componentes principlaes e independientes con la ayuda de la función preProcess::caret. Para PCA e ICA indicamos explícitamente el número de componentes. Para ICA no vamos a indicar el método de normalización.
require(caret)
evalq({
prePCA <- preProcess(x.cap,
pcaComp = 5,
method = Hmisc::Cs(center, scale, pca))
preICA <- preProcess(x.cap,
n.comp = 3,
method = "ica")
}, env)
Vamos a echar un vistazo a los parámetros de transformación:> str(env$prePCA) List of 20 $ dim : int [1:2] 7906 11 $ bc : NULL $ yj : NULL $ et : NULL $ invHyperbolicSine: NULL $ mean : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ std : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ ranges : NULL $ rotation : num [1:11, 1:5] -0.428 -0.091 -0.437 -0.107 -0.32 ... ..- attr(*, "dimnames")=List of 2 .. ..$ : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ... $ method :List of 4 ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ pca : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ ignore: chr(0) $ thresh : num 0.95 $ pcaComp : num 5 $ numComp : num 5 $ ica : NULL $ wildcards :List of 2 ..$ PCA: chr(0) ..$ ICA: chr(0) $ k : num 5 $ knnSummary :function (x, ...) $ bagImp : NULL $ median : NULL $ data : NULL - attr(*, "class")= chr "preProcess"
Nos interesan tres espacios: prePCA$mean y prePCA$std (parámetros de normalización) y prePCA$rotation (matriz de rotación y cargas).
> str(env$preICA) List of 20 $ dim : int [1:2] 7906 11 $ bc : NULL $ yj : NULL $ et : NULL $ invHyperbolicSine: NULL $ mean : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ std : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ ranges : NULL $ rotation : NULL $ method :List of 4 ..$ ica : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ ignore: chr(0) $ thresh : num 0.95 $ pcaComp : NULL $ numComp : NULL $ ica :List of 3 ..$ row.norm: logi FALSE ..$ K : num [1:11, 1:3] -0.214 -0.0455 -0.2185 -0.0534 -0.1604 ... ..$ W : num [1:3, 1:3] -0.587 0.77 -0.25 -0.734 -0.636 ... $ wildcards :List of 2 ..$ PCA: chr(0) ..$ ICA: chr(0) $ k : num 5 $ knnSummary :function (x, ...) $ bagImp : NULL $ median : NULL $ data : NULL - attr(*, "class")= chr "preProcess"Aquí tenemos los mismos $mean y $std y las dos matrices $K y $W. El paquete caret para calcular ICA, a su vez, usa el paquete fastICA, cuyo algoritmo es el siguiente:
- la matriz original se centra (es posible normalizar las líneas), obtenemos la matriz Х
- después la matriz Х se proyecta en la dirección de los componentes principales, obtenemos PCA = X * K
- después de ello, multiplicando PCA por la matriz unmixing, obtenemos los componentes independientes ICA = X * K * W
Calculamos PCA e ICA de las dos formas, usando la función predict::caret y los parámetros obtenidos con la función preProcess.
require(magrittr)
evalq({
pca <- predict(prePCA, x.cap)
ica <- predict(preICA, x.cap)
pca1 <- ((x.cap %>% scale(prePCA$mean, prePCA$std)) %*%
prePCA$rotation)
ica1 <- ((x.cap %>% scale(preICA$mean, preICA$std)) %*%
preICA$ica$K) %*% preICA$ica$W
colnames(ica1) <- colnames(ica1, do.NULL = FALSE, prefix = 'ICA')
},env)
evalq(all_equal(pca, pca1), env)
# [1] TRUE
evalq(all_equal(ica, ica1), env)
# [1] TRUE
El resultado es idéntico, lo cual resulta comprensible.
Un método más fiable de cálculo de PCA es el uso del paquete pcaPP, que define los componentes principales con mayor precisión.
El paquete fastICA contiene muchas posibilidades y parámetros adicionales para que el cálculo de los componentes principales resulte más flexible y completo. Nosotros recomendamos usar este paquete, y no la función en caret.
2.3 Análisis probabilístico de los componentes principales (PPCA)
Para el método de los componentes principales se puede formular un modelo de probabilidad (probabilistic PCA, PPCA). La reformulación del método en términos probabilísticos da una serie de ventajas.
- La posibilidad de usar un algoritmo ЕМ para buscar la solución. Para el algoritmo PCA ЕМ resulta más efectivo en cuanto al cálculo el procedimiento en las situaciones cuando d ≪ D
- Corregir correctamente los valores ausentes. Simplemente son añadidos a la lista de variables ocultas del modelo de probabilidad, para el cual se aplica después el algoritmo EM existente
- La posibilidad de pasar al modelo mixto de distribuciones probabilísticas, que amplía significativamente la esfera de aplicación del método
- La posibilidad de usar el así llamado enfoque bayesiano para solucionar las tareas de selección de modelos. En particular, aquí podemos construir (de una forma teóricamente fundamentada) un esquema de selección de las dimensiones del espacio reducido d (mírese [24, 25])
- La posibilidad de generar nuevos objetos del modelo probabilístico
- Para las tareas de clasificación: la posibilidad de modelar la distribución de clases aparte de los objetos para su posterior uso en los esquemas de clasificación
- El valor de la función de verosimilitud, un criterio universal que permite comparar los diferentes modelos probabilísticos entre sí. En particular, con la ayuda del valor de verosimilitud se pueden determinar con sencillez los valores atípicos en los datos.
Como sucede con el modelo PCA clásico, el modelo probabilístico de PCA es invariante con respecto a la elección de la base en el hiperplano.
A diferencia del modelo PCA clásico, en el que se restaura solo el hiperplano que mejor explica los datos, el modelo probabilístico restaura todo el modelo de variabilidad de los datos. En particular, describe la dispersión de los datos en todas direcciones. Por lo tanto, la solución incluye no solo los vectores de base de dirección, indicados por los propios vectores de la matriz de covariación, sino también las longitudes de estos vectores de base.
Para usar РРСА y otros métodos no lineales de obtención de los componentes principales, se puede usar el paquete pcaMethods.
El paquete pcaMethods ofrece un conjunto de diversas implementaciones de PCA, así como herramientas para la comprobación cruzada y la visualización de resultados. Los métodos en general permiten aplicar PCA a los datos incompletos, y eso significa que se los puede usar para valorar los valores ausentes (NA). El paquete se encuentra en el repositorio Bioconductor y se instala así:
source("https://bioconductor.org/biocLite.R") biocLite("pcaMethods") library(pcaMethods)
Todos los métodos del paquete retornan la clase general pcaRes, que contiene el resultado. Esto garantiza la máxima flexibilidad para el usuario. La función de envoltorio pca() proporciona acceso a todos los tipos deseados de РСА a través del argumento de denominación. Lista de algoritmos con una breve descripción:
- svdPCA — función de envoltorio para la función estándar prcomp.
- svdImpute — implementación del algoritmo para la imputación de NA. Tolera un gran número de NA (>10%).
- Probabilistic PCA (ppca) — PPCA es tolerante a un número de NA entre 10% y 15%.
- Bayesian PCA (bpca) — semejante al PCA probabilístico, usa un enfoque con EM junto con un modelo bayesiano para calcular la probabilidad de restauración del valor. El algoritmo es tolerante con respecto a un gran número de datos ausentes (> 10%). Las cuentas y las cargas obtenidas con este método se diferencian un poco de las obtenidas con la ayuda de РСА. Esto se relaciona con el hecho de que BPCA se ha desarrollado especialmente para la valoración de valores ausentes y se basa en la estructura bayesiana de variación (VBF) con definición automática de la relevancia (ARD). El argumento no fuerza la ortogonalidad entre cargas. Los que es más, los autores del documento BPCA detectaron que la activación del criterio de ortogonalidad empeoraba el pronóstico.
- Inverse non-linear PCA (NLPCA) es especialmente adecuado para los datos de los experimentos en los que la relación entre los predictores y la variable objetivo no es lineal. NLPCA se basa en el entrenamiento de la parte decodificadora de la red neuronal autoasociativa (autoencoder). Las cargas se pueden ver en la capa oculta de la neurored. Los valores ausentes en los datos de aprendizaje simplemente se ignoran al calcular el error durante la propagación inversa. De esta forma, NLPCA puede usarse para procesar los valores ausentes de la misma forma que para el РСА normal. La única diferencia es que las cargas P se presentan ahora como red neuronal. Más abajo analizaremos aparte con más detalle esta variante de reducción de las dimensiones en el apartado "Autoencoder".
- Nipals PCA — es una valoración lineal por mínimos cuadrados parciales iterativos. Este algoritmo está en la raíz de la regresión de PLS, que puede ejecutar PCA con los valores ausentes, simplemente dejándolos fuera de los respectivos productos internos. Es resistente a cantidades altas (como norma, no superiores al 5%) de datos ausentes.
- Local least squares (LLS) imputation — es un algoritmo/función llsImpute() para valorar los valores ausentes, basado en la combinación lineal de los k vecinos más cercanos de una variable incompleta. La distancia entre variables se define como el valor absoluto de los coeficientes de correlación de Pearson, Spearman o Kendall. La combinación lineal se encuentra mediante la solución de la tarea local de localización de los mínimos cuadrados.
En la implementación actual se presentan dos métodos un tanto diferentes de valoración de los valores ausentes. El primero implica la limitación de la búsqueda de vecinos en el subconjunto de variables completas. Este método es preferible cuando hay relativamente pocas variables indefinidas. En el segundo método, como candidatos se contemplan todas las variables. Aquí los valores ausentes son inicialmente sustituidos por el valor medio de las columnas. A continuación, el método realiza la iteración usando la valoración actual como entrada para la regresión LLS hasta que los cambios entre la nueva valoración y la antigua caigan por debajo de umbral determinado (0,001).
Por desgracia, el tema del artículo y su volumen no nos permiten deternernos con detalle en todos los algoritmos propuestos por este magnífico paquete. Solo vamos a analizar NLPCA en comparación con el autoencoder de más abajo.
2.4. Autoencoder
Las redes autoasociativas se han aplicado ampliamente desde que comenzaron a usarse las redes neuronales. En uno de mis artículos anteriores ya analizamos con detalle la estructura y las peculiaridades del entrenamiento de los autoencoders (АЕ), los autoencoders complejos (Stacked AE), la máquina restringida de Boltzmann (RBM), etcétera.
Recordemos que el autoencoder es una neurored con una o varias capas ocultas cuyo número de neuronas en la capa de entrada es igual al número de neuronas de la capa de salida. La principal tarea del АЕ es reproducir los datos de entrada con la mayor precisión posible. Para entrenar el АЕ se usan los mismos métodos de entrenamiento, regularización y activación de neuronas usados para las neuroredes normales. Es posible construir un modelo de АЕ usando cualquier paquete de construcción de NN que permita extraer la matriz de pesos de las capas ocultas. Vamos a utilizar el paquete autoencoder. Como ejemplo, recordaremos las posibles estructuras del АЕ:
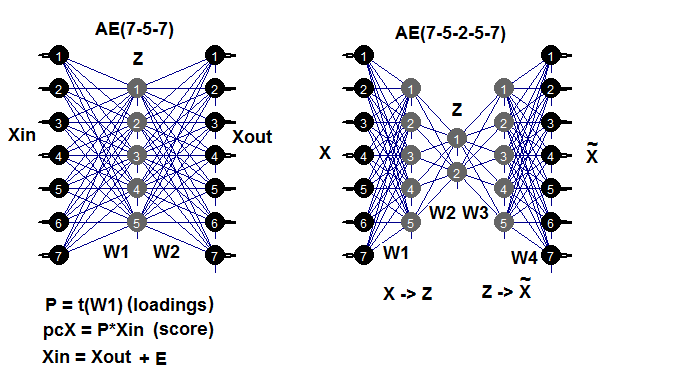
Fig. 7. Esquema estructural de los autoencoders (de tres y cinco capas)
La matriz de pesos W1 entre la primera capa (de entrada) y la capa oculta es precisamente la obtenida tras el entrenamiento de la carga. Después de proyectar (multiplicación) la matriz de entrada Xin en la carga Р obtenemos la matriz reducida (propiamente, los componentes principales. Obtendremos el mismo resultado usando predict(). Esta función permite recibir la salida o bien de la capa oculta (con hidden.output = TRUE), o bien de la capa de salida del autoencoder (con hidden.output = FALSE).
Después de entrenar el AE, podemos extraer del modelo la matriz de pesos W1 y el error de recuperación al realizar el entrenamiento. Si hemos proporcionado también el conjunto de prueba, podremos obtener del modelo el error de prueba. El error de entrenamiento depende de los parámetros del АЕ y (en mucha medida) de la proporción n.hidden/n.in. Cuanto menor sea, mayor será el error de recuperación. Si nuestra misión es lograr una gran reducción de las dimensiones, podemos conectar dos АЕ de forma consecutiva. Por ejemplo, con 12 entradas podremos entrenar el modelo 12-7-12, ejecutar predict() de la capa oculta e insertarla en un autoencoder 7-3-7. Obtendremos la reducción 12 -> 3. ¡Experimente!
Destacaremos aparte que, aunque en el paquete se anuncia la posibilidad de crear y entrenar un AE multicapa, no lo hemos conseguido.
Vamos a realizar un experimento. Usted ya ha cargado Part_1.RData con los resultados del cálculo de la primera parte del artículo. Secuencia del cálculo (brevemente):
- a partir de la muestra dataSet, creamos la muestra train/val/test, obtenemos la lista DT;
- imputamos los valores atípicos, obtenemos la lista DTcap;
- normalizamos nuestras muestras sucesivamente usando los métodos con("center", "scale", "spatialSign"). Usted puede usar las otras variantes de transformación y normalización que ya hemos analizado antes;
- entrenamos el modelo de autoencoder con tres neuronas en la capa oculta. Usted puede investigar otras variantes. Aumentando el número de neuronas ocultas, se reduce el error de recuperación;
- usando el modelo entrenado y predict(), obtenemos el resultado de la capa oculta. Se trata, en esencia, de una matriz reducida (РСА). Le añadimos una variable objetivo;
- construimos los gráficos de variación y covariación de las muestras reducidas train/val/test/.
require(FCNN4R)
require(deepnet)
require(darch)
require(tidyverse)
require(magrittr)
#----Clean---------------------
require(caret)
require(pipeR)
evalq(
{
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
dataSet %>%
preProcess(., method = c("zv", "nzv", "conditionalX")) %>%
predict(., dataSet) %>%
na.omit -> dataSetClean
list(train = dataSetClean[train, ],
val = dataSetClean[val, ],
test = dataSetClean[test, ]) -> DT
rm(dataSetClean, train, val, test)
},
env)
#------outlier-------------
require(foreach)
evalq({
DTcap <- list()
foreach(i = 1:3) %do% {
DT[[i]] %>%
select(-c(Data, Class)) %>%
as.data.frame() -> x
if (i == 1) {
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
prep.outlier(x[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
}
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = x[ ,i], impute = T, fill = T,
lower = lower, upper = upper,
med = med, cap1 = cap1, cap2 = cap2)
} %>% as.data.frame() -> x.cap
colnames(x.cap) <- colnames(x)
return(x.cap)
} -> DTcap
foreach(i = 1:3) %do% {
cbind(DTcap[[i]], Class = DT[[i]]$Class)
} -> DTcap
DTcap$train <- DTcap[[1]]
DTcap$val <- DTcap[[2]]
DTcap$test <- DTcap[[3]]
rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
#------normalize-----------
evalq(
{
method <- c("center", "scale", "spatialSign") #, "expoTrans") #"YeoJohnson",
# "spatialSign"
preProcess(DTcap$train, method = method) -> preproc
list(train = predict(preproc, DTcap$train),
val = predict(preproc, DTcap$val),
test = predict(preproc, DTcap$test)
) -> DTcap.n
#foreach(i = 1:3) %do% {
# cbind(DTcap.n[[i]], Class = DT[[i]]$Class)
#} -> DTcap.n
},
env)
#----train-------
require(autoencoder)
evalq({
train <- DTcap.n$train %>% select(-Class) %>% as.matrix()
val <- DTcap.n$val %>% select(-Class) %>% as.matrix()
test <- DTcap.n$test %>% select(-Class) %>% as.matrix()
## Set up the autoencoder architecture:
nl = 3 ## number of layers (default is 3: input, hidden, output)
unit.type = "tanh" ## specify the network unit type, i.e., the unit's
## activation function ("logistic" or "tanh")
N.input = ncol(train) ## number of units (neurons) in the input layer (one unit per pixel)
N.hidden = 3 ## number of units in the hidden layer
lambda = 0.0002 ## weight decay parameter
beta = 0 ## weight of sparsity penalty term
rho = 0.01 ## desired sparsity parameter
epsilon <- 0.001 ## a small parameter for initialization of weights
## as small gaussian random numbers sampled from N(0,epsilon^2)
max.iterations = 3000 ## number of iterations in optimizer
## Train the autoencoder on training.matrix using BFGS
##optimization method
AE_13 <- autoencode(X.train = train, X.test = val,
nl = nl, N.hidden = N.hidden,
unit.type = unit.type,
lambda = lambda,
beta = beta,
rho = rho,
epsilon = epsilon,
optim.method = "BFGS", #"BFGS", "L-BFGS-B", "CG"
max.iterations = max.iterations,
rescale.flag = FALSE,
rescaling.offset = 0.001)}, env)
## Report mean squared error for training and test sets:
#cat("autoencode(): mean squared error for training set: ",
# round(env$AE_13$mean.error.training.set,3),"\n")
## Extract weights W and biases b from autoencoder.object:
#evalq(P <- AE_13$W, env)
#-----predict-----------
evalq({
#Train <- predict(AE_13, X.input = train, hidden.output = FALSE)
pcTrain <- predict(AE_13, X.input = train, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$train$Class)
#Val <- predict(AE_13, X.input = val, hidden.output = FALSE)
pcVal <- predict(AE_13, X.input = val, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$val$Class)
#Test <- predict(AE_13, X.input = test, hidden.output = FALSE)
pcTest <- predict(AE_13, X.input = test, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$test$Class)
}, env)
#-----graph---------------
require(GGally)
evalq({
ggpairs(pcTrain,columns = 1:ncol(pcTrain),
mapping = aes(color = Class),
title = "pcTrain")},
env)
evalq({
ggpairs(pcVal,columns = 1:ncol(pcVal),
mapping = aes(color = Class),
title = "pcVal")},
env)
evalq({
ggpairs(pcTest,columns = 1:ncol(pcTest),
mapping = aes(color = Class),
title = "pcTest")},
env)
Veamos los gráficos
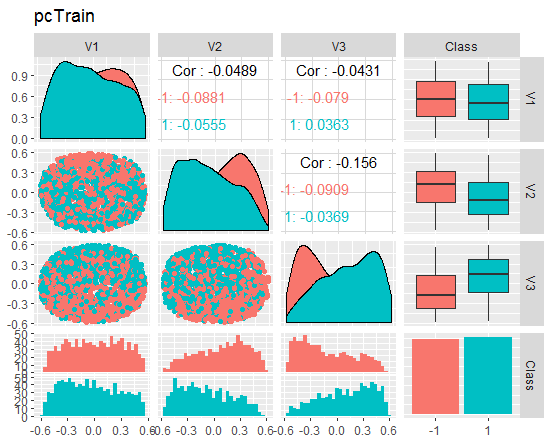
Fig. 8. Variación y covariación del conjunto reducido train
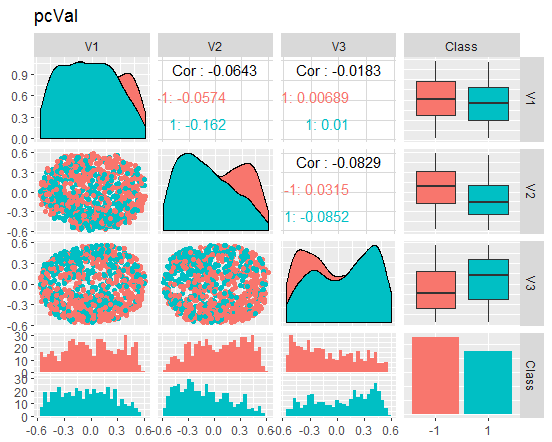
Fig. 9. Variación y covariación del conjunto reducido val
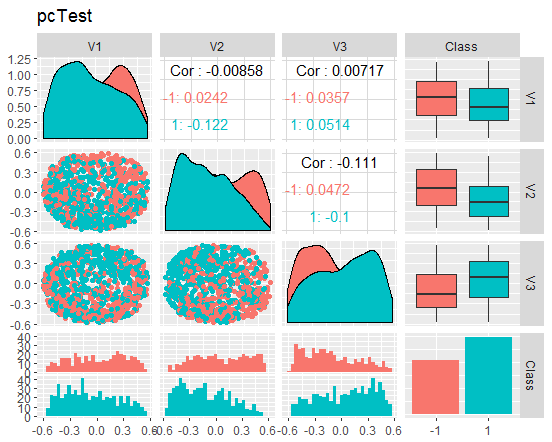
Fig. 10. Variación y covariación del conjunto reducido test
¿Qué podemos hacer según los gráficos? Podemos que ver que los "componentes principales" (V1, V2, V3) están bien divididos según los niveles de la variable objetivo, mientras que las distribuciones en los conjuntos train/val/test son irregulares. Podríamos descartar las muestras de ruido y ver cuánto mejora el asunto. Dejaremos a la discreción del lector esta idea, para que la analice por sí mismo.
Una pequeña digresión: NLPCA
Para descomponer los datos por componentes principales, es importante distinguir las aplicaciones de reducción pura de las dimensiones de las aplicaciones donde el mayor interés lo supone la identificación y reconocimento de los componentes únicos y significativos, normalmente llamada extracción de características (feature extraction).
En las aplicaciones para la reducción pura de las dimensiones con un interés principal por la supresión de ruido y la compresión de datos, solo se requiere un poco de espacio con gran capacidad descriptiva. Los métodos en que los componentes por separado forman este subespacio no están limitados, y por consiguiente, no deben ser únicos obligatoriamente. El único requerimiento consiste en que el subespacio explique el máximo de información en el sentido del cuadrado del error (MSE). Puesto que ciertos componentes que abarcan este espacio se procesan de la misma forma, con un algoritmo sin ningún tipo concreto de orden o ponderación diferenciada, este tipo se llama tipo simétrico de entrenamiento. Incluye un PCA lineal y una red neuronal autoasociativa estándar ejecutable (autoencoder), que por ello se llama NLPCA. En el anterior apartado ya analizamos esta variante.
Por el contrario, el PCA jerárquico no lineal (h-NLPCA) ofrece, no solo un subespecio lineal óptimo abarcado por componentes, sino que también limita los componentes lineales en el PCA estándar. La jerarquía en este contexto se explica con dos propiedades: la escalabilidad y la estabilidad. La escalabilidad implica que los primeros n componentes explican la dispersión máxima que puede ser cubierta por un subespacio n dimensional. La estabilidad significa que el i-ésimo componente de la solución n-componente es idéntico al i-ésimo componente de la solución m-componente.
El orden jerárquico de componentes no correlacionados. La no linealidad también significa que h-NLPCA es capaz de eliminar correlaciones lineales complejas entre componentes. Esto ayuda a filtrar los compnentes útiles y significativos. Además, escalando un componente no correlacionado no lineal con respecto a la dispersión única, obtenemos el blanqueo no lineal complejo (transformación esférica). Se trata de un procesamiento preliminar para aplicaciones tales como la regresión, la clasificación o la división ciega de fuentes. Dado que el blanqueo no lineal elimina la no-linealidad en los datos, como consecuencia, los métodos utilizados pueden ser lineales. Esto es especialmente importante para el ICA, que puede ampliarse hasta un enfoque no lineal con el uso de este blanqueo no lineal.
¿Cómo podemos alcanzar un orden jerárquico? Una simple clasificación de componentes procesados simétricamente según la dispersión no nos dará el orden jerárquico requerido: ni lineal, ni no lineal. En principio, es posible alcanzar la jerarquía mediante dos métodos interrelacionados: o bien mediante la limitación de la dispersión en el espacio de los componentes, o bien mediante la limitación del cuadrado del error de reconstrucción en el espacio original. De forma semejante a PCA, el i-ésimo componente está obligado a tener en cuenta la i-ésima dispersión más alta.
Pero desde un punto de vista no lineal, esta limitación puede resultar inefectiva o singular sin limitaciones adicionales. Por el contrario, un error de recuperación puede controlarse mucho mejor, puesto que se trata de una magnitud absoluta, invariante ante cualquier escala de transformación. Por eso, la limitación jerárquica del error es un método bastante más efectivo. En un caso lineal simple, podemos alcanzar el orden jerárquico de componentes mediante el enfoque secuencial (deflacional), en el que los componentes se extraen secuencialmente uno tras otro en la dispersión restante, establecida por el error cuadrático de las anteriores. Sin embargo, esto no funciona en el caso no lineal: ni de forma secuencial, ni simultáneamente mediante el entrenamiento de varias redes de manera paralela. La dispersión restante no puede ser interpretada con el error cuadrático, independientemente de la transformación no lineal. La solución es usar solo una red con una jerarquía de subredes. Esto nos permite formular la jerarquía directamente en la función del error.
2.5. PCA inverso no lineal
En este apartado, el PCA no lineal resolverá la tarea inversa. Si consideramos que el problema original consiste en pronosticar la salida de la entrada esteblecida, la tarea inversa será valorar qué entrada se corresponde de la mejor forma con el resultado establecido. Puesto que no conocemos ni el modelo, ni el proceso de generación de datos, nos encontramos ante una así llamada "tarea inversa ciega".
Un PCA lineal sencillo se puede considerar igualmente bueno tanto en una tarea directa, como en una inversa, dependiendo de si se predicen los componentes deseados como salidas o si se valoran como datos de entrada según un algoritmo existente. La red autoasociativa (АЕ) modela simultáneamente tanto el modelo directo, como el indirecto.
El modelo directo es definido por la primera parte del АЕ mediante la función de extracción Fextr: X → Z. El modelo inverso es definido por la segunda parte, mediante la función de generación Fgen: Z → X. El primer modelo conviene más para el PCA lineal, y menos para el PCA no lineal. Esto sucede porque este modelo puede resultar funcionalmente muy complejo y difícil de solucionar, a causa del problema de representación «uno para muchos». Dos muestras X idénticas pueden corresponder a diferentes resultados de los componentes Z.
Para un РСА lineal inverso, solo se requiere la segunda parte de la red autoasociativa (fig.11), lo cual se ilustra con la red 3-7-12. Esta parte de la generación supone la representación inversa de Fgen, que genera o reconstruye patrones de gran tamaño de Х a partir de sus imágenes Z de dimensiones más pequeñas. Estos valores de los componentes Z ahora son entradas desconocidas que se pueden valorar propagando errores parciales σ de vuelta a la capa de entrada Z.
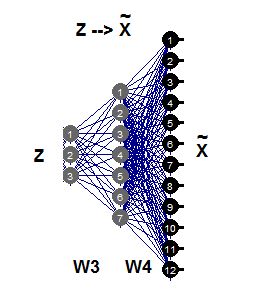
Fig. 11. Modelo РСА inverso no lineal
Vamos a comparar los resultados obtenidos con la ayuda del АЕ y a través de la función nlpca::pcaMethods. Esta función se muestra brevemente más arriba. Ahora calculamos con los mismos datos y con los mismos requisitos originales de reducción 12->3 y comparamos los resultados.
Para ello, tomaremos el conjunto DTcap.n$train, eliminaremos de él la variable objetivo Class y la convertiremos en matriz, después de lo cual, centraremos el conjunto. Definiremos la estructura de la neurored como (3,8,12), los demás parámetros se pueden ver en el script de más abajo. Después de obtener el resultado, individualizamos los componentes principales (puntuación), le añadimos la variable objetivo y construimos el gráfico.
Conviene mencionar que el algoritmo es muy lento, y cada nuevo inicio da un resultado diferente del anterior.
require(pcaMethods)
evalq({
DTcap.n$train %>% tbl_df %>%
select(-Class) %>% as.matrix() %>%
prep(scale = "none", center = TRUE) -> train
resNLPCA <- pca(train,
method = "nlpca", weightDecay = 0.01,
unitsPerLayer = c(3, 8, 12),
center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
nPcs = 3, completeObs = FALSE,
subset = NULL, cv = "none", # "none""q2"), ...)
maxSteps = 1100)
rm(train)},
env)
#--------
evalq(
pcTrain <- resNLPCA@scores %>% tbl_df %>%
cbind(., Class = DTcap.n$train$Class)
, env)
#------graph-------
require(GGally)
evalq({
ggpairs(pcTrain,columns = 1:ncol(pcTrain),
mapping = aes(color = Class),
title = "pcTrain -> NLPCA(3-8-12) wd = 0.01")},
env)
#----------
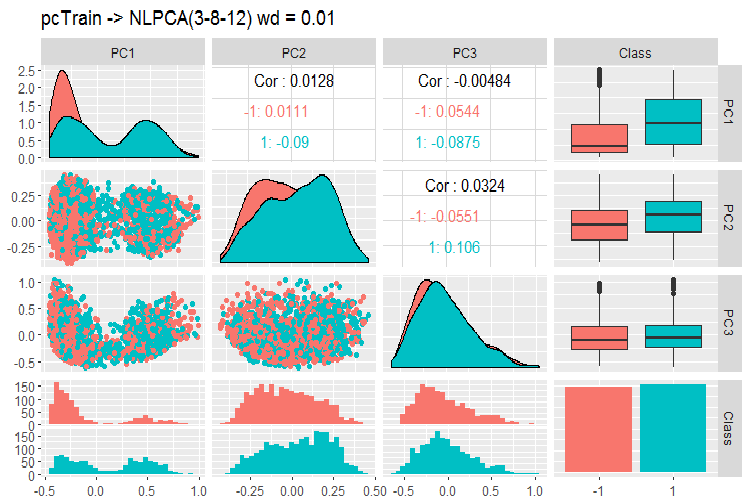
Fig. 12. Variación y covariación de componentes principales obtenidos con la ayuda de NLPCA
¿Qué vemos en el gráfico? Los componentes son bien divididos por los niveles de la variable objetivo y tienen una correlación muy baja. El tercer componente parece sobrar. Vamos a ver la información general del modelo.
> print(env$resNLPCA) nlpca calculated PCA Importance of component(s): PC1 PC2 PC3 R2 0.3769 0.2718 0.09731 Cumulative R2 0.3769 0.6487 0.74599 12 Variables 2000 Samples 0 NAs ( 0 %) 3 Calculated component(s) Data was mean centered before running PCA Data was NOT scaled before running PCA Scores structure: [1] 2000 3 Loadings structure: Inverse hierarchical neural network architecture 3 8 12 Functions in layers linr tanh linr hierarchic layer: 1 hierarchic coefficients: 1 1 1 0.01 scaling factor: 0.3260982
Tenemos otro problema: el resultado no retorna las matrices de peso W3 y W4. En otras palabras, no tenemos un P de carga, y no podemos obtener los componentes principales S (puntuación) en los conjuntos de prueba y validación. El mismo problema tienen otros dos buenos métodos de reducción de las dimensiones: tSNE, ICS. Por supuesto que, aplicando un poco de gimnasia mental, podremos resolver estos problemas, pero será mejor no seguir este dudoso camino, pues su destino resulta desconocido.
En el paquete se proponen otros dos métodos: el РСА probabilístico y el bayesiano. Son rápidos y retornan las cargas, lo que permite obtener con facilidad los componentes principales en los conjuntos val/test. Vamos a mostrar un ejemplo solo para PPCA.
#=======PPCA===================
evalq({
DTcap.n$train %>% tbl_df %>%
select(-Class) %>% as.matrix() -> train
DTcap.n$val %>% tbl_df %>%
select(-Class) %>% as.matrix() -> val
DTcap.n$test %>% tbl_df %>%
select(-Class) %>% as.matrix() -> test
resPPCA <- pca(train, method = "ppca",
center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
nPcs = 3, completeObs = FALSE,
subset = NULL, cv = "none", # "none""q2"), ...)
maxIterations = 3000)
},
env)
#-----------
>print(env$resPPCA)
ppca calculated PCA
Importance of component(s):
PC1 PC2 PC3
R2 0.2873 0.2499 0.1881
Cumulative R2 0.2873 0.5372 0.7253
12 Variables
2000 Samples
0 NAs ( 0 %)
3 Calculated component(s)
Data was mean centered before running PCA
Data was NOT scaled before running PCA
Scores structure:
[1] 2000 3
Loadings structure:
[1] 12 3
Construimos un gráfico para las cargas y puntuaciones para los componentes 1 y 2:
slplot(env$resPPCA, pcs = c(1,2), lcex = 0.9, sub = "Probabilistic PCA")
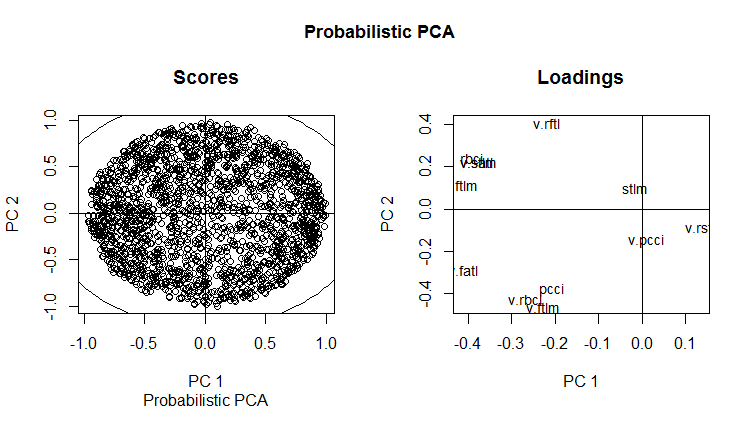
Fig. 13. РСА probabilístico de РС1 y РС2 (cargas y puntuaciones)
Los gráficos de variación y covariación de los componentes pricipales de las muestras PPCA train/val/test se representan más abajo. Vea los scripts en GitHub.
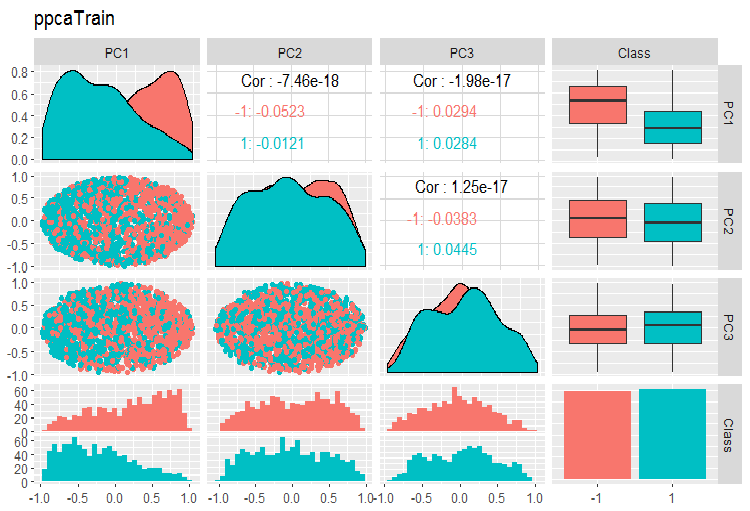
Fig. 14. Variación y covariación de los componentes pricipales de la muestra train obtenidos con la ayuda de PPCA
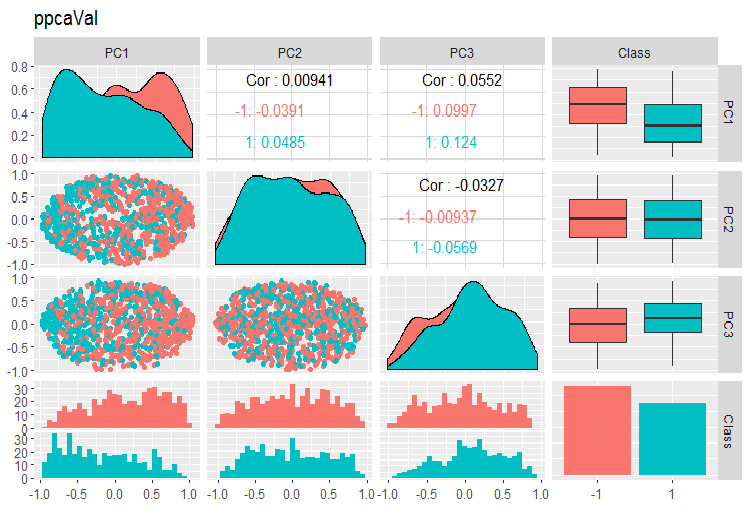
Fig. 15. Variación y covariación de los componentes pricipales de la muestra val obtenidos con la ayuda de PPCA
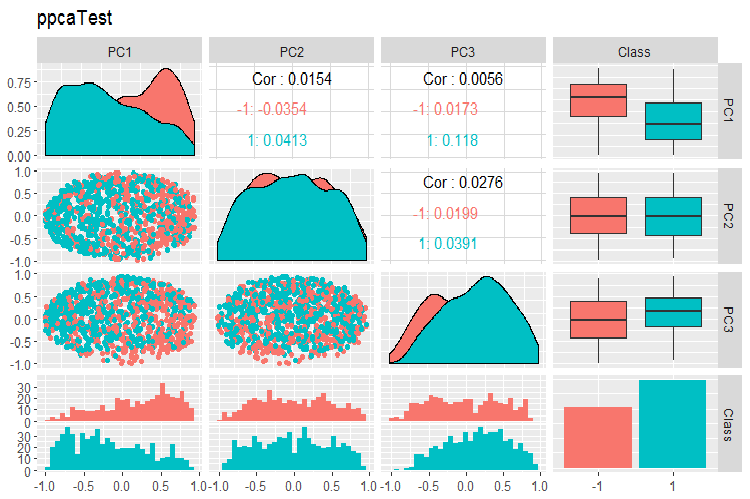
Fig. 16. Variación y covariación de los componentes pricipales de la muestra test obtenidos con la ayuda de PPCA
No podemos decir que la división por los niveles de la variable objeto de los componenetes principales, obtenidos con la ayuda de PPCA sea mejor o tenga mayor calidad que la misma reducción con la ayuda del autoencoder, analizada más arriba. La ventaja de PPCA y BPCA reside en su velocidad y sencillez. La calidad se deberá comprobar cada vez con la ayuda de un modelo de clasificación completo.
3.División del conjunto en train/valid/test
En esta parte nada cambia con respecto a lo descrito en los artículos anteriores. Al entrenar: train/valid/test, ventana móvil, ventana de crecimiento, en ocasiones: bootstrap. Al elegir el modelo: la validación cruzada. Permanece abierta la cuestión de la definición del tamaño suficiente de estas muestras.
Querríamos mencionar aparte las interesantes afirmaciones de la empresa Win Wector LLC sobre el uso de los conjuntos train en las transformaciones de pre-procesamiento. Aseguran que si en el conjunto de entrenamiento hemos definido los componentes principales, entonces deberemos entrenar el modelo con los componentes principales obtenidos en el conjunto de validación. Es decir, no se puede usar para entrenar un modelo una muestra ya utilizada. Podremos comprobar esto al entrenar la neurored.
Conclusión
En las tres partes del artículo hemos analizado todas las etapas de la preparación de datos, para el entrenamiento de las neuroredes profundas. Como podemos ver, se trata de una etapa laboriosa y compleja. Pero sin la comprensión y el conocimiento adecuados de la preparación de datos, todas las etapas y acciones posteriores no tendrán ningún sentido.
Si no controlamos visualmente todos los cálculos en la etapa de preparación de datos, no será posible obtener un buen resultado. Para los usuarios más perezosos e impacientes se han desarrollado los paquetes "preprocomb" y "metaheur", que pueden seleccionar automáticamente (según su criterio) las etapas de preparación preliminar más adecuadas.
Anexos
Los scripts usados en el artículo se muestran en GitHub/Part_III.