Predicción de series de tiempo usando el ajuste exponencial

Victor | 12 marzo, 2014

Introducción

Hay actualmente un gran número de métodos de predicción bien conocidos que se basan solo en el análisis de los valores pasados de una secuencia temporal, es decir, métodos que emplean los principios normalmente utilizados en el análisis técnico. El instrumento principal de estos métodos es la extrapolación, donde las propiedades de la serie identificadas en un determinado retraso temporal van más allá de sus límites.

Al mismo tiempo, se asume que las propiedades de la serie en el futuro serán las mismas que en el pasado y el presente. Un esquema de extrapolación más complejo implica el estudio de la dinámica de los cambios en las características de la serie, sin olvidar que dicha dinámica en el intervalo de predicción es usada con menor frecuencia en predicción.

Los métodos de predicción basados en la extrapolación más conocidos son quizás aquellos que utilizan el modelo de media móvil integrado autorregresivo (ARIMA). La popularidad de estos métodos se debe, principalmente, a los trabajos de Box y Jenkins, quienes propusieron y desarrollaron un modelo ARIMA integrado. Por supuesto, hay otros modelos y métodos de predicción además de los modelos de Box y Jenkins.

Este artículo trata brevemente sobre más modelos simples - modelos de ajuste exponencial propuestos por Holt y Brown antes de la aparición de los trabajos de Box y Jenkins.

A pesar de utilizar herramientas matemáticas más simples y claras, la predicción mediante modelos de ajuste exponencial conduce a menudo a resultados comparables a los obtenidos mediante el uso del modelo ARIMA. Esto no es muy sorprendente ya que los modelos de ajuste exponencial son un caso especial del modelo ARIMA. En otras palabras, cada modelo de ajuste exponencial estudiado en este artículo posee un modelo ARIMA equivalente. Estos modelos equivalentes no serán considerados en el artículo y solo se mencionan a título informativo.

Es sabido que la predicción requiere, en cada caso particular, un enfoque determinado que normalmente implica un número de procedimientos.

Por ejemplo:

1. Análisis de lla serie de tiempo para detectar valores omitidos y atípicos. Ajuste de estos valores.
2. Identificación de la tendencia y su tipo. Determinación de la periodicidad de la serie.
3. Comprobación de la estacionariedad de la serie.
4. Análisis de preprocesado de la serie (tomando logaritmos, diferenciando, etc.).
5. Selección del modelo.
6. Determinación del parámetro del modelo. Pronóstico basado en el modelo elegido.
7. Evaluación de la exactitud de la predicción del modelo.
8. Análisis de los errores del modelo elegido.
9. Cálculo de la idoneidad del modelo elegido y, de ser necesario, sustitución del modelo y vuelta a los elementos anteriores.

Esta no es, ni mucho menos, la lista completa de las acciones que se requieren para una predicción eficaz.

Debe destacarse aquí que el cálculo del parámetro del modelo y la obtención de los resultados de la predicción es tan solo una parte del proceso general de predicción. Pero parece imposible cubrir en un artículo todo el rango de problemas que, de una u otra forma, están involucrados en la predicción.

Por ello, este artículo solo tratará los modelos de ajuste exponencial y el uso de cotizaciones monetarias no preprocesadas como series de prueba. No es posible evitar por completo las cuestiones que entran en juego, pero serán tratadas solo en la medida en que sean necesarias para la revisión de los modelos.

1. Estacionariedad

El concepto de extrapolación implica que el desarrollo futuro del proceso en estudio será el mismo para el pasado y el presente. En otras palabras, trata sobre la estacionariedad del proceso. Los procesos estacionarios son muy atractivos desde el punto de vista de la predicción, pero, por desgracia, no existen en la naturaleza, ya que cualquier proceso real está sujeto a cambio en el curso de su desarrollo.

Los procesos reales pueden tener una expectativa, varianza y distribución marcadamente distinta a lo largo del tiempo, pero los procesos cuyas características cambian muy lentamente pueden ser atribuidos a los procesos estacionarios. "Muy lentamente" significa en este caso que los cambios en las características del proceso dentro del intervalo de observación finito parecen ser tan insignificantes que pueden ser descartados.

Está claro que cuanto más breve sea el intervalo de observación (muestra breve), mayor será la probabilidad de tomar una decisión equivocada en relación con la estacionariedad del proceso en su conjunto. Por otro lado, si estamos más interesados en el estado del proceso en un momento posterior y pensamos hacer un pronóstico a corto plazo, la reducción del tamaño de la muestra puede conducir, en algunos casos, a aumentar la precisión de dicho pronóstico.

Si el proceso está sujeto a cambios, los parámetros de la serie determinados en el intervalo de la observación serán distintos fuera de sus límites. De esta forma, cuanto más amplio sea el intervalo de predicción, mayor será el efecto de la variabilidad de las características de la serie sobre el error de predicción. Debido a esto, tenemos que limitarnos solo a una predicción a corto plazo, una reducción significativa del intervalo de predicción nos permite esperar que el cambio lento de características de la serie no provocará errores de predicción considerables.

Además, la variabilidad de los parámetros de la serie conduce al hecho de que el valor obtenido al estimar en el intervalo de observación es promediado, ya que los parámetros no permanecen constantes en el intervalo. Los valores del parámetro obtenidos no estarán relacionados con el último instante de este intervalo pero reflejarán un cierto valor medio. Por desgracia, es imposible eliminar por completo este desagradable fenómeno, pero puede atenuarse si se reduce al máximo la longitud del intervao de observación implicado en la estimación del parámetro del modelo (intervalo de estudio).

Al mismo tiempo, el intervalo de estudio no puede acortarse indefinidamente ya que si se reduce demasiado puede disminuir la precisión de la estimación del parámetro de la predicción. Uno debe buscar un compromiso entre el efecto de los errores asociados con la variabilidad de las caracerísticas de la serie y el incremento de errores debido a la excesiva reducción del intervalo de estudio.

Todo lo anterior es completamente aplicable a la predicción mediante el uso de modelos de ajuste exponencial, ya que estos están basados en la hipótesis de la estacionariedad de los procesos, como los modelos ARIMA. No obstante, para simplificar asumiremos a partir de ahora que los parámetros de todas las series consideradas varían en el intervalo de observación pero de una forma tan lenta que estos cambios pueden obviarse.

Así pues, el artículo tratará las cuestiones relacionadas con la predicción de series a corto plazo con características de cambio lento en base a los modelos de ajuste exponencial. La expresión "predicción a corto plazo" debe entenderse, por tanto, como una predicción para uno, dos o más intervalos de tiempo en el futuro, en lugar de una predicción para un periodo inferior a un año, como habitualmente se entiende en el ámbito de la economía.

2. Series de prueba

Al escribir este artículo se usaron las cotizaciones en EURRUR, EURUSD, USDJPY y XAUUSD, previamente guardadas, para M1, M5, M30 y H1. Cada uno de los archivos guardados contienen 1100 valores "abiertos"- El valor más "antiguo" se encuentra al principio del archivo y el más "reciente" al final. El último valor guardado en el archivo corresponde al momento en el que se creó el archivo. Los archivos que contienen series de prueba se crearon usando el script HistoryToCSV.mq5. Los archivos de datos y scripts que usan los que hemos creado se encuentran al final del artículo en el archivo Files.zip.

Como ya se ha dicho, las cotizaciones guardadas se usan en este artículo sin ser procesadas a pesar de los problemas obvios a los que me gustaria que prestarán atención. Por ejemplo, las cotizaciones EURRUH_H1 durante el día desde la barra 12 a la 13, cotizaciones XAUUSD de los viernes con una barra menos que en otros días. Estos ejemplos demuestran que las cotizaciones se generan a intervalos irregulares. Esto es totalmente inaceptable para los algoritmos diseñados para funcionar con series de tiempo correctas que sugieren tener un intervalo de cuatificación uniforme.

Incluso si los valores perdidos de las cotizaciones se generan mediante extrapolación, la cuestión de la falta de cotizaciones en los fines de semana sigue abierta. Podemos suponer que los eventos que ocurren en el mundo los fines de semana tienen el mismo impacto en la economía mundial que los que ocurren el resto de días. En cualquier momento pueden ocurrir eventos como revoluciones, fenómenos naturales, escándalos, cambios gubernamentales y otros más o menos importantes. Si ocurre un evento de este tipo un sábado, es dificil que tenga un menor impacto en los mercados mundiales que si ocurriera en un día de la semana.

Quizá sean estos eventos los que provocan lapsos en las cotizaciones tan frecuentemente observados al final de la semana. Aparentemente, el mundo sigue con sus propias reglas incluso cuando el mercado FOREX no opera. Todavía no está claro si los valores de las cotizaciones correspondientes a los fines de semana destinados al análisis técnico deben reproducirse y qué beneficio generarían.

Obviamente, estas cuestiones quedan fuera del alcance de este artículo pero, a primera vista, la serie sin lapsos parece ser más adecuada para el análisis, al menos para la detección de componentes cíclicos (estacionales).

La importancia de una preparación premilinar de la información para el análisis posterior no debe sobreestimarse. En nuestro caso es una cuestión independiente ya que las cotizaciones, en la forma en la que estas aparecen en el terminal, no son realmente adecuadas para un análisis técnico. Además de las cuestiones relacionadas con los lapsos a las que nos hemos referido, hay una gran cantidad de problemas adicionales.

Al crearse las cotizaciones, por ejemplo, se asigna a un punto del tiempo fijo los valores "abierto" y "cerrado" que no pertenecen a él. Estos valores corresponden al momento de la formación del tick de un momento fijo de un periodo de tiempo seleccionado del gráfico, donde se sabe que los ticks son a veces muy raros.

Puede verse otro ejemplo completamente al margen del teorema de la muestra, ya que nadie puede garantizar que el ratio de muestreo, incluso en un intervalo de un minuto, satisfaga el teorema anterior (por no mencionar otros intervalos mayores). Además, debemos tener en cuenta la presencia de un margen diferencial variable que, en algunos casos, puede ser impuesto a la fuerza sobre los valores de las cotizaciones.

Pero vamos a dejar estas cuestiones al margen de este artículo y volvamos al asunto principal.

3. Ajuste exponencial.

Vamos a ver el modelo más simple.

,

donde:

• X(t) – (simulado) proceso en estudio,
  
• L(t) – nivel de proceso variable,
  
• r(t) – variable aleatoria de media cero.

Como puede verse, este modelo comprende la suma de dos componentes. Estamos especialmente interesados en el nivel de proceso L(t) y vamos a intentar centrarnos en él.

Es bien conocido que el promedio de una serie aleatoria puede generar una varianza menor, es decir, un ratio de la desviación de la media reducido. Podemos por tanto asumir que si el proceso descrito por nuestro modelo simple se expone a la promediación (ajuste), puede que no podamos deshacernos de un componente aleatorio r(t) por completo, pero podremos al menos debilitarlo de forma considerable y de esta forma destacar el nivel objetivo L(t).

Para este propósito usaremos un ajuste exponencial simple (SES).

En esta conocida fórmula, el grado de ajuste se define a través del coeficiente alfa que puede adquirir valores entre 0 y 1. Si a alfa se le asigna el valor cero, los nuevos valores que llegan de la serie de entrada X no producirán ningún efecto en el resultado del ajuste. El resultado del ajuste para cualquier punto en el tiempo será un valor constante.

Por tanto, en casos extremos como este, el incómodo componente aleatorio será eliminado por completo aunque el nivel del proceso considerado sea ajustado a una línea horizontal. Si a alfa se le asigna el valor de uno, la serie de entrada no se verá afectada por el ajuste en absoluto. El nivel considerado L(t) no se verá afectado en este caso y el componente aleatorio tampoco será suprimido.

Está claro que al seleccionar el valor de alfa, uno debe satisfacer simultaneamente los requisitos en conflicto. Por un lado, el valor de alfa debe estar cerca de cero para suprimir eficazmente el componente aleatorio r(t). Por otro, es aconsejable establecer el valor de alfa cercano a la unidad para no distorsionar el componente L(t) en el que estamos tan interesados. Para obtener el valor óptimo de alfa necesitamos identificar un criterio por el que dicho valor pueda ser optimizado.

Para determinar dicho criterio, debemos recordar que este artículo trata sobre la predicción y no sobre el ajuste de series.

En este caso, en relación al modelo simple de ajuste exponencial es habitual considerar el valor obtenido en un momento determinado como predicción para un número de pasos futuros.

donde es el pronóstico para m pasos en el futuro en el momento t.

Así pues, la predicción del valor de la serie en el momento t será la previsión realizada en el paso previo para un paso en el futuro.

En este caso podemos usar el error de la predicción para un paso en el futuro como criterio de optimización del valor del coeficiente alfa.

De esta forma, minimizando la suma de los cuadrados de estos errores en toda la muestra podemos determinar el valor óptimo del coeficiente alfa para una serie dada. El mejor valor alfa será desde luego aquel en el que la suma de los cuadrados de los errores sea mínima.

La Figura 1 muestra la suma de los cuadrados de los errores de la predicción sobre un paso en el futuro frente al valor del coeficiente alfa para un fragmento de la serie de prueba USDJPY M1.

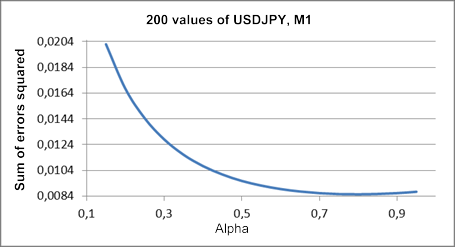
Figura 1. Ajuste exponencial simple

El mínimo en el gráfico resultante es apenas discernible y está situado cerca del valor alfa de casi 0,8. Pero esto no es lo que siempre ocurre en el caso del ajuste exponencial simple. Al intentar obtener el valor alfa óptimo para los fragmentos de la serie de prueba utilizados en el artículo, obtendremos en la mayoría de las ocasiones un gráfico que se acerca constantemente a la unidad.

Estos valores tan altos del coeficiente de ajuste sugieren que el modelo simple no es muy adecuado para describir nuestras series de prueba (cotizaciones). Ocurre que, o bien el nivel de proceso L(t) cambia demasiado rápido o que hay una tendencia en el proceso.

Vamos a hacer nuestro modelo un poco más complejo añadiendo otro componente

,

donde:

• X(t) – (simulado) proceso en estudio,
  
• L(t) – nivel de proceso variable,
  
• T(t) - tendencia lineal,
  
• r(t) – variable aleatoria de media cero.

Se sabe que los coeficientes de una regresión lineal pueden determinarse ajustando doblemente una serie:

Para los coeficientes a1 y a2 obtenidos de esta forma, la predición de un paso en el futuro en el momento t serán iguales

Debe tenerse en cuenta que el coeficiente alfa de la muestra se utiliza en las fórmulas anteriores para el ajuste primero y el repetido. A este modelo se le conoce como modelo de un parámetro aditivo de crecimiento lineal.

Vamos a ver la diferencia entre el modelo simple y el modelo de crecimiento lineal.

Supongamos que durante un largo periodo, el proceso a estudio ha representado un componente constante, es decir, apareció en el gráfico como una línea recta horizontal pero en un cierto punto comenzó a surgir una tendencia lineal. En la Figura 2 se muestra una predicción de este proceso utilizando los modelos anteriores.

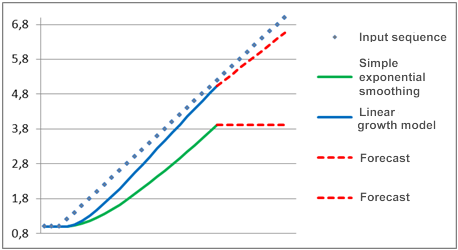
Figura 2. Comparación de modelos

Como puede verse, el modelo de ajuste exponencial simple está detrás de la serie de entrada variante linealmente de forma apreciable, y la predicción realizada utilizando este modelo se aleja aún más. Podemos ver un patrón muy diferente cuando se usa el modelo de crecimiento lineal. Cuando surge la tendencia, este modelo está mas cerca de la dirección de los valores de entrada variables como si intentara sugerir la serie variable linealmente.

Si el coeficiente de ajuste del ejemplo dado fuera mayor, el modelo de crecimiento lineal podría "alcanzar" la señal de entrada en el momendo dado y su pronóstico casi coincidiría con la serie de entrada.

A pesar del hecho de que el modelo de crecimiento lineal en el estado estacionario da buenos resultados en presencia de una tendencia lineal, es fácil ver que le lleva un cierto tiempo "alcanzar" la tendencia. Por lo tanto, siempre habrá un lapso entre el modelo y la serie de entrada si la dirección de una tendencia cambia con frecuencia. Además, si la tendencia crece de forma no lineal y sigue la ley cuadrática, el modelo de crecimiento lineal no podrá "alcanzarla". Pero a pesar de estos inconvenientes, este modelo es más ventajoso que el modelo de ajuste exponencial simple en presencia de una tendencia lineal.

Como ya se ha mencionado, hemos utilizado un modelo de un parámetro de crecimiento lineal. Para encontrar el valor óptimo del parámetro alfa para un fragmento de la serie de prueba USDJPY M1, vamos a construir un gráfico de la suma de los cuadrados de los errores de predicción con vistas a un paso en el futuro frente al valor del coeficiente alfa.

Este gráfico, basado en el mismo fragmento de serie de la Figura 1, se muestra en la Figura 3.

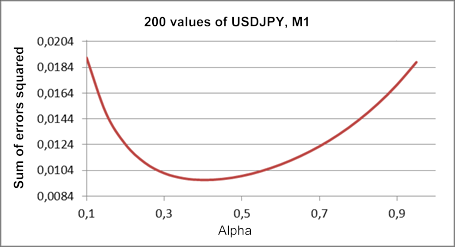
Figura 3. Modelo de crecimiento lineal

Comparándolo con el resultado de la Figura 1, el valor óptimo del coeficiente alfa ha disminuido 0,4 aproximadamente. El primer y segundo ajuste tienen los mismos coeficientes en este modelo, aunque teóricamente sus valores puedan ser diferentes. Más tarde veremos el modelo de crecimiento lineal con dos coeficientes de ajuste distintos.

Los dos modelos de ajuste exponencial tienen sus análogos en MetaTrader 5 donde existen en forma de indicadores. Estos son los conocidos EMA y DEMA que no están pensados para predecir sino para ajustar los valores de la serie.

Debe tenerse en cuenta que cuando se utiliza el indicador DEMA, se muestra un valor correspondiente al coeficiente a1 en lugar del valor de la predicción con vistas a un paso en el futuro. En este caso, el coeficiente a2 (véanse las formulas anteriores para el modelo de crecimiento lineal) no se calcula ni se utiliza. Además, el coeficiente de ajuste se calcula en términos del periodo equivalente n

Por ejemplo, alfa igual 0.8 corresponde a un valor de n aproximadamente igual a 2, y si alfa es 0,4 entonces n es igual a 4.

4. Valores iniciales

Como ya se ha mencionado, debe obtenerse, de una forma o de otra, un valor del coeficiente de ajuste en la aplicación del ajuste exponencial. Pero parece que esto no es suficiente. Como en el ajuste exponencial, el valor actual se calcula sobre la base del valor previo, hay un momento en que dichos valores ya no existen en el momento cero. En otras palabras, el valor inicial de S o S1 y S2 en el modelo de crecimiento lineal debe de algún modo ser calculado en el momento cero.

El problema de obtener los valores iniciales no es siempre fácil de resolver. Si (como ocurre cuando se utiliza la cotización en Meta Trader 5) tenemos un historial muy largo disponible, la curva de ajuste exponencial, habiendo sido inexactamente determinados los valores iniciales, tendrá tiempo de estabilizarse en un cierto punto, habiendo corregido nuestro error inicial. Esto requerirá entre 10 y 200 (y algunas veces aún más) periodos dependiendo del valor del coeficiente de ajuste.

En este caso sería suficiente estimar a groso modo los valores iniciales y comenzar el proceso de ajuste exponencial 200-300 periodos antes del periodo de tiempo objetivo. Es más difícil, no obstante, cuando la muestra disponible solo contiene, p. ej., 100 valores.

Hay varias recomendaciones en la bibliografía en relación a la elección de los valores iniciales. Por ejemplo, el valor inicial en el ajuste exponencial simple puede igualarse al primer elemento en una serie o calcularse como la media de tres o cuatro elementos inciales en una serie sin perder de vista los valores atípicos aleatorios del ajuste. Los valores iniciales S1 y S2 en el modelo de crecimiento lineal pueden determinarse en base a la hipótesis de que el nivel inicial de la curva de predicción debe ser igual al primer elemento de una serie y la pendiente de la tendencia lineal debe ser cero.

Podemos encontrar aún más recomendaciones en las diferentes fuentes relativas a la elección de los valores inciales, pero ninguna de ellas nos puede asegurar la ausencia de errores apreciables en las etapas tempranas del algoritmo de ajuste. Es particularmente apreciable con el uso de coeficientes de ajuste de bajo valor cuando se requiere un gran número de periodos para lograr un estado estacionario.

Por tanto, para minimizar el impacto de los problemas asociados con la elección de valores inciales (especialmente para series cortas), algunas veces usamos un método que implica una búsqueda de dichos valores que resultará en un error de predicción mínimo. Es cuestión de calcular un error de predicción para los valores inciales variando en pequeños incrementos sobre toda la serie.

La variante más apropiada puede elegirse después de calcular el error dentro del rango de todas las posibles combinaciones de valores inciales. Sin embargo, este método es muy laborioso y requiere muchos cálculos y casi nunca se usa en su forma directa.

El problema descrito tiene que ver con la optimización o búsqueda de un valor de función multivariable mínimo. Dichos problemas pueden resolverse utilizando varios algoritmos desarrollados para reducir de forma considerable el alcande de los cálculos requeridos. Volveremos a las cuestiones sobre la optimización de los parámetros de ajuste y los valores inciales en la predicción un poco más tarde.

5. Evaluación de la exactitud de la predicción.

El procedimeinto de predicción y elección de los valores o parámetros del modelo inicial da lugar al problema de estimar la exactitud de la predicción. La evaluación de la exactitud también es importante al comparar dos modelos diferentes o determinar la coherencia de la predicción obtenida. Hay un gran número de estimaciones para la evaluación de la exactitud de la predicción, pero el cálculo de cualquiera de ellas requiere el conocimiento del error de predicción en cada paso.

Como ya se ha mencionado, un error de predicción sobre un paso en el futuro en el tiempo t es igual a

donde:

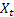• – valor de la serie de entrada en el momento t;
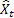• – predicción en el momento t realizada en el paso previo.

Probablemente, la estimación de la exactitud de predicción más común es el error cuadrado medio (ECM):

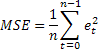
donde n es el número de elementos en una serie.

La sensibilidad extrema a los errores únicos ocasionales de valor grande es a veces señalado como una desventaja del ECM. Deriva del hecho de que el valor del error al calcular ECM es cuadrado. Como alternativa, es aconsejable usar en este caso el error medio absoluto (EMA).

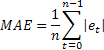
Aquí, el error cuadrado se reemplaza por el valor absoluto del error. Se asume que las estimaciones obtenidas utilizando el EMA son más estables.

Ambas estimaciones son muy adecuadas para, por ejemplo, la evaluación de la exactitud de la predicción de la misma serie usando diferentes parámetros del modelo o distintos modelos, pero parecen ser de poca utilidad para comparar los resultados de las predicciones recibidos en distintas series.

Además, los valores de estas estimaciones no sugieren expresamente la calidad del resultado de la predicción. Por ejemplo, no podemos decir si un EMA de 0,03 que hayamos obtenido u otro valor es bueno o malo.

Para poder comparar la exactitud de la predicción de distintas series, podemos usar estimaciones relativas RelMSE y RelMAE:

Las estimaciones obtenidas para la exactitud de la predicción se dividen aquí por las estimaciones respectivas obtenidas usando el método de prueba de la predicción. Como método de prueba es apto para el llamado método ingenuo, sugiriendo que el valor futuro del proceso será igual al valor actual.

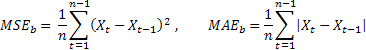
Si la media de los errores de predicción se iguala al valor de los errores obtenidos utilizando el método ingenuo, el valor de estimación relativo será igual a uno. Si el valor de estimación relativo es menor que uno, significa que, de media, el valor del error de predicción es menor que en el método ingenuo. En otras palabras, la exactitud de los resultados de la predicción es mayor que la del método ingenuo. Y al contrario, si el valor de estimación relativo es mayor que uno, la exactitud de los resultados de la predicción es, de media, inferior que en el método ingenuo de predicción.

Estas estimaciones también son aptas para la evaluación de la exactitud de la predicción de dos o más pasos en el futuro. Un error en los cálculos de una predicción a un paso en el futuro requiere ser reemplazado por el valor de los errores de predicción para el número adecuado de pasos hacia adelante.

Como ejemplo, la tabla a continuación contiene errores de predicción un paso hacia delante utilizando ReIMAE en un modelo de un parámetro de crecimiento lineal. Los errores se calcularon utilizando los últimos 200 valores de cada serie de prueba.

Alfa = 0,03 Alfa = 0,04 Alfa = 0,05 EURRUR M1 1,14 1,10 1,09 EURRUR M30 1,14 1,11 1,14 EURUSD M1 1,17 1,11 1,10 EURUSD M30 1,17 1,11 1,11 USDJPY M1 1,10 1,08 1,10 USDJPY M30 1,17 1,13 1,13 XAUUSD M1 1,20 1,11 1,10 XAUUSD M30 1,11 1,12 1,13

Tabla 1. Errores de predicción un paso hacia delante estimados utilizando ReIMAE.

La estimación ReIMAE nos permite comparar la efectividad de un método cuando hacemos predicciones sobre varias series. Como sugieren los resultados de la Tabla 1, nuestra predicción nunca fue más exacta que el método ingenuo - todos los valores de ReIMAE son mayores que uno.

6. Modelos aditivos

Había un modelo anterior en el artículo que comprendía la suma del nivel del proceso, la tendencia lineal y una variable aleatoria. Ampliaremos la lista de los modelos revisados en este artículo añadiendo otro modelo que, además de los anteriores componentes, incluye un componente cíclico y estacional.

Los modelos de ajuste exponencial que comprenden todos los componentes como una suma se llaman modelos aditivos. Aparte de estos modelos, hay modelos multiplicativos donde uno o más o incluso todos los componentes se componen de un producto. Vamos a revisar el grupo de modelos aditivos.

El error de predicción a un paso en el futuro ha sido repetidamente mencionado antes en este artículo. Este error tuvo que ser calculado en casi todas las aplicaciones relacionadas con la predicción basadas en el ajuste exponencial. Conociendo el valor del error de predicción, las fórmulas para los modelos de ajuste exponencial presentadas antes pueden mostrarse de una forma diferente (forma de corrección de error).

La forma de representación del modelo que vamos a usar en nuestro caso contiene un error en sus expresiones que es añadido, parcialmente o en su totalidad, a los valores obtenidos previamente. Dicha representación se llama modelo de error aditivo. Los modelos de ajuste exponencial también pueden expresarse en forma de error multiplicativo que sin embargo no será usada en este artículo.

Vamos a echar un vistazo a los modelos de ajuste exponencial aditivos:

Ajuste exponencial simple:

Modelo equivalente – ARIMA(0,1,1):

Modelo de crecimiento lineal aditivo:

Al contrario del modelo de crecimiento lineal de un parámero presentado antes, aquí se usan dos parámetros de ajuste distintos.

Modelo equivalente – ARIMA(0,2,2):

Modelo de crecimiento lineal con amortiguación:

El significado de dicha amortiguación es que la pendiente de dicha tendencia disminuirá en cada paso en la predicción correspondiente dependiendo del valor del coeficiente de amortiguación. Este efecto se muestra en la Fig. 4.

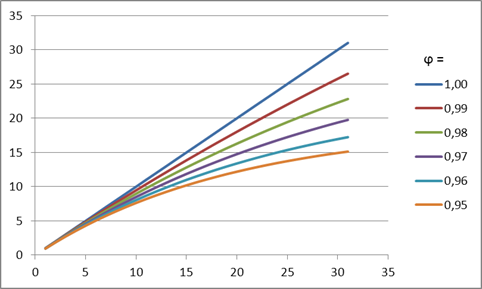
Figura 4. Efecto del coefciente de amortiguación

Como puede verse en la figura, cuando hacemos una predicción, un valor decreciente del coeficiente de amortiguación hará que la tendencia pierda su fuerza con más rapidez, y por tanto el crecimiento lineal estará cada vez mas amortiguado.

Modelo equivalente – ARIMA (1,1,2):

Añadiendo un componente estacional como la suma de cada uno de estos tres modelos obtendremos tres modelos más.

Modelo simple con estacionalidad aditiva:

Modelo de crecimiento lineal con estacionalidad aditiva:

Modelo de crecimiento lineal con estacionalidad de amortiguación y aditiva:

Hay también modelos ARIMA equivalentes a los modelos con estacionalidad pero no los trataremos aquí ahora ya que no tienen apenas utilidad práctica.

Las notaciones utilizadas en las fórmulas son las siguientes:

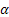• – parámetro de ajuste para el nivel de la serie, [0:1];
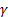• – parámetro de ajuste para la tendencia, [0:1];
• – parámetro de ajuste para los índices estacionales, [0:1];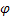
• – parámetro de amortiguación, [0:1];
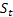• – nivel ajustado de la serie calculado en el momento t despues de que 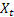ha sido observado;
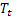• – tendencia aditiva ajustada calculada en el momento t;
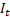• – índice aditivo ajustado calculado en el momento t;
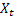• – valor de la serie en el momento t;
• m – número de pasos en el futuro para los que se realiza la predicción;
• p – número de periodos en el ciclo estacional;
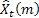• – predicción en m pasos en el futuro en el momento t;
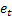• – predicción en un paso en el futuro en el momento t, .

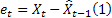Es fácil ver que las fórmulas para el último modelo incluyen seis variantes.

Si en las fórmulas para el modelo de crecimiento lineal con estacionalidad de amortiguación y aditiva tomamos la estacionalidad

,

esta será obviada en la predicción. Además, donde , se generará un modelo de crecimiento lineal y donde , obtendremos un modelo de crecimiento lineal con amortiguación.

El modelo de ajuste exponencial simple se corresponderá con .

Al emplear los modelos que utilizan la estacionalidad, la presencia de ciclos y periodo de ciclo será en primer lugar determinada usando cualquier método disponible para usar luego estos datos para la inicialización de valores de índices estacionales.

No logramos detectar una dinámica cíclica estable de cierta envergadura en los fragmentos de las series de prueba en nuestro caso, donde las predicciones se realizan en intervalos de tiempo cortos. Por tanto, en este artículo no daremos ejemplos ni nos extenderemos en las características asociadas con la estacionalidad.

Para determinar los intervalos de predicción de probabilidad con relación a los modelos considerados, usaremos la derivación analítica encontrada en la literatura [3]. La media de la suma de los cuadrados de un error de predicción a un paso en el futuro calculado sobre toda la muestra de tamaño n se usará como la varianza estimada de tales errores.

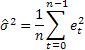
Luego la siguiente expresión será cierta para la determinacicón de la varianza estimada en una predicción para dos y más pasos por delante para los modelos considerados:

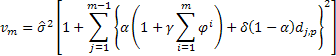
don se iguala a uno si j modulo p es cero, si no es cero.

Una vez calculada la varianza estimada de la predicción para cada paso m, podemos hallar los límites del intervalo de predicción del 95%:

Acordaremos el nombre de dicho intervalo de predicción como el intervalo de confianza de la predicción.

Vamos a implementar las expresiones para los modelos de ajuste exponencial en una clase escrita en MQL5.

7. Implementación de la clase AdditiveES

La implementación de la clase implicó el uso de las expresiones para el modelo de crecimiento lineal con estacionalidad de amortiguación y aditiva.

Como mencionamos antes, pueden derivarse otros modelos de este a partir de una adecuada selección de parámetros.

//-----------------------------------------------------------------------------------
//                                                                     AdditiveES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

//-----------------------------------------------------------------------------------
// Forecasting. Ajuste exponencial. Modelos aditivos
// References:
// 1. Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II.
//    June 3, 2005.
// 2. Rob J Hyndman. Forecasting based on state space models for exponential
//    smoothing. 29 August 2002.
// 3. Rob J Hyndman et al. Prediction intervals for exponential smoothing
//    using two new classes of state space models. 30 January 2003.
//-----------------------------------------------------------------------------------
class AdditiveES:public CObject
  {
protected:
  double Alpha;    // Smoothed parameter for the level of the series
  double Gamma;    // Smoothed parameter for the trend
  double Phi;      // Autoregressive or damping parameter
  double Delta;    // Smoothed parameter for seasonal indices
  int    nSes;     // Number of periods in the seasonal cycle
  double S;        // Smoothed level of the series, computed after last Y is observed
  double T;        // Smoothed additive trend
  double Ises[];   // Smoothed seasonal indices
  int    p_Ises;   // Pointer for Ises[] shift register
  double F;        // Forecast for 1 period ahead from origin t

public:
         AdditiveES();
  double Init(double s,double t,double alpha=1,double gamma=0,
              double phi=1,double delta=0,int nses=1);
  double GetS()                 { return(S); }
  double GetT()                 { return(T); }
  double GetF()                 { return(F); }
  double GetIs(int m);
  void   IniIs(int m,double is);  // Initialization of smoothed seasonal indices
  double NewY(double y);          // Next calculating step
  double Fcast(int m);            // m-step ahead forecast
  double VarCoefficient(int m);   // Coefficient for calculating prediction intervals

  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void AdditiveES::AdditiveES()
  {
  Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0; S=0; T=0;
  }
//-----------------------------------------------------------------------------------
// Initialization
//-----------------------------------------------------------------------------------
double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0,
                       double phi=1,double delta=0,int nses=1)
  {
  S=s; T=t;
  Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1;
  Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1;
  Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1;
  Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1;
  nSes=nses; if(nSes<1)nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0;
  F=S+Phi*T;
  return(F);
  }
//-----------------------------------------------------------------------------------
// Calculations for the new Y
//-----------------------------------------------------------------------------------
double AdditiveES::NewY(double y)
  {
  double e;
  
  e=y-F;
  S=S+Phi*T+Alpha*e;
  T=Phi*T+Alpha*Gamma*e;
  Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e;
  p_Ises++; if(p_Ises>=nSes)p_Ises=0;
  F=S+Phi*T+GetIs(0);
  return(F);
  }
//-----------------------------------------------------------------------------------
// Return smoothed seasonal index
//-----------------------------------------------------------------------------------
double AdditiveES::GetIs(int m)
  {
  if(m<0)m=0;
  int i=(int)MathMod(m+p_Ises,nSes);
  return(Ises[i]);
  }
//-----------------------------------------------------------------------------------
// Initialization of smoothed seasonal indices
//-----------------------------------------------------------------------------------
void AdditiveES::IniIs(int m,double is)
  {
  if(m<0)m=0;
  if(m<nSes)
    {
    int i=(int)MathMod(m+p_Ises,nSes);
    Ises[i]=is;
    }
  }
//-----------------------------------------------------------------------------------
// m-step-ahead forecast
//-----------------------------------------------------------------------------------
double AdditiveES::Fcast(int m)
  {
  int i,h;
  double v,v1;

  if(m<1)h=1; else h=m;  
  v1=1; v=0;
  for(i=0;i<h;i++){v1=v1*Phi; v+=v1;}
  return(S+v*T+GetIs(h));
  }
//-----------------------------------------------------------------------------------
// Coefficient for calculating prediction intervals
//-----------------------------------------------------------------------------------
double AdditiveES::VarCoefficient(int m)
  {
  int i,h;
  double v,v1,a,sum,k;
  
  if(m<1)h=1; else h=m;
  if(h==1)return(1);
  v=0; v1=1; sum=0;
  for(i=1;i<h;i++)
    {
    v1=v1*Phi; v+=v1;
    if((int)MathMod(i,nSes)==0)k=1; else k=0;
    a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha);
    sum+=a*a;
    }
  return(1+sum);
  }
//-----------------------------------------------------------------------------------

Vamos a revisar brevemente los métodos de la clase AdditiveES.

Método Init

Parámetros de entrada:

• double s - establece el valor inicial del nivel ajustado;
• double t - establece el valor inicial de la tendencia ajustada;
• double alpha=1 - establece el parámetro de ajuste para el nivel de la serie;
• double gamma=0 - establece el parámetro de ajuste para la tendencia;
• double phi=1 - establece el parámetro de amortiguación;
• double delta=0 - establece el parámetro de ajuste para los índices estacionales;
• int nses=1 - establece el número de periodos en el ciclo estacional.

Valor devuelto:

• Devuelve una predicción a un paso en el futuro calculada en base a los valores iniciales establecidos.

El método Init deber ser llamado en primer lugar. Esto es necesario para establecer los parámetros de ajuste y los valores iniciales. Debe señalarse que el método Init no contempla la inicialización de índices estacionales en valores arbitrarios. Cuando se llama a este método, los índices estacionales siempre se establecerán a cero.

Método Inils

Parámetros de entrada:

• Int m - número de índice estacional;
• double is - establece el valor del índice estacional número m.

Valor devuelto:

• Ninguno

El método Inils(...) es llamado cuando es necesario que los valores iniciales de los índices estacionales sean distintos a cero. Los índices estacionales deben ser inicializados justo después de llamar al método Init(...).

Método NewY

Parámetros de entrada:

• double y – nuevo valor de la serie de entrada

Valor devuelto:

• Devuelve una predicción a un paso en el futuro calculada en base al nuevo valor de la serie.

El método está pensado para calcular un predicción a un paso en el futuro cada vez que se introduce un nuevo valor de la serie de entrada. Solo debe ser llamado después de la inicialización de la clase por Init y, cuando sea necesario, por los métodos Inils.

Método Fcast

Parámetros de entrada:

• int m – predicción de un horizonte de 1,2,3,… periodos;

Valor devuelto:

• Devuelve el valor de predicción en m pasos en el futuro.

Este método calcula solo el valor de predicción sin afectar al estado del proceso de ajuste. Normalmente es llamado después del método NewY.

Método VarCoefficient

Parámetros de entrada:

• int m – predicción de un horizonte de 1,2,3,… periodos;

Valor devuelto:

• Devuelve el valor del coeficiente para calcular la varianza de la predicción.

El valor de este coeficiente muestra el aumento de la varianza de una predicción a m pasos en el futuro comparada con la varianza de la predicción a un paso en el futuro.

Métodos GetS, GetT, GetF y GetIs

Estos métodos proporcionan acceso a las variables protegidas de la clase. GetS, GetT y GetF devuelven valores del nivel ajustado, la tendencia ajustada y la predicción a un paso en el futuro, respectivamente. El método Getls proporciona acceso a los índices estacionales y requiere indicar el número de índice m como argumento de entrada.

El modelo más complejo de todos los que hemos revisado es el modelo lineal con estacionalidad de amortiguación y aditiva en base al cual se ha creado la clase AdditiveES. Esto suscita una pregunta razonable: ¿para qué son necesarios los demás modelos simples?

A pesar del hecho de que los modelos más complejos deben tener aparentemente una ventaja sobre los simples, no siempre es así en la realidad. Los modelos simples con menos parámetros darán, en la mayoría de casos, una menor varianza en los errores de predicción, es decir, su operación será más estable. Este hecho es utilizado en la creación de algoritmos de predicción en operaciones paralelas simultáneas de todos los modelos disponibles, desde los más simples a los más complejos.

Una vez que la serie ha sido procesada con éxito, se selecciona el modelo de predicción que haya mostrado el menor error dado el número de sus parámetros (es decir, su complejidad). Hay un número de criterios que se han desarrollado para esta finalidad, p. ej. el Criterio de información de Akaike (AIC). Esto dará como resultado la elección de un modelo que se espera que proporcione la predicción más estable.

Para mostrar el uso de la clase AdditiveES se creó un indicador simple en el que todos los parámetros de ajuste se establecieron manualmente.

El código fuente del indicador AdditiveES_Test.mq5 se muestra a continuación.

//-----------------------------------------------------------------------------------
//                                                                AdditiveES_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"      // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "PInterval+"    // Prediction interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCadetBlue
#property indicator_style3  STYLE_SOLID
#property indicator_width3  1
#property indicator_label4  "PInterval-"    // Prediction interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCadetBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  1

double HIST[];
double FORE[];
double PINT1[];
double PINT2[];

input double Alpha=0.2;     // Smoothed parameter for the level
input double Gamma=0.2;     // Smoothed parameter for the trend
input double Phi=0.8;       // Damping parameter
input double Delta=0;       // Smoothed parameter for seasonal indices
input int    nSes=1;        // Number of periods in the seasonal cycle
input int    nHist=250;     // History bars, nHist>=100
input int    nTest=150;     // Test interval, 50<=nTest<nHist
input int    nFore=12;      // Forecasting horizon, nFore>=2

#include "AdditiveES.mqh"
AdditiveES fc;

int    NHist;               // history bars
int    NFore;               // forecasting horizon
int    NTest;               // test interval
double ALPH;                // alpha
double GAMM;                // gamma
double PHI;                 // phi
double DELT;                // delta
int    nSES;                // Number of periods in the seasonal cycle
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NHist=nHist; if(NHist<100)NHist=100;
  NFore=nFore; if(NFore<2)NFore=2;
  NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50;
  ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1;
  GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1;
  PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1;
  DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1;
  nSES=nSes; if(nSES<1)nSES=1;

  MqlRates rates[];
  CopyRates(NULL,0,0,NHist,rates);           // Load missing data
  
  SetIndexBuffer(0,HIST,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,FORE,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFore);
  SetIndexBuffer(2,PINT1,INDICATOR_DATA);
  PlotIndexSetString(2,PLOT_LABEL,"Conf+");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFore);
  SetIndexBuffer(3,PINT2,INDICATOR_DATA);
  PlotIndexSetString(3,PLOT_LABEL,"Conf-");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFore);
  
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
  int i,j,init,start;
  double v1,v2;
  
  if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1)
    {init=1; start=rates_total-NHist;}
  else
    {init=0; start=prev_calculated;}
  if(start==rates_total)return(rates_total);    // New tick but not new bar
//-----------------------
  if(init==1)                                   // Initialization
    {
    i=start;
    v2=(open[i+2]-open[i])/2;
    v1=(open[i]+open[i+1]+open[i+2])/3.0-v2;
    fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES);
    ArrayInitialize(HIST,EMPTY_VALUE);
    }
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore);

  for(i=start;i<rates_total;i++)                // History
    {
    HIST[i]=fc.NewY(open[i]);
    }
  v1=0;
  for(i=0;i<NTest;i++)                          // Variance
    {
    j=rates_total-NTest+i;
    v2=close[j]-HIST[j-1];
    v1+=v2*v2;
    }
  v1/=NTest;                                    // v1=var
  j=1;
  for(i=rates_total-NFore;i<rates_total;i++)
    {
    v2=1.96*MathSqrt(v1*fc.VarCoefficient(j));  // Prediction intervals
    FORE[i]=fc.Fcast(j++);                    // Forecasting
    PINT1[i]=FORE[i]+v2;
    PINT2[i]=FORE[i]-v2;
    }
  
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

Una llamada o una inicialización repetida del indicador establece los valores iniciales de ajuste exponencial

No hay ajustes iniciales para los índices estacionales en este indicador, sus valores iniciales son por tanto iguales a cero. Con dicha inicialización, la influencia de la estacionalidad sobre los resultados de la predicción se incrementará gradualmente desde cero hasta un cierto valor estable con la introducción de nuevos valores.

El número de ciclos requeridos para alcanzar una condición de funcionamiento estable depende del valor del coeficiente de ajuste para los índices estacionales: cuanto menor sea el valor del coeficiente de ajuste, mayor tiempo requerirá.

El resultado de la operación del indicador AdditiveES_Test.mq5 con ajustes por defecto se muestra en la Figura 5.

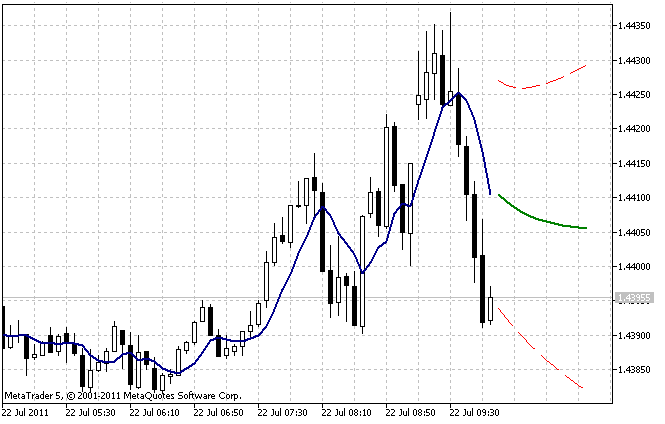
Figura 5. Indicador AdditiveES_Test.mq5

Aparte de la predicción, el indicador muestra una línea adicional correspondiente a la predicción a un paso por delante para los valores pasados de la serie y los límites del intervalo de confianza de la predicción al 95%.

El intervalo de confianza se basa en la varianza estimada de error a un paso hacia delante. Para reducir el efecto de la imprecisión de los valores iniciales elegidos, la varianza estimada no se calcula sobre toda la longitud de nHist sino solo con relación a las últimas barras cuyo número se especifica en el parámetro de entrada nTest.

El archivo Files.zip al final de este artículo incluye los archivos AdditiveES.mqh y AdditiveES_Test.mq5. Al compilar el indicador es necesario que el archivo include AdditiveES.mqh se ubique en el mismo directorio que AdditiveES_Test.mq5.

Mientras que el problema de seleccionar los valores iniciales se solucionó hasta cierto punto al crear el indicador AdditiveES_Test.mq5, el problema de seleccionar los valores óptimos de los parámetros de ajuste aún está abierto.

8. Selección óptima de los valores del parámetro

El modelo de ajuste exponencial simple tiene un solo parámetro de ajuste y su valor óptimo puede encontrarse usando el método de enumeración simple. Después de calcular los valores del error de predicción sobre toda la serie, se cambia el valor del parámetro en un pequeño incremento y se realiza de nuevo un cálculo completo. Este procedimiento se repite hasta que todos los valores de los parámetros posibles han sido enumerados. Ahora solo necesitamos elegir el valor del parámetro con el menor valor del error.

Para encontrar un valor óptimo del coeficiente de ajuste en el rango de 0,1 a 0,9 en incrementos de 0,05, todo el cálculo del valor del error de predicción deberá realizarse diecisiete veces. Como puede verse el número de cálculos requeridos no es tan grande. Pero el modelo de crecimiento lineal con amortiguación implica la optimización de los parámetros de ajuste y en este caso llevará la realización de 4.913 cálculos para enumerar todas las combinaciones en el mismo rango en los mismos incrementos de 0,05.

El número de ejecuciones completas para la enumeración de todos los valores de los parámetros posibles se incrementará rápidamente con el aumento del número de parámetros, la disminución del incremento y el aumento de la amplitud del rango de enumeración. Si es necesario optimizar más los valores iniciales de los modelos, además de los parámetros de ajuste, será muy difícil conseguirlo usando el método de enumeración simple.

Los problemas que surgen a la hora de encontrar el mínimo de una función de varias variables se han estudiado bien y hay muy pocos algoritmos de este tipo. La descripción y comparación de los distintos métodos para encontrar el mínimo de una función se encuentran disponibles en la bibliografía [7]. Todos estos métodos pretenden, fundamentalmente, reducir el número de llamadas a la función objetivo, es decir, reducir los esfuerzos de cálculo en el proceso de búsqueda del mínimo.

A menudo, se encuentran distintas fuentes con una referencia a los llamados métodos de optimización cuasi-newtonianos. Más bien tiene que ver con su gran eficiencia, pero la implementación de un método más simple debe ser también suficiente para mostrar un enfoque de la optimización de la predicción. Vamos a elegir el método de Powell. El método de Powell no requiere cálculos de derivadas de la función objetivo y pertenece a los métodos de búsqueda.

Este método, como cualquier otro, puede ser implementado programáticamente de varias formas. La búsqueda debe completarse cuando se alcanza una cierta precisión del valor o argumento de la función objetivo. Además, una cierta implementación puede incluir la posibilidad de usar limitaciones del rango permisible de los cambios en el parámetro de la función.

En nuestro caso, el algoritmo para encontrar un mínimo no restringido utilizando el método Powell se implementa en PowellsMethod.class. El algoritmo deja de buscar una vez que se logra una cierta precisión del valor de la función objetivo. En la implementación de este método se usó como prototipo un algoritmo encontrado en la bibliografía [8].

A continuación se muestra el código fuente de la clase PowellsMethod.

//-----------------------------------------------------------------------------------
//                                                                  PowellsMethod.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

#define GOLD   1.618034
#define CGOLD  0.3819660
#define GLIMIT 100.0
#define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d);
#define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a))
#define FMAX(a,b) (a>b?a:b)
//-----------------------------------------------------------------------------------
// Minimization of Functions.
// Unconstrained Powell’s Method.
// References:
// 1. Numerical Recipes in C. The Art of Scientific Computing.
//-----------------------------------------------------------------------------------
class PowellsMethod:public CObject
  {
protected:
  double P[],Xi[];
  double Pcom[],Xicom[],Xt[];
  double Pt[],Ptt[],Xit[];
  int    N;
  double Fret;
  int    Iter;
  int    ItMaxPowell;
  double FtolPowell;
  int    ItMaxBrent;
  double FtolBrent;
  int    MaxIterFlag;
public:
  void   PowellsMethod(void);
  void   SetItMaxPowell(int n)           { ItMaxPowell=n; }
  void   SetFtolPowell(double er)        { FtolPowell=er; }
  void   SetItMaxBrent(int n)            { ItMaxBrent=n;  }
  void   SetFtolBrent(double er)         { FtolBrent=er;  }
  int    Optimize(double &p[],int n=0);
  double GetFret(void)                   { return(Fret);  }
  int    GetIter(void)                   { return(Iter);  }
private:
  void   powell(void);
  void   linmin(void);
  void   mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc);
  double brent(double ax,double bx,double cx,double &xmin);
  double f1dim(double x);
  virtual double func(const double &p[]) { return(0); }
  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void PowellsMethod::PowellsMethod(void)
  {
  ItMaxPowell= 200;
  FtolPowell = 1e-6;
  ItMaxBrent = 200;
  FtolBrent  = 1e-4;
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::powell(void)
  {
  int i,j,m,n,ibig;
  double del,fp,fptt,t;
  
  n=N; Fret=func(P);
  for(j=0;j<n;j++)Pt[j]=P[j];
  for(Iter=1;;Iter++)
    {
    fp=Fret; ibig=0; del=0.0;
    for(i=0;i<n;i++)
      {
      for(j=0;j<n;j++)Xit[j]=Xi[j+n*i];
      fptt=Fret;
      linmin();
      if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;}
      }
    if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return;
    if(Iter>=ItMaxPowell)
      {
      Print("powell exceeding maximum iterations!");
      MaxIterFlag=1; return;
      }
    for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];}
    fptt=func(Ptt);
    if(fptt<fp)
      {
      t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt);
      if(t<0.0)
        {
        linmin();
        for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];}
        }
      }
    }
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::linmin(void)
  {
  int j,n;
  double xx,xmin,fx,fb,fa,bx,ax;

  n=N;
  for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];}
  ax=0.0; xx=1.0;
  mnbrak(ax,xx,bx,fa,fx,fb);
  Fret=brent(ax,xx,bx,xmin);
  for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];}
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::mnbrak(double &ax,double &bx,double &cx,
                                 double &fa,double &fb,double &fc)
  {
  double ulim,u,r,q,fu,dum;

  fa=f1dim(ax); fb=f1dim(bx);
  if(fb>fa)
    {
    SHFT(dum,ax,bx,dum)
    SHFT(dum,fb,fa,dum)
    }
  cx=bx+GOLD*(bx-ax); fc=f1dim(cx);
  while(fb>fc)
    {
    r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa);
    u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r));
    ulim=bx+GLIMIT*(cx-bx);
    if((bx-u)*(u-cx)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;}
      else if(fu>fb){cx=u; fc=fu; return;}
      u=cx+GOLD*(cx-bx); fu=f1dim(u);
      }
    else if((cx-u)*(u-ulim)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc)
        {
        SHFT(bx,cx,u,cx+GOLD*(cx-bx))
        SHFT(fb,fc,fu,f1dim(u))
        }
      }
    else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);}
      else {u=cx+GOLD*(cx-bx); fu=f1dim(u);}
    SHFT(ax,bx,cx,u)
    SHFT(fa,fb,fc,fu)
    }
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::brent(double ax,double bx,double cx,double &xmin)
  {
  int    iter;
  double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm;

  a=(ax<cx?ax:cx); b=(ax>cx?ax:cx);
  d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x);
  for(iter=1;iter<=ItMaxBrent;iter++)
    {
    xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19);
    if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);}
    if(fabs(e)>tol1)
      {
      r=(x-w)*(fx-fv); q=(x-v)*(fx-fw);
      p=(x-v)*q-(x-w)*r; q=2.0*(q-r);
      if(q>0.0)p=-p; q=fabs(q);
      etemp=e; e=d;
      if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x))
        d=CGOLD*(e=(x>=xm?a-x:b-x));
      else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);}
      }
    else d=CGOLD*(e=(x>=xm?a-x:b-x));
    u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d));
    fu=f1dim(u);
    if(fu<=fx)
      {
      if(u>=x)a=x; else b=x;
      SHFT(v,w,x,u)
      SHFT(fv,fw,fx,fu)
      }
    else
      {
      if(u<x)a=u; else b=u;
      if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;}
      else if(fu<=fv||v==x||v==w){v=u; fv=fu;}
      }
    }
  Print("Too many iterations in brent");
  MaxIterFlag=1; xmin=x;
  return(fx);
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::f1dim(double x)
  {
  int j;
  double f;
  
  for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j];
  f=func(Xt);
  return(f);
  }
//-----------------------------------------------------------------------------------
int PowellsMethod::Optimize(double &p[],int n=0)
  {
  int i,j,k,ret;
  
  k=ArraySize(p);
  if(n==0)N=k;
  else N=n;
  if(N<1||N>k)return(0);
  ArrayResize(P,N); ArrayResize(Xi,N*N);
  ArrayResize(Pcom,N); ArrayResize(Xicom,N);
  ArrayResize(Xt,N); ArrayResize(Pt,N);
  ArrayResize(Ptt,N); ArrayResize(Xit,N);
  for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0);
  for(i=0;i<N;i++)P[i]=p[i];
  MaxIterFlag=0;
  powell();
  for(i=0;i<N;i++)p[i]=P[i];
  if(MaxIterFlag==1)ret=-1;
  else ret=Iter;
  return(ret);
  }
//-----------------------------------------------------------------------------------

El método Optimize es el método principal de la clase.

Método Optimize

Parámetros de entrada:

• double &p[] - matriz que a la entrada contiene los valores iniciales de los parámetros de los valores óptimos que deben encontrarse. Los valores óptimos obtenidos de estos parámetros están en la salida de la matriz.
• int n=0 - número de argumentos en la matriz p[]. Con n=0 es el número de parámetros considerados iguales al tamaño de la matriz p[].

Valor devuelto:

• Devuelve el número de iteraciones necesarias para la operación del algoritmo, o -1 si se ha alcanzado el número máximo permisible.

Al buscar los valores del parámetro óptimos, tiene lugar una aproximación interactiva al mínimo de la función objetivo. El método Optimize devuelve el número de iteraciones necesarias para alcanzar el mínimo de la función con una precisión dada. La función objetivo es llamada varias veces en cada iteración, es decir, el número de llamadas de la función objetivo puede ser significativamente mayor (diez e incluso cien veces) que el número de iteraciones devueltas por el método Optimize.

Otros métodos de la clase.

El método SetItMaxPowell

Parámetros de entrada:

• Int n - número de iteraciones máximo permitido en el método Powell. El valor por defecto es 200.

Valor devuelto:

• Ninguno.

Establece el número máximo permitido de iteraciones. Una vez que se alcanza este número, la búsqueda habrá terminado con independencia de si se ha encontrado el mínimo de la función objetivo con una precisión dada. Y se añadirá al registro el mensaje correspondiente.

Método SetFtolPowell

Parámetros de entrada:

• double er - precisión. Si se alcanza este valor de derivación a partir del valor mínimo de la función objetivo, el método Powell deja de buscar. El valor por defecto es 1E-6.

Valor devuelto:

• Ninguno.

Método SetItMaxBrent

Parámetros de entrada:

• Int n - número de iteraciones máximo permitido en el método auxiliar de Brent. El valor por defecto es 200.

Valor devuelto:

• Ninguno.

Establece el máximo número de iteraciones permitido. Una vez que se alcanza, el método auxiliar de Brent dejará de buscar y se añadirá al registro el mensaje correspondiente.

Método SetFtolBrent

Parámetros de entrada:

• double er - precisión. Este valor establece la precisión en la búsqueda del mínimo para el método auxiliar de Brent. El valor por defecto es 1E-4.

Valor devuelto:

• Ninguno.

Método GetFret

Parámetros de entrada:

• Ninguno.

Valor devuelto:

• Devuelve el valor mínimo de la función objetivo obtenida.

Método GetIter

Parámetros de entrada:

• Ninguno.

Valor devuelto:

• Devuelve el número de iteraciones necesarias para el funcionamiento del algoritmo.

Función virtual func(const double &p[])

Parámetros de entrada:

• const double &p[] – dirección de la matriz que contiene los parámetros optimizados. El tamaño de la matriz se corresponde con el número de parámetros de la función.

Valor devuelto:

• Devuelve el valor de la función correspondiente a los parámetros pasados a esta.

La función virtual func() debe, en todos los casos particulares, redefinirse en una clase derivada de la clase PowellsMethod. La función func() es la función objetivo cuyos argumentos corresponden al valor mínimo devuelto por la función obtenida al aplicar el algoritmo de búsqueda.

Esta implementación del método Powell utiliza el método de interpolación parabólica de una variable de Brent para determinar la dirección de búsqueda con relación a cada parámetro. La precisión y el número máximo admitido de iteraciones para estos métodos pueden establecerse por separado llamando a SetItMaxPowell, SetFtolPowell, SetItMaxBrent y SetFtolBrent.

Por tanto, las características por defecto del algoritmo pueden cambiarse de esta forma. Esto puede parecer útil cuando la precisión por defecto que se establece para una función objetivo resulta ser demasiado alta y el algoritmo necesita demasiadas iteraciones en el proceso de búsqueda. El cambio en el valor de la precisión necesaria puede optimizar la búsqueda con relación a las diferentes categorías de funciones objetivo.

A pesar de esta aparente complejidad del algoritmo que utiliza el método Powell, es muy sencillo de usar.

Vamos a ver un ejemplo. Supongamos que tenemos una función

y que necesitamos encontrar los valores de los parámetros y en los que la función tendrá el menor valor.

Vamos a escribir un script que muestra la solución a este problema.

//-----------------------------------------------------------------------------------
//                                                                        PM_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
class PM_Test:public PowellsMethod
  {
public:
  void   PM_Test(void) {}
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
double PM_Test::func(const double &p[])
  {
  double f,r1,r2;
  
  r1=p[0]-0.5;
  r2=p[1]-6.0;
  f=r1*r1*4.0+r2*r2;
  return(f);
  }
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  int it;
  double p[2];

  p[0]=8; p[1]=9;                                 // Initial point
  PM_Test *pm = new PM_Test;
  it=pm.Optimize(p);
  Print("Iter= ",it,"        Fret= ",pm.GetFret());
  Print("p[0]= ",p[0],"    p[1]= ",p[1]);
  delete pm;
  }
//-----------------------------------------------------------------------------------

Al escribir este script primero creamos la función func() como miembro de la clase PM_Test que calcula el valor de la función de prueba dada usando los valores pasados de los parámetros p[0] y p[1]. Luego, en el cuerpo de la función OnStart(), los valores iniciales se asignan a los parámetros requeridos. La búsqueda empezará a partir de estos valores.

Además, se crea una copia de la clase PM_Test y la búsqueda de los valores requeridos p[0] y p[1] comienza con la llamada al método Optimize. Los métodos de la clase matriz PowellsMethod llamarán a la función func() redefinida. Al completarse la búsqueda, el número de iteraciones, el valor de la función en el punto mínimo y los valores del parámetro obtenidos p[0]=0.5 y p[1]=6 se añadirán al registro.

PowellsMethod.mqh y un caso de prueba PM_Test.mq5 se encuentran al final del artículo en el archivo Files.zip. Para compilar PM_Test.mq5 debe ubicarse en el mismo directorio que PowellsMethod.mqh.

9. Optimización de los valores del parámetro del modelo

La sección anterior del artículo trató la implementación del método para encontrar el mínimo de la función y mostró un ejemplo simple de su uso. Ahora veremos los aspectos relacionados con la optimización de los parámetros del modelo de ajuste exponencial.

Para empezar, vamos a simplificar la clase mostrada anteriormente AdditiveES al máximo eliminando de ella todos los elementos asociados con un componente estacional, ya que los modelos que tienen en cuenta la estacionalidad no van a ser considerados más en este artículo. Esto permitirá que el código fuente de la clase sea mucho más sencillo de entender y reducirá el número de cálculos. Además, también excluiremos todos los cálculos relacionados con la predicción y cómputos de los intervalos de confianza de la predicción para una demostración sencilla de un enfoque de la optimización de los parámetros del modelo de crecimiento lineal con amortiguación.

//-----------------------------------------------------------------------------------
//                                                                     OptimizeES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class OptimizeES
//-----------------------------------------------------------------------------------
class OptimizeES:public PowellsMethod
  {
protected:
  double Dat[];            // Input data
  int    Dlen;             // Data lenght
  double Par[5];           // Parameters
  int    NCalc;            // Number of last elements for calculation
public:
  void   OptimizeES(void) {}
  int    Calc(string fname);
private:
  int    readCSV(string fnam,double &dat[]);
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// Calc
//-----------------------------------------------------------------------------------
int OptimizeES::Calc(string fname)
  {
  int i,it;
  double relmae,naiv,s,t,alp,gam,phi,e,ae,pt;
  
  if(readCSV(fname,Dat)<0){Print("Error."); return(-1);}
  Dlen=ArraySize(Dat);
  NCalc=200;                               // number of last elements for calculation
  if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);}
  Par[0]=Dat[Dlen-NCalc];                  // initial S
  Par[1]=0;                                // initial T
  Par[2]=0.5;                              // initial Alpha
  Par[3]=0.5;                              // initial Gamma
  Par[4]=0.5;                              // initial Phi
  it=Optimize(Par);                        // Powell's optimization
  s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4];
  relmae=0; naiv=0;
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t);
    relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]);
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  relmae/=naiv;
  PrintFormat("%s:    N=%i,  RelMAE=%.3f",fname,NCalc,relmae);
  PrintFormat("Iter= %i,  Fmin= %e",it,GetFret());
  PrintFormat("p[0]= %.5f,  p[1]= %.5f,  p[2]= %.2f,  p[3]= %.2f,  p[4]= %.2f",
                                             Par[0],Par[1],Par[2],Par[3],Par[4]);
  return(0);
  }
//-----------------------------------------------------------------------------------
// readCSV
//-----------------------------------------------------------------------------------
int OptimizeES::readCSV(string fnam,double &dat[])
  {
  int n,asize,fhand;
    
  fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
  if(fhand==INVALID_HANDLE)
    {
    Print("FileOpen Error!");
    return(-1);
    }
  asize=512;
  ArrayResize(dat,asize);
  n=0;
  while(FileIsEnding(fhand)!=true)
    {
    dat[n++]=FileReadNumber(fhand);
    if(n+128>asize)
      {
      asize+=128;
      ArrayResize(dat,asize);
      }
    }
  FileClose(fhand);
  ArrayResize(dat,n-1);
  return(0);

  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double OptimizeES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}                 // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}                 // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}                 // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}                 // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }                 // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}                 // Phi     < 0.05
  sse=0; 
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(NCalc*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

La clase OptimizeES deriva de la clase PowellsMethod e incluye la redefinición de la función virtual func(). Como se mencionó antes, los parámetros cuyo valor calculado será minimizado durante la optimización deben pasarse a la entrada de esta función.

De acuerdo con el método de máxima verosimilitud, la función func() calcula el logaritmo de la suma de los cuadrados de los errores de predicción a un paso en el futuro. Los errores se calculan en un bucle con relación a los valores recientes de NCalc de la serie.

Para preservar la estabilidad del modelo, debemos imponer limitaciones al rango de cambios en sus parámetros. Este rango para los parámetros Alpha y Gamma será de 0,05 a 0,95 y para el parámetro Phi de 0,05 a 1,0. Pero para la optimización en nuestro caso usamos un método para encontrar un mínimo no restringido que no implique el uso de limitaciones de los argumentos de la función objetivo.

Intentaremos convertir el problema de encontrar el mínimo de una función con múltiples variables en el problema de encontrar un mínimo no restringido para poder tener en cuenta todas las limitaciones impuestas a los parámetros sin cambiar el algoritmo de búsqueda. Para esta finalidad, se usará el llamado método de la función de penalización. Este método puede demostrarse fácilmente para un caso de una dimensión.

Supongamos que tenemos una función de un solo argumento (cuyo dominio es desde 2,0 a 3,0) y un algoritmo que en el proceso de búsqueda pueda asignar cualquier valor a este parámetro de la función. En este caso, podemos hacer lo siguiente: si el algoritmo de búsqueda ha pasado un argumento que excede el máximo valor permitido, p. ej. 3,5, la función puede calcularse para un argumento igual a 3 y el resultado obtenido se multiplica luego por un coeficiente proporcional al exceso sobre el valor máximo, por ejemplo k=1+(3,5-3)*200.

Si se realizan operaciones similares con relación a los valores del argumento que resultó estar por debajo del valor mínimo admitido, se garantiza que la función objetivo resultante se incrementará fuera del rango permisible de cambios en su argumento. Dicho incremento artificial en el valor resultante de la función objetivo permite mantener el algoritmo de búsqueda sin que este sea consciente de que el argumento pasado a la función fue de cualquier modo limitado y garantiza que el mínimo de la función resultante estará comprendido dentro de los límites del argumento. Dicho enfoque se aplica fácilmente a una función de varias variables.

El método principal de la clase OptimizeES es el método Calc. Una llamada de este método es la responsable de leer los datos en un archivo, buscar los valores del parámetro óptimo de un modelo y estimar la precisión de la predicción usando ReIMAE para los valores del parámetro obtenidos. El número de valores procesados de la serie leída del archivo se establece en este caso en la variable NCalc.

A continuación se muestra un ejemplo del script Optimization_Test.mq5 que usa la clase OptimizeES.

//-----------------------------------------------------------------------------------
//                                                              Optimization_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "OptimizeES.mqh"

OptimizeES es;
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  es.Calc("Dataset\\USDJPY_M1_1100.TXT");
  }
//-----------------------------------------------------------------------------------

Después de la ejecución de este script, el resultado obtenido se muestra a continuación.

 

Figura 6. Resultado del script Optimization_Test.mq5

Aunque podemos encontrar ahora valores del parámetro y valores iniciales óptimos del modelo, hay aún otro parámetro que no puede optimizarse usando herramientas simples: el número de valores de la serie utilizados en la optimización. En la optimización de una serie de gran longitud, obtendremos los valores del parámetro óptimos que, de media, aseguren un error mínimo sobre toda la longitud de la serie.

Sin embargo, si la naturaleza de la serie varió dentro de este intervalo, los valores obtenidos para algunos de sus fragmentos ya no serán óptimos. Por otro lado, si la longitud de la serie disminuye drásticamente, no hay garantías de que los parámetros óptimos obtenidos para un intervalo tan corto sean óptimos durante un espacio de tiempo más prolongado.

OptimizeES.mqh y Optimization_Test.mq5 se encuentran al final del artículo en el archivo Files.zip. Al compilar, es necesario que OptimizeES.mqh y PowellsMethod.mqh estén ubicados en el mismo directorio que el archivo Optimization_Test.mq5 compilado. En el ejemplo mostrado se usa el archivo USDJPY_M1_1100.TXT que contiene la serie de prueba y que debe ubicarse en el directorio \MQL5\Files\Dataset\.

La Tabla 2 muestra las estimaciones de la precisión de la predicción obtenida usando ReIMAE por medio de este script. La predicción se hizo respecto a las ocho series de prueba mencionadas antes en el artículo usando los últimos 100, 200 y 400 valores de cada una de estas series.

N=100 N=200 N=400 EURRUR M1 0,980 1,000 0,968 EURRUR M30 0,959 0,992 0,981 EURUSD M1 0,995 0,981 0,981 EURUSD M30 1,023 0,985 0,999 USDJPY M1 1,004 0,976 0,989 USDJPY M30 0,993 0,987 0,988 XAUUSD M1 0,976 0,993 0,970 XAUUSD M30 0,973 0,985 0,999

Tabla 2. Errores de predicción estimados utilizando ReIMAE.

Como puede verse, las estimacioens del error de predicción están cerca de la unidad pero en la mayoría de casos la predicción para las series dadas en este modelo es más precisa que en el método simple.

10. El indicador IndicatorES.mq5

El indicador AdditiveES_Test.mq5 basado en la clase AdditiveES.mqh se mencionó antes al revisar la clase. Todos los parámetros de ajuste en este indicador se establecieron manualmente.

Ahora, después de considerar el método que permite optimizar los parámetros del modelo, podemos crear un indicador donde los valores del parámetro óptimos o los valores iniciales se determinen automáticamente y solo sea necesario establecer manualmente la longitud de la muestra procesada. Dicho esto, excluiremos todos los cálculos relativos a la estacionalidad.

El código fuente de la clase CIndiсatorES usada al crear el indicador se muestra a continuación.

//-----------------------------------------------------------------------------------
//                                                                   CIndicatorES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class CIndicatorES
//-----------------------------------------------------------------------------------
class CIndicatorES:public PowellsMethod
  {
protected:
  double Dat[];                                              // Input data
  int    Dlen;                                               // Data lenght
  double Par[5];                                             // Parameters
public:
  void   CIndicatorES(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)            { if(n>=0||n<5)return(Par[n]); else return(0); }
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// CalcPar
//-----------------------------------------------------------------------------------
void CIndicatorES::CalcPar(double &dat[])
  {

  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayCopy(Dat,dat);
 
  Par[0]=Dat[0];                                             // initial S
  Par[1]=0;                                                  // initial T
  Par[2]=0.5;                                                // initial Alpha
  Par[3]=0.5;                                                // initial Gamma
  Par[4]=0.5;                                                // initial Phi
  Optimize(Par);                                             // Powell's optimization
  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double CIndicatorES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}           // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}           // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}           // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}           // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }           // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}           // Phi     < 0.05
  sse=0; 
  for(i=0;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(Dlen*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

Esta clase contiene los métodos CalcPar y GetPar. El primero está pensado para el cálculo de los valores del parámetro óptimo del modelo y el segundo está destinado a acceder a estos valores. Además, la clase CIndicatorES comprende la redefinición de la función virtual func().

El código fuente del indicador IndicatorES.mq5:

//-----------------------------------------------------------------------------------
//                                                                    IndicatorES.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"                 // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "ConfUp"                   // Confidence interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCrimson
#property indicator_style3  STYLE_DOT
#property indicator_width3  1
#property indicator_label4  "ConfDn"                   // Confidence interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCrimson
#property indicator_style4  STYLE_DOT
#property indicator_width4  1

input int nHist=80; // History bars, nHist>=24

#include  "CIndicatorES.mqh"
#define   NFORE 12

double    Hist[],Fore[],Conf1[],Conf2[];
double    Data[];
int       NDat;

CIndicatorES   Es;
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NDat=nHist; if(NDat<24)NDat=24;
  MqlRates rates[];
  CopyRates(NULL,0,0,NDat,rates);                   // Load missing data
  ArrayResize(Data,NDat);
    
  SetIndexBuffer(0,Hist,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,Fore,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFORE);
  SetIndexBuffer(2,Conf1,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(2,PLOT_LABEL,"ConfUp");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFORE);
  SetIndexBuffer(3,Conf2,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(3,PLOT_LABEL,"ConfDN");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFORE);
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int  &spread[])
  {
  int i,start;
  double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci;
  
  if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar
  start=rates_total-NDat;
//-----------------------
  PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat);
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE);
  
  for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data
  Es.CalcPar(Data);                                    // Optimization of parameters
  s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4);
  f=(s+phi*t); var=0;
  for(i=0;i<NDat;i++)                                // History
    {
    e=Data[i]-f; var+=e*e;
    a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
    f=(s+phi*t); Hist[start+i]=f;
    }
  var/=(NDat-1); a1=1; a2=0; a3=1;
  for(i=rates_total-NFORE;i<rates_total;i++)
    {
    a1=a1*phi; a2+=a1;
    Fore[i]=s+a2*t;                                 // Forecast
    ci=1.96*MathSqrt(var*a3);                        // Confidence intervals
    a=alp*(1+a2*gam); a3+=a*a;
    Conf1[i]=Fore[i]+ci;
    Conf2[i]=Fore[i]-ci;
    }
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

Con cada nueva barra, el indicador encuentra valores óptimos de los parámetros del modelo, hace los cálculos en el modelo para un número definido de barras NHist, realiza una predicción y define los límites de confianza de la predicción.

El único parámetro del indicador es la longitud de la serie procesada cuyo valor mínimo está limitado a 24 barras. Todos los cálculos en el indicador se realizan en base a los valores de open[]. El horizonte de la predicción es 12 barras. El código del indicador IndicatorES.mq5 y el archivo CIndicatorES.mqh se encuentran al final del artículo en el archivo Files.zip.

 

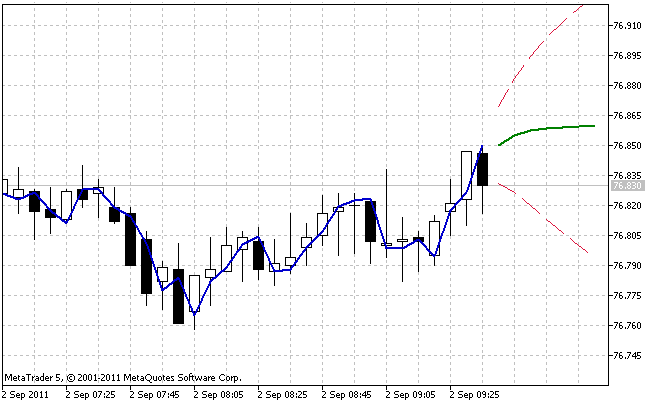
Figura 7. Resultado de la operación del indicador IndicatorES.mq5

En la Figura 7 se muestra un ejemplo del resultado de la operación del indicador IndicatorES.mq5. Durante la operación del indicador, el intervalo de confianza de la predicción del 95% tomará los valores correspondientes a los parámetro sóptimos obtenidos del modelo. Cuanto mayores sean los valores del parámetro de ajuste, más rápido será el incremento del intervalo de confianza sobre el horizonte de la predicción.

Con una simple mejora el indicador IndicatorES.mq5 puede usarse no solo para la precisión de la predicción sino también para los valores de predicción de varios indicadores o datos preprocesados.

Conclusión

El objetivo principal de este artículo fue familiarizar al lector con los modelos de ajuste exponencial aditivos usados en la predicción. Al demostrar su uso práctico hemos visto también algunas cuestiones relacionadas. Sin embargo, los materiales que se proporcionan en este artículo solo pueden considerarse una mera introducción al gran abanico de problemas y soluciones asociados con la predicción.

Me gustaría llamar la atención sobre el hecho de que las clases, funciones, scripts e indicadores proporcionados se crearon durante la escritura de este artículo y están pensados sobre todo para que sirvan de ejemplo a los materiales del artículo. Por tanto, no se ha realizado ninguna prueba importante sobre la estabilidad y los errores. Además, los indicadores que se muestran en el artículo deben considerarse solo una demostración de la implementación de los métodos utilizados.

La precisión de la predicción del indicador presentada en este artículo puede ser mejorada usando las modificaciones del modelo aplicado más adecuado en términos de las peculiaridades de las cotizaciones consideradas. El indicador puede ser también ampliado por otros modelos. Pero estas cuestiones quedan fuera del alcance de este artículo.

En conclusión, debe señalarse que los modelos de ajuste exponencial pueden, en ciertos casos, producir predicciones de la misma precisión que las obtenidas aplicando modelos más complejos, probando una vez más que incluso el modelo más complejo no siempre es el mejor.

Bibliografía

1. Everette S. Gardner Jr. Exponential Smoothing: The State of the Art – Part II. //    June 3, 2005.
2. Rob J Hyndman. Forecasting Based on State Space Models for Exponential Smoothing. 29 August 2002.
3. Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30 January 2003.
4. Rob J Hyndman and Muhammad Akram. Some Nonlinear Exponential Smoothing Models Are Unstable. 17 January 2006.
5. Rob J Hyndman and Anne B Koehler. Another Look at Measures of Forecast Accuracy. 2 November 2005.
6. Yu. P. Lukashin. Adaptive Methods for Short-Term Forecasting of Time Series: Textbook. - М.: Finansy i Statistika, 2003.-416 pp.
7. D. Himmelblau. Applied Nonlinear Programming. М.: Mir, 1975.
8. Numerical Recipes in C. The Art of Scientific Computing. Second Edition. Cambridge University Press.