Análisis de las Características Principales de las Series Cronológicas
Victor | 31 marzo, 2014
Introducción
El análisis de procesos representado por series de precio es una difícil tarea que a menudo requiere una cantidad de tiempo y esfuerzo significativa. Esto es a causa de las peculiaridades de las secuencias que se estudian, así como el hecho de que a pesar del gran número de publicaciones que hay al respecto, a veces es complicado adecuar una solución de programación a un problema determinado.
Aún si se encuentra un script o indicador adecuado, no significa que su código fuente no necesite ser ajustado para la tarea que tenemos entre manos.
Además, incluso en soluciones de problemas simples, estos programas pueden requerir el uso de parámetros de entrada, cuya función es bien conocida por los desarrolladores, pero no siempre está clara para un usuario.
Estas dificultades no son en absoluto un obstáculo insalvable en investigación, pero cuando una persona desea comprobar una sugestión, o simplemente satisfacer su curiosidad, a menudo se debe quedar con las ganas. Por eso se me ocurrió crear una herramienta de programación universal que permitiera el análisis preliminar fácil de las características principales y parámetros de una secuencia de entrada.
Esta herramienta debería ser muy sencilla para instalar, sin requerir parámetros de entrada para simplificar su uso al máximo. Al mismo tiempo, los parámetros y características calculadas deberían reflejar adecuada y claramente la naturaleza de la secuencia que estamos considerando.
El cálculo preliminar de características podría ayudar a determinar la forma para un estudio en profundidad, o rechazar cualquier sugestión en una etapa temprana y evitar la pérdida de tiempo que ello supondría.
Es bien sabido que el software universal a menudo resulta pobre en comparación con software personalizado en términos de características. Este es un precio habitual por esa universalidad, que casi siempre se consigue por medio de un sistema entero de compromisos. No obstante, este artículo representa un esfuerzo por crear una herramienta universal que permite facilitar al máximo el análisis preliminar de características de secuencias.
Instalación y Capacidad
El archivo TSAnalysis.zip, que se puede encontrar al final del artículo, incluye el directorio \TSAnalysis con todos los archivos requeridos para el trabajo. Tras descomprimirlo, debe copiar el directorio con todos sus componentes (sin cambiar su nombre) en la carpeta \MQL5\Scripts. El directorio copiado \TSAnalysis contiene un script de prueba TSAexample.mq5, que se puede usar tras su compilación.
Este script preparará todos los datos y llamará al navegador por defecto para mostrarlos usando la clase TSAnalysis. Note que el uso de DLLs externos se debe activar en el terminal para la operación correcta de la clase TSAnalysis. Para desinstalarlo, basta con eliminar el directorio \TSAnalysis.
El código fuente completo usado para este análisis de secuencias se representa por la clase TSAnalysis y solo se puede encontrar en el archivo TSAnalysis.mqh.
Al usar esta clase para una secuencia de entrada, calcula y puede mostrar la siguiente información:
- Número de elementos en la secuencia;
- Valores máximo y mínimo de la secuencia (max, min);
- Mediana;
- Media;
- Diferencia;
- Desviación estándar;
- Diferencia objetiva;
- Desviación estándar objetiva;
- Oblicuidad;
- Kurtosis;
- Kurtosis excesiva;
- Test Jarque-Bera;
- Valor p de test Jarque-Bera;
- Test Jarque-Bera ajustado;
- Valores p de test Jarque-Bera ajustado
- Límites de valores que no pertenecen a la secuencia especificada (outliers);
- Datos de histograma;
- Datos de Dibujo de Probabilidad Normal (Normal Probability Plot);
- Datos de correlograma;
- Bandas de confianza al 95% para la función de autocorrelación;
- Datos del Dibujo Espectral (Spectral Plot) calculados a través de la función de autocorrelación;
- Datos del Dibujo de la Función de Autocorrelación Parcial (Partial Autocorrelation Function Plot);
- Datos del Dibujo de Cálculo Espectral (Spectral Estimation Plot) calculados usando el método de máxima entropía.
Para mostrar los resultados obtenidos de forma visual en la clase TSAnalysis que estamos considerando se usa un método de visualización virtual que se encarga solo de un método de visualización de información preparado previamente.
Por tanto, redefiniendo este método en los descendientes de la clase TSAnalysis podremos distribuir el formato de los resultados como queramos, no solo usando un archivo HTML como clase base donde, con cada generación de un archivo de datos para la visualización en gráficos, se llama a un navegador.
Antes de seguir con la revisión de la clase TSAnalysis ilustraremos los resultados de su uso a través de una secuencia de datos de prueba. La figura de abajo muestra el resultado de la ejecución del script TSAexample.mq5.
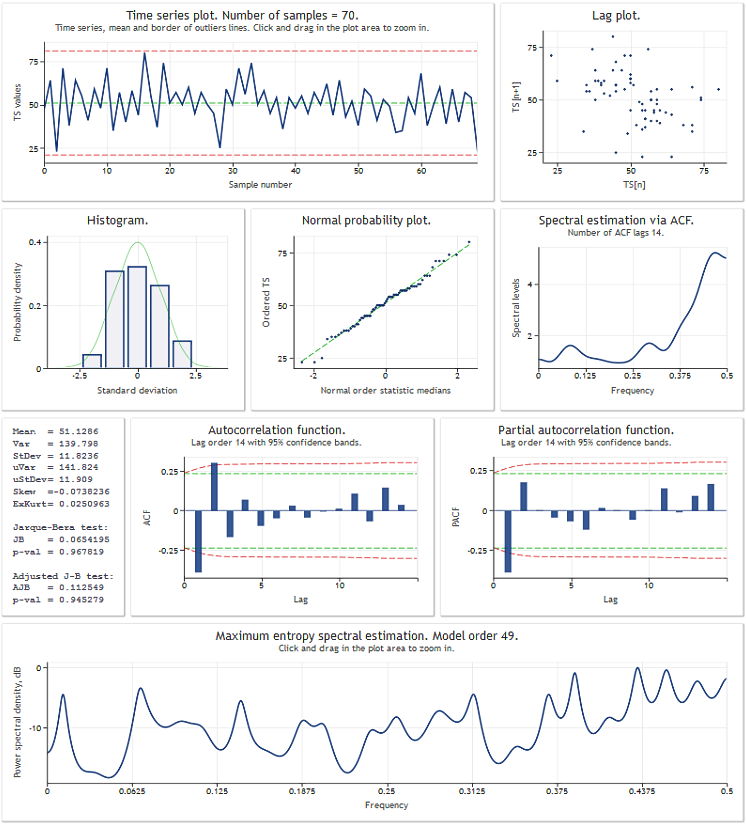
Figura 1. Resultado de la ejecución del script TSAexample.mq5.
Tras una breve introducción a la capacidad de la clase TSAnalysis, ahora procederemos a una consideración más detallada de la clase misma.
Clase TSAnalysis
La clase TSAnalysis (vea el script TSAnalysis.mqh) incluye solo un método disponible (público), Calc, que se encarga de todos los cálculos necesarios que siguen a la llamada del método de visualización virtual. El método de visualización se revisará brevemente después, y ahora procederemos a una aclaración paso a paso del principal objetivo de los cálculos hechos.
Al usar la clase TSAnalysis se impusieron algunos límites en la secuencia de entrada que estamos estudiando.
Primero, la secuencia deberá constar de al menos ocho elementos. Este límite probablemente no es muy rígido, puesto que apenas es necesario estudiar secuencias tan cortas por propósitos prácticos.
Además del límite de longitud mínima de secuencia, el valor de diferencia de la secuencia de entrada debe ser un valor diferente a cero. Este requisito se debe al hecho de que el valor de la diferencia se usa en otros cálculos y no puede ser menor que un valor determinado para conseguir un resultado estable.
Las secuencias con un valor de diferencia muy bajo no son muy comunes, de modo que este límite probablemente no nos supondrá una desventaja notable. Si la secuencia es demasiado corta, o si hay un valor de diferencia cercano a cero, los cálculos se interrumpirán, y aparecerá un mensaje de error en el registro.
Hay otro límite implícito relativo a la longitud máxima permitida para una secuencia de entrada. Este límite no se establece explícitamente, y depende del rendimiento de un ordenador y su capacidad de memoria. Se determina de forma puramente subjetiva por el tiempo requerido para la ejecución del script y la velocidad de dibujo de los resultados en un navegador web. Se supone que el procesamiento de secuencias que constan de 2.000 o 3.000 elementos no debería causar serias dificultades.
El cálculo de parámetros estadísticos de la secuencia se basará en el fragmento de abajo del código fuente del método Calc (vea TSAnalysis.mqh).
Puede encontrar la descripción del algoritmo empleado en el siguiente enlace: "Algorithms for Calculating Variance" ("Algoritmos para Calcular Diferencia").
. . . Mean=0; sum2=0; sum3=0; sum4=0; for(i=0;i<NumTS;i++) { n=i+1; delta=TS[i]-Mean; a=delta/n; Mean+=a; // Mean (average) sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // sum of fourth degree b=TS[i]-Mean; sum3+=a*(b*delta*(n-2.0)-3.0*sum2); // sum of third degree sum2+=delta*b; // sum of second degree } . . .
Como resultado de la ejecución de este fragmento, se calculan los siguientes valores
![]()
donde n = NumTS es el número de elementos en la secuencia.
Usando los valores obtenidos, calculamos los siguientes parámetros.
Diferencia y desviación estándar:
![]()
Diferencia objetiva y desviación estándar:
![]()
Oblicuidad:
![]()
Kurtosis. La kurtosis mínima es 1, la kurtosis de la secuencia distribuida normalmente será 3.
![]()
Kurtosis excesiva:
![]()
En este caso, la kurtosis mínima es -2, y la kurtosis de la secuencia distribuida normalmente será 0.
Convencionalmente, al ejecutar el primer test goodness-of-fit (adecuación del ajuste) en una secuencia, la estadística Jarque-Bera se usa, lo que se calcula fácilmente usando los valores conocidos de oblicuidad y kurtosis. El significado estadístico (valor p) para la estadística Jarque-Bera con el aumento de la longitud de secuencia tiende asintóticamente a la función de distribución inversa χ² con dos grados de libertad.
Por tanto,
![]()
Donde la secuencia sea corta, el valor p obtenido de esta manera tendrá un error apreciable. A pesar de ello, esta misma opción de cálculo se usa mucho. Es difícil decir por qué. Quizás sea por las fórmulas simples y claras que se usan en él, o puede ser el hecho de que la estadística Jarque-Bera misma no representa un test de adecuación del ajuste ideal, y por tanto no tiene sentido en hacer cálculos más precisos.
En nuestro caso, la estadística Jarque-Bera y el valor p relevante se calculan en el método Calc (TSAnalysis.mqh), de acuerdo con las fórmulas de arriba.
Además, se calcula también un test Jarque-Bera ajustado:
![]()
donde
![]()
La versión ajustada del test Jarque-Bera para secuencias cortas reduce el error del valor p calculado de la forma especificada, pero no lo elimina del todo.
Se supone que el resultado final del análisis incluye un gráfico de secuencia de entrada que muestra la línea correspondiente con la media y las líneas que definen los límites fuera de la zona en la que los valores se pueden considerar no válidos y que no pertenecen a la secuencia especificada (outliers).
Estos límites se calculan en este caso de la siguiente manera:
![]()
![]()
Esta fórmula viene en el libro de S. V. Bulashev "Statistics for Traders" ("Estadísticas para Traders") con una referencia al libro de P. V. Novitsky y I.A. Zograf "Estimation of Error in Measurement Results" ("Cálculo de Error en Resultados de Medición"). Tras determinar los límites, no se pretende llevar a cabo un procesamiento de la secuencia de entrada; los límites solo se deberían mostrar para dar información.
Además del gráfico de secuencia de entrada, se debería mostrar un histograma que refleje un cálculo empírico de la distribución de secuencia de entrada. El número de intervalos para el histograma se define de la siguiente manera (S. V. Bulashev "Statistics for Traders" ("Estadísticas para Traders"):
![]()
El resultado redondeado hacia abajo, hacia el valor íntegro impar más cercano. Si el valor obtenido es menor de cinco, se usa el valor 5.
El número de elementos en arrays de datos para el eje X y el eje Y del histograma se corresponde con el número obtenido de intervalos más dos, puesto que una columna de valor cero se añade a la izquierda y a la derecha del histograma.
Abajo puede ver un fragmento del código (vea TSAnalysis.mqh) que prepara los datos para construir un histograma.
. . . n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0); if((n&0x01)==0)n--; if(n<5)n=5; // Number of bins ArrayResize(XHist,n); ArrayResize(YHist,n); ArrayInitialize(YHist,0.0); a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean); if(a<b)a=b; v=Mean-a; delta=2.0*a/n; for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // Histogram. X-axis for(i=0;i<NumTS;i++) { k=(int)((TS[i]-v)/delta); if(k>(n-1))k=n-1; YHist[k]++; } for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev; // Histogram. Y-axis . . .
En el código de arriba:
- NumTS es el número de elementos en la secuencia,
- XHist[] y YHist[] son arrays que contienen valores para el eje X y el eje Y, respectivamente,
- TSort[] es el array que contiene una secuencia de entrada ordenada.
Usando este método, los valores del eje X se expresarán en unidades de desviación estándar, y los valores del eje Y se corresponderán con la densidad de probabilidad.
Para el propósito de construir un gráfico con el eje de distribución normal, la secuencia de entrada ordenada en orden ascendente se usa como valores de eje Y. El número de valores de los ejes Y X debería ser igual. Para calcular los valores del eje X, primero hay que encontrar los valores de la mediana como se muestran en la ley de distribución uniforme:
![]()
![]()
![]()
Después se usarán para calcular los valores del eje X por medio de la función de distribución normal inversa (vea el método ndtri).
Para crear un dibujo de función de autocorrelación (ACF por sus siglas en inglés), un dibujo de función de autocorrelación parcial (PACF por sus siglas en inglés) y calcular el cálculo espectral usando el método de entropía máxima, los valores de función de autocorrelación se debería encontrar en la secuencia de entrada.
Definiremos el número valores que deberían mostrarse en los dibujos ACF y PACF de la siguiente manera:
![]()
![]()
![]()
El número de valores determinado de la manera especificada debería ser suficiente para la visualización de la función de autocorrelación en el dibujo, pero para más cálculos de cálculo espectral se recomienda tener un mayor número de valores ACF calculados, que en nuestro caso deberá ser igual al orden del modo autorregresivo empleado.
La orden del modelo IP se definirá con el valor NLags obtenido:
![]()
![]()
Es bastante difícil formalizar el proceso para determinar el orden óptimo del modelo de cálculo espectral. Un modelo de orden bajo nos traerá resultados extremadamente suavizados, mientras que un modelo de orden alto nos llevará probablemente a un cálculo espectral inestable con un gran intervalo de valores.
Además, el orden de modelo también se verá afectado por la naturaleza de la secuencia de entrada, por tanto el orden IP determinada usando la fórmula de arriba será en algunos casos demasiado alto, y en otros casos demasiado bajo. Desafortunadamente, no hemos encontrado un enfoque efectivo para determinar el orden de modelo requerido.
Por tanto, para la secuencia de entrada se debería determinar el número de valores ACF igual al orden de modelo IP, que se usa para el cálculo espectral de la secuencia.
. . . ArrayResize(cor,IP); a=0; for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i]; for(i=1;i<=IP;i++) { c=0; for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i]; cor[i-1]=c/a; // Autocorrelation } . . .
Este fragmento del código fuente (veaTSAnalysis.mqh) ilustra el proceso de cálculo de la función de autocorrelación (ACF). El resultado del cálculo se colocará en el array cor[]. Como puede ver, primero se calcula un coeficiente de autocorrelación cero, seguido del cálculo y normalización de los coeficientes restantes en el bucle. Tras esta normalización, el coeficiente cero siempre será igual al uno, de modo que no es necesario guardarlo en el array cor[].
Este array contiene el número de coeficientes igual a IP empezando desde el primero. Al calcular el ACF, se usa el array TSCenter[]; contiene la secuencia de entrada de los elementos desde todos aquellos de los que se sustrajo el valor de la media.
Para reducir el tiempo requerido para calcular el ACF se pueden usar métodos que empleen algoritmos de transformación rápida, como por ejemplo FFT. Pero en este caso, el tiempo requerido para calcular el ACF es bastante aceptable, de modo que probablemente no necesitamos complicar el código de programación.
Un dibujo de ACF (correlograma) se puede construir fácilmente usando los valores obtenidos de los coeficientes de correlación. Para mostrar las bandas de confianza al 95% en este dibujo, sus valores se pueden calcular usando las fórmulas de abajo.
Para las bandas usadas para las pruebas de aleatoriedad:
![]()
Para las bandas usadas para determinar el orden de modelo ARIMA:
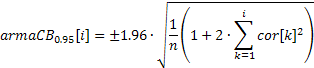
El valor de la banda de confianza en el primer caso será constante, y en el segundo caso irá aumentando con el aumento del coeficiente de autocorrelación.
En ocasiones nos interesará una respuesta de frecuencia suavizada de la secuencia de entrada que refleje solo la tendencia general de la distribución de frecuencia. Por ejemplo, los aumentos considerables en intervalo de frecuencia alta o baja, predominio de frecuencias de intervalo medio, etc.
Se recomienda mostrar esta respuesta de frecuencia en escala lineal para enfatizar con fuerza los intervalos de frecuencia dominantes. Esta respuesta de amplitud y frecuencia (AFR, por sus siglas en inglés) se puede dibujar basándonos en los coeficientes de autocorrelación obtenidos anteriormente. Para el cálculo de la AFR usaremos el número de coeficientes igual al número mostrado en el dibujo ACF.
Puesto que este número no es grande, los cálculos espectrales obtenidos como resultado deberían ser bastante suaves.
La respuesta de frecuencia de la secuencia en este caso se puede expresar por medio del coeficientes de autocorrelación de la siguiente manera:
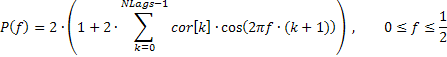
Puede encontrar abajo un fragmento del código (vea TSAnalysis.mqh) que se usa para calcular el AFR basándonos en la fórmula facilitada:
. . . n=320; // Number of X-points ArrayResize(Spect,n); v=M_PI/n; for(i=0;i<n;i++) { a=i*v; b=0; for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1)); Spect[i]=2.0*(1+2*b); // Spectrum Y-axis } . . .
Note que los valores de coeficiente de correlación en el código de arriba se multiplican por la función de ventana triangular para un mayor suavizado.
Para un análisis espectral más detallado, se seleccionó el método de entropía máxima como otro compromiso. La selección de un método universal de cálculo espectral es bastante difícil. Las desventajas asociadas con los métodos clásicos no paramétricos de análisis espectral son muy conocidos.
Los métodos de periodograma y correlograma pueden servir como ejemplos de tales métodos que se implementan fácilmente usando algoritmos de transformación Fourier rápida. Pero a pesar de la alta estabilidad de los resultados, estos métodos requieren secuencias de entrada muy largas para obtener un poder de resolución adecuado. En contraste, los métodos paramétricos de cálculo espectral (es decir, métodos autorregresivos) pueden asegurar una resolución mucho más alta para secuencias cortas.
Desafortunadamente, al usarlos se debe tener en consideración no solo las peculiaridades de ciertas implementaciones de estos métodos, sino también la naturaleza de la secuencia de entrada. Al mismo tiempo es difícil determinar el orden de modelo de AR óptimo cuyo aumento lleva a un aumento del poder de resolución, pero también a resultados desordenados. Si se usan modelos de orden muy alto, estos métodos comienzan a dar resultados inestables.
Las características comparativas de diferentes algoritmos de cálculo espectral se pueden encontrar en el libro de S. L. Marple "Digital Spectral Analysis with Applications" ("Análisis Espectral Digital con Aplicaciones"). Como ya menxionamos, en este caso se seleccionó el método de entropía máxima. Este método resulta en lo que probablemente sea el poder de resolución más bajo en comparación con otros métodos autorregresivos, pero se seleccionó para obtener cálculos espectrales más estables.
Echemos un vistazo al orden de cálculos espectrales autorregresivos. La elección del orden de modelo ya se trató antes, así que supondremos que ya se seleccionó un orden de modelo igual al IP, y los coeficientes de autocorrelación del I^P cor[] ya se calcularon.
Para obtener los coeficientes autorregresivos usando los coeficientes de autocorrelación conocidos se usa el algoritmo Levinson-Durbin, implementado como el método LevinsonRecursion.
//----------------------------------------------------------------------------------- // Calculate the Levinson-Durbin recursion for the autocorrelation sequence R[] // and return the autoregression coefficients A[] and partial autocorrelation // coefficients K[] //----------------------------------------------------------------------------------- void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[]) { int p,i,m; double km,Em,Am1[],err; p=ArraySize(R); ArrayResize(Am1,p); ArrayInitialize(Am1,0); ArrayInitialize(A,0); ArrayInitialize(K,0); km=0; Em=1; for(m=0;m<p;m++) { err=0; for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1]; km=(R[m]-err)/Em; K[m]=km; A[m]=km; for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]); Em=(1-km*km)*Em; ArrayCopy(Am1,A); } return; }
El método tiene tres parámetros de entrada. Los tres parámetros son referencias a arrays. Al llamar a este método, los coeficientes de autocorrelación de entrada se deberían colocar en el primer array R[]. Estos valores no cambian durante el curso de los cálculos.
Los coeficientes de autocorrelación obtenidos se colocarán en el array A[]. Además de eso, el array K[] contendrá valores de la función de autocorrelación parcial iguales a los coeficientes de reflejo de modelo autorregresivo obtenidos con el signo opuesto. El orden de modelo no se pasa como un parámetro de entrada; se supone que es igual al número de elmentos en el array de entrada R[].
Los tamaños del array de salida, por tanto, no pueden ser menores que el tamaño del array de entrada; el cumplimiento de este requisito no se comprueba dentro de la función. Al completar los cálculos, el coeficiente autorregresivo cero y el coeficiente cero de la función de autocorrelación parcial no se guardan en los arrays A[] y K[].
Se supone que siempre son iguales a uno. Por tanto, los arrays de salida contendrán, al igual que la secuencia de entrada, coeficientes con índices desde 1 a IP (no los confunda con los índices de array que empiezan desde 0).
Los valores obtenidos de la función de autocorrelación parcial se usan después solo para la visualización en un dibujo, y los coeficientes autorregresivos sirven como la base para los cálculos de la respuesta de frecuencia, que se define con la siguiente fórmula:
![]()
La respuesta de frecuencia se calcula para 4.096 valores de frecuencia normalizada en el intervalo de 0 a 0,5. El cálculo directo de valores AFR usando la fórmula de arriba lleva demasiado tiempo, que se puede reducir sustancialmente usando el algoritmo de transformación Fourier rápida para calcular la suma de exponenciales complejos.
Para ello, el método Calc emplea la transformación Hartley rápida (FHT), en lugar de la transformación Fourier rápida.
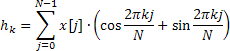
La transformación Hartley no incluye operaciones complejas, y tanto la secuencia de entrada como la de salida son válidas. La transformación Hartley invertida se calcula usando la misma fórmula, requiriendo solo un factor adicional 1/N.
En una secuencia de entrada válida hay una conexión simple entre los coeficientes de esta transformación y los coeficientes de la transformación Fourier.
![]()
Puede encontrar información sobre los algoritmos de transformación Hartley rápida aquí: "FXT algorithm library" ("Biblioteca de algoritmo FXT") y "Discrete Fourier and Hartley Transforms" ("Transformaciones Hartley y Fourier Discretas").
En la siguiente implementación, la función de transformación Hartley rápida se representa con el método fht.
//----------------------------------------------------------------------------------- // Radix-2 decimation in frequency (DIF) fast Hartley transform (FHT). // Length is N = 2 ** ldn //----------------------------------------------------------------------------------- void TSAnalysis::fht(double &f[], ulong ldn) { const ulong n = ((ulong)1<<ldn); for (ulong ldm=ldn; ldm>=1; --ldm) { const ulong m = ((ulong)1<<ldm); const ulong mh = (m>>1); const ulong m4 = (mh>>1); const double phi0 = M_PI / (double)mh; for (ulong r=0; r<n; r+=m) { for (ulong j=0; j<mh; ++j) { ulong t1 = r+j; ulong t2 = t1+mh; double u = f[t1]; double v = f[t2]; f[t1] = u + v; f[t2] = u - v; } double ph = 0.0; for (ulong j=1; j<m4; ++j) { ulong k = mh-j; ph += phi0; double s=MathSin(ph); double c=MathCos(ph); ulong t1 = r+mh+j; ulong t2 = r+mh+k; double pj = f[t1]; double pk = f[t2]; f[t1] = pj * c + pk * s; f[t2] = pj * s - pk * c; } } } if(n>2) { ulong r = 0; for (ulong i=1; i<n; i++) { ulong k = n; do {k = k>>1; r = r^k;} while ((r & k)==0); if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;} } } }
Al llamar a este método se introducen una referencia al array de entrada de datos f[] y el número íntegro no firmado Idn que define la longitud de transformación N = 2 ** ldn. El tamaño del array f[] no puede ser menor que la longitud de transformación N. Tenga en cuenta que esto no se comprueba dentro de la función. Recuerde también que el resultado de la transformación se guarda en el array donde se colocaron los datos de entrada.
Después de la transformación, los datos de entrada no se guardan. En el método Calc que estamos considerando se usa una transformación de longitud N=8192 para calcular 4096 valores AFR. Después del cálculo del cuadrado de la magnitud de la transformación y tomando la recíproca, el resultado obtenido se normaliza a su valor máximo y se escala logarítmicamente.
Aparte de eso, no hay mayores peculiaridades en el método Calc; si es necesario, se puede mirar más detalladamente su implementación en el archivo TSAnalysis.mqh.
Todos los valores obtenidos y preparados para su visualización como resultado de los cálculos se guardan en variables que son los miembros de la clase TSAnalysis. Por tanto, no deben pasarse como argumentos al llamar la visualización del método virtual para mostrar los resultados.
Visualización
Como ya mencioné, el método de visualización se declara como virtual. De modo que, al redefinirlo, se puede implementar el método requerido para mostrar los resultados de cálculo que serían diferentes de los propuestos. La visualización en la clase propuesta TSAnalysis se lleva a cabo por medio de preparación de archivo de datos y llamando a un navegador web para mostrar los datos.
Para que un navegador web pueda mostrar estos datos se usa el archivo TSA.htm, localizado en el mismo directorio que el resto de los archivos del proyecto. Este método para mostrar información gráfica se describió anteriormente en el artículo "Graphs and Diagrams in HTML" ("Gráficos y Diagramas en HTML").
La clase TSAnalysis del método de visualización se encarga de dar formato y guardar todos los resultados de los cálculos que se deben mostrar en una variable de tipo cadena de caracteres (vea TSAnalysis.mqh). Se generará una larga línea de esta forma, y se guardará en TSDat.txt en un solo paso. La creación de este archivo y el almacenamiento de datos en él se lleva a cabo usando las herramientas estándares de MQL5. Por tanto, el archivo se crea en el directorio \MQL5\Files.
Este archivo, a continuación, se mueve al directorio de este proyecto llamando a las funciones de sistema externas. A esto le sigue la llamada a un navegador web que muestre el archivo TSA.htm, que usa datos de TSDat.txt. Puesto que las funciones de sistema se llaman en el método de visualización, el uso de DLLs externos se deberá activar en el terminal para trabajar con la clase TSAnalysis.
Ejemplos
El archivo TSAexample.mq5, incluido en la carpeta de archivos TSAnalysis.zip, es un ejemplo de uso de la clase TSAnalysis.
//----------------------------------------------------------------------------------- // TSAexample.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "TSAnalysis.mqh" //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50, 60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52, 38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23}; TSAnalysis *tsa=new TSAnalysis; tsa.Calc(bd); delete tsa; }
Como puede ver, la referencia a la clase es bastante simple; si hay un array preparado que contiene la secuencia de entrada, no requerirá mucho esfuerzo pasarla al método Calc para su análisis. Además, debe acordarse de liberar memoria llamando a la función de eliminación. El resultado de la ejecución de este script ya se facilitó al comienzo del artículo.
Para demostrar la eficiencia de los cálculos espectrales producidos, fijémonos en ejemplos adicionales donde se usarán las secuencias generadas.
Para empezar, usaremos una secuencia consistente de dos sinusoides.
int i,n; double a,x[]; n=400; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);
La figura de abajo demuestra el cálculo de la respuesta de frecuencia de esta secuencia.
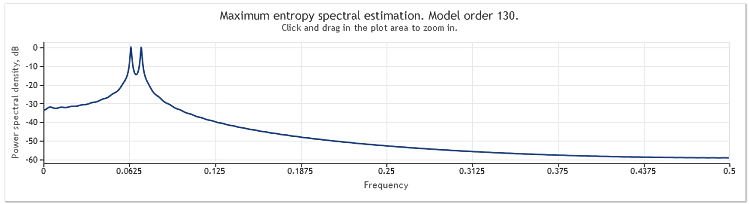
Figura 2. Cálculo espectral. Dos sinusoides.
Aunque ambos sinusoides son fácilmente observables, al ampliar en el gráfico el área de interés podemos descubrir que los picos están localizados en frecuencias de 0,0637 y 0,0712. En otras palabras, son algo diferentes de los valores verdaderos. Cuando una secuencia consta de un solo sinusoide, no se tiene en cuenta esta parcialidad de un cálculo. Consideremos esta ocurrencia como el efecto del método seleccionado de análisis espectral.
Complicaremos la tarea aún más añadiendo un componente aleatorio a nuestra secuencia. Para ello se usará un generación de secuencias pseudo-aleatorio representado por la clase RNDXor128, que se puede encontrar en el archivo RNDXor128.zip al final del archivo.
El fragmento de código de abajo se usó para generar una señal de prueba.
int i,n; double a,x[]; RNDXor128 *rnd=new RNDXor128; n=800; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm(); delete rnd;
En este ejemplo se añadió una señal aleatoria con distribución normal y diferencia de unidad a dos sinusoides.
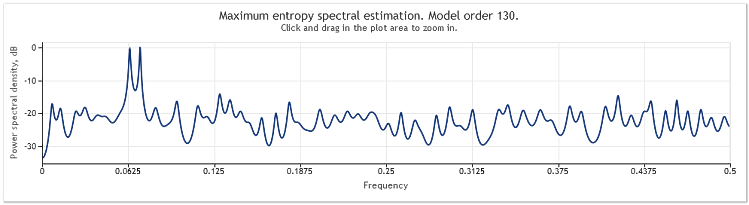
Figura 3. Cálculo espectral. Dos sinusoides más una señal aleatoria.
En este caso, los componentes sinusoidales se mantienen bien perceptibles.
Una quintuplicación de la amplitud del componente aleatorio resulta en sinusoides sustancialmente ocultos.
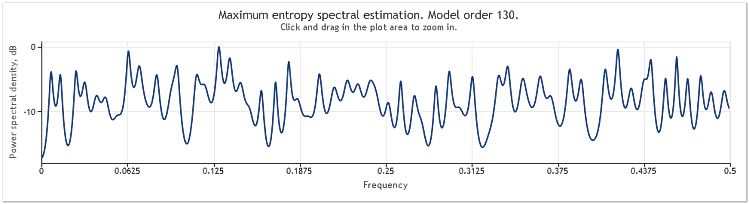
Figura 4. Cálculo espectral. Dos sinusoides más una señal aleatoria con mayor amplitud.
Cuando la longitud de secuencia aumenta de 400 a 800 elementos, los sinusoides vuelven a ser fácilmente observables de nuevo.
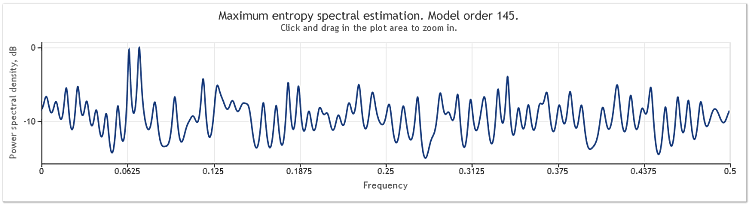
Figura 5. Dos sinusoides más una señal aleatoria con mayor amplitud N=800.
El orden de modelo autorregresivo ha aumentado aquí de 130 a 145. El aumento en la longitud de secuencia condujo a un orden más alto del modelo, y como resultado, el poder de resolución del cálculo espectral aumentó. Los picos del gráfico se volvieron marcadamente afilados.
El cálculo espectral de las cuotas para EURUSD, D1 durante dos años (2009 y 2010) será tal y como se muestra a continuación.

Figura 6. Cuotas EURUSD. 2009-2010. Período D1.
La secuencia de entrada constó de 519 valores, y el orden de modelo, tal y como se muestra en la figura, pareció ser 135.
Como puede ver, este cálculo espectral contiene un número de picos distintivos. Pero este cálculo por sí solo no es suficiente para determinar si estos picos son componentes periódicos de las cuotas.
La aparición de picos en la respuesta de frecuencia puede ser causada por un componente aleatorio de alto nivel presente en las cuotas, o por la no-estacionalidad explícita de la secuencia en cuestión.
Por tanto, siempre es recomendable verificar los resultados obtenidos usando los datos de otra fracción de la secuencia u otro intervalo de tiempo antes de llegar a una conclusión final respecto a la presencia del componente periódico. Además, al estudiar recurrencias cíclicas, puede intentar usar las diferencias de la secuencia, en lugar de la secuencia en sí misma.
Conclusión
Puesto que el método de cálculo espectral empleado en el artículo se basa en coeficientes de autocorrelación, la media de la secuencia de entrada siempre parece haber sido eliminada de la secuencia con la aplicación del método. A menudo es absolutamente necesario eliminar un componente constante de la secuencia de entrada, pero al usar los métodos autorregresivos, esta eliminación puede causar en algunos casos distorsiones del cálculo espectral en el intervalo de baja frecuencia.
Un ejemplo de estas distorsiones se puede ver al final del capítulo "Summary of Results Regarding Spectral Estimates" ("Resumen de Resultados Respecto a Cálculos Espectrales") en el libro de by S. L. Marple "Digital Spectral Analysis with Applications" ("Análisis Espectral Digital con Aplicaciones"). En nuestro caso, el método de análisis espectral empleado no nos deja otra opción que simplemente tener en cuenta que el cálculo espectral siempre se lleva a cabo con respecto a una secuencia con una media eliminada.
Referencias
- Wuertz, Diethelm y Katzgraber, Helmut (2009): Precise finite-sample quantiles of the Jarque-Bera adjusted Lagrange multiplier test (Cuantiles de muestra finita precisos del test multiplicador Lagrange ajustado Jarque-Bera), Instituto Federal Suizo de Tecnología, Zúrich,2009.
- Tanweer-ul-Islam, Asad Zaman, Normality Testing - A new Direction (Test de Normalidad - Una Nueva Dirección), IIE, Universidad Islámica Internacional, Islamabad, Pakistán, 2008.
- Carlos M. Urzua, Portable and powerful tests for normality (Tests portátiles y eficaces de normalidad), Tecnológico de Monterrey, Campus Ciudad de México, 2007.
- Comparison of Common Tests for Normality (Comparación de Tests Comunes de Normalidad)
- S. V. Bulashev. Statistics for Traders (Estadísticas para Traders). - М.: Kompania Sputnik +, 2003. - 245 pp.
- P. V. Novitsky, I. A. Zograf. Estimation of Error in Measurement Results (Cálculo dee Error en Resultados de Medición) Energoatomizdat, 1991.
- S. L. Marple, Jr. Digital Spectral Analysis with Applications (Análisis Espectral Digital con Aplicaciones). Moscú: Mir, 1990.
- David J. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures (Manual de Procedimientos Estadísticos Paramétricos y No-Paramétricos), Chapman y Hall/CRC.