Análisis de los gráficos mediante métodos econométricos

Denis Kirichenko | 3 abril, 2014

Las teorías sin hechos pueden ser estériles, pero los hechos sin teorías no tienen sentido.

 K. Boulding

Introducción

Oigo a menudo que los mercados son volátiles e inestables. Y esto explica el motivo por el cual el trading a largo plazo no tiene éxito. Pero, ¿es cierto? Vamos a tratar de analizar este problema desde un punto de vista científico. Y vamos a elegir el método de análisis econométrico. ¿Por qué los métodos econométricos? En primer lugar, a la comunidad MQL le encanta la precisión, algo que proporcionan las matemáticas y las estadísticas. En segundo lugar, si no me equivoco, esto no se ha tratado antes.

Cabe señalar que el problema del éxito del trading a largo plazo no se puede solucionar en un solo artículo. En este artículo, voy a describir solamente algunos métodos de diagnóstico para el modelo seleccionado, esperando que sean útiles para su uso futuro.

Además, voy a hacer lo mejor para describir de un modo claro algunos conceptos aburridos que incluyen fórmulas, teoremas e hipótesis. Sin embargo, espero que los lectores ya conocen algunos conceptos básicos de estadísticas, tales como: hipótesis, significación estadística, estadísticas (normas estadísticas), dispersión, distribución, probabilidad, regresión, autocorrelación, etc.

1. Características de las series temporales

Está claro que el objeto del análisis son las series del precio (sus derivadas), que son series temporales.

Los econometristas estudian las series del tiempo mediante métodos del dominio de la frecuencia (análisis espectral, análisis de ondas) y métodos del dominio temporal (análisis de correlación cruzada, análisis de autocorrelación). Ya se le ha proporcionado al lector el artículo "Construyendo un analizador de espectro" que describe los métodos del dominio de la frecuencia. Propongo ahora centrarse en los métodos del dominio temporal, en el análisis de la autocorrelación y el análisis de la varianza condicional en particular.

Para describir el comportamiento de las series temporales del precio, los modelos no lineales son mejores que los modelos lineales. Es por ello que en este artículo nos centramos en el estudio de los modelos no lineales.

Las series temporales del precio tienen unas características especiales que se pueden tener en cuenta únicamente con unos modelos econométricos concretos. En primer lugar, estas características incluyen: el escaso apuntamiento o "curtosis" (fat tail), la agrupación (clusterization) de la volatilidad y el efecto del apalancamiento.      

                                                                                                                

 

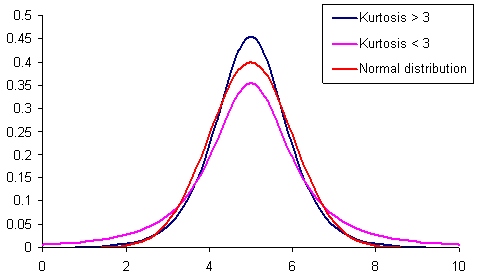
Figura 1. Distribuciones con distintas curtosis.

En la figura 1 se muestran 3 distribuciones con diferentes curtosis (apuntamiento). La distribución con un apuntamiento inferior al de la distribución normal, tiene efecto "fat tails" (escaso apuntamiento) con más frecuencia que las demás. Es la distribución de color rosa.

Necesitamos la distribución para mostrar la densidad de probabilidad de un valor aleatorio, que se usa para calcular los valores de las series.

Con clusterization (agrupación) (de concentración de clúster o grupo) de la volatilidad, nos referimos a lo siguiente. A un período de tiempo de alta volatilidad le sigue uno igual y a un período de tiempo de baja volatilidad le sigue también uno igual. Si los precios fluctuaban ayer, es muy probable que lo hagan hoy. Por tanto, hay una inercia de volatilidad. La figura 2 muestra que la volatilidad tiene una forma agrupada.

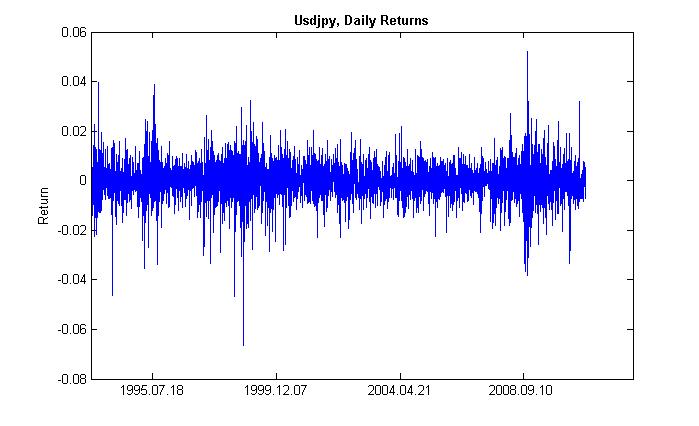
Figura 2. Volatilidad del retorno diario de USDJPY, su agrupación.

Con el efecto del apalancamiento nos referimos a cuando la volatilidad en un mercado a la baja es superior a la volatilidad en un mercado al alza. Está sujeto al incremento del coeficiente de apalancamiento, que depende de la relación de los activos prestados y los propios, cuando caen los precios de las acciones. No obstante, se aplica este efecto al mercado de valores, pero no al mercado de divisas. No tendremos más en cuenta este efecto.

2. El modelo GARCH

Bien, nuestro objetivo principal es la predicción de la tasa de cambio (precio) mediante algún modelo. Los econometristas usan modelos matemáticos que describen uno u otro efecto que se puede estimar en términos cuantitativos. En resumen, adaptan una fórmula a un evento. Y de este modo, describen este evento.

Teniendo en cuenta que estas series temporales analizadas tienen las propiedades mencionadas anteriormente, el modelo ideal para estas propiedades sería no lineal. Uno de los modelos no lineales más genéricos es el modelo GARCH. ¿Cómo puede ayudarnos? En su parte principal (función), considerará la volatilidad de las series, es decir, la variabilidad de la dispersión con distintos períodos de observación. Los econometristas llaman a este efecto con el término abstruso; heterocedasticidad (del griego - hetero - differente, skedasis - dispersión).

Si echamos un vistazo a la propia fórmula, veremos que este modelo implica que la variabilidad de dispersión (σ²t) se ve afectada por los cambios anteriores de los parámetros (ϵ²t-i) y las estimaciones anteriores de la dispersión (llamadas "noticias viejas") (σ²t-i):

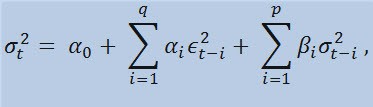
con los límites

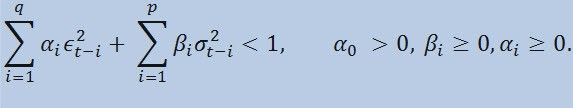
donde: ϵt son las novedades no normalizadas; α0 , βi , αi , q (orden de los miembros de ARCH ϵ²), p (orden de los miembros de GARCH σ²)   son los parámetros y orden estimados de los modelos.

3. El indicador de retornos

En realidad, no vamos a hacer la estimación de las series del precio en sí, sino de las series de retornos. Se determina el cambio logarítmico del precio (continuamente cargado de retornos) como un logaritmo natural de porcentajes de retornos:

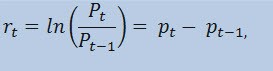
donde:

• Pt es el valor de las series temporales en el instante t;
  
• Pt -1 es el valor de las series temporales en el instante t-1;
  
• pt = ln(Pt)   es el logaritmo natural de Pt.
  

En la práctica, la razón principal por la que se trabaja con los retornos, son sus mejores características estadísticas.

Así que, vamos a crear un indicador par los retornos ReturnsIndicator.mq5, que nos va a ser muy útil. Voy a hacer referencia al artículo "Indicadores personalizados para principiantes en MQL5" que describe de manera sencilla el algoritmo de creación de un indicador. Es por ello que voy a mostrar únicamente la parte del código donde aparece la fórmula mencionada. Creo que es bastante sencillo y no requiere explicaciones.

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,      // size of the array price[]
                const int prev_calculated,  // number of bars available at the previous call
                const int begin,            // index of the array price[] the reliable data starts from
                const double& price[])      // array for the calculation itself

  {
//---
   int start;
   if(prev_calculated<2) start=1;  // start filling ReturnsBuffer[] from the 1-st index, not 0.
   else start=prev_calculated-1;   // set 'start' equal to the last index in the arrays
   for(int i=start;i<rates_total;i++)
     {
      ReturnsBuffer[i]=MathLog(price[i]/price[i-1]);
     }
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

Lo único que quiero destacar es que las series de retornos son siempre inferiores a las series primarias de 1 elemento. Es por ello que vamos a comenzar el cálculo de la matriz de retornos a partir del segundo elemento, y el primero será siempre igual a cero.

Por tanto, mediante el indicador ReturnsIndicator hemos obtenido las series temporales aleatorias que usaremos en nuestro trabajo.

4. Pruebas estadísticas

Ahora es el turno de las pruebas estadísticas. Se llevan a cabo para determinar si las series temporales tienen cualquier indicio que confirme la conveniencia de uso de un modelo u otro. En nuestro caso, se trata del modelo GARCH.

Mediante la prueba Q de Ljung-Box-Pierce, comprobamos si las autocorrelaciones de las series son aleatorias o siguen una relación. Para este propósito, tenemos que escribir una nueva función. Me refiero con autocorrelación a la correlación (conexión probabilística) entre los valores de la misma serie temporal X (t) en los instantes t1 y t2. Si los momentos t1 y t2 son adyacentes (uno después del otro), buscamos una relación entre los miembros de las series y los miembros de las mismas series desplazado por una unidad de tiempo: x1, x2, x3,... y x1+1, x2+1, x3+1,... Este efecto de miembros desplazados, se llama desfase (latencia, retardo). El valor del desfase puede ser cualquier número positivo.

Quiero hacer la siguiente observación. Que yo sepa, ni C++, ni MQL5 disponen de librerías estándar que cubren los cálculos estadísticos complejos y de promedios. Por lo general, estos cálculos se llevan a cabo mediante unas herramientas estadísticas especiales. Para mí, es más fácil utilizar Matlab, STATISTICA 9, etc., para solucionar el problema. Sin embargo, he decidido no recurrir a librerías externas, en primer lugar, para demostrar lo potente que es el lenguaje MQL5 para los cálculos y en segundo lugar... He aprendido por mí mismo al escribir el código MQL.

Hay resaltar lo siguiente. Para llevar a cabo la prueba Q, necesitamos números complejos. Es por ello que he creado la clase Complex. Idealmente, debería llamarse CComplex. Bueno, me voy a relajar un poco. Estoy seguro que mis lectores están preparados y no tengo que explicar lo que es un número complejo. Personalmente, no me gustan las funciones que calculan la transformada de Fourier publicadas en MQL5 y MQL4; se usan los números complejos de forma implícita. Además, existe otro obstáculo, la imposibilidad de cancelar los operadores aritméticos en MQL5. Así que tuve que buscar otros métodos y evitar la notación estándar de "C". He implementado la función de los números complejos del siguiente modo:

class Complex
  {
public:
   double            re,im; //re -real component of the complex number, im - imaginary
public:
   void              Complex(){};                                   //default constructor
   void              setComplex(double rE,double iM){re=rE; im=iM;}; //set method (1-st variant)
   void              setComplex(double rE){re=rE; im=0;};           //set method (2-nd variant)  
   void              ~Complex(){};                                  //destructor
   void              opEqual(const Complex &y){re=y.re;im=y.im;};   //operator=
   void              opPlus(const Complex &x,const Complex &y);      //operator+   
   void              opPlusEq(const Complex &y);                    //operator+=
   void              opMinus(const Complex &x,const Complex &y);     //operator-
   void              opMult(const Complex &x,const Complex &y);      //operator*   
   void              opMultEq(const Complex &y);                    //operator*= (1-st variant)     
   void              opMultEq(const double y);                       //operator*= (2-nd variant)    
   void              conjugate(const Complex &y);                   //conjugation of complex numbers
   double            norm();                                       //normalization 
 };

Por ejemplo, se puede llevar a cabo la operación de la suma de dos números complejos mediante el método opPlus, la sustracción mediante opMinus, etc. Si solo escribimos c = a + b (donde a, b, с son números complejos), el compilador mostrará un error. Pero aceptaría la siguiente expresión: c.opPlus(a,b).

Si es necesario, el usuario puede ampliar los métodos de la clase Complex. Por ejemplo, podemos añadir un operador de división. 

Además, nos hacen falta unas funciones adicionales para procesar las matrices de los números complejos. Es por ello que las he implementado fuera de la clase Complex, no en el bucle de procesamiento de los elementos de la matriz, sino directamente con las matrices asignadas por referencia. En total, hay tres de estas funciones:

1. getComplexArr (devuelve una matriz bidimensional de números reales a partir de una matriz de números complejos);
2. setComplexArr (devuelve una matriz de números complejos a partir de una matriz unidimensional de números reales);
3. setComplexArr2 (devuelve una matriz de números complejos a partir de una matriz bidimensional de números reales).
   

Hay que tener en cuenta que estas funciones devuelven matrices pasadas por referencia. Es el motivo por el cual no incluyen el operador "return". Pero razonando con lógica, creo que podemos hablar de retorno a pesar del tipo void. 

Se describen las funciones adicionales y la clase de los números complejos en el archivo de cabecera Complex_class.mqh.

Más a delante, al realizar las pruebas, nos harán falta la función de autocorrelación y la función de la transformada de Fourier. Por tanto, necesitamos crear una nueva clase, la llamaremos CFFT. Procesará las matrices de los números complejos para las transformadas de Fourier. A continuación, se muestra la clase de Fourier:

class CFFT
  {
public:
   Complex           Input[];  //input array of complex numbers
   Complex           Output[]; //output array of complex numbers
public:
   bool              Forward(const uint N);                                   //direct Fourier transformation
   bool              InverseT(const uint N,const bool Scale=true);            //weighted reverse Fourier transformation
   bool              InverseF(const uint N,const bool Scale=false);           //non-weighted reverse Fourier transformation
   void              setCFFT(Complex &data1[],Complex &data2[],const uint N); //set method(1-st variant)
   void              setCFFT(Complex &data1[],Complex &data2[]);              //set method (2-nd variant)
protected:
   void              Rearrange(const uint N);                                 // regrouping
   void              Perform(const uint N,const bool Inverse);                // implementation of transformation
   void              Scale(const uint N);                                     // weighting
  };

Hay que tener en cuenta que todas las transformaciones de Fourier se llevan a cabo con matrices, cuyo tamaño cumple con la condición 2^N (donde N es una potencia de dos). A menudo, el tamaño de la matriz es distinto de 2^N. En este caso, se incrementa el tamaño de la matriz al valor de 2^N para 2^N  >= n, donde n es el tamaño de la matriz. Los elementos añadidos a la matriz son iguales a 0. Se lleva a cabo este procesamiento de la matriz en la función autocorr mediante la función adicional nextpow2 y la función pow:

int nFFT=pow(2,nextpow2(ArraySize(res))+1);      //power rate of two

Así que, si tenemos una matriz inicial cuyo tamaño (n) es igual a 73585, la función nextpow2 devolverá el valor 17, donde 2^17 = 131072. En otras palabras, el valor devuelto es superior a n con pow(2, ceil(log(n)/log(2))). A continuación, vamos a calcular el valor de nFFT: 2^(17+1) = 262144. Este será el tamaño de la matriz adicional, cuyos elementos del 73585 al 262143 serían iguales a cero.

Se describe la clase Fourier en el archivo de cabecera FFT_class.mqh.

Para ahorrar espacio, voy a saltar la descripción de la implementación de la clase CFFT. Aquellos lectores interesados, la pueden encontrar en el archivo adjunto. Ahora, vamos a pasar a la función de correlación.

void autocorr(double &ACF[],double &res[],int nLags)  //1-st variant of function 
/* selective autocorrelation function (ACF)  for unidimensional stochastic time series 
   ACF - output array of calculated values of the autocorrelation function;
   res - array of observation of stochastic time series;
   nLags - maximum number of lags the ACF is calculated for.
*/
  {
   Complex Data1[],Data21[], //input arrays of complex numbers
   Data2[],Data22[],         //output arrays of complex numbers
   cData[];                  //array of conjugated complex numbers           
   double rA[][2];           //auxiliary two-dimensional array of real numbers

   int nFFT=pow(2,nextpow2(ArraySize(res))+1);      //power rate of two
   ArrayResize(rA,nFFT);ArrayResize(Data1,nFFT);    //correction of array sizes
   ArrayResize(Data2,nFFT);ArrayResize(Data21,nFFT);
   ArrayResize(Data22,nFFT);ArrayResize(cData,nFFT);

   double rets1[];                   //an auxiliary array for observing the series
   double m=mean(res);               //arithmetical mean of the array res
   ArrayResize(rets1,nFFT);          //correction of array size
   for(int t=0;t<ArraySize(res);t++) //copy the initial array of observation 
       // to the auxiliary one with correction by average
     rets1[t]=res[t]-m;
   setComplexArr(Data1,rets1); //set input array of complex numbers   
   CFFT F,F1;                  //initialize instances of the CFFT class
   F.setCFFT(Data1,Data2);     //initialize data-members for the instance F
   F.Forward(nFFT);            //perform direct Fourier transformation
   for(int i=0;i<nFFT;i++)
     {
      Data21[i].opEqual(F.Output[i]);//assign the values of the F.Output array to the Data21 array;
      cData[i].conjugate(Data21[i]); //perform conjugation for the array Data21
      Data21[i].opMultEq(cData[i]);  //multiplication of the complex number by the one adjacent to it 
                     //results in a complex number that has only real component not equal to zero
     }
   F1.setCFFT(Data21,Data22);   //initialize data-members for the instance F1   
   F1.InverseT(nFFT);           //perform weighter reverse Fourier transformation
   getComplexArr(rA,F1.Output); //get the result in double format after
                     //weighted reverse Fourier transformation   
   for(int i=0;i<nLags+1;i++) 
     {
      ACF[i]=rA[i][0];          //in the output ACF array save the calculated values
                    //of autocorrelation function
      ACF[i]=ACF[i]/rA[0][0];   //normalization relatively to the first element
     }
  }

De modo que hemos calculado los valores de ACF (función de autocorrelación) para el valor indicado de desfase. Ahora podemos utilizar la función de autocorrelación para la prueba Q. El código de la función de prueba es el siguiente:

void lbqtest(bool &H[],double &rets[])
/* Function that implements the Q test of Ljung-Box-Pierce
   H - output array of logic values, that confirm or disprove
    the zero hypothesis on the specified lag;
   rets - array of observations of the stochastic time series;
*/
  {
   double lags[3]={10.0,15.0,20.0};       //specified lags 
   int maxLags=20;                        //maximum number of lags
   double ACF[]; ArrayResize(ACF,21);     //epmty ACF array
   double acf[]; ArrayResize(acf,20);     //alternate ACF array
   autocorr(ACF,rets,maxLags);            //calculated ACF array
   for(int i=0;i<20;i++) acf[i]=ACF[i+1]; //remove the first element - one, fill
                                          //alternate array                            
   double alpha[3]={0.05,0.05,0.05};      //array of levels of significance of the test

/*Calculation of array of Q statistics for selected lags according to the formula:            
                  L
                |----|
                 \
       Q = T(T+2) || (rho(k)^2/(T-k)), 
                 /  
                |----| 
                  k=1
  where: T is range, L is the number of lags, rho(k) is the value of ACF at the k-th lag.
*/

   double idx[]; ArrayResize(idx,maxLags);     //auxiliary array of indexes
   int len=ArraySize(rets);                    //length of the array of observations
   int arrLags[];ArrayResize(arrLags,maxLags); //auxiliary array of lags
   double stat[]; ArrayResize(stat,maxLags);   //array of Q statistics
   double sum[]; ArrayResize(sum,maxLags);     //auxiliary array po sums
   double iACF[];ArrayResize(iACF,maxLags);    //auxiliary ACF array
   for(int i=0;i<maxLags;i++)
     {                                         //fill:
      arrLags[i]=i+1;                          //auxiliary array of lags     
      idx[i]=len-arrLags[i];                   //auxiliary array of indexes      
      iACF[i]=pow(acf[i],2)/idx[i];            //auxiliary ACF array     
     }
   cumsum(sum,iACF);                           //sum the auxiliary ACF array 
                                               //by progressive total                        
   for(int i=0;i<maxLags;i++)
      stat[i]=sum[i]*len*(len+2);              //fill the array Q statistics
   double stat1[];                             //alternate of the array of Q statistics
   ArrayResize(stat1,ArraySize(lags));
   for(int i=0;i<ArraySize(lags);i++)
      stat1[i]=stat[lags[i]-1];                //fill the alternate array of specified lags

   double pValue[ArraySize(lags)];             //array of 'p' values
   for(int i=0;i<ArraySize(lags);i++)
     {
      pValue[i]=1-gammp(lags[i]/2,stat1[i]/2); //calculation of 'p' values
      H[i]=alpha[i]>=pValue[i];                //estimation of zero hypothesis
     }
  }

Por consiguiente, nuestra función lleva a cabo la prueba Q de Ljung-Box-Pierce y devuelve la matriz de los valores lógicos del desfase indicado. Hay que señalar que la prueba de Ljung-Box se llama la prueba "portmanteau" (prueba combinada). Esto significa que para confirmar la presencia de la autocorrelación, se comprueban algunos desfases hasta el desfase indicado. Normalmente, se comprueba la autocorrelación hasta el desfase número 10, 15 y 20 incluido. Se derivan las conclusiones acerca de la presencia de la autocorrelación en todas las series en base al último valor de la matriz H, es decir, desde el primer desfase hasta el nº 20.

Si el elemento de la matriz es igual a false, se acepta la hipótesis cero, que indica que no hay autocorrelación en los desfases anteriores y seleccionados. En otras palabras, no hay correlación cuando el valor es false. De lo contrario, la prueba confirma la presencia de la autocorrelación. Con lo cual se acepta una alternativa a la hipótesis cero cuando el valor es true.

A veces, ocurre que las autocorrelaciones no se encuentran en la series de retornos. En este caso, para más precisión, se prueban los cuadrados de los retornos. Se toma la decisión final sobre la aceptación o el rechazo de la hipótesis cero del mismo modo que en la prueba inicial de las series de retornos. ¿Por qué tenemos que utilizar los cuadrados de los retornos? De este modo, incrementamos artificialmente la posible componente no aleatoria de autocorrelación de las series analizadas, que se determina más adelante dentro de los límites de los valores iniciales de confianza. En teoría, podemos utilizar los cuadrados y otras potencias de retornos. Pero es una carga estadística innecesaria, que le resta sentido a la prueba.

Al final de la parte principal de la función de prueba Q, cuando se calcula el valor de "p", aparece la función gammp(x1/2,x2/2). Permite calcular la función gamma incompleta de los elementos correspondientes. De hecho, nos hace falta la función acumulativa χ2-distribution (distribución de chi cuadrado). Pero es un caso particular de la distribución Gamma.

En general, para confirmar si es conveniente usar el modelo GARCH, basta con obtener un valor positivo de cualquier desfase de la prueba Q. Además, los econometristas hacen otra prueba, es la prueba ARCH de Engel, que comprueba la presencia de una heterocedasticidad convencional. No obstante, supongo que la prueba Q es suficiente de momento. Es la prueba más común. 

Ahora que ya tenemos todas las funciones necesarias para llevar a cabo la prueba, tenemos que pensar en la representación de los resultados obtenidos en la pantalla. Para ello, he escrito la función lbqtestInfo que muestra el resultado de la prueba econométrica en forma de un mensaje en una ventana y el diagrama de correlación directamente en el gráfico del símbolo analizado.

Veamos los resultados a través de un ejemplo. He elegido usdjpy como primer símbolo para el análisis. En primer lugar, abro el gráfico de líneas del símbolo (mediante los precios de cierre) y cargo el indicador personalizado ReturnsIndicator para mostrar las series de retornos. El gráfico está comprimido al máximo para una mejor visualización de la agrupación de la volatilidad del indicador. A continuación, ejecuto el script GarchTest. Seguramente, la configuración de su pantalla es distinta de la mía, así que el script le va a preguntar acerca del tamaño deseado del diagrama en píxeles. Yo uso 700*250.

Se muestran varios resultados de las pruebas en la figura 3.

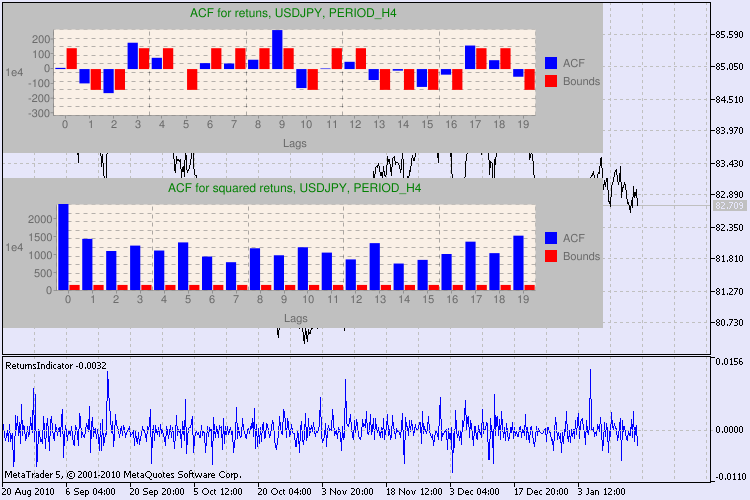
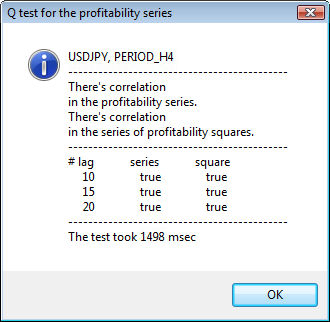
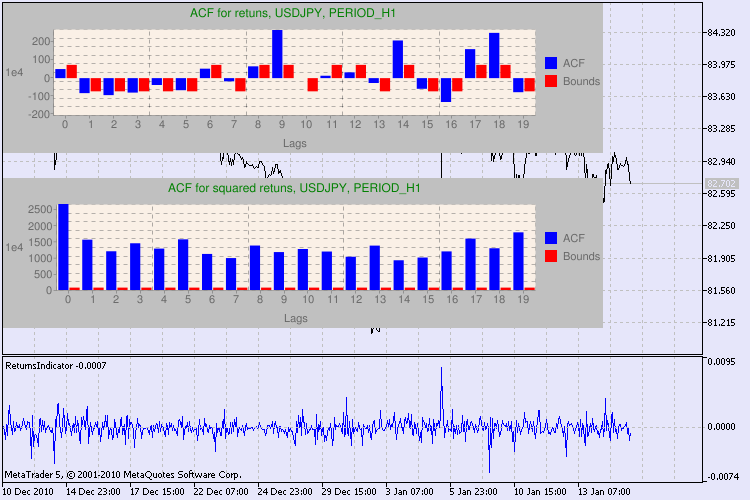
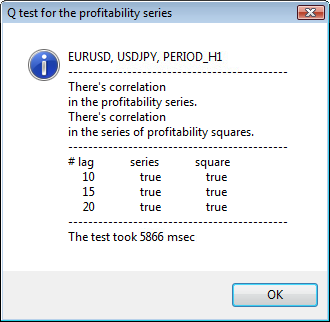
Figura 3. El resultado de la prueba Q y el diagrama de la autocorrelación de USDJPY con distintos períodos de tiempo.

Sí, he tenido que buscar mucho para encontrar la manera de mostrar el diagrama en el gráfico del símbolo en MetaTrader 5. Y he decidido que lo ideal sería usar la librería del dibujo de diagramas mediante Google Chart API, que está descrita en el artículo correspondiente.

¿Cómo tenemos que interpretar esta información? Echemos un vistazo. La parte superior del gráfico contiene el diagrama de la función de autocorrelación (ACF) de las series iniciales de retornos. En el primer diagrama, analizamos las series de usdjpy con el período de tiempo H4. Podemos observar que varios valores de ACF (barras azules) superan los límites (barras rojas). En otras palabras, observamos una pequeña autocorrelación en las series iniciales de retornos. El siguiente diagrama es el de la función de autocorrelación (ACF) de las series de los cuadrados de los retornos del símbolo indicado. Está muy claro, ganan las barras azules. Se analizan los diagramas de H1 del mismo modo.

He aquí una breve descripción de los ejes del diagrama. El eje x está claro; muestra los índices de los desfases. En el eje y se puede ver el valor exponencial, por el cual se multiplica el valor de ACF. Con lo cual, 1e4 significa que el valor inicial se multiplica por 1e4 (1e4=10.000), y 1e2 quiere decir que se multiplica por 100, etc. Se hace está multiplicación para facilitar la comprensión del gráfico. 

La parte superior de la ventana de diálogo muestra el nombre del símbolo o el par cruzado y su período de tiempo. Después del nombre se pueden ver dos frases que informan sobre la presencia u ausencia de la autocorrelación en las series iniciales de retornos y en todas las series de los cuadrados de los retornos. A continuación, se muestra el desfase nº 10, 15 y 20, además del valor de la autocorrelación en las series iniciales y en las series de los cuadrados. Se muestra aquí un valor relativo de la autocorrelación; un flag de tipo bool que durante la prueba Q determina si existe autocorrelación en las los flags anteriores y el flag especificado.

Al final, si vemos que existe autocorrelación en los flags anteriores y el especificado, el flag será igual a true, de lo contrario, será false. En el primer caso, nuestras series son del tipo "cliente" para el modelo GARCH no lineal, en el segundo caso, tenemos que usar modelos analíticos más sencillos. Un lector atento, se dará cuenta de que las series iniciales de retornos del par USDJPY presentan una ligera correlación entre sí, en particular con el mayor período de tiempo. Pero las series de los cuadrados de los retornos muestran una autocorrelación.

En la parte inferior de la ventana, se muestra el tiempo que ha tardado la prueba.

Todas las pruebas se han llevado a cabo mediante el script GarchTest.mq5.

Conclusiones:

En este artículo, he descrito cómo analizan los econometristas las series temporales, o más precisamente, cómo empiezan a estudiarlas. A lo largo del artículo, he tenido que escribir muchas funciones y codificar algunos tipos de datos (por ejemplo, los números complejos). Seguramente, la estimación gráfica de las series de datos proporciona casi el mismo resultado que la estimación econométrica. No obstante, hemos decidido usar únicamente métodos precisos. Sabemos que un buen médico puede establecer un diagnóstico sin utilizar métodos y tecnologías complejas. Pero en cualquier caso, hará un diagnóstico cuidadoso y meticuloso al paciente.

¿Qué hemos conseguido del método descrito en este artículo? El uso de los modelos GARCH no lineales permite la representación formal de las series analizadas desde un punto de vista matemático y crear predicciones para un número determinado de pasos. Además, nos ayudará a simular el comportamiento de las series en los períodos de predicción y probar cualquier Expert Advisor existente mediante la información pronosticada.

Ubicación de los archivos:

#	Archivo	Ruta
1	ReturnsIndicator.mq5	%MetaTrader%\MQL5\Indicators
2	Complex_class.mqh	%MetaTrader%\MQL5\Include
3	FFT_class.mqh	%MetaTrader%\MQL5\Include
4	GarchTest.mq5	%MetaTrader%\MQL5\Scripts

Se pueden descargar los archivos y la descripción de las librerías google_charts.mqh y Libraries.rar a partir del artículo mencionado anteriormente.

Referencias bibliográficas:

1. Analysis of Financial Time Series, Ruey S. Tsay, 2nd Edition, 2005. - 638 pp.
   
2. Applied Econometric Time Series,Walter Enders, John Wiley & Sons, 2nd Edition, 1994. - 448 pp.
   
3. Bollerslev, T., R. F. Engle, and D. B. Nelson. "ARCH Models." Handbook of Econometrics. Vol. 4, Chapter 49, Amsterdam: Elsevier Science B.V.
4. Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Upper Saddle River, NJ: Prentice-Hall, 1994.
5. Numerical Recipes in C, The Art of Scientific Computing, 2nd Edition, W.H. Press, B.P. Flannery, S. A. Teukolsky, W. T. Vetterling, 1993. - 1020 pp.
   
6. Gene H. Golub, Charles F. Van Loan. Matrix computations, 1999.
   
7. Porshnev S. V. "Computing mathematics. Series of lectures", S.Pb, 2004.