Revisión de la gestión del dinero

Hide | 29 octubre, 2015

Epígrafe:

Introducción

El trading puede dividirse en dos partes relativamente independientes. La primera parte, la relacionada con los sistemas de trading (Trading System, TS), analiza la situación actual del mercado con el objetivo de tomar decisiones, definiendo cuál es el mejor momento para entrar en el mismo, así como el tipo de posición que se debe ejecutar: compra o venta. La segunda parte es la referente a la gestión del dinero, y engloba todo lo relacionado con los fondos que se utilizan en cada operación. En este artículo intentamos analizar algunas estrategias MM en función de los cambios producidos en sus parámetros. Se ha seleccionado un método de simulación para el análisis. Sin embargo, en algunos casos se consideran también los resultados de decisiones analíticas. Las herramientas de análisis utilizadas son el terminal de trading MT4 y Excel. También se utilizan librerías para la generación de números pseudoaleatorios (PRNG) [1], funciones estadísticas [2] y un módulo para transmitir datos de МТ4 a Excel [3].

Suponemos que toda actividad de trading (Trading Activity, TA) tiene un cierto grado de incertidumbre. En otras palabras, los parámetros TA se conocen con una determinada precisión pero nunca se pueden terminar de establecer. La estrategia de las "apuestas al azar" puede tomarse como un ejemplo sencillo de TA. En esta estrategia, un trader apuesta de forma aleatoria (por ejemplo, lanzando una moneda) si una divisa determinada subirá o bajará un número de puntos con respecto a otra. Lo más probable es que la generación de los tipos de cambio no esté relacionada con los resultados que se obtienen al lanzar una moneda. Por lo tanto, tenemos un TA donde los resultados de las transacciones no se relacionan entre sí (Bernoulli). Además, no podemos definir el resultado del siguiente lanzamiento de la moneda, ni predecir si en el futuro coincidirá con la dirección de la divisa. Solo sabemos que la correspondencia ocurrirá aproximadamente en el 50 por 100 de los casos, siempre que exista un número suficientemente grande de intentos. Muchos traders creen que su actividad comercial es diferente de lo expuesto anteriormente. Tal vez estén en lo cierto, pero primero tenemos que analizar este caso particular. Así pues a continuación analizaremos el comportamiento y el rendimiento del sistema que puede predecir más del 50 por 100 de los casos.

Este artículo se organiza de forma estructural, de modo que los parámetros MM más interesantes se analizan primero con ejemplos teóricos. A continuación, intentaremos modelar el comportamiento de MM con datos parecidos a los de las condiciones reales del trading Forex. No analizaremos ningún TS específico. Suponemos que se utiliza cualquier TS, proporcionando datos de pérdidas y ganancias con una probabilidad especificada, así como valores preestablecidos de los mismos. Tampoco consideraremos las cuestiones relativas a la definición de la independencia (Bernoulli) de los resultados de las transacciones reales, ni la evaluación de la estacionariedad de TS en el tiempo.

Como se indicó antes, se lleva a cabo una simulación. La esencia de la simulación reside en el hecho de que el resultado de la siguiente jugada (ganancia o pérdida) se define en base a la generación de números pseudoaleatorios con parámetros preestablecidos. El tamaño de la jugada queda definido en la estrategia MM seleccionada. En caso de pérdida, la jugada colocada se resta de los fondos actuales del trader. Y en caso de ganancia, los fondos se incrementan. Se simula un número especificado de operaciones y después se calculan los resultados totales. Luego se repite el proceso varias veces (desde unos cientos de veces a varios cientos de miles); y finalmente se calcula el promedio de los resultados de la forma más adecuada.

Términos básicos y abreviaturas

Primero hay que mencionar el concepto de Riqueza Terminal Relativa (Terminal Wealth Relative, TWR ). Representa el beneficio total de la serie de operaciones como un multiplicador del capital inicial. En otras palabras, si dividimos el saldo final por el inicial, obtendremos el TWR. Por ejemplo, si el beneficio representa el 12%, TWR=1.12. si las pérdidas comprenden el 18%, TWR=0.82. Es posible comparar los resultados de varios TAs independientemente del valor absoluto de los fondos iniciales. El término TWR se utiliza por analogía con [4], [5] y [6].

Otra cosa importante es el concepto de "ganancia". Un resultado se considera ganancia si su valor supera el inicial. En otras palabras, una ganancia sucede cuando TWR>1. De igual modo, una pérdida es un resultado que no satisface la condición mencionada, es decir, TWR<=1. Así, cuando los fondos finales son iguales a los iniciales, TWR=1, y también se considera una pérdida. Pero este caso se considerará por separado si es necesario. El concepto de "pérdida" indica la pérdida de fondos, ya sea como resultado de una transacción individual o como una serie de transacciones que impiden continuar la actividad de trading. Por ejemplo, puede tratarse de la pérdida de todos los fondos (TWR<=0) o éstos pueden ser menores que un determinado mínimo (depósito de seguridad).

Ahora vamos a considerar los signos convencionales utilizados en este artículo. La probabilidad de ganancia se denota con el símbolo p. Su dimensión normal son las fracciones unitarias. Lo mismo se aplica a la probabilidad de pérdida, q=1- p. Número total de transacciones - N, número de transacciones rentables - V, número de transacciones perdedoras - L. El tamaño de las operaciones ganadoras se define en términos absolutos como a, y el tamaño de las perdedoras - como b, el ratio beneficio/pérdida es k= a/b. En relación a los tamaños de las operaciones ganadoras/perdedoras con respecto al tamaño de los fondos, los símbolos son a% y b% respectivamente. El ratio de a% a b% es k. El tamaño de la apuesta o jugada con respecto a los fondos se denota como f.

La probabilidad de los eventos recibidos durante los cálculos se denota como Prob. Si es necesario se implementarán otros signos.

Por otro lado, este artículo no diferencia los conceptos "apuesta" y "transacción". Se refieren a la misma cosa: una sola operación de trading (Single Trading Operation, STO). Una serie de tales SОT recibe el nombre de juego o trading, dependiendo del contexto. A muchos traders no les gusta, pero la palabra juego caracteriza adecuadamente la incerteza inherente en el trading.

Antecedentes históricos

Desde hace tiempo se vienen investigado las propiedades de los TS que consisten en lanzar una moneda. En su forma más simple se trata de apuestas de "cara o cruz". En el juego participan dos jugadores que inicialmente cuentan con fondos. Se lanza una moneda, y el jugador que elige cara recibe una parte de los fondos del otro jugador. De otro modo, el jugador tiene que entregar una parte de sus fondos a su contrincante. Es el clásico problema matemático de "la ruina del jugador". Este problema es clásico, y los resultados que dependen de los parámetros iniciales son bien conocidos.

Los resultados fundamentales de resolver el problema de "la ruina del jugador jugando contra un rival muy rico" son importantes para los traders. Aquí, el rival muy rico se representa con un centro de operaciones (Dealing Center, DC). Si está seguro de no actuar en contra del DC, puede considerar que los demás participantes del mercado Forex son oponentes muy ricos.

¿Cuál es el problema en este tipo de juegos? Nosotros no vamos a discutir los casos del juego infinito. Nadie puede jugar infinitamente; los posibles resultados son deplorables de todos modos. Consideramos que el juego es finito y que consiste de N operaciones. Supongamos que la probabilidad de acertar es p>0.50, y que los valores de las ganancias y de las pérdidas son iguales, a=b. Supongamos también que usted desea ganar con N transacciones.

En este juego, la mejor estrategia para lograr el máximo beneficio consiste en colocar la apuesta máxima posible, es decir, todos los fondos que usted tiene. Sin embargo, se ha demostrado matemáticamente que en este caso la probabilidad de ruina puede calcularse con la ecuación 1-(p^N) y que la probabilidad depende de N. [7][8] Cuanto mayor es el valor de N, esto es, el número de apuestas, tanto más alta es la probabilidad de ruina. En consecuencia, la ruina es menos probable si N=1 en caso de jugada obligatoria. Si la jugada no es obligatoria, la estrategia ganadora consiste en no jugar porque la probabilidad de ruina es cero.

Nota: hay una idea errónea común. Muchas personas creen que si las probabilidades de juego son iguales, entonces la ganancia posible es aproximadamente cero. Esto sería así si jugaran contra un oponente con un volumen de fondos similar.

En el trading real significa que incluso si usted gana en 2 ocasiones de 3 poniendo todos sus fondos en juego cada vez, sucederá lo siguiente. La probabilidad de ruina en la primera transacción es igual a 1/3. Es un resultado bueno, que valdrá ~0.98 sobre la décima operación.

De este modo, el requisito para maximizar los beneficios conduce a una situación absurda cuando se tienen que poner en juego todos los fondos, pero sólo una vez, no obstante. Ciertamente no es un resultado deseable si usted espera de su juego un beneficio final mayor en tanto que hace más apuestas.

Se puede incrementar la duración de tal juego y reducir la probabilidad de ruina al eliminar el requisito del beneficio máximo. O dicho de otro modo, sólo debería utilizar una parte de los fondos en sus apuestas. Si dicha parte es muy pequeña, el juego puede durar bastante tiempo. Se ha demostrado matemáticamente. [7][8] Sin embargo en este caso la ganancia final también será pequeña. Las apuestas altas aumentan el beneficio potencial, aumentando también el riesgo de pérdida. Las apuestas bajas reducen el riesgo, disminuyendo la ganancia potencial. Por lo tanto debemos hacernos la siguiente pregunta: qué tanto por ciento de los fondos es razonable utilizar en el juego (desde cierto punto de vista).

Son líneas de razonamiento normales e hipótesis. Este tema se ha estudiado minuciosamente. De hecho, el campo de la "Gestión del dinero" surge para resolver este problema. Hay varios métodos MM que ofrecen oportunidades que cumplen con los requisitos de la probabilidad de ruina y el beneficio. No los examinaremos todos por falta de espacio sino que nos centraremos en dos de ellos: el método basado en la definición de apuestas de tamaño fijo y el método que consiste en poner en juego una fracción fija de los fondos.

Un poco de teoría

Omitiendo el sentido común matemático, el momento clave de todo MM es una pregunta que puede formularse así. ¿Cuál es la probabilidad de que ocurra un evento (por ejemplo, el crecimiento de los fondos o la ruina) transcurrido un cierto período de tiempo (por ejemplo, el número de transacciones)? Esta pregunta puede analizarse desde diferentes puntos de vista, por lo tanto, el tiempo puede ser fijo y se pueden considerar sólo dos parámetros: la probabilidad del evento y el evento en sí.

Si consideramos el juego de "cara o cruz" en su forma más simple, podemos calcular algunas cosas de forma sencilla si conocemos el número N de apuestas. Por ejemplo, la esperanza matemática (МО) de los ingresos por apuesta (1) o los ingresos esperados de una serie de apuestas (2). Nótese que МО se define aquí en relación a los fondos iniciales. Esto significa que tenemos una esperanza positiva cuando МО>0 y si МО<0, se espera que la apuesta promedio sea perdedora.

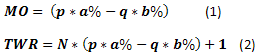
En el caso mencionado en [9]: p=0.45, q=0.55, a%=0.08, b%=0.05, N=20, los resultados son MO=0.0085, TWR=1.170. Este caso es interesante porque con una probabilidad de ganar de p<0.5, МО sigue siendo positiva en una apuesta y en consecuencia se espera un beneficio de ~17% con respecto a los fondos iniciales.

Advertencia: se examina otro método MM en [9]. Por lo tanto, los resultados serán diferentes a pesar de contar con unos datos de entrada parecidos.

Sin embargo, esa esperanza se parece a la media en todos los sentidos. No dice nada sobre la probabilidad de ocurrencia de algunos resultados en función del número de apuestas ganadoras, que complican la evaluación de los riesgos. Vamos pues a introducir dos ecuaciones más; para calcular el beneficio de una determinada cantidad de apuestas ganadoras (3) y para calcular la probabilidad de ocurrencia de una cantidad determinada de apuestas ganadoras en una serie (4):

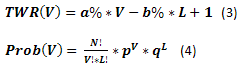
Ahora, solo tenemos que calcular los valores V= 0,1,...,N, L=N-V y crear el gráfico de dependencia de Prob(V) a partir de TWR(V). En el caso descrito anteriormente el gráfico es como sigue. Cabe señalar que el gráfico muestra los ejes Prob y TWR sin el índice (V). Esto se ha hecho únicamente para que resulte menos complicado.

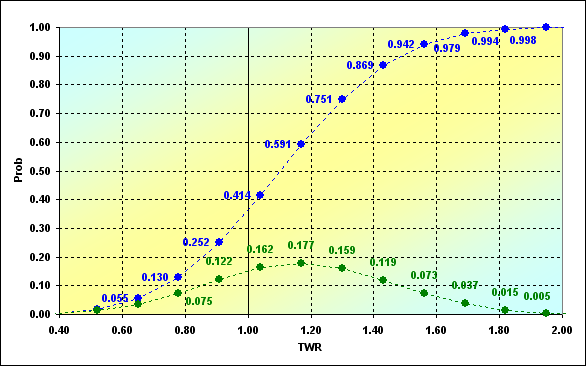
Fig. 1

Los puntos verdes son los resultados de nuestros cálculos utilizando las ecuaciones (3) y (4). El gráfico se puede interpretar de la siguiente manera. Por ejemplo, la probabilidad de que se produzcan los resultados de la serie de operaciones donde TWR=1.04, es 0.162. La mayoría de veces, con probabilidad 0.177, TWR=1.170 y así sucesivamente. Los puntos azules representan los mismos datos en forma de probabilidad acumulativa. Por lo tanto, la probabilidad de pérdida (esto es, algunas de las rondas del juego tienen TWR<=1.00) de nuestros datos de entrada es 0.252. Los valores extremos no se muestran en el gráfico. El caso de ruina (TWR=0.00) tiene Prob=6.4E-06. La ganancia máxima TWR=2.60, - Prob=1.2E-07. Se trata de probabilidades muy pequeñas. Sin embargo su existencia plantea cuestiones importantes.

Vamos a demostrarlo ahora con el siguiente ejemplo. Los cálculos se llevan a cabo con estas condiciones: p=0.45, q=0.55, a%=0.05, b%=0.05, N=50. Los resultados se muestran en el gráfico.

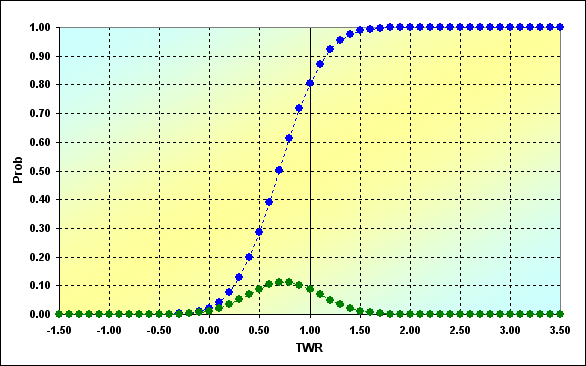
Fig. 2

Como vemos, TWR toma valores entre -1.50 y 3.50. TWR=-1.50 es posible solo si el juego se desarrolla con unos fondos menores a 0.0. Entonces las ecuaciones que utilizamos no tienen en cuenta el hecho de que los fondos se agotan en una de las operaciones intermedias y el juego no puede continuar. La cuestión que surge en este momento se llama "problema de absorción del límite". Esta cuestión considera que existe algún límite en los fondos existentes. Cuando se alcanza dicho límite el juego se detiene. En su forma más simple, se asume que el límite =0. No obstante, nos interesa más el caso que puede tomar valores arbitrarios. En [7] se revelan algunos aspectos de la solución analítica de este problema.

Rango de oportunidades

En primer lugar, vamos a intentar solucionar este problema numéricamente por medio de cálculos iterativos; y en segundo lugar modelando simulaciones basadas en métodos estocásticos (método de Monte Carlo) Comencemos pues examinando la figura e intentemos resolver el problema.

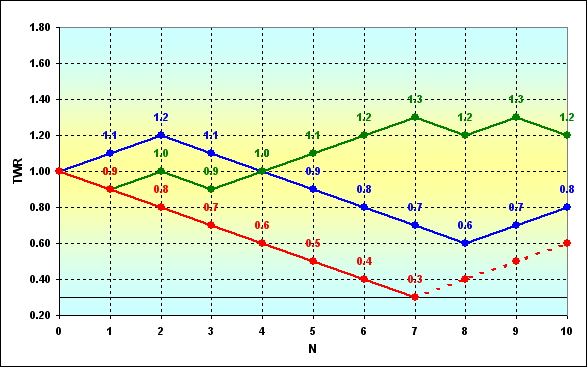
Fig. 3

La figura representa esquemáticamente posibles trayectorias de cambio de los fondos durante el juego. Se muestran tres casos aunque hay muchos más, por supuesto. Se asume que los jugadores cuyos fondos superan, por ejemplo, 0.3 (requisitos de garantía) pueden participar en el juego. Supongamos que el juego toma el camino rojo y resulta imposible seguir jugando. Entonces ocurre la absorción del límite de la trayectoria, lo que significa la ruina completa. El jugador ha quedado fuera de juego, a diferencia de los juegos que siguen los caminos verdes o azules. Así, tenemos que definir la probabilidad de ruina de los pasos anteriores.

La técnica más sencilla, intuitiva y clásica que podemos utilizar para llevar a cabo estos cálculos es el triángulo de Pascal. Este es un procedimiento recursivo donde el valor siguiente se calcula utilizando las anteriores. El triángulo ligeramente modificado se muestra a continuación.

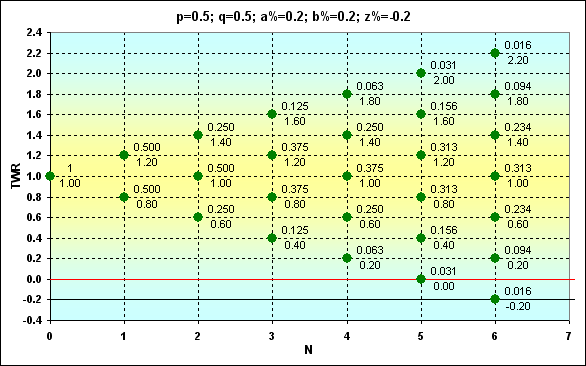
Fig. 4

Los puntos verdes indican las posiciones del gráfico TWR por donde la trayectoria puede pasar. En este caso, TWR se puede calcular con la ecuación (3). Los puntos tienen valores Prob (numerador) y valores TWR (denominador). El símbolo z% señala el valor del límite donde la absorción se produce (línea negra). La línea horizontal roja se dibuja con el valor z%+b%.

¿Qué representa la posición de los puntos en relación a la línea roja? Si el punto está más alto, es posible la próxima ronda. Cuando la línea roja cruza el punto, es la última oportunidad de dar un paso más. En caso de éxito el juego continúa; de lo contrario, se produce la absorción. Los puntos entre las líneas rojas y las líneas negras se pueden alcanzar, pero el siguiente paso fuera de ellas es imposible, ya que los fondos son insuficientes para la apuesta siguiente. En otras palabras, no es una ruina completa pero el juego no puede continuar.

Nota: por supuesto, este no es el caso de las apuestas enteras, como por ejemplo las monedas, pero si la apuesta es igual a, digamos el 0.15 de los fondos, el panorama es exactamente como el descrito antes.

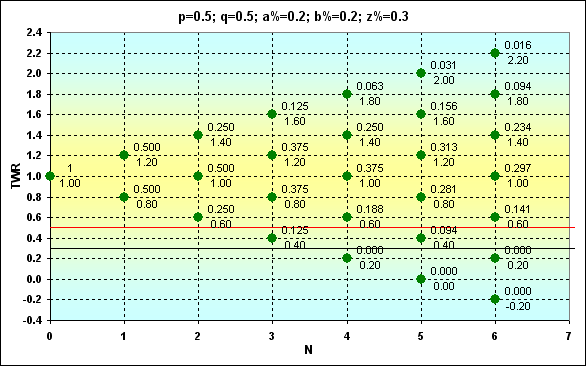
Fig. 5

A continuación se muestra otra figura de resultados para diferentes condiciones límite. Si la comparamos con la anterior notaremos la diferencia.

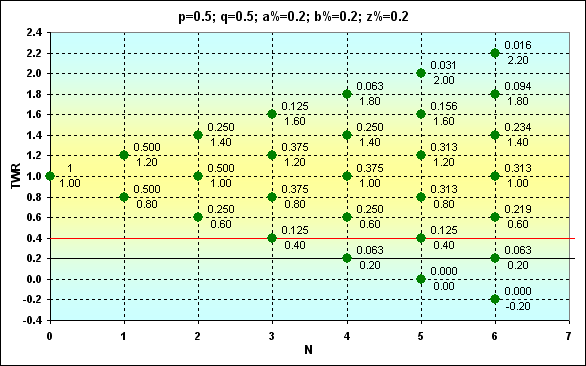
Fig. 6

Ahora, con estos datos, podemos conocer la probabilidad de cualquier evento. Por ejemplo, ¿cuál es el valor Prob de TWR=1.4 cuando N=6 en Fig. 6? La respuesta es 0.234. ¿O cuál es el valor Prob de TWR>1 cuando N=6? Los valores correspondientes de Prob se tienen que sumar. La respuesta es 0.344. ¿Qué valor tiene Prob para TWR=1.1 cuando N=6? La respuesta es 0. Y así sucesivamente.

El último ejemplo de esta serie tras haber "desfigurado" los valores de entrada: p=2/3, q=1/3, a%=0.1, b%=0.2, z%=0.2 ilustra cómo Prob y TWR cambian en este caso. Como se puede ver, la probabilidad de ganar dobla la de perder. Pero la victoria es la mitad que la pérdida.

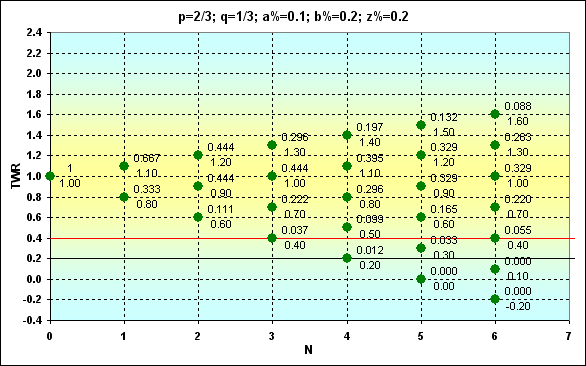
Fig. 7

Si TWR>1, Prob=0.351. Este valor Prob se acerca mucho al caso mostrado en la figura 6. Claramente los valores TWR que se pueden conseguir en un número comparable de apuestas son muchos menos.

Hay una cosa importante que no hemos debatido todavía sobre el parámetro f que indica la proporción de los fondos involucrados en la apuesta. De hecho, esta es la parte de los fondos utilizados en la transacción, es decir, b%. En el clásico "cara o cruz" se puede perder solamente un número contable de "monedas". Por lo tanto, una expresión como 1/f muestra el número de derrotas consecutivas que llevan a la ruina. El parámetro 1/f puede ser no integral en nuestro caso. Al mismo tiempo, el número de apuestas no puede ser no integral, considerando la no divisibilidad de las apuestas. Esto significa que aún puede quedar una parte de los fondos cuando el juego no puede seguir (y esta parte será menor que b%). En otras palabras, esta parte está absolutamente libre de riesgo porque no se puede perder. En este sentido la cantidad real de fondos involucrada en el juego es menor por este valor. Así, el parámetro real z% es mayor por este valor (ver Fig. 5). Es este caso si z%>0, entonces f tiende a superar b%. De acuerdo a todo lo anterior, la f real se puede calcular de la siguiente manera:

donde el símbolo int significa truncamiento. En el ejemplo que muestra la Fig. 5, b%=1/5, pero f=1/3.

Duración de las oportunidades

Vamos a considerar nuestros resultados como una correspondencia entre Prob y TWR. Se han seleccionado como ejemplo varios conjuntos diferentes como datos de entrada. Todas las series tienen la misma longitud - N=15.

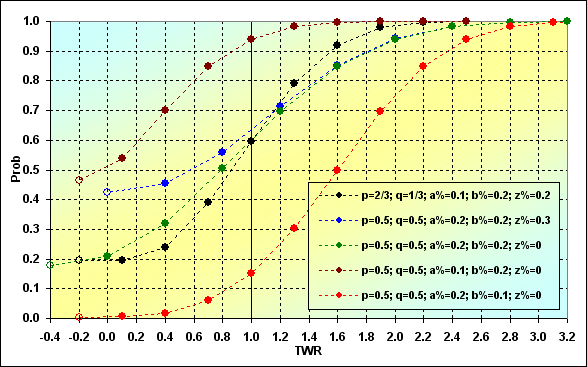
Fig. 8

A continuación explicamos qué se representa en el gráfico, y cómo. Cada curva comienza con un punto "vacío" (si se observa de izquierda a derecha). Estos son puntos condicionales (en algunos casos) que pueden no existir realmente. Sin embargo, se aplican indicando la probabilidad de absorción que ocurre en algunos de los pasos intermedios. En otras palabras, esta es la probabilidad que tiene la trayectoria de no alcanzar el último paso. El siguiente punto de la gráfica representa los datos reales sobre la probabilidad de absorción en el último paso, teniendo en cuenta todas las ruinas anteriores (con algunas excepciones que aquí no son importantes).

La siguiente imagen demuestra cómo cambia la probabilidad de ruina dependiendo de la longitud N de la serie. En este ejemplo se utilizan los mismos datos de entrada de Fig. 8. Como veremos más adelante, los resultados son significativamente diferentes.

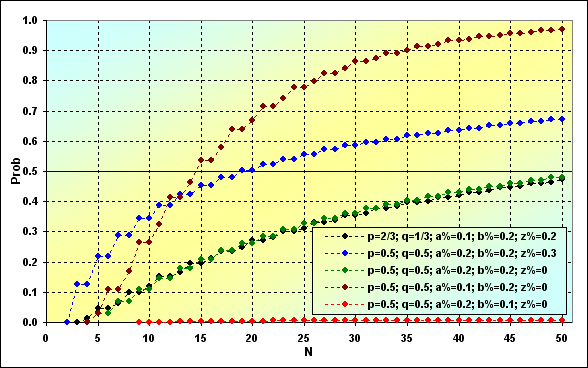
Fig. 9

Lo más importante es que si la longitud de la serie aumenta, también lo hace la probabilidad de ruina. Esta cuestión fundamental no puede eliminarse de un juego de absorción límite. Pero no todo es tan malo como parece a primera vista. La probabilidad de ruina puede ser muy pequeña dependiendo de los parámetros TS (ver línea roja). Si los parámetros TS no son muy acertados, la ruina se produce rápidamente (véase la línea marrón).

Otra cuestión importante es la probabilidad de victoria total. Antes hemos considerado el caso de TWR<(z%+b%), ahora vamos a definir el comportamiento de probabilidad TWR>1 dependiendo de N.

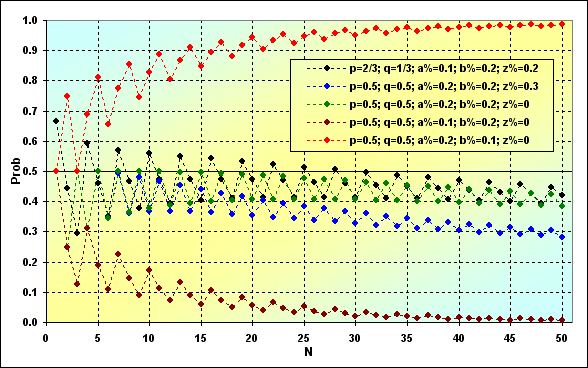
Fig. 10

El caso pintado de verde y negro ilustra las estrategias neutrales, esto es, aquellas con MO=0, de modo que podemos esperar que la probabilidad de ganar sea alrededor de 0.5. Sin embargo, este no es el caso. Esto tiene que ver con la absorción del límite.

Este es el aspecto que tiene la probabilidad de posibles TWR ocurriendo en un paso determinado. En este caso N=50 y se parece al valor de Fig. 10.

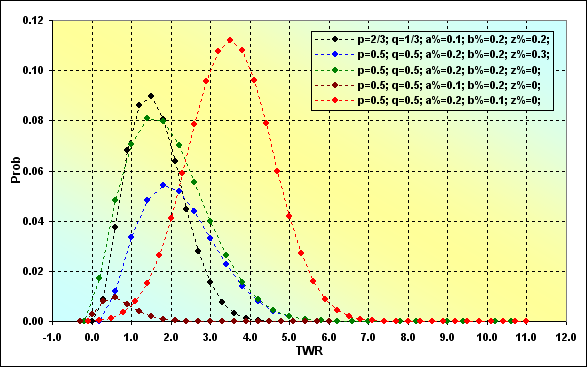
Fig. 11

Estas son curvas normales de distribución. Se diferencian de la curva de distribución convencional en que son asimétricas en relación a su valor máximo, así como en sus TWR mínimo y máximo. Además, algunas curvas están notablemente torcidas y se parecen a las curvas lognormales. Otra cosa interesante es que si comparamos las figuras 10 y 11 observaremos lo siguiente. Mientras que en la figura 11 la mayoría de distribuciones tiene el valor TWR más probable, superior a 1, la probabilidad de que el TWR sea superior a 1 es menor a 0.5. Además, en los casos donde MO=0 (líneas negras y verdes), el TWR más probable no es igual a 1, como cabría esperar. Esto no es ninguna paradoja.

Ahora ya podemos terminar nuestro examen breve sobre el problema de la "absorción de límite". Ahora vamos a realizar una simulación estocástica, comparando los resultados obtenidos con los presentados previamente, con el objetivo de evaluar la exactitud de nuestro razonamiento, así como la precisión de nuestra simulación.

Simulación

En general, se utiliza el siguiente algoritmo de simulación. Se comprueban los fondos disponibles antes del lanzamiento de cada "moneda". Si no hay fondos suficientes para continuar con el juego, se detiene. Si el juego puede seguir, PRNG se utiliza para definir si la apuesta es ganadora o perdedora. Los fondos aumentan o disminuyen de acuerdo a los resultados. El algoritmo es el mismo hasta el final del juego. Se llevan a cabo una gran cantidad de rondas, los resultados se promedian. Todo es muy sencillo. El único problema de los métodos estocásticos reside en su exactitud. Se ha demostrado matemáticamente que, con este método, es imposible encontrar la solución exacta de la tarea (ver paradoja de Moivre). Por lo tanto, antes de utilizar este modelo en otros cálculos, primero tenemos que definir en qué medida los resultados son consistentes con otros.

Vamos a comparar dos casos de solución para estos parámetros: p=0.5, q=0.5, a%=0.2, b%=0.1, z%=0.0. A continuación se presentan dos figuras (12 y 13) con la correspondencia de los resultados.

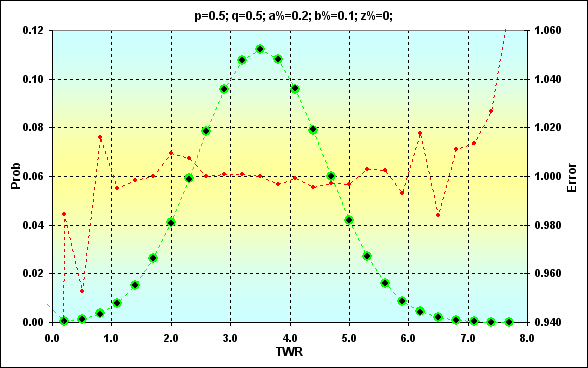
Fig. 12

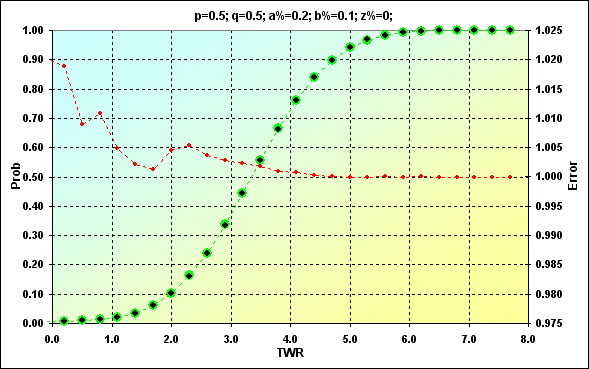
Fig. 13

Los valores obtenidos anteriormente se muestran en verde. Los puntos negros representan el resultado de la simulación. El color rojo representa el error, la relación entre el valor esperado y el de la simulación. La figura 12 muestra los valores, mientras que la figura 13 es una suma acumulada. La comparación es bastante buena. La tasa de error en el punto medio de los valores es menor que 0.5%. Por supuesto, la tasa de error es mayor en los bordes del rango. No nos preocupemos por ello. Lo tendremos en consideración el el futuro. Por otro lado, nos interesa más la suma acumulada. Ahí la tasa de error es mucho menor, dada la característica de las curvas acumulativas, donde los errores de algunos valores se cancelan mutuamente.

Otra característica de los resultados de la simulación es que es casi imposible recibir la probabilidad de los valores extremadamente raros. En el ejemplo anterior, el máximo TWR=11, mientras que Prob= 8.88E-16. Estos valores no se pudieron obtener en la simulación.

Otro ejemplo que demuestra el hecho mencionado arriba en el caso de N=250: p=0.5, q=0.5, a%=0.1, b%=0.1, z%=0.0. En esta ocasión no hacen falta más comentarios.

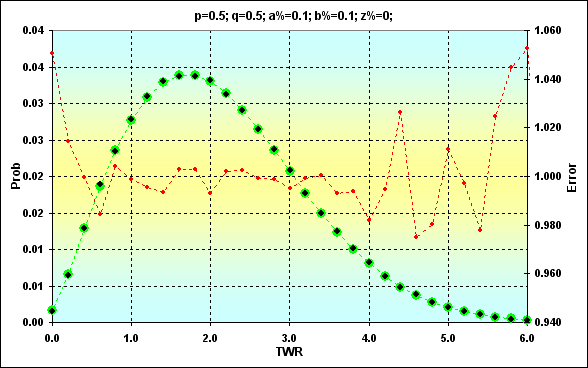
Fig. 14

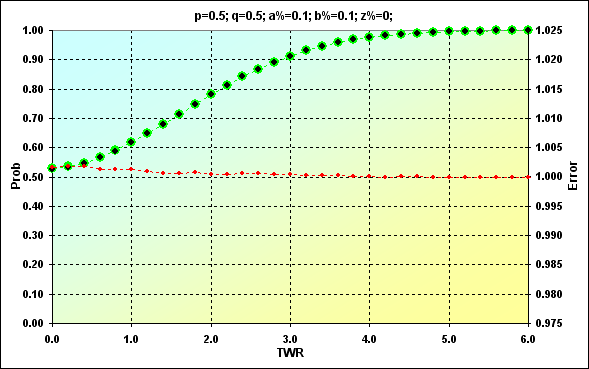
Fig. 15

Ahora podemos utilizar este modelo como base para resolver el problema más complejo que el considerado previamente.

Operaciones de trading

Antes de continuar esta exposición me gustaría que nos centráramos en algunos conceptos y ecuaciones. A primera vista, el trading real es bastante diferente al juego descrito de "cara o cruz"; esta consideración requiere un esfuerzo adicional en la simulación. Por lo tanto, es necesario aclarar de inmediato lo que tendremos que afrontar en el futuro. Por supuesto, la mayoría de los lectores tiene sus propias ideas acerca de esta afirmación. A continuación se presentan algunos conceptos y notaciones útiles.

Nota: por simplicidad sólo se examinarán aquellas operaciones con pares de "cotización directa", como EURUSD y GBPUSD. Los pares de "cotización indirecta" y los tipos de cambio cruzados se calculan de otra manera. En los tipos de cambio indirecto el precio del punto cambia de acuerdo a la cotización actual. En los tipos cruzados se considera adicionalmente la cotización actual de la divisa base a USD. Por otro lado, nosotros no utilizamos aquí los conceptos ASK y BID.

Los fondos utilizados en el trading se llaman Deposit. Podemos comprar y vender contratos con un LotSize determinado, utilizando Leverage. Como el contrato puede ser fraccional necesitamos el concepto de Lots como parámetro para indicar el tamaño del contrato aplicado. En consecuencia, el tamaño real del lote utilizado en la divisa base se llamará LotPrice. Tenemos que pagar Margin por el derecho a comprar o vender. Si expresamos Margin como parte de Deposit, recibiremos el parámetro Margin%. También utilizaremos StopOut para indicar la parte mínima de Margin. Alcanzarlo implica el cierre de la operación actual y el trading se para forzosamente. Por lo tanto, hay dos situaciones diferentes donde no se puede hacer trading y realizar operaciones futuras (en la tasa deseada de LotPrice), es decir, el caso de la ruina. También se incluye otro parámetro, Sigma. Esta es la relación de los fondos utilizados en el trading con el depósito. El ratio de los fondos empleados con respecto al capital real es como un apalancamiento, aunque se aplica a la totalidad de Deposit en lugar de LotPrice.

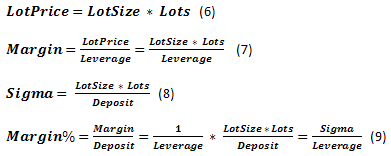
Uno de los conceptos básicos que caracterizan el proceso de negociación es Quote - tipo de cambio actual. La tasa mínima es Tick. El tamaño del cambio mínimo de la tasa del símbolo es TickPrice considerado como parte de Deposit - Tick%.

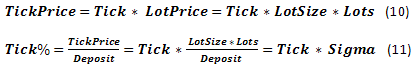
Por otro lado, hay otros parámetros relacionados con la tasa de cambio: el así llamado TP (TakeProfit) y SL (StopLoss) - cambio de tasa en que se fija la ganancia o la pérdida. Expresando estos parámetros en divisas, se llamará TPprice y SLprice. Los expresados como parte de Deposit se llamarán TP% y SL%. Además, están las comisiones del broker, incluyendo Spread, Swap etc. No examinaremos en su totalidad todos estos parámetros, sino que nos centraremos en Spread, que suele mostrarse en los puntos del cambio de tarifa. Si es necesario, los datos Swap se pueden tener en cuenta fácilmente si también se representan con puntos. Si Swap se representa como una tasa de interés real sobre los fondos prestados, con la ayuda del apalancamiento, la situación resulta algo más complicada.

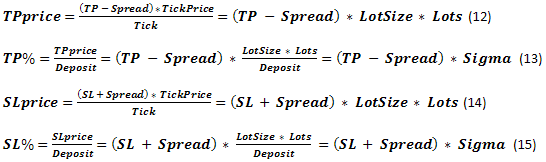
Comparemos los parámetros obtenidos con los utilizados en el problema de la "absorción del límite". SL% se corresponde claramente con b%, mientras que TP% = a%. Los fondos iniciales se representan como TWR=1. El caso actual es parecido, ya que nuestros cálculos se basan en parámetros que representan fracciones de unidad. Puede considerarse el valor límite z%+b% como Margin%. Si bien es cierto que hay alguna diferencia entre estos conceptos, no es tan crítica si no consideramos la existencia de StopOut. Parece que las tareas son parecidas tras una primera aproximación. Comprobaremos esta afirmación más adelante.

Si examinamos atentamente las ecuaciones (9, 11, 13, 15), veremos que el parámetro Sigma está en todas ellas. Como ya se mencionó, esto equivale a utilizar un apalancamiento en todas las ecuaciones fundamentales. Leverage solo puede afectar directamente aMargin%.

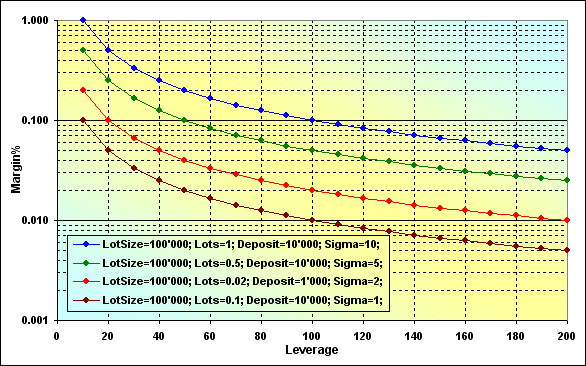
Fig. 16

La exactitud de los cálculos se puede comprobar en el siguiente ejemplo. Supongamos que si Leverage=100, LotSize=100000, Lots=0.1, Deposit=10000, el tamaño del margen es 100. Echando un vistazo al gráfico correspondiente (marrón), comprobamos que Margin%=0.01. Si Deposit=10000, recibiremos 100.

Los gráficos muestran dos características. En primer lugar, cuanto más grande es el valor de Sigma, tanto más lo es Margin%, o en otras palabras, hay menos fondos libres para destinar al trading. En segundo lugar, cuando el valor de Leverage disminuye, entonces aumenta Margin%. Analicemos los casos parecidos de la figura 9 (líneas azules y verdes). Estos casos solo se diferencian en el valor de z%. Se observa que el aumento del valor límite conduce a un aumento en la probabilidad de ruina, en igualdad de condiciones.

Puesto que no hay ninguna relación directa entre SL% y Leverage, examinemos cómo depende este parámetro de Sigma y de (SL+Spread).

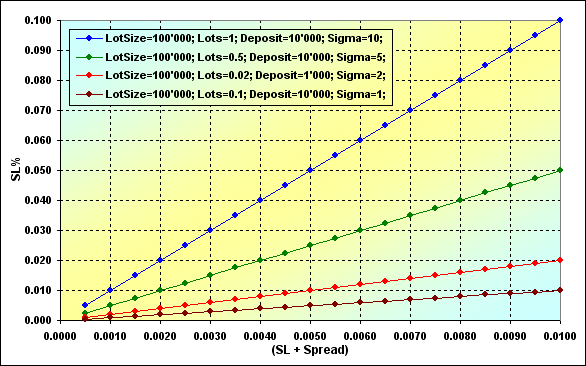
Fig. 17

Un incremento en el parámetro Sigma implica un incremento de SL%. De nuevo la ruina vuelve a ser mucho más probable. Esta dependencia es lineal. Resulta que para disminuir SL%, hace falta disminuir (SL+Spread) o Lots, ya que el resto de valores incluidos en Sigma probablemente no se pueden cambiar.

Entonces terminamos con las ecuaciones. Ahora vamos a describir brevemente cómo se ha llevado a cabo la simulación. El proceso es casi el mismo que el anterior. Hemos verificado la posibilidad de negociar, la operación de compra se ha realizado con las condiciones actuales del mercado, la tasa se ha determinado con la ayuda de PRNG, la operación de venta se ha llevado a cabo, y se ha calculado el nivel actual de los fondos. Todo esto se ha repetido muchas veces en el bucle. Los resultados de trading han quedado finalmente definidos. No se han utilizado técnicas analíticas específicas, sino que la simulación entera se ha ejecutado así. No ha hecho falta utilizar Tick ni otros conceptos relacionados; tampoco hay Swap.

Con el fin de evaluar los resultados de la simulación hemos utilizado un ejemplo con estos parámetros básicos: Deposit=1000, Leverage=100, LotSize=100000, Lots=0.1, TP=0.0040, SL=0.0040, Spread=0.0002, p=0.5, N=250. El valor de la longitud de la serie es aproximadamente igual al número de días laborables por año. Por tanto, asumiendo que se ejecuta una operación por día (transacción intradía, entonces no hay Swap), los resultados se anualizan. Tras aplicar las ecuaciones (9, 13, 15), obtenemos estos resultados: TP%=0.038=a%, SL%=0.042=b%, Margin%=0.1 (en consecuencia, z%=0.058). Vamos a realizar la simulación estocástica y a hacer nuestros cálculos tal y como hicimos en la figura 4.

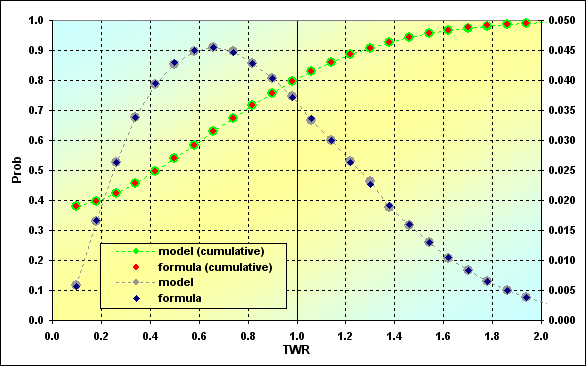
Fig. 18

Comparamos las ecuaciones y los cálculos de la simulación. Como vemos, la coincidencia de los resultados es buena. Esta es otra razón para afirmar que el proceso de trading no es muy diferente del clásico juego de "cara o cruz", en lo que se refiere al problema de la "absorción del límite".

A continuación se muestran unos breves comentarios sobre el gráfico. El punto extremo más pequeño a la izquierda de la línea verde muestra la probabilidad de ruina. En nuestro caso, es TWR<= Margin% - 0.375. La probabilidad de pérdida es cuando TWR<=1, - 0.795, de modo que la probabilidad de ganancia es 0.205.

ММ - Tamaño fijo (FixSize)

La idea principal de este método MM consiste en utilizar cada vez una parte fija de los fondos iniciales independientemente de las circunstancias. De hecho, las características convencionales de gestión del tamaño del lote que los brokers proporcionan a los traders se corresponden con este método. Además, este método se implementa en el juego de "cara o cruz". Puesto que antes ya hemos cubierto las características básicas de este método, procedamos ahora a la cuestión de los parámetros individuales que afectan al sistema. Vamos a utilizar nuestro modelo para abordar esta cuestión.

Como consideramos una solución numérica más que analítica, la única manera de evaluar el efecto de los cambios en los parámetros de entrada es comparar los resultados de los cálculos. Corregiremos la información, cambiando algunos datos en un cierto rango, y observaremos los cambios.

Retomemos el caso mostrado en la figura 16. Realizamos los cálculos con los siguientes parámetros: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL= { 0.0030, 0.0040, 0.0050, 0.0060}, Spread=0.0002, p=0.5, N=250, Leverage= { 3, 4, 5, 6, 7, 10, 25, 50, 75, 100}.

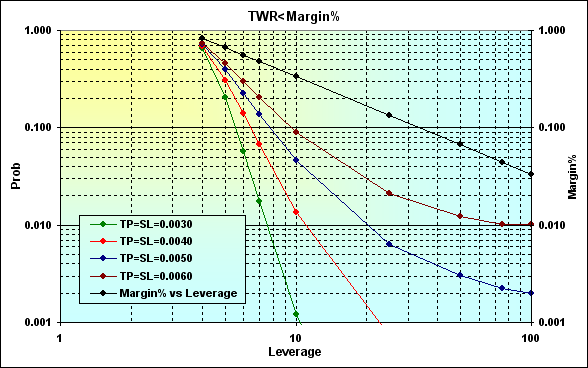
Fig. 19

Los resultados de los cálculos se muestran en escala logarítmica para mayor claridad. Para ser exactos, la disminución de Leverage implica el incremento de Margin% (línea negra) mejorando así la probabilidad de ruina. La correlación entre la probabilidad de ruina y el apalancamiento es no lineal y su mayor impacto se puede sentir en el área de pequeños valores Leverage. El efecto negativo causado por la disminución de Leverage se puede reducir al disminuir los niveles TP y SL. Pero incluso si el valor de Leverage es suficientemente pequeño (en nuestro caso es 4), la probabilidad de ruina es suficientemente alta todavía. Además, esta figura muestra otra característica.

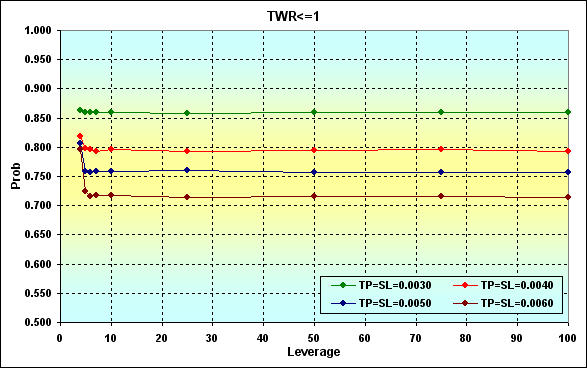
Fig. 20

La figura ilustra cómo cambia la probabilidad de pérdida al alterar el valor de Leverage. Como vemos, la pérdida es más probable cuando TP y SL disminuyen.

Si incrementamos los fondos hasta, digamos 10 000, la ruina se vuelve imposible en el caso de N=250. Al comparar las figuras 20 y 21 veremos que los resultados coinciden en el área Leverage>10.

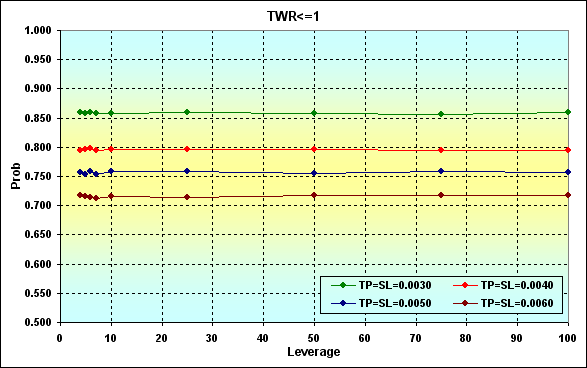
Fig. 21

Consideremos otro ejemplo donde la probabilidad de ganar una operación es mayor que la probabilidad de perder, en otras palabras, p>0.50. Hagamos los cálculos con estos parámetros: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL={ 0.0030, 0.0040, 0.0050, 0.0060}, Spread=0.0002, p=0.52, N=250, Leverage={ 3, 4, 5, 6, 7, 10, 25, 50, 75, 100}.

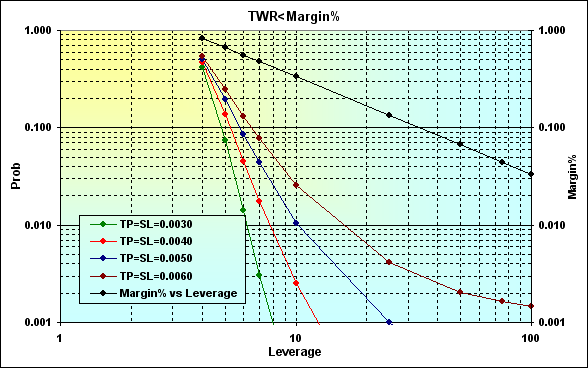
Fig. 22

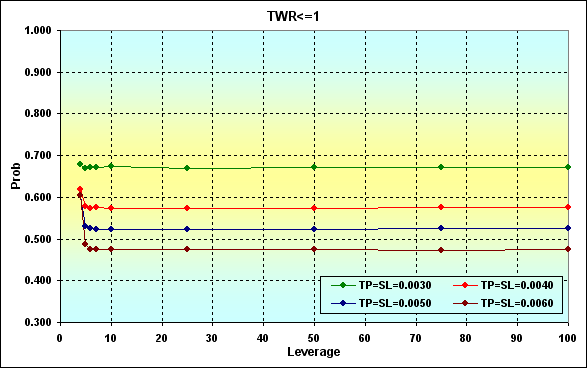
Fig. 23

Si comparamos los resultados de cálculo de la figura 19, veremos que incrementando la ganancia en una operación disminuyen las probabilidades de ruina y de pérdida. Este es un resultado esperado y natural.

En el ejemplo siguiente vemos cómo la probabilidad de ganar afecta a la de perder en una transacción, considerando los niveles TP, SL. Los parámetros son así: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52, 0.53, 0.54, 0.55, 0.56, 0.57}, N=250, Leverage=100.

Nota: este ejemplo se ha seleccionado para que la probabilidad de ruina sea despreciable y se pueda ignorar. La probabilidad más alta de ruina en el peor caso es aproximadamente 0.04.

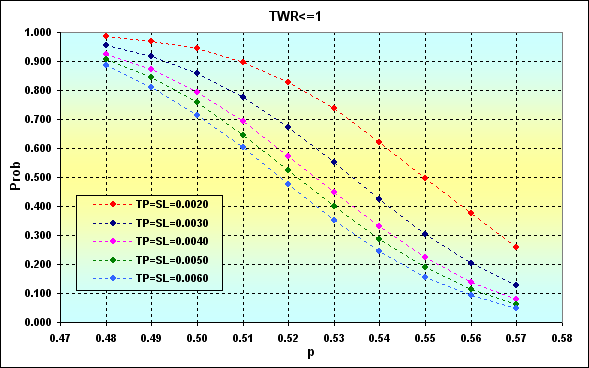
Fig. 24

Es importante señalar que al aumentar p disminuye la probabilidad de pérdida. La disminución de los niveles TP y SL tiene el efecto contrario. Esto sucede debido al valor fijo de Spread. Otra conclusión que podemos extraer de estos resultados es que operar con bajos niveles en cada operación es bastante arriesgado.

El siguiente ejemplo ilustra hasta qué punto el valor Spread puede afectar a la probabilidad de pérdida. Parámetros principales de la simulación: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}, Spread={ 0.00000, 0.00005, 0.00010, 0.00015, 0.00020, 0.00025, 0.00030, 0.00035, 0.00040, 0.00045}, p=0.55, N=250, Leverage=100.

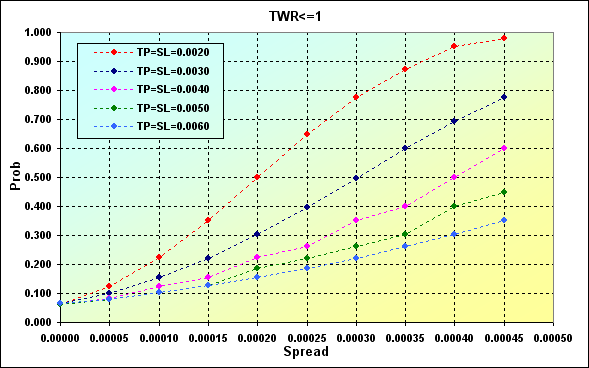
Fig. 25

Esta otra figura muestra la correspondencia entre la probabilidad de pérdida y el MO de la transacción calculada con la ecuación (1) para los datos mostrados en la Fig. 24. En lugar de los valores a% y b%, se han utilizado los TP% y SL% adecuados.

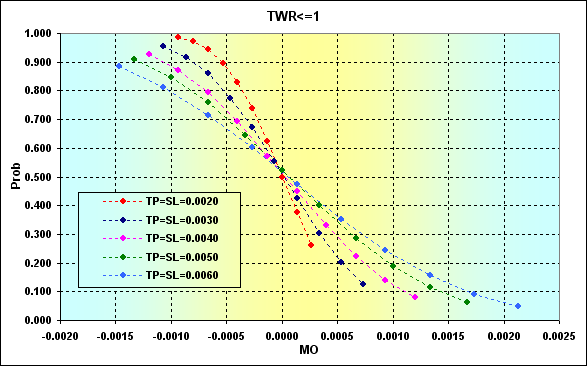
Fig. 26

Como vemos, incrementar en MO la operación disminuye la probabilidad de pérdida, aunque no se puede reducir a cero. Significa que un MO positivo no garantiza él solo una protección contra la pérdida y la ruina. Unos niveles mayores de TP y SL reducen claramente la probabilidad de pérdida. Pero al mismo tiempo (ver las figuras 19 y 22), se incrementa la probabilidad de ruina.

Dicho de otro modo, hemos vuelto a la afirmación anterior que hicimos al describir el juego clásico de "cara o cruz". Aumentar las apuestas implica aumentar las ganancias posibles (y reduce la probabilidad de pérdida), pero la ruina es más probable. Lamentablemente, no existe ningún método matemático para seleccionar el volumen de la operación cuando se aplica este método MM. Tan solo podemos utilizar nuestras preferencias personales acerca de qué nivel de ruina o pérdida es aceptable en cada caso.

Determinemos la probabilidad de alcanzar un cierto nivel TWR durante el juego. Parámetros principales de la simulación: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL= 0.0030, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52}, N=250, Leverage=100.

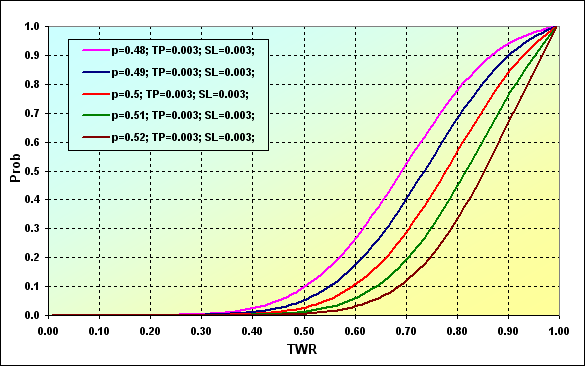
Fig. 27

Los datos del gráfico se pueden interpretar de la siguiente manera. La probabilidad de que el valor TWR disminuya a ~0.90 en caso de p=0.48 es ~0.93. Si p=0.52, el valor es ~0.68.

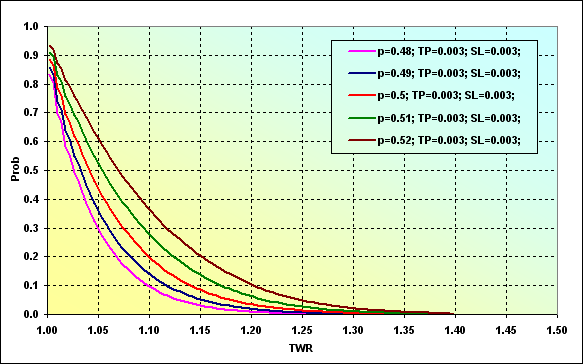
Fig. 28

La figura muestra la probabilidad que tiene el nivel TWR de incrementarse hasta un cierto valor durante el juego. Por ejemplo, la probabilidad de que TWR alcance ~1.10 con p=0.48 es ~0.09. Si p=0.52, el valor es ~0.37. Es bastante lógico que un aumento de la probabilidad de ganar una operación implique un aumento de la probabilidad de alcanzar un determinado nivel.

Ahora vamos a dedicar unas líneas a Drawdown. Para evaluar este parámetro hemos utilizado el script [10] con algunos cambios menores. Además, a diferencia del script original, los cálculos se han hecho teniendo en cuenta el Spread.

Principales parámetros de la simulación: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL=0.0030, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52}, N=250, Leverage=100.

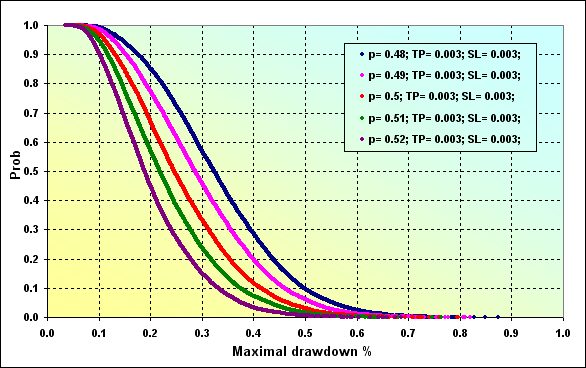
Fig. 29

Los parámetros iniciales son como en la Fig. 27, la probabilidad de Maximal Drawdown % ~0.20 en p=0.48 es ~0.85. En caso de p=0.52, el valor es ~0.47.

Ya para terminar, este ejemplo: Deposit=2000, LotSize=100000, Lots=0.1, TP=SL={ 0.0020, 0.0030, 0.0040, 0.0050, 0.0060}, Spread=0.0002, p=0.50, N=250, Leverage= 100.

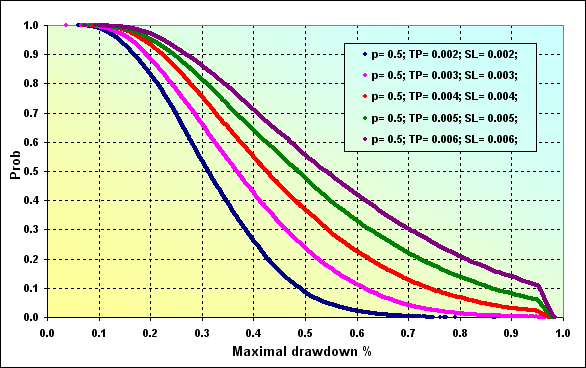
Fig. 30

Una pequeña nota sobre la figura 30. El nivel de Maximal Drawdown % es 0.96 coincidiendo aproximadamente con el nivel de Margin. Por esto se observa una ruptura en las líneas de los gráficos. Como vemos, la probabilidad de alcanzar valores Maximal Drawdown % mayores ha aumentado, en comparación con la figura 29 (línea roja).

Antes de terminar nuestra discusión sobre las características de MM con tamaño fijo, examinemos dos distribuciones de tales características del modelo, como Profit Factor y Expected Payoff.

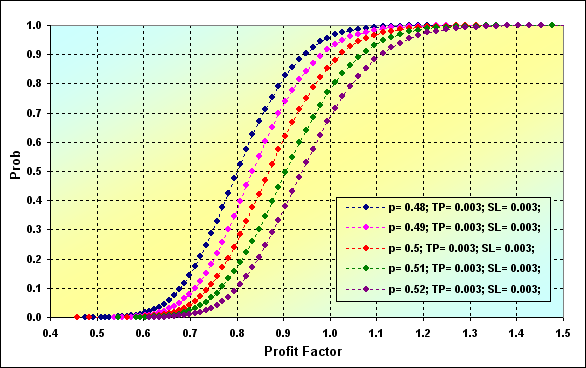
Fig. 31

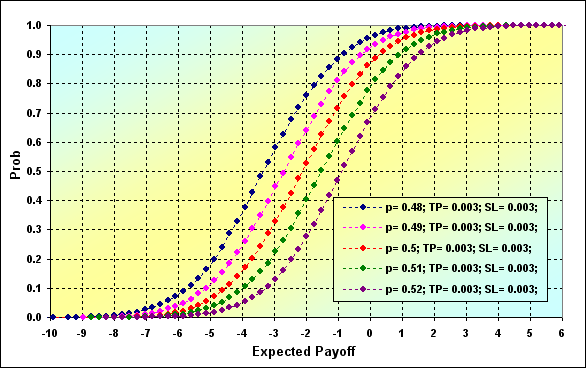
Fig. 32

Parámetros principales de la simulación de las figuras 31 y 32: Deposit=3000, LotSize=100000, Lots=0.1, TP=SL= 0.0030, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52}, N=250, Leverage=100.

ММ - Fracción Fija (FixFrac)

Este método comprende ММ con una apuesta como fracción fija de los fondos actuales. El tamaño de la operación se determina inicialmente, por ejemplo el 10%. La cantidad de fondos utilizados en las transacciones se calcula en base a la cantidad total de los mismos, independientemente de los resultados. Por lo tanto, cada operación exitosa aumenta el volumen de la siguiente y viceversa. A veces este sistema se llama anti-martingala (aunque estrictamente hablando esta denominación es incorrecta). Este sistema supone la reinversión del beneficio posible, a diferencia de MM con tamaño fijo.

Son bien conocidas las ventajas y desventajas de este método MM. Este método proporciona un rápido crecimiento de los fondos cuando las operaciones tienen éxito. Este crecimiento tiene la forma de una progresión geométrica, a diferencia del método de tamaño fijo, que tiene una aritmética. En teoría, este método evita la pérdida completa de los fondos en un caso de divisibilidad infinita de apuestas (aunque, por supuesto, esto no sucede en el trading real).

Uno de los inconvenientes del método es el así llamado efecto apalancamiento asimétrico. Esto significa que la siguiente apuesta después de las pérdidas tiene menor volumen. Así, un jugador necesita más operaciones ganadoras que perdedoras para recuperar las pérdidas. Además, las series ocultas pueden afectar los resultados de este método (no-Bernoulli).

Durante su uso práctico, este método MM puede plantear un problema para seleccionar la parte de los fondos que proporcione la mejor tasa de crecimiento en combinación con una probabilidad de ruina aceptable. Esta estrategia de juego asintóticamente óptima ha sido propuesta por Kelly.

Pero primero examinemos algo de teoría y algunas ecuaciones. Conociendo el número de apuestas ganadoras y perdedoras, así como los valores de las victorias y derrotas por apuesta, podemos calcular TWR(V) y Prob(V) de la misma manera que en el método de tamaño fijo. La ecuación (17) se parece a (4).

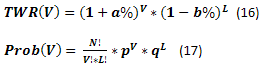
A continuación se muestra un ejemplo de cálculo utilizando las ecuaciones (16) y (17). La probabilidad de alcanzar diferentes valores TWR se muestra como un valor acumulado.

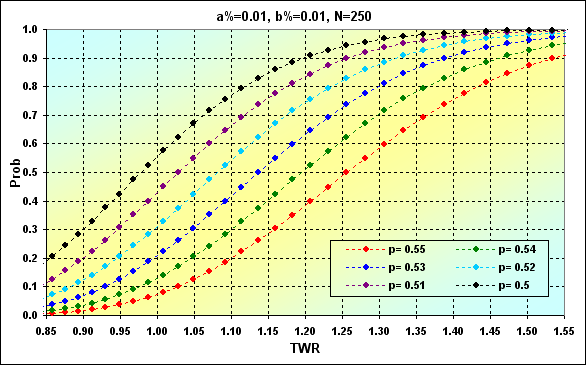
Fig. 33

La siguiente figura muestra dos casos que tienen condiciones parecidas pero diferentes MM. El caso de tamaño fijo se ha tomado de la figura. 8. El MM de tamaño fijo (FixSize) se representa en rojo, y la fracción fija (FixFrac) en negro.

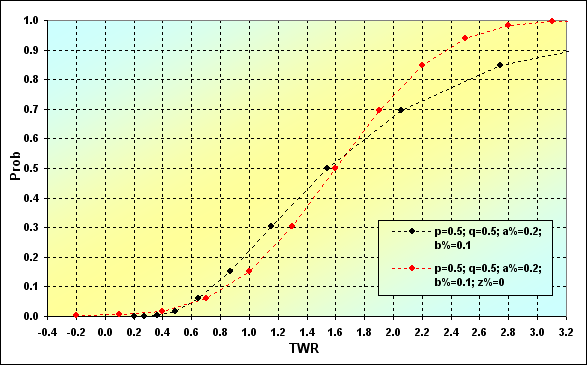
Fig. 34

Esta es la ecuación que describe la velocidad de crecimiento de los fondos cuando las pérdidas y las ganancias son iguales.

Con sencillas transformaciones y razonamientos [8], y minimizando el crecimiento geométrico promedio esperado, podemos producir la siguiente ecuación que muestra el tamaño óptimo f* de la apuesta.

Este es el así llamado criterio de Kelly. La idea es bastante sencilla. En un ТS con probabilidad ganadora superior a 0.5, mientras los valores de las pérdidas y de las ganancias sean iguales, hay que utilizar la cantidad de fondos que indica la ecuación (19) en el momento de colocar una orden. Por ejemplo, p=0.55, en cuyo caso, f*=0.55-0.45=0.10. Esto significa que para que sus fondos crezcan eficientemente usted debe utilizar una décima parte de sus fondos en su apuesta.

Advertencia: tenga en cuenta que la apuesta óptima de Kelly es diferente a la de Vince en [4]. Un poco más adelante explicaré que no hay ningún error en la versión de Vince.

Nota: si calculamos el valor de la cantidad de fondos óptima para p=0.50, entonces obtendremos 0.00 naturalmente. En otras palabras, no es para nada recomendable jugar.

Cuando las ganancias y las pérdidas son k veces diferentes tenemos que utilizar otras ecuaciones diferentes a (18) y (19). [8][5].

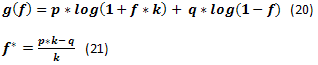
Si creamos el gráfico de cambio g(f) a partir de f con la ecuación (20) obtendremos algo como la figura siguiente. Obsérvese en la figura el punto f*. Este es el punto más alto del gráfico donde la tasa de crecimiento de los fondos alcanza su máximo. También está el punto fc, que representa el punto de intersección entre el gráfico y la línea cero. Es el punto donde la tasa de crecimiento de los fondos es cero.

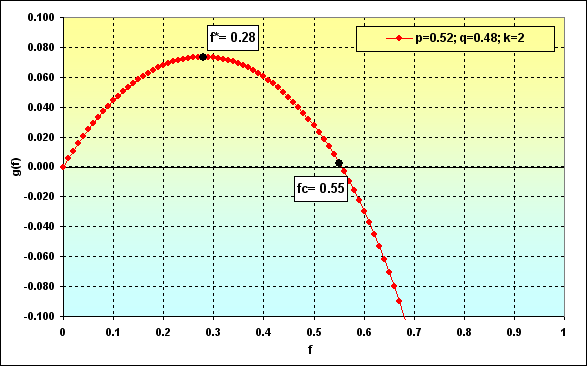
Fig. 35

Nota: se ha seleccionado k=2 como ironía dirigida a los gráficos correspondientes de los libros de Vince. Sin embargo, tal valor k proporciona una mayor "claridad" y "belleza" a los métodos por los que aboga el autor.

En [8], se afirma que si el juego se lleva a cabo en las condiciones especificadas, entonces f* proporciona la tasa de crecimiento de fondos máxima y la probabilidad de ruina cero. Si se utiliza una cantidad menor que f*, la probabilidad de ruina también es cero, pero la tasa de crecimiento de los fondos es menor. La ruina es inminente si la cantidad de fondos es superior a fc. Si los fondos están comprendidos entre f* y fc, la tasa de crecimiento también es más lenta que el máximo, aunque no hay ninguna probabilidad de ruina.

Los resultados son bastante impresionantes. Sin embargo, estos cálculos teóricos no tienen en cuenta algunas características del mundo real. Por lo tanto, Vince recomienda calcular fс óptima teniendo en cuenta las pérdidas máximas. Esto nos lleva a que el valor de su f* se vuelve menor que el calculado estrictamente de forma matemática, con todas las consecuencias resultantes.

Intentemos plasmar esto en los gráficos. Tomemos este caso: Deposit=1000, LotSize=100000, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.01, Spread=0.0000, p=0.51, N=250, Leverage= 100. Con estos datos de entrada, Lots=0.01 y TP%=SL%=0.01. Además, f*=0.02 y fc=0.04, tal y como ilustra la siguiente figura.

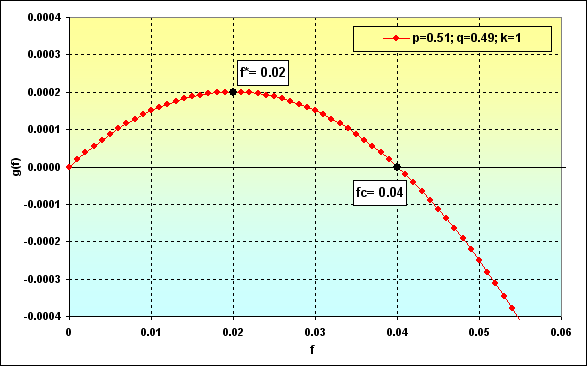
Fig. 36

Si f cambia, tendremos las siguientes correlaciones entre Prob y TWR. Hagamos los siguientes cálculos para demostrar esto.

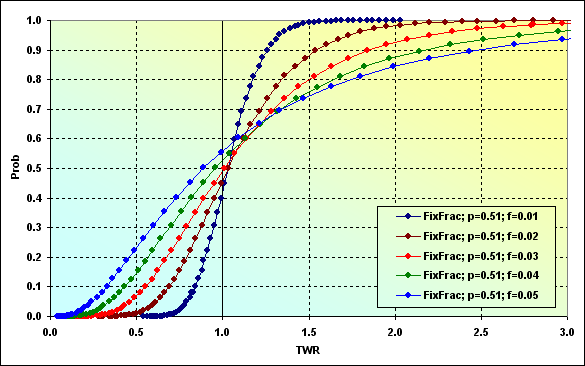
Fig. 37

Analicemos esto más detalladamente. La línea correspondiente a f=0.01 demuestra el caso expuesto anteriormente; f<f* cuando la tasa de crecimiento de los fondos es inferior al máximo posible, mientras que la probabilidad de ruina es cero. En este caso, la probabilidad de pérdida TWR<=1 es igual a ~0.40.

El caso siguiente, f=0.02 es cuando los fondos utilizados son óptimos. La probabilidad de pérdida es ~0.45. En otras palabras, se espera que sean rentables más de la mitad de las rondas del juego.

Versión del cálculo f*<f<fc, es decir f=0.03. La probabilidad de pérdida es ~0.45. La ruina es imposible dadas las condiciones del juego. Sin embargo, los valores TWR que pueden descender son más significativos que en los casos previos. Los grandes beneficios también son posibles.

Ahora la probabilidad de pérdida es ~0.50, es decir f=fc=0.04. Se indica que en este caso, TWR fluctuará seguramente entre 0 y +infinito.

Y el último caso, f>fc. La probabilidad de pérdida es ~0.55. En tal caso puede producirse una ganancia considerable, pero los fondos se perderán en el largo plazo (infinito) y TWR se reducirá a un nivel que puede clasificarse como ruina.

Unas cuantas ecuaciones más. La tasa de crecimiento de los fondos g(f) puede evaluarse con las ecuaciones (18) y (20). Dado que se conoce la tasa de crecimiento g(f) y el número de transacciones N, TWR puede calcularse con la ecuación (22). Además, sería más correcto evaluar el beneficio promedio esperado de la operación con MM utilizando una parte fija de los fondos como ilustra la media geométrica Gmean de la ecuación (23), en lugar de una media aritmética.

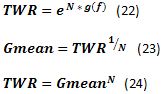
Recomendación: estaría bien incluir el cálculo de la media geométrica de las operaciones en el informe estándar del probador de MT. Esto permitiría a los usuarios evaluar más correctamente sus sistemas de trading de fracción fija.

A continuación se muestran dos ejemplos de cálculo realizados con las ecuaciones (23) y (24), y con los datos de la figura 36.

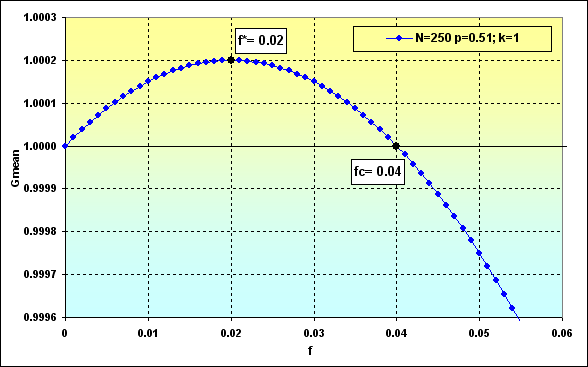
Fig. 38

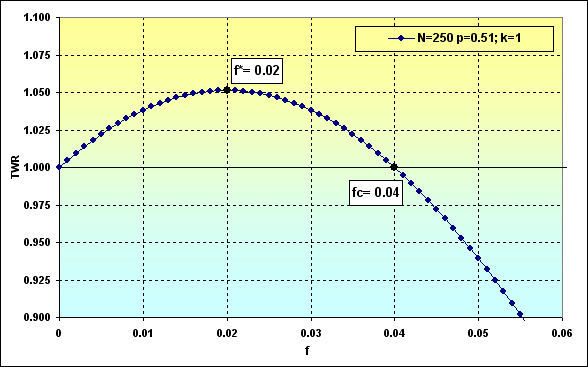
Fig. 39

Por lo tanto, bajo estas condiciones, y de acuerdo a la figura 39, los fondos totales tienden a TWR=1.05 con la participación óptima en las apuestas. Como vemos en la figura 37, la probabilidad de pérdida es ~0.45.

Sería interesante ver cómo se comportan otros MM con las mismas condiciones iniciales. Con los datos de la figura 36 se obtiene lo siguiente.

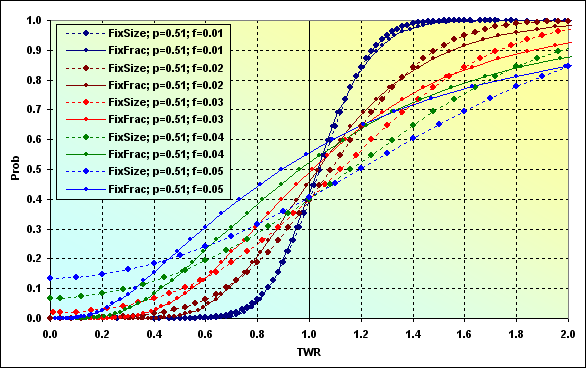
Fig. 40

En el caso de f=0.01 los gráficos son muy parecidos; los MM son diferentes. En otras palabras, bajo determinadas condiciones se obtienen resultados similares. Los otros casos demuestran que, en igualdad de condiciones, la probabilidad de pérdida de MM de tamaño fijo es menor (TWR<=1) que la fracción fija.

Advertencia: la observación anterior solo se aplica a los datos de entrada seleccionados. En ningún caso puede considerarse como una regla general.

Ahora vamos a exponer otra circunstancia interesante; una correlación de valores a los que TWR tiende, con la cantidad de fondos utilizada en una operación. El cálculo de estos valores se puede realizar para MM de tamaño fijo como multiplicación de MO por N, mientras que la ecuación (22) se utiliza para MM de fracción fija.

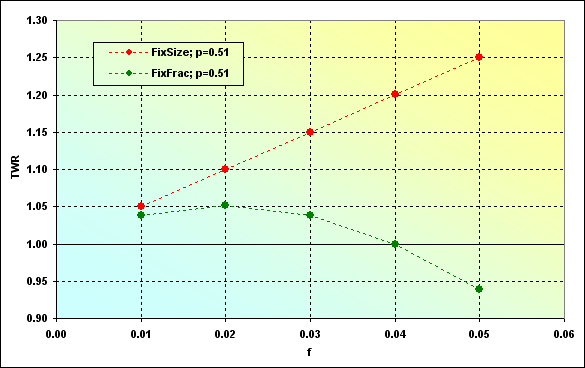
Fig. 41

Como se observa, el beneficio esperado es mayor cuando se utiliza MM de tamaño fijo (para los datos de entrada empleados). Sin embargo, esto no siempre es así.

Las correlaciones a las que TWR tiende cambian en función de la probabilidad ganadora de una transacción. Los gráficos de la longitud N=250 de la serie se muestran a continuación.

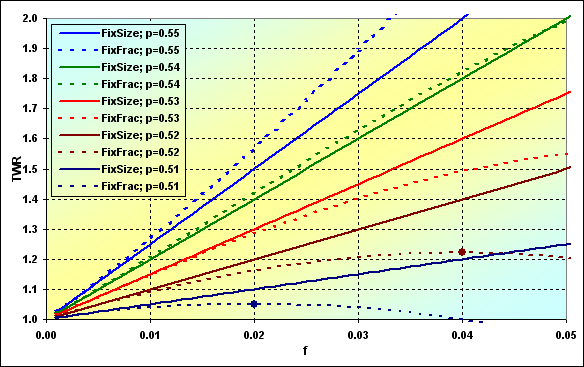
Fig. 42

En términos del TWR esperado, existen situaciones en las que el ММ de tamaño fijo es preferible al de fracción fija. Sin embargo, si consideramos esta cuestión junto con la probabilidad de ruina, las cosas no son tan obvias como parecen.

Además, el valor del TWR esperado, se ve significativamente afectado por la longitud N de la serie. En general, el beneficio del MM de fracción fija es mayor cuanto más larga es la serie.

Ahora vamos a terminar nuestro análisis de los aspectos teóricos y vamos a pasar a la simulación. De hecho, en nuestro modelo inicial no ha cambiado nada, salvo el hecho de que hay que añadir los conceptos de lote mínimo y máximo, MinLot y MaxLot. También necesitaremos el valor LotStep para caracterizar el mínimo paso posible de cambio de lote. El algoritmo de cálculo general sigue siendo el mismo. Inicialmente se presentó el concepto MinDeposit como valor mínimo posible del depósito. Por lo tanto, el trading puede continuar si el valor del depósito supera Margin y MinDeposit.

El siguiente ejemplo simula varios MMs con estos datos de entrada. Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0.01, LotStep=0.01, MaxLot=100, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.01, Spread=0.0000, p=0.54, N=250, Leverage=100. Obsérvese que en este cálculo no se utiliza Spread.

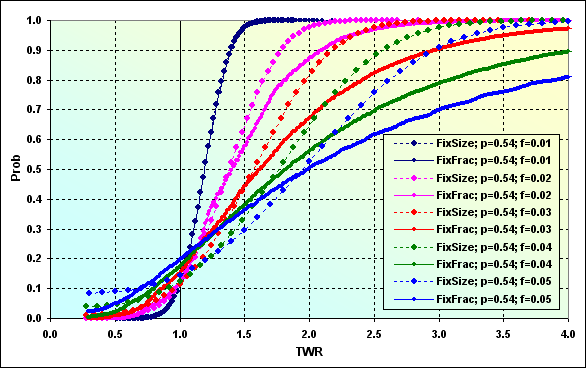
Fig. 43

La introducción de MinDeposit en los cálculos implica que el ММ de fracción fija, que tenía teóricamente una probabilidad de ruina cero (con f<fc), ahora tiene una diferente de cero. Además, la discretización, así como las limitaciones del tamaño de lote, también conducen a la probabilidad de ruina en determinadas condiciones (que no se muestran aquí). El impacto de estos factores negativos puede reducirse tomando como fondos iniciales la diferencia de los valores Deposit y MinDeposit. De hecho, eso es lo que propone Vince: sólo hay que utilizar una parte de los fondos para calcular la parte óptima. Parece una decisión inteligente pero naturalmente implica la disminución de TWR.

Permítame que haga algunas aclaraciones más sobre la figura 43. Echemos un vistazo a "FixFrac; p=0.54; f=0.05" en el gráfico donde se corresponde con Prob=0.50. Esta es la mediana, el valor done se localizan el 50% de todos los valores, en la parte superior y en la parte inferior. En este caso corresponde a TWR~2.00. En otras palabras, la mitad de los juegos ha conseguido duplicar los fondos iniciales. La probabilidad de pérdida es ~0.20, y la probabilidad de ruina es ~0.03. En comparación con el gráfico "FixSize; p=0.54; f=0.05", se observa que la probabilidad de ruina se puede incrementar hasta ~0.08, mientras que la probabilidad de pérdida desciende a ~0.14, pero la mediana se corresponde aproximadamente con TWR~2.00. Si tenemos la suerte de alcanzar la cantidad de casos donde TWR>2.00, el resultado probablemente será menor que cuando se utiliza MM de fracción fija.

Comparando las gráficas de las figuras 42 y 43, cabe señalar que los valores de la figura 42 a los que tiende TWR, no son más que la mediana de la figura 43.

Ahora consideremos el caso de la figura 43 con Spread=0.0002. Los demás datos de entrada permanecen iguales.

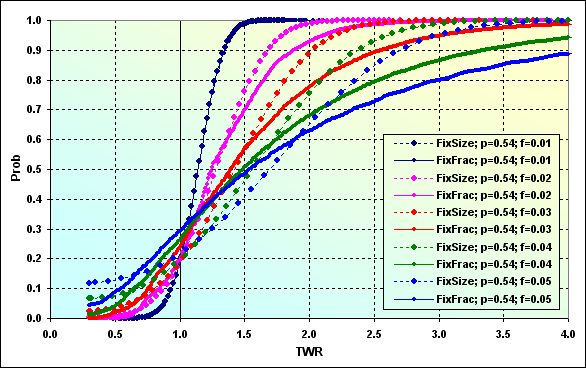
Fig. 44

Como vemos, el Spread comprendido entre el 0.4% y el 2% del nivel ganancia/pérdida por transacción implica el cambio considerable de la figura. Esto se ve mejor en la siguiente figura, donde se comparan dos casos de cálculo (los de las figuras 43 y 44).

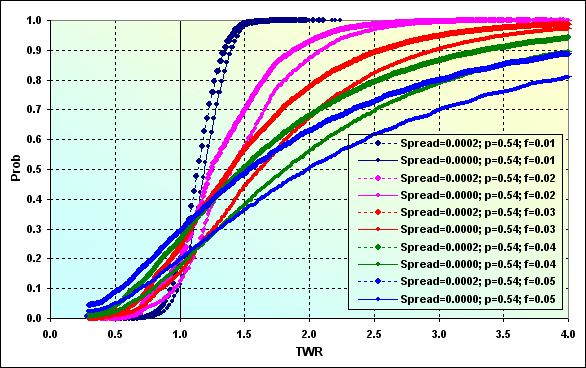
Fig. 45

Por consiguiente, el Spread disminuye el TWR medio (por ejemplo las líneas azules) desde 2.00 hasta 1.50. La probabilidad de pérdida ha aumentado de 0.20 hasta 0.30. La diferencia no parece muy importante, solo 0.10; uno de cada jugadores pierde (aunque no se arruina) en el primer caso, mientras que en el segundo caso es uno de cada tres.

Vamos a examinar los cambios en la probabilidad de pérdida inducidos por la probabilidad de ganancia por operación, teniendo en cuenta diversos f, simulando varios ММs con estos datos de entrada: Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0.01, LotStep=0.01, MaxLot=100, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.0100, Spread=0.0002, p={ 0.48, 0.49, 0.50, 0.51, 0.52, 0.53, 0.54, 0.55, 0.56, 0.57}, N=250, Leverage=100.

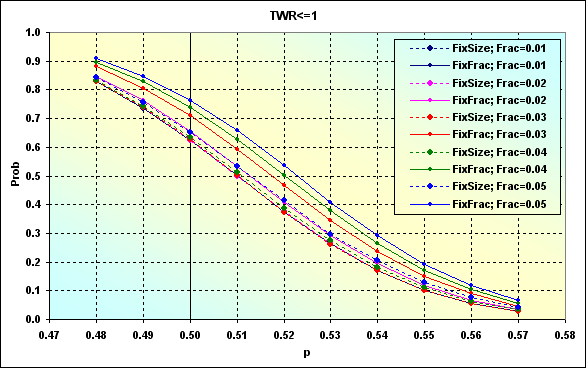
Fig. 46

Este ejemplo se diferencia del de la figura 24 en que los niveles TP y SL son fijos pero el el tamaño del lote puede variar. La Figura 47 muestra un caso con datos parecidos a los de la figura 46; TP=SL=0.0050.

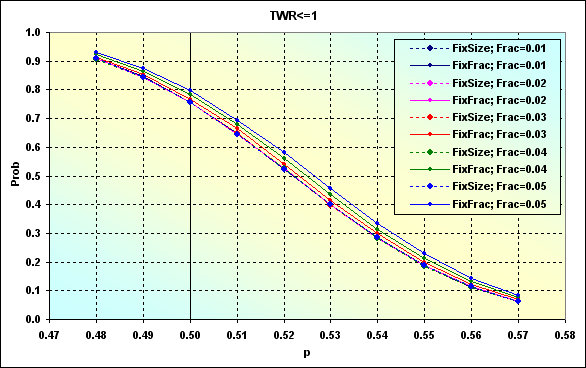
Fig. 47

De modo parecido en la figura 24, la disminución de los niveles TP y SL induce un incremento en la probabilidad de pérdida. Además, la dispersión de los valores en los diferentes casos disminuye. Los gráficos se han vuelto más "densos". En otras palabras, el efecto del valor f ha disminuido. Esto es particularmente evidente en la siguiente figura.

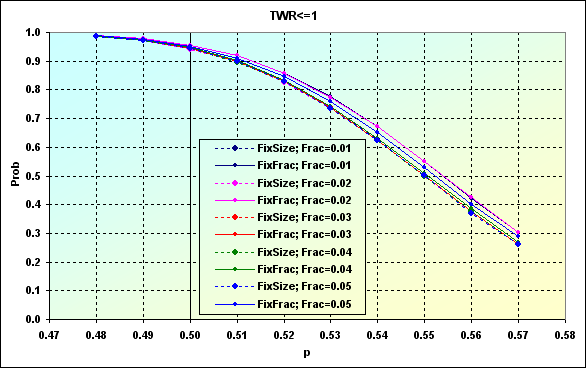
Fig. 48

En este caso se han utilizado los niveles TP=SL=0.0020. Como podemos ver, para compensar la influencia Spread y reducir la probabilidad de pérdida hasta menos de 0.50, necesitamos un TS capaz de proporcionar p=>0.56. Pero generalmente, si un TS solo es rentable en el 50 por 100 de los casos, los resultados permanecen iguales; la probabilidad de pérdida después de 250 operaciones es ~0.95 independientemente de los tipos de MM y f.

Hagamos el cálculo y veamos cómo será TWR cuando TP=SL=0.0020 y p=0.56. A continuación se muestra el resultado. En realidad se trata de un caso con probabilidad de pérdida 0.40, como en la figura 48, mientras que el valor TWR esperado es 1.01...1.04. ММs diferentes muestran valores parecidos.

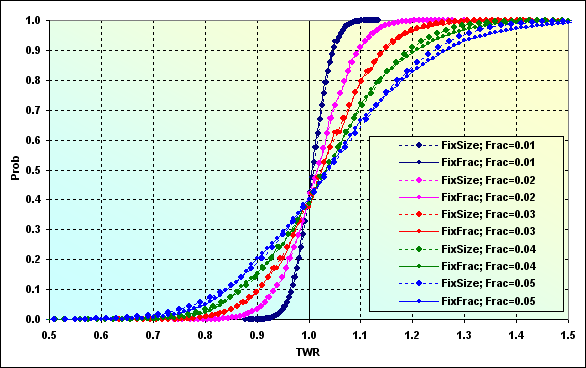
Fig. 49

Como ya mencioné, esto es típico en los casos con niveles pequeños. Si Spread hubiera sido un valor flotante y se hubiera cargado como un porcentaje del tamaño de la apuesta, el resultado habría cambiado. Eso es exactamente lo que sucede en otros mercados aparte del "Forex para una amplia variedad de clientes".

Volvamos a los cálculos con los siguientes datos: Deposit=1000, MinDeposit=300, LotSize=100000, MinLot=0.01, LotStep=0.01, MaxLot=100, f={ 0.01, 0.02, 0.03, 0.04, 0.05}, TP=SL=0.0100, Spread=0.0002, p=0.51, N=250, Leverage=100. Veamos cómo la probabilidad de disminución TWR busca un nivel determinado.

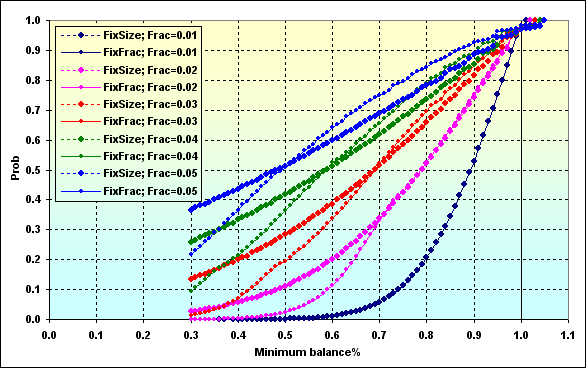
Fig. 50

La interpretación de los datos del gráfico es como en la figura 27. La probabilidad de que el valor TWR descienda a ~0.70 en f=0.05 es ~0.76 si se utiliza fracción fija MM. Si f=0.02, el valor es ~0.34.

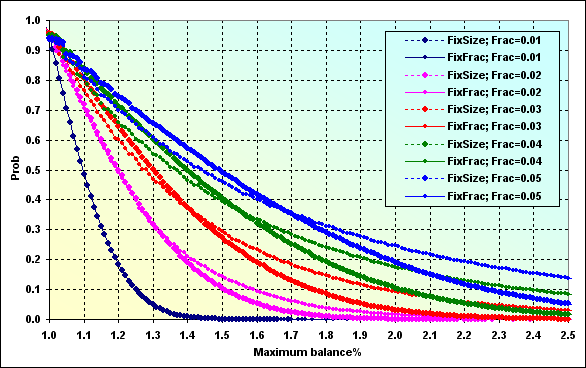
Fig. 51

Y para un determinado valor esa es la probabilidad de incremento del depósito durante el juego. La interpretación de este gráfico es como en la figura 28.

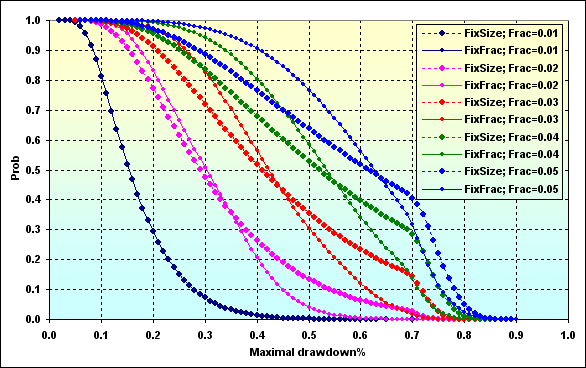
Fig. 52

El último gráfico muestra la probabilidad Maximal Drawdown % de un determinado valor en función de los fondos utilizados. Como norma general, podemos asumir que la fracción fija MM lleva a un Drawdown mayor que cuando se utiliza una de tamaño fijo. Esto puede explicarse con el efecto de la palanca asimétrica. Además, con fc>f>f*, se puede esperar un Drawdown menor, mientras que el beneficio se puede parecer al caso f<f*.

Conclusión

Hemos examinado dos métodos de gestión de dinero y hemos analizado su desarrollo; también hemos aprendido algunos aspectos teóricos sobre este tema, presentando unas cuantas ecuaciones sencillas. Hemos llevado a cabo una investigación de simulación estocástica evaluando los resultados obtenidos, comparando varios métodos. Posiblemente, la conclusión más importante que puede extraerse de este estudio es que es imposible seleccionar el método definitivo de los dos examinados. La eficiencia de MM depende de muchos factores. Los resultados pueden variar dependiendo de cómo se combinen estos factores. Por lo tanto, en cada caso hay que seleccionar el MM más apropiado en función de sus propiedades TS, tratando las condiciones centrales, así como las posibilidades del trader y sus preferencias. Nuestro artículo ha puesto en relieve algunas soluciones posibles y algunas características esenciales. Espero que algunos traders hayan encontrado útil este texto. ¡Buena suerte a todos!

Entre mis planes futuros están el análisis de martingala (en mi opinión, esa parte no debería tomar mucho tiempo y espacio, puesto que las propiedades de ese método son bastante obvias), y la revisión del método de R. Jones (el autor afirma que se ha desarrollado como una combinación de ventajas de los dos métodos MM analizados).

Referencias y enlaces (en orden de aparición en el texto)

Agner Fog - Pseudo random number generators - http://www.agner.org/random
strator - Probability Library (parte de Cephes) - https://www.mql5.com/ru/code/10101 (en ruso)
Suvorov V. - MS Excel: Data Exchange and Management - https://www.mql5.com/en/code/8175
Vince R. - The Mathematics of Money Management.
Bershadsky А.V. - Research and Development of Risk Management Scenario Methods. - Dissertation, 2002 (en ruso).
Smirnov А.V., Guryanova Т.V. - On Ralph Vince's "optimal f" (en ruso).
W. Feller - An Introduction to Probability Theory and Its Applications.
E. Thorp - The Kelly Criterion in Blackjack, Sports Betting, and the Stock Market.
S. Bulashov - Statistics for Traders. (versión online, p. 199, en ruso)
Starikoff S. - How to Evaluate the Expert Testing Results - https://www.mql5.com/en/articles/1403

Ejemplos

A continuación se adjuntan las librerías, públicamente disponibles, que se han utilizado para escribir este artículo. Las secuencias de comandos y la aplicación no se adjuntan, no obstante. Esto se ha hecho deliberadamente para estimular el desarrollo de emuladores de servidor de trading entre los miembros de la comunidad MQL. En la simulación se ha utilizado un emulador de servidor de trading.

Exención de responsabilidad (también conocido como excusa)

El autor de este artículo no se responsabiliza de nada. Se aceptan quejas y sugerencias por escrito, en la sección de debate o por correo electrónico. Se tendrán en cuenta las sugerencias sensatas y se omitirán las que no tengan sentido. Se especifican todos los derechos de autor si son conocidos. De lo contrario, el autor los desconoce o bien éstos se han perdido.

El autor admite que el texto y los cálculos pueden tener inexactitudes o errores. Los errores son inevitables porque el texto es extenso y el tema complicado. En consecuencia, el autor ha querido asignar un premio de $1 por cada fallo detectado, como hizo D. Knuth. Pero la vida ha hecho algunos ajustes. Los vientos fríos de la crisis financiera global soplan todavía furiosos en el país. Los más vulnerables y los más débiles entre nosotros - los niños sin padres - son los que suelen sufrir más en tiempos como estos. Para ayudarles, el autor ha decidido destinar la cuota completa obtenida de la revisión de los errores a fines benéficos. He seleccionado unos cuantos orfanatos de provincias rusas remotas y he enviado allí mi modesta aportación.

Tuve una sensación indescriptible al recibir una respuesta de uno de los responsables de los orfanatos. Era una carta sencilla escrita a mano en una hoja de papel, tomada de un libro cuadrado. Claro que tenía palabras de agradecimiento, pero lo más importante es que había una lista de artículos comprados. Aquella sabia mujer no se gastó aquella aportación en un ordenador nuevo para copiar y pegar cartas de agradecimiento, ni tampoco en cortinas nuevas para la oficina, ni en alimentos proporcionados por el Estado. Los fondos se invirtieron en la educación de los niños.

Libros, marcadores, bolígrafos, juegos para aprender, libretas de ejercicios, pinturas. Se trataba de materiales necesarios para el desarrollo de los niños y niñas que viven en un pequeño pueblo provincial, o en un viejo edificio de madera posiblemente construido por nuestros antepasados que regresaron de la Gran Guerra Patria. Por lo tanto, si usted puede, si tiene algo de dinero, por favor ayúdeles, no sea codicioso o perezoso. Esto no pasará desapercibido. De hecho no estoy seguro. Tal vez, esa carta la escribiría algún vigilante nocturno para olvidar el regalo inesperado. En realidad no me interesa y nunca sabré la verdad. Sólo hice una apuesta, si bien muy pequeña, de que la probabilidad de que vivo entre gente normal es mucho mayor. A diferencia del juego de cara o cruz, este juego es justo para nosotros.