Análisis fractal de los movimientos de la moneda común

Руслан | 4 septiembre, 2015

Introducción

A menudo se puede oír gente discutir de las relaciones entre diferentes monedas en el mercado Forex.

El principal punto en cuestión generalmente viene de factores fundamentales, la experiencia práctica o meras especulaciones que resultan de estereotipos personales del parlante. Una hipótesis de una o más monedas 'globales' 'arrastra' a todo el resto, puede considerarse un caso extremo.

De hecho, ¿cuál es la naturaleza de las relaciones entre varias cotizaciones? ¿Son sus movimientos coordinados o ningún movimiento de una de las monedas sugiere el movimiento de la otra? El artículo describe un intento de abordar esta cuestión mediante la dinámica no lineal y los métodos de geometría fractal.

1. Parte teórica

1.1. Variables dependientes e independientes

Tengamos la mirada en dos variables (cotizaciones) x e y. En un momento dado, los valores instantáneos de estas variables determinan un punto en el plano XY (Fig. 1). El movimiento del punto en el curso de tiempo forma una trayectoria. La forma y el tipo de tal trayectoria dependerá del tipo de relación entre las variables.

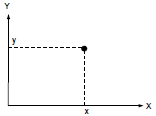
Figura 1. Punto en el plano

Por ejemplo, si la variable x no tiene relación con la variable y, se puede observar un estructura irregular - llenará uniformemente el plano XY con los puntos, siempre que su número sea suficiente (Fig. 2)-

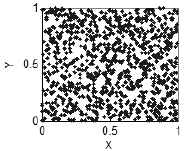
Figura 2. No hay correlación - plano uniforme lleno

Si, sin embargo, existe una relación entre x e y, aparecerá una estructura regular, en el caso más simple, que representa una curva (Fig. 3),

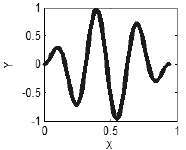
Figura 3. Presencia de correlaciones -una curva de

o incluso una estructura más compleja (Fig. 4).

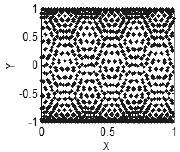
Figura 4. Presencia de correlaciones - una estructura en el plano

El mismo es característico con un tres- y más dimensiones del espacio: Si todas las variables están interrelacionadas o interdependientes, los puntos forman una curva (Fig. 5), si hay dos variables independientes en un conjunto, los puntos formarán una superficie (Fig. 6), en el caso de tres variables independientes, los puntos llenarán el espacio tridimensional, etc.

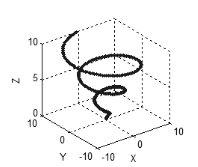
Figura 5. Curva en el espacio tridimensional

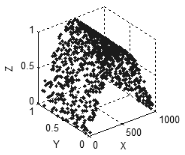
Figura 6. Superficie en el espacio tridimensional

Si no hay ninguna relación entre las variables, los puntos se distribuyen de manera uniforme en todas las dimensiones disponibles (Fig. 7). Así, podemos hablar acerca de la naturaleza de las relaciones entre variables basadas en la forma de que los puntos de llenan el espacio.

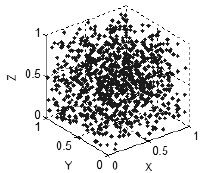
Figura 7. No hay correlación - puntos distribuidos uniformemente en el espacio

La forma de la estructura resultante (línea, superficie, 3D de la forma, etc.) en este caso no tiene importancia.

Lo que importa es una dimensión fractal de la estructura: 1 para sistemas que describen líneas, 2 para sistemas que describen superficies, 3 para conjuntos que describen volúmenes, etc.. Generalmente se asume que un valor de dimensión fractal corresponde al número de variables independientes en un conjunto de datos.

También podemos encontramos una dimensión fraccionaria, por ejemplo 1.61 o 2.68. Este puede ser el caso si la estructura resultante es un conjunto fractal , es decir, un conjunto auto-similar de dimensión no integral. En la figura 8 se da un ejemplo de un fractal, su dimensión es aproximadamente 1.89, es decir, no es una línea (dimensión 1) y tampoco una superficie (dimensión 2).

Figura 8. La alfombra de Sierpinski

Una dimensión fractal de un mismo conjunto puede ser diferente en diferentes escalas.

Por ejemplo, si usted toma una mirada en el conjunto en la figura 9 de 'lejos', claramente se verá la línea, es decir, la dimensión fractal del conjunto dado es de 1. Una mirada a 'primer plano' en el mismo conjunto no revelará una línea sino un 'tubo fuzzy' donde los puntos no forman una línea clara, pero se acumulan alrededor de él al azar. Una dimensión fractal de ese 'tubo' será igual a la dimensión del espacio en el cual nuestra estructura se considera como puntos en el 'tubo' distribuidos uniformemente en todas las dimensiones disponibles.

Un aumento en la dimensión fractal en escalas más pequeñas permite estimar una dimensión en la que las relaciones entre las variables se convierten en imperceptibles debido a la presencia de ruido aleatorio.

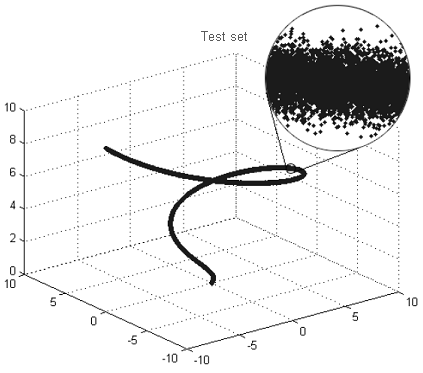
Figura 9. Ejemplo de un fractal 'tubo'

1.2. Estimar la dimensión fractal

Una dimensión fractal puede estimarse utilizando el método de conteo de caja basado en el análisis de la dependencia del número de cajas que contienen los puntos de un conjunto en la longitud del lado de la caja (no tiene que ser un cuadro 3D - una 'caja' en el espacio unidimensional estará representada por un segmento, en el espacio bidimensional de un recuadro etc.)

Teóricamente, esta dependencia está dada por N (ε) ~1/ε^D, donde D es la dimensión fractal del conjunto, ε es la longitud de la caja, N(ε) – es el número de puntos del conjunto de cajas medianas en ε. Permite estimar la dimensión fractal

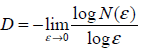
Sin entrar en mucho detalle, el funcionamiento del algoritmo puede ser descrito como sigue:

1. Un conjunto determinado de puntos se divide en cajas de ε-tamaño y se cuenta el número de N cajas que contienen al menos un punto del conjunto.

2. Para varios ε se determina un valor de N respectivo, es decir, que acumulamos datos para trazar la dependencia N(ε).

3. La dependencia N(ε) se traza en coordenadas logarítmicas dobles donde la pendiente de la dependencia corresponderá al valor de la dimensión fractal.

Por ejemplo, la figura 10 muestra dos conjuntos: una figura del plano (a) y una línea (b). Se llenan las celdas que contienen puntos del conjunto en gris. Contando el número de células 'gris' con tamaños de célula diferente, obtenemos las dependencias ilustradas en la figura 11. La pendiente de las rectas aproximadas a estas dependencias ayuda a calcular las dimensiones fractales: Da≈2, Db≈1.

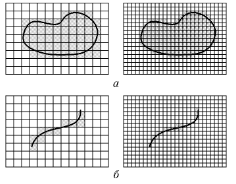
Figura 10. Sistemas de medición

Normalmente, una dimensión fractal se estima en la práctica utilizando el algoritmo de Grassberger Procaccia en lugar del método de box-counting, que arroja resultados más precisos en espacios de alta dimensión. La idea del algoritmo es obtener una dependencia С(ε) de la probabilidad de dos puntos de un conjunto de entrar en una celda de tamaño de ε del tamaño celular y determinar la pendiente de un tramo lineal de tal dependencia.

Desafortunadamente, es imposible cubrir todos los aspectos de estimación de la dimensión fractal en el ámbito de este artículo. Para obtener más información, si es necesario, puede encontrarse en literatura especializada.

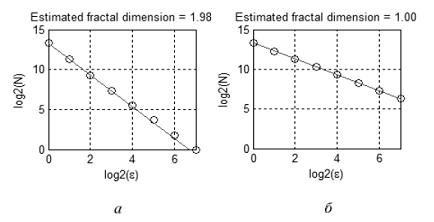
Figura 11. Estimado de conjuntos de dimensión fractal

1.3. Ejemplo de estimación de la dimensión fractal

Para verificar el rendimiento de la técnica propuesta, debemos determinar el nivel de ruido y el número de variables independientes para el sistema mostrado en la figura 9. Este conjunto tridimensional consiste en 3000 puntos y representa una línea (una variable independiente) con ruido superpuesto. El ruido se distribuye normalmente, con error medio de la raíz cuadrada de 0.01.

La figura 12 muestra la dependencia С(ε) en escala logarítmica. Hay dos secciones lineales que se intersectan en el ε≈2^-4.6≈0.04. La pendiente de la primera línea es ≈2.6, la pendiente de la segunda línea es ≈1.0.

Los resultados obtenidos sugieren que el equipo de prueba tiene sólo una variable independiente en la escala de más de 0.0 y 'casi tres' variables independientes o ruido superpuesto en la escala de menos de 0.04. Esto es en acuerdo con los datos iniciales: según la regla de tres sigma, 99.7% de puntos forman un 'tubo' con un diámetro de 2 * 3 * 0.01≈0.06.

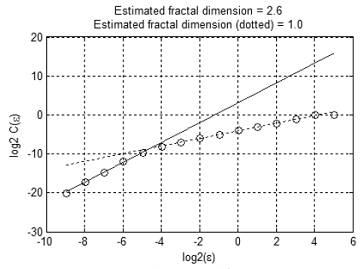
Figura 12. Dependencia c (e) en escala logarítmica

2. Parte práctica

2.1. Datos iniciales

La propiedades del fractal del mercado Forex se estudiaron utilizando datos públicos que cubren el período de 2000 a 2009 inclusive. El estudio se realizó sobre los precios de cierre de siete pares de divisas principales: EURUSD, USDJPY, GBPUSD, AUDUSD, USDCHF, USDCAD, NZDUSD.

2.2. Implementación

Los algoritmos para estimar la dimensión fractal se aplicaron en forma de funciones MATLAB de medio ambiente basados en los avances hechos por el Dr. Michael Small (http://www.eie.polyu.edu.hk/~ensmall/matlab/). Las funciones con ejemplos de implementación están disponibles en el archivo frac.rar adjunto a este artículo.

Para acelerar los cálculos, la parte más desperdiciadora de tiempo fue escrita en lenguaje C. Antes de empezar, compilar la función C "interbin.c" usando el comando MATLAB "mex interbin.c".

2.3. Resultados del estudio

La figura 13 muestra un movimiento conjunto de precios EURUSD y GBPUSD desde 2000 a 2010. Los valores de precio como tal se demuestran en las figuras 14 y 15.

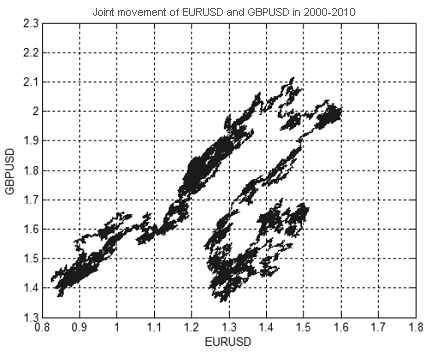
Figura 13. Movimiento articular de precios EURUSD y GBPUSD desde 2000 a 2010

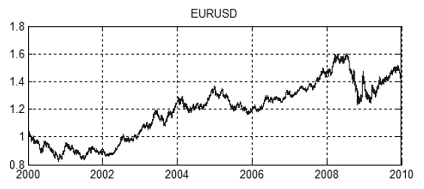
Figura 14. Tabla de precios EURUSD desde 2000 a 2010

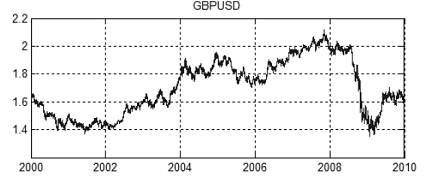
Figura 15. Tabla de precios GBPUSD desde 2000 a 2010

Una dimensión fractal del conjunto que se muestra en la figura 13 es aproximadamente igual a 1.7 (Fig. 16). Esto significa que este movimineto EURUSD + GBPUSD no representa un paseo 'puramente' aleatorio, de lo contrario su dimensión hubiera sido 2 (dimensión de una recorrido aleatorio en espacios de dos y más dimensiones es siempre igual a 2).

Sin embargo, puesto que el movimiento de precios es muy similar al recorrido aleatorio, no podemos analizar los valores de precio por sí mismos - los cambios de dimensión fractal soninsignificantes cuando se añaden nuevos pares de divisas (tabla 1) y es imposible sacar cualquier conclusión.

Pares de divisas	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
Dimensión	1.7	1.9	1.9	1.9	1.9	1.9

Tabla 1. Cambio de dimensión en aumento en el número de monedas

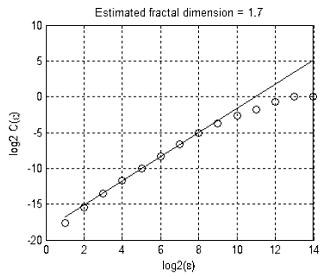
Figura 16. Dimensión fractal Estimado

Para obtener resultados más interesantes, debemos proceder de las cotizaciones a los cambios en ellos.

Dimensión valores para diferentes intervalos de incremento y diverso número de pares moneda son proporcionados en la tabla 2.

	Fechas	Número de puntos de	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
M5	14 Agosto de 2008 — 31 de diciembre de 2009	100000	1.9	2.8	3.7	4.4	5.3	6.2
M15	18 Nov de 2005 – 31 de diciembre de 2009	100000	2	2.8	3.7	4.5	5.9	6.7
M30	16 Noviembre de 2001 — 31 de diciembre de 2009	100000	2	2.8	3.7	4.5	5.7	6.8
H1	03 De enero de 2000 – 31 de diciembre de 2009	61765	2	2.9	3.8	4.6	5.6	6.5
H4	03 De enero de 2000 – 31 de diciembre de 2009	15558	2	3	4	4.8	5.9	6.3
D1	03 De enero de 2000 – 31 de diciembre de 2009	2601	2	3	4	5.1	5.7	6.5

Table 2. Cambio de dimensión en intervalos de incremento diferentes

Si las monedas están interrelacionadas, la dimensión fractal, cada vez que se agrega en el nuevo par de divisas, y debe aumentar significativamente menos para finalmente llegar a un cierto valor que determinará el número de variables' libres' en el mercado de cambio de moneda.

Si también suponemos, que el "ruido de mercado" se superpone sobre los precios, todas las dimensiones disponibles pueden quedar llenas de ruido en timeframes breves (М5, М15, М30) y este efecto debe bajar en timeframes más largos 'revelando' dependencias entre las cotizaciones (como en el ejemplo de la prueba).

Como indica la tabla 2, esta hipótesis no fue confirmada por los datos reales: el conjunto se distribuye en todas las dimensiones disponibles en todos los timeframes, es decir, todas las monedas son independientes unas de otras.

It is somewhat in conflict with intuitive assumptions regarding currency relationships. Parece ser que cerca de las monedas, por ejemplo, GBP y CHF o AUD y NZD deben exhibir dinámicas similares. Por ejemplo, la figura 17 muestra incremento de dependencias entre NZDUSD y AUDUSD en los timeframes M5 (coeficiente de correlación: 0.54) y D1 (coeficiente de correlación: 0.84).

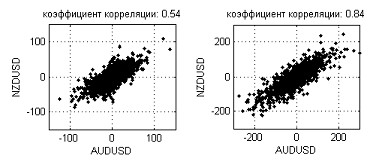
Figura 17. Incremento de dependencias entre NZDUSD y AUDUSD en timeframes M5 (0.54) y D1 (0,84)

Como puede verse en esta figura, la dependencia se obtiene más y más lejos y se extendía diagonalmente y el valor del coeficiente de correlación aumenta a medida que aumenta el intervalo. Sin embargo, en términos de dimensión fractal, el nivel de ruido es demasiado alto como para considerar que dicha dependencia es una línea unidimensional. Las dimensiones fractales en intervalos más largos (semanas, meses) tal vez convergen en un valor determinado pero no nos dan las facilidades para ello debido al número insuficiente de puntos para una estimación de la dimensión.

Conclusión

Sin duda sería más interesante restringir los movimientos de las monedas a una o más variables independientes para simplificar considerablemente la tarea de reconstrucción del atractor de mercado y pronóstico de precios. El mercado sin embargo produce un resultado diferente: las dependencias son mal pronunciadas y "bien ocultas" en una gran cantidad de ruido. El mercado es muy eficiente en este sentido.

Los métodos de dinámicas no lineales que constantemente producen buenos resultados en áreas como la medicina, física, química, biología y otros, requieren una atención especial y cuidadosa interpretación de los resultados cuando se utilizan en el análisis del precio de mercado.

Los resultados obtenidos no indican expresamente la presencia o ausencia de relaciones entre las monedas. Sólo podemos decir que el nivel de ruido en los timeframes dados son comparable a la 'fuerza' de la relación por lo que la cuestión de las relaciones entre las monedas permanece abierta.