Neural networks made easy (Part 32): Distributed Q-Learning
Dmitriy Gizlyk | 11 January, 2023
Introduction
We got acquainted with the Q-learning method in the article "Neural networks made easy (Part 27): Deep Q-Learning (DQN)". In that article, we approximated the Q-function which is a function of dependence of the reward on the state of the system and the action taken. But the problem is that the real world is multifaceted. When assessing the current state, we cannot always take into account all the influencing factors. Therefore, there is no direct relationship between the estimated parameters describing the system state, the action performed, and the rewards. As a result of the Q-function approximation, we only get the averaged most probable value of the expected reward. In this process, we do not see the entire distribution of rewards received in the model training process. Also, the average value is subject to distortion as a result of significant sharp outliers. Two articles were released in 2017. Their authors proposed algorithms to study the distribution of values of the rewards received. In both articles, the authors managed to significantly improve the results of classical Q-learning in Atari computer games.
1. Features of Distributed Q-learning
Distributed Q-learning, like the original Q-learning, approximates the action utility function. Again, we will approximate the Q-function for predicting the expected reward. The main difference is that we will not approximating a single reward value for the completed action in a particular state, but the whole probability distribution of the expected reward. Of course, we cannot estimate the probability of the occurrence of each individual reward value due to limited resources. But we can split the range of possible rewards into multiple ranges, i.e., quantiles.
Additional parameters are introduced to determine the quantiles. These are the minimum (Vmin) and maximum (Vmax) values in the range of expected rewards, as well as the number of quantiles (N). The following formula is used to calculate the range of values for one quantile.
![]()
Unlike the original Q-learning method which implied the approximation of the natural reward value, the distributed Q-learning algorithm approximates the probability distribution of receiving a reward within a quantile when performing a certain action in a particular state. By transforming the problem into the probability distribution task, we can convert the Q-Function approximation problem into a standard classification problem. This leads to a change in the loss function. The original Q-learning uses standard deviation as a loss function, but the distributed Q-learning method will use LogLoss. We have considered this function earlier, when studying Policy Gradient.
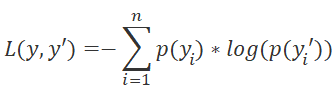
This way, we can approximate the probability distribution of the reward for each State-Action pair. Therefore, when selecting the action, we can determine the expected reward and its probability with a higher level of accuracy. Another advantage is the ability to estimate the probabilities of a particular reward level rather than of the average reward. This allows the use of a risk-based approach when assessing the probability of receiving positive and negative rewards after performing an action from the current state of the system.
The greatest effect is achieved when, as a result of the same action from similar situations, the environment returns both positive and negative rewards. With the original Q-learning algorithm using averaging of the expected reward, we would most often get a value close to 0 in such cases. As a result, the action will be skipped. When using the distributed Q-learning algorithm, we can evaluate the probability of receiving real rewards. The use of a risk-based approach will assist in making the right decision.
Pay attention that when the agent performs any of the possible actions, the environment definitely gives a reward. Therefore, for any action of the agent performed from the current state of the environment, we expect to receive a reward with 100% probability. The sum of probabilities for each agent action should equal 1. This result can be achieved by using the SoftMax function in terms of possible actions.
We will still use all the tools of the original Q-learning algorithm. These include the experience replay buffer and the Target Net model to predict future rewards. Naturally, we will use a discount factor for future rewards.
Model training is based on the principles of the original Q-learning. The process itself is based on the Bellman equation.
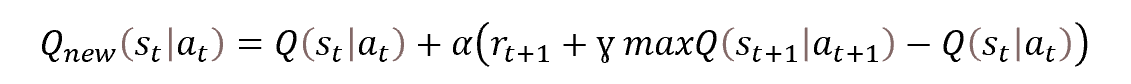
As mentioned above, we will evaluate the predicted values of future rewards using Target Net, which is a "frozen" copy of the model being trained. I would like to dwell on the approaches to its use.
One of the features of reinforcement learning and Q-learning is the ability to build action strategies in an effort to obtain the best possible result. To enable the building of a strategy, the Bellman equation includes a value of the future state. In fact, the evaluation of the future state of the environment should include the maximum possible reward from the state to the end of the session. Without this metric, the model would only be trained to predict the expected reward for the current transition to a new state.
But let's look at the process from the other side. We do not have a real full reward until the end of the session. Therefore, we use a second neural network to predict the missing data. To avoid training two models in parallel, we use a copy of the trainable model with frozen weights to predict rewards from the future state. Will the predictions from an untrained model be accurate? Most likely they will be completely random. But by introducing random values for the training model targets, we distort the perception of the environment and lead the training in the wrong direction.
By excluding the use of Target Net at the initial stage, we can train the model to predict the reward for the current transition with some accuracy. Well, the model will not be able to build a strategy. But this is only the first stage of learning. If we have a model that is able to give reasonable predictions one step ahead, we can use it as a Target Net. After that we can additionally train the model to build a strategy two steps ahead.
This approach with the phased updated of Target Net and with the use of reasonable predictive future state values will enable the model to build the right strategy. This way we can get the desired result.
I would like to add a few more words about the discount factor for the value of future rewards. This is the tool to manage model foresight in strategy building. This hyperparameter largely affects the type of strategy being build. The use of a coefficient close to 1 instructs the model to build long strategies. In this case, the model will build strategies for long-term investments.
On the contrary, a decrease in this parameter and values closer to 0 forces the model to forget about future rewards and to pay more attention to making a profit in the short term. So, the model will build a scalping strategy. Of course, the position holding time will be affected by the timeframe used.
Let's summarize the above.
- The distributed Q-learning method is based on the classical Q-learning and complements it.
- A neural network is used as a model.
- In the process of training, we approximate the probability distribution of the expected reward for the transition to a new state, depending on the State-Action pair.
- The distribution is represented by a set of quantiles of a fixed remuneration range.
- The number of quantiles and the range of possible values are determined by hyperparameters.
- The distribution for each possible action is represented by the same probability vector.
- To normalize the probability distribution, we use the SoftMax function in the context of each individual action.
- The model is trained on the basis of the Bellman equation.
- The probabilistic approach to solving the problem requires the use of LogLoss as a loss function.
- To stabilize the learning process, we use heuristics of the original Q-learning algorithm (Target Net, experience playback buffer).
As always, the theoretical part is followed by the practical implementation of the approach using MQL5.
2. Implementation using MQL5
Prior to proceeding to implementing the distributed Q-learning method using MQL5, let's draw up a work plan. As mentioned in the theoretical part, the method is based on the original Q-learning algorithm. We have already implemented this algorithm before. Therefore, we can create an Expert Advisor based on the previously used one.
The use of the probabilistic approach will require changes in the block where the target values of the model are transmitted.
At the model output, we need to normalize data using the SoftMax function. We have already met this function and implemented it in the article about Policy Gradient. In that article, we also normalized the probabilities. That time we used the probabilities of choosing actions. Data were normalized within the entire neural layer. Now we need to normalize the probabilities of the distribution for each action separately. This means that we cannot use the previously created CNeuronSoftMaxOCL class in its pure form.
So, we have 2 options. We can create a new class or modify the existing one. I decided to use the second option. The structure of the previously created class was as follows.
class CNeuronSoftMaxOCL : public CNeuronBaseOCL { protected: virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; } public: CNeuronSoftMaxOCL(void) {}; ~CNeuronSoftMaxOCL(void) {}; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual bool calcOutputGradients(CArrayFloat *Target, float& error) override; //--- virtual int Type(void) override const { return defNeuronSoftMaxOCL; } };
First, we add a variable to store the number of normalizable vectors iHeads and the method for specifying this parameter - SetHeads. By default, we will specify 1 vector. This corresponds to the normalization of data within the entire layer.
class CNeuronSoftMaxOCL : public CNeuronBaseOCL { protected: uint iHeads; ......... ......... public: CNeuronSoftMaxOCL(void) : iHeads(1) {}; ~CNeuronSoftMaxOCL(void) {}; ......... ......... virtual void SetHeads(int heads) { iHeads = heads; } ......... ......... };
As you know, the addition of a new variable does not change the logic of the class methods. Next, we should modify the algorithm of the methods. We are primarily interested in the feed forward and back propagation approaches. The feed forward pass is implemented in the feedForward method. Please note this method only implements an auxiliary algorithm for calling the corresponding kernel of the OpenCL program. All computations are performed on the OpenCL context side, in the multi-threaded mode. Therefore, before making changes to the operations related to the placing of the kernel in the execution queue, we need to make changes on the OpenCL side of the program.
Let's reason. The specific feature of the SoftMax function is the normalization of the data in such a way that the sum of the entire result vector is equal to 1. The mathematical formula of the function is shown below.
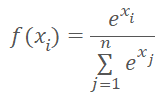
As you can see, the data is normalized using the sum of the exponential values of the entire source data vector. Using a local data array, we transfer data between separate threads of the same kernel. This enables the creation of a multi-threaded implementation of the function on the OpenCL context side. The algorithm that we have created runs in a one-dimensional problem space. It normalizes data within a single vector. To solve the problems of the new algorithm, we need to divide the entire volume of initial data into several equal parts and normalize each part separately. The difficulty here is that we don't know the number of such parts.
But there is also a good side of the coin. Each individual block can be normalized independently of each other. This is fully compliant with our concept of multi-threaded computing. So, for distributed data normalization, we can run additional instances of the previously created kernel.
We only need to distribute the total volume of source data buffers and result buffers into corresponding blocks. Previously, we launched the kernel in the one-dimensional task space. OpenCL technology enables the use of the three-dimensional task space. In this case, we do not need the third dimension. Anyway, we can use the second dimension to identify the normalization block.
Thus, by adding another dimension of the task space, we enable the distributed normalization in the previously created SoftMax_FeedForward class. We still need to make changes in the kernel code. But these changes will be minor. We need to add the processing of the second task space dimension onto the kernel algorithm.
Kernel parameters remain unchanged. In the parameters, we pass pointers to data buffers and the size of one data normalization vector.
__kernel void SoftMax_FeedForward(__global float *inputs, __global float *outputs, const uint total) { uint i = (uint)get_global_id(0); uint l = (uint)get_local_id(0); uint h = (uint)get_global_id(1); uint ls = min((uint)get_local_size(0), (uint)256); uint shift_head = h * total;
In the kernel body, we request the thread IDs in both dimensions. They define the amount of work for the current thread and offsets in the data buffers to the elements being processed. The first dimension indicates where the thread is in the data normalization algorithm. By the second dimension, we determine the offset in the data buffers. In the code above, I highlighted the added lines.
Next, the kernel algorithm has a loop of the first stage where the exponential values of the initial data are summed. Add adjustment to jump to the first element of the source data block being normalized (highlighted in the code).
Note that we are only using the offset for the global source data buffer. We ignore it for the local data array. This is because each work-group works in isolation and uses its own local data array.
__local float temp[256]; uint count = 0; if(l < 256) do { uint shift = shift_head + count * ls + l; temp[l] = (count > 0 ? temp[l] : 0) + (shift < ((h + 1) * total) ? exp(inputs[shift]) : 0); count++; } while((count * ls + l) < total); barrier(CLK_LOCAL_MEM_FENCE);
In the previous block, we collected parts of the total in the elements of a local array. This is followed by a loop where the total sum of the local array values is consolidated. Here we only work with a local array. This process is absolutely independent of the second dimension of our task space and remains unchanged.
count = ls; do { count = (count + 1) / 2; if(l < 256) temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- float sum = temp[0];
At the end of the kernel, we normalize the initial data and save the resulting value in the result buffer. Here, as in the first loop, we use the previously calculated offset in the global data buffers.
if(sum != 0) { count = 0; while((count * ls + l) < total) { uint shift = shift_head + count * ls + l; if(shift < ((h + 1) * total)) outputs[shift] = exp(inputs[shift] / 10) / (sum + 1e-37f); count++; } } }
We use a similar approach when making changes to the kernel with gradient distribution to the previous layer SoftMax_HiddenGradient. Add an offset in the global data buffers without changing the general algorithm of the kernel.
__kernel void SoftMax_HiddenGradient(__global float* outputs, __global float* output_gr, __global float* input_gr) { size_t i = get_global_id(0); size_t outputs_total = get_global_size(0); size_t h = get_global_id(1); uint shift = h * outputs_total; float output = outputs[shift + i]; float result = 0; for(int j = 0; j < outputs_total ; j++) result += outputs[shift + j] * output_gr[shift + j] * ((float)(i == j) - output); input_gr[shift + i] = result; }
No changes need to be made in the SoftMax_OutputGradient kernel which determines the deviation from the reference distribution. This is because the offset in this kernel is determined for a specific element in the sequence, regardless of which block a particular element is a part of.
__kernel void SoftMax_OutputGradient(__global float* outputs, __global float* targets, __global float* output_gr) { size_t i = get_global_id(0); output_gr[i] = targets[i] / (outputs[i] + 1e-37f); }
This completes operations on the OpenCL program side. Let's get back to the code of our CNeuronSoftMaxOCL class. We started with changes in the feed forward kernel. Similarly, let's make changes to the methods of our class.
We did not add or change parameters in the kernels. Therefore, the data preparation algorithm and the kernel call remain unchanged. The only changes will be done in how the task space is specified.
First, we define the dimension of one data normalization vector. It can be easily determined by simply dividing the result buffer size by the number of vectors to normalize. We save the resulting value in a local variable size. Here we also fill the global_work_size array of the global task space. In the first dimension, indicate the size of one normalization vector calculated above. And in the second dimension, indicate the number of such vectors.
To enable the synchronization of threads and data exchange between threads, we have previously created a working group equal to the global task space. This is because we normalized data within the entire data buffer. Now the situation is a little different. We need to normalize several individual blocks in the data buffer. When building the feed forward kernel, we noticed that the work with the local data array remained unchanged. This was made possible by planning to separate the normalization of each vector into a separate working group. So, in this case, we need to create a separate array for the local group task space local_work_size.
The dimensions of the global and local task spaces must be the same. Therefore, we need to define a two-dimensional local task space. The number of global threads must be a multiple of the number of local threads in each individual task space dimension.
Previously we specified the global ask space in terms of one normalizable vector in the first dimension and the number of such vectors in the second dimension. In each working group, we plan to normalize only one vector. Logically, we should indicate the size of one normalizable vector in the first dimension of the local task space. We will indicate 1 in the second dimension. This corresponds to one vector.
Below is the modified code of the feedForward method. All changes are highlighted. As you can see, there are not so many changes. But it is very important to take into account all the key points.
bool CNeuronSoftMaxOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!OpenCL || !NeuronOCL) return false; uint global_work_offset[2] = {0, 0}; uint size = Output.Total() / iHeads; uint global_work_size[2] = { size, iHeads }; uint local_work_size[2] = { size, 1 }; OpenCL.SetArgumentBuffer(def_k_SoftMax_FeedForward, def_k_softmaxff_inputs, NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_SoftMax_FeedForward, def_k_softmaxff_outputs, getOutputIndex()); OpenCL.SetArgument(def_k_SoftMax_FeedForward, def_k_softmaxff_total, size); if(!OpenCL.Execute(def_k_SoftMax_FeedForward, 2, global_work_offset, global_work_size, local_work_size)) { printf("Error of execution kernel SoftMax FeedForward: %d", GetLastError()); return false; } //--- return true; }
Similar changes have been made to the method that propagates the error gradient to the previous layer: calcInputGradients. But in this case we did not create working groups.
bool CNeuronSoftMaxOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID) return false; uint global_work_offset[2] = {0, 0}; uint size = Output.Total() / iHeads; uint global_work_size[2] = {size, iHeads}; OpenCL.SetArgumentBuffer(def_k_SoftMax_HiddenGradient, def_k_softmaxhg_input_gr, NeuronOCL.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_SoftMax_HiddenGradient, def_k_softmaxhg_output_gr, getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_SoftMax_HiddenGradient, def_k_softmaxhg_outputs, getOutputIndex()); if(!OpenCL.Execute(def_k_SoftMax_HiddenGradient, 2, global_work_offset, global_work_size)) { printf("Error of execution kernel SoftMax InputGradients: %d", GetLastError()); return false; } //--- return true; }
The addition of distributed normalization is a design feature and should be reflected in file handling methods. Let's continue with the CNeuronSoftMaxOCL class. We have not created file methods for this class before. The functionality of similar methods of the parent class was enough. But the addition of a new variable whose values must be saved for a correct recovery of object operation, requires redefining of such methods.
Again, we start with the data saving method Save. Its algorithm is quite simple. The method receives in parameters the file handle to write data. Usually, such methods begin with checking the correctness of the received handle. We will not create a block of controls. Instead, we will call a similar method of the parent class and pass the received handle to it. With this approach, we solve two tasks with one line of code. All necessary controls are already implemented in the parent class method. This means that it performs a control function. In addition, it implements the saving of all inherited objects and variables. Therefore, the data saving function is also executed. We only need to check the result of the parent class method to find out the execution state of the specified functionality.
After the successful execution of the parent class method, we save the value of the new variable and complete the method.
bool CNeuronSoftMaxOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; if(FileWriteInteger(file_handle, iHeads) <= 0) return false; //--- return true; }
The data loading method CNeuronSoftMaxOCL follows a similar operation sequence. It additionally controls the minimum number of normalizable methods.
bool CNeuronSoftMaxOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false; iHeads = (uint)FileReadInteger(file_handle); if(iHeads <= 0) iHeads = 1; //--- return true; }
This concludes our work with the CNeuronSoftMaxOCL class. What is left is to add the possibility for the user to specify the number of vectors to be normalized. We will not make any changes to the neural layer description object. We will use the step parameter to specify the number of vectors to be normalized. In the neural network initialization method CNet::Create, at the time the SoftMax layer is created, we will pass the specified parameter to the created CNeuronSoftMaxOCL class instance. The changes are highlighted in the code below.
void CNet::Create(CArrayObj *Description) { ......... ......... //--- for(int i = 0; i < total; i++) { ......... ......... if(!!opencl) { ......... ......... CNeuronSoftMaxOCL *softmax = NULL; switch(desc.type) { ......... ......... case defNeuronSoftMaxOCL: softmax = new CNeuronSoftMaxOCL(); if(!softmax) { delete temp; return; } if(!softmax.Init(outputs, 0, opencl, desc.count, desc.optimization, desc.batch)) { delete softmax; delete temp; return; } softmax.SetHeads(desc.step); if(!temp.Add(softmax)) { delete softmax; delete temp; return; } softmax = NULL; break; ......... ......... } } ......... ......... //--- return; }
No other changes in the architecture of the neural network are required to implement the method.
The model learning process is implemented in the "DistQ-learning.mq5" EA. The EA has been created based on the Q-learning.mq5 EA, which was used to train the model with the original Q-learning method.
According to the distributed Q-learning algorithm, we need to introduce additional hyper parameters that determine the range of expected rewards and the number of quantiles in the probability distribution.
In the proposed implementation, I approached this issue from a different angle. As in the previous tests, we will create the model using the NetCreator tool. The number of quantiles is determined based on the size of the layer with the model operation results. This takes into account the number of possible actions which is specified by the EA's Action parameter.
int Actions = 3;
In the learning process, we need to match a specific reward value from the environment with a certain quantile. Let's make the following assumptions. According to the reward policy we have developed, there can be both positive and negative rewards. They can be referred to as rewards and penalties. We assume that the median of the vector will correspond to zero reward. To measure the size of the quantile in physical reward terms, we introduce an external parameter Step.
input double Step = 5e-4;
The EA's other external parameters remain unchanged.
In the EA initialization function OnInit, after successful loading of the model, we determine the number of quantiles by the size of the neural layer of the model output and the number of the median quantile.
int OnInit() { ......... ......... //--- float temp1, temp2; if(!StudyNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false) || !TargetNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false)) return INIT_FAILED; if(!StudyNet.TrainMode(true)) return INIT_FAILED; //--- if(!StudyNet.GetLayerOutput(0, TempData)) return INIT_FAILED; HistoryBars = TempData.Total() / 12; StudyNet.getResults(TempData); action_dist = TempData.Total() / Actions; if(action_dist <= 0) return INIT_PARAMETERS_INCORRECT; action_midle = (action_dist + 1) / 2; //--- ......... ......... //--- return(INIT_SUCCEEDED); }
Next, move on to the model training function. The data preparation block remained unchanged, since we do not change any data for the training sample. The changes affect only the block indicating the target results for predicting the expected reward.
First, let us prepare a vector of predicted future state costs. This vector will contain three elements, one value for each action. We will use vector operations to calculate the values of the vector. First, we transfer the result buffer Target Net into a row matrix. Then we reformat the matrix into a table of 3 rows, one row for each action. In each row, find the element with the maximum probability. Translate the quantiles of the maximum elements into natural reward expression.
void Train(void) { //--- ......... ......... //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { ......... ......... for(int batch = 0; batch < (Batch * UpdateTarget); batch++) { ......... ......... //--- vectorf add = vectorf::Zeros(Actions); if(use_target) { if(!TargetNet.feedForward(GetPointer(State2), 12, true)) return; TargetNet.getResults(TempData); vectorf temp; TempData.GetData(temp); matrixf target = matrixf::Zeros(1, temp.Size()); if(!target.Row(temp, 0) || !target.Reshape(Actions, action_dist)) return; add = DiscountFactor * (target.ArgMax(1) - action_midle) * Step; }
After determining the predicted value of the future state, we can prepare a buffer of target values for our model. First, we will do a little preparatory work. Fill the reward buffer with zero values and determine the potential profit from the current state of the system one candlestick ahead.
Rewards.BufferInit(Actions * action_dist, 0); double reward = Rates[i].close - Rates[i].open;
Further steps depend on the candlestick direction. In the case of a bullish candlestick, create a positive reward to a buy action and an increased negative reward to a sell action. In addition, we set a negative reward to the out-of-the-market state as a penalty for lost profits. Then we add the calculated value of the future state to the reward received. But when building the original Q-learning algorithm, we indicated the reward in the target results buffer as a natural expression. This time we determine the reward quantile of each action and write down the probability of 1 for the corresponding event. The remaining elements of the buffer will have zero probabilities.
if(reward >= 0) { int rew = (int)fmax(fmin((2 * reward + add[0]) / Step + action_midle, action_dist - 1), 0); if(!Rewards.Update(rew, 1)) return; rew = (int)fmax(fmin((-5 * reward + add[1]) / Step + action_midle, action_dist - 1), 0) + action_dist; if(!Rewards.Update(rew, 1)) return; rew = (int)fmax(fmin((-reward + add.Max()) / Step + action_midle, action_dist - 1), 0) + 2 * action_dist; if(!Rewards.Update(rew, 1)) return; }
The algorithm of actions for a bearish candlestick is similar. The only difference is the reward and penalty for buying and selling actions.
else { int rew = (int)fmax(fmin((5 * reward + add[0]) / Step + action_midle, action_dist - 1), 0); if(!Rewards.Update(rew, 1)) return; rew = (int)fmax(fmin((-2 * reward + add[1]) / Step + action_midle, action_dist - 1), 0) + action_dist; if(!Rewards.Update(rew, 1)) return; rew = (int)fmax(fmin((reward + add.Max()) / Step + action_midle, action_dist - 1), 0) + 2 * action_dist; if(!Rewards.Update(rew, 1)) return; }
The rest of the function code remains unchanged, as well as all the EA's code not described here. The full EA code can be found in the attachment.
3. Testing
The created EA was used to train the model consisting of:
- 3 convolutional data preprocessing layers,
- 3 fully connected hidden layers of 1000 neurons each,
- 1 fully connected decision layer of 45 neurons (15 neurons for each of the three probabilistic distributions of actions),
- 1 SoftMax layer for normalization of probability distributions.
The model was trained using historical EURUSD data for the last two years. Timeframe used: H1. The same list of indicators and the same indicator parameters are used throughout the series of articles.
The trained model was tested in the strategy tester using historical data for the last two weeks; this data was not included in the training sample. This ensures a pure experiment, as the model is tested using new data.
To test the model in the strategy tester, we have created the "DistQ-learning-test.mq5" EA. The EA is almost a complete copy of "Q-learning-test.mq5" which was used to test the model trained using the original Q-learning method. The only change in the EA code is the addition of an action selection function GetAction.
The function receives in parameters a pointer to the probability distribution buffer which is obtained as a result of the model's assessment of the current situation. This buffer contains probability distributions over all possible values. To make data processing more convenient, let us move the buffer values to a matrix and change the matrix format to tabular. The number of rows in it its equal to the number of possible actions of the agent.
Next, we determine the quantiles with the most probable reward for each individual action.
int GetAction(CBufferFloat* probability) { vectorf prob; if(!probability.GetData(prob)) return -1; matrixf dist = matrixf::Zeros(1, prob.Size()); if(!dist.Row(prob, 0)) return -1; if(!dist.Reshape(Actions, prob.Size() / Actions)) return -1; prob = dist.ArgMax(1);
After that, we compare the expected return from buying and selling in the current state. If the expected returns are equal, we choose the action with the highest probability of receiving a reward.
if(prob[0] == prob[1]) { if(prob[2] > prob[0]) return 2; if(dist[0, (int)prob[0]] >= dist[1, (int)prob[1]]) return 0; else return 1; }
Otherwise, we choose the action with the maximum expected reward.
//--- return (int)prob.ArgMax(); }
As you can see, in this case we use a greedy strategy for choosing the action with the highest return.
The full EA code can be found in the attachment.
While the testing EA was running in the MetaTrader 5 strategy tester for two weeks, trading based on the model signals, it generated a profit of about $20. All operations had a minimum lot. The below graph demonstrates a clear upward trend in the balance value.
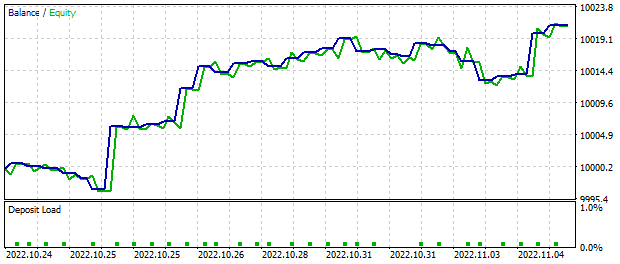
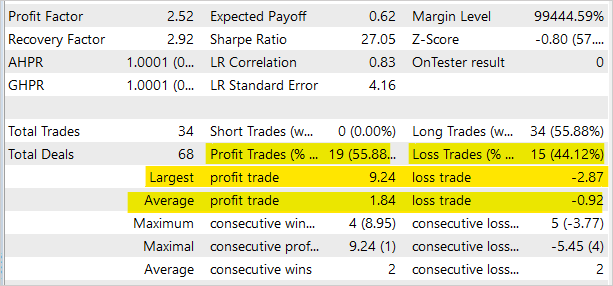
Trading operations statistics shows that almost 56% of operations were profitable. However, please note that the EA is intended solely for testing the model in the strategy tester and is not suitable for real trading in the financial markets.
The full code of all programs used in the article is available in the attachment.
Conclusion
In this article, we got acquainted with another reinforcement training algorithm: Distributed Q-Learning. With this algorithm, the model studies the probabilistic distribution of rewards when performing an action in a particular state of the environment. By studying the probability distribution instead of predicting the average value of the reward we can obtain more information about the nature of the reward and increase the stability in model training. In addition, when we know the probability distribution of the expected return, we can better assess risks when making trading operations.
Model testing in the MetaTrader 5 strategy tester demonstrated the potential profitability of the approach. The algorithm can be further developed and used to build trading decisions.
Find the entire code of all programs and libraries in the attachment.
References
- Neural networks made easy (Part 26): Reinforcement learning
- Neural networks made easy (Part 27): Deep Q-Learning (DQN)
- Neural networks made easy (Part 28): Policy gradient algorithm
- A Distributional Perspective on Reinforcement Learning
- Distributional Reinforcement Learning with Quantile Regression
Programs used in the article
| # | Issued to | Type | Description |
|---|---|---|---|
| 1 | DistQ-learning.mq5 | EA | EA for optimizing the model |
| 2 | DistQ-learning-test.mq5 | EA | An Expert Advisor to test the model in the Strategy Tester |
| 3 | NeuroNet.mqh | Class library | Library for creating neural network models |
| 4 | NeuroNet.cl | Code Base | OpenCL program code library to create neural network models |
| 5 | NetCreator.mq5 | EA | Model building tool |
| 6 | NetCreatotPanel.mqh | Class library | Class library for creating the tool |