Schätzung der Kerndichte einer unbekannten Wahrscheinlichkeitsverteilung
Victor | 13 Mai, 2016
Einleitung
Verbesserungen der Programmiersprache MQL5 hinsichtlich ihrer Verarbeitungsgeschwindigkeit sowie die ständig wachsende PC-Leistung haben dazu geführt, dass die Nutzer der Plattform MetaTrader 5 begonnen haben, sich zur Analyse des Marktes immer häufiger hoch komplexer und entwickelter mathematischer Verfahren zu bedienen. Diese Verfahren können unterschiedlichen Gebieten der Wirtschaftswissenschaften, Ökonometrie und Statistik entstammen, gleichwie begegnen wir bei ihrer Anwendung stets dem Begriff der Wahrscheinlichkeitsdichtefunktion.
Zahlreiche verbreitete Analysemethoden wurden ausgehend von der Annahme der Normalverteilung der Daten selbst oder der Normalität der Fehler in dem verwendeten Modell entwickelt. Außerdem muss man zur Berechnung der Analyseergebnisse häufig die Verteilung der unterschiedlichen Bestandteile des verwendeten Modells kennen. In beiden Fällen ist es erforderlich, ein möglichst universelles „Werkzeug“ zur Abschätzung einer unbekannten Wahrscheinlichkeitsdichte zu entwickeln.
In diesem Beitrag versuchen wir, eine Klasse anzulegen, die einen mehr oder weniger universellen Algorithmus zur Schätzung einer unbekannten Wahrscheinlichkeitsdichtefunktion umsetzen. Die ursprüngliche Idee bestand darin, dazu keine externen Mittel zu verwenden, also davon auszugehen, dass alles ausschließlich mit den Mitteln von MQL5 erfolgen kann. Von dieser ursprünglichen Vorstellung mussten wir allerdings etwas abweichen. Es versteht sich, dass die Aufgabe der visuellen Schätzung der Wahrscheinlichkeitsdichte aus zwei eigenständigen Teilen besteht.
Die eigentliche Berechnung der Schätzung sowie ihre Veranschaulichung, das heißt ihre Wiedergabe in Form eines Schaubildes oder Diagramms. Die Berechnungen wurden natürlich mittels MQL5 ausgeführt, während die Veranschaulichung mithilfe einer in einem geeigneten Programm angezeigten HTML-Seite umgesetzt werden musste. Diese Lösung wurde gewählt, weil wir am Ende eine grafische Abbildung in vektorieller Form erhalten wollen.
Da der Berechnungsteil und die Wiedergabe der Ergebnisse der Berechnung unabhängig voneinander umgesetzt werden, kann die Veranschaulichung natürlich auch mit einem anderen Mittel erfolgen. Zumal wir erwarten können, dass es in MetaTrader 5 in naher Zukunft unterschiedliche Bibliotheken, darunter vermutlich auch solche mit Grafiken, geben wird (dem Vernehmen nach laufen die Arbeiten dieser Richtung bereits). Sollten tatsächlich einmal im Lieferumfang von MetaTrader 5 hoch entwickelte Mittel zum Anlegen von Schaubildern und Diagrammen vorhanden sein, dürfte es nicht schwierig sein, den Abbildungsteil auf Wunsch in der angebotenen Lösung zu überarbeiten.
Es sei gleich darauf hingewiesen, dass die Aufstellung eines wirklich universellen Algorithmus zur Schätzung der Wahrscheinlichkeitsdichte von Folgen sich in der Realität als unerreichbar erwiesen hat. Obwohl die in diesem Beitrag vorgeschlagene Lösung nicht gerade hoch spezialisiert ist, können wir sie auch nicht als wirklich universell bezeichnen. Die Schwierigkeit besteht darin, dass sich zum Beispiel bei glockenförmigen, der normalen oder exponentiellen nicht unähnlichen Verteilungen die Optimalitätskriterien bei der Dichteschätzung als vollkommen unterschiedlich erweisen können.
Deshalb kann, wenn man über Informationen über den Charakter der zu berechnenden Verteilung verfügt, die für jeden Einzelfall jeweils passendste Lösung auswählen. Nichtsdestoweniger sollten wir jedoch im weiteren Verlauf davon ausgehen, dass uns über den Charakter der zu berechnenden Dichte nichts bekannt ist. Höchstwahrscheinlich wird ein solches Vorgehen die Qualität der Berechnungen in gewissem Umfang beeinträchtigen, aber wir wollen hoffen, dass das durch die Möglichkeit zur Berechnung ihrer Art nach vollkommen unterschiedlicher Dichten ausgeglichen wird.
Da wir es bei der Analyse von Marktdaten häufig mit nicht stationären Folgen zu tun haben, könnte die Berechnung der Dichte von Folgen mit geringer bis mittlerer Länge von besonderem Interesse sein. Das ist der entscheidende Augenblick, von dem die Auswahl des verwendeten Rechenverfahrens in vielem bestimmt wird.
Für wirklich lange Folgen mit über einer Million Werten lassen sich recht erfolgreich Histogramme und P-Splines verwenden. Folgen mit 10 - 20 Werten dagegen stellen die erfolgreiche Anlage von Histogrammen vor einige Probleme. Deshalb orientieren wir uns im weiteren Verlauf dieses Beitrages in erster Linie an Folgen mit Längen von 10 bis 10.000 Werten.
1. Verfahren zur Schätzung der Dichte der Wahrscheinlichkeitsverteilung
Heute kennen wir eine große Zahl mehr oder weniger beliebter Verfahren zur Schätzung der Wahrscheinlichkeitsdichte. Hinweise auf sie findet man im Internet, wenn man beispielsweise Suchbegriffe eingibt wie „Wahrscheinlichkeitsdichteschätzung“, „Wahrscheinlichkeitsdichte“, „density estimation“ usw. Leider gelingt es nicht, unter allen Fundstellen die geeignetste ausfindig zu machen. Sie weisen alle in vergleichbarem Umfang Stärken und Schwächen auf.
Traditionell werden Histogramme [1] zur Schätzung der Dichte verwendet. Die Verwendung von Histogrammen oder geglätteten Histogrammen ermöglicht die Gewinnung qualitativ guter Schätzungen der Wahrscheinlichkeitsdichte, jedoch nur bei Folgen von großer Länge. Wie bereits erwähnt ist es unmöglich, eine kurze Folge in eine große Zahl von Gruppen zu untergliedern, wogegen ein aus 2 bis 3 Spalten bestehendes Histogramm keine Vorstellung von der Verteilungsgesetzmäßigkeit der Wahrscheinlichkeitsdichte dieser Folge vermitteln kann. Deshalb müssen wir auf die Verwendung von Histogrammen verzichten.
Ein anderes recht bekanntes Schätzverfahren ist die Kerndichteschätzung (KDE) [2]. Gute Abbildungen, die das Wesen der Verwendung der Kernel-Regression (Kernglättung) veranschaulichen, finden sich in den Literaturhinweisen unter [3]. Letztlich haben wir uns aller ihm anhaftenden Nachteile für genau dieses Verfahren entschieden. Einige mit seiner Umsetzung verbundene Aspekte werden wir weiter unten kurz behandeln.
Von den übrigen Verfahren zur Dichteschätzung sei ein besonders interessantes erwähnt, das einen Algorithmus zur Maximierung der Erwartung (Expectation-Maximization) [4] umsetzt. Dieser Algorithmus ermöglicht die Aufgliederung der Folge in Einzelbestandteile, die beispielsweise eine Normalverteilung aufweisen. Nach Festlegung der Kennziffern der einzelnen Bestandteile lässt sich durch Aufsummierung der resultierenden Graphen eine Dichteschätzung gewinnen. Mehr zu diesem Verfahren bietet Literaturhinweis [5]. Es wurde übrigens wie eine Vielzahl anderer Verfahren bei der Arbeit an diesem Beitrag weder umgesetzt noch geprüft. Die bloße Menge der in unterschiedlichsten Quellen vorgeschlagenen Dichteschätzverfahren macht es praktisch unmöglich, jedes einzelne davon zu untersuchen.
Kommen wir also zur Betrachtung der Kerndichteschätzung, des Verfahrens, das wir umsetzen wollen.
2. Schätzung der Kerndichte einer Wahrscheinlichkeitsverteilung
Die Schätzung der Kerndichte einer Wahrscheinlichkeitsverteilung beruht auf dem Verfahren der Kernel-Regression (Kernglättung). Die Grundlagen dieses Verfahrens finden sich in den Literaturhinweisen beispielsweise unter [6] und [7].
Der Grundgedanke der Kernglättung ist recht simpel. Verwender von MetaTrader 5 sind mit dem Indikator des gleitenden Durchschnittswertes, Moving Average (MA), gut vertraut. Die Funktionsweise dieses Indikators kann man sich leicht in Form eines an einer Folge entlang gleitenden Fensters vorstellen, in dem die Mittelung der gewichteten Werte der Folge vonstattengeht. Dabei kann die Form des Fensters rechteckig, exponentiell oder irgendwie anders sein. Es lässt sich leicht feststellen, dass wir so ein gleitendes Fenster auch bei der Kernglättung sehen werden (zum Beispiel in Literaturhinweis [3]), nur dass es hier symmetrisch ist.
Beispiele für die bei der Kernglättung am häufigsten verwendeten Fenster finden sich in den Literaturhinweisen unter [8]. Wird bei der Kernglättung eine Regression der Ordnung Null verwendet, so werden die gewichteten Werte der Folge, die in das Fenster (den Kern) geraten, wie bei dem MA nur einfach gemittelt. Dieselbe Anwendung der Fensterfunktion können wir auch sehen, wenn wir auf das Problem der Filterung treffen. Nur dass wir dasselbe Verfahren jetzt in leicht veränderter Form darstellen: unter Einbeziehung des Amplitudenfrequenz- und des Phasenfrequenzgangs, während der Kern (das Fenster) als Impulskennlinie des Filters bezeichnet wird.
Die aufgeführten Beispiele veranschaulichen den Umstand, dass ein und dieselbe Erscheinung auf unterschiedliche Weise dargestellt werden kann. Was zweifelsohne unser mathematisches Arsenal bereichert, mitunter jedoch bei der Erörterung mit diesem Thema verbundener Fragen auch zu Verwirrung führen kann.
Obwohl bei der Kerndichteschätzung dieselben Prinzipien zur Anwendung kommen, die wir bereits von der Kernglättung kennen, weist ihr Algorithmus gewisse Besonderheiten auf.
Wir wenden uns dem Ausdruck zu, der das Vorgehen bei der Dichteschätzung in einem Punkt bestimmt.
![]()
mit
- x für eine Folge mit der Länge n;
- K für den symmetrischen Kern; und
- h für den Bereich, den Glättungsparameter.
Im weiteren Verlauf werden wir für die Dichteschätzung nur noch den Gaußkern verwenden.
![]()
Wie aus dem erwähnten Ausdruck folgt, wird die Dichte am Punkt X als die Summe der Kernwerte für die durch die Differenzen zwischen dem Wert X und den Werten der Folge bestimmten Größen berechnet. Dabei dürfen die Punkte X, an denen die Dichte berechnet wird, nicht mit den Werten der Folge selbst zusammenfallen.
Wir stellen die grundlegenden Schritte zur praktischen Umsetzung des Algorithmus der Kerndichteschätzung (kurz: KDE) vor:
- Wir berechnen den Durchschnittswert und die Standardabweichung der Eingangsfolge.
- Wir normalisieren die Eingangsfolge. Von jedem ihrer Werte subtrahieren wir den zuvor ermittelten Durchschnittswert und dividieren ihn durch den Wert der Standardabweichung. Nach dieser Normalisierung besitzt die ursprüngliche Folge den Durchschnittswert „0“ und eine Standardabweichung gleich „1“. Zur Berechnung der Dichte ist diese Normalisierung nicht unmittelbar erforderlich, aber sie ermöglicht die Vereinheitlichung der resultierenden Diagramme, da zu jeder Folge auf der X-Achse in Einheiten der Standardabweichung ausgedrückte Werte liegen.
- Wir finden den höchsten und den kleinsten Wert in der normalisierten Folge.
- Wir legen zwei Datenfelder an, deren Größe der gewünschten Anzahl der in dem resultierenden Diagramm abzubildenden Punkte entsprechen muss. Wenn zum Beispiel ein Diagramm mit 200 Punkten erstellt werden soll, müssen die Datenfelder dementsprechend jeweils 200 Werte beinhalten.
- Eines der angelegten Datenfelder behalten wir der Speicherung des Ergebnisses vor, in dem anderen bilden wir die Werte der Punkte, für die die Dichteschätzung erfolgt. Dazu bilden wir in dem Bereich zwischen dem zuvor ermittelten größten und kleinsten Wert 200 (für das aktuelle Beispiel) Werte in gleichbleibendem Abstand und speichern sie in dem vorbereiteten Datenfeld.
- Unter Verwendung des oben angeführten Ausdrucks berechnen wir die Dichte der 200 (für das aktuelle Beispiel) Versuchspunkte und speichern das Ergebnis in dem in Schritt 4 angelegten Datenfeld.
Es folgt eine Umsetzung dieses Algorithmus in Programmform:
//+------------------------------------------------------------------+ //| CDens.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CDens:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth public: void CDens(void); int Density(double &x[],double hh); void NTpoints(int n); private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CDens::CDens(void) { NTpoints(200); // Default number of test points } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CDens::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Density | //+------------------------------------------------------------------+ int CDens::Density(double &x[],double hh) { int i; double a,b,min,max,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) min=X[ArrayMinimum(X)]; max=X[ArrayMaximum(X)]; b=(max-min)/(Np-1.0); for(i=0;i<Np;i++)T[i]=min+b*(double)i; // Create test points //-------------------------------- Bandwidth selection h=hh; if(h<0.001)h=0.001; H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Gaussian kernel density estimation | //+------------------------------------------------------------------+ void CDens::kdens(double h) { int i,j; double a,b,c; c=MathSqrt(M_PI+M_PI)*N*h; for(i=0;i<Np;i++) { a=0; for(j=0;j<N;j++) { b=(T[i]-X[j])/h; a+=MathExp(-b*b*0.5); } Y[i]=a/c; // pdf } } //--------------------------------------------------------------------
Die Methode NTpoints() ermöglicht die Festlegung der erforderlichen Anzahl an Versuchspunkten in gleichbleibendem Abstand, deren Dichte geschätzt werden soll. Der Aufruf dieser Methode muss vor dem Aufruf der Methode Density() erfolgen. Beim Aufruf der Methode Density() muss die Verknüpfung zu dem Datenfeld, das die Eingangsdaten und den Bereichswert enthält, als Parameter an sie weitergegeben werden (als Glättungsparameter).
Bei einer erfolgreichen Ausführung gibt die Methode Density() „0“ aus, während in den Datenfeldern T[] und Y[] dieser Klasse die Werte der Versuchspunkte bzw. die Ergebnisse der Schätzung abgelegt werden.
Die Größe dieser Datenfelder wird beim Aufruf von NTpoints() festgelegt, die Voreinstellung liegt bei 200 Werten.
Das folgende Beispielskript veranschaulicht das Vorgehen bei der Verwendung der vorgestellten Klasse CDens.
#include "CDens.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i; int ndata=1000; // Input data length int npoint=300; // Number of test points double X[]; // Array for data double T[]; // Test points for pdf estimating double Y[]; // Array for result ArrayResize(X,ndata); ArrayResize(T,npoint); ArrayResize(Y,npoint); for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data CDens *kd=new CDens; kd.NTpoints(npoint); // Setting number of test points kd.Density(X,0.22); // Density estimation with h=0.22 ArrayCopy(T,kd.T); // Copy test points ArrayCopy(Y,kd.Y); // Copy result (pdf) delete(kd); // Result: T[]-test points, Y[]-density estimation } //--------------------------------------------------------------------
In diesem Beispiel werden Datenfelder für die Speicherung der Eingangsfolge der Versuchspunkte sowie der Ergebnisse der Schätzung vorbereitet. Anschließend wird das Datenfeld X[] zu Vorführzwecken mit Zufallswerten gefüllt. Nach Abschluss der Aufbereitung der Daten wird eine Instanz der Klasse CDens angelegt.
Des Weiteren wird durch den Aufruf der Methode NTpoints() die erforderlichen Anzahl an Versuchspunkten festgelegt, hier bspw. npoint = 300). Wenn die Voreinstellung der Punktezahl nicht geändert werden muss, kann der Aufruf der Methode NTpoints() ausgelassen werden.
Nach Aufruf der Methode Density() werden die berechneten Werte in die vorbereiteten Datenfelder gespeichert und anschließend die zuvor angelegte Instanz der Klasse CDens entfernt. Dieses Beispiel zeigt lediglich die Interaktion mit der Klasse CDens. An den gewonnenen Ergebnissen (in den Datenfeldern T[] und Y[]) werden keine weiteren Manipulationen vorgenommen.
Wenn diese Ergebnisse zur Erstellung eines Diagramms verwendet werden sollen, so ist das nicht schwer, indem man die Werte aus dem Datenfeld T[] auf der X-Achse verschiebt und auf der Y-Achse die entsprechenden Werte aus Y[].
3. Die Auswahl des optimalen Bereichs
Die Abbildung 1 zeigt Darstellungen der Dichteschätzungen für eine Folge mit Normalverteilung und unterschiedlichen Werten im Bereich h.
Die Schätzungen werden mithilfe der oben eingeführten Klasse CDens ausgeführt. Die Diagramme wurden als Webseiten im Format HTML angelegt. Am Ende dieses Beitrages wird das hier zur Erstellung derartiger Diagramme verwendete Verfahren vorgestellt. Mehr zur Erstellung von Schaubildern und Diagrammen im HTML-Format findet sich in den Literaturhinweisen unter [9].
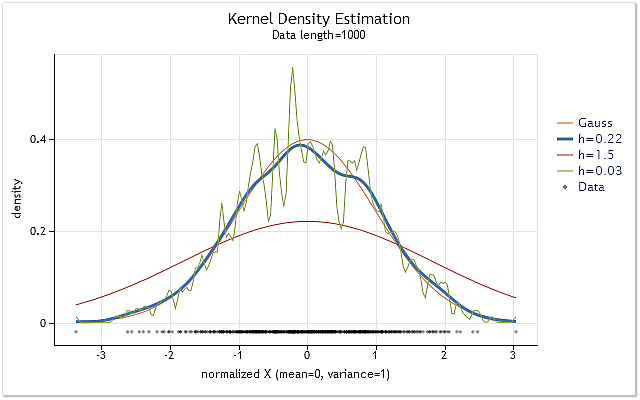
Abb. 1. Dichteschätzung für unterschiedliche Werte des Bereichs h
Die Abbildung 1 zeigt neben den drei Dichteschätzungen auch die tatsächliche Dichtekurve einer Normalverteilung (Gaußverteilung). Es ist unschwer zu erkennen, dass das annehmbarste Schätzergebnis in diesem Fall bei h = 0,22 erhalten wurde. In zwei anderen Fällen lässt sich eine deutliche „Über-“ bzw. „Unterglättung“ beobachten.
Die Abbildung 1 macht klar, wie wichtig die richtige Wahl des Bereiches h bei der Anwendung der Kerndichteschätzung (KDE) ist. Sollte der Wert für h falsch gewählt werden, erfährt die Schätzung entweder eine starke Verschiebung in Richtung der tatsächlichen Dichtekurve oder eine viel zu große Streuung.
Auf die optimale Auswahl des Bereiches h wird viel Arbeit verwendet. Häufig wird zur Auswahl von h die von Silverman vorgeschlagene recht einfache und bewährte Daumenregel verwendet (siehe [10]).
![]()
Hier ist A der kleinere der Werte der Standardabweichung und des Interquartilabstandes der Folge geteilt durch 1,34.
Wenn wir berücksichtigen, dass die Eingangsfolge in der oben eingeführten Klasse CDens nach der Normalisierung eine Standardabweichung von „1“ aufweist, ist diese Regel nicht schwer umzusetzen, wenn wir folgenden Codeausschnitt verwenden:
ArraySort(X); i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb
Diese Schätzung eignet sich gut für Folgen mit einer Wahrscheinlichkeitsdichte, deren Form nicht weit von der normalen entfernt ist.
In nicht wenigen Fällen ermöglicht die Berücksichtigung des Abstandes zwischen den Quartilen bei einer Abweichung der Form der zu schätzenden Dichte von der Normalform eine Korrektur des Wertes der Größe h nach unten, wodurch das vorgeschlagene Schätzverfahren hinreichend universell wird. Deshalb ist es sinnvoll, diese empirische Regel als anfängliche Grundeinschätzung des Wertes h zu verwenden, zumal dabei keine umständlichen Berechnungen benötigt werden.
Außer den asymptotischen und empirischen Schätzungen des Wertes für den Bereich h gibt es weitere Verfahren auf der Grundlage der unmittelbaren vorläufigen Analyse der Eingangsfolge selbst. In diesem Fall wird der optimale Wert für h unter Berücksichtigung der vorläufigen Schätzung der Eigenschaften der unbekannten Dichte bestimmt. Einen Vergleich der Aussagekraft einiger dieser Verfahren findet man in den Literaturhinweisen unter [11] und [12].
Laut in verschiedenen Quellen veröffentlichten Versuchsergebnissen ist die Plug-In-Methode nach Sheather und Jones (im Weiteren kurz: SJPI) eines der effektivsten Verfahren zur Schätzung des Bereichs. Wir entscheiden uns für genau dieses Verfahren. Um diesen Beitrag nicht mit unhandlichen mathematischen Ausdrücken zu überfrachten, beschäftigen wir uns später lediglich mit einigen Besonderheiten der genannten Methode. Falls erforderlich können die mathematischen Grundlagen in den Literaturhinweisen unter [13] nachgelesen werden.
Der von uns verwendete Gaußkern ist ein Kern mit einem unbegrenzten Träger (d. h., er wird bei Änderung seines Parameters von minus auf plus unendlich festgelegt). Aus dem oben angeführten Ausdruck folgt, dass wir bei einem unmittelbaren Rechenverfahren und einem Kern mit unbegrenztem Träger zur Berechnung der Dichte von M Punkten einer Folge mit der Länge N O(M*N) Operationen benötigen. Wenn es erforderlich die Berechnung für jeden Punkt der Folge auszuführen, steigt dieser Wert auf O(N*N) Operationen, und die für die Berechnungen benötigte Zeit wird proportional zum Quadrat der Länge der Folge zunehmen.
Ein derart großer Bedarf an Rechnerkapazität ist einer der Hauptnachteile der Kernglättung (Kernel-Regression). Bei Umsetzung des SJPI-Verfahrens sieht die Sache hinsichtlich des erforderlichen Rechenaufkommens nicht viel besser aus. Ohne ins Detail gehen zu wollen, halten wir fest, dass wir bei der Umsetzung dieses Verfahrens zunächst zweimal die Summe der Ableitungen von der Dichte über die gesamte Länge der Eingangsfolge berechnen müssen.
Anschließend müssen wir unter Verwendung der gewonnenen Ergebnisse mehrmals den Schätzwert berechnen, der gleich „0“ sein muss. Für die Suche nach dem Argument, bei dem diese Funktion gleich Null ist, können wir uns der Methode von Newton und Raphson [14] bedienen. Bei der direkten Methode kann die Berechnung des optimalen Wertes für den Bereich mithilfe des SJPI-Verfahrens bis zu etwa zehnmal so viel Zeit in Anspruch nehmen wie bei der unmittelbaren Berechnung der Dichteschätzung selbst.
Wir kennen unterschiedliche Verfahren zur Beschleunigung der Berechnungen bei der Kernglättung und der Kerndichteschätzung. In unserem Fall setzen wir auf den Gaußkern, dessen Wert bei Argumenten, deren Wert größer ist als 4, vernachlässigt werden kann. Deshalb kann die Berechnung des Wertes des Kerns bei Argumentwerten >4 unterbleiben, wodurch die Anzahl der erforderlichen Berechnungen herabgesetzt wird. Beim Anlegen des Diagramms für diese Schätzung lässt sich kaum ein Unterschied von der vollständigen Variante der Berechnung feststellen.
Als weiteres einfaches Verfahren zur Beschleunigung der Berechnungen kann die Verringerung der Anzahl der Punkte dienen, für die die Schätzung erfolgt. Wie bereits gesagt, verringert sich bei M < N die Anzahl der erforderlichen Rechenoperationen von O(N*N) auf O(M*N). Bei einer langen Folge mit, sagen wir, N = 100.000 können wir, indem wir die Berechnung nur in M = 200 Punkten durchführen, beträchtliche Gewinne bei der Rechenzeit verbuchen.
Zur Verringerung der Anzahl der erforderlichen Berechnungen werden auch komplexere Verfahren eingesetzt, zum Beispiel Schätzungen unter Verwendung des Algorithmus der schnellen Fourier-Transformation oder Wavelet-Transformationen. Bei wirklich langen Folgen können auch auf die Verringerung der Dimension der Eingangsfolge aufsetzende Verfahren mit Erfolg eingesetzt werden, so etwa das Data binning [15].
Neben den aufgeführten Verfahren zur Beschleunigung der Berechnungen kann bei Verwendung des Gaußkerns auch die schnelle Gaußtransformation [16] zur Anwendung kommen. Zur Umsetzung des SJPI-Verfahrens zur Berechnung des Bereichswertes verwendeten wir den auf der Gaußtransformation beruhenden Algorithmus aus Literaturhinweis [17]. Dort finden sich auch Veröffentlichungen mit einer Beschreibung des Verfahrens sowie Programmcodes, die den vorgeschlagenen Algorithmus umsetzen.
4. Sheather-Jones Plug-In (SJPI)
Wie bereits im Fall der mathematischen Ausdrücke zur Bestimmung des Kerns der Methode SJPI werden wir auch jetzt nicht die mit der Umsetzung des in den Literaturhinweisen unter [17] vorgestellten Algorithmus verbundenen mathematischen Berechnungen in diesen Beitrag kopieren. Wer möchte, kann sich damit gerne selbst befassen: [17].
Auf der Grundlage der unter [17] abgelegten Materialien wurde die Klasse CSJPlugin erstellt. Sie dient der Berechnung des optimalen Wertes für den Bereich h und besteht aus nur einer öffentlich zugänglichen (public) Methode, die da heißt: double CSJPlugin::SelectH(double &px[],double h,double stdev=1).
Beim Aufruf dieser Methode werden folgende Argumente als Parameter an sie weitergegeben:
- double &px[] – die Verknüpfung zu dem Datenfeld mit der ursprünglichen Folge;
- double h – der ursprüngliche Wert für den Bereich h, in Bezug auf den die Suche bei der Lösung von Gleichungen mit dem Algorithmus von Newton und Raphson ausgeführt wird. Es wäre zu wünschen, dass dieser Wert möglichst dicht bei dem Gesuchten liegt. Das würde die zur Lösung der Gleichungen benötigte Zeit sowie die Wahrscheinlichkeit des Auftretens von Situationen, in denen das Verfahren nach Newton und Raphson seine Stabilität einbüßen könnte, beträchtlich verringern. Als Anfangsgröße für h kann der nach der empirischen Regel von Silverman ermittelte Wert verwendet werden;
- double stdev=1 – der Wert der Standardabweichung der ursprünglichen Folge. Die Standardeinstellung lautet „1“. In unserem Fall muss diese Voreinstellung nicht geändert werden, da vorgesehen ist, dass dieses Verfahren gemeinsam mit der weiter oben eingeführten Klasse CDens verwendet wird, in der die ursprüngliche Folge bereits normalisiert wurde und stets eine Standardabweichung = 1 aufweist.
Bei erfolgreicher Ausführung gibt die Methode SelectH() den ermittelten optimalen Bereichswert für h aus. Im Fall eines Misserfolgs wird der ursprüngliche Wert für h ausgegeben. Der Quellcode der Klasse CSJPlugin befindet sich in der Datei CSJPlugin.mqh.
Einige Besonderheiten dieser Umsetzung gilt es zu erläutern.
Die Ausgangsfolge wird sofort in das Intervall [0,1] umgewandelt, während der ursprüngliche Wert für den Bereich h proportional zu dem Maßstab der Umwandlung der Ausgangsfolge normalisiert wird. Auf den als Ergebnis der Berechnungen gefundenen optimalen Wert für h wird eine umgekehrte Normalisierung angewandt.
Im Konstruktor der Klasse CSJPlugin wird die Genauigkeit der Berechnungen der Dichteschätzungen und ihrer Ableitungen auf eps=1e-4 sowie die zulässige Höchstzahl der Iterationen innerhalb des Algorithmus auf P_UL=500 festgelegt. Mehr dazu siehe [17].
In der Methode SelectH() wird die Höchstzahl der zulässigen Iterationen für das Verfahren von Newton und Raphson auf IMAX=20 und die Genauigkeit der Gleichungslösung mit seiner Hilfe auf PREC = 1e-4 festgelegt.
Für gewöhnlich erfordert die Verwendung des Verfahrens nach Newton und Raphson die Berechnung des Wertes derselben Zielfunktion und ihrer Ableitung an dem jeweiligen Punkt für jede Iteration. Hier wurde die Berechnung der Ableitung durch ihren mithilfe der Hinzufügung eines geringfügigen Inkrements zum Wert ihres Argumentes berechneten Schätzwert ersetzt.
In der Abbildung 2 findet sich ein Anwendungsbeispiel zweier unterschiedlicher Schätzverfahren für den optimalen Wert für den Bereich h
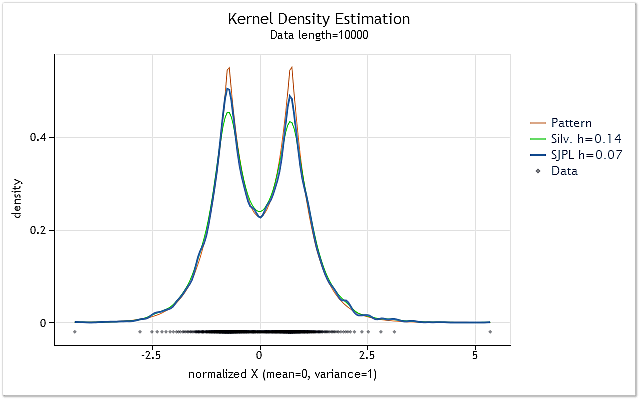
Abb. 2. Vergleich der Schätzungen des optimalen Wertes für den Bereich h
In der Abbildung 2 werden zwei Schätzungen für eine Zufallsfolge vorgestellt, deren tatsächliche Dichte (Pattern) in dem Diagramm in rot wiedergegeben wird.
Die Schätzungen erfolgten für eine Folge mit einer Länge von 10.000 Elementen. Mithilfe der empirischen Regel von Silverman wurde für diese Folge ein Wert von 0,14 für den Bereich h ermittelt, während dieser bei Verwendung des SJPI-Verfahrens bei 0,07 lag.
Vergleicht man die in der Abbildung 2 wiedergegebenen Ergebnisse der Kerndichteschätzung für diese beiden Werte von h, ist schwerlich zu übersehen, dass das SJPI-Verfahren im Vergleich zu der Regel von Silverman ein ansprechenderes Ergebnis für h liefert Wir sehen, dass die spitzen Ausschläge bei h = 0,07 erkennbar deutlicher herausgearbeitet sind, während bei den sanften Abschwächungen de facto keine Erhöhung der Streuung zu erkennen ist.
Wie zu erwarten war, ermöglicht das SJPI-Verfahren in vielen Fällen die Gewinnung recht ordentlicher Schätzwerte für den Bereich h. Ungeachtet des Umstandes, dass beim Anlegen der Klasse CSJPlugin ziemlich schnelle Algorithmen [17] eingesetzt wurden, kann die Berechnung des Wertes für h mit diesem Verfahren bei langen Folgen immer noch zu viel Zeit verschlingen.
Ein weiterer Schwachpunkt dieses Verfahrens ist seine Neigung zur „Überschätzung“ des Wertes für h bei kurzen Folgen aus nicht mehr als 10 bis 30 Werten. Dabei können die mithilfe des SJPI-Verfahrens ermittelten Schätzwerte über den mithilfe der empirischen Regel von Silverman gewonnenen liegen.
Um diesen Schwächen in gewisser Hinsicht Rechnung zu tragen, halten wir uns bei der weiteren Umsetzung an folgende Regeln:
- Als Voreinstellung zur Schätzung für den Bereich h gilt das Schätzverfahren nach Silverman, das SJPI-Verfahren kann mit einem gesonderten Befehl aufgerufen werden;
- Bei Verwendung des SJPI-Verfahrens wird als resultierende Größe h stets der kleinere der beiden mithilfe der genannten Verfahren gewonnenen Werte gewählt.
5. Randeffekt
Der Wunsch, bei der Dichteschätzung einen möglichst optimalen Bereichswert zu wählen, hat dazu geführt, dass wir die recht sperrige Klasse CSJPlugin angelegt haben. Aber neben den mit der Bestimmung des Bereichswertes und dem hohen Rechenleistungsbedarf des Verfahrens zur Kernglättung verbundenen Schwierigkeiten besteht ein weiteres Problem, der so genannte Randeffekt.
Die Sache ist im Kern ganz einfach. Wir veranschaulichen das ganze am Beispiel der Verwendung eines auf das Intervall [-1,1] festgelegten Kerns. Einen solchen Kern bezeichnet man als einen Kern mit einem endlichen (finiten) Träger. Außerhalb des angegebenen Wertebereichs ist er gleich Null (das heißt, er ist nicht vorhanden.
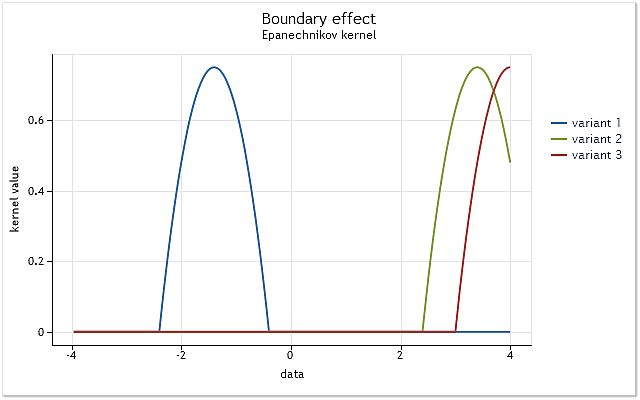
Abb. 3. Beschneiden des Kerns an der Bereichsgrenze
Wie in Abbildung 3 zu sehen ist, umfasst der Kern im ersten Fall alle in dem Intervall [-1,1] in Bezug auf seinen Mittelpunkt liegenden Ausgangsdaten. In Abhängigkeit von der Verlagerung des Kerns (z. B. nach rechts) entsteht eine Situation, in der die Daten zur vollständigen Nutzung der gewählten Funktion des Kerns nicht mehr ausreichen.
Dabei umfasst der Kern bereits weniger Daten als im ersten Fall. Im schlimmsten Fall liegt der Mittelpunkt des Kerns am Rand der Datenfolge. Die Anzahl der von dem Kern umfassten Daten schrumpft dabei auf 50%. Eine derartige Verringerung der zur Schätzung der Dichte verwendeten Datenmenge führt zu einer erheblichen Verschiebung der Schätzungen und zu einer Vergrößerung ihrer Streuung an den Punkten in der Nähe der Bereichsränder.
In der Abbildung 3 wird ein Beispiel für die Beschneidung eines Kerns mit endlichem Träger (eines Epanetschnikov-Kerns) am Rand des Bereichs wiedergegeben. Es sei darauf hingewiesen, dass wir bei der Umsetzung des Verfahrens zur Kerndichteschätzung einen über einen unbegrenzten Bereich (unbegrenzten Träger) definierten Gaußkern verwendet haben. Theoretisch erfolgt die Beschneidung eines solchen Kerns immer. Aber eingedenk der Tatsache, dass der Wert dieses Kerns bei großen Argumenten praktisch gleich Null ist, sind die Randeffekte für ihn dieselben wie für Kerne mit einem endlichen Träger.
In den Beispielen der Abbildungen 1 und 2 konnte die genannte Erscheinung die Ergebnisse der Dichteschätzung nicht wesentlich beeinflussen, da die Schätzung in beiden Fällen für Folgen ausgeführt wurde, deren Wahrscheinlichkeitsdichte an den Rändern faktisch auf Null fiel.
Um den Einfluss der Kernbeschneidung an den Bereichsrändern zu veranschaulichen, bilden wir eine Folge unter Verwendung einer Reihe positiver ganzer Zahlen X = 1,2,3,4,5,6,…n. Eine solche Folge weist eine gleichmäßige Verteilung der Wahrscheinlichkeitsdichte auf. Das bedeutet, dass die Schätzung der Dichte dieser Folge eine waagerechte Gerade auf einer von „0“ verschiedenen Ebene darstellen muss.
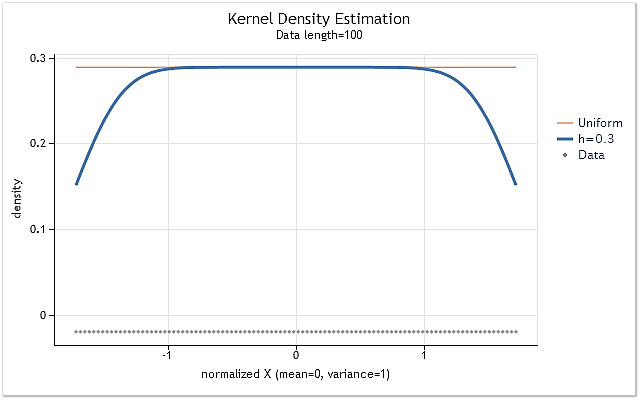
Abb. 4. Dichteschätzung für eine Folge mit gleichmäßiger Verteilung
Aus der Abbildung 4 wird ersichtlich, dass an den Bereichsrändern wie vermutet eine beträchtliche Verlagerung der Dichteschätzungen zu beobachten ist. Um die an den Rändern entstehende Verlagerung in mehr oder weniger großem Umfang zu verringern, kommen unterschiedliche Verfahren zur Anwendung, die grob in folgende Gruppen unterteilt werden können:
- Methoden zur Spiegelung von Daten
- Methoden zur Umwandlung von Daten
- Methoden für Pseudodaten
- Methoden für Randkerne
Die Idee hinter der Verwendung gespiegelter Daten besteht darin, die Eingangsfolge künstlich zu vergrößern, indem man sie um Daten erweitert, die gleichsam ihr Spiegelbild in Bezug auf die Bereichsgrenzen der Folge sind. Nach dieser Erweiterung erfolgt die Dichteschätzung für dieselben Punkte wie bei der ursprünglichen Folge, nur dass in diese Schätzung auch schon die künstlich hinzugefügten Daten einbezogen werden.
Die Methoden, die eine Umwandlung der Daten nahelegen, orientieren sich an der Umwandlung der Folge in der Nähe der Ränder ihres Bereichs. Man kann beispielsweise eine logarithmische oder irgendeine andere Umwandlung verwenden, die es möglich macht, den Maßstab der Daten im Verlauf der Dichteschätzung bei einer Annäherung an einen Rand des Bereiches irgendwie umzuformen.
Zur künstlichen Erweiterung (Vergrößerung) der Ausgangsfolge können so genannte Pseudodaten verwendet werden. Dabei handelt es sich um Daten, die auf der Grundlage der Werte der ursprünglichen Folge errechnet werden. Sie sind dazu gedacht, deren Verhalten an den Rändern zu erfassen und sie in der entsprechenden optimalen Weise zu ergänzen.
Eine Fülle von Veröffentlichungen widmet sich den Methoden für Randkerne. Bei diesen Methoden ändert der Kern bei Annäherung an eine Grenze seine Form in mehr oder weniger großem Umfang. Die Form des Kerns ändert sich so, dass die an den Rändern auftretende Verlagerung der Schätzungen ausgeglichen wird.
Der Literaturhinweis [18] stellt einige Methoden zum Ausgleich von an den Bereichsrändern entstehenden Verzerrungen vor, vergleicht sie miteinander und bewertet ihre Erfolgsaussichten.
Nach einigen kurzen Experimenten wurde zur weiteren Verwendung die Methode der Spiegelung von Daten gewählt. Diese Wahl wurde durch den Umstand beeinflusst, dass es bei Verwendung dieser Methode nicht zu Situationen kommt, in denen die Dichteschätzung einen negativen Wert annehmen kann Außerdem erfordert sie keine komplexen mathematischen Berechnungen. Dabei nimmt die Gesamtzahl der Operationen aufgrund der Notwendigkeit, jede Schätzung für eine Folge mit künstlich erweiterter Länge ausführen zu müssen, natürlich dennoch zu.
Zur Umsetzung dieser Methode gibt es zwei mögliche Vorgehensweisen: Erstens kann man die Ausgangsfolge sofort um die erforderlichen Daten erweitern, wodurch ihre Größe verdreifacht wird. Danach werden alle Schätzungen genauso ausgeführt wie es bei der weiter oben eingeführten Klasse CDens gezeigt wurde. Zweitens kann man aber auch auf die Erweiterung des ursprünglichen Datenfeldes mit den Werten der Folge verzichten und stattdessen einfach in einer vorgegebenen Weise immer wieder Daten aus ihm entnehmen. Wir haben uns bei der praktischen Umsetzung für die zweite Vorgehensweise entschieden.
In der bereits erwähnten Klasse CDens wurde die Dichteschätzung in der Funktion void kdens(double h) umgesetzt. Wir wandeln diese Funktion ab, indem wir sie um eine Korrektur der Randverzerrungen erweitern.
Die erweiterte Funktion könnte etwa so aussehen:
//+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
Die Umsetzung der Funktion erfolgt unter Berücksichtigung des Umstandes, dass die Ausgangsdaten im Datenfeld X[] bereits geordnet sind, wenn die Funktion aufgerufen wird. Dadurch können die beiden den Extremwerten des Bereichs entsprechenden Elemente der Folge problemlos von der wiederholten Verarbeitung ausgenommen werden. Bei der Umsetzung dieser Funktion wurde der Versuch unternommen, die mathematischen Operationen möglichst nach außerhalb der Zyklen zu verlagern. In der Folge lässt die Funktion das Wesen des verwendeten Algorithmus weniger deutlich erkennen.
Weiter oben wurde bereits darauf hingewiesen, dass die Anzahl der Berechnungen ein wenig herabgesetzt werden kann, wenn der Wert des Kerns bei hohen Argumentwerten nicht berechnet wird. Eben das wird in der angegebenen Funktion umgesetzt. Dabei sind nach dem Anlegen des Diagramms der zu schätzenden Dichte praktisch keine Veränderungen zu erkennen.
Bei Verwendung der überarbeiteten Fassung der Funktion kdens() verwandelt sich die in Abbildung 4 dargestellte Dichteschätzung in eine Gerade, und die Absenkungen an den Rändern verschwinden ganz. Eine derart ideale Korrektur ist allerdings nur in dem Fall zu erreichen, wenn die Verteilung in den randnahen Abschnitten einen Gradienten von „0“ aufweist, sich also als waagerechte Linie darstellt.
Wenn die geschätzte Dichte der Verteilung in Nähe der Ränder stark zu- oder abnimmt, ist die gewählte Methode zur Spiegelung der Daten nicht mehr in der Lage, den Randeffekt vollständig zu korrigieren. Diese Ausführungen werden durch die folgenden Abbildungen veranschaulicht:
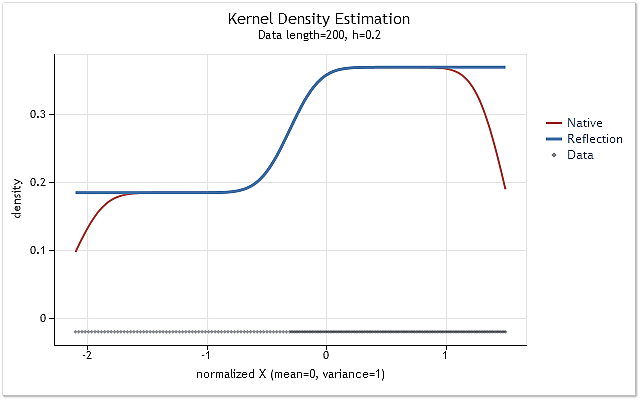
Abb. 5. Sich stufenweise ändernde Wahrscheinlichkeitsdichtefunktion
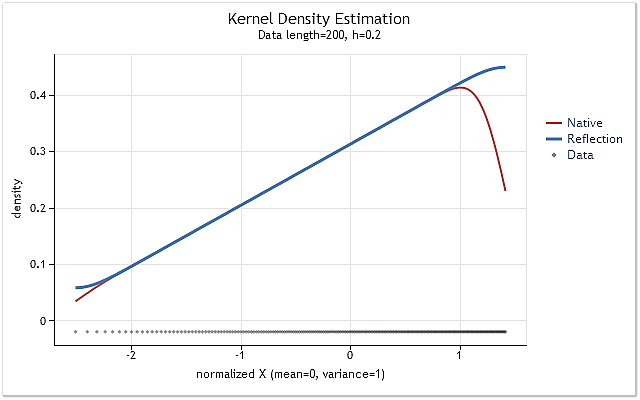
Abb. 6. Linear ansteigende Wahrscheinlichkeitsdichtefunktion
In den Abbildungen 5 und 6 ist die mithilfe der ursprünglichen Fassung der Funktion kdens() ermittelte Dichteschätzung rot dargestellt, während blau die Schätzung anzeigt, die unter Berücksichtigung der an ihr vorgenommenen Änderungen zur Umsetzung der Methode zur Spiegelung der Daten zustande gekommen ist. Während der Randeffekt in dem in der Abbildung 5 wiedergegebenen Fall vollständig korrigiert wurde, sehen wir in der Abbildung 6, dass die Verschiebung an den Rändern nicht ganz verschwunden ist. Wenn die zu schätzende Dichte an einem Rand stark zu- oder abnimmt, dann erscheint sie in der Nähe dieses Randes ein wenig geglättet.
Die zur Korrektur des Randeffektes gewählte Methode zur Spiegelung von Daten ist weder das beste noch das schlechteste aller bekannten Verfahren. Auch wenn diese Methode nicht in allen Fällen den Randeffekt ganz beseitigen kann, so ist sie doch recht stabil und vor allem leicht umzusetzen. Dieses Verfahren gewährleistet die Gewinnung eines folgerichtigen und stets vorhersagbaren Ergebnisses.
6. Abschließende Umsetzung. Die Klasse CKDensity
Wir erweitern die oben angelegte Klasse CDens um die Möglichkeit der automatischen Auswahl des Bereichswertes h und um die Korrektur des Randeffekts.
Es folgt der Quellcode der überarbeiteten Klasse:
//+------------------------------------------------------------------+ //| CKDensity.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #include "CSJPlugin.mqh" //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CKDensity:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth int Pflag; // SJ plug-in bandwidth selection flag public: void CKDensity(void); int Density(double &x[],double hh=-1); void NTpoints(int n); void PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;} private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CKDensity::CKDensity(void) { NTpoints(200); // Default number of test points Pflag=0; // Not SJ plug-in } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CKDensity::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Bandwidth selection and kernel density estimation | //+------------------------------------------------------------------+ int CKDensity::Density(double &x[],double hh=-1) { int i; double a,b,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); // Sort input data Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) a=X[0]; b=(X[N-1]-a)/(Np-1.0); for(i=0;i<Np;i++)T[i]=a+b*(double)i; // Create test points //-------------------------------- Bandwidth selection if(hh<0) { i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb if(Pflag==1) { CSJPlugin *plug=new CSJPlugin(); a=plug.SelectH(X,h); // SJ Plug-in delete plug; h=MathMin(a,h); } } else {h=hh; if(h<0.005)h=0.005;} // Manual select H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void CKDensity::kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
Die Hauptmethode dieser Klasse ist: Density(double &x[],double hh=-1). Ihr erstes Argument ist die Verknüpfung mit dem Datenfeld x[], das die zu untersuchende Ausgangsfolge enthalten muss. Die Länge der Eingangsfolge muss mindestens acht Elemente betragen. Das zweite (nicht verbindliche) Argument dient der obligatorischen Bestimmung des Bereichswertes h.
Dabei kann eine beliebige positive Zahl angegeben werden. Der festgelegte Wert für h ist nach unten stets durch den Wert 0,005 begrenzt. Hat dieser Parameter ein negatives Vorzeichen, dann wird die Bereichsgröße automatisch festgelegt. Bei erfolgreicher Erledigung gibt die Methode Density() „0“ aus bzw. „-1“ bei einer fehlgeschlagenen.
Nach dem Aufruf und den erfolgreichen Ausführung der Methode Density() enthält das Datenfeld T[] die Werte der Versuchspunkte, für die die Dichteschätzung erfolgt ist, während das Datenfeld Y[] die Werte dieser Schätzungen enthält. Das Datenfeld X[] enthält die normalisierte und geordnete Eingangsfolge. Dabei ist der Durchschnittswert dieser Folge gleich Null, ihre Standardabweichung hat den Wert „1“.
Die Variablen, die zu dieser Klasse gehören, beinhalten folgende Werte:
- N – die Länge der Eingangsfolge
- Np – die Anzahl der Versuchspunkte, für die die Dichteschätzung erfolgt ist
- Mean – den Durchschnittswert der Eingangsfolge
- Var – die Varianz (Streuung) der Eingangsfolge
- StDev – die Standardabweichung der Eingangsfolge
- H – den Bereichswert (Glättungsparameter)
- Pflag – die Markierung der Verwendung des SJPI-Verfahrens zur Bestimmung des optimalen Wertes für den Bereich h.
Die Methode NTpoints(int n) kommt zur Anwendung, um die Anzahl der Versuchspunkte festzulegen, für die die Dichteschätzung erfolgen soll. Die Anzahl der Versuchspunkte muss vor dem Aufruf der Hauptmethode Density() festgelegt worden sein. Wird die Methode NTpoints(int n) nicht verwendet, bleibt es bei der Voreinstellung von 200 Punkten.
Die Methode PluginMode(int m) ermöglicht die Zulassung oder Verweigerung der Verwendung des SJPI-Verfahrens zur Ermittlung des optimalen Bereichswertes. Wenn nach dem Aufruf dieser Methode der Parameter „1“ verwendet wird, kommt das SJPI-Verfahren zur Bestimmung des Bereichswertes h zum Einsatz. Bei jedem von „1“ verschiedenen Parameterwert wird das SJPI-Verfahren nicht angewendet. Sollte die Methode PluginMode(int m) nicht aufgerufen werden, bleibt das SJPI-Verfahren entsprechend der Voreinstellung abgeschaltet.
7. Anlegen von Diagrammen
Beim Schreiben dieses Beitrages wurde zur Erstellung der Diagramme ein Verfahren verwendet, das in den Literaturhinweisen unter [9] bereits vorgestellt wurde. In der betreffenden Veröffentlichung wurde vorgeschlagen, eine im Vorfeld angelegte Webseite im Format HTML zu verwenden, die die JavaScript-Bibliothek highcharts [19] sowie die vollständige Festlegung all ihrer Aufrufe beinhaltet. Des Weiteren wurde in einem MQL-Programm eine Textdatei mit den zur Wiedergabe vorgesehenen Daten angelegt und mit der genannten HTML-Seite verknüpft.
Bei einem solchen Vorgehen muss die HTML-Seite bearbeitet werden, um den in ihr enthaltenen JavaScript-Code zu ändern, wenn Änderungen am Aufbau der abzubildenden Grafiken vorgenommen werden sollen. Um das zu umgehen, wurde eine einfache Benutzeroberfläche entwickelt, mit deren Hilfe die Methoden der JavaScript-Bibliothek „highcharts“ unmittelbar aus dem MQL-Programm aufgerufen werden können.
Bei der Erstellung der Benutzeroberfläche gehörte die Ermöglichung des Zugriffs auf das gesamte Potenzial der „highcharts“-Bibliothek nicht zur Aufgabestellung. Es wurden lediglich die Möglichkeiten umgesetzt, die zum Zeitpunkt der Verfassung dieses Beitrages keine Korrektur der im Vorfeld angelegten HTML-Datei zuließen.
Weiter unten folgt der Quellcode der Klasse CLinDraw, die zur Herstellung der Verbindung zu den Methoden der „highcharts“-Bibliothek verwendet wurde. Dieser Code sollte nicht als abschließende Umsetzung in Programmform betrachtet werden, er ist vielmehr ein Beispiel zur Veranschaulichung der Möglichkeit, mit der Grafiksammlung von JavaScript eine Benutzeroberfläche anzulegen.
//+------------------------------------------------------------------+ //| CLinDraw.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #import "shell32.dll" int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters, string lpDirectory,int nShowCmd); #import #import "kernel32.dll" int DeleteFileW(string lpFileName); int MoveFileW(string lpExistingFileName,string lpNewFileName); #import //+------------------------------------------------------------------+ //| type = "line","spline","scatter" | //| col = "r,g,b,y" | //| Leg = "true","false" | //| Reference: http://www.highcharts.com/ | //+------------------------------------------------------------------+ class CLinDraw:public CObject { protected: int Fhandle; // File handle int Num; // Internal number of chart line string Tit; // Title chart string SubTit; // Subtitle chart string Leg; // Legend enable/disable string Ytit; // Title Y scale string Xtit; // Title X scale string Fnam; // File name public: void CLinDraw(void); void Title(string s) { Tit=s; } void SubTitle(string s) { SubTit=s; } void Legend(string s) { Leg=s; } void YTitle(string s) { Ytit=s; } void XTitle(string s) { Xtit=s; } int AddGraph(double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double y,string type,string name,int w=0,string col=""); int LDraw(int ashow=1); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CLinDraw::CLinDraw(void) { Num=0; Tit=""; SubTit=""; Leg="true"; Ytit=""; Xtit=""; Fnam="CLinDraw.txt"; Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI); if(Fhandle<0) { Print(__FUNCTION__,": Error! FileOpen() error."); return; } FileSeek(Fhandle,0,SEEK_SET); // if file exists } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(y); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("%.5g,",y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("%.5g]},\n",y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| LDraw | //+------------------------------------------------------------------+ int CLinDraw::LDraw(int ashow=1) { int i,k; string pfnam,to,p[]; FileWriteString(Fhandle,"]});\n});"); if(Fhandle<0)return(-1); FileClose(Fhandle); pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\"+Fnam; k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("\\",0),p); to=""; for(i=0;i<k-1;i++)to+=p[i]+"\\"; to+="ChartTools\\"; // Folder name DeleteFileW(to+Fnam); MoveFileW(pfnam,to+Fnam); if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1); return(0); }
Damit diese Klasse normal funktioniert, benötigen wir eine vorgefertigte HTML-Seite mit angeschlossenen JavaScript-Bibliotheken, die auch die Größe und die Lage des zur anschließenden Anlage eines oder mehrerer Diagramme vorgesehenen Feldes bestimmt. Ein Beispiel für die Umsetzung einer solchen Webseite findet sich in den Dateien im Anhang zu diesem Beitrag.
Beim Aufruf der Methode AddGraph() wird in einer Textdatei, die anschließend mit der zuvor erstellten HTML-Seite verknüpft wird, der entsprechende JavaScript-Code angelegt. Dieser Code gewährleistet durch Abrufen der Bibliothek mit den Grafiken die Erstellung des Diagramms anhand der als Argument an die Methode AddGraph() weitergegebenen Daten. Bei dem erneuten Aufruf dieser Methode kann das Ausgabefeld um ein oder mehrere Diagramme erweitert werden.
Die Klasse CLinDraw enthält drei Varianten der Erweiterungsfunktion AddGraph(). An eine davon muss lediglich ein Datenfeld mit den gespiegelten Daten als Argument weitergegeben werden. Diese Variante ist zur Erstellung eines Diagramms gedacht, in dem die Kennziffern der Elemente dieser Folge auf der X-Achse abgebildet werden.
Eine andere Variante erhält als Argument zwei Datenfelder, in denen die Werte enthalten sind, die auf der X- bzw. der Y-Achse angezeigt werden. Die dritte Variante ermöglicht die Festlegung eines festen Wertes für die Y-Achse. Sie kann zum Anlegen einer waagerechten Linie verwendet werden. Die übrigen Argumente sind bei diesen Funktionen identisch:
- string type – die Art des abgebildeten Diagramms. Möglich sind die Werte „line“, „spline“ und „splatter“;
- string name – die dem Diagramm zugeordnete Bezeichnung;
- int w=0 – die Linienstärke. Ein nicht obligatorisches Argument. Ist der erhaltene Wert gleich „0“, wird die voreingestellte Stärke 2 verwendet;
- string col="" – die Farbe der Linie und ihre Deckkraft. Ein nicht obligatorisches Argument.
Die Methode LDraw() muss zuletzt aufgerufen werden. Sie schließt die Überführung des JavaScript-Codes und der Daten in die standardmäßig in dem Verzeichnis \MQL5\Files\ angelegte Textdatei ab. Anschließend wird diese Datei in das Verzeichnis verlegt, in dem sich die Dateien mit den Grafiksammlungen und die HTML-Datei befinden.
Die Methode LDraw() kann nur ein einziges nicht obligatorisches Argument aufnehmen. Wenn für dieses Argument kein oder der Wert „1“ festgelegt wird, erfolgt nach der Verschiebung der Datei mit den Daten in das entsprechende Verzeichnis der Aufruf des Standard-Webbrowsers zur Anzeige des Diagramms. Bei einem anderen Wert als „1“ für das Argument wird die Datei mit den Daten zwar vollständig angelegt, aber der automatische Aufruf des Webbrowsers unterbleibt.
Weitere verfügbare Methoden der Klasse CLinDraw ermöglichen die Angabe einer Kopfzeile für das Diagramm und die Beschriftung seiner Achsen. Die mit der Anwendung der Bibliothek „highcharts“ und der Klasse CLinDraw verbundenen Fragen werden wir in diesem Beitrag nicht ausführlicher behandeln. Umfassende Informationen zu der Grafiksammlung „highcharts“ bietet der Literaturhinweis [19], Anwendungsbeispiele bei der Erstellung von Schaubildern und Diagrammen finden sich in [9] und [20].
Damit die Klasse CLinDraw normal funktioniert, muss in der Programminstanz auf dem Ausgabegerät (Terminal) die Verwendung externer Bibliotheken zugelassen sein.
8. Beispiel einer Dichteschätzung und Ablage der Dateien
Alles in allem haben wir jetzt drei Klassen, CKDensity, CSJPlugin und CLinDraw.
Es folgt der Ausgangscode eines Beispiels zur Veranschaulichung ihrer jeweiligen Verwendung:
//+------------------------------------------------------------------+ //| KDE_Example.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CKDensity.mqh" #include "ChartTools\CLinDraw.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double a; int ndata=1000; // Input data length double X[]; // Array for data double Z[]; // Array for graph of a Laplace distribution double Sc[]; // Array for scatter plot //-------------------------- Preparation of the input sequence ArrayResize(X,ndata+1); i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X); if(i!=ndata+1) { Print("Not enough historical data."); return; } for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns ArrayResize(X,ndata); //-------------------------- Kernel density estimation CKDensity *kd=new CKDensity; kd.PluginMode(1); // Enable Plug-in mode kd.Density(X); // Density estimation //-------------------------- Graph of a Laplace distribution n=kd.Np; // Number of test point ArrayResize(Z,n); for(i=0;i<n;i++) { a=MathAbs(kd.T[i]*M_SQRT2); Z[i]=0.5*MathExp(-a)*M_SQRT2; } //-------------------------- Scatter plot n=kd.N; // Data length if(n<400) { ArrayResize(Sc,n); for(i=0;i<n;i++)Sc[i]=kd.X[i]; } else // Decimation of data { ArrayResize(Sc,400); for(i=0;i<400;i++) { a=i*(n-1.0)/399.0+0.5; Sc[i]=kd.X[(int)a]; } } //-------------------------- Visualization CLinDraw *ld=new CLinDraw; ld.Title("Kernel Density Estimation"); ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H)); ld.YTitle("density"); ld.XTitle("normalized X (mean=0, variance=1)"); ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1"); ld.AddGraph(kd.T,kd.Y,"line","Estimation"); ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4"); ld.LDraw(); // With WEB-browser autostart // ld.LDraw(0); // Without autostart delete(ld); delete(kd); }
Am Anfang des Skripts KDE_Example.mq5 werden die Daten aufbereitet, für die die Schätzung der Wahrscheinlichkeitsdichtefunktion vorgenommen wird. Dazu werden die „offenen“ (open) Werte des betreffenden Finanzinstrumentes (Kürzels) sowie der aktuelle Zeitraum in das Datenfeld X[] kopiert. Danach wird auf deren Grundlage die logarithmierte Rendite, der „logarithmic return“, berechnet.
Im nächsten Schritt wird eine Instanz der Klasse CKDensity angelegt. Der Aufruf ihrer Methode PluginMode() ermöglicht die Verwendung des SJPI-Verfahrens zur Schätzung des Bereichs h. Danach erfolgt die Dichteschätzung für die in dem Datenfeld X[] angelegte Folge. Damit ist der Schätzvorgang beendet. Im Weiteren folgen die mit der Veranschaulichung der erhaltenen Dichteschätzung verbundenen Schritte.
Zum Vergleich der erhaltenen Schätzung mit einer beliebigen bekannten Verteilungsgesetzmäßigkeit werden in dem Datenfeld Z[] Werte gebildet, die der Laplace-Verteilung entsprechen. Im Anschluss daran werden die normalisierten und geordneten Eingangsdaten in dem Datenfeld Sc[] gespeichert. Bei einer Länge der Eingangsfolge von mehr als 400 Elementen werden nicht alle Werte der Eingangsfolge von dem Datenfeld Sc[] erfasst, ein Teil von ihnen wird zurückgewiesen. Folglich bietet die Größe des Datenfeldes Sc[] niemals mehr als 400 Elementen Platz.
Sobald alle für die Wiedergabe erforderlichen Informationen aufbereitet sind, wird eine Instanz der Klasse CLinDraw erstellt. Als Nächstes werden die Kopfzeilen festgelegt und mithilfe der Methode AddGraph() die für die Abbildung vorgesehenen Grafiken hinzugefügt.
Als Erste von ihnen folgt das als Muster angelegte Diagramm einer Laplace-Verteilung. Anschließend kommt ein aus der Dichteschätzung für die Eingangsdaten gewonnenes Diagramm. Und zum Abschluss wird im unteren Teil ein Diagramm hinzugefügt, das die Gruppierung der Ausgangsdaten veranschaulicht. Nachdem alle für die Wiedergabe erforderlichen Elemente bestimmt sind, erfolgt der Aufruf der Methode LDraw().
Als Ergebnis erhalten wir das in der Abbildung 7 vorgestellte Diagramm:
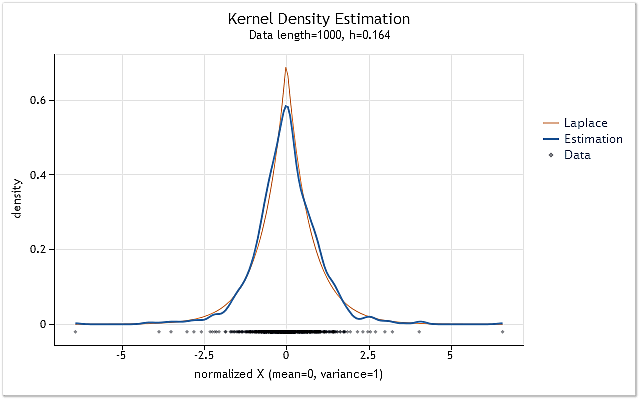
Abb. 7. Dichteschätzung für logarithmierte Renditen (USDJPY, Daily)
Die Schätzung in der Abbildung 7 wurde für 1.000 Werte der logarithmierten Rendite des Kürzels USDJPY, Daily, durchgeführt. Unverkennbar ähnelt die Schätzung sehr der Kurve der Laplace-Verteilung.
Alle zur Schätzung der Dichte sowie zu deren Veranschaulichung erforderlichen Dateien befinden sich am Ende dieses Beitrages in der gepackten Datei KDEFiles.zip. Dabei handelt es sich um folgende Dateien:
- DensityEstimation\ChartTools\CLinDraw.mqh – die Klasse für die Interaktion mit der Bibliothek highcharts.js;
- DensityEstimation\ChartTools\highcharts.js - die Bibliothek Highcharts JS v2.2.0 (2012-02-16);
- DensityEstimation\ChartTools\jquery.js – die Bibliothek jQuery v1.7.1;
- DensityEstimation\ChartTools\LinDraw.htm – die für die Wiedergabe vorgesehene HTML-Seite;
- DensityEstimation\CKDensity.mqh – die Klasse zur Ausführung der Dichteschätzung;
- DensityEstimation\CSJPlugin.mqh – die Klasse zur Ausführung des SJPI-Verfahrens zur Schätzung der optimalen Bereichsgröße;
- DensityEstimation\KDE_Example.mq5 – Beispiel der Dichteschätzung für logarithmierte Renditen.
Nach dem Entpacken der Datei muss das Verzeichnis DensityEstimation\ mit seinem gesamten Inhalt in dem Verzeichnis Scripts (oder Indicators) des Ausgabegerätes (Terminals) abgelegt werden. Danach kann das Beispiel KDE_Example.mq5 unmittelbar zusammengestellt und aufgerufen werden. Gegebenenfalls kann das Verzeichnis DensityEstimation umbenannt werden, ohne dass die Arbeit des Programms dadurch beeinträchtigt wird.
Es sei daran erinnert, dass, um die normale Funktion der Klasse CLinDraw zu gewährleiten, die Verwendung externer Bibliotheken in dem Ausgabegerät (Terminal) zugelassen sein muss.
Das Verzeichnis DensityEstimation\ umfasst das eingebettete Unterverzeichnis ChartTools\ mit allen für die Abbildung der Schätzungsergebnisse vorgesehenen Elementen. Die mit der Veranschaulichung verbundenen Dateien sind in einem gesonderten Unterverzeichnis zu Gruppen zusammengefasst, um das Verzeichnis DensityEstimation\ nicht zu überfrachten, sodass sein Inhalt einfacher zu identifizieren ist. Die Bezeichnung des Unterverzeichnisses ChartTools\ wird unverzüglich in die Quellcodes eingetragen, weswegen sie nicht geändert werden sollte. Wenn seine Umbenennung unerlässlich ist, müssen alle Quellcodes entsprechend angepasst werden.
Es wurde bereits darauf hingewiesen, dass bei der Umsetzung der Veranschaulichung eine Textdatei mit allen für die Diagrammerstellung benötigten Angaben angelegt wird. Diese Datei befindet sich ursprünglich in dem eigens dafür vorgesehenen Verzeichnis „Dateien“ (Files) auf dem Ausgabegerät. Anschließend wird sie jedoch in das bereits erwähnte Verzeichnis ChartTools verschoben. Somit bleiben weder in dem Dateien-Verzeichnis Files\ noch in einem anderen Verzeichnis auf dem Ausgabegerät Spuren unseres Versuchsbeispiels zurück. Deshalb genügt die Löschung des Verzeichnisses DensityEstimation samt seinem gesamten Inhalt, um die für diesen Beitrag angelegten Dateien vollständig zu entfernen.
Fazit
Beim Verfassen dieses Beitrages wurden einige das Wesen des einen oder anderen Verfahrens erläuternde mathematische Ausdrücke weggelassen. Das geschah bewusst, um das Lesen selbst zu erleichtern. Falls erforderlich sind alle mathematischen Berechnungen in der umfangreichen Fachliteratur zu finden. Ein kleiner Teil wird in den Literaturhinweisen zu diesem Beitrag ausgewiesen.
Die in dem Beitrag angeführten Quellcodes wurden keiner ernsthaften Überprüfung unterzogen, weshalb sie lediglich als Veranschaulichungen für das in dem Beitrag vorgestellte Material zu betrachten sind, keinesfalls jedoch als fertige Programme.
Literaturhinweise:
- Histogramm.
- Kerndichteschätzer.
- Kernglätter (Kernel smoother).
- EM-Algorithmus (Expectation-Maximization Algorithm).
- А.V. Batov, V.J. Korolev, А.J. Kortschagin. Ein EM-Algorithmus mit zahlreichen Bestandteilen als Mittel zur Erstellung nichtparametrischer Dichteschätzungen (nur in russischer Sprache).
- Hardle W., Angewandte nichtparametrische Regression (Applied Nonparametric Regression).
- Kernel (statistics).
- Schaubilder und Diagramme in HTML (Charts and diagrams in HTML).
- Simon J. Sheather. (2004) Dichteschätzung (Density Estimation).
- Max Kohler, Anja Schindler, Stefan Sperlich. (2011) A Review and Comparison of Bandwidth Selection Methods for Kernel Regression (Prüfung und Vergleich der Verfahren zur Bandbreitenauswahl bei der Kernglättung).
- Clive R. Loader. (1999) Bandbreitenauswahl: Klassisch oder Plug-In? (Bandwidth Selection: Classical or Plug-In?).
- S. J. Sheather, M. C. Jones. (1991) Ein zuverlässiges Verfahren zur Auswahl der Bandbreite bei der Kerndichteschätzung (A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation).
- Das Newton-Verfahren.
- Einteilung von Daten in Klassen (Data binning).
- Changjiang Yang, Ramani Duraiswami und Larry Davis. (2004) Effiziente Kernberechnungen mittels schneller Gaußtransformation (Efficient Kernel Machines Using the Improved Fast Gauss Transform).
- Schnelle Ermittlung der optimalen Bandbreite für die KDE (Fast optimal bandwidth estimation for univariate KDE).
- R.J. Karunamuni und T. Alberts. (2005) Ein örtlich anpassungsfähiges Umwandlungsverfahren zur Randkorrektur bei der Kerndichteschätzung (A Locally Adaptive Transformation Method of Boundary Correction in Kernel Density Estimation).
- Highcharts JS.
- Analyse der wesentlichen Merkmale von Zeitreihen.