Tiefe neuronale Netzwerke (Teil II). Ausarbeitung und Auswahl von Prädiktoren
Vladimir Perervenko | 5 Oktober, 2017
Inhalt
- Einführung
- 1. Erstellen der Merkmale
- 2. Prädiktoren Auswahl
- Schlussfolgerung
- Anwendung
Einführung
Im vorherigen Artikel haben wir verschiedene Aspekte der Beschaffung und Aufbereitung der Eingangsdaten und der Zielvariablen betrachtet. Um die Skripte des ersten Artikels zu erhalten, müssen Sie entweder alle Skripte des ersten Teils implementieren oder die Berechnungsergebnisse aus dem ersten Teil des Programms RStudio herunterladen.
1. Erstellen der Merkmale
Das Erstellen von Eigenschaften ist die Wissenschaft (und Kunst) des Ermittelns weiterer Informationen aus den vorhandenen Daten. Unser Ziel ist es nicht, neue Daten hinzuzunehmen, sondern die vorhandenen zu nutzen. Neue Möglichkeiten erlauben es uns, zusätzliche Eigenschaften aus den Datensätzen zu extrahieren. Diese Eigenschaften ermöglichen eine präzisere Kennzeichnung, Charakterisierung und Aufteilung der Daten für das Training. Das führt zu einer erhöhten Genauigkeit.
Dieser Vorgang kann in zwei Phasen unterteilt werden:
- Transformation. Je nach Szenario kann es sich dabei um eine von vier Transformationsarten handeln: Normalisierung der Daten, Beseitigung der Schiefe von Variablen, Entfernen von Ausreißern (outlier) und eine Diskretisierung.
- Erstellen der Merkmale. Das Extrahieren einer neuen Variable aus den vorhandenen Variablen wird als Erstellen eines neuen Merkmals bezeichnet. Diese kann versteckte Zusammenhänge in den Daten hervorbringen.
1.1. Transformation von Merkmalen
1.1.1. Transformation
Was ist die Transformation einer Variablen?
In der Datenmodellierung ist eine Transformation das Ersetzen einer Variablen durch eine Funktion dieser Variablen. Dies kann z. B. die Änderung der Variablen x durch eine Quadrat- oder Kubikwurzel oder den Logarithmus von x sein. Mit anderen Worten, eine Transformation ist ein Prozess, der die Verteilung einer Variablen und das Verhältnis dieser Variablen zu anderen verändert.
Erinnern wir uns, wann die Transformationen einer Variablen sinnvoll sind.
- Wenn wir den Maßstab einer Variablen ändern oder ihre Werte für ein besseres Verständnis standardisieren wollen. Diese Transformation wird benötigt, wenn verschiedene Datensätze mit unterschiedlichen Maßstäben vorliegen. Die Verteilungsform selbst ändert sich dadurch nicht.
- Wenn komplexe, nichtlineare und krümmungslineare Beziehungen zwischen Variablen in eine lineare Beziehung umgewandelt werden müssen. Dies ist anschaulicher und bietet eine bessere Prognosefähigkeit. In einem solchen Fall kann ein Punktdiagramm verwendet werden, um eine Beziehung zwischen zwei kontinuierlichen Variablen zu finden. Normalerweise wird dafür eine logarithmische Transformation verwendet.
- Wenn eine asymmetrische Verteilung für eine leichtere Interpretation und Analyse in eine symmetrische umgewandelt werden soll. Einige Modellierungsmethoden erfordern normalverteilte Variablen. Wenn wir es also mit einer uneinheitlichen Verteilung zu tun haben, können wir die Transformationen verwenden, um die Schiefe verringern. Für eine rechtsschiefe Verteilung nehmen wir eine Quadrat- oder Kubikwurzel oder den Logarithmus einer Variablen, während eine linksschiefe Verteilung durch Quadrierung/Kubatur oder eine Exponentialfunktion angeglichen wird.
- Wenn eine kontinuierliche Variable in eine diskrete umgewandelt werden soll. Die Methode einer solchen Transformation nennt man Diskretisierung.
Was sind die allgemeinen Methoden der Transformation?
Es gibt verschiedene Methoden Variablen zu transformieren. Einige davon haben wir bereits erwähnt: Quadrat- und Kubikwurzel, Logarithmen, trigonometrische Funktionen und Segmentierung. Lassen Sie uns einige Methoden im Detail betrachten und ihre Vor- und Nachteile aufzeigen.
- Der Logarithmus. Dies ist eine allgemeine Transformationsmethode, um die Form der Verteilung einer Variablen zu ändern. Sie wird in der Regel verwendet, um eine Rechtsschiefe zu verringern. Diese Funktion ist nicht anwendbar auf Null und auf negative Werte.
- Quadrat-/Kubikwurzel. Diese Funktionen haben einen signifikanten Einfluss auf die Verteilung der Variablen, wenn auch nicht so stark wie der Logarithmus. Der Vorteil der Kubikwurzel ist, dass sie für Werte kleiner gleich Null verwendet werden kann. Die Quadratwurzel akzeptiert nur Werte größer gleich Null.
- Diskretisieren/Klassifizieren. Diese wird für ein Kategorisierung der Werte verwendet. Die Diskretisierung eignet sich für Originaldaten, Prozentsätze und Frequenzen. Die Auswahl der Kategorisierungsmethode richtet sich nach der Art der Daten. Wir können eine gemeinsame Segmentierung von voneinander abhängigen Variablen durchführen.
Jede Transformation von Daten führt zu einer Änderung der Verteilung. Um dies zu veranschaulichen, verwenden wir beispielsweise zwei Transformationsmethoden.
Zwei Probleme unseres anfänglichen Datensatzes sind Ausreißer und eine Rechtsschiefe. Wir haben bereits überlegt, wie wir Ausreißer entfernen können. Lassen Sie uns nun zunächst versuchen, die Asymmetrie zu entfernen/reduzieren und dann die Ausreißer zu eliminieren.
Methode 1.
Um die starke Rechtsschiefe der X-Daten zu beseitigen, nehmen wir den Logarithmus zur Basis 2 und entfernen dann die Ausreißer. Da die Werte der Variablen der Anfangsdaten viel kleiner als 1 sind und es negative Werte gibt, nehmen wir den Logarithmus der Variablen, zu denen jeweils 1 addiert wird, um Genauigkeit zu erhöhen. Schauen wir, was mit der Kurve passiert.
evalq({x.ln <- apply(x, 2, function(x) log2(x + 1))
sk.ln <- skewness(x.ln)},
env)
> env$sk.ln
ftlm stlm rbci pcci v.fatl
Skewness -0.2715663 -2.660613 -4.484301 0.4267873 1.253008
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 1.83489 2.065224 -0.0343451 -15.62414 0.01529019
v.pcci
Skewness 0.1811206
Drei Variablen — stlm, rbci and v.ftlm zeigen eine Linksschiefe. Die Variablen v.fatl, v.satl and v.rftl sind aber immer noch rechtsschief. Die Schiefe der anderen Variablen hat sich ausgeglichen. Lassen Sie uns die Ausreißer aus diesem Daten entfernen und begrenzen und dann betrachten wir die Schiefe und Verteilung der Variablen:
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
remove_outliers(x.ln[ ,i])
} -> x.ln.out
colnames(x.ln.out) <- colnames(x.ln)
},
env)
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
capping_outliers(x.ln[ ,i])
} -> x.ln.cap
colnames(x.ln.cap) <- colnames(x.ln)
},
env)
evalq({
sk.ln.out <- skewness(x.ln.out)
sk.ln.cap <- skewness(x.ln.cap)
},
env)
> env$sk.ln.out
ftlm stlm rbci pcci
Skewness -0.119055 -0.3549119 -0.1099921 -0.01476384
v.fatl v.satl v.rftl v.rstl
Skewness -0.02896319 -0.03634833 -0.06259749 -0.2120127
v.ftlm v.stlm v.pcci
Skewness -0.05819699 -0.01661317 -0.05420077
> env$sk.ln.cap
ftlm stlm rbci pcci
Skewness -0.1814781 -0.4582045 -0.1658855 -0.02849945
v.fatl v.satl v.rftl v.rstl
Skewness -0.04336238 -0.04400781 -0.0692754 -0.2269408
v.ftlm v.stlm v.pcci
Skewness -0.06184128 -0.02856397 -0.06258243
Die Daten in beiden Gruppen (x.out und x.cap) sind fast symmetrisch. Die Verteilung ist in den folgenden Diagrammen dargestellt.
par(mfrow = c(2,2)) boxplot(env$x.ln, main = "x.ln with outliers", xlab = "") boxplot(env$x.ln.out, main = "x.ln.out without outliers", xlab = "") boxplot(env$x.ln.cap, main = "x.ln.cap with imputed outliers", xlab = "") par(mfrow = c(1,1))
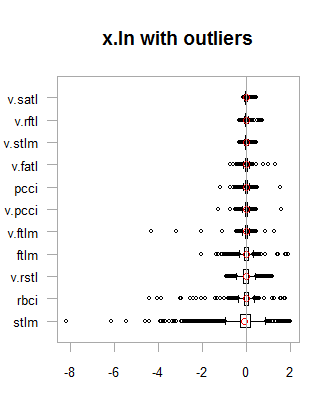

Abb. 1. Log-transformierte Daten mit und ohne Ausreißer
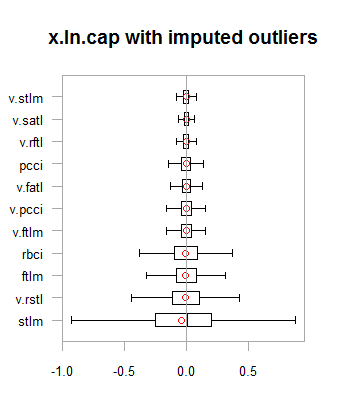
Abb. 2. Log-transformierte Daten mit begrenzten Ausreißern
Die Ergebnisse sind mit einer Ausnahme der vorherigen Transformation sehr ähnlich. Das Ausmaß der Veränderung der Variablen ist größer geworden.
Transformieren wir nun die Daten von x.ln.cap und sehen uns deren Variation und Kovariation an:
evalq(x.ln.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetLnCap, env)
Zeichnen des Diagramms:
require(GGally) evalq(ggpairs(dataSetLnCap, columns = 2:7, mapping = aes(color = Class), title = "PredLnCap1"), env) evalq(ggpairs(dataSetLnCap, columns = 8:13, mapping = aes(color = Class), title = "PredLnCap2"), env)
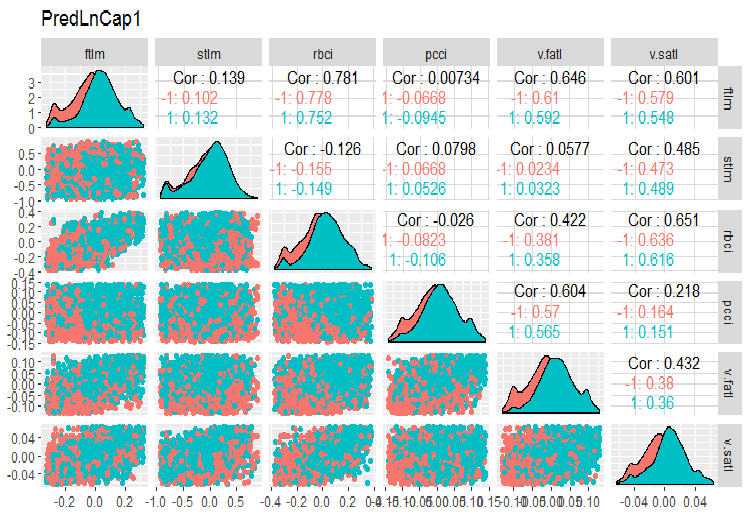
Abb. 3. Parameter von logarithmisch transformierten Daten, Teil 1
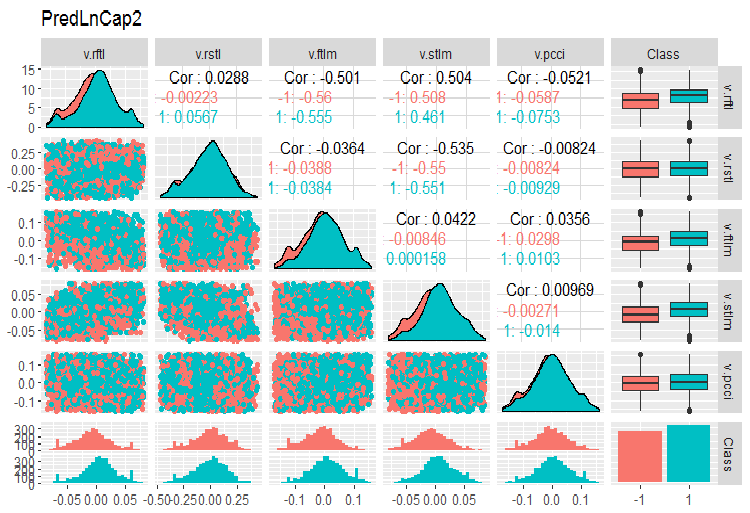
Abb. 4. Parameter von logarithmisch transformierten Daten, Teil 2
Methode 2.
Die Daten werden mit der Funktion sin(2*pi*x) transformiert, die Ausreißer entfernt und begrenzt, und anschließend kann die Schiefe, die Verteilung der Ausreißer und Kovariation transformierter Variablen in Diagrammen bewertet werden.
evalq({x.sin <- apply(x, 2, function(x) sin(2*pi*x))
sk.sin <- skewness(x.sin)
},
env)
#----------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
remove_outliers(x.sin[ ,i])
} -> x.sin.out
colnames(x.sin.out) <- colnames(x.sin)
},
env)
#-----------------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
capping_outliers(x.sin[ ,i])
} -> x.sin.cap
colnames(x.sin.cap) <- colnames(x.sin)
},
env)
#-----------
evalq({
sk.sin.out <- skewness(x.sin.out)
sk.sin.cap <- skewness(x.sin.cap)
},
env)
Wie ist jetzt die Schiefe dieser transformierten Daten?
env$sk.sin ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.0009679463 v.fatl v.satl v.rftl v.rstl Skewness 0.03280465 0.5217757 0.05611136 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.04923953 -0.2123434 0.01738377 > env$sk.sin.out ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03532892 v.fatl v.satl v.rftl v.rstl Skewness 0.00360966 -0.02380975 -0.05336561 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.0009366441 0.01835948 0.0008843329 > env$sk.sin.cap ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03283132 v.fatl v.satl v.rftl v.rstl Skewness 0.007588308 -0.02424707 -0.04106469 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.007003051 0.009237835 0.002101687
Wie Sie sehen können, sind durch diese Transformation alle Daten symmetrisch. Mal sehen, wie sie jetzt aussehen:
par(mfrow = c(2, 2)) boxplot(env$x.sin, main = "x.sin with outlier") abline(h = 0, col = 2) boxplot(env$x.sin.out, main = "x.sin.out without outlier") abline(h = 0, col = 2) boxplot(env$x.sin.cap, main = "x.sin.cap with capping outlier") abline(h = 0, col = 2) par(mfrow = c(1, 1))
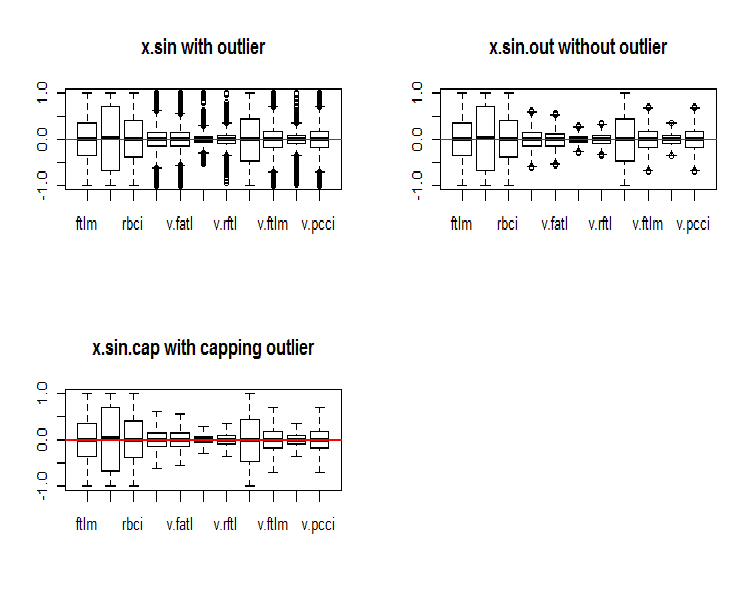
Abb. 5. Daten, die durch die Funktion sin() transformiert wurden
Auf den ersten Blick sehen diese Daten besser aus als die vorherigen (die ursprünglichen und transformierten).
Jetzt wollen wir die Verteilung von NA (ohne Wert) in Variablen sehen, nachdem die Ausreißer entfernt wurden.
require(VIM)
evalq(a <- aggr(x.sin.out), env)
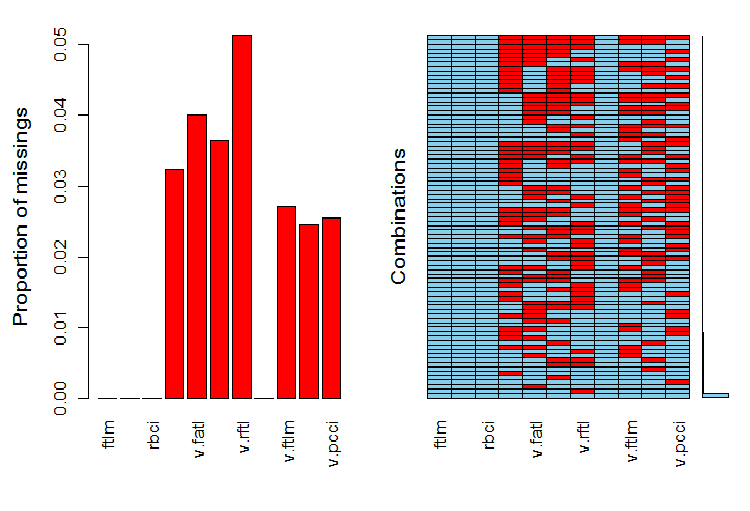
Abb. 6. Verteilung von NA in den Daten
Der linke Teil des Diagramms zeigt die relative Anzahl undefinierter Daten in jeder Variablen. Die rechte Seite zeigt die Kombinationen von Beispielen mit einer unterschiedlichen Anzahl von NA (von unten nach oben steigend). Wir sehen die Werte:
> print(env$a) Missings in variables: Variable Count pcci 256 v.fatl 317 v.satl 289 v.rftl 406 v.ftlm 215 v.stlm 194 v.pcci 201
Was ist die Verteilung der NA in den Variablen?
par(mfrow = c(3, 4)) evalq( foreach(i = 1:ncol(x.sin.out)) %do% { barMiss(x.sin.out, pos = i, only.miss = TRUE, main = "x.sin.out without outlier") }, env ) par(mfrow = c(1, 1))
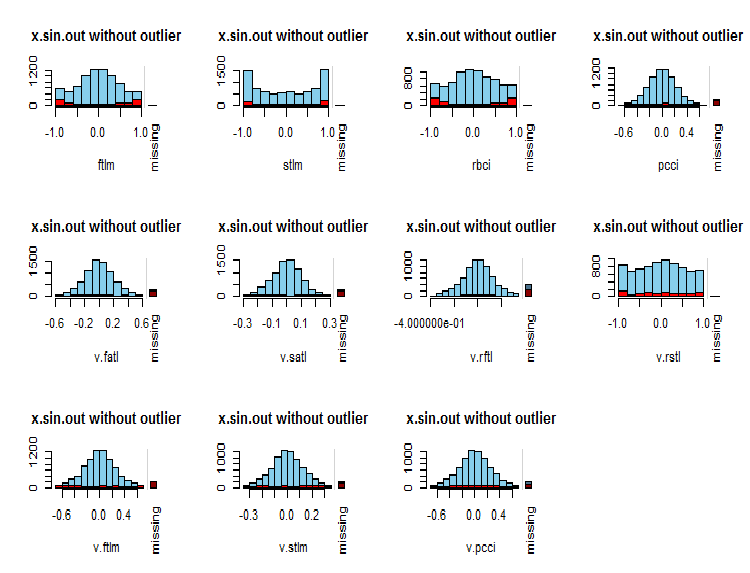
Abb. 7. Verteilung der NA in den Variablen
Beobachtete Werte der Variablen werden blau und die Anzahl der NA anderer Variablen in verschiedenen Bereichen der Werte der aktuellen Variablen rot dargestellt. Der Balken auf der rechten Seite stellt den Beitrag der aktuellen Variable zur Gesamtzahl der NA aller Variablen dar.
Abschließend noch ein Blick auf die Variation und Kovariation der transformierten Daten mit begrenzten Ausreißern.
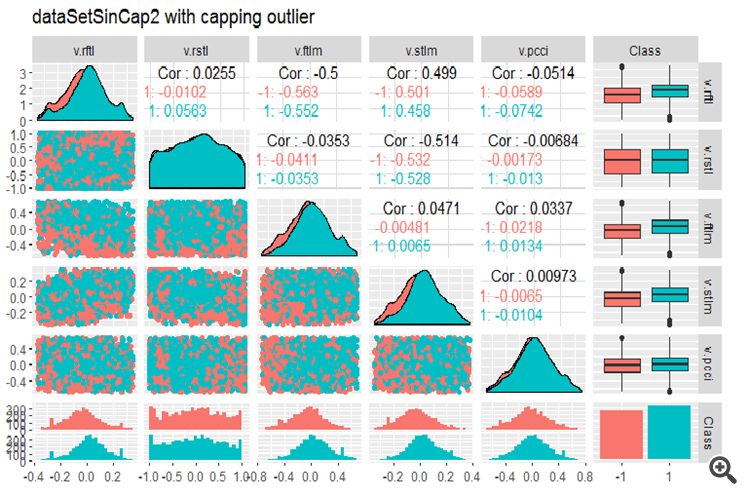
#--------------- evalq(x.sin.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetSinCap, env) require(GGally) evalq(ggpairs(dataSetSinCap, columns = 2:7, mapping = aes(color = Class), title = "dataSetSinCap1 with capping outlier "), env) evalq(ggpairs(dataSetSinCap, columns = 8:13, mapping = aes(color = Class), title = "dataSetSinCap2 with capping outlier"), env) #---------------------------
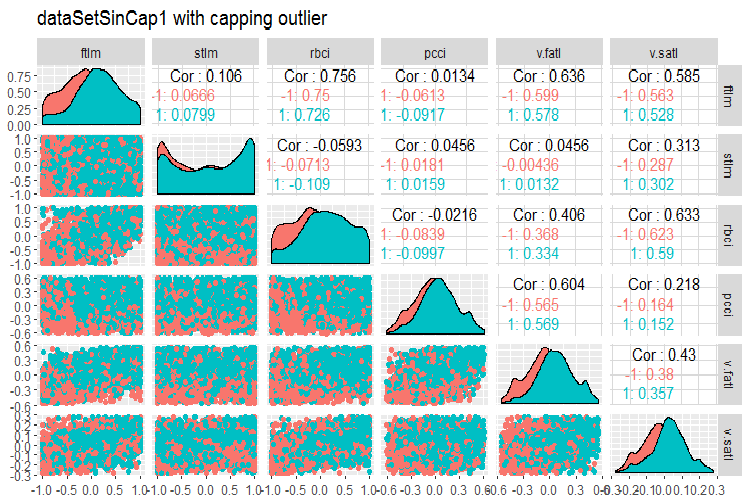
Abb. 8. Parameter von sin()-transformierte Daten, Teil 1
Abb. 9. Parameter von sin()-transformierte Daten, Teil 2
1.1.2. Normalisierung
Wir bereiten die Daten für ein neuronales Netz vor, daher müssen Variablen im Bereich von { -1... +1 } gebracht werden. Dazu wird die Funktion preProcess()::caret mit der Methode = "spatialSign" verwendet. Alternativ können die Daten vor der Normalisierung zentriert oder skaliert werden. Dies ist ein sehr einfacher Prozess, den wir in diesem Artikel nicht beschreiben werden.
Eines sollte man aber nicht vergessen. Die aus dem Trainingsdaten gewonnenen Normalisierungsparameter sind für die Test- und Validierungsdaten zu verwenden.
Zur weiteren Verwendung der Daten aus den früheren Berechnungen (dataSet, ohne hochkorrelierte Werte zu entfernen), teilen wir sie auf in train/test/val (Training/Test/Werte) und bringen sie ohne Standardisierung in den Bereich (-1, +1).
Bei der Normalisierung mit Standardisierung ist zu beachten, dass bei der Definition der Normierungsparameter (mean/median, sd/mad) auch die Parameter der begrenzten Ausreißer zu definieren sind. Später werden sie für train/val/test verwendet werden. Weiter oben in diesem Artikel beschrieben wir zwei Funktionen: prep.outlier() und treatOutlier(). Sie wurden für diesen Zweck erstellt.
Reihenfolge der Vorgehens:
- Definieren der Parameter der Ausreißer train
- Entfernen der Ausreißer in train
- Definieren der Parameter für die Standardisierung in train
- Begrenzen der Ausreißer in train/val/test
- Normalisieren von train/val/test.
Diese Variante werden wir hier nicht betrachten. Sie können sie selbst studieren.
Aufteilen der Daten in train/val/test:
evalq(
{
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(clean = data.frame(dataSet) %>% na.omit(),
train = clean[train, ],
val = clean[val, ],
test = clean[test, ]) -> DT
}, env)
Definieren der Parameter der Normalisierung für den Datensatz train und Normalisieren der Ausreißer in train/test/val:
require(foreach)
evalq(
{
preProcess(DT$train, method = "spatialSign") -> preproc
list(train = predict(preproc, DT$train),
val = predict(preproc, DT$val),
test = predict(preproc, DT$test)
) -> DTn
},
env)
Werfen wir einen Blick auf die Gesamtstatistik des Datensatze train:
> table.Stats(env$DTn$train %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5909 -0.7624 -0.6114 -0.8086 Quartile 1 -0.2054 -0.2157 -0.2203 -0.2110 Median 0.0145 0.0246 0.0147 0.0068 Arithmetic Mean 0.0070 0.0190 0.0085 0.0028 Geometric Mean -0.0316 -0.0396 -0.0332 -0.0438 Quartile 3 0.2139 0.2462 0.2341 0.2277 Maximum 0.6314 0.8047 0.7573 0.7539 SE Mean 0.0060 0.0073 0.0063 0.0065 LCL Mean (0.95) -0.0047 0.0047 -0.0037 -0.0100 UCL Mean (0.95) 0.0188 0.0333 0.0208 0.0155 Variance 0.0719 0.1058 0.0784 0.0848 Stdev 0.2682 0.3252 0.2800 0.2912 Skewness -0.0762 -0.0221 -0.0169 -0.0272 Kurtosis -0.8759 -0.6688 -0.8782 -0.7090 v.fatl v.satl v.rftl v.rstl Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5160 -0.5943 -0.6037 -0.7591 Quartile 1 -0.2134 -0.2195 -0.1988 -0.2321 Median 0.0015 0.0301 0.0230 0.0277 Arithmetic Mean 0.0032 0.0151 0.0118 0.0177 Geometric Mean -0.0323 -0.0267 -0.0289 -0.0429 Quartile 3 0.2210 0.2467 0.2233 0.2657 Maximum 0.5093 0.5893 0.6714 0.7346 SE Mean 0.0058 0.0063 0.0062 0.0074 LCL Mean (0.95) -0.0082 0.0028 -0.0003 0.0033 UCL Mean (0.95) 0.0146 0.0274 0.0238 0.0321 Variance 0.0675 0.0783 0.0757 0.1083 Stdev 0.2599 0.2798 0.2751 0.3291 Skewness -0.0119 -0.0956 -0.0648 -0.0562 Kurtosis -1.0788 -1.0359 -0.7957 -0.7275 v.ftlm v.stlm v.rbci v.pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5627 -0.6279 -0.5925 -0.7860 Quartile 1 -0.2215 -0.2363 -0.2245 -0.2256 Median -0.0018 0.0092 -0.0015 -0.0054 Arithmetic Mean -0.0037 0.0036 -0.0037 0.0013 Geometric Mean -0.0426 -0.0411 -0.0433 -0.0537 Quartile 3 0.2165 0.2372 0.2180 0.2276 Maximum 0.5577 0.6322 0.5740 0.9051 SE Mean 0.0061 0.0065 0.0061 0.0070 LCL Mean (0.95) -0.0155 -0.0091 -0.0157 -0.0124 UCL Mean (0.95) 0.0082 0.0163 0.0082 0.0150 Variance 0.0732 0.0836 0.0742 0.0975 Stdev 0.2706 0.2892 0.2724 0.3123 Skewness 0.0106 -0.0004 -0.0014 0.0232 Kurtosis -1.0040 -1.0083 -1.0043 -0.4159
Diese Tabelle zeigt uns, dass die Variablen symmetrisch sind und sehr ähnliche Parameter haben.
Werfen wir nun einen Blick auf die Verteilung der Variablen in den Datensätzen train/val/test:
boxplot(env$DTn$train %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Train") abline(v = 0, col = 2) boxplot(env$DTn$test %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Test") abline(v = 0, col = 2) boxplot(env$DTn$val %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Val") abline(v = 0, col = 2)
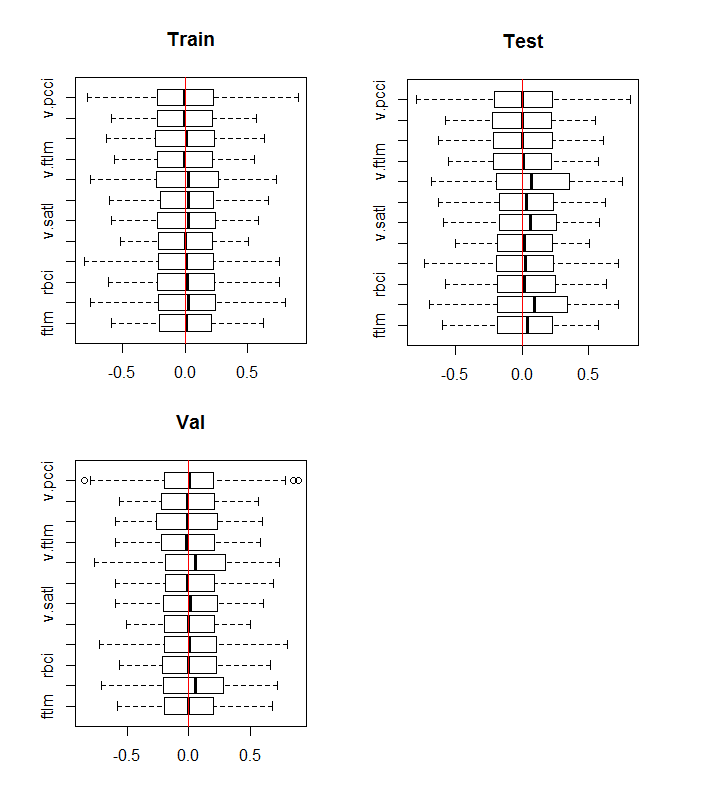
Abb. 10. Verteilung der Variablen im train/val/test nach der Normalisierung
Fast die gleiche Verteilung in allen Datensätzen. Wir müssen aber auch Korrelation und Kovariation der Variablen in train berücksichtigen:
require(GGally) evalq(ggpairs(DTn$train, columns = 2:7, mapping = aes(color = Class), title = "DTn$train1 "), env) evalq(ggpairs(DTn$train, columns = 8:14, mapping = aes(color = Class), title = "DTn$train2"), env)
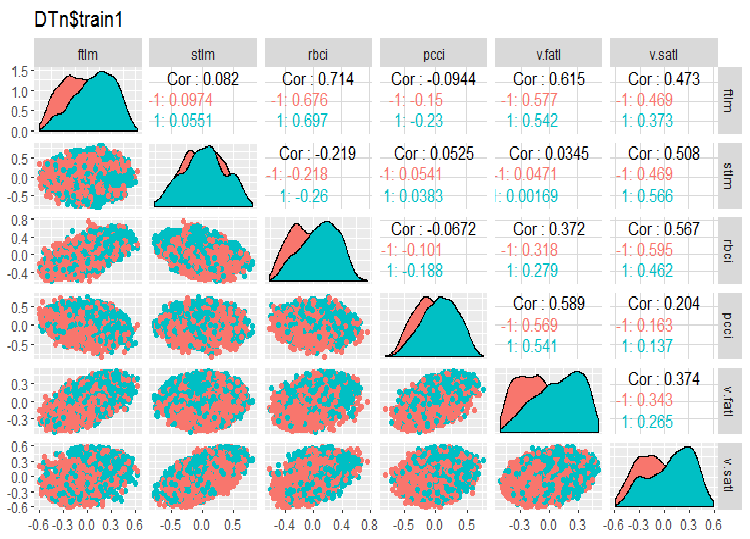
Abb. 11. Variation und Kovariation des Datensatzes 1 von train
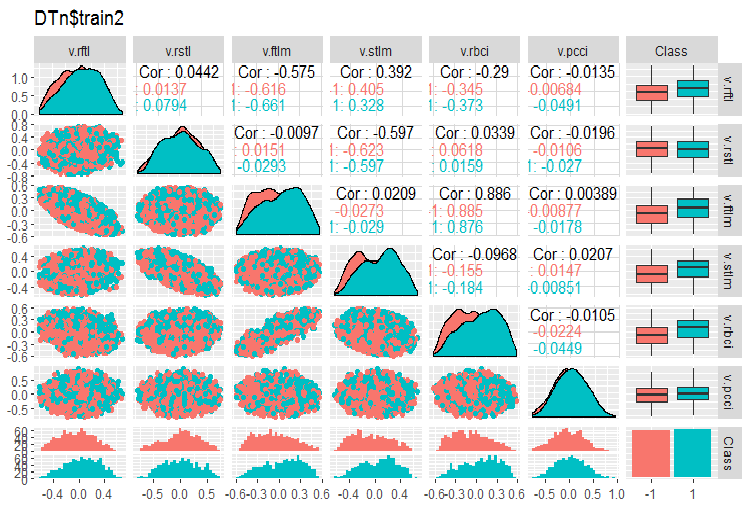
Abb. 12. Variation und Kovariation des Datensatzes 2 von train
Es gibt keine hochgradig korrelierten Daten, die Verteilung ist gepackt und hat keine Ausreißer. Die Daten sind gut unterteilbar. Auf den ersten Blick gibt es nur zwei problematische Variablen - stlm und v.rstl. Wir werden diese Frage später überprüfen, wenn wir die Relevanz der Prädiktoren (= Variablen zur Wertevorhersage anderen Variablen) beurteilen. Jetzt können wir uns die Korrelation dieser Prädiktoren und der Zielvariablen ansehen:
> funModeling::correlation_table(env$DTn$train %>% tbl_df %>% + select(-Data), str_target = 'Class') Variable Class 1 Class 1.00 2 v.fatl 0.38 3 ftlm 0.34 4 rbci 0.28 5 v.rbci 0.28 6 v.satl 0.27 7 pcci 0.24 8 v.ftlm 0.22 9 v.stlm 0.22 10 v.rftl 0.18 11 v.pcci 0.08 12 stlm 0.03 13 v.rstl -0.01Die genannten Variablen befinden sich am Ende der Tabelle und haben sehr kleine Korrelationskoeffizienten. Die Relevanz der Variablen v.pcci Variable muss ebenfalls verifiziert werden. Überprüfen wir die Variable v. fatl aus dem Datensatz train/val/test:
require(ggvis) evalq( DTn$train %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$train$v.fatl"), env) evalq( DTn$val %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$val$v.fatl"), env) evalq( DTn$test %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$test$v.fatl"), env)
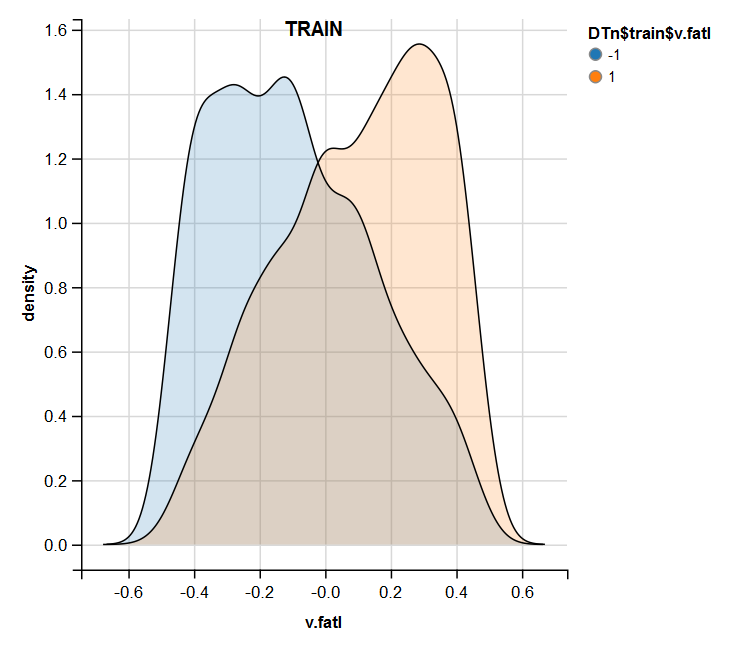
Abb. 13. Verteilung der Variablen v.fatl im Datensatz train nach der Normalisierung
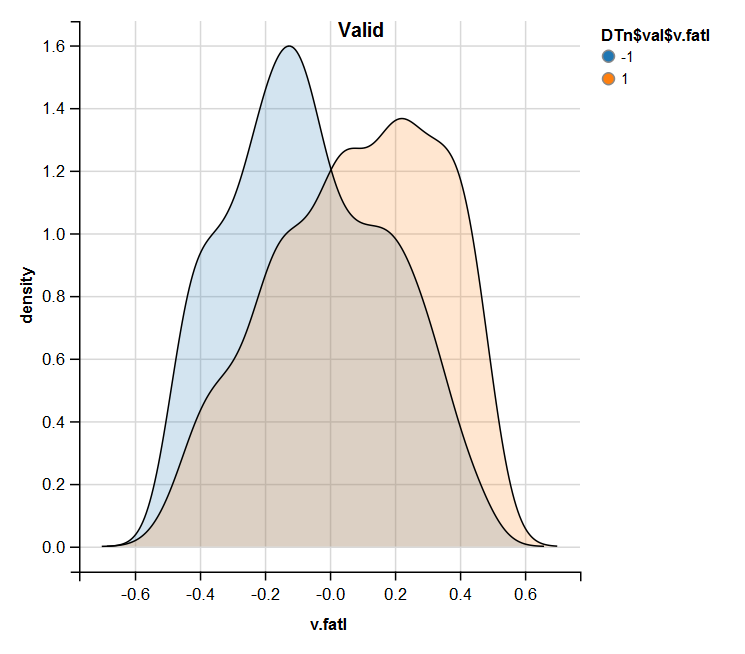
Abb. 14. Die Verteilung der Variablen v.fatl im gültigen Datensatz nach der Normalisierung
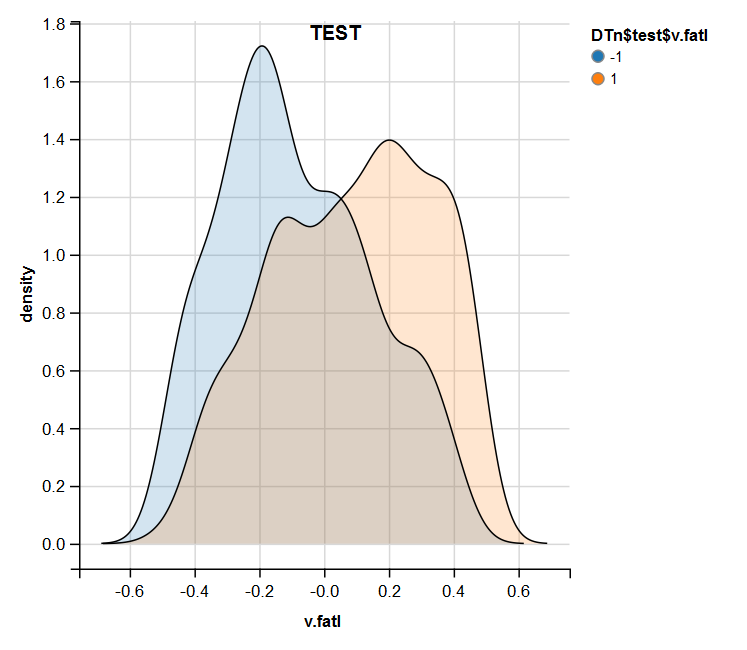
Abb. 15. Verteilung der Variablen v.fatl im Datensatz test nach der Normalisierung
Die durchgeführte Analyse zeigt, dass die Normalisierung oft eine gute Verteilung der Prädiktoren ohne Ausreißer und hochkorrelierten Daten liefert. Im Großen und Ganzen hängt dies vom Charakter der Rohdaten ab.
1.1.3. Diskretisierung
Unter Diskretisierung versteht man den Prozess der Umwandlung einer kontinuierlichen in eine diskrete Variable, indem man ihre Werte in Teilbereiche unterteilt. Die Grenzen dieser Teilbereiche können mit verschiedenen Methoden bestimmt werden.
Die Methoden zur Teilung lassen sich in zwei Gruppen einteilen: quantitative Methoden, die nicht die Beziehung zur Zielvariablen beinhalten und Methoden, die den Bereich der Zielvariablen berücksichtigen.
Die erste Gruppe der Methoden wird durch die Funktion cut2()::Hmisc fast vollständig abgedeckt. Die Stichprobe kann in eine voreingestellte Anzahl von Teilbereichen mit festgelegten Grenzen, in Quartile, in Teilbereiche mit einer minimalen oder einer gleichen Anzahl von Beispielen aufgeteilt werden.
Die zweite Gruppe der Methoden ist interessanter, weil sie die Variable in Teilbereiche unterteilt, die mit den Niveaus der Zielvariablen verbunden sind. Betrachten wir einige Programme zur Realisierung dieser Methoden.
Diskretisierung. Dieses Programmpaket ist ein Satz von Algorithmen der Diskretisierung mit einem Trainer. Diese kann auch mit den Begriffen "von oben nach unten" und "von unten nach oben" kategorisiert werden, die die Diskretisierungsalgorithmen umsetzen. Betrachten wir einige davon am Beispiel unseres dataSet.
Zuerst bereinigen wir den Datensatz (ohne hoch korrelierte Variablen zu entfernen) und teilen es dann in die Datensätze train/val/test im Verhältnis 2000/1000/1000 auf.
require(discretization)
require(caret)
require(pipeR)
evalq(
{
dataSet %>%
preProcess(.,
method = c("zv", "nzv", "conditionalX")) %>%
predict(., dataSet) %>%
na.omit -> dataSetClean
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(train = dataSetClean[train, ],
val = dataSetClean[val, ],
test = dataSetClean[test, ]) -> DT
},
env)
Wir verwenden die Funktion mdlp()::discretization, die eine Diskretisierung mit minimaler Beschreibungslänge durchführt. Diese Funktion diskretisiert kontinuierliche Attribute der Matrix durch das Entropiekriterium mit der minimalen Beschreibungslänge als Stoppregel.
evalq(
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()}) -> mdlp.train, envir = env)
Die Funktion gibt zwei Listen zurück. Sie sind: cutp - ein Datenrahmen mit Trennungspunkten für jede Variable und Disc.data - ein Datenrahmen mit markierten Variablen.
> env$mdlp.train%>%str() List of 2 $ cutp :List of 12 ..$ : num [1:2] -0.0534 0.0278 ..$ : chr "All" ..$ : num -0.0166 ..$ : num [1:2] -0.0205 0.0493 ..$ : num [1:3] -0.0519 -0.0055 0.019 ..$ : num 0.000865 ..$ : num -0.00909 ..$ : chr "All" ..$ : num 0.0176 ..$ : num [1:2] -0.011 0.0257 ..$ : num [1:3] -0.03612 0.00385 0.03988 ..$ : chr "All" $ Disc.data:'data.frame': 2000 obs. of 13 variables: ..$ ftlm : int [1:2000] 3 3 3 3 3 2 1 1 1 1 ... ..$ stlm : int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ rbci : int [1:2000] 2 2 2 2 2 2 1 1 1 1 ... ..$ pcci : int [1:2000] 2 2 1 2 2 1 1 2 3 2 ... ..$ v.fatl: int [1:2000] 4 4 3 4 3 1 1 2 3 2 ... ..$ v.satl: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rftl: int [1:2000] 1 2 2 2 2 2 2 2 1 1 ... ..$ v.rstl: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ v.ftlm: int [1:2000] 2 2 1 1 1 1 1 1 2 1 ... ..$ v.stlm: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rbci: int [1:2000] 4 4 3 3 2 1 1 2 3 2 ... ..$ v.pcci: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ...
Was zeigt uns die erste Liste?
Wir haben drei unmarkierte Variablen mit Werten, die nicht mit der Zielvariablen verbunden sind. Es sind dies 2, 8 und 12 (stlm, v.rstl, v.pcci). Sie können ohne Verlust an der Qualität der Daten entfernt werden. Bitte beachten Sie, dass diese Variablen im vorherigen Teil des Artikels als irrelevant definiert wurden.
Vier Variablen werden in zwei Klassen, drei Variablen in drei Klassen und zwei Variablen in vier Klassen unterteilt.
Zerlegen Sie die Datensätze val/test anhand der Trennungspunkte aus dem Datensatz train. Entfernen Sie dazu die nicht markierten Variablen aus train und speichern Sie sie im Datenrahmen train.d. Benutzen Sie dann die Funktion findInterval(), um die Datensätze test/val mit den zuvor erhaltenen Trennpunkten zu markieren.
evalq(
{
mdlp.train$cutp %>%
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> train.d
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> test.d
colnames(test.d) <- colnames(train.d)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> val.d
colnames(val.d) <- colnames(train.d)
},env
)
Wie sehen diese Datensätze aus?
> env$train.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 3 2 2 4 1 1 2 1 4 1 2 3 2 2 4 1 2 2 1 4 1 3 3 2 1 3 1 2 1 1 3 1 4 3 2 2 4 2 2 1 2 3 1 5 3 2 2 3 2 2 1 2 2 1 6 2 2 1 1 1 2 1 1 1 -1 > env$test.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 1 1 1 2 1 1 1 1 2 -1 2 1 1 3 3 1 1 2 2 3 -1 3 1 1 2 2 1 1 1 2 2 -1 4 2 1 2 3 1 1 2 2 3 1 5 2 2 2 3 1 1 1 2 3 1 6 2 2 2 4 1 1 2 2 3 1 > env$val.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 2 2 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 1 2 2 1 3 2 2 2 3 2 2 1 2 2 1 4 2 2 2 4 2 2 2 2 3 1 5 2 2 2 3 2 2 1 2 2 1 6 2 2 2 3 2 2 2 2 2 1 > env$train.d$v.fatl %>% table() . 1 2 3 4 211 693 519 577 > env$test.d$v.fatl %>% table() . 1 2 3 4 49 376 313 262 > env$val.d$v.fatl %>% table() . 1 2 3 4 68 379 295 258
Die weitere Verwendung der Datensätze mit diskreten Daten ist modellabhängig. Wenn es sich um ein neuronales Netz handelt, müssen die Prädiktoren in Dummy-Variablen umgewandelt werden. Wie gut sind diese Klassen durch diese Variablen getrennt? Wie gut korrelieren sie mit der Zielvariablen? Stellen wir diese Beziehungen mit der Funktion cross-plot()::funModeling dar. Cross_plot zeigt, wie die Eingangsvariable mit der Zielvariablen korreliert, die den Wahrscheinlichkeitskoeffizienten für jeden Teilbereich jeder Eingang empfängt.
Betrachten wir drei Variablen v.fatl, ftlm und v.satl, aufgeteilt in 4,3 und 2 Teilbereiche. Charts: Zeichnen des Diagramms:
evalq(
cross_plot(data = train.d,
str_input = c("v.fatl", "ftlm", "v.satl"),
str_target = "Class",
auto_binning = F,
plot_type = "both"), #'quantity' 'percentual'
env
)
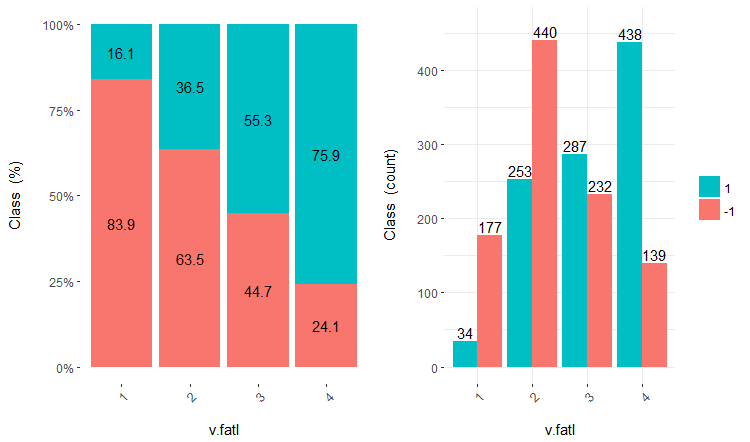
Abb. 16. Cross-plot der Variablen für v.fatl/Class
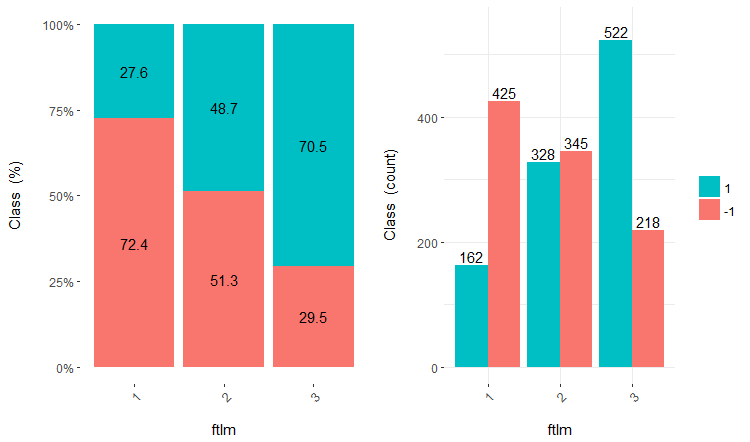
Abb. 17. Cross-plot der Variablen für ftlm/Class
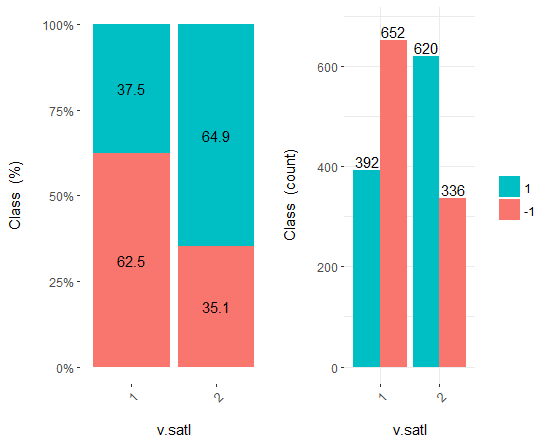
Abb. 18. Cross-plot der Variablen für v.satl/Class
Sie können sehen, die Prädiktoren korrelieren gut mit den Niveaus der Zielvariable, sie haben gut ausgeprägte Schwellenwerte, die die Niveaus der Zielvariablen trennen.
Prädiktoren können einfach in gleiche Teilbereiche aufgeteilt werden (nicht optimal), um zu sehen, in welchem Fall sie mit der Zielvariablen korrelieren. Lasst uns drei vorhergehende und zwei schlechte Variablen (stlm, v.rstl) aus dem Datensatz von train in 10 Teilbereiche mit gleicher Anzahl aufteilen und deren Kreuzdiagramm mit der Zielvariablen betrachten:
evalq(
cross_plot(
DT$train %>% select(-Data) %>%
select(c(v.satl, ftlm, v.fatl, stlm, v.rstl, Class)) %>%
as.data.frame(),
str_input = Cs(v.satl, ftlm, v.fatl, stlm, v.rstl),
str_target = "Class",
auto_binning = T,
plot_type = "both"), #'quantity' 'percentual'
env
)
Zeichnen von 5 Diagrammen dieser Variablen:
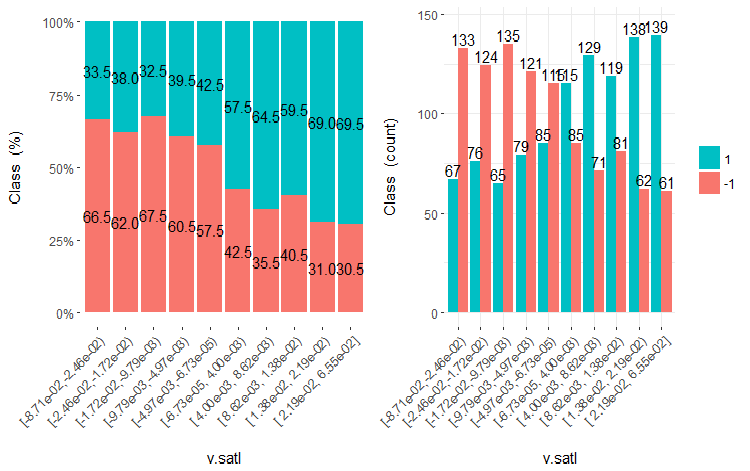
Abb. 19. Cross-plot der Variablen v.satl (10 Teilbereiche) versus Klasse
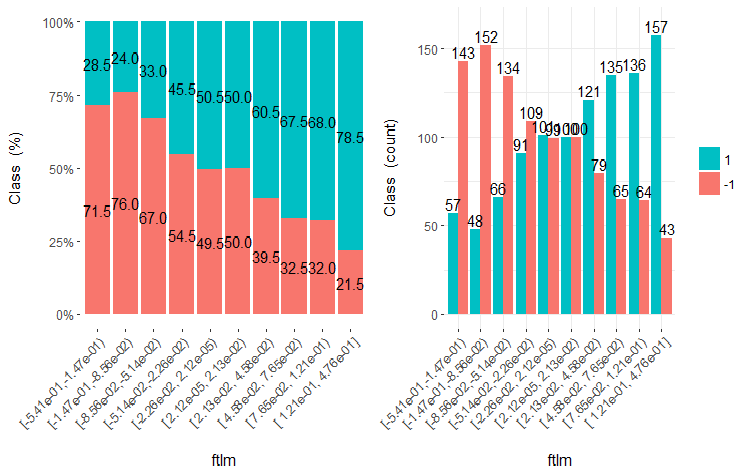
Abb. 20. Cross-plot der Variablen ftlml (10 Teilbereiche) versus Klasse
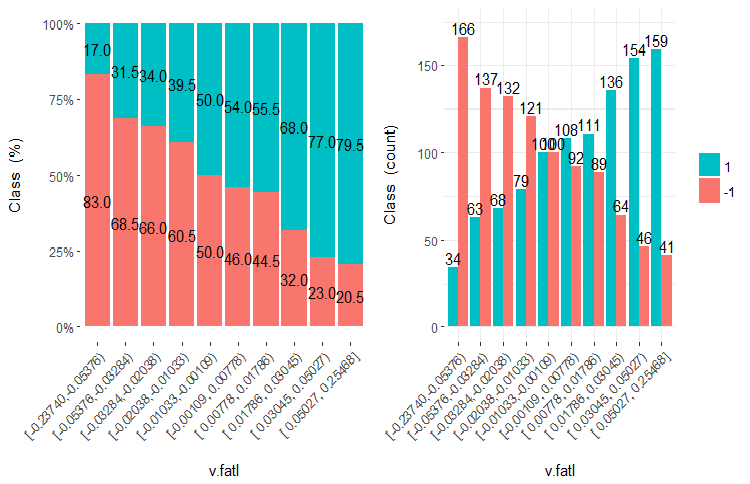
Abb. 21. Cross-plot der Variablen v.fatl (10 Teilbereiche) versus Klasse
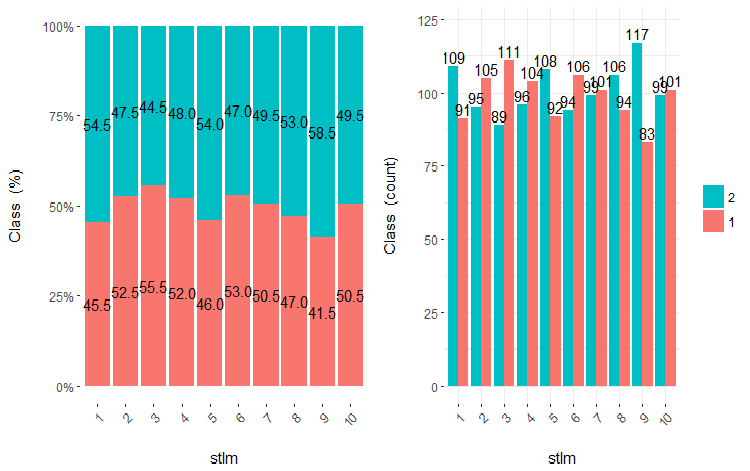
Abb. 22. Cross-plot der Variablen stlm (10 Teilbereiche) versus Klasse
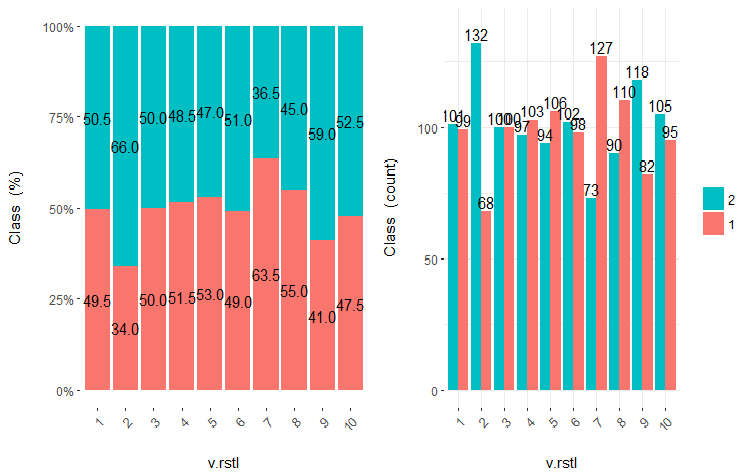
Abb. 23. Cross-plot der Variablen v.rstl (10 Teilbereiche) versus Klasse
Aus den Diagrammen wird deutlich, dass selbst wenn Variablen in 10 diskrete Teilbereiche mit gleicher Anzahl aufgeteilt wurden, haben die Variablen v.fatl, ftlm und v.satl eine gut ausgeprägte Schwelle von Teilungsstufen der Variablen. Es ist klar, warum die beiden anderen Variablen (stlm, v.rstl) irrelevant sind. Dies ist ein effizienter Weg, um die Bedeutung der Prädiktoren zu erkennen. Darauf werden wir später in diesem Artikel zurückkommen.
Nun wollen wir sehen, wie die Eingangsvariable mit der Zielvariablen korreliert, indem wir sie mit der Bayes'schen Methode der posterioren Konversionsrate vergleichen. Es ist sinnvoll, kategoriale Werte ohne eigene Ordnung zu vergleichen. Dazu verwenden wir die Funktion bayes_plot::funModeling. Nehmen wir die Variablen v.fatl, ftlm und v.satl aus den Datensätzen train.d, val.d und test.d.
#------BayesTrain------------------- evalq( { bayesian_plot(train.d, input = "v.fatl", target = "Class", title = "Bayesian comparison train$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "ftlm", target = "Class", title = "Bayesian comparison train$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "v.satl", target = "Class", title = "Bayesian comparison train$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------BayesTest------------------------ evalq( { bayesian_plot(test.d, input = "v.fatl", target = "Class", title = "Bayesian comparison test$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "ftlm", target = "Class", title = "Bayesian comparison test$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "v.satl", target = "Class", title = "Bayesian comparison test$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #-------------BayesVal--------------------------------- evalq( { bayesian_plot(val.d, input = "v.fatl", target = "Class", title = "Bayesian comparison val$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "ftlm", target = "Class", title = "Bayesian comparison val$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "v.satl", target = "Class", title = "Bayesian comparison val$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------------------------------------
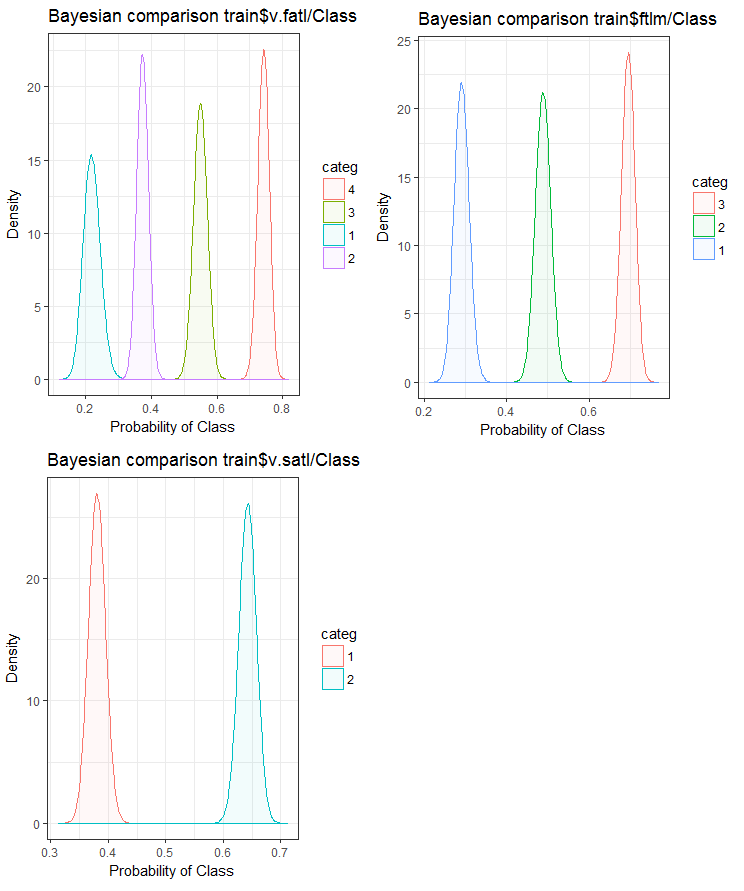
Abb. 24. Bayes'scher Vergleich von Variablen mit der Zielvariablen des Datensatzes train
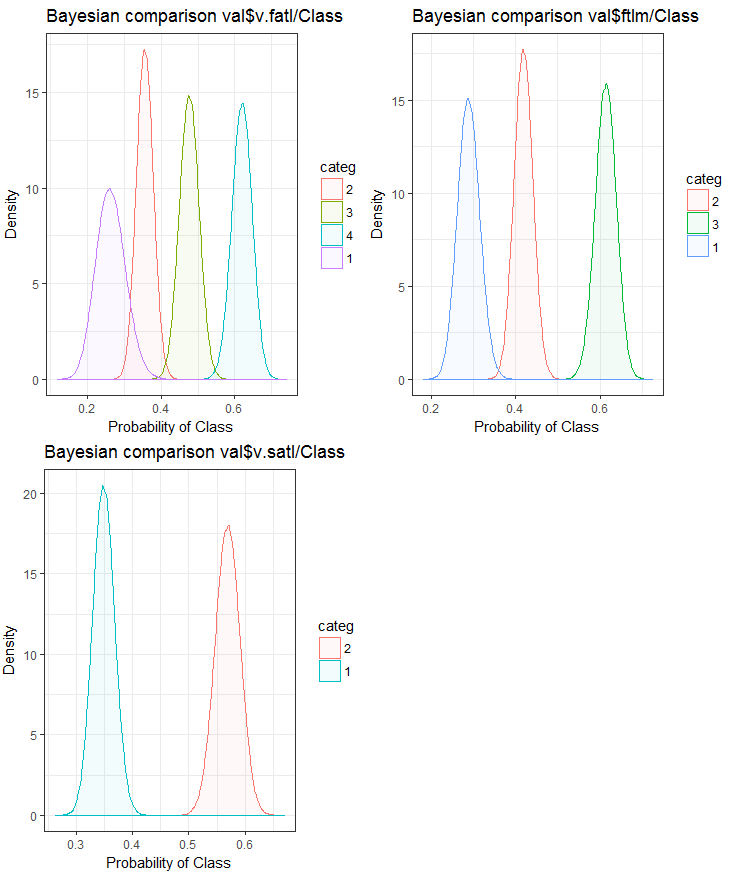
Abb. 25. Bayes'scher Vergleich von Variablen mit der Zielvariablen des Datensatzes val
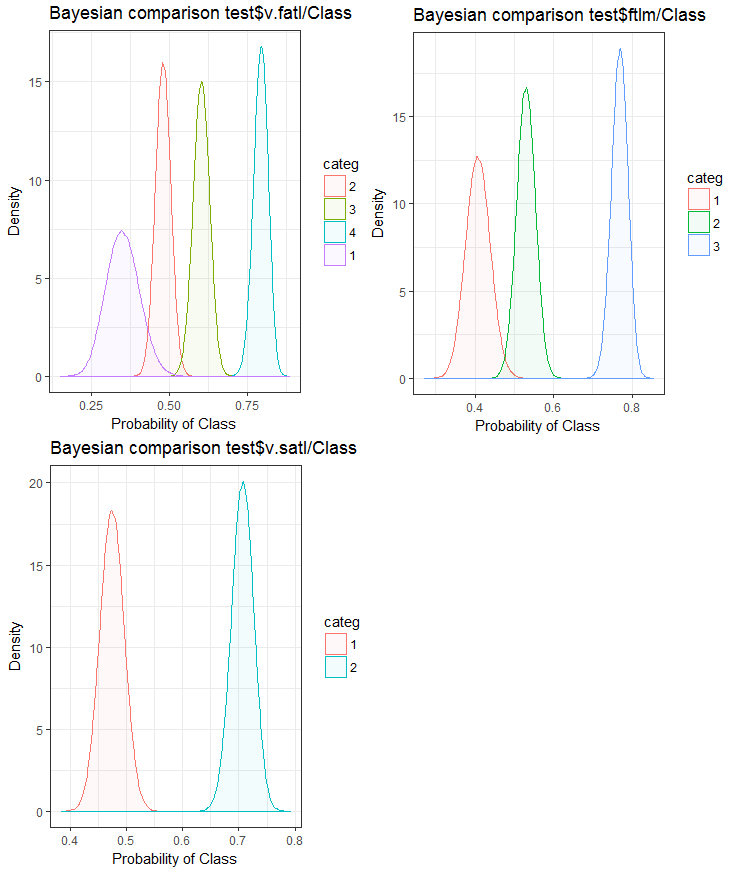
Abb. 26. Bayes'scher Vergleich von Variablen mit der Zielvariablen des Datensatzes test
Wir können sehen, dass die Korrelation der Prädiktoren mit der Zielvariable mehr in Richtung der Variable mit 4 und mehr Ebenen tendiert. Diese Tendenz ist bei den Variablen mit zwei Gruppen kleiner. Künftig wird es sinnvoll sein zu überprüfen, wie sich die Genauigkeit des Modells durch die Verwendung von Prädiktoren mit nur zwei Teilbereichen beeinflussen lässt.
Die gleiche Aufgabe, eine Variable in Teilbereiche zu unterteilen, die eng mit den Ebenen der Zielvariablen übereinstimmen, kann auf eine andere Weise gelöst werden - mit dem Programmpaket smbinning. Das können Sie selbst überprüfen. Der vorhergehende Artikel beschreibt eine andere interessante Methode der Diskretisierung. Sie kann mit dem Programmpaket "RoughSets" implementiert werden.
Die Diskretisierung ist eine effiziente Methode der Transformation von Prädiktoren. Leider können nicht alle Modelle mit Faktorvorhersagen arbeiten.
1.2. Erstellen neuer Merkmale
Das Erstellen einer Variablen ist ein Vorgang, der einer neue Variablen aus den existierenden erstellt. Betrachten wir den Datensatz, in dem das Datum (tt-mm-jj) eine Eingangsvariable ist. Wir können neue Variablen erstellen, die besser mit der Zielvariabelen verbunden werden - Tag, Monate, Jahr, Wochentag. Dieser Schritt wird verwendet, um verborgene Beziehungen in der Variablen aufzudecken.
Das Erstellen von abgeleiteten Variablen bezieht sich auf den Prozess des Erstellen einer neuen Variablen mit Hilfe einer Reihe von Funktionen und verschiedener Methoden aus den bestehenden Variablen. Die Art der zu erstellenden Variablen hängt von der Neugier des Wirtschaftsanalysten, dessen verschiedenen Hypothesen und seinen theoretischen Kenntnissen ab. Die Methodenauswahl ist umfangreich. Die Funktionen wie der Logarithmus, die Segmentierung oder die n-te Potenz sind nur einige Beispiele für Transformationsmethoden.
Das Erstellen von Dummy-Variablen ist eine weitere, beliebte Methode, mit Variablen zu arbeiten. Üblicherweise werden Dummy-Variable bei der Umwandlung von kategorialen in numerische Variablen verwendet. Die kategoriale Variable kann Werte von 0 und 1 annehmen. Wir können Dummy-Variablen für mehr als zwei Klassen aus kategorialen Variablen mit N und N-1 Variablen erstellen.
In diesem Artikel besprechen wir Situationen, die uns als Analysten täglich begegnen. Nachfolgend sind mehrere Möglichkeiten aufgeführt, um das Maximum an Information aus einem Datensatz zu extrahieren.
- Verwenden Sie Datums- und Zeitwerte als Variablen. Neue Variablen können unter Berücksichtigung von Datums- und Zeitdifferenzen angelegt werden.
- Erstellen Sie neue Verhältnisse und Proportionen. Anstatt vergangene Ein- und Ausgänge im Datensatz zu speichern, können auch deren Verhältnisse einbezogen werden. Dies kann eine größere Bedeutung haben.
- Verwenden Sie Standardtransformationen. Betrachtet man die Schwankungen und Bereiche der Variablen zusammen mit der Ausgabe, so kann man sehen, ob sich die Korrelation nach grundlegenden Transformationen verbessert. Am häufigsten werden dabei logarithmische, exponentielle, quadratische und trigonometrische Variationen verwendet.
- Variablen auf Saisonalität prüfen und ein Modell für den gewünschten Zeitraum (Woche, Monat, Session etc.) erstellen.
Intuitiv ist einem klar, dass das Verhalten des Marktes am Montag anders ist als am Mittwoch und Donnerstag. Der Wochentag ist also ein wichtiges Merkmal. Ebenso wichtig für den Markt ist die Tageszeit. Sie zeigt an, ob es sich um asiatische, europäische oder amerikanische Handelszeiten handelt. Wie können wir diese Merkmale definieren?
Wir werden dafür das Programmpaket timekit verwenden. tk_augment_timeseries_signature() ist die zentrale Funktion des Pakets. Sie ergänzt eine Reihe von Zeitbezeichnungen den Daten des Anfangsdatensatzes pr, die sowohl als Zusatzfunktionen als auch als Parameter der Gruppe nützlich werden können. Welche Daten sind das?
| Index | den Wert des Index, der ermittelt wurde |
| Index.num | der numerische Wert des Index in Sekunden, Basis ist “1970-01-01 00:00:00” |
| diff | Differenz in Sekunden zum vorherigen numerischen Wert des Index |
| Year | Jahr, Komponente des Index |
| half | die Hälfte der Komponente des Index |
| quarter | Quartal, Komponente des Index |
| month | Monat, Komponente des Index |
| month.xts | Monat, Komponente des Index mit der Basis 0, so wie in xts |
| month.lbl | Monatsnamen in geordneter Folge. Beginnt mit Januar und endet mit Dezember |
| day | Tag, Komponente des Index |
| hour | Stunde, Komponente des Index |
| minute | Minute, Komponente des Index |
| second | Sekunde, Komponente des Index |
| hour12 | Stunde, Komponente des Index im 12-Stunden Format |
| am.pm | Vormittag (am) = 1, Nachmittag (pm) = 2 |
| wday | Wochentag aus Basis 1 Sonntag = 1, Samstag = 7 |
| wday.xts | Wochentag auf Basis 0, so wie in xts. Sonntag = 0, Samstag = 6 |
| wday.lbl | Name des Wochentages in geordneter Folge Beginnt mit Sonntag und endet mit Samstag |
| mday | Tag des Monats |
| qday | Tag des Quartals |
| yday | Tag des Jahres. |
| mweek | Woche des Monats |
| week | Woche des Jahres (beginnend mit Sonntag) |
| week.iso | Woche des Jahres nach ISO (beginnend mit Montag) |
| week2 | Modul für eine 2-Wochen Frequenz |
| week3 | Modul für eine 3-Wochen Frequenz |
| week4 | Modul für eine 4-Wochen Frequenz |
Wir nehmen den Anfangsdatensatz pr, verstärken ihn mit der Funktion tk_augment_timeseries_signature(), fügen dem Anfangsdatensatz die Variablen mday, wday.lbl, hour, hinzu, entfernen undefinierte Variablen (NA) und gruppieren die Daten nach Wochentagen.
evalq(
{
tk_augment_timeseries_signature(pr) %>%
select(c(mday, wday.lbl, hour)) %>%
cbind(pr, .) -> pr.augm
pr.compl <- pr.augm[complete.cases(pr.augm), ]
pr.nest <- pr.compl %>% group_by(wday.lbl) %>% nest()
},
env)
> str(env$pr.augm)
'data.frame': 8000 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..................................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ mday : int 10 10 10 10 10 10 10 10 10 10 ...
$ wday.lbl: Ord.factor w/ 7 levels "Sunday"<"Monday"<..: 3 3 3 3 3 3 3 3 3 3 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ...
Dasselbe Ergebnis kann erreicht werden, wenn wir die Bibliothek Lubridate nutzen, nachdem wir Daten für Samstag gelöscht haben.
require(lubridate)
evalq({pr %>% mutate(.,
wday = wday(Data), #label = TRUE, abbr = TRUE),
day = day(Data),
hour = hour(Data)) %>%
filter(wday != "Sat") -> pr1
pr1.nest <- pr1 %>% na.omit %>%
group_by(wday) %>% nest()},
env
)
#-------
str(env$pr1)
'data.frame': 7924 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..........................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ wday : int 3 3 3 3 3 3 3 3 3 3 ...
$ day : int 10 10 10 10 10 10 10 10 10 10 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ...
Die nach Wochentagen gruppierten Daten sehen wie folgt aus (Sonntag = 1, Montag = 2 usw.):
> env$pr1.nest # A tibble: 5 × 2 wday data <int> <list> 1 4 <tibble [1,593 Ч 32]> 2 5 <tibble [1,632 Ч 32]> 3 6 <tibble [1,624 Ч 32]> 4 2 <tibble [1,448 Ч 32]> 5 3 <tibble [1,536 Ч 32]>
Zusätzlich können auf den letzten drei Balken die Variablen dL, dH aus dem Datensatz pr verwendet werden.
2. Prädiktoren Auswahl
Es gibt viele Möglichkeiten und Kriterien, die Bedeutung von Prädiktoren zu bewerten. Einige davon wurden in den vorherigen Artikeln besprochen. Da in diesem Artikel der Schwerpunkt auf der Visualisierung liegt, vergleichen wir eine visuelle und eine analytische Methode zur Bewertung der Bedeutung von Prädiktoren.
2.1. Visuelle Auswertung
Wir werden das Programmpaket smbinning verwenden. Früher verwendeten wir das Paket funModeling zur Beurteilung der Prädiktoren. Wir kamen zu dem Schluss, dass die Visualisierung einer Beziehung eine einfache und zuverlässige Möglichkeit zur Identifizierung der Relevanz von Prädiktoren ist. Wir werden testen, wie das Paket smbinning mit normalisierten und transformierten Daten umgehen wird. Wir werden auch herausfinden, wie sich die Transformation von Prädiktoren auf deren Bedeutung auswirkt.
Versammeln Sie in einem Datensatz log-transformierte, sin-transformierte, tanh-transformierte und normalisierte Daten und bewerten Sie die Abhängigkeit der Zielvariablen und der Prädiktoren in diesem Datensatz.
Die Reihenfolge der Abarbeitung des primären Datensatzes (siehe Abbildung unten) ist wie folgt: Bereinigen der Rohdaten im dataSet (ohne hochkorrelierte Daten zu entfernen), Aufteilen des dataSet in die Datensätze train/val/test auf und Holen des Datensatzes DT. Dann wird alles für jede der Transformationen gemäß dem Blockdiagramm berechnet. Fassen wir alles in einem Drehbuch zusammenfassen:
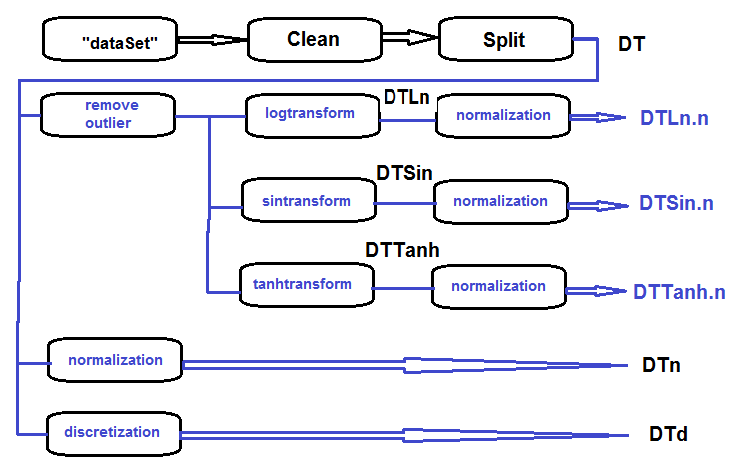
Abb. 27. Blockschaltbild der Vorverarbeitung
Säubern des Datensatz, Unterteilen der Datensätze train/val/test und Entfernen der unnötige Daten:
#----Clean--------------------- require(caret) require(pipeR) evalq( { train = 1:2000 val = 2001:3000 test = 3001:4000 DT <- list() dataSet %>% preProcess(., method = c("zv", "nzv", "conditionalX")) %>% predict(., dataSet) %>% na.omit -> dataSetClean list(train = dataSetClean[train, ], val = dataSetClean[val, ], test = dataSetClean[test, ]) -> DT rm(dataSetClean, train, val, test) }, env)
Alle Ausreißer in allen Datensätzen verarbeiten:
#------outlier-------------
evalq({
# define the new list for the result
DTcap <- list()
# go through the three sets
foreach(i = 1:3) %do% {
DT[[i]] %>%
# remove columns with (Data, Class)
select(-c(Data, Class)) %>%
# transform into data.frame and store in the temporary variable x
as.data.frame() -> x
if (i == 1) {
# define parameters of outliers in the first input
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
prep.outlier(x[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
}
# substitute outliers for 5/95 % and store the result in x.cap
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = x[ ,i], impute = T, fill = T,
lower = lower, upper = upper,
med = med, cap1 = cap1, cap2 = cap2)
} %>% as.data.frame() -> x.cap
colnames(x.cap) <- colnames(x)
return(x.cap)
} -> Dtcap
#remove unnecessary variables
rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
Transformieren der Variablen in allen Datensätzen Dtcap ohne die Ausreißer mit der Funktion log(x+1). Holen der Liste DTLn mit den drei Datensätzen der log-transformierten Variablen.
#------logtrans------------
evalq({
DTLn <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) log2(x + 1)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTLn
},
env)
Transformieren der Variablen in allen Datensätzen Dtcap ohne die Ausreißer mit der Funktion sin(2*pi*x). Holen der Liste DTSin mit den drei Datensätzen der log-transformierten Variablen.
#------sintrans--------------
evalq({
DTSin <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) sin(2*pi*x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTSin
},
env)
Transformieren der Variablen in allen Datensätzen Dtcap ohne die Ausreißer mit der Funktion tanh(x). Holen der Liste DTTanh mit den drei Datensätzen der log-transformierten Variablen.
#------tanhTrans----------
evalq({
DTTanh <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) tanh(x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTTanh
},
env)
Normalisieren der Datensätze DT, DTLn, DTSin, DTTanh.
#------normalize----------- evalq( { # define parameters of normalization preProcess(DT$train, method = "spatialSign") -> preproc list(train = predict(preproc, DT$train), val = predict(preproc, DT$val), test = predict(preproc, DT$test) ) -> DTn }, env) #--ln--- evalq( { preProcess(DTLn[[1]], method = "spatialSign") -> preprocLn list(train = predict(preprocLn, DTLn[[1]]), val = predict(preprocLn, DTLn[[2]]), test = predict(preprocLn, DTLn[[3]]) ) -> DTLn.n }, env) #---sin--- evalq( { preProcess(DTSin[[1]], method = "spatialSign") -> preprocSin list(train = predict(preprocSin, DTSin[[1]]), val = predict(preprocSin, DTSin[[2]]), test = predict(preprocSin, DTSin[[3]]) ) -> DTSin.n }, env) #-----tanh----------------- evalq( { preProcess(DTTanh[[1]], method = "spatialSign") -> preprocTanh list(train = predict(preprocTanh, DTTanh[[1]]), val = predict(preprocTanh, DTTanh[[2]]), test = predict(preprocTanh, DTTanh[[3]]) ) -> DTTanh.n }, env)
Diskretisieren des Datensatzes DT mit der Funktion mdlp::discretization
##------discretize----------
#--------preCut---------------------
# define the cutpoints
require(pipeR)
require(discretization)
evalq(
#require(pipeR)
# takes some time !
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()
}) -> mdlp.train,
env)
#-------cut_opt----------
evalq(
{
DTd <- list()
mdlp.train$cutp %>%
# define the columns that have to be discretized
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> DTd$train
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
# rearrange data according to calculated ranges
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> DTd$test
colnames(DTd$test) <- colnames(DTd$train)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
# rearrange data according to calculated ranges
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> DTd$val
colnames(DTd$val) <- colnames(DTd$train)
# tidy up
rm(test.d, val.d)
},
env
)
Erinnern wir uns daran, welche Variablen des ursprüngliche Datensatzes DT$train enthält:
require(funModeling)
plot_num(env$DT$train %>% select(-Data), bins = 20)
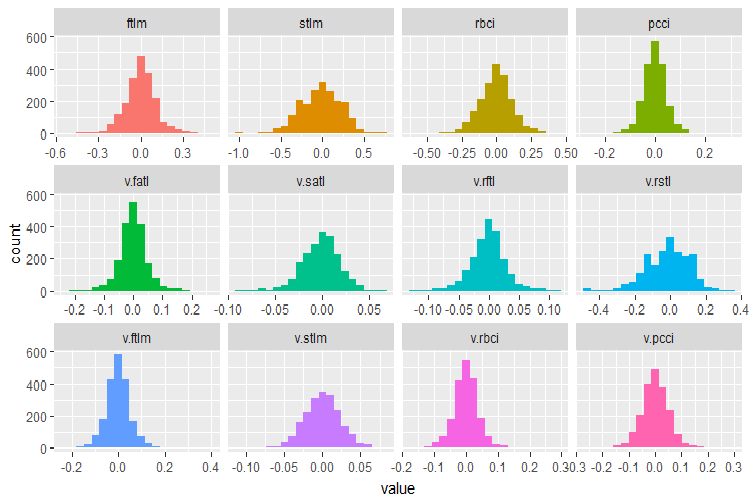
Abb. 28. Verteilung der Variablen im Datensatz DT$train
Benutzen Sie die Fähigkeiten des Paketes smbinning, um relevante Prädiktoren im Datensatz train aus allen normalisierten Datensätze zu identifizieren, die Sie zuvor erhalten haben (Dtn, DTLn.n, DTSin.n und DTTanh.n). Die Zielvariable in diesem Paket muss numerisch sein und Werte (0,1) haben. Lassen Sie uns eine Funktion für die notwendige Konvertierungen schreiben.
#-------------------------------- require(smbinning) targ.int <- function(x){ x %>% tbl_df() %>% mutate(Cl = (as.numeric(Class) - 1) %>% as.integer()) %>% select(-Class) %>% as.data.frame() }
Außerdem akzeptiert dieses Paket keine Variablen mit einem Punkt im Namen. Die Funktion unten wandelt alle Variablennamen mit einem Punkt in einen mit einem Unterstrich um.
renamepr <- function(X){
X %<>% rename(v_fatl = v.fatl,
v_satl = v.satl,
v_rftl = v.rftl,
v_rstl = v.rstl,
v_ftlm = v.ftlm,
v_stlm = v.stlm,
v_rbci = v.rbci,
v_pcci = v.pcci)
return(X)
}
Berechnen und Zeichnen des Diagramms mit den relevanten Prädiktoren.
par(mfrow = c(2,2)) #--Ln-------------- evalq({ df <- renamepr(DTLn.n[[1]]) %>% targ.int sumivt.ln.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.ln.n, cex = 0.7) rm(df) }, env) #---Sin----------------- evalq({ df <- renamepr(DTSin.n[[1]]) %>% targ.int sumivt.sin.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.sin.n, cex = 0.7) rm(df) }, env) #---norm------------- evalq({ df <- renamepr(DTn[[1]]) %>% targ.int sumivt.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.n, cex = 0.7) rm(df) }, env) #-----Tanh---------------- evalq({ df <- renamepr(DTTanh.n[[1]]) %>% targ.int sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.7) rm(df) }, env) par(mfrow = c(1,1))
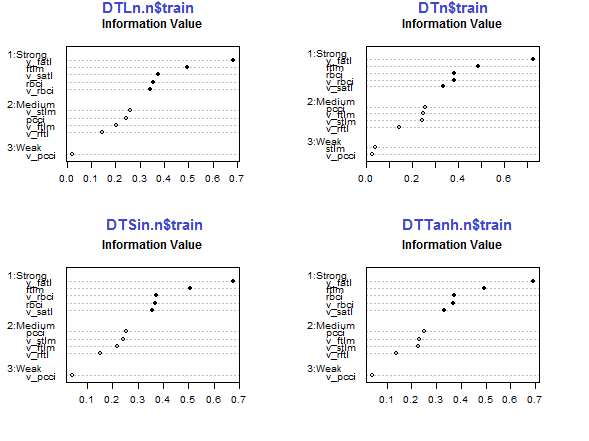
Abb. 29. Bedeutung von Prädiktoren im Datensatz train, einer der normalisierten Datensätzen
Die fünf Prädiktoren v_fatl, ftlm, v_satl, rbci, v_rbci sind in allen Datensätzen stark, auch wenn ihre Reihenfolge unterschiedlich ist. Die vier Prädiktoren pcci, v_ftlm, v_stlm, v_rftl haben eine mittlere Stärke. Die Prädiktoren v_pcci and stlm sind schwach. Die Verteilung der Variablen ist für jeden Datensatz in der Reihenfolge ihrer Wichtigkeit ersichtlich:
env$sumivt.ln.n Char IV Process 5 v_fatl 0.6823 Numeric binning OK 1 ftlm 0.4926 Numeric binning OK 6 v_satl 0.3737 Numeric binning OK 3 rbci 0.3551 Numeric binning OK 11 v_rbci 0.3424 Numeric binning OK 10 v_stlm 0.2591 Numeric binning OK 4 pcci 0.2440 Numeric binning OK 9 v_ftlm 0.2023 Numeric binning OK 7 v_rftl 0.1442 Numeric binning OK 12 v_pcci 0.0222 Numeric binning OK 2 stlm NA No significant splits 8 v_rstl NA No significant splits
Die letzten drei Variablen können verworfen werden. So bleiben nur noch die fünf Stärksten und vier durchschnittlich Starke übrig. Definieren wir die Namen der besten Variablen (IV > 0.1).
evalq(sumivt.sin.n$Char[sumivt.sin.n$IV > 0.1] %>% na.omit %>% as.character() -> best.sin.n, env) > env$best.sin.n [1] "v_fatl" "ftlm" "rbci" "v_rbci" "v_satl" "pcci" [7] "v_ftlm" "v_stlm" "v_rftl"
Schauen wir uns die Variablen v_fatl und ftlm genauer an.
evalq({
df <- renamepr(DTTanh.n[[1]]) %>% targ.int
x = 'v_fatl'
y = 'Cl'
res <- smbinning(df = df,
y = y,
x = x)
#res$ivtable # Tabulation and Information Value
#res$iv # Information value
#res$bands # Bins or bands
#res$ctree # Decision tree from partykit
par(mfrow = c(2,2))
sub = paste0(x, " vs ", y) #rbci vs Cl"
boxplot(df[[x]]~df[[y]],
horizontal = TRUE,
frame = FALSE, col = "lightblue",
main = "Distribution")
mtext(sub,3) #ftlm
smbinning.plot(res, option = "dist",
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "goodrate", #"badrate"
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "WoE",
sub = sub) #"pcci vs Cl")
par(mfrow = c(1, 1))
}, env)
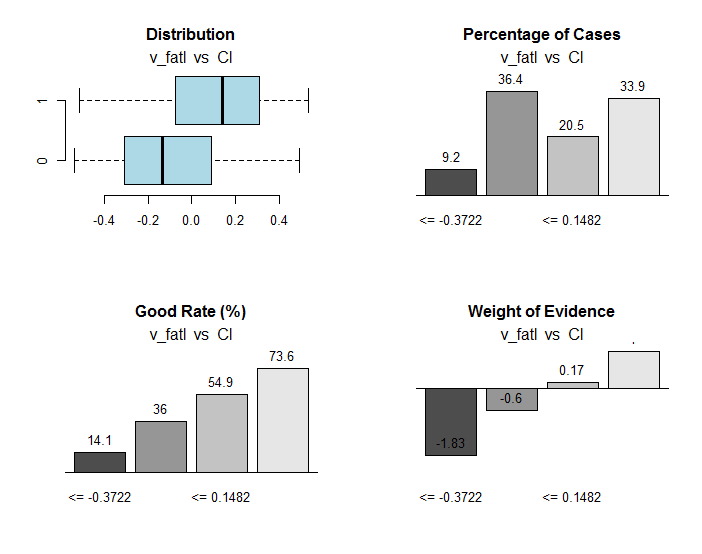
Abb. 30. Verbindung der Bereiche der Variablen v_fatl mit der Zielvariablen Cl
Neben nützlichen Informationen enthält das Objekt res die Punkte der Aufteilung der Variablen in Teilbereiche, die optimal mit der Zielvariablen verknüpft sind. In unserem speziellen Fall gibt es vier Bereiche.
> env$res$cuts [1] -0.3722 -0.0433 0.1482
Wir werden die gleiche Berechnung für die Variable ftlm durchführen und das Diagramme zeichnen:
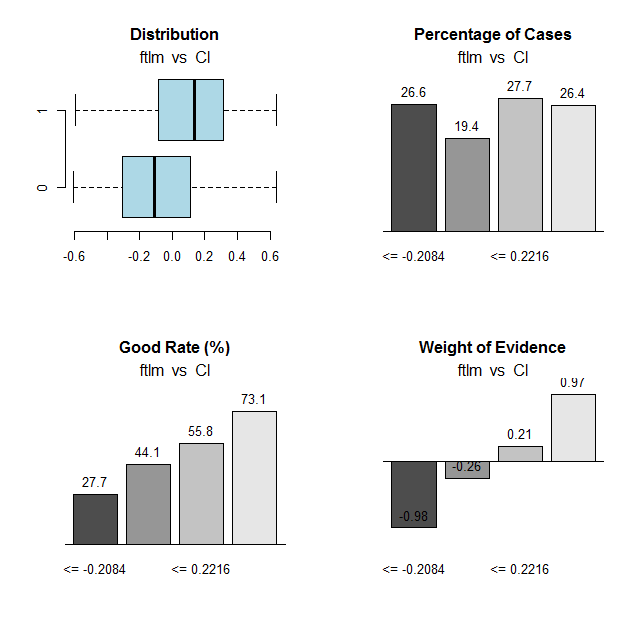
Abb. 31. Verbindung der Bereiche der Variablen ftlm mit der Zielvariablen Cl
Bereich der Trennpunkte:
> env$res$cuts [1] -0.2084 -0.0150 0.2216
Anhand der Trennpunkte können wir die Variablen in unseren Datensätzen diskretisieren und sehen, wie sehr sich die folgenden Punkte unterscheiden:
- wichtige Variablen, die zuvor mit der Funktion mdlp::discretization unter Verwendung der Definition der Variablen mit der Funktion smbinning::smbinning; bestimmt wurden
- Aufteilen der Variablen in Teilbereiche.
Wir haben bereits einen der Datensätze mit der Funktion mdlp::discretization DTd diskretisiert. Wir wiederholen das, aber diesmal verwenden wir die Funktion smbinning::smbinning nur für den Datensatz train.
Definieren der Trennpunkte:
evalq({
res <- list()
DT$train %>% renamepr() %>% targ.int() -> df
x <- colnames(df)
y <- "Cl"
foreach(i = 1:(ncol(df) - 1)) %do% {
smbinning(df, y = y, x = x[i])
} -> res
res %>% lapply(., function(x) x[1] %>% is.list) %>%
unlist -> idx
}, env)
Diskretisieren von DT$train:
evalq({
DT1.d <- list()
DT$train %>% renamepr() %>%
targ.int() %>% select(-Cl) -> train
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(train[ ,i],
vec = res[[i]]$cuts,
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$train$Class) -> DT1.d$train
colnames(DT1.d$train) <- colnames(train)[idx] %>%
c(., 'Class')
},
env)
Identifizieren der besten Variablen mit der Wichtigkeit größer als 0,1 in aufsteigender Reihenfolge:
evalq({
DT$train %>% renamepr() %>% targ.int() -> df
sumivt.dt1.d = smbinning.sumiv(df = df, y = 'Cl')
sumivt.dt1.d$Char[sumivt.dt1.d$IV > 0.1] %>%
na.omit %>% as.character() -> best.dt1.d
rm(df)
},
env)
Zeichnen des Diagramms der Aufteilung der Variablen im Datensatz DTd$train:
require(funModeling) plot_num(env$DTd$train)
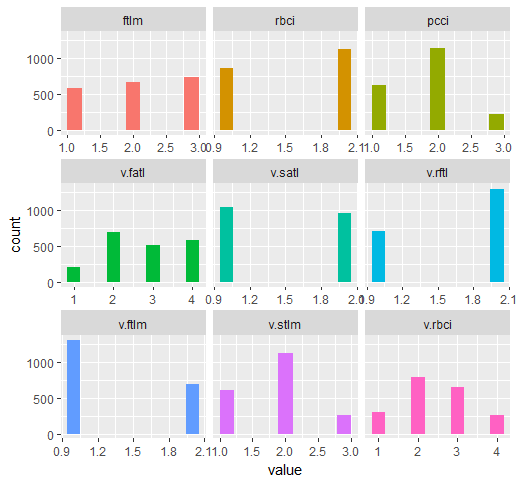
Abb. 32. Die Variablen von DT$train, diskretisiert mit der Funktion mdlp
Das Diagramm des Datensatzes DT1.d mit allen Variablen, die Besten sind unten dargestellt.
plot_num(env$DT1.d$train)
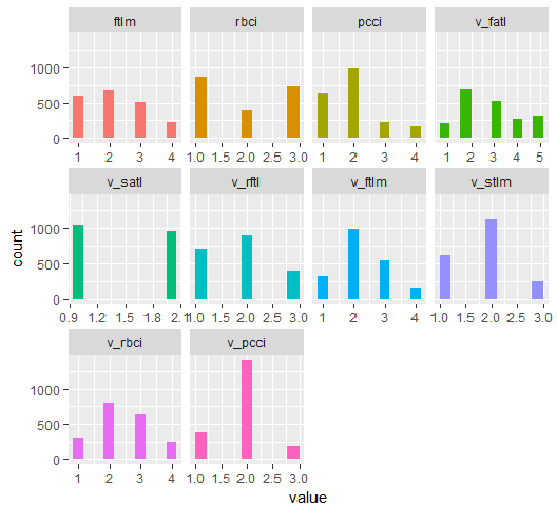
Abb. 33. Die Variablen des Datensatzes DT1.d$train diskretisiert mit der Funktion smbinning
plot_num(env$DT1.d$train[ ,env$best.dt1.d])
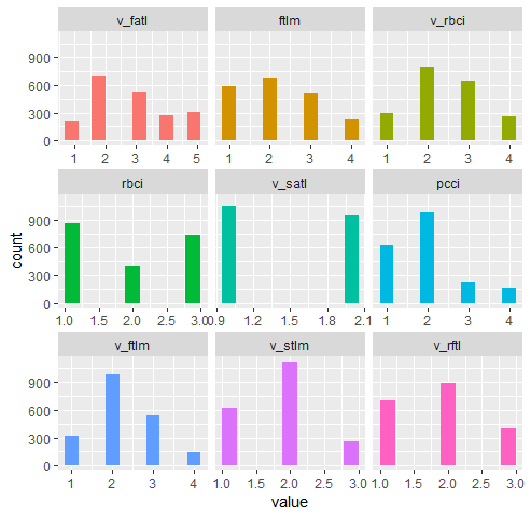
Abb. 34. Variablen des Datensatzes DT1.d$train diskretisiert mit der Funktion Smbinning (die besten sind in aufsteigender Reihenfolge der Informationsrelevanz angeordnet)
Was können wir auf dem Diagramm erkennen? In beiden Fällen sind die als wichtig definierten Variablen gleich, wenn auch die Aufteilung in Teilbereiche unterschiedlich ist. Es muss getestet werden, welche Variante die bessere Vorhersage des Modell ermöglicht.
2.2. Analytische Auswertung
Es gibt viele analytische Methoden, um die Bedeutung von Prädiktoren anhand verschiedener Kriterien zu identifizieren. Wir haben einige bereits besprochen. Nun möchte ich noch einen ungewöhnlichen Ansatz bei der Auswahl der Prädiktoren testen.
Wir werden das Programmpaket varbvs verwenden. In der Funktion varbvs sind implementiert: Schnelle Algorithmen für die Installation der Bayes'schen Modelle zur Variablenauswahl und zur Berechnung der Bayes'schen Koeffizienten, bei denen das Ergebnis (oder die Zielvariable) mit linearer Regression oder logistischer Regression abgebildet wird. Diese Algorithmen basieren auf den Variationsapproximation, die in "Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies" (P. Carbonetto and M. Stephens, Bayesian Analysis 7,2012, Seiten 73-108) beschrieben sind. Diese Software wurde für die Arbeit mit großen Datensätzen mit mehr als einer Million Variablen und Tausenden von Stichproben konzipiert und verwendet.
Die Funktion varbvs() übernimmt eine Matrix und die Zielvariable erhält als Eingabedaten einen numerischen Vektor (0,1). Mit dieser Methode testen wir, welche Prädiktoren in unserem Datensatz mit den normalisierten Daten DTTanh.n$train als wichtig definiert werden.
require(varbvs)
evalq({
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
fit <- varbvs(X = train[ ,-ncol(train)] ,
Z = NULL,
y = train[ ,ncol(train)] %>% as.vector(),
"binomial",
logodds = seq(-2,-0.5,0.1),
optimize.eta = T,
initialize.params = T,
verbose = T, nr = 100
)
print(summary(fit))
}, env)
Welcome to -- * *
VARBVS version 2.0.3 -- | | |
large-scale Bayesian -- || | | | || | | |
variable selection -- | || | | | | || || |||| || | ||
****************************************************************************
Copyright (C) 2012-2017 Peter Carbonetto.
See http://www.gnu.org/licenses/gpl.html for the full license.
Fitting variational approximation for Bayesian variable selection model.
family: binomial num. hyperparameter settings: 16
samples: 2000 convergence tolerance 1.0e-04
variables: 12 iid variable selection prior: yes
covariates: 0 fit prior var. of coefs (sa): yes
intercept: yes fit approx. factors (eta): yes
Finding best initialization for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00018 -1.204193e+03 6.1e-05 0003.3 NA 3.3e+00
Computing marginal likelihood for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00002 -1.204193e+03 3.2e-05 0003.3 NA 3.3e+00
Summary of fitted Bayesian variable selection model:
family: binomial num. hyperparameter settings: 16
samples: 2000 iid variable selection prior: yes
variables: 12 fit prior var. of coefs (sa): yes
covariates: 1 fit approx. factors (eta): yes
maximum log-likelihood lower bound: -1204.1931
Hyperparameters:
estimate Pr>0.95 candidate values
sa 3.49 [3.25,3.6] NA--NA
logodds -0.75 [-1.30,-0.50] (-2.00)--(-0.50)
Selected variables by probability cutoff:
>0.10 >0.25 >0.50 >0.75 >0.90 >0.95
3 3 3 3 3 3
Top 5 variables by inclusion probability:
index variable prob PVE coef* Pr(coef.>0.95)
1 1 ftlm 1.0000 NA 2.442 [+2.104,+2.900]
2 4 pcci 1.0000 NA 2.088 [+1.763,+2.391]
3 3 rbci 0.9558 NA 0.709 [+0.369,+1.051]
4 10 v.stlm 0.0356 NA 0.197 [-0.137,+0.529]
5 6 v.satl 0.0325 NA 0.185 [-0.136,+0.501]
*See help(varbvs) about interpreting coefficients in logistic regression.
Wie Sie sehen können, wurden die fünf beste Prädiktoren identifiziert (ftlm, pcci, rbci, v.stlm, v.satl). Sie gehören zu den Top Ten, die wir früher, wenn auch in anderer Reihenfolge und mit anderen Wichtungen identifiziert haben. Da wir bereits ein Modell haben, lassen Sie uns prüfen, welches Ergebnis wir mit den Validierungs- und Testdaten erhalten.
Validierungsdaten:
#-----------------
evalq({
val <- DTTanh.n$val %>% targ.int() %>%
as.matrix()
y = val[ ,ncol(val)] %>% as.vector()
pr <- predict(fit, X = val[ ,-ncol(val)] ,
Z = NULL)
}, env)
cm.val <- confusionMatrix(table(env$y, env$pr))
> cm.val
Confusion Matrix and Statistics
0 1
0 347 204
1 137 312
Accuracy : 0.659
95% CI : (0.6287, 0.6884)
No Information Rate : 0.516
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.3202
Mcnemar's Test P-Value : 0.0003514
Sensitivity : 0.7169
Specificity : 0.6047
Pos Pred Value : 0.6298
Neg Pred Value : 0.6949
Prevalence : 0.4840
Detection Rate : 0.3470
Detection Prevalence : 0.5510
Balanced Accuracy : 0.6608
'Positive' Class : 0
Das Ergebnis sieht nicht gerade beeindruckend aus. Testdaten:
evalq({
test <- DTTanh.n$test %>% targ.int() %>%
as.matrix()
y = test[ ,ncol(test)] %>% as.vector()
pr <- predict(fit, X = test[ ,-ncol(test)] ,
Z = NULL)
}, env)
cm.test <- confusionMatrix(table(env$y, env$pr))
> cm.test
Confusion Matrix and Statistics
0 1
0 270 140
1 186 404
Accuracy : 0.674
95% CI : (0.644, 0.703)
No Information Rate : 0.544
P-Value [Acc > NIR] : < 2e-16
Kappa : 0.3375
Mcnemar's Test P-Value : 0.01269
Sensitivity : 0.5921
Specificity : 0.7426
Pos Pred Value : 0.6585
Neg Pred Value : 0.6847
Prevalence : 0.4560
Detection Rate : 0.2700
Detection Prevalence : 0.4100
Balanced Accuracy : 0.6674
'Positive' Class : 0
Das Ergebnis ist fast das gleiche. Dies bedeutet, dass das Modell nicht umgeschult wurde, und es gut die Daten verallgemeinert.
Ergo gemäß varbvs sind die besten ftlm, pcci, rbci, v.stlm, v.satl.
2.3. Neuronales Netz
Da wir uns mit neuronalen Netzen beschäftigen, sollten wir testen, welche Prädiktoren das neuronale Netz als die wichtigsten auswählen wird.
Wir werden das Programmpaket FCNNN4R verwenden, das die Schnittstelle für die Kernprogramme aus der Bibliothek FCNN C++ bereitstellt. FCNN basiert auf einer völlig neuen Realisierung des neuronalen Netzes, die Effizienz, Modularität und Erweiterbarkeit beinhaltet. FCNN4R ermöglicht standardmäßiges Lernen (backpropagation, Rprop, simulated annealing, stochastischer Gradient) und Algorithmen des Trimmens (Pruning) (Mindestgröße, Optimal Brain Surgeon), obwohl ich dieses Paket vor allem als leistungsfähige Rechenmaschine betrachte.
Benutzer können ihren Algorithmus mit der schnellen Gradientenmethoden und der Funktion zur Wiederherstellung des Netzwerks (Entfernen von Gewichten und überzähligen Neuronen, Neuordnung von Eingangsdaten und Zusammenführung von Netzwerken) einfach implementieren.
Netzwerke können in die C-Funktionen exportiert werden, um in jede Programmlösung integriert werden zu können.
Erstellen eines vollständig verbundenen Netzes mit zwei verdeckten Schichten. Die Anzahl der Neuronen in jeder Schicht sind: input = 12 (Anzahl der Prädiktoren), output = 1. Initialisieren der Neuronen mit Zufallsgewichten im Bereich +/- 0,17. Bestimmen der Aktivierungsfunktionen in jeder Schicht des neuronalen Netzes (außer der Eingangsfunktion) = c("tanh","tanh","sigmoid"). Vorbereiten der Datensätze train/val/test.
Das folgende Skript führt diese Aktionen in der angegebenen Reihenfolge aus.
require(FCNN4R)
evalq({
mlp_net(layers = c(12, 8, 5, 1), name = "n.tanh") %>%
mlp_rnd_weights(a = 0.17) %>%
mlp_set_activation(layer = c(2, 3, 4),
activation = c("tanh", "tanh", "sigmoid"), #"threshold", "sym_threshold",
#"linear", "sigmoid", "sym_sigmoid",
#"tanh", "sigmoid_approx",
#"sym_sigmoid_approx"),
slope = 0) -> Ntanh #show()
#-------
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
test <- DTTanh.n$test %>% targ.int() %>% as.matrix()
val <- DTTanh.n$val %>% targ.int() %>% as.matrix()
}, env)
Wir werden die Trainingsmethode rprop verwenden. Festlegen der Konstanten: tol - der Fehler, der das Training stoppt, wenn dieser Wert erreicht ist, max_ep - die maximale Anzahl der Durchläufe, nach denen das Training abbricht, l2reg - der Regularisierungskoeffizient. Trainieren Sie das Netzwerk mit diesen Parametern und beurteilen Sie visuell, welches Netzwerk und welchen Trainingsfehler wir haben.
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
net_rp <- mlp_teach_rprop(Ntanh,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_epochs = max_ep,
l2reg = l2reg,
u = 1.2, d = 0.5,
gmax = 50, gmin = 1e-06,
report_freq = 100)
}, env)
plot(env$net_rp$mse, t = "l",
main = paste0("max_epochs =", env$max_ep, " l2reg = ", env$l2reg))
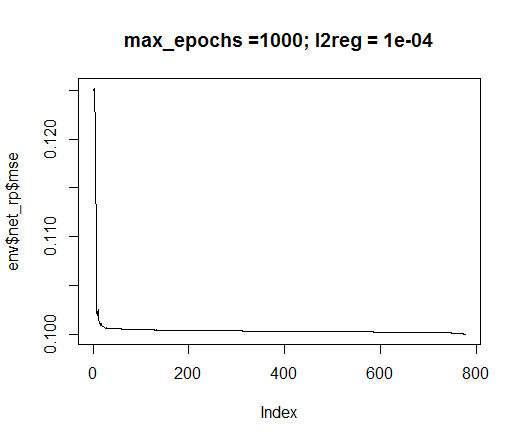
Abb. 35. Fehler des neuronalen Netzes
evalq(mlp_plot(net_rp$net, FALSE), envir = env)
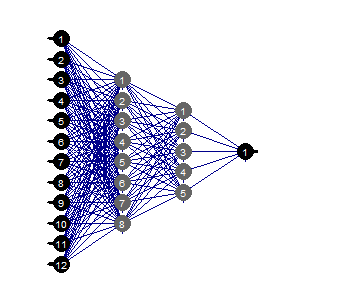
Abb. 36. Struktur des neuronalen Netzes
Trimmen (Prune)
Das Trimmen des kleinsten Wertes ist ein einfach zu verwendender Algorithmus. Dabei werden bei jedem Schritt die Gewichte mit dem kleinsten Absolutwert abgeschaltet. Dieser Algorithmus erfordert ein Netzwerkrelais fast bei jedem Schritt und liefert suboptimale Ergebnisse.
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
mlp_prune_mag(net_rp$net,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_reteach_epochs = max_ep,
report = FALSE,
plots = TRUE) -> net_rp_prune
}, env)
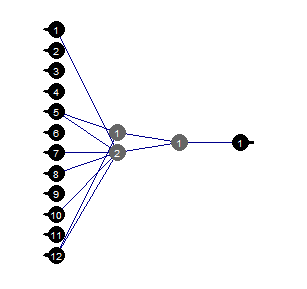
Abb. 37. Getrimmtes neuronales Netz
Wir können sehen, dass bei einer bestimmten Struktur des neuronalen Netzes, der Initialisierung, der Aktivierungsfunktionen und der Lernfehler, das neuronale Netz mit der Struktur (12,2,1,1) ausreichend ist. Welche Prädiktoren wurden vom neuronalen Netz ausgewählt?
evalq( best <- train %>% tbl_df %>% select(c(1,5,7,8,10,12)) %>% colnames(), env) env$best [1] "ftlm" "v.fatl" "v.rftl" "v.rstl" "v.stlm" [6] "v.pcci"
Die Variablen v.rstl und v.pcci gehören nicht zu den besten neun Variablen, die zuvor definiert wurden.
Ich möchte betonen, dass wir hier gezeigt haben, dass ein neuronales Netz selbständig und automatisch wichtige Prädiktoren auswählen kann. Diese Wahl hängt nicht nur von den Prädiktoren, sondern auch von der Struktur und den Parametern des Netzwerks ab.
Fröhliches Experimentieren!
Schlussfolgerung
Im folgenden Teil werden wir über Möglichkeiten sprechen, wie man Beispiele von Rauschen aus den Daten entfernen kann, wie man die Größe der Eingaben verringert und welche Auswirkungen das hat, sowie eine Aufteilung der Originaldaten in train/val/test.
Anwendung
1. Sie können die Skripte FeatureTransformation.R, FeatureSelect.R, FeatureSelect_analitic.R, FeatureSelect_NN.R und die Diagramme, die die Arbeit der Skripte von Part_1 dieses Artikels zeigen, von Git /Part_II herunterladen.