Die Berechnung des Hurst-Exponenten
Dmitriy Piskarev | 24 April, 2017
Einführung
Das Bestimmen der Marktentwicklung ist einer Hauptaufgaben eines Händlers. Oft ist es aber zu schwierig, das mit den technischen Standardmitteln der Analyse zu bewältigen. Zwar zeigen zum Beispiel ein МА oder der MACD einen Trend, dennoch werden weitere Instrumente zur Auswertung der Stärke und Beständigkeit benötigt. Am Ende ist es dann doch nur eine kurze Spitze, die schnell "verglüht".
Sie kennen wahrscheinlich das Sprichwort: um im Forexhandel erfolgreich zu sein, muss man mehr wissen als die anderen Marktteilnehmer. In diesem Fall kann man bei der Auswahl der besten Einstiegspunkte zum Erzielen und Absichern eines Profits einen Schritt im Vorteil sein. Erfolgreiches Handeln ist eine Kombination mehrerer Vorteile, einschließlich der Platzierung von Kauf/Verkaufsaufträgen, gerade bei einer Trendumkehr, geschickte Verwendung von fundamentalen und technischen Daten, sowie der kompletten Absenz von Emotionen. All dies sind zentrale Elemente einer erfolgreichen Händlerkarriere.
Die Fraktalanalyse könnte eine umfassende Lösung vieler Fragen an den Markt bieten. Fraktale werden oft zu Unrecht von Händlern und Investoren vernachlässigt, obwohl eine fraktale Analyse eine effiziente Auswertung des Trends mit seiner Zuverlässigkeit im Markt ermöglicht. Die Hurst Exponent ist einer der grundlegenden Werte einer fraktalen Analyse.
Vor der Erklärung seiner Berechnung betrachten wir kurz die wichtigsten Regeln der fraktalen Analyse und schauen genauer auf den Hurst-Exponenten.
1. Fraktale Hypothese des Marktes (FMH). Fraktale Analyse
Ein Fraktal ist eine mathematische Menge mit der Eigenschaft der Selbstähnlichkeit. Ein selbstähnliches Objekt ist genau oder fast genau gleich zu einem Teil seiner selbst (d.h. das Ganze hat dieselbe Form wie eins oder mehrerer seiner Teile). Die anschaulichste Beispiel für eine fraktale Struktur ist der "fraktale Baum":

Ein selbstähnliches Objekt bleibt sich gleich, nur mit einem anderen Maßstab — räumlich oder zeitlich.
Angewendet auf dem Markt bedeutet "fraktal" so etwas wie "wiederkehrend" oder "zyklisch".
Die fraktal Dimension definiert, wie ein Objekt oder eine Prozess den Raum füllt, und wie sich seine Struktur in unterschiedlichen Maßstäben ändert. Wenden wir diese Definition auf Finanzmärkte (in unserem Fall dem Forexmarkt) an, können wir erkennen, dass die fraktale Dimension ein Maß der "Irregularität" (Variabilität) einer Zeitreihe ist. So ist die Dimension d einer Graden gleich 1 und die des Random Walk 1,5, während für eine fraktale Zeitreihe gilt 1<d<1.5 oder 1.5<d<1.
"Das Ziel der FMH ist ein Modell des Verhaltens der Investoren und der Preisbewegungen des Marktes entsprechend unserer Beobachtungen... Nicht immer sind alle verfügbaren Informationen in den Preisen enthalten, sondern nur die des Anlagehorizontes" — E. Peters, Fraktale Analyse der Finanzmärkte.
Wir gehen nicht näher auf das Konzept der Fraktale ein, da angenommen wird, dass unsere Leser bereits eine Vorstellung von dieser analytischen Methode haben. Die ausführliche Beschreibung seiner Anwendung auf den Finanzmärkten findet sich in "Fraktale und Finanzen: Märkte zwischen Risiko, Rendite und Ruin" von B. Mandelbrot und R. Hudson, so wie "Fractal Market Analysis" und "Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility" von Edgar E. Peters.
2. R/S Analyse und der Hurst-Exponent
2.1. R/S Analyse
Der Schlüsselparameter einer fraktalen Analyse ist der Hurst-Exponent für die Untersuchung der Zeitreihe. Je größer die Verzögerung zwischen zwei ähnlichen Wertepaaren einer Zeitreihe, desto kleiner ist der Hurst-Exponent.
Der Exponent wurde von Harold Edwin Hurst eingeführt — ein herausragender, britischer Hydrologe, der am Nilstaudamm mitgearbeitet hat. Für den Baubeginn benötigte Hurst eine Schätzung der Änderungen der Wasserstände. Anfangs ging man davon aus, dass der Wasserzulauf ein reiner Zufallsprozess ist. Nach der Analyse der Aufzeichnungen der Hochwasser des Nils über neun Jahrhunderte konnte Hurst jedoch ein Muster entdecken. Das war der Beginn seiner Studien. Es stellte sich heraus, dass nach überdurchschnittlichen Überschwemmungen noch stärkere folgten. Danach drehte sich diese Entwicklung und nach unterdurchschnittlichen Überschwemmungen folgten schwächere. Das waren klare, nicht-periodische Zyklen.
Das statistische Modell von Hurst beruht auf Albert Einsteins Arbeit zur Brownschen Bewegung, ein Modell auf Basis des Random Walks der Teilchen. Die Idee hinter der Theorie ist, dass ein Abstand (R), den ein Partikel zurücklegt (walked), proportional zur Quadratwurzel der Zeit (T) ansteigt:
![]()
An dieser Gleichung angelehnt: Im Fall einer großen Zahl von Tests wäre die Variationsbreite (R) gleich der Quadratwurzel der Anzahl der Tests (T). Diese Gleichung verwendete Hurst für den Beweis, dass die Hochwasser nicht zufällig sind.
Für seine Methode verwendete der Hydrologe eine Zeitreihe X1..Xn für die Hochwasser. Der folgende Algorithmus verwendet die Rescaled Range Methode oder die R/S Analyse:
- Berechnung des Durchschnitts der Zeitreihe X1..Xn
- Berechnung der der Standardabweichung S
- Normalisieren der Zeitreihe durch die Subtraktion des Durchschnitts Zr (mit r=1..n) von jedem Wert
- Erstellen einer kumulierten Zeitreihe Y1=Z1+Zr, mit r=2..n
- Berechnung der Größenordnung der kumulierten Zeitreihe R=max(Y1..Yn)-min(Y1..Yn)
- Division der Größenordnung der kumulierten Zeitreihe durch die Standardabweichung (S).
Hurst verallgemeinert Einsteins Gleichung:
![]()
mit der Konstanten с.
Der Wert von R/S verändert den Maßstab mit steigenden Zeitintervall gemäß der Grad der Abhängigkeit von H, dem Hurst-Exponenten.
Nach Hurst müsste H den Wert von 0,5 haben, wenn die Hochwasser zufällig wären. Seinen Beobachtungen nach gilt aber H=0.91! Das heißt aber, die normalisierte Höhe ändert sich schneller als die Quadratwurzel der Zeit. Oder anders ausgedrückt, vergangene Ereignisse haben einen höheren Einfluss auf die Gegenwart und die Zukunft als der reine Zufall.
2.2. Anwendung der Theorie auf die Märkte
Unten wenden wir die Berechnung des Hurst-Exponent auf Finanz- und Aktienmärkte an. Die Daten werden auf einen Durchschnitt von Null normalisiert und mit einer Standardabweichung zur Kompensation der Inflation berechnet. Anders ausgedrückt, wir arbeiten wieder mit der R/S Analyse.
Wie aber ist der Hurst-Exponent auf den Märkten zu interpretieren?1. Ist der Hurst-Exponent zwischen 0.5 und 1 und weicht von der Erwartung um zwei oder mehr Standardabweichung ab, zeichnet sich der Prozess durch ein Langzeitgedächtnis aus. Oder er ist persistent.
Das heißt, alles Ereignisse hängen innerhalb einer Zeitspanne stark von vorherigen ab. Die Charts der Kurse der wichtigsten und einflussreichsten Firmen zeigen am deutlichsten persistente Zeitreihen. US-Konzerne wie Apple, GE, Boeing oder russische, wie Rosneft, Aeroflot und VTB können als Beispiel dafür benannt werden. Die Kurscharts dieser Firmen sind unten zu sehen. Ich glaube, jeder Investor erkennt ein vertrautes Bild beim Betrachten dieses Charts — jedes neue Hoch oder Tief ist höher als das Vorherige.
Aeroflot Aktienkurse:
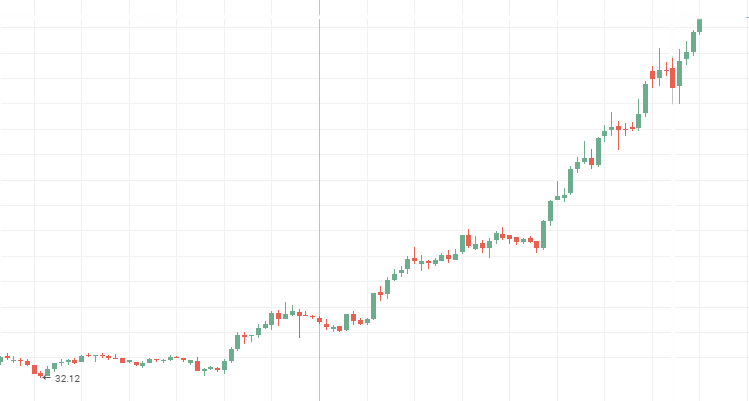
Rosneft Aktienkurse:
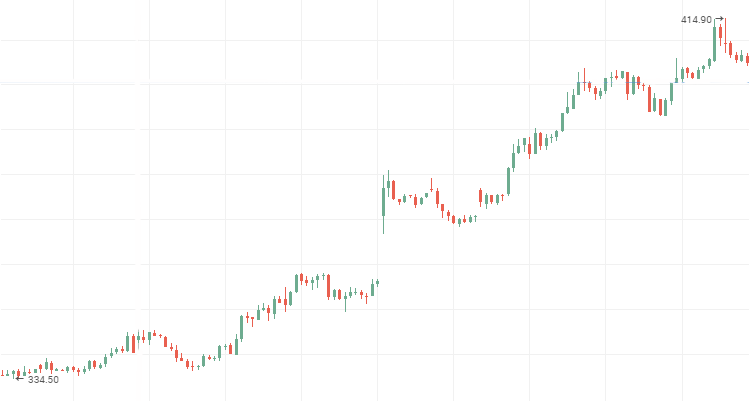
VTM Aktienkurse, eine persistente, fallende Zeitreihe
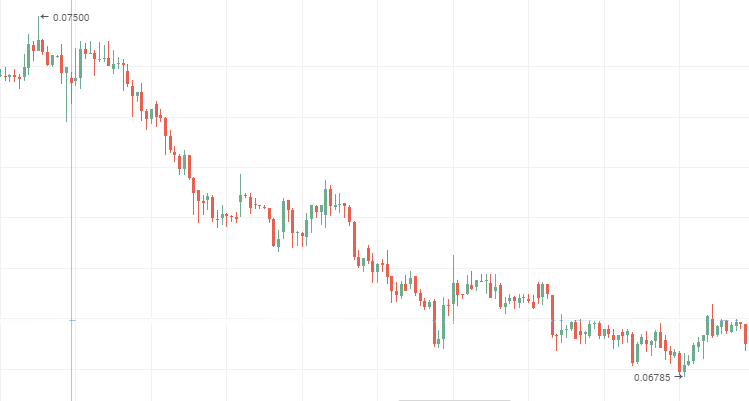
2. Unterscheidet sich der Hurst-Exponent von seinem absoluten Erwartungswert um zwei oder mehr Standardabweichung und ist zwischen 0 und 0,5 bedeutet das, das die Zeitreihe anti-persistent ist.
Die Werte ändern sich schneller als es ein Zufallsprozess tun würde, d.h. er ist anfällig für häufige, kleine Fluktuationen. Eine anti-persistente Zeitreihe ist deutlich in den Kursen von Tier 2 Aktien zu sehen. Während einer Seitwärtsbewegung zeigen auch die so genannten "blue chip" ein anti-persistentes Verhalten. Die Aktienkurse von Mechel, AvtoVAZ und Lenenergo sind klare Beispiele anti-persistenter Zeitreihen.
Mechel Vorzugaktien:
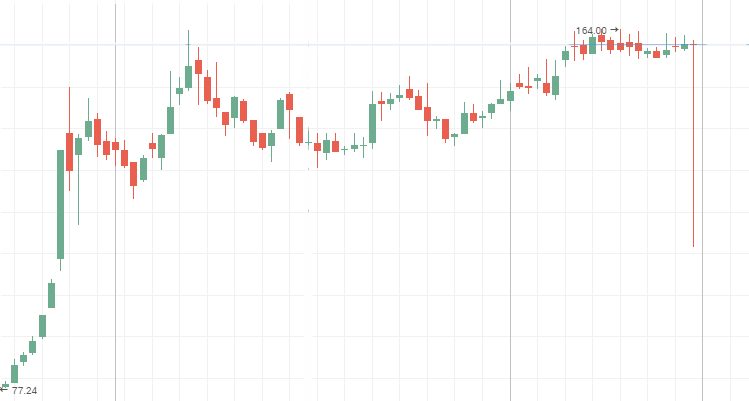
AvtoVAZ Stammaktien während einer Seitwärtsbewegung
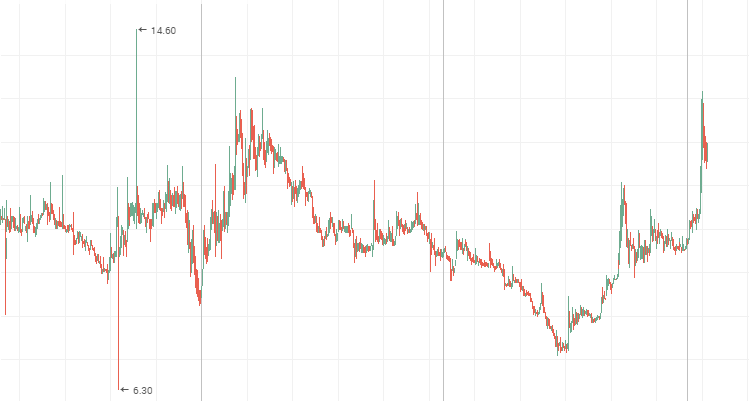
Lenenergo:
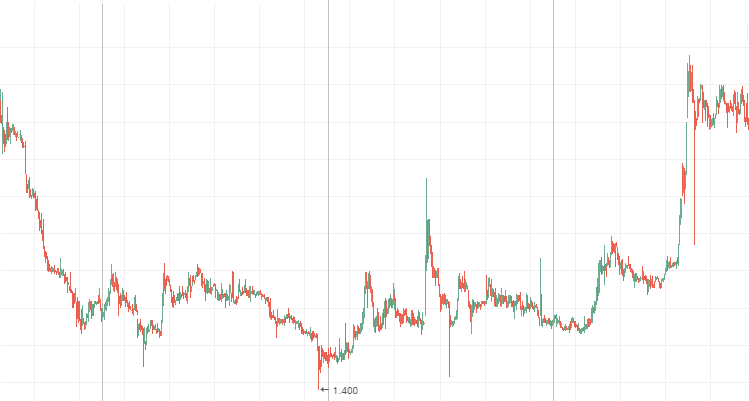
3. Ist der Hurst-Exponent 0,5 oder weicht sein Wert vom Erwartungswert um weniger als zwei Standardabweichung ab, wird der Prozess als Random Walk angesehen. Weder kurz- noch langfristige Zyklen sind zu erwarten. Für das Handeln bedeutet das, dass eine technische Analyse keine große Hilfe ist, da der aktuellen Wert von vorherigen nicht beeinflusst wird. Daher ist eine fundamentale Analyse besser.
Beispiele für den Hurst-Exponent für eine Gruppe von Aktien (Wertpapiere verschiedener Firmen, Industrieunternehmen und Rohstoffe) sind in der Tabelle unten aufgeführt. Der Berechnungszeitraum umfasst 7 Jahre. Die "Blue Chips" haben durch die Konsolidierung in der Finanzkrise einen kleinen Wert. Interessanterweise zeigen viele Papiere des Tier-2 Marktes eine gewisse Robustheit gegen diese Krise.
| Name | Hurst-Exponent H |
|---|---|
| Gazprom |
0.552 |
| VTB |
0.577 |
| Magnit |
0.554 |
| MTS |
0.543 |
| Rosneft |
0.648 |
| Aeroflot | 0.624 |
| Apple | 0.525 |
| GE | 0.533 |
| Boeing | 0.548 |
| Rosseti |
0.650 |
| Raspadskaya |
0.656 |
| TGC-1 |
0.641 |
| Tattelecom |
0.582 |
| Lenenergo |
0.642 |
| Mechel |
0.635 |
| AvtoVAZ |
0.574 |
| Petrol | 0.586 |
| Tin | 0.565 |
| Palladium | 0.564 |
| Natural gas | 0.560 |
| Nickel | 0.580 |
3. Erkennen von Zyklen. Das Gedächtnis in der fraktalen Analyse
Wie können wir sicher sein, unsere Ergebnisse sind nicht zufällig (trivial)? Um diese Frag zu beantworten, müssen wir zuerst die RS Analyse unter der Annahmen betrachten, sie sei zufällig. Anders gesagt, wir prüfen zunächst die Nullhypothese, dass der Prozess ein Random Walk ist und seine Struktur unabhängig und normal verteilt ist.
3.1. Berechnung des Erwartungswertes der R/S Analyse
Wir definieren den Erwartungswert der R/S Analyse.
1976 leiteten Anis und Lloyd eine Gleichung ab für den erforderlichen Erwartungswert:
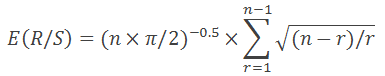
mit n der Anzahl der Beobachtungen, und r einem Wert zwischen 1 und n-1.
Wie in "Fractal Market Analysis" ausgeführt, ist sie nur gültig für n>20. Für n<20 verwenden wir folgende Gleichung:
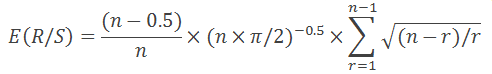
Alles ist ganz einfach:
- Berechnung des Erwartungswertes für jede Zahl von Beobachtungen und eine Anzeige einer Grafik von Log(E(R/S)) von Log(N) zusammen mit Log(R/S) ab Log(N);
- Berechnung der zu erwartenden Varianz des Hurst-Exponenten mittels der in der Statistik wohl bekannten Gleichung
![]()
mit H als Hurst-Exponent;
N – Anzahl der Beobachtungen in der Stichprobe S;
3. Überprüfen der Relevanz der erhaltenen Hurst-Verhältnisse durch die Auswertung der Anzahl von Standardabweichungen, durch die H den Wert von E(H) übersteigt. Ein Ergebnis gilt als relevant,wenn er 2 übersteigt.
3.2. Bestimmen von Zyklen
Betrachten wir folgendes Beispiel. Zeichnen wir die Grafiken für die RS Statistik und den Erwartungswert E(R/S) und vergleichen sie mit der Marktentwicklung, um herauszufinden, welche von beiden dem Kursverlauf entspricht.
In seinen Arbeiten stellt Peter fest, der beste Weg einen existierenden Zyklus bestimmen zu können, ist eine Grafik der V-Statistik mit logarithmischen Maßstab einer Anzahl von Beobachtungen einer Untergruppe zu erstellen.
Die erhaltenen Ergebnisse sind leicht zu bewerten:
- zeigt die Grafik im logarithmischen Maßstab eine Horizontale auf beiden Achsen, dann haben wir es mit einem unabhängigen, zufälligen Prozess zu tun;
- zeigt die Grafik einen positiven, nach oben gerichteten Winkel ist es ein persistenter Prozess. Wie bereits erwähnt, heißt das, die Änderungen des R/S erscheinen schneller als die Quadratwurzel der Zeit;
- und schließlich, wenn die Grafik einen Abwärtstrend zeigt, haben wir es mit einem anti-persistenten Prozess zu tun.
3.3. Das Gedächtniskonzept der fraktalen Analyse und wie ihre Tiefe definiert ist
Für ein besseres Verständnis der fraktalen Analyse, führen wir das Konzept Gedächtnisses ein.
Wie bereits erwähnt verwenden wir lang- und kurzfristiges Gedächtnis. In der fraktalen Analyse ist das Gedächtnis eine Zeitspanne, während der der Markt sich der Vergangenheit erinnert und diese so einem Einfluss auf die Gegenwart und die Zukunft hat. Diese Zeitspanne ist die Gedächtnistiefe (memory depth), die in gewissem Maße die gesamte Kraft und die Besonderheiten der fraktalen Analyse enthält. Diese Daten sind wichtig für die technische Analyse, um die Relevanz der früheren, technisch gefundenen Muster zu bestimmen.
Es ist keine übermäßige Rechenleistung nötig, um die Gedächtnistiefe zu bestimmen. Eine reine visuelle Analyse der logarithmischen V-Statistik ist ausreichend.
- Ziehen Sie eine Linie durch alle Punkte der Grafik.
- Stellen Sie sicher, diese Linie ist keine Horizontale.
- Bestimmen Sie die Spitzen der Kurve oder wo die Kurve ihr Maximum erreicht. Diese Maxima dienen als erste Hinweis für einen existierenden Zyklus.
- Bestimmen der X-Koordinate der Grafik auf dem logarithmischen Maßstab und Umrechnen der Zahl, um sie leichter verstehen zu können: Periodenlänge = exp^(Periodenlänge im logarithmischen Maßstab). Wenn Sie also Daten von 12000 GBPUSD Stunden analysieren und Sie erhalten eine 8,2 im logarithmischen Maßstab, hat der Zyklus eine Dauer von exp^8.2=3772 Stunden oder 157 Tage.
- Jeder richtige Zyklus sollte im gleichen Zeitrahmen gesichert werden, aber mit einem anderen Zeitrahmen als Basis. So haben wir unter 4. Daten über 12000 GBPUSD Stunden untersucht und eine Zyklus von 157 Tagen ermittelt. Wechseln wir auf H4 und analysieren 12000/4=3000 Daten. Wenn der 157-Tageszyklus tatsächlich existiert, dann ist die Annahmen wahrscheinlich korrekt. Falls nicht, sollte es möglich sein, einen kürzeren Zyklus zu finden.
3.4. Der aktuelle Hurst-Exponent für Währungspaare
Wir haben die Einführung in die Grundlagen der Fraktalanalyse beendet. Bevor wir fortfahren, die RS-Analyse mit der MQL5-Sprache umzusetzen, schauen wir uns ein paar Beispiele an.
Die Tabelle unten zeigt die Hurst-Exponenten von 11 Forex-Währungspaaren in verschiedenen Zeitrahmen und Anzahl von Bars. Die Zahlen wurden durch die Lösung der Regression mit der Methode der kleinsten Quadrate (LS) ermittelt. Wie wir sehen können, zeigen die meisten Paare einen persistenten Prozess, obwohl es auch anti-persistente gibt. Aber ist das Ergebnis signifikant? Können wir den Zahlen trauen? Wir werden das später diskutieren.
Tabelle 1. Analyse der Hurst-Exponenten für 2000 Bars
| Symbol | H (D1) | H (H4) | H (H1) | H(15M) | H (5M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.559 | 0.513 | 0.567 | 0.577 |
| EURCHF | 0.520 | 0.468 | 0.457 | 0.463 | 0.522 | 0.577 |
| EURJPY | 0.574 | 0.501 | 0.527 | 0.511 | 0.546 | 0.577 |
| EURGBP | 0.553 | 0.571 | 0.540 | 0.562 | 0.550 | 0.577 |
| EURRUB | insufficient bars | 0.536 | 0.521 | 0.543 | 0.476 | 0.577 |
| USDJPY | 0.591 | 0.563 | 0.583 | 0.519 | 0.565 | 0.577 |
| USDCHF | insufficient bars | 0.509 | 0.564 | 0.517 | 0.545 | 0.577 |
| USDCAD | 0.549 | 0.569 | 0.540 | 0.519 | 0.565 | 0.577 |
| USDRUB | 0.582 | 0.509 | 0.564 | 0.527 | 0.540 | 0.577 |
| AUDCHF | 0.522 | 0.478c | 0.504 | 0.506 | 0.509 | 0.577 |
| GBPCHF | 0.554 | 0.559 | 0.542 | 0.565 | 0.559 | 0.577 |
Tabelle 2. Analyse der Hurst-Exponenten für 400 Bars
| Symbol | H (D1) | H (H4) | H (H1) | H(15M) | H (5M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.513 | 0.604 | 0.617 | 0.578 |
| EURCHF | 0.471 | 0.460 | 0.522 | 0.603 | 0.533 | 0.578 |
| EURJPY | 0.545 | 0.494 | 0.562 | 0.556 | 0.570 | 0.578 |
| EURGBP | 0.620 | 0.589 | 0.601 | 0.597 | 0.635 | 0.578 |
| EURRUB | 0.580 | 0.551 | 0.478 | 0.526 | 0.542 | 0.578 |
| USDJPY | 0.601 | 0.610 | 0.568 | 0.583 | 0.593 | 0.578 |
| USDCHF | 0.505 | 0.555 | 0.501 | 0.585 | 0.650 | 0.578 |
| USDCAD | 0.590 | 0.537 | 0.590 | 0.587 | 0.631 | 0.578 |
| USDRUB | 0.563 | 0.483 | 0.465 | 0.531 | 0.502 | 0.578 |
| AUDCHF | 0.443 | 0.472 | 0.505 | 0.530 | 0.539 | 0.578 |
| GBPCHF | 0.568 | 0.582 | 0.616 | 0.615 | 0.636 | 0.578 |
Tabelle 3. Berechnung der Hurst-Exponent für M15 und M5
| Symbol | H (15M) | Significance | H (5M) | Significance | E(H) |
|---|---|---|---|---|---|
| EURUSD | 0.543 | insignificant | 0.542 | insignificant | 0.544 |
| EURCHF | 0.484 | significant | 0.480 | significant | 0.544 |
| EURJPY | 0.513 | insignificant | 0.513 | insignificant | 0.544 |
| EURGBP | 0.542 | insignificant | 0.528 | insignificant | 0.544 |
| EURRUB | 0.469 | significant | 0.495 | significant | 0.544 |
| USDJPY | 0.550 | insignificant | 0.525 | insignificant | 0.544 |
| USDCHF | 0.551 | insignificant | 0.525 | insignificant | 0.544 |
| USDCAD | 0.519 | insignificant | 0.550 | insignificant | 0.544 |
| USDRUB | 0.436 | significant | 0.485 | significant | 0.544 |
| AUDCHF | 0.518 | insignificant | 0.499 | significant | 0.544 |
| GBPCHF | 0.533 | insignificant | 0.520 | insignificant | 0.544 |
E. Peters empfiehlt die Analyse einiger, wichtiger Zeitrahmen und diese für die Suche nach Zyklen in den Zeitreihen zu suchen. Dann muss man die analysierte Zeitspanne auf einem anderen Zeitrahmen mit weniger Bars wiederholen mit einer "passenden" Gedächtnistiefe. Das impliziert folgendes:
Existiert ein Zyklus im Basiszeitrahmen, kann dessen Gültigkeit bewiesen werden, wenn er in einem anderen Zeitrahmen wiedergefunden werden kann.
Die Verwendung unterschiedlicher Kombinationen der verfügbaren Bars, lässt uns die nicht-periodischen Zyklen finden. Ihre Länge kann Zweifel über die Sinnhaftigkeit der Verwendung früherer Signale technischer Indikatoren eliminieren.
4. Von der Theorie zur Praxis
Nachdem wir jetzt alles Wichtige über die fraktale Analyse, den Hurst-Exponenten und die Interpretation seiner Werte kennen, wird es Zeit, die Idee mittels MQL5 zu realisieren.
Legen wir die technischen Voraussetzungen folgendermaßen fest: Wir benötigen ein Programm, das den Hurst-Exponenten für 1000 Bars der Historie eines bestimmten Währungspaares berechnet.
Schritt 1. Erstellen eines neuen Skriptes
Wir sehen eine Eingabemaske, die es auszufüllen gilt. Wir ergänzen weiters #property script_show_inputs, um so ein Währungspaar zu Beginn wählen zu können.
//+------------------------------------------------------------------+ //| New.mq5 | //| Copyright 2016, Piskarev D.M. | //| piskarev.dmitry25@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Piskarev D.M." #property link "piskarev.dmitry25@gmail.com" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| Script Programm Start Funktion | //+------------------------------------------------------------------+ void OnStart() { //--- } //+------------------------------------------------------------------+
Schritt 2. Deklarieren eines Arrays für die Preise und Überprüfen, ob die Historie aktuell für das gewählte Paar über 1001 Bars verfügt.
Warum verwenden wir 1001 Bars, wenn wir uns doch nur auf 1000 Bars festgelegt haben? Antwort: Für die Berechnung benötigen wir zu jedem Wert seinen Vorgänger.
double close[]; //Deklaration des dynamischen Arrays der Schlusskurse int copied=CopyClose(symbol,timeframe,0,barscount1+1,close); //kopieren der Schlusskurse des ausgewählten Paares in //den Array close[] ArrayResize(close,1001); //Festlegen der Arraygröße ArraySetAsSeries(close,true); if(bars<1001) //Überprüfen der Existenz von 1001 Bars { Comment("Too few bars are available! Try another timeframe."); Sleep(10000); //10 Sek. Verzögerung für die Anzeige des Kommentars Comment(""); return; }
Schritt 3. Erzeugen eines Arrays für die logarithmischen Ergebnisse.
Es wird angenommen, dass der Array LogReturns bereits deklariert wurde und der Befehl ArrayResize(LogReturns,1001) ausgeführt wurde.
for(int i=1;i<=1000;i++) LogReturns[i]=MathLog(close[i-1]/close[i]);
Schritt 4. Berechnen des Hurst-Exponenten.
Für eine korrekte Berechnung müssen wir die analysierten Zahl von Bars in Untergruppen aufteilen, so dass in keiner Gruppe weniger als 10 Bars sind. Mit anderen Worten, wir müssen einen Divisor für 1000 finde, so dass das Ergebnis größer als 10 ist. Es gibt 11 Möglichkeiten:
//--- Anzahl der Elemente in jeder Untergruppe num1=10; num2=20; num3=25; num4=40; num5=50; num6=100; num7=125; num8=200; num9=250; num10=500; num11=1000;
Da wir die Daten für die RS-Statistik 11 mal berechnen müssen, wäre sinnvoll dafür eine Funktion zu schreiben. Die Indizes der ersten und letzten Untergruppe, für die die RS-Statistik berechnet werden soll, so wie die Anzahl der zu analysierenden Bars werden als Parameter der Funktion übergeben. Der Algorithmus ist ganz ähnlich dem zu Anfang des Artikels beschriebenen.
//+----------------------------------------------------------------------+ //| Funktion zur Berechnung von R/S | //+----------------------------------------------------------------------+ double RSculc(int bottom,int top,int barscount) { Sum=0.0; //Anfangswert ist Null DevSum=0.0; //Anfangswert ist Null // //--- Berechnen der Summer der LogReturns for(int i=bottom; i<=top; i++) Sum=Sum+LogReturns[i]; //Aufsummieren //--- Berechnen des Durchschnitts M=Sum/barscount; //--- Berechnen der summierten Abweichungen for(int i=bottom; i<=top; i++) { DevAccum[i]=LogReturns[i]-M+DevAccum[i-1]; StdDevMas[i]=MathPow((LogReturns[i]-M),2); DevSum=DevSum+StdDevMas[i]; //Komponente zur Berechnung der Abweichung if(DevAccum[i]>MaxValue) //Falls der Array kleiner als a ist MaxValue=DevAccum[i]; //Maximum eins, der Wert des Elements des Arrays DevAccum wird //dem Maximum zugewiesen if(DevAccum[i]<MinValue) //identische Logik MinValue=DevAccum[i]; } //--- Berechnen der Amplitude R und der Abweichung S R=MaxValue-MinValue; //Die Amplitude ist die Differenz von Maximum und MaxValue=0.0; MinValue=1000; //Minimum S1=MathSqrt(DevSum/barscount); //Berechnen der Standardabweichung //--- Berechnen der R/S-Parameter if(S1!=0)RS=R/S1; //Ausschließen einer Division durch Null // else Alert("Zero divide!"); return(RS); //Rückgabe der RS-Statistik }
Berechnen mittels switch-case.
//--- Berechnen der Log(R/S) for(int A=1; A<=11; A++) //Die Schleife erlaubt die Reduktion von Code { //und berücksichtigen alle möglichen Divisoren switch(A) { case 1: // 100 Gruppen mit je 10 Elementen { ArrayResize(rs1,101); RSsum=0.0; for(int j=1; j<=100; j++) { rs1[j]=RSculc(10*j-9,10*j,10); //Aufruf der Funktion RScuclc RSsum=RSsum+rs1[j]; } RS1=RSsum/100; LogRS1=MathLog(RS1); } break; case 2: // 50 Gruppen mit je 20 Elementen { ArrayResize(rs2,51); RSsum=0.0; for(int j=1; j<=50; j++) { rs2[j]=RSculc(20*j-19,20*j,20); //Aufruf der Funktion RScuclc RSsum=RSsum+rs2[j]; } RS2=RSsum/50; LogRS2=MathLog(RS2); } break; ... ... ... case 9: // 125 and 16 groups { ArrayResize(rs9,5); RSsum=0.0; for(int j=1; j<=4; j++) { rs9[j]=RSculc(250*j-249,250*j,250); RSsum=RSsum+rs9[j]; } RS9=RSsum/4; LogRS9=MathLog(RS9); } break; case 10: // 125 and 16 groups { ArrayResize(rs10,3); RSsum=0.0; for(int j=1; j<=2; j++) { rs10[j]=RSculc(500*j-499,500*j,500); RSsum=RSsum+rs10[j]; } RS10=RSsum/2; LogRS10=MathLog(RS10); } break; case 11: //200 and 10 groups { RS11=RSculc(1,1000,1000); LogRS11=MathLog(RS11); } break; } }
Schritt 5. Die Nutzerfunktion zur Berechnung der linearen Regression mittels der Methode der kleinsten Quadrate (LS).
Die Eingabeparameter sind die Werte aus der berechneten RS-Statistik.
double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6, double Y7,double Y8,double Y9,double Y10,double Y11) { double SumY=0.0; double SumX=0.0; double SumYX=0.0; double SumXX=0.0; double b=0.0; double N[]; //Array zur Sicherung des logarithmischen Divisors double n={10,20,25,40,50,100,125,200,250,500,1000} //Divisor-Array //---Berechnen von N Verhältnissen for (int i=0; i<=10; i++) { N[i]=MathLog(n[i]); SumX=SumX+N[i]; SumXX=SumXX+N[i]*N[i]; } SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11; SumYX=Y1*N1+Y2*N2+Y3*N3+Y4*N4+Y5*N5+Y6*N6+Y7*N7+Y8*N8+Y9*N9+Y10*N10+Y11*N11;
//---Berechnen des Beta-Verhältnisses der Regression oder den notwendigen Hurst-Exponenten
b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX); return(b); }
Schritt 6. Nutzerfunktion zur Berechnung des Erwartungswertes der RS-Statistik. Die Berechnung wurde im theoretischen Teil hergeleitet.
//+----------------------------------------------------------------------+ //| Funktion zur Berechnung des Erwartungswertes E(R/S) | //+----------------------------------------------------------------------+ double ERSculc(double m) //m - 1000 Divisoren { double e; double nSum=0.0; double part=0.0; for(int i=1; i<=m-1; i++) { part=MathPow(((m-i)/i), 0.5); nSum=nSum+part; } e=MathPow((m*pi/2),-0.5)*nSum; return(e); }
Der Code des ganzen Programm könnte wie folgt aussehen:
//+------------------------------------------------------------------+ //| hurst_exponent.mq5 | //| Copyright 2016, Piskarev D.M. | //| piskarev.dmitry25@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Piskarev D.M." #property link "piskarev.dmitry25@gmail.com" #property version "1.00" #property script_show_inputs #property strict input string symbol="EURUSD"; // Symbol input ENUM_TIMEFRAMES timeframe=PERIOD_D1; // Timeframe double LogReturns[],N[], R,S1,DevAccum[],StdDevMas[]; int num1,num2,num3,num4,num5,num6,num7,num8,num9,num10,num11; double pi=3.14159265358979323846264338; double MaxValue=0.0,MinValue=1000.0; double DevSum,Sum,M,RS,RSsum,Dconv; double RS1,RS2,RS3,RS4,RS5,RS6,RS7,RS8,RS9,RS10,RS11, LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,LogRS9, LogRS10,LogRS11; double rs1[],rs2[],rs3[],rs4[],rs5[],rs6[],rs7[],rs8[],rs9[],rs10[],rs11[]; double E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11; double H,betaE; int bars=Bars(symbol,timeframe); double D,StandDev; //+------------------------------------------------------------------+ //| Script Programm Start Funktion | //+------------------------------------------------------------------+ void OnStart() { double close[]; //Deklaration des dynamischen Arrays der Schlusskurse int copied=CopyClose(symbol,timeframe,0,1001,close); //kopieren der Schlusskurse des ausgewählten Paares in //den Array close[] ArrayResize(close,1001); //Festlegen der Arraygröße ArraySetAsSeries(close,true); if(bars<1001) //Überprüfen der Existenz von 1001 Bars { Comment("Too few bars are available! Try another timeframe."); Sleep(10000); //10 Sek. Verzögerung für die Anzeige des Kommentars Comment(""); return; } //+------------------------------------------------------------------+ //| Vorbereiten der Arrays | //+------------------------------------------------------------------+ ArrayResize(LogReturns,1001); ArrayResize(DevAccum,1001); ArrayResize(StdDevMas,1001); //+------------------------------------------------------------------+ //| Array der Logarithmen | //+------------------------------------------------------------------+ for(int i=1;i<=1000;i++) LogReturns[i]=MathLog(close[i-1]/close[i]); //+------------------------------------------------------------------+ //| | //| R/S Analyse | //| | //+------------------------------------------------------------------+ //--- Anzahl der Elemente in jeder Untergruppe num1=10; num2=20; num3=25; num4=40; num5=50; num6=100; num7=125; num8=200; num9=250; num10=500; num11=1000; //--- Berechnen der Log(R/S) for(int A=1; A<=11; A++) { switch(A) { case 1: { ArrayResize(rs1,101); RSsum=0.0; for(int j=1; j<=100; j++) { rs1[j]=RSculc(10*j-9,10*j,10); RSsum=RSsum+rs1[j]; } RS1=RSsum/100; LogRS1=MathLog(RS1); } break; case 2: { ArrayResize(rs2,51); RSsum=0.0; for(int j=1; j<=50; j++) { rs2[j]=RSculc(20*j-19,20*j,20); RSsum=RSsum+rs2[j]; } RS2=RSsum/50; LogRS2=MathLog(RS2); } break; case 3: { ArrayResize(rs3,41); RSsum=0.0; for(int j=1; j<=40; j++) { rs3[j]=RSculc(25*j-24,25*j,25); RSsum=RSsum+rs3[j]; } RS3=RSsum/40; LogRS3=MathLog(RS3); } break; case 4: { ArrayResize(rs4,26); RSsum=0.0; for(int j=1; j<=25; j++) { rs4[j]=RSculc(40*j-39,40*j,40); RSsum=RSsum+rs4[j]; } RS4=RSsum/25; LogRS4=MathLog(RS4); } break; case 5: { ArrayResize(rs5,21); RSsum=0.0; for(int j=1; j<=20; j++) { rs5[j]=RSculc(50*j-49,50*j,50); RSsum=RSsum+rs5[j]; } RS5=RSsum/20; LogRS5=MathLog(RS5); } break; case 6: { ArrayResize(rs6,11); RSsum=0.0; for(int j=1; j<=10; j++) { rs6[j]=RSculc(100*j-99,100*j,100); RSsum=RSsum+rs6[j]; } RS6=RSsum/10; LogRS6=MathLog(RS6); } break; case 7: { ArrayResize(rs7,9); RSsum=0.0; for(int j=1; j<=8; j++) { rs7[j]=RSculc(125*j-124,125*j,125); RSsum=RSsum+rs7[j]; } RS7=RSsum/8; LogRS7=MathLog(RS7); } break; case 8: { ArrayResize(rs8,6); RSsum=0.0; for(int j=1; j<=5; j++) { rs8[j]=RSculc(200*j-199,200*j,200); RSsum=RSsum+rs8[j]; } RS8=RSsum/5; LogRS8=MathLog(RS8); } break; case 9: { ArrayResize(rs9,5); RSsum=0.0; for(int j=1; j<=4; j++) { rs9[j]=RSculc(250*j-249,250*j,250); RSsum=RSsum+rs9[j]; } RS9=RSsum/4; LogRS9=MathLog(RS9); } break; case 10: { ArrayResize(rs10,3); RSsum=0.0; for(int j=1; j<=2; j++) { rs10[j]=RSculc(500*j-499,500*j,500); RSsum=RSsum+rs10[j]; } RS10=RSsum/2; LogRS10=MathLog(RS10); } break; case 11: { RS11=RSculc(1,1000,1000); LogRS11=MathLog(RS11); } break; } } //+----------------------------------------------------------------------+ //| Berechnen des Hurst-Exponenten | //+----------------------------------------------------------------------+ H=RegCulc1000(LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8, LogRS9,LogRS10,LogRS11); //+----------------------------------------------------------------------+ //| Berechnen des Erwartungswertes log(E(R/S)) | //+----------------------------------------------------------------------+ E1=MathLog(ERSculc(num1)); E2=MathLog(ERSculc(num2)); E3=MathLog(ERSculc(num3)); E4=MathLog(ERSculc(num4)); E5=MathLog(ERSculc(num5)); E6=MathLog(ERSculc(num6)); E7=MathLog(ERSculc(num7)); E8=MathLog(ERSculc(num8)); E9=MathLog(ERSculc(num9)); E10=MathLog(ERSculc(num10)); E11=MathLog(ERSculc(num11)); //+----------------------------------------------------------------------+ //| Berechnen des Beta des Erwartungswertes E(R/S) | //+----------------------------------------------------------------------+ betaE=RegCulc1000(E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11); Alert("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3)); Comment("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3)); } //+----------------------------------------------------------------------+ //| Funktion zur Berechnung von R/S | //+----------------------------------------------------------------------+ double RSculc(int bottom,int top,int barscount) { Sum=0.0; //Anfangswert ist Null DevSum=0.0; //Anfangswert ist Null // //--- Berechnen der Summer der LogReturns for(int i=bottom; i<=top; i++) Sum=Sum+LogReturns[i]; //Aufsummieren //--- Berechnen des Durchschnitts M=Sum/barscount; //--- Berechnen der summierten Abweichungen for(int i=bottom; i<=top; i++) { DevAccum[i]=LogReturns[i]-M+DevAccum[i-1]; StdDevMas[i]=MathPow((LogReturns[i]-M),2); DevSum=DevSum+StdDevMas[i]; //Komponente zur Berechnung der Abweichung if(DevAccum[i]>MaxValue) //Falls der Array kleiner als a ist MaxValue=DevAccum[i]; //Maximum eins, der Wert des Elements des Arrays DevAccum wird //dem Maximum zugewiesen if(DevAccum[i]<MinValue) //identische Logik MinValue=DevAccum[i]; } //--- Berechnen der Amplitude R und der Abweichung S R=MaxValue-MinValue; //Die Amplitude ist die Differenz von Maximum und MaxValue=0.0; MinValue=1000; //Minimum S1=MathSqrt(DevSum/barscount); //Berechnen der Standardabweichung //--- Berechnen der R/S-Parameter if(S1!=0)RS=R/S1; //Ausschließen einer Division durch Null // else Alert("Zero divide!"); return(RS); //Rückgabe der RS-Statistik } //+----------------------------------------------------------------------+ //| Berechnung er Regression | //+----------------------------------------------------------------------+ double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6, double Y7,double Y8,double Y9,double Y10,double Y11) { double SumY=0.0; double SumX=0.0; double SumYX=0.0; double SumXX=0.0; double b=0.0; //Array zur Sicherung des logarithmischen Divisors double n[]={10,20,25,40,50,100,125,200,250,500,1000}; //---Berechnen von N Verhältnissen ArrayResize(N,11); for (int i=0; i<=10; i++) { N[i]=MathLog(n[i]); SumX=SumX+N[i]; SumXX=SumXX+N[i]*N[i]; } SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11; SumYX=Y1*N[0]+Y2*N[1]+Y3*N[2]+Y4*N[3]+Y5*N[4]+Y6*N[5]+Y7*N[6]+Y8*N[7]+Y9*N[8]+Y10*N[9]+Y11*N[10]; //---Berechnen des Beta-Verhältnisses der Regression oder den notwendigen Hurst-Exponenten b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX); return(b); } //+----------------------------------------------------------------------+ //| Funktion zur Berechnung des Erwartungswertes E(R/S) | //+----------------------------------------------------------------------+ double ERSculc(double m) //m - 1000 Divisoren { double e; double nSum=0.0; double part=0.0; for(int i=1; i<=m-1; i++) { part=MathPow(((m-i)/i), 0.5); nSum=nSum+part; } e=MathPow((m*pi/2),-0.5)*nSum; return(e); }
Sie können den Code nach eigenem Ermessen ändern, um weitere Merkmale zu berechnen oder eine benutzerfreundliche Schnittstelle zu erstellen.
Im letzten Kapitel diskutieren wir bestehende Softwareversionen.
5. Softwareversionen
Es gibt mehrere Versionen des Algorithmus zur R/S-Analyse. Die Umsetzung ist in der Regel jedoch verkürzt und überlässt die analytische Arbeit dem Nutzer. Ein solch ein Beispiel ist das Matlab Paket.
Es gibt auch für MetaTrader 5 im Market solch ein Programm namens Fractal Analysis, das es dem Nutzer eine fraktale Analyse der Finanzmärkte erlaubt. Schauen wir es uns genauer an.
5.1. Eingaben
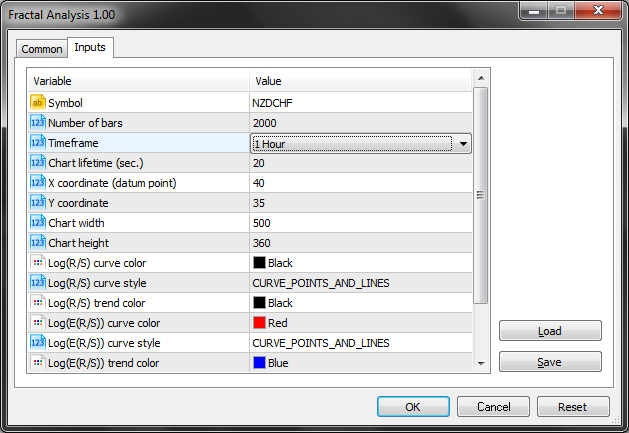
Tatsächlich benötigen wir nur drei Eingabeparameter (Symbol, Anzahl der Bars Number und den Zeitrahmen) aus allen Möglichkeiten.
Wie der Screenshot unten zeigt, erlaubt Fractal Analysis die Auswahl des Währungspaares unabhängig vom Chart auf dem es gestartet wurde: Das wichtigste ist Bestimmung des Symbols im Eingabefenster.
Bestimmen der Anzahl der Bars eines Zeitrahmens durch den Parameter darunter.
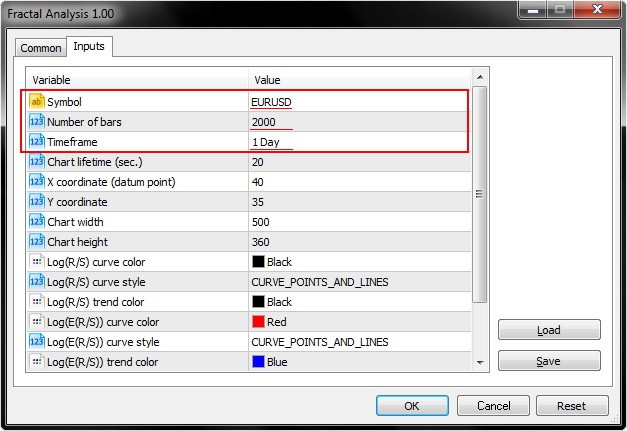
Beachten Sie auch den Laufzeitparameter, der die Anzahl der Sekunden festlegt, innerhalb derer Sie mit dem Programm arbeiten wollen. Nach dem Klick auf OK, erscheint die Analyse in der unteren linken Ecke des MetaTrader 5 Terminals. Ein Beispiel zeigt der Screenshot unten.
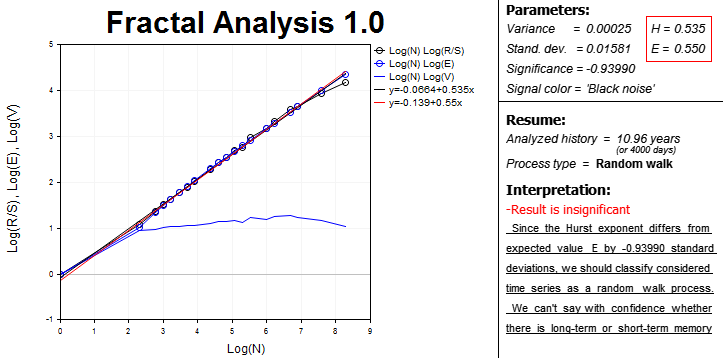
Es werden alle Daten und Ergebnisse der fraktalen Analyse auf dem Chart in zwei Blöcken angezeigt.
Links ist der Bereich mit der grafischen Abhängigkeiten im logarithmischen Maßstab:
- R/S-Statistik der Anzahl von Beobachtungen;
- Der Erwartungswert der R/S-Statistik E(R/S) der Anzahl von Beobachtungen;
- Die V-Statistik der Anzahl von Beobachtungen.
Es ist ein interaktiver Bereich, der die Verwendung von Werkzeugen des MetaTrader 5 für die Chartanalyse beinhaltet, da es manchmal recht schwierig ist, die Länge des Zyklus „nach Augenmaß“ zu finden.
Die Gleichungen der Kurven und der Trendlinie werden auch gezeigt. Die Steigungen der Trendlinien werden für die Bestimmung des Hurst-Exponent (H) verwendet. Der Erwartungswert des Hurst-Exponenten (E) wird auch berechnet. Diese Gleichungen finden sich im rechten Block. Varianz, Signifikanz Analyse und die Farbe des Signals finden sich auch da.
Der Übersichtlichkeit wegen berechnet das Programm die Länge der analysierten Periode in Tagen. Bedenke Sie das, wenn Sie die Signifikanz auf der historischen Basis beurteilen.
Die Zeile "Process type" bestimmt den Parameter der Zeitreihen:
- persistent;
- anti-persistent;
- Random Walk.
Schließlich zeigt der Interpretationsblock eine kurze Zusammenfassung, die Anfängern der fraktalen Analyse die Interpretation der Ergebnisse erleichtert.
5.2. Anwendungsbeispiel
Wir müssen angeben, welches Symbol mit welchem Zeitrahmen analysiert werden soll. Nehmen wir NZDCHF und verwenden die Kurse des Zeitrahmens H1.
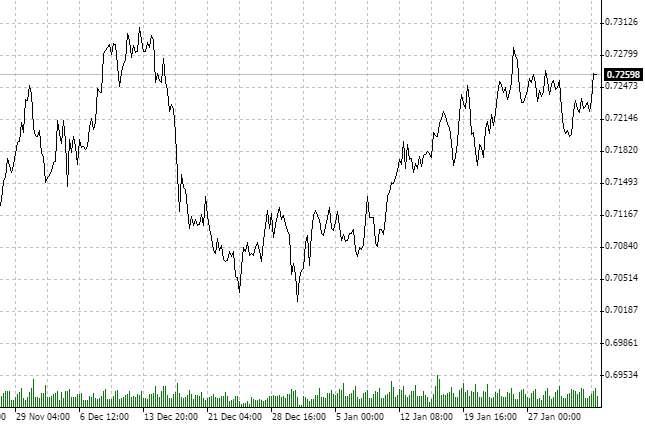
Bitte beachten Sie, dass der Markt sich über die letzten zwei Monate in einer Konsolidierung befindet. Nochmal, wir sind NICHT an anderen Anlagehorizonten interessiert. Es ist durchaus möglich, dass der D1-Chart einen Auf- oder Abwärtstrend zeigen könnte. Wir haben H1 und eine bestimmte Menge an historischen Daten ausgewählt.
Augenscheinlich ist der Prozess anti-persistent. Prüfen wir das mit der fraktalen Analyse.
Vom 21.11 bis 3.02, haben wir eine Historie von 75 Tagen. Nach der Umwandlung der 75 Tage in Stunden erhalten wir Daten über 1800 Stunden. Da diese Zahl nicht allzu groß ist nehmen wir eine runde Näherung — 2000 Stunden für die Analyse.
Die Ergebnisse sind unten aufgeführt:
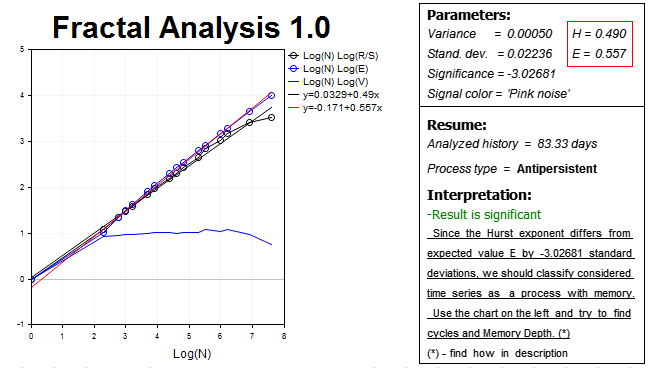
Unsere Hypothese wurde bestätigt, der Markt zeigt einen erheblichen nicht-persistenten Prozess in diesem Zeithorizont — der Hurst-Exponent H=0.490, was praktisch 3 Standardabweichungen kleiner ist als der Erwartungswert E=0.557.
Korrigieren wir das Ergebnis durch die Verwendung eines etwas höheren Zeitrahmens (H2) und demgemäß einer halb so großen Zahl von Bars (1000 Werte). Die Ergebnisse sind wie folgt:
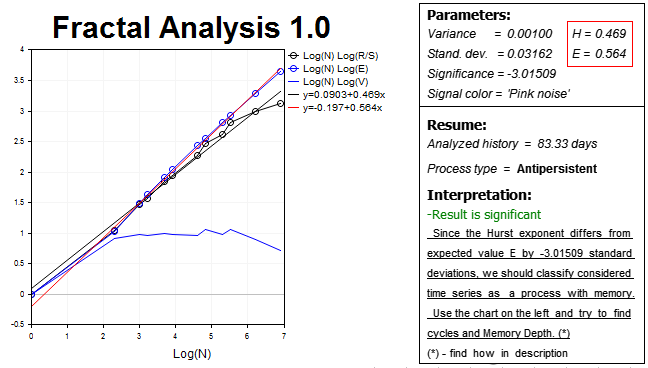
Wir sehen wieder einen anti-persistenten Prozess. Der Hurst-Exponent H=0.469 ist mehr als drei Standardabweichungen kleiner als der Erwartungswert E=0.564.
Versuchen wir nun Zyklen zu finden.
Wir kehren zurück zu H1 und definieren den Moment, da die R/S-Kurve sich von E(R/S) löst. Dieser Punkt ist durch die Bildung von Scheitelpunkten in der graphischen Darstellung der V-Statistik gekennzeichnet. So können wir die ungefähre Zyklenlänge bestimmen.
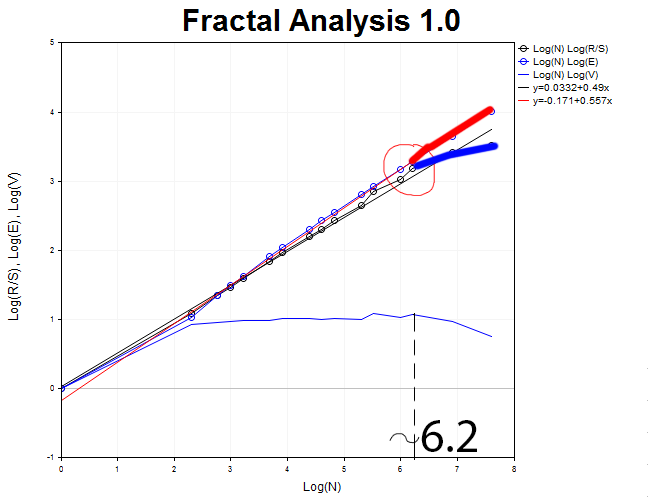
Sie ist ungefähr N1 = 2.71828^6.2 = 493 Stunden oder 21 Tage.
Natürlich garantiert ein einzelnes Experiment keine allgemeine Gültigkeit der Ergebnisse. Wie bereits erwähnt, muss man verschiedene Zeitrahmen und alle Arten von Kombinationen von "Zeitrahmen — Anzahl Bars" auswählen, um die Gültigkeit der Ergebnisse sicherzustellen.
Führen wir eine Analyse mit 1000 Bars des H2-Zeitrahmens durch.
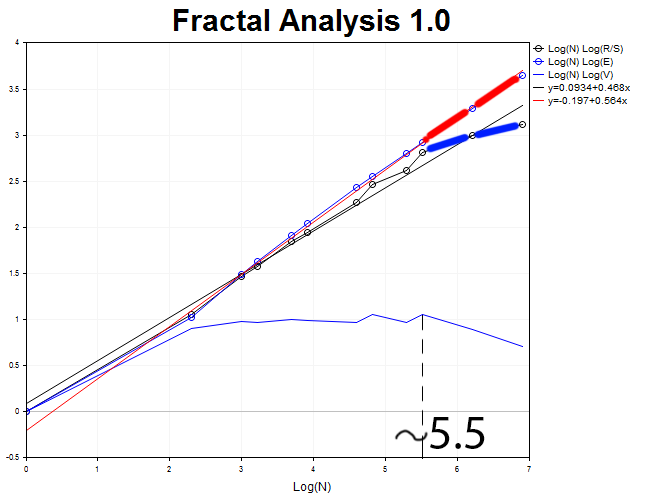
Die Zyklenlänge ist N2 = 2.71828^5.5 = 245 Zwei-Stundenperiode (ungefähr zwanzig Tage).
Analysieren wir jetzt den Zeitrahmen M30 mit 4000 Werten. Wir erhalten einen anti-persistenten Prozess mit dem Hurst-Exponenten H = 0.492 und dem Erwartungswert E=0.55, der H um 3,6 Standardabweichungen überschreitet.
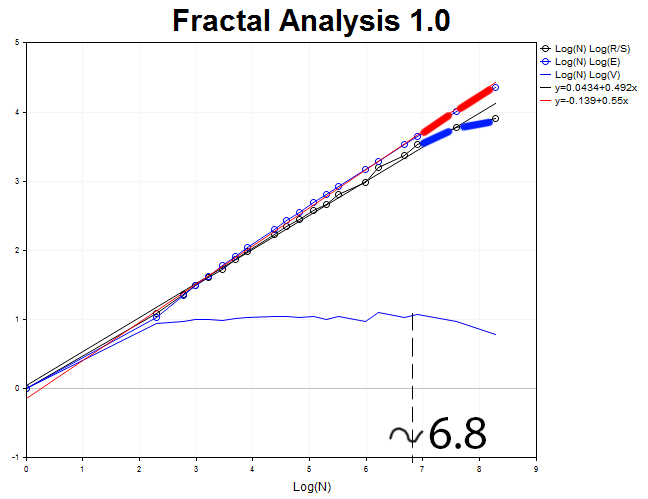
Zykluslänge N3 = 2.71828^6.8 = 898 Halbstundenperioden (18.7 days).
Drei Tests mögen als Trainingsbeispiele ausreichen. Finden wir einen Mittelwert der ermittelten Zyklenlängen M= (N1 + N2 + N3)/3 = (21 + 20 + 18.7)/3 = 19.9 (20 days).
Im Ergebnis erhalten wir eine Zeitspanne, innerhalb der sich technischen Daten als zuverlässig erwiesen haben und sich die Entwicklung einer Handelsstrategie lohnen sollte. Wie bereits erwähnt, ist die Berechnung und Analyse für einen Investmenthorizont von zwei Monaten gedacht. Das heißt, die Analyse ist für einen Intratageshandel nicht relevant, da hier ultra kurze zyklische Prozesse auftreten, deren An- oder Abwesenheit wir bestätigen wollen. Werden dies Zyklen nicht erkannt, verliert die technischen Analyse ihre Relevanz und Effizienz. In diesem Fall sind "News_Trading" und die Bestimmung des "Market-Sentiments" die vernünftigsten Lösungen.
Schlussfolgerung
Die Fraktale Analyse ist eine Synergie aus technischen, fundamentalen und statistischen Ansätzen für eine Prognose der Dynamik des Marktes. Dies ist eine vielseitige Daten-Verarbeitung-Methode: Die R/S-Analyse und die Hurst-Exponenten werden erfolgreich in Geographie, Biologie, Physik und Wirtschaftswissenschaften eingesetzt. Die Fraktale Analyse kann für die Entwicklung von Wertungs- oder Schätzmodelle angewendet werden, die von Banken zur Analyse der Zahlungsfähigkeit von Kreditnehmern verwendet wird.
Wie bereits zu Beginn gesagt: Um im Forexmarkt erfolgreich handeln zu können, sollten wir etwas mehr wissen als die anderen. Etwaige Missverständnisse vorwegnehmend möchte ich den Leser warnen, dass der Markt dazu tendiert den Analysten zu "täuschen". Daher ist es wichtig das Vorhandensein von nicht-periodischen Zyklen höherer oder kleinerer Zeitrahmen zu prüfen. Können sie in anderen Zeitrahmen nicht entdeckt werden, sind sie wohl nur ein Marktrauschen.