Ökonometrischer Ansatz zur Chartanalyse
Denis Kirichenko | 14 März, 2016
Theorien ohne Fakten sind manchmal etwas dürftig, aber Fakten ohne Theorien sind absolut nutzloss
K. Boulding
Einleitung
Ich höre es oft: die Märkte sind volatil und es gibt keine Stabilität. Und das macht langfristiges Handeln mit Erfolg unmöglich. Doch stimmt das auch? Versuchen wir diese Aussage wissenschaftlich zu analysieren, und zwar mit Hilfe der ökonometrischen Analysemethode. Warum gerade sie? Zum einen steht die MQL-Community auf Exaktheit, die von Mathematik und Statistik ja geliefert wird. Und zum anderen ist das noch nie so beschreiben worden, wenn ich mich nicht irre .
Hier möchte ich gleich anmerken, dass das Problem langfristigen Handels mit Erfolg nicht in einem einzigen Beitrag gelöst werden kann. Ich beschreibe hier nur einige Diagnosemethoden für das ausgewählte Modell, die sich hoffentlich für weitere Verwendung als nützlich erweisen.
Zusätzlich dazu versuche ich so klar wie möglich den trockenen Stoff voller Formeln. Theoreme und Hypothesen zu erläutern. Ich erwarte jedoch von den Lesern, dass sie sich mit den Grundlagen der Statistik auskennen, wie z.B. Hypothese, statistische Signifikanz, Statistik (statistisches Kriterium), Streuung, Verteilung, Regression, Autokorrelation usw.
1. Charakteristika von Zeitreihen
Es ist klar, dass der Gegenstand der Analyse eine Kursreihe (seine Derivate) ist, die ihrerseits eine Zeitreihe darstellt.
Ökonometriker untersuchen Zeitreihen vom Standpunkt der Häufigkeitsmethoden (Spektralanalyse, Wavelet-Analyse) und den Methoden des Zeitbereichs aus (Kreuz-Korrelationsanalyse, Autokorrelationsanalyse). Dem Leser liegt ja bereits der Beitrag "Aufbau der Spektralanalyse" vor, der die Häufigkeitsmethoden beschreibt. Ich schlage hier einen Blick auf die Zeitbereichsmethoden , die Autokorrelationsanalyse und insb. die Analyse von bedingten Varianzen vor.
Nicht-linear Modelle beschreiben das Verhalten von Kurs-Zeitreihen besser als lineare. Deshalb konzentrieren wir uns in diesem Beitrag aucf auf nicht-lineare Modelle.
Kurs-Zeit reihen weisen bestimmte Merkmale auf, die nur von gewissen ökonometrischen Modellen berücksichtigt werden können. Derartige Merkmale umfassen: "fat tail" ("fette Zipfel") Clusterbildung von Volatilität und den Leverage-Effekt.
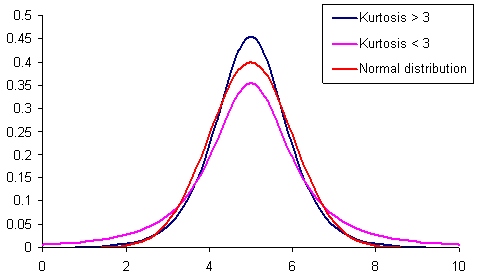
Abb. 1 Verteilungen mit unterschiedlicher Wölbung.
Abb. 1 zeigt drei Verteilungen mit unterschiedlicher Wölbung (Spitzigkeit). Eine Verteilung, deren Spitze geringer als die normale Verteilung ist, hat öfter als andere die sog. "fette Zipfel", sie sind in rosa dargestellt.
Für uns muss die Verteilung die Wahrscheinlichkeitsdichte eines zufälligen Wertes zeigen, die zum Zählen der Werte der untersuchten Reihen verwendet wird
Mit Clusterbildung der Volatilität meinen wir folgendes Phänomen: Einem Zeitraum hoher Volatilität folgt der gleiche Zeitraum und einem geringer Volatilität folgt ebenso der gleiche. Wenn Kurse gestern fluktuierten, dann wird das heute höchstwahrscheinlich auch der Fall sein. Es gibt als eine gewisse Trägheit der Volatilität. Abb. 2 zeigt, dass Volatilität in Clustens auftritt.
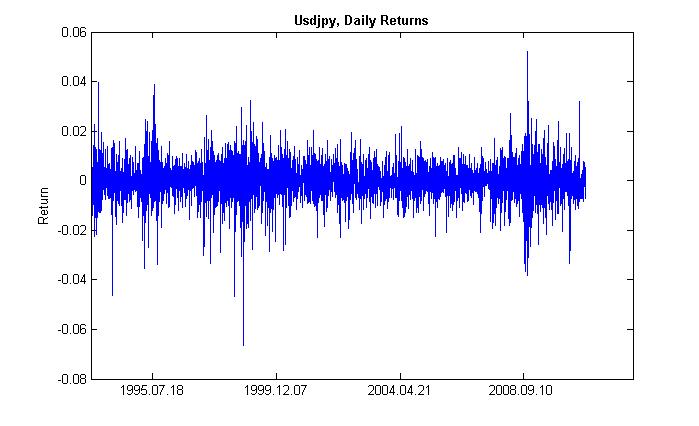
Abb. 2 Volatilität der täglichen 'Returns' von USDJPY, ihre Clusterbildung.
Der Leverage-Effekt besteht in der Volatilität eines fallenden Marktes und ist höher als der eines steigenden Marktes . Dies wird durch den Anstieg des Leverage-Koeffizienten, wenn die Aktienkurse fallen, gefordert, der vom Verhältnis zwischen geliehenem und eigenem Kapital abhängt. Dieser Effekt betrifft jedoch den Aktienmarkt und nicht den Devisenmarkt. Ihn werden wir jedoch nicht weiter betrachten.
2. Das GARCH-Modell
Unser Hauptanliegen ist die Prognose des Wechselkurses mit Hilfe eines Modells. Ökonometriker beschreiben mittels mathematischer Modelle den einen oder anderen Effekt, der in Bezug auf seine Menge abgeschätzt werden kann. Einfacher ausgedrückt: Sie passen einem Erigenis eine Formel entsprechend an und beschreiben so das Ereignis.
Vor dem Hintergrund der Tatsache, dass die analysierten Zeitreihen Eigenschaften besitzen (wie oben bereits gesagt), ist das optimale Modell zur Berücksichtigung dieser Eigenschaften ein nicht-lineares Modell. Und das GARCH-Modell ist halt eins der universellsten nicht-linearen Modelle. Wie kann es uns helfen? Innerhalb seines Korpus (Funktion), betrachtet es die Volatilität einer Reihe, d.h. die Variabilität der Verteilung zu unterschiedlichen Punkten der Beobachtung. Ökonometriker haben diesem Effekt einen abstrusen Namen gegeben: Heteroskedastizität (vom griech. - hetero = unterschiedlich und skedasis = Verteilung).
Wenn wir uns die Formel an sich betrachten, sehen wir, dass dieses Modell impliziert, dass die aktuelle Streuungsvariabilität (σ2t) sowohl von vorausgegangenen Änderungen der Parameter (ϵ2t-i) als auch vorausgegangegnen Einschätzungen der Streuung (sog. «Old News») (σ2t-i) beeinflusst wird:
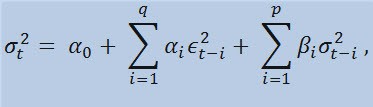
mit Grenzen,
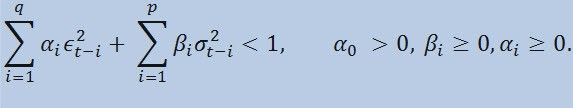
wobei: ϵt - nicht-normalisierte Innovationen; α0 , βi , αi , q (Reihenfolge der ARCH-Mitglieder ϵ2), p (Reihenfolge der GARCH-Mitglieder σ2) - abgeschätzte Parameter und Reihenfolge der Modelle ist.
3. Return-Indikator
Wir schätzen tatsächlich nicht die Kursreihen selbst ab, sondern die Return-Reihen Der Logarithmus der Kursveränderung (konstant beladene Returns) ist als ein natürlicher Logarithmus des Return-Prozentwerts festgelegt:
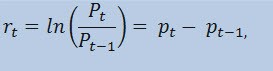
wobei:
- Pt - den Wert der Kursreihe zu einer Zeit t darstellt;
- Pt-1 - den Wert der Kursreihe zu einer Zeit t -1 darstellt;
- pt = ln(Pt) - den natürlichen Logarithmus Pt darstellt.
Der Hauptgrund warum die Arbeit mit Returns empfehlenswerter ist als die Arbeit mit Kurses, liegt ganz praktisch darin, dass Returns besser statistische Merkmale haben.
Daher erzeugen wir einen Return-IndikatorReturnsIndicator.mq5, der uns viele Dienste erweisen wird. An dieser Stelle verweise ich auf den Betrag "Angepasste Indikatoren für Neulinge", der den Algorithmus der Erzeugung von Indikatoren verständlich erklärt. Deshalb finden Sie hier nur den Code, wo die erwähnte Formel implementiert ist. Meiner Meinung nach ist er recht einfach und muss nicht ausführlich erklärt werden.
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // size of the array price[] const int prev_calculated, // number of bars available at the previous call const int begin, // index of the array price[] the reliable data starts from const double& price[]) // array for the calculation itself { //--- int start; if(prev_calculated<2) start=1; // start filling ReturnsBuffer[] from the 1-st index, not 0. else start=prev_calculated-1; // set 'start' equal to the last index in the arrays for(int i=start;i<rates_total;i++) { ReturnsBuffer[i]=MathLog(price[i]/price[i-1]); } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
Ich möchte nur auf eines hinweisen: die Reihe an Returns ist immer um 1 Element kleiner als die primäre Reihe. Daher berechnen wir das Array der Returns mit Beginn beim zweiten Element, und das erste wird immer = 0 sein.
Mit Hilfe des ReturnsIndicator Indikators, haben wir also eine zufällige Zeitreihe erhalten, die wir für unsere Untersuchungen verwenden wollen.
4. Statistische Tests
Jetzt sind die statistischen Tests dran. Sie werden durchgeführt, um festzustellen, ob die Zeitreihe irgendwelche Zeichen aufweist, die belegen, dass der Einsatz eines oder des anderen Modells passen würde. In unserem Fall, ist so ein Modell das GARCH-Modell.
Mit Hilfe des Q-Tests von Ljung-Box-Pierce prüfen Sie, ob die Autokorrelationen der Reihen zufällig sind oder ob es eine Beziehung/Zusammenhang gibt. Dafür müssen wir eine neue Funktion schreiben. Mit Autokorrelation meine ich hier eine Korrelation (wahrscheinlicher Zusammenhang) zwischen den Werten derselben Zeitreihe X (t) zu den Zeitmomenten t1 und t2. Grenzen beide Momente (t1 und t2) aneinander (einer folgt dem anderen), suchen wir nach einem Zusammenhang zwischen den Mitgliedern der Reihe und den Mitgliedern derselben Reihe, die um eine Zeiteinheit verschoben ist: x1, x2, x3, ... и x1+1, x2+1, x3+1, ... Diesen Effekt verschobener Mitglieder nennt man Verzögerung. Der Wert dieser Verzögerung kann jede positive Ziffer haben.
Die folgende Bemerkung kommt quasi in Klammern, doch möchte ich Ihnen folgendes mitteilen. so weit ich weiß, besitzen weder С++, noch MQL5 Standard-Libraries, die komplexe und durchschnittliche statistische Berechnungen leisten können. Derartige Berechnungen werden meist mittels spezielleer Statistik-Tools angestellt. Für mich ist es zur Lösung unseres Problems leichter, Tools wie z.B. Matlab, STATISTICA 9 usw. zu verwenden. Ich habe mich jedoch gegen die Verwendung von externen Libraries entscheiden, zum einen, um zu zeigen, wie leistungsstark die MQL5-Sprache für Berechnungen ist und zweitens... habe ich selbst eine Menge gelernt, als ich den MQL-Code geschrieben habe.
Wir müssen uns also jetzt folgendes merken:. Um den Q-Test ausführen zu können, brauchen wir komplexe Zahlen, und deshalb habe ich die Complex-Klasse geschaffen, die man am besten CComplex nennt. Und an diesem Punkt habe ich mich ein wenig zurück gelehnt. Ich bin sicher, dass meine Leser gut vorbereitet sind, daher verzichte ich auf eine Erklaärung, was eine komplexe Zahl ist. Ich persönlich mag die Funktionen, die die Fourier-Transformationen-Transformation berechnen, die mit MQL5 und MQL4 veröffentlicht wurden, nicht besonders, da hier stillschweigend komplexe Zahlen verwendet werden. Und außerdem gibt es noch einen Stolperstein - mathematische Operators können in MQL5 nicht aufgehoben werden. Also musste ich nach anderen Ansätzen suchen und die Standard 'C'-Bezeichnung vermeiden. Ich habe die Klasse der komplexen zahl folgendermaßen implementiert:
class Complex { public: double re,im; //re -real component of the complex number, im - imaginary public: void Complex(){}; //default constructor void setComplex(double rE,double iM){re=rE; im=iM;}; //set method (1-st variant) void setComplex(double rE){re=rE; im=0;}; //set method (2-nd variant) void ~Complex(){}; //destructor void opEqual(const Complex &y){re=y.re;im=y.im;}; //operator= void opPlus(const Complex &x,const Complex &y); //operator+ void opPlusEq(const Complex &y); //operator+= void opMinus(const Complex &x,const Complex &y); //operator- void opMult(const Complex &x,const Complex &y); //operator* void opMultEq(const Complex &y); //operator*= (1-st variant) void opMultEq(const double y); //operator*= (2-nd variant) void conjugate(const Complex &y); //conjugation ofcomplexnumbers double norm(); //normalization };
So kann z.B. die Addition zweier komplexer Zahlen mit Hilfe der Methode opPlus vonstatten gehen und Subtraktion funktioniert mit Hilfe der Methode opMinus, usw. Wenn Sie nur den Code c = a + b schreiben (wobei a, b und c komplexe Zahlen sind), zeigt Ihnen der Compiler eine Fehlermeldung an. Folgenden Ausdruck nimmt er jedoch an: c.opPlus(a,b).
Und jeder Anwender kann ggf. die Reihe der Methoden der Complex-Klasse ausweiten. Sie können beispielsweise einen Divisions-Operator hinzufügen.
Des Weiteren brauche ich Hilfsfunktionen, die die Arrays der komplexen Zahlen verarbeiten. Und diese habe ich außerhalb der Complex-Klasse implementiert,. damit sie nicht die Verarbeitung der Array-Elemente in der Klasse zyklisch ausführen, sondern direkt mit den Arrays via einer Übertragung per Verweis arbeiten. Insgesamt gibt es drei Funktionen:
- getComplexArr (liefert ein zweidimensionales Array echter Zahlen von einem Array komplexer Zahlen);
- setComplexArr (liefert ein Array komplexer Zahlen von einem eindimensionalen Array echter Zahlen);
- setComplexArr2 (liefert ein Array komplexer Zahlen von einem zweidimensionalen Array echter Zahlen ).
Hier muss angemerkt werden, dass die Funktionen Arrays liefern, die via Verweis übertragen werden. Deshalb enthält ihr Korpus ja auch keinen 'liefern'-Operator. Doch bei logischem Schlussfolgern können wir trotzdem von einem Return sprechen, trotz des Typs 'nichtig'.
Die Klasse der komplexen Zahlen und Hilfsfunktionen sind in der Header-Datei Complex_class.mqh beschrieben.
Wenn wir dann Tests durchführen, brauchen wir dazu die Autokorrelationsfunktion und die Funktion der Fourier-Transformationen. Daher müssen wir eine neue Klasse erzeugen, die wir CFFT nennen. Sie verarbeitet die Arrays komplexer Zahlen für die Fourier-Transformationen Und so sieht die Fourier-Transformationen-Klasse aus:
class CFFT { public: Complex Input[]; //input array of complex numbers Complex Output[]; //output array of complex numbers public: bool Forward(const uint N); //direct Fourier transformation bool InverseT(const uint N,const bool Scale=true); //weighted reverse Fourier transformation bool InverseF(const uint N,const bool Scale=false); //non-weighted reverse Fourier transformation void setCFFT(Complex &data1[],Complex &data2[],const uint N); //set method(1-st variant) void setCFFT(Complex &data1[],Complex &data2[]); //set method (2-nd variant) protected: void Rearrange(const uint N); // regrouping void Perform(const uint N,const bool Inverse); // implementation of transformation void Scale(const uint N); // weighting };
Hier sei darauf hingewiesen, dass alle Fourier-Transformationen mit Arrays ausgeführt werden, deren Länge die Bedingung 2^N erfüllt (wobei N eine Zweierpotenz ist). Normalerweise entspricht die Arraylänge nicht 2^N, doch in diesem Fall wird die Arraylänge auf den Wert 2^N für 2^N >= n erhöht, wobei 'n' die Arraylänge bezeichnet. Dem Array hinzugefügte Elemente = 0. Eine solche Verarbeitung von Arrays findet innerhalb des Korpus der autocorr Funktion mit Hilfe der Hilfsfunktion nextpow2 und der pow Funktion statt:
int nFFT=pow(2,nextpow2(ArraySize(res))+1); //power rate of two
Haben wir also ein ursprüngliches Array, dessen Länge (n) = 73585, dann liefert uns die nextpow2 Funktion den wert 17, wobei 2^17 = 131072 ist. Anders gesagt: der erhaltene Wert ist größer als n mal pow(2, ceil(log(n)/log(2))). Danach berechnen wir den Wert von nFFT: 2^(17+1) = 262144. Dies ist die Länge des Hilfsarrays, dessen Elemente von 73585 bis 262143 alle = 0 sind.
Die Fourier-Transformationen-Klasse ist in der Header-Datei FFT_class.mqh beschrieben.
Aus Platzgründen, spare ich mir die Beschreibung der Implementierung der CFFT Klasse. Für alle Interessierten unter Ihnen: die Beschreibung findet sich in der dem Beitrag angehängten 'Include'-Datei. Kommen wir nun zur Autokorrelationsfunktion.
void autocorr(double &ACF[],double &res[],int nLags) //1-st variant of function /* selective autocorrelation function (ACF) for unidimensional stochastic time series ACF - output array of calculated values of the autocorrelation function; res - array of observation of stochastic time series; nLags - maximum number of lags the ACF is calculated for. */ { Complex Data1[],Data21[], //input arrays of complex numbers Data2[],Data22[], //output arrays of complex numbers cData[]; //array of conjugated complex numbers double rA[][2]; //auxiliary two-dimensional array of real numbers int nFFT=pow(2,nextpow2(ArraySize(res))+1); //power rate of two ArrayResize(rA,nFFT);ArrayResize(Data1,nFFT); //correction of array sizes ArrayResize(Data2,nFFT);ArrayResize(Data21,nFFT); ArrayResize(Data22,nFFT);ArrayResize(cData,nFFT); double rets1[]; //an auxiliary array for observing the series double m=mean(res); //arithmetical mean of the array res ArrayResize(rets1,nFFT); //correction of array size for(int t=0;t<ArraySize(res);t++) //copy the initial array of observation // to the auxiliary one with correction by average rets1[t]=res[t]-m; setComplexArr(Data1,rets1); //set input array of complex numbers CFFT F,F1; //initialize instances of the CFFT class F.setCFFT(Data1,Data2); //initialize data-members for the instance F F.Forward(nFFT); //perform direct Fourier transformation for(int i=0;i<nFFT;i++) { Data21[i].opEqual(F.Output[i]);//assign the values of the F.Output array to the Data21 array; cData[i].conjugate(Data21[i]); //perform conjugation for the array Data21 Data21[i].opMultEq(cData[i]); //multiplication of the complex number by the one adjacent to it //results in a complex number that has only real component not equal to zero } F1.setCFFT(Data21,Data22); //initialize data-members for the instance F1 F1.InverseT(nFFT); //perform weighter reverse Fourier transformation getComplexArr(rA,F1.Output); //get the result in double format after //weighted reverse Fourier transformation for(int i=0;i<nLags+1;i++) { ACF[i]=rA[i][0]; //in the output ACF array save the calculated values //of autocorrelation function ACF[i]=ACF[i]/rA[0][0]; //normalization relatively to the first element } }
Wir haben jetzt die AFC-Werte für eine festgelegte Anzahl an Verzögerungen berechnet, sodass wir jetzt die Autokorrelationsfunktion für den Q-Test verwenden können. Die Testfunktion an sich sieht so aus:
void lbqtest(bool &H[],double &rets[]) /* Function that implements the Q test of Ljung-Box-Pierce H - output array of logic values, that confirm or disprove the zero hypothesis on the specified lag; rets - array of observations of the stochastic time series; */ { double lags[3]={10.0,15.0,20.0}; //specified lags int maxLags=20; //maximum number of lags double ACF[]; ArrayResize(ACF,21); //epmty ACF array double acf[]; ArrayResize(acf,20); //alternate ACF array autocorr(ACF,rets,maxLags); //calculated ACF array for(int i=0;i<20;i++) acf[i]=ACF[i+1]; //remove the first element - one, fill //alternate array double alpha[3]={0.05,0.05,0.05}; //array of levels of significance of the test /*Calculation of array of Q statistics for selected lags according to the formula: L |----| \ Q = T(T+2) || (rho(k)^2/(T-k)), / |----| k=1 where: T is range, L is the number of lags, rho(k) is the value of ACF at the k-th lag. */ double idx[]; ArrayResize(idx,maxLags); //auxiliary array of indexes int len=ArraySize(rets); //length of the array of observations int arrLags[];ArrayResize(arrLags,maxLags); //auxiliary array of lags double stat[]; ArrayResize(stat,maxLags); //array of Q statistics double sum[]; ArrayResize(sum,maxLags); //auxiliary array po sums double iACF[];ArrayResize(iACF,maxLags); //auxiliary ACF array for(int i=0;i<maxLags;i++) { //fill: arrLags[i]=i+1; //auxiliary array of lags idx[i]=len-arrLags[i]; //auxiliary array of indexes iACF[i]=pow(acf[i],2)/idx[i]; //auxiliary ACF array } cumsum(sum,iACF); //sum the auxiliary ACF array //by progressive total for(int i=0;i<maxLags;i++) stat[i]=sum[i]*len*(len+2); //fill the array Q statistics double stat1[]; //alternate of the array of Q statistics ArrayResize(stat1,ArraySize(lags)); for(int i=0;i<ArraySize(lags);i++) stat1[i]=stat[lags[i]-1]; //fill the alternate array of specified lags double pValue[ArraySize(lags)]; //array of 'p' values for(int i=0;i<ArraySize(lags);i++) { pValue[i]=1-gammp(lags[i]/2,stat1[i]/2); //calculation of 'p' values H[i]=alpha[i]>=pValue[i]; //estimation of zero hypothesis } }
Unsere Funktion führt also den Q-Test von Ljung-Box-Pierce aus und liefert das Array der logischen Werte für festgelegte Verzögerungen. Hier sei klargestellt, das der Test von Ljung-Box ein sog. Portmanteau-Test (kombinierter Test) ist. D.h., dass eine Gruppe Verzögerungen bis zu einer festgelegten Verzögerung auf das Vorhandensein von Autokorrelation getestet wird. Meist wird bis zur 10., 15. und 20. Verzögerung (einschließlich) auf Autokorrelation geprüft. Ein Schlussfolgerung bzgl. des Vorhandenseins von Autokorrelation in der gesamten Reihe erfolgt auf Grundlage des letzten Elementwerts des H-Arrays, d.h. von der 1. bis zu 20. Verzögerung.
Entspricht das Element des Arrays einem 'false', wird die Null-Hypothese, die besagt, dass es auf den vorherigen und ausgewählten Verzögerungen keine Autokorrelation gab/gibt, nicht zurückgewiesen. Oder: gibt es keine Autokorrelation, dann erhalten wir 'false' als Wert. Ansonsten belegt der Test das Vorhandensein von Autokorrelation. Sobald der Wert 'true' ist, wird eine Alternative zur Null-Hypothese akzeptiert.
Manchmal kann es vorkommen, dass Autokorrelationen in Return-Reihen nicht gefunden werden. In so einem Fall, werden, um sicher zu gehen, die Quadratpotenzen der Returns getestet. Die letztendliche Entscheidung über die Annahme oder Ablehnung der Null-Hypothese erfolgt auf die gleiche Art und Weise, wie bei den Tests der ursprünglichen Return-Reihen. Und warum sollten wir die Quadratpotenzen von Returns verwenden? Weil wir auf diese Weise die mögliche, nicht-zufällige Autokorrelationskomponente der analysierten Reihen künstlich anheben, die weiter innerhalb der Grenzen der ursprünglichen Werte von vertrauenswürdigen Limits festgelegt ist. Theoretisch können Sie die Quadrat- und andere Potenzen verwenden. Doch das ist nur unnötiges statistisches Laden, das den Sinn des Testens zunichte macht.
Am Ende des Korpus der Q-Testfunktion, wenn der 'p'-Wert berechnet wird, ist nun die gammp(x1/2,x2/2) Funktion aufgetaucht. Mit ihr kann man eine unvollständige gamma-Funktion für die entsprechenden Elemente berechnen. Wir brauchen tatsächlich eine kumulative Funktion der χ2-Verteilung (chi-Quadrat-Verteilung). Das ist jedoch ein Spezialfall der Gamma-Verteilung.
Um zu beweisen, dass das GARCH-Modell für eine Verwendung passt, genügt es generell, im Q-Test einen positiven Wert bei einer der Verzögerung zu bekommen. Ökonometriker führen hier zusätzlich noch einen weiteren Test aus - den ARCH-Test von Engle, der nach dem Vorhandensein einer konventionellen Heteroskedastizität sucht. Doch für jetzt finde ich, reicht der Q-Test schon mal aus. Er ist einfach der universellste.
Da wir jetzt all zur Durchführung des Tests benötigten Funktionen zusammen haben, müssen wir uns überlegen, wie wir die Testergebnisse auf dem Bildschirm darstellen wollen. Zu diesem Zweck habe ich eine weitere Funktion geschrieben - lbqtestInfo, die das Ergebnis des ökonometrischen Tests in Form eines Nachrichtenfenster und des Autokorrelationsdiagramm - rechts auf dem Chart des analysierten Symbols - anzeigt.
Zeigen wir das Ergebnis doch am besten an einem Beispiel. Ich habe als das erste Symbol für die Analyse usdjpy gewählt. Zuerst öffne ich dazu das Linienchart des Symbols (nach Schlusskurs) und alde den angepassten Indikator ReturnsIndicator zur Veranschaulichung der Return-Reihen. Das Chart ist maximal zusammengezogen, um die Clusterbildung der Volatilität des Indikators besser veranschaulichen zu können. Dann führe ich das SkriptGarchTest aus. Wahrscheinlich haben Sie eine andere Bildschirmauflösung, sodass das Skript Sie nach der gewünschten Auflösung des Diagramms in Pixel fragen wird. Ich verwende 700 c 250.
Abb. 3 zeigt verschiedene Beispiele des Tests
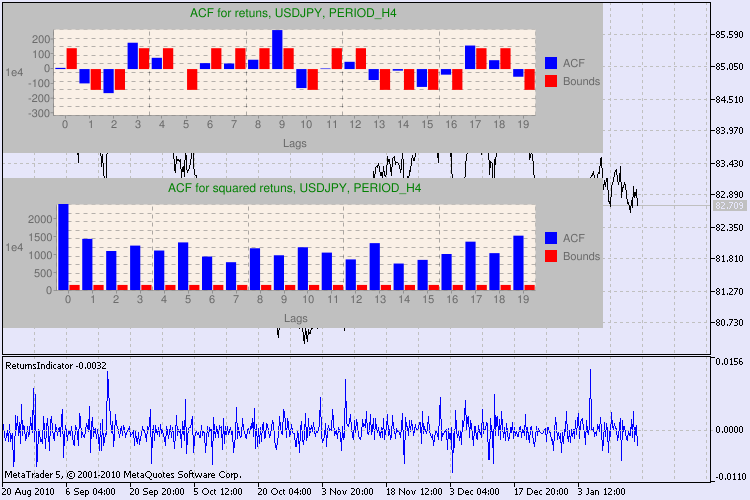
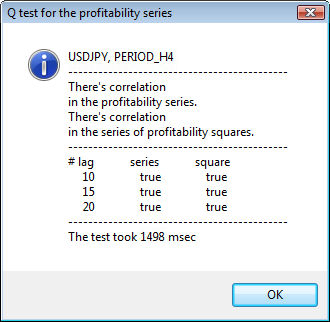
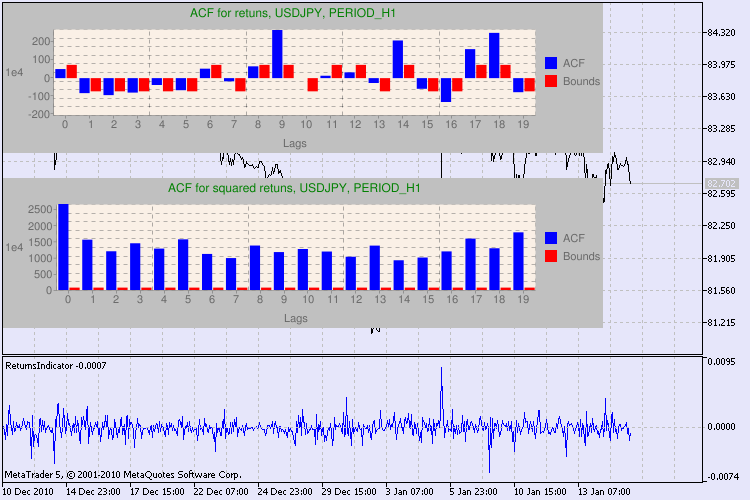
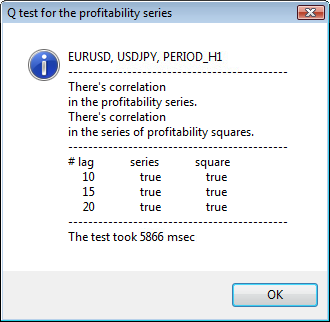
Abb. 3 Das Ergebnis des Q-Tests und das Diagramm der Autokorrelation für USDJPY für unterschiedliche Zeitrahmen.
Ja stimmt, ich habe ganz schön lange gesucht, um eine Variante zu finden, das Diagramm auf einem Symbolchart in MetaTrader 5 abbilden zu können. Und meiner Meinung nach ist die optimalste Variante, eine Library von Zeichnungsdiagrammen mit Hilfe der Google Chart Programmierschnittstelle zu verwenden, die im entsprechenden Beitrag beschrieben ist
Was sollten wir mit dieser Information machen? Nach sehen wir's uns mal an. Der obere Teil des Charts enthält das Diagramm der Autokorrelationsfunktion (AKF) für die ursprüngliche Return-Reihe. Im ersten Diagramm analysieren wir die Reihe von usdjpy im H4 Zeitrahmen. Wir erkennen, dass einige AKF-Werte (blaue Balken) die Limits (rote Balken) überschreiten. Anders ausgedrückt: in der ursprünglichen Returnreihe erkennen wir eine kleine Autokorrelation. Das Diagramm unten ist das Diagramm der Autokorrelationsfunktion (AKF) für die Reihe derReturn-Quadratpotenzen des festgelegten Symbols. Und hier ist alles klar: die blauen Balken haben gesiegt. Die H1 Diagramme werden auf die gleiche Art analysiert.
Noch ein paar Worte zur Beschreibung der Diagrammachsen. Die x-Achse ist klar - sie zeigt die Indices der Verzögerungen an. Auf der Y- Achse erkennen Sie den Exponentialwert mit dem der ursprüngliche AKF-Wert multipliziert wird . Also: 1e4 bedeutet, der ursprüngliche Wert wird mit 1e4 multipliziert (1e4=10000); 1e2 bedeutet analog eine Multiplikation mit 100 usw. Eine derartige Multiplikation wird durchgeführt, um das Diagramm besser verständlich zu machen.
Der obere Teil des Dialogfensters zeigt ein Symbol oder Kreuzpaar-Namen und seinen Zeitrahmen an. Danach stehen zwei Sätze, die uns über das Vorhandensein oder Fehlen von Autokorrelation in der ursprünglichen Return-Reihe und in der Reihe der Return-Quadratpotenzen Aufschluss geben. Dann folgen die 10., 15. und 20. Verzögerung sowie der Wert der Autokorrelation in den ursprünglichen Reihen und den Quadratpotenz-Reihen. Hier wird ein relativer Autokorrelationswert gezeigt - eine boolesche Flagge während des Q-Tests, der feststellt ob bei den vorherigen und den festgelegten Flaggen Autokorrelation vorkommt.
Wenn wir dann schließlich sehen, dass bei den vorherigen und den festgelegten Flaggen Autokorrelation vorkommt, entspricht die Flagge 'true', ansonsten eben 'false'. Im ersten fall ist unsere Reihe ein "Fall" für die Anwendung des nicht-linearen GARCH-Modells; im zweiten, müssen wir uns mit einfacheren Analysemodellen behelfen. Dem aufmerksamen Leser ist vielleicht aufgefallen, das die ursprünglichen Return-Reihen des USDJPY Paares leicht miteinander korrelieren, insbesondere die mit dem größeren Zeitrahmen. Doch die Reihe der Return-Quadratpotenzen zeigen Autokorrelation.
Die Zeit, die das Testen gebraucht hat, wird im unteren Bereich des Fensters angezeigt.
Der komplette Test wurde mit Hilfe des GarchTest.mq5 Skripts durchgeführt
Fazit
Ich habe in diesem Beitrag beschrieben, wie Ökonometriker Zeitreihen analysieren, oder genauer gesagt: wie sie ihre Untersuchungen beginnen. Ich musste während des Verfassens meiner Erläuterungen viele Funktionen schreiben und mehrere Datentypen codieren (z.B. komplexe Zahlen). Wahrscheinlich bringt die visuelle Einschätzung einer ursprünglichen Serie annähernd dasselbe Ergebnis wie eine ökonometrische Abschätzung. Doch wir haben uns ja darauf geeignet, nur mit präzisen Methoden zu arbeiten. Sie wissen ja, ein erfahrener Arzt stellt eine Diagnose auch ohne komplexe Technologie und Methoden aus. Doch auf jeden Fall untersucht er den Patienten sorgfältig und gründlich.
Und was bringt uns der in diesem Beitrag dargestellt Ansatz? Der Einsatz von nicht linearen GARCH-Modellen ermöglicht die formale Repräsentation der analysierten Reihen von einem mathematischen Standpunkt aus und erzeugt eine Prognose für eine festgelegte Anzahl an Schritten. Des Weiteren können wir so das Verhalten von Reihen zu Prognoseperioden leichter simulieren und jeden einsatzbereiten Expert Advisor mit Hilfe der prognostizierten Information prüfen.
Standort der Dateien:
| # | Datei | Pfad |
|---|---|---|
| 1 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators |
| 2 | Complex_class.mqh | %MetaTrader%\MQL5\Include |
| 3 | FFT_class.mqh | %MetaTrader%\MQL5\Include |
| 4 | GarchTest.mq5 | %MetaTrader%\MQL5\Scripts |
Die Dateien und die Beschreibung der Library google_charts.mqh und Libraries.rar stehen im eingangs erwähnten Beitrag als Downloads zur Verfügung.
Für diesen Beitrag verwendete Literatur:
- Analyse of Financial Time Series, Ruey S. Tsay, 2nd Edition, 2005. - 638 pp.
- Applied Econometric Time Series,Walter Enders, John Wiley & Sons, 2nd Edition, 1994. - 448 pp.
- Bollerslev, T., R. F. Engle, and D. B. Nelson. "ARCH Models." Handbook of Econometrics. Vol. 4, Chapter 49, Amsterdam: Elsevier Science B.V.
- Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Upper Saddle River, NJ: Prentice-Hall, 1994.
- Numerical Recipes in C, The Art of Scientific Computing, 2nd Edition, W.H. Press, B.P. Flannery, S. A. Teukolsky, W. T. Vetterling, 1993. - 1020 pp.
- Gene H. Golub, Charles F. Van Loan. Matrix computations, 1999.
- Porshnev S. V. "Computing mathematics. Series of lectures", S.Pb, 2004.