Fractal Analyse von Gemeinschaften Währungsbewegungen

Руслан | 20 April, 2016

Einführung

Häufig hören Sie Menschen über die Beziehungen zwischen den verschiedenen Währungen am Devisenmarkt diskutieren.

Der wichtigste Streitpunkt bezieht sich in der Regel auf fundamentale Faktoren, praktische Erfahrung oder reine Spekulationen, resultierend aus persönlichen Stereotypen des Redners. Eine Hypothese, von einer oder mehr 'globalen' Währungen, die alle übrigen 'zieht', kann als Extremfall betrachtet werden.

Nun, was ist die Natur der Beziehungen zwischen verschiedenen Währungen? Sind ihre Bewegungen koordiniert oder sagt die Bewegung einer Währung nichts aus über die Bewegung einer anderen? Der Artikel beschreibt einen Versuch dieses Problem in Angriff mit nicht-linearer Dynamik und Fraktal-Geometrie-Methoden in Angriff zu nehmen.

1. Theoretischer Teil

1.1. Abhängige und unabhängige Variablen

Werfen wir einen Blick auf die zwei Variablen (Kurse) x und y. Zu jeder gegebenen Zeit bestimmen momentane Werte einen Punkt in der XY-Ebene (Abb.1). Die Bewegung des Punktes bildet im Laufe der Zeit eine Bahn. Die Form und Art einer solchen Bahn hängt ab von der Art der Beziehung zwischen den Variablen.

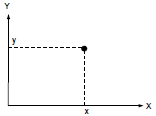
Abbildung 1. Punkt in der Ebene

Zum Beispiel, wenn die Variable x keine Beziehung zu der Variable y hat, werden Sie keine normale Struktur beobachten - die XY-Ebene wird gleichmäßig mit den Punkten gefüllt, vorausgesetzt ihre Anzahl ist ausreichend.(Abb).2).

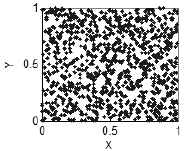
Abbildung 2. Keine Korrelation - gleichmäßig gefüllte Ebene

Gibt es jedoch eine Beziehung zwischen x und y, wird eine normale Struktur sichtbar, im einfachsten Fall eine Kurve darstellend.(Abb. 3),

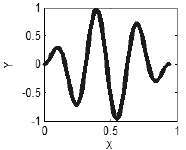
Abbildung 3. Vorhandensein von Korrelationen - eine Kurve

oder auch komplexere Strukturen (Abb. 4).

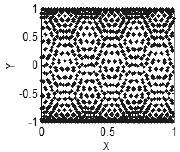
Abbildung 4. Vorhandensein von Korrelationen - eine Struktur in der Ebene

Das gleiche ist charakteristisch für einen drei- oder mehrdimensionalen Raum: wenn alle Daten zusammenhängend oder ineinandergreifend sind, werden die Punkte eine Kurve bilden (Abb. 5), wenn dort zwei unabhängige Variablen in einer Reihe sind, werden die Punkte eine Fläche bilden (Abb. 6), im Fall von drei unabhängigen Variablen, werden die Punkte den dreidimensionalen Raum ausfüllen, usw.

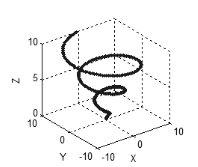
Abbildung 5. Eine Kurve in dem dreidimensionalen Raum

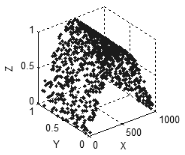
Abbildung 6. Eine Fläche im dreidimensionalen Raum

Wenn es keine Beziehung zwischen den Variablen gibt, werden die Punkte gleichmäßig über die verfügbaren Dimensionen verteilt (Abb. 7). So können wir über die Natur der Beziehungen zwischen Variablen sprechen, basierend auf der Art, in der die Punkte den Raum füllen

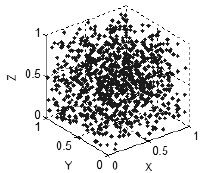
Abbildung 7. Keine Korrelation - Punkte gleichmäßig im Raum verteilt

Die Form der resultierenden Struktur (Linie, Fläche, 3D-Form, usw.) ist in diesem Fall nicht von Bedeutung.

Was zählt, ist eine fraktale Dimension dieser Struktur: 1 für Linien beschreibende Sätze, 2 für Flächen beschreibende Sätze, 3 für Volumen beschreibende Sätze, usw. Es wird in der Regel angenommen, dass ein fraktaler Dimensionswert der Anzahl unabhängiger Variablen in einem Datensatz entspricht.

Wir können auch auf eine fraktale Dimension treffen, z.B. 1,61 oder 2,68. Dies kann der Fall sein, wenn die resultierende Struktur ein Fraktal ist, das heißt, ein selbstähnlicher Satz von nicht-integraler Dimension ist. Ein Beispiel eines Fraktals ist in Abbildung 8 gegeben, seine Dimension ist ungefähr 1,89, d.h. dies ist nicht länger eine Linie (Dimension 1) und noch keine Fläche (Dimension 2).

Abbildung 8. Der Sierpinski Teppich

Eine fraktale Dimension aus ein und demselben Satz kann auf verschiedenen Ebenen unterschiedlich sein.

Zum Beispiel, wenn Sie 'aus der Ferne' einen Blick auf die Abbildung 9 werfen, werden Sie deutlich eine Linie erkennen, d.h. eine fraktale Dimension des gegebenen Satzes ist 1. Ein 'näherer' Blick auf den gleichen Satz wird nicht länger eine Linie offenbaren, sondern ein 'verschwommenes Rohr', wobei die Punkte keine klare Linie bilden, sondern auf zufällige Weise angesammelt sind. Eine Fraktal-Dimension dieses 'Rohrs' sollte gleich sein zu der Dimension des Raums in dem die Struktur betrachtet wird, da die Punkte in dem 'Rohr' über alle Dimensionen gleichmäßig verteilt werden.

Eine Erhöhung der fraktale Dimension in kleineren Maßstäben ermöglicht eine Dimension einzuschätzen, bei der die Beziehung zwischen Variablen durch das Vorhandensein von zufälligem Rauchen ununterscheidbar werden.

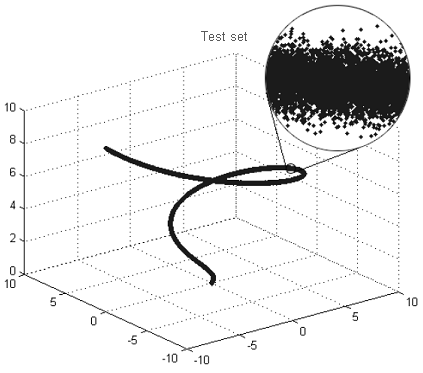
Abbildung 9. Beispiel eines Fractal-'Rohrs'

1.2. Einschätzen der fraktalen Dimension

Eine fraktale Dimension kann mit der Box-Zählmethode eingeschätzt werden, auf Grundlage der Analyse der Abhängigkeit der Anzahl der Boxen die Punkte eines Satzes des Seitenlänge der Box enthalten (es muss keine 3D-Box sein - eine 'Box' in dem eindimensionalen Raum wird durch ein Segment dargestellt, in dem zweidimensionalen Raum durch ein Quadrat, usw.).

Theoretisch ist diese Abhängigkeit durch N(e)~1/e^D gegeben, wobei D die fraktale Dimension des Satzes ist, e ist die Seitenlänge der Box, N(e) - ist die Anzahl von e-Größe Boxen die Punkte aus dem Satz enthalten. Es ermöglich die fraktale Dimension einzuschätzen.

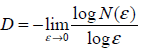
Ohne zu sehr ins Detail zu gehen, kann die Arbeitsweise des Algorithmus wie folgt beschrieben werden:

1. Ein gegebener Satz an Punkten wird auf e-Größe Boxen heruntergebrochen und die Anzahl an Boxen N, die mindestens einen Punkt enthalten, wird gezählt.

2. Für verschiedene e wird ein entsprechender N-Wert bestimmt, d.h. wir sammeln Daten um die Abhängigkeit N(e) zu zeichnen.

3. Die Abhängigkeit N(e) wird auf doppelten Logarithmus-Koordinaten gezeichnet, wobei die Neigung der Abhängigkeit dem Wert der fraktalen Dimension entspricht.

Beispielsweise zeigt Abbildung 10 zwei Sätze: eine ebene Figur (a) und eine Linie (b). Zellen, die Punkte des Satzes enthalten, sind grau gefüllt. Zählen wir die Anzahl der 'grauen' Zellen mit unterschiedlicher Zellengröße, erhalten wir die in Abbildung 11 dargestellten Abhängigkeiten. Die Neigung der geraden Annäherung an diese Abhängigkeiten hilft die fraktalen Dimensionen einzuschätzen: Da≈2, Db≈1.

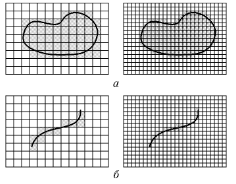
Abbildung 10. Messsätze

Normalerweise wird eine fraktale Dimension in der Praxis mit dem Grassberger-Procaccia Algorithmus geschätzt, anstatt mit der Box-Zählmethode, da es genauere Ergebnisse in hochdimensionalen Räumen ergibt. Der Grundgedanke des Algorithmus ist es, eine Abhängigkeit С(e) der Wahrscheinlichkeit von zwei Punkten eines Satzes zu erhalten, die in einer e-Größe Zellen auf bei der Zellengröße und die Neigung eines linearen Bereichs einer solchen Abhängigkeit zu bestimmen.

Leider ist es unmöglich alle Aspekte der Schätzung der fraktalen Dimension im Rahmen dieses Artikels abzudecken. Weitere Informationen können, wenn notwendig, in spezialisierter Literatur gefunden werden.

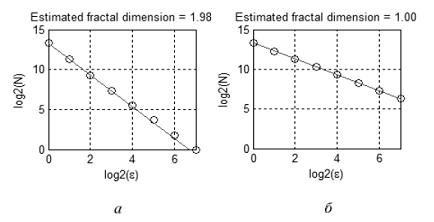
Abbildung 11. Geschätzte fraktale Dimensionen von Sätzen

1.3. Beispiel des Einschätzens fraktaler Dimension

Um die Leistung der vorgeschlagenen Technik zu überprüfen, wollen wir das Rauschniveau und die Anzahl der unabhängigen Variablen für den in Abbildung 9 gezeigten Satz bestimmen. Dieser dreidimensionale Satz besteht aus 3000 Punkten und stellt eine Linie (eine unabhängige Variable) mit überlagertem Rauschen dar. das Rauschen ist normal verteilt, mit der Wurzel aus der mittleren quadratischen Abweichung von 0.01.

Abbildung 12 zeigt die Abhängigkeit C(e) in logarithmischen Maßstab. Es überschneiden sich zwei lineare Abschnitte bei e≈2^-4.6≈0.04. Die Neigung der ersten Zelle ist ≈2.6, die Neigung der zweiten Linie ist ≈1.0.

Die erhaltenen Ergebnisse deuten darauf hin, dass der Testsatz nur eine unabhängige Variable hat, auf der Skala mehr als 0,0 und 'fast drei' unabhängige Variablen oder überlagertes Rauschen auf der Skala weniger als 0,04. Dies ist eine gute Übereinstimmung mit den Anfangsdaten: nach der Drei-Sigma Regel, 99,7% der Punkte eines 'Rohrs' mit einem Durchmesser von 2*3*0.01≈0.06.

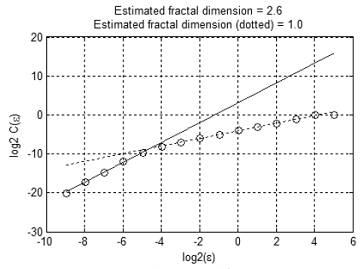
Abbildung 12. Abhängigkeit C(e) in logarithmischem Maßstab

2. Praktischer Teil

2.1. Anfangsdaten

Fraktale Eigenschaften für den Devisenmarkt wurden mit öffentlichen Daten für den Zeitraum von 2000 bis einschließlich 2009 untersucht. Die Untersuchung wurde auf Schlusskursen der sieben wichtigsten Währungspaaren durchgeführt: EURUSD, USDJPY, GBPUSD, AUDUSD, USDCHF, USDCAD, NZDUSD.

2.2. Umsetzung

Algorithmen zum Einschätzen von fraktalen Dimensionen wurden umgesetzt in Form von MATLAB-Umgebung Funktionen, basierend auf Entwicklungen von Dr. Michael Small (http://www.eie.polyu.edu.hk/~ensmall/matlab/). Funktionen mit Umsetzung-Beispielen sind verfügbar in dem frac.rar Archiv, das an diesen Artikel angehangen ist.

Um Berechnungen zu Beschleunigen, wurde der zeitaufwändigste Teil in der C-Sprache geschrieben. Bevor Sie anfangen, kompilieren Sie die C Funktion "interbin.c" mit dem MATLAB Befehl "mex interbin.c".

2.3. Ergebnisse der Untersuchung

Abbildung 13 zeigt eine gemeinsame Bewegung von EURUSD und GBOUSD Kursen von 2000 bis 2010. Die Kurswerte als solche, werden in den Abbildungen 14 und 15 dargestellt.

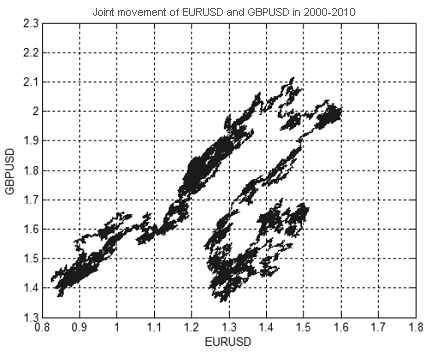
Abbildung 13. Gemeinsame Bewegung von EURUSD und GBPUSD Kursen von 2000 bis 2010

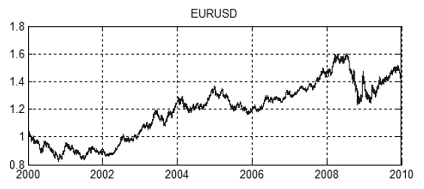
Abbildung 14. EURUSD Kurs-Chart vom 2000 bis 2010

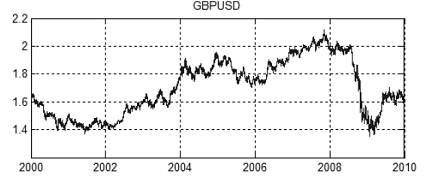
Abbildung 15. GBPUSD Kurs-Chart vom 2000 bis 2010

Eine fraktale Dimension des in Abbildung 13 gezeigten Satzes ist annähernd gleich zu 1,7 (Abb. 16). Das Bedeutet, dass EURUSD + GBPUSD Bewegung keinen 'reinen' Random Walk darstellt, andernfalls wäre ihre Dimension 2 gewesen. (Dimensionen in zwei- oder mehrdimensionalen Räumen ist immer gleich 2).

Allerdings, da die Kursbewegung sehr ähnlich zu einem Random Walk ist, können wir die Kurse selbst nicht analysieren - die fraktale Dimension ändert sich unwesentlich, wenn neue Währungspaare hinzugefügt werden (Tabelle 1) und es ist unmöglich irgendwelche Schlüsse zu ziehen.

Währungspaare	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
Dimension	1.7	1.9	1.9	1.9	1.9	1.9

Tabelle 1. Veränderung der Dimension durch Zunahme der Anzahl an Währungen

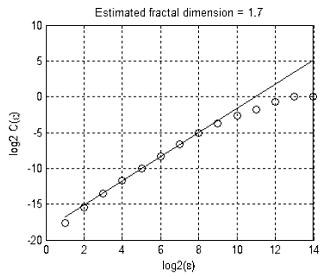
Abbildung 16. Geschätzte fraktale Dimension

Um interessantere Ergebnisse zu erhalten, sollten wir von den Kursen zu den Veränderungen in ihnen kommen.

Dimension-Werte für verschiedene Inkrement-Intervalle und unterschiedliche Anzahl an Währungspaaren sind in Tabelle 2 bereitgestellt.

	Datum	Anzahl an Punkten	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
M5	14 Aug 2008 — 31 Dez 2009	100000	1.9	2.8	3.7	4.4	5.3	6.2
M15	18 Nov 2005 — 31 Dez 2009	100000	2	2.8	3.7	4.5	5.9	6.7
M30	16 Nov 2001 — 31 Dez 2009	100000	2	2.8	3.7	4.5	5.7	6.8
H1	03 Jan 2000 — 31 Dez 2009	61765	2	2.9	3.8	4.6	5.6	6.5
H4	03 Jan 2000 — 31 Dez 2009	15558	2	3	4	4.8	5.9	6.3
D1	03 Jan 2000 — 31 Dez 2009	2601	2	3	4	5.1	5.7	6.5

Tabelle 2. Veränderung der Dimension bei verschiedenen Inkrement-Intervallen

Wenn Währungen miteinander in Beziehung stehen, sollte die fraktale Dimension, jedes Mal wenn ein neues Währungspaar hinzugefügt wird, immer weniger deutlich werden, um schließlich zu einem bestimmten Wert zu kommen, der die Anzahl an 'freien Variablen' am Devisenmarkt bestimmt.

Wenn wir außerdem annehmen, dass das 'Marktrauschen' durch Kurse Überlagert wird, können alle Dimensionen auf kurzen Zeitrahmen mit dem Rauschen gefüllt werden (M5. M15, M30), und dieser Effekt sollte auf längeren Zeitrahmen, die Abhängigkeiten zwischen den Kursen 'enthüllend' nachlassen (wie in dem Test-Beispiel).

Wie Tabelle 2 andeutet, wurde diese Hypothese nicht durch die tatsächlichen Daten bestätigt: Der Sat wird über alle verfügbaren Dimensionen auf allen Zeitrahmen verteilt, das heißt, alle Währungen sind voneinander unabhängig.

Es steht etwas in Konflikt mit intuitiven Annahmen zu Währungsrelationen. Es scheint, dass nahe Währungen, z.B. GBP und CHF oder AUD und NZD eine ähnliche Dynmaik aufweisen. Abbildung 17 zeigt beispielsweise Inkrement-Abhängigkeiten zwischen NZDUSD und AUDUSD auf M5 (Korrelation-Koeffizient: 0.54) und D1 (Korrelation-Koeffizient: 0.84)Zeitrahmen.

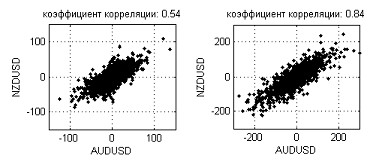
Abbildung 17. Inkrement Abhängigkeiten zwischen NZDUSD und AUDUSD auf M5 und (0.54) und D1 (0.84) Zeitrahmen

Wie in dieser Abbildung zu sehen ist, wird die Abhängigkeit weiter und weiter diagonal gedehnt und die Korrelation-Koeffizient Werte steigen wie der Intervall ansteigt. Allerdings, in Bezug auf die fraktale Dimension, ist das Rausch-Niveau zu hoch, um eine solche Abhängigkeit als eindimensionale Linie zu betrachten. Fraktale Dimensionen auf längeren Intervallen (Wochen, Monate) werden vielleicht zu einem bestimmten Wert konvergieren, aber wir verfügen nicht über die Einrichtungen, um dies zu prüfen, durch die unzureichende Anzahl an Punkten zum Einschätzen der Dimension

Fazit

Es wäre sicherlich interessanter die Bewegungen von Währungen auf eine oder mehr unabhängige Variablen einzuengen, um die Aufgabe der Rekonstruktion des Markt-Anziehungspunkts und der Kurs-Prognosen erheblich zu vereinfachen. Der Markt ergibt jedoch ein anderes Ergebnis: Abhängigkeiten sind schlecht ausgeprägt und "gut versteckt" in einer großen Menge an Rauschen. Der Markt ist in dieser Hinsicht sehr effizient.

Methoden der nichtlinearen Dynamik, die stetig gute Ergebnisse in Bereichen wie Medizin, Physik, Chemie, Biologie und anderen ergeben, erfordern besondere Aufmerksamkeit und sorgfältige Interpretation der Feststellungen, wenn sie in der Analyse der Marktkurse verwendet werden.

Die erhaltenen Ergebnisse deuten nicht ausdrücklich das Vorhandensein oder das Fehlen von Abhängigkeiten zwischen Währungen an. Wir können nur sagen, dass das Niveau des Rauschens auf dem gegebenen Zeitrahmen vergleichbar ist mit der "Stärke" der Beziehung, so dass die Frage nach den Beziehungen zwischen Währungen offen bleibt.